La barrera de potencial

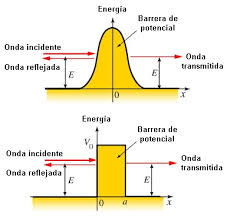
barrera-emenorv_la-mecanica-cuantica-blogspot

La barrera de potencial

Función potencial $V(x)$ :
$V(x) = \left \{ \begin{matrix} 0 & \mbox{si } x \le 0\;:\; zona \;\; I \\ V_o > 0 & \mbox{si } 0 < x < a \;,\, a > 0 \;:\; zona \; \;II \\ 0 & \mbox{si } x \ge a\;: \; zona \;\; III \; \end{matrix}\right.$
-Se trata de una función continua a trozos, con discontinuidades de primera especie en los puntos $x=0$ y $x=a$ .
Problema de autovalores de energía:
$\frac{d^2\psi}{dx^2}-\frac{2m}{\hbar^2}[V(x)-E]\psi(x)=0$ ,
y buscamos soluciones $\psi(x)$ que sean funciones ella y su derivada primera $\psi'(x)$ continuas $\forall x$ (siempre que $V(x)$ sea finito $\forall x$ ).
Dependiendo de la región espacial considerada, la forma concreta de la EDO planteada es:
Zonas I y III: $\quad \frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}E\psi(x)=0$
Zona II: $\quad \frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}[E-V_{o}]\psi(x)=0$
La solución general de una EDO
$\frac{d^2\psi}{dx^2}\mp a^2\psi=0$ ,
donde $a>0$ , $a \in \mathbb{R}$ , tiene la expresión:
-Signo (-) : $\psi(x)=C_1 \ e^{ax} + C_2\ e^{-ax}$
con $C_1,C_2$ escalares arbitrarios.
-Signo (+) : $\psi(x)=C_1 \ e^{+iax} + C_2\ e^{-iax}=C'_1 \ cos\ ax + C'_2\ sen \ ax$
con $C_1,C_2,C'_1,C'_2$ escalares arbitrarios.
Se presentan pues los casos:
1. :
  1. Zonas I y III: $x \le 0$ y $x \ge a$ , respectivamente:
    $\psi(x)=A \ e^{k_Ix} + B\ e^{-k_Ix}$
    $\psi(x)=C \ e^{k_Ix} + D\ e^{-k_Ix}$
    ambas con el mismo $k_I=\frac{+\sqrt{2m(-E)}}{\hbar}>0$ y $A,B,C,D$ escalares arbitrarios.
  2. Zona II: $0 < x < a$ :
    $\psi(x)=F\ e^{k_{II}x} + G\ e^{-k_{II}x}$ con $k_{II}=\frac{+\sqrt{2m(V_o-E)}}{\hbar}>0$
    y $F,G$ escalares arbitrarios.
  3. Imponiendo las condiciones para que la solución sea físicamente aceptable:
    -Acotación $x \rightarrow -\infty \Rightarrow B = 0$
    -Acotación $x \rightarrow +\infty \Rightarrow C=0$
    -Continuidad de $\psi$ en $x=0$ : $A=F+G$
    -Continuidad de $\psi'$ en $x=0$ : $Ak_I=(F-G)k_{II}$
    -Continuidad de $\psi$ en $x=a$ : $F e^{k_{II}a} + G e^{-k_{II}a} = D e^{-k_Ia}$
    -Continuidad de $\psi'$ en $x=a$ : $k_{II}( F\ e^{+k_{II}a}-G\ e^{-k_{II}a})=-Dk_{I}\ e^{-k_Ia}$
    -Puesto que este conjunto de condiciones conduce a la solución trivial, la conclusión es que no existen efectivamente soluciones físicamente aceptables del problema de autovalores de energía para valores del parámetro de separación $E<0$ .
2. :
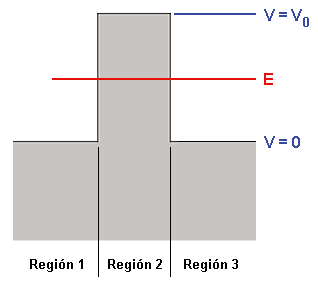
  Imagen del blog la-mecanica-cuantica.blogspot.com .
  1. Expresión de la función de onda en cada zona:
    1. Zonas I y III: $x \le 0$ y $x \ge a$ , respectivamente:
      $\psi(x)=A \ e^{ik_Ix} + B\ e^{-ik_Ix}$
      $\psi(x)=C\ e^{ik_Ix} + D\ e^{-ik_Ix}$
      con un común $k_I = \frac{+\sqrt{2mE}}{\hbar} >0$
      y $A,B,C,D$ escalares arbitrarios.
    2. Zona II: $0 < x < a$ :
      $\psi(x)=F\ e^{k_{II}x} + G\ e^{-k_{II}x}$ ; con $k_{II}=\frac{+\sqrt{2m(V_o-E)}}{\hbar}>0$
      y $F,G$ escalares arbitrarios.
  2. Elegimos uno de los dos sentidos de incidencia posibles (según el principio de reciprocidad, de aplicación también en este problema, los resultados son indiferentes a esta elección); por ejemplo: incidencia desde la izquierda (extremo $-\infty$ ), es decir, $D=0$ .
  3. Imponiendo las condiciones de contorno:
    -Continuidad de $\psi$ en $x=0$ : $A+B=F+G$
    -Continuidad de $\psi'$ en $x=0$ : $ik_I(A-B)=k_{II}(F-G)$
    -Continuidad de $\psi$ en $x=a$ : $F\ e^{+k_{II}a} + G\ e^{-k_{II}a}=C\ e^{+ik_Ia}$
    -Continuidad de $\psi'$ en $x=a$ : $k_{II}(F\ e^{+k_{II}a} - G\ e^{-k_{II}a})=C\ ik_{I}\ e^{+ik_Ia}$
  4. Cálculos:
    -Eliminando $F$ y $G$ :
    $G=A\frac{-ik_I+k_{II}}{2k_{II}}+B\frac{ik_I+ k_{II}}{2k_{II}}$
    $F=A\frac{ik_I+k_{II}}{2k_{II}}+B\frac{-ik_I+ k_{II}}{2k_{II}}$
    $\frac{B}{A}=\frac{(k_I^2+k_{II}^2)(e^{2k_{II}a}-1)}{e^{2k_{II}a}(k_I+ik_{II})^2-(k_I-ik_{II})^2}$
    $|\frac{B}{A}|^2=[1+\frac{4k_I^2k_{II}^2}{(k_I^2+k_{II}^2)^2\ senh^2 (k_{II}a)}]^{-1}$
    $\frac{C}{A}=\frac{4ik_Ik_{II}e^{-ik_{I}a}e^{k_{II}a}}{e^{2k_{II}a}(k_I+ik_{II})^2-(k_I-ik_{II})^2}$
    $|\frac{C}{A}|^2=[1+\frac{(k_I^2+k_{II}^2)^2\ senh^2\ (k_{II}a)}{4k_I^2k_{II}^2}]^{-1}$
    $\Rightarrow \psi_E(x) = \left \{ \begin{matrix} A\ e^{iK_Ix} + A\frac{(k_I^2+k_{II}^2)(e^{2k_{II}a}-1)}{e^{2k_{II}a}(k_I+ik_{II})^2-(k_I-ik_{II})^2} e^{-ik_Ix} & \mbox{si } x \le 0 \\ A[\frac{ik_I+k_{II}}{2k_{II}} + \frac{(k_I^2+k_{II}^2)(e^{2k_{II}a}-1)}{e^{2k_{II}a}(k_I+ik_{II})^2-(k_I-ik_{II})^2} \cdot \frac{-ik_I+ k_{II}}{2k_{II}} ]e^{k_{II}x} \\ +A[\frac{-ik_I+k_{II}}{2k_{II}}+\frac{(k_I^2+k_{II}^2)(e^{2k_{II}a}-1)}{e^{2k_{II}a}(k_I+ik_{II})^2-(k_I-ik_{II})^2}\cdot \frac{ik_I+ k_{II}}{2k_{II}} ]e^{-k_{II}x} & \mbox{si } 0 < x < a \\ A\frac{4ik_Ik_{II}e^{-ik_{I}a}e^{k_{II}a}}{e^{2k_{II}a}(k_I+ik_{II})^2-(k_I-ik_{II})^2} e^{ik_Ix} & \mbox{si } x \ge a \end{matrix}\right.$
    -En las regiones I y II ( $x <0$ y $x \ge a$ , respectivamente) presenta un carácter oscilatorio, teniéndose en la región I la interferencia entre dos ondas; como se tiene $|B| < |A|$ , ni la función de onda ni la densidad de probabilidad presentan en rigor nodos en la región I; en muchos casos, no obstante, $|B/A| \approx 1$ .
  5. La forma general característica que presentan las funciones y densidades de probabilidad (por unidad de volumen) en estos problemas, para $E <V_o$ , se representa en la siguiente figura:
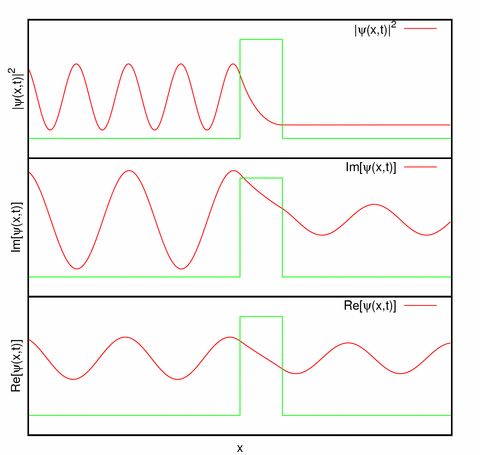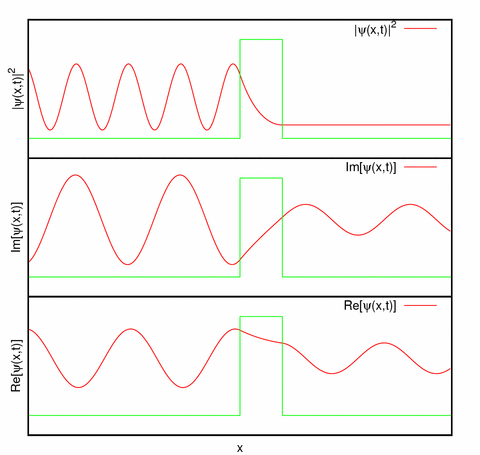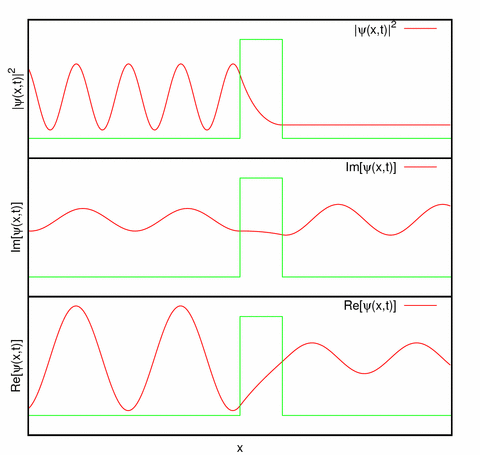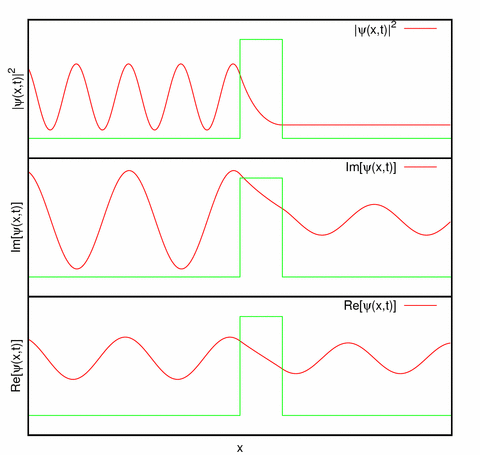
    Imagen de la Wikipedia (imagen por Agualin): representación de la parte real, parte imaginaria y la densidad de probabilidad de un estado estacionario $\Psi_E(x,t)=\psi_E(x) e^{-iEt/\hbar} con E < V_0$ . Nótese que la densidad de probabilidad no varía con el tiempo.
    
    -Proporciona una probabilidad no nula constante de encontrar a la partícula en la zona III. Este hecho no se produce en Física Clásica, donde la región al otro lado de la barrera resulta estrictamente prohibida o inaccesible a la partícula con energía menor que la altura de la barrera. En cambio, en Física Cuántica hay probabilidad no nula de atravesar la barrera, produciéndose una transmisión: se trata del denominado efecto túnel, muy frecuente en procesos atómicos, nucleares y de estado sólido y manifestación de la naturaleza cuántica del fenómeno (en la referencia http://www.met.reading.ac.uk/pplato2/h-flap/phys11_1.html puede leerse la explicación del fenómeno de la desintegración $\alpha$ nuclear vía un efecto túnel: las partículas $\alpha$ observadas no poseerían la energía suficiente para escapar del núcleo sin este efecto; al final, en páginas complementarias, hay más referencias).
    
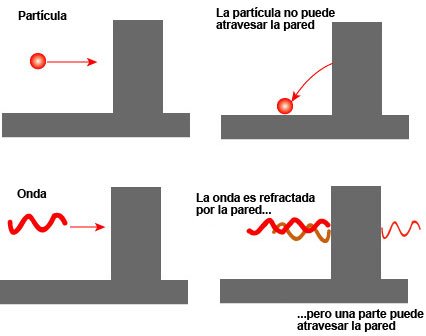
    Imagen de Javier Canteros, tomada del blog https://dandax.wordpress.com/2007/09/19/el-final-de-la-ley-de-moore-y-la-computacion-cuantica/.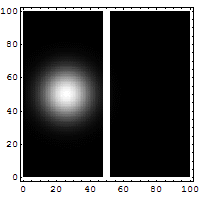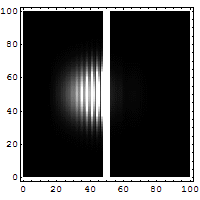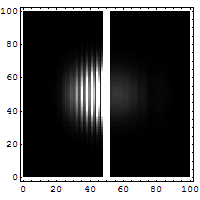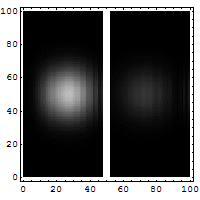
    
    Reflexión y «tunelado» de un electrón dirigido hacia una barrera de potencial. El punto resplandeciente moviéndose de derecha a izquierda es la sección reflejada del paquete de onda. Un vislumbre puede observarse a la derecha de la barrera. Esta pequeña fracción del paquete de onda atraviesa el túnel de una forma imposible para los sistemas clásicos. También es notable la interferencia de los contornos entre las ondas de emisión y de reflexión (de Wikipedia; imagen de Jean-Christophe BENOIST).
  6. Vídeo ilustrativo en términos de paquetes de ondas:
    https://youtu.be/_3wFXHwRP4s :
    
    -Vídeo y texto por «nageljr»: FDTD simulation of a Gaussian wave packet with kinetic energy of $500\ eV$ . The potential barrier has a height of $600\ eV$ , and a thickness of $25\ pm$ . The black line represents the real part of the wave function, while the red line represents the imaginary part. The actual probability amplitude is found by taking the magnitude-square of the total wave function. The wave packet partially tunnels through the barrier, giving a total probability of about 17% of finding the particle on the other side.
  7. En las regiones I y III, la solución se expresa en términos de ondas planas viajeras:
    -Zona I: $\Psi_E(x;t)=e^{-iEt/\hbar}\ (A\ e^{+ik_Ix} + B\ e^{-ik_Ix})$ ,
    -Zona III: $\Psi_E(x;t)=C\ e^{-iEt/\hbar}\ e^{ik_Ix}$ ,
    asociadas interpretativamente a movimientos de la partícula con sentidos positivo para las ondas de amplitud $A$ y $C$ , y negativo para la de amplitud $B$ ; los correspondientes vectores de densidad de corriente de probabilidad total en cada una de estas dos regiones son:
    $j_I(x;t)=|\vec{v}|[|A|^2-|B|^2]$ ,
    $j_{III}(x;t)=v|C|^2$
    donde $|\vec{v}|=\frac{\hbar k_I}{m}$ .
    -Así pues, interpretamos el sumando $A \ e^{-iEt/\hbar} \ e^{+ik_Ix}$ , región I, como una onda viajera incidente desde la izquierda (desde $x \rightarrow -\infty$ ) hacia la barrera de potencial, mientras que el sumando $B\ e^{-iEt/\hbar}\ e^{-ik_Ix}$ se asocia con una onda viajera reflejada, viajando hacia la izquierda (hacia $x \rightarrow -\infty$ ), también en la región I. La función en la zona III, por su parte, corresponde a la onda transmitida, viajando hacia la derecha (hacia $x \rightarrow +\infty$ ).
    -Ley de conservación del flujo: $|A|^2-|B|^2=|C|^2$ .
  8. Coeficientes de reflexión $R$ y transmisión $T$ :
    -Recordemos la definición del vector densidad de corriente de probabilidad:
    $\vec{j}(\vec{r};t)= -\frac{i\hbar}{2m}[ \Psi^*( \nabla \Psi)-(\nabla\Psi^*) \Psi ] =Re\{ -\frac{i\hbar}{m}\Psi^*( \nabla \Psi) \}$
    -Se define el coeficiente de reflexión $R$ como el cociente entre los módulos de los vectores densidad de corriente reflejada e incidente:
    $R=\frac{|\vec{j}_{refl}(x;t)|}{|\vec{j}_{inci}(x;t)|}$
    -Se define el coeficiente de transmisión $T$ como el cociente entre los módulos de los vectores densidad de corriente transmitida e incidente:
    $T=\frac{|\vec{j}_{trans}(x;t)|}{|\vec{j}_{inci}(x;t)|}$
    (ambos independientes de la normalización aplicada).
    -Se relacionan según: $R+T=1$ .
  9. En el caso presente, , los coeficientes valen:
    1. Coeficiente de reflexión:
      $R_<=\frac{|\vec{v}||B|^2}{|\vec{v}||A|^2}=\frac{|B|^2}{|A|^2}=[1+\frac{4E(V_o-E)}{V_o^2 senh^2(k_{II}a)}]^{-1} < 1$
      -Por tanto, no se produce reflexión total, frente a la predicción en física de partículas clásica: aparece un efecto túnel o fenómeno en el que una partícula asociada a una autofunción de energía, para autovalor $E$ menor que la altura de la barrera, puede atravesar esta y ser localizada en la región III.
      -Cuando $|B/A| \approx 1$ se tiene $R \approx 1$ .
    2. Coeficiente de transmisión:
      
      , es decir, , se puede producir un efecto túnel (cuando se tiene ).
      -Propiedades:
      1. $\lim_{E\rightarrow 0}T_<(E)=0$ ; $\Rightarrow \lim_{E\rightarrow 0}R_<(E)=1$
      2. En el límite $E \rightarrow V_o^{-}$ :
        $k_{II} \rightarrow 0 \Rightarrow senh(k_{II}a) \approx k_{II}a$
        $\Rightarrow \lim_{E\rightarrow V_o^{-}}T_<(E) \approx \lim_{E\rightarrow V_o^{-}} [1+\frac{mV_o^2a^2}{2E\hbar^2}]^{-1}$
        $=\frac{1}{1+\frac{mV_oa^2}{2\hbar^2}}< 1$
        -De manera que, conforme $E$ aumenta hacia el valor $V_o$ , la altura de la barrera, el parámetro real adimensional $\frac{mV_oa^2}{2\hbar^2}$ puede considerarse como la medida de la opacidad, o impenetrabilidad, de la barrera: será más improbable que se atraviese la barrera cuánto mayores sean $m$ , $V_o$ y $a$ .
      3. En el límite $\hbar \rightarrow 0$ , se tiene $T_<(E) \xrightarrow{\hbar \rightarrow 0} 0$ , recuperándose el resultado clásico de transmisión cero para $0 < E \le V_o$ .
      4. Si la barrera es ancha y alta, $k_{II}a > > 1$ , la probabilidad de transmisión es baja: $senh(k_{II}a) \approx \frac{1}{2}e^{k_{II}a}$ y el coeficiente de transmisión toma el valor
        $T_<(E) \approx \frac{4E(V_o-E)}{4E(V_o-E)+V_o^2\frac{1}{4}e^2(k_{II}a)}$
        que resulta tanto más pequeño cuanto menor sea $E$ y cuanto mayores sean $m$ , $V_o$ y $a$ .
        
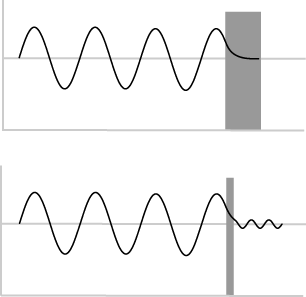
        «Quantum mechanics tells us that electrons have both wave and particle like properties. Tunneling is an effect of the wavelike nature. The top image shows us that when an electron (the wave) hits a barrier, the wave doesn’t abruptly end, but tapers off very quickly – exponentially. For a thick barrier, the wave doesn’t get past. The bottom image shows the senario if the barrier is quite thin (about a nanometer). Part of the wave does get through, and therefore some electrons may appear on the other side of the barrier» (imagen y texto de: http://www.teachnano.com/education/STM.html).
        
        -Las siguientes figuras ilustran el comportamiento descrito para el coeficiente de transmisión $T$ (tramo $0<E<V_o$ ):
        
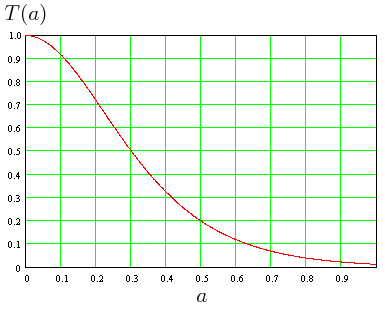
        Transmisión para un valor constante Vo = 15 MeV para E menor que Vo. Para una anchura de la barrera igual a cero en el cual a = 0 (no hay barrera de potencial alguna) tendremos una transmisión perfecta de todas las partículas. Conforme la anchura de la barrera de potencial va en aumento (en este caso, cuando se acerca a 1 fermi) el coeficiente de transmisión cae hasta haber una reflexión casi total de partículas para todos los fines prácticos (imagen y texto del blog la.mecanica.cuantica.blogspot.com).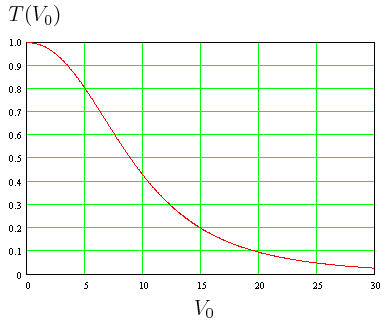
        
        Transmisión para una barrera de potencial con una anchura fija tomando el valor a = 0.5 fermi (E menor que Vo), conforme la altura Vo de la barrera de potencial es reducida el coeficiente de transmisión T se acerca a la unidad indicando una transmisión casi total (imagen y texto del blog la.mecanica.cuantica.blogspot.com).
    3. La siguiente figura ilustra los valores de los coeficientes $R_<(E) \;,\; T_<(E)$ :
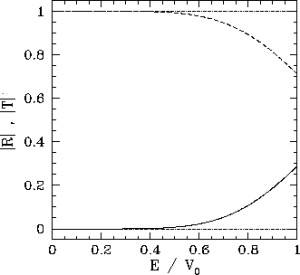
      Transmission (solid-curve) and reflection (dashed-curve) probabilities for a square potential barrier of width a=0.5 $\lambda$ , where $\lambda$ is the free-space de Broglie wavelength, as a function of the ratio of the energy, $E$ , of the incoming particle to the height, $V_0$ , of the barrier (imagen de http://farside.ph.utexas.edu/teaching/qmech/Quantum/node48.html).
  10. Interpretación en términos de paquetes de onda: Para tiempos remotos, se considera un paquete de ondas incidente, que generará en el futuro sendos paquetes de ondas reflejado y transmitido, superpuestos. Simulaciones numéricas disponibles en internet ilustran esta situación; por ejemplo:
    –http://www.uco.es/hbarra/index.php/fc/appletsfc/67-schrodinger-barrera .
    -YouTube: https://youtu.be/_3wFXHwRP4s (la anterior).
  11. Una simulación en 3D del proceso, por Eugene Khutoryansky:
    Quantum tunneling explained with 3D simulations of Schrodinger’s equation for quantum wave functions.
  12. Conforme al principio de reciprocidad, los resultados que se obtienen considerando incidencia desde la derecha (extremo $+\infty$ ) son por completo análogos: basta tomar $A=0$ y proceder en consecuencia.
  13. En resumen: hemos encontrado dos soluciones linealmente independientes $\forall E$ en el rango $0<E<V_o$ , de forma que todos estos puntos $E$ reales pertenecen a la parte continua del espectro $\sigma(H)$ y son doblemente degenerados (en este rango de energías el problema de autovalores tiene dos soluciones físicamente aceptables linealmente independientes, que se pueden escoger como las correspondientes a sendas incidencias desde la izquierda y desde la derecha).
3. :
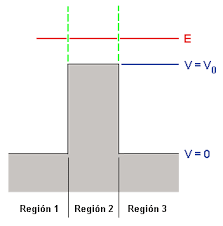
  Imagen del blog la-mecanica-cuantica.blogspot.com.
  1. En este caso la función de onda es combinación de funciones oscilatorias en las tres zonas:
    $\psi(x) = \left \{ \begin{matrix} A \ e^{ik_Ix} + B\ e^{-ik_Ix} & \mbox{si } x \le 0\;:\; zona \;\; I \\ F\ e^{+ik'_{II}x} + G\ e^{-ik'_{II}x} > 0 & \mbox{si } 0 < x < a \;,\, a > 0 \;:\; zona \; \;II \\ C\ e^{+ik_{I}x} + D\ e^{-ik_{I}x} & \mbox{si } x \ge a\;: \; zona \;\; III \; \end{matrix}\right.$
    con $A,B,C,D,E,F$ escalares arbitrarios;
    $k_I=\frac{+\sqrt{2mE}}{\hbar}>0\;\;,\;\;k'_{II}=\frac{+\sqrt{2m(E-V_o)}}{\hbar}>0$ .
  2. Elegimos uno de los dos sentidos de incidencia posibles (según el principio de reciprocidad, los resultados son indiferentes a esta elección); por ejemplo: incidencia desde la izquierda (extremo $-\infty$ ), es decir, $D=0$ .
  3. Imponiendo las condiciones de contorno:
    -Continuidad de $\psi$ en $x=0$ : $A+B=F+G$
    -Continuidad de $\psi'$ en $x=0$ : $ik_I(A-B)=ik'_{II}(F-G)$
    -Continuidad de $\psi$ en $x=a$ : $F\ e^{+ik'_{II}a} + G\ e^{-ik'_{II}a}=C\ e^{+ik_Ia}$
    -Continuidad de $\psi'$ en $x=a$ : $ik'_{II}(F\ e^{+ik'_{II}a} - G\ e^{-ik'_{II}a})=C\ ik_{I}\ e^{+ik_Ia}$
  4. Cálculos:
    -Eliminando $F$ y $G$ :
    $G=Ai\frac{-k_I+k'_{II}}{2ik'_{II}}+Bi\frac{k_I+ k'_{II}}{2ik'_{II}}$
    $F=A\frac{k_I+k'_{II}}{2k'_{II}}+B\frac{-k_I+ k'_{II}}{2k'_{II}}$
    $\frac{B}{A}=\frac{(k_I^2-k_{II}^{'^{2}})(1-e^{2ik'_{II}a})}{(k_I+k'_{II})^2-(k_I-k'_{II})^2e^{2ik'_{II}a}}$
    $|\frac{B}{A}|^2=[1+\frac{4k_I^2k_{II}^{'^{2}}}{(k_I^2-k_{II}^{'^{2}})\ sen^2 (k'_{II}a)}]^{-1}$
    $\frac{C}{A}=\frac{4k_Ik'_{II}e^{+i(k'_{II}-k_I)a}}{(k_I+k'_{II})^2-(k_I-k'_{II})^2e^{2ik'_{II}a}}$
    $|\frac{C}{A}|^2=[1+\frac{(k_I^2-k_{II}^{'^{2}})^2\ sen^2 (k^{\prime}_{II}a)}{4k_I^2k_{II}^{'^{2}}}]^{-1}$
  5. Función de onda:
    $\Rightarrow \psi_E(x) = \left \{ \begin{matrix} A\ e^{ik_Ix} + A\frac{(k_I^2-k'_{II})^2(1-e^{2ik'_{II}a})}{(k_I+k'_{II})^2-(k_I-k'_{II})^2e^{2ik'_{II}a}} e^{-ik_Ix} & \mbox{si } x \le 0 \\ A[ \frac{k_I+k'_{II}}{2k'_{II}}+\frac{(k_I^2-k'_{II})^2(1-e^{2ik'_{II}a})}{(k_I+k'_{II})^2-(k_I-k'_{II})^2e^{2ik'_{II}a}}\cdot \frac{-k_I+ k'_{II}}{2k'_{II}} ]e^{ik'_{II}x} \\ +A[i\frac{-k_I+k'_{II}}{2ik'_{II}}+i\frac{(k_I^2-k'_{II})^2(1-e^{2ik'_{II}a})}{(k_I+k'_{II})^2-(k_I-k'_{II})^2e^{2ik'_{II}a}}\cdot \frac{k_I+ k'_{II}}{2ik'_{II}}]e^{-ik'_{II}x} & \mbox{si } 0 < x < a \\ A\frac{4k_Ik'_{II}e^{+i(k'_{II}-k_I)a}}{(k_I+k'_{II})^2-(k_I-k'_{II})^2e^{2ik'_{II}a}} e^{ik_Ix} & \mbox{si } x \ge a \end{matrix}\right.$
  6. En este caso , los coeficientes y valen:
    -Recordemos de nuevo la definición del vector densidad de corriente de probabilidad:
    .
    1. Coeficiente de reflexión:
      $R_>=\frac{|\vec{v}||B|^2}{|\vec{v}||A|^2}=\frac{|B|^2}{|A|^2}=[1+\frac{4E(E-V_o)}{V_o^2 sen^2(k'_{II}a)}]^{-1} \le 1$
      -Por tanto, puede producirse reflexión, frente a la predicción de física de partículas clásica: a veces una partícula asociada a una autofunción de energía para autovalor $E$ mayor que la altura de la barrera no la atraviesa y no puede ser localizada en la región III.
    2. Coeficiente de transmisión:
      
      , es decir, el coeficiente de transmisión puede ser en algunos casos inferior a la unidad.
      -Propiedades:
      1. Cuando $E > > V_o$ , se tiene que el coeficiente de transmisión $T_>(E)$ tiende asintóticamente al valor unidad:
        $\lim_{E\rightarrow +\infty}T_>(E)=1$ ; $\Rightarrow \lim_{E\rightarrow +\infty} R_>(E)=0$ ·
      2. Si se va aumentando la altura $V_o$ de la barrera, manteniendo constante su anchura $a$ , el factor de transmisión $T_>(E)$ disminuye, tendiendo asintóticamente a cero; al disminuir $V_o$ , tiende al valor $1$ :
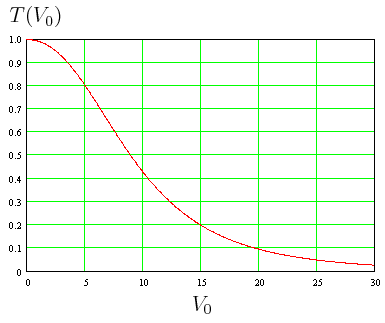
        Variación del coeficiente de transmisión T cuando, manteniendo constante la anchura de la barrera, varía el potencial Vo: a medida que el potencial cae a cero el coeficiente de transmisión tiende a la unidad; imagen del blog la.mecanica.cuantica.blogspot.com.
      3. Casos en que la transmisión es total (certeza de atravesar la barrera, es decir, probabilidad cero de reflexión):
        $T=1 \Leftrightarrow k'_{II}a=n\pi\;,\;n=1,2\ldots \Leftrightarrow a=\frac{n\pi}{k'_{II}}=\frac{n}{2}\lambda'$
        -Es decir: no hay reflexión cuando la anchura de la barrera $a$ es un número entero ( $n=2,4\ldots$ , par) o semi-impar ( $n=1,3\ldots$ , impar) de veces la longitud de onda de de Broglie asociada a la partícula en el interior de la barrera. Se trata de un efecto de interferencia destructiva entre las ondas reflejadas en $x=0$ y $x=a$ .
        
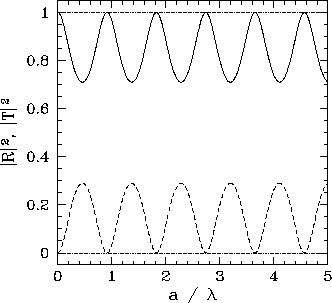
        Transmission (solid-curve) and reflection (dashed-curve) probabilities for a particle of energy $E$ incident on a square potential barrier of height $V_0 = 0.75 E$ , as a function of the ratio of the width of the barrier, $a$ , to the free-space de Broglie wavelength, $\lambda$ (imagen de http://farside.ph.utexas.edu/teaching/qmech/Quantum/node48.html).
        
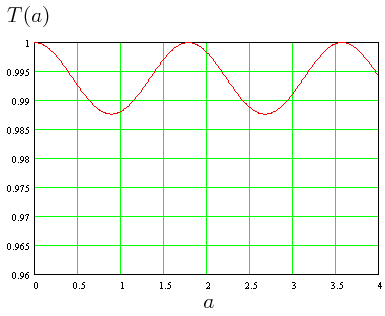
        Coeficiente de transmisión T para una partícula con energía en reposo mc² = 3758 MeV; energía E = 5 MeV; Vo = 1 MeV (imagen del blog la.mecanica.cuantica.blogspot.com).
      4. En el límite $E \rightarrow V_o^{+}$ , es decir, cuando $E$ va disminuyendo hacia el valor de altura de la barrera:
        $E \rightarrow V_o^{+} \Rightarrow k'_{II} \rightarrow 0 \Rightarrow sen (k'_{II}a) \approx k'_{II}a$
        $\Rightarrow \lim_{E\rightarrow V_o^{+}}T_>(E) \approx \lim_{E\rightarrow V_o^{+}} [1+\frac{mV_o^2a^2}{2E\hbar^2}]^{-1}$
        $=\frac{1}{1+\frac{mV_oa^2}{2\hbar^2}} = \lim_{E\rightarrow V_o^{-}}T_<(E) < 1$
        confirmando así el carácter continuo de la función $T(E)$ .
    3. Las siguientes figuras ilustran los valores de estos coeficientes:
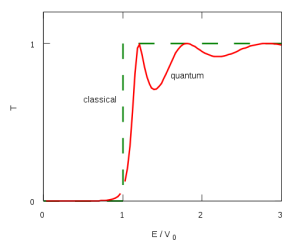
      Probabilidad de transmisión a través de una barrera de potencial finita para $\sqrt{2m V_0}a/\hbar=7$ . Línea discontinua: resultado clásico. Línea sólida: resultado mecano-cuántico. (Imagen de Wikipedia por Bamse).
      
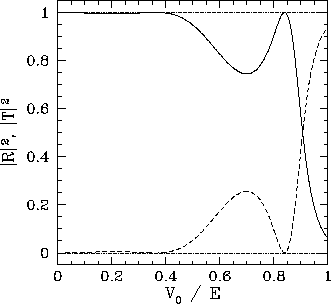
      Transmission (solid-curve) and reflection (dashed-curve) probabilities for a square potential barrier of width $a=1.25 \lambda$ , where $\lambda$ is the free-space de Broglie wavelength, as a function of the ratio of the height of the barrier, $V_0$ , to the energy, $E$ , of the incident particle (imagen de http://farside.ph.utexas.edu/teaching/qmech/Quantum/node48.html).
  7. Interpretación en términos de paquetes de onda: Para tiempos iniciales, se considera un paquete de ondas, incidente desde uno de los dos lados y lejos de la zona de la barrera, que generará en el futuro sendos paquetes de ondas reflejado y transmitido, superpuestos. Las simulaciones al final de la entrada ilustran esta situación; por ejemplo:
    http://www.uco.es/hbarra/index.php/fc/appletsfc/67-schrodinger-barrera .
  8. Conforme al principio de reciprocidad, los resultados que se obtienen considerando incidencia desde la derecha (extremo $+\infty$ ) son por completo análogos: basta tomar $A=0$ y proceder en consecuencia.
  9. En resumen: hemos encontrado dos soluciones linealmente independientes $\forall E$ en el rango $E>V_o$ , de forma que todos estos puntos $E$ reales pertenecen a la parte continua del espectro $\sigma(H)$ y son doblemente degenerados (en este rango de energías el problema de autovalores tiene dos soluciones linealmente independientes y físicamente aceptable, que se pueden escoger como las correspondientes a sendas incidencias desde la izquierda y desde la derecha).
Reuniendo resultados, en las siguientes figuras se representan de nuevo los coeficientes de reflexión y transmisión en todo el rango de autovalores para varios casos:
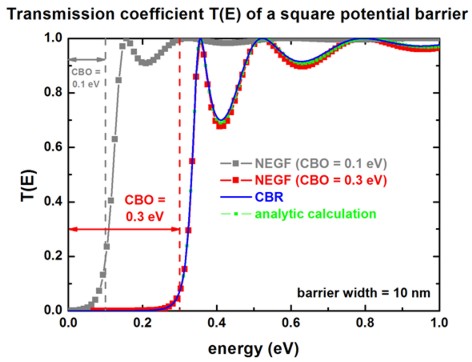
Imagen de http://www.nextnano.de/nextnano3/tutorial/1Dtutorial_Transmission_NEGF.htm.

-Obsérvese que en efecto se satisface:
$\lim_{E \rightarrow V_o^+}T_{>}(E)=\lim_{E \rightarrow V_o^-}T_{>}(E)$ .
En el problema estudiado, Hamiltoniano de una barrera de potencial, resulta por tanto que $\sigma(H)=(0\, ,+\infty)$ , donde todos los puntos son doblemente degenerados.

Referencias

[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.

[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.

[SCH-68] Schiff,L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.

Páginas complementarias

http://www.uco.es/hbarra/index.php/fc/apuntesfc/330-fc0302

www.lfp.uba.ar/es/notas%20de%20cursos/notasmecanicacuantica/09Ejemplos.pdf

http://la-mecanica-cuantica.blogspot.com.es/2010/07/transmision-y-reflexion-de-particulas.html

http://la-mecanica-cuantica.blogspot.com.es/2010/07/transmision-y-reflexion-de-particulas_06.html

http://www.met.reading.ac.uk/pplato2/h-flap/phys11_1.html

http://farside.ph.utexas.edu/teaching/qmech/Quantum/node48.html

http://desayunoconfotones.org/2014/06/05/el-efecto-tunel-la-desintegracion-alfa-y-los-origenes-de-la-mecanica-cuantica/

Microscopio de efecto túnel (divulgación animada muy básica)

Efecto túnel y microscopio de efecto túnel (divulgación)

APPS

http://www.sc.ehu.es/sbweb/fisica/cuantica/tunel/tunel.htm
https://phet.colorado.edu/sims/quantum-tunneling/quantum-tunneling_en.jnlp
http://www.uco.es/hbarra/index.php/fc/appletsfc/66-barrera
http://www.uco.es/hbarra/index.php/fc/appletsfc/67-schrodinger-barrera
http://www.uco.es/hbarra/index.php/fc/appletsfc/69-transmision-barrera
http://www.sc.ehu.es/sbweb/fisica/cuantica/nucleo/nucleo.htm
Transmission and Reflection Coefficients of Quantum Particles from the Wolfram Demonstrations Project by Reinhard Tiebel
http://phys.educ.ksu.edu/vqm/html/qtunneling.html
http://physics.oregonstate.edu/~roundyd/COURSES/ph365x/366.html
Universidad de Colorado, animación PHeT (https://phet.colorado.edu/en/simulation/legacy/quantum-tunneling):
Animaciones desde la Universidad de Oregón, proyecto desarrollado por David Roundy:
-Paquete de ondas para una partícula confinada en una caja:

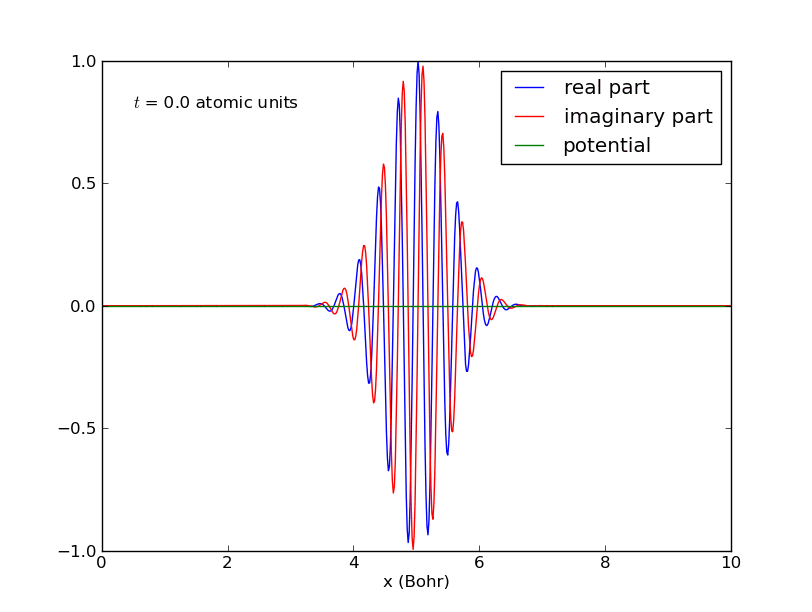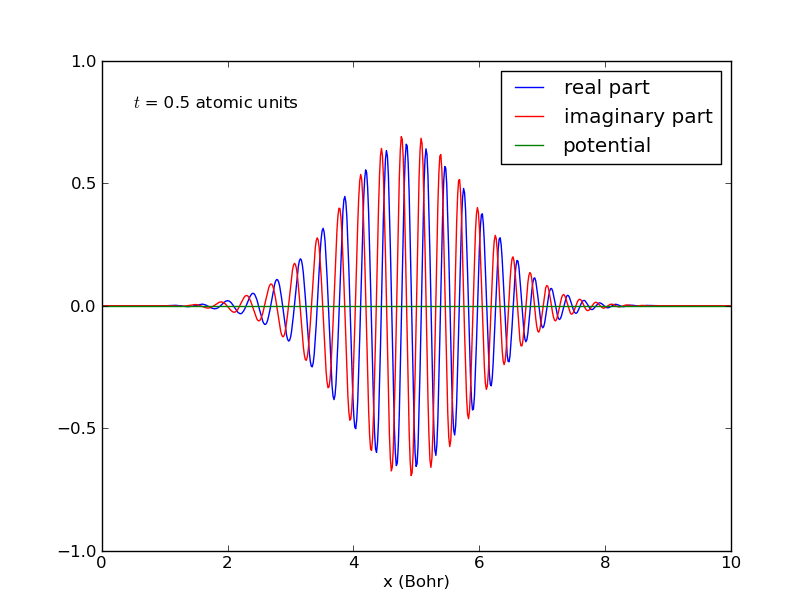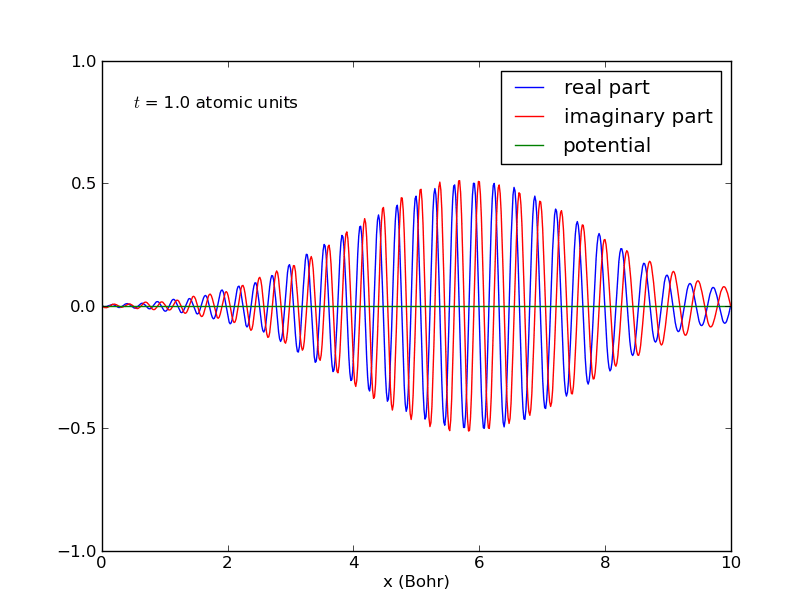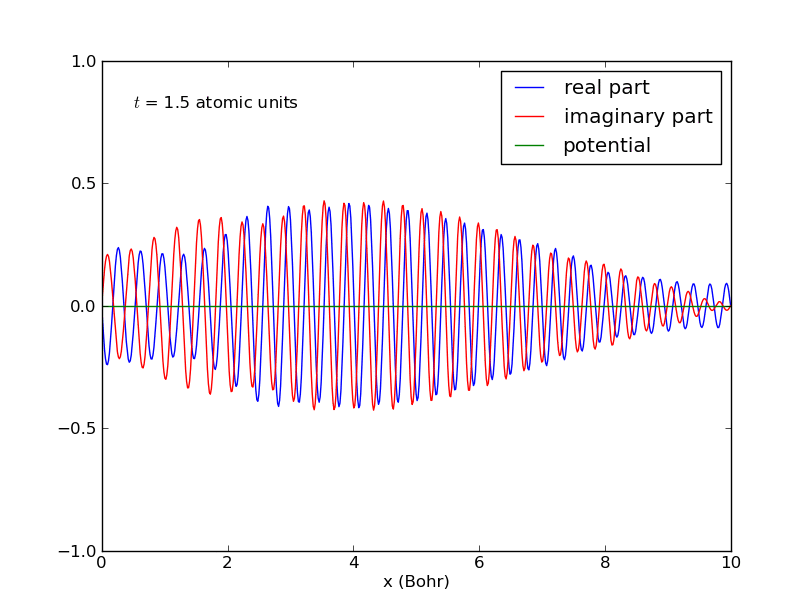
-Comportamiento del anterior paquete de ondas cuando interacciona con una barrera de potencial en el centro de la caja: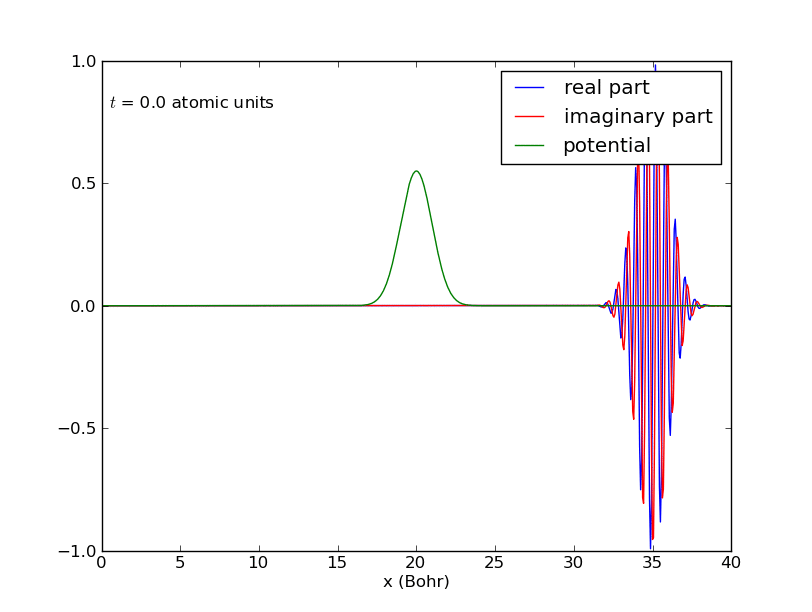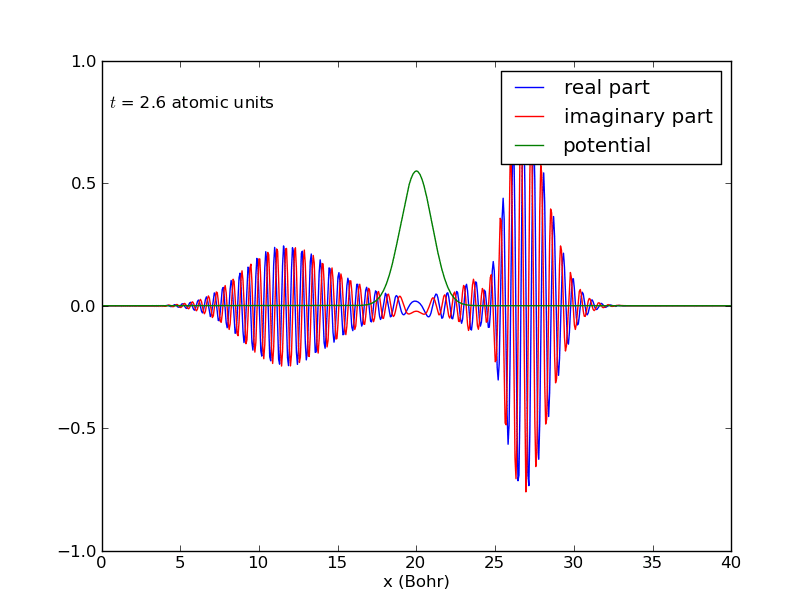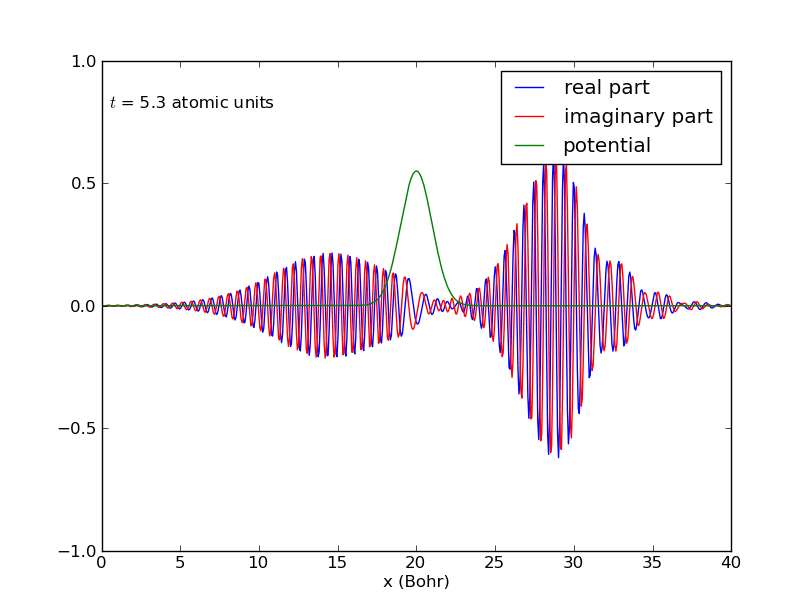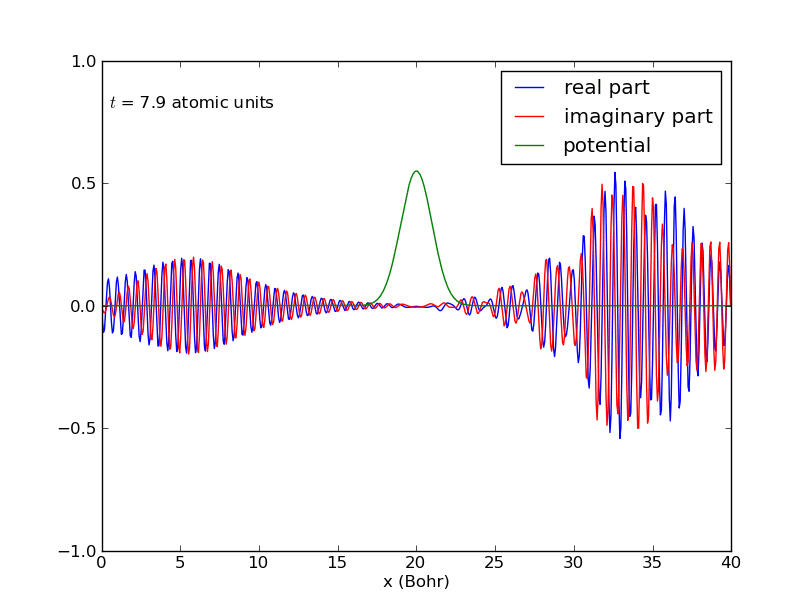
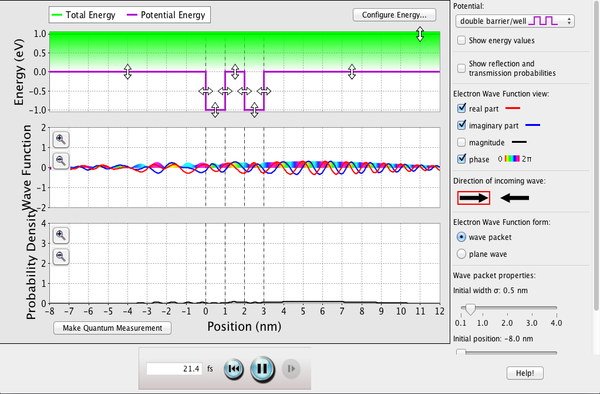
Vídeos en YouTube para un paquete de ondas incidiendo sobre una barrera de potencial:
–https://youtu.be/_3wFXHwRP4s (incidencia con energía menor que la altura de la barrera):

–https://youtu.be/cV2fkDscwvY (varios casos, primero un pozo finito y luego una barrera):

Juan
10/03/2017 a las 20:59

Buenas tardes, quería comentar una pequeña errata que he detectado.
En el apartado donde se habla sobre los casos en que la transmisión es total (certeza de atravesar la barrera, es decir, probabilidad cero de reflexión), en el caso de la barrera de potencial: se comenta que la transmisión es total cuando la anchura de la barrera es un número semientero de longitudes de onda de De Broglie, pero si aplicamos la ecuación podemos observar que la transmisión será total también en el caso cuando es un numero entero de longitudes de De Broglie: n=1,2,… a=n*lambda/2.

Responder
- FCenRed
  14/03/2017 a las 15:46
  
  ¡Gracias! Corregido.
  
  Responder

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

La barrera de potencial

2 comentarios

Responder a Juan Cancelar la respuesta