El calor específico de los sólidos

moglft0304_calor_solidos_algarabia_wikipedia

Calor específico de los sólidos

Otro fenómeno que la Física Clásica se mostraba incapaz de explicar teóricamente era el comportamiento del calor específico o molar a volumen constante $C_V$ (equivalentemente, a presión constante, $C_P$ ) de los sólidos.
Clásicamente, la energía interna de un sólido radica en las vibraciones de sus constituyentes: átomos, iones, moléculas… Estas vibraciones, descompuestas en tres ejes coordenados, permiten representar cada ente constituyente como tres osciladores, que según la teoría clásica, teorema de equipartición de la energía, tendrían cada uno, en el equilibrio térmico, una energía media de $K_B T$ .
Así, cada átomo en un sólido tendría una energía $3K_B T$ ; de esta forma la energía interna total $E$ a temperatura absoluta $T$ resultaría ser $E= 3N_AK_B T=3RT$ , donde $R$ representa la constante universal de los gases, $R=8,31 \times 10^3 J mol^{-1}K^{-1}=1,99 \ cal \cdot mol^{-1} \cdot K^{-1}$ .
Consecuentemente, el calor específico a volumen constante sería $C_V=(\frac{\partial E}{\partial T} )_{V_{cte}}=3R=24,93 \times 10^3 J mol^{-1}K^{-1}=5,97 cal \cdot mol^{-1} \cdot K^{-1}$ , expresión que constituye la denominada ley de Dulong-Petit (de 1819, anterior a la Mecánica Estadística), quienes habían comprobado que $C_{V} \approx 3R$ , unos 25 J/(mol·K) = 6 cal/(mol·K), para muchos elementos en estado sólido (con excepciones), a temperatura ambiente y superiores. Así pues, y a pesar de su simplicidad, la ley de Dulong-Petit ofrece una buena predicción de la capacidad calorífica de los sólidos con estructuras cristalinas relativamente simples, especialmente a altas temperaturas.
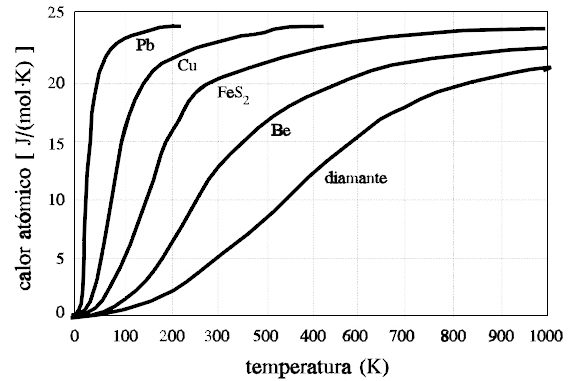
Pero datos experimentales adicionales mostraban los resultados de la siguiente figura:

*Calor específico de sólidos. Imagen por Algarabia, Wikipedia.*

El hecho experimental es que la ley de Dulong-Petit falla para elementos ligeros, como Boro, Berilio, Carbón… (calores específicos respectivos de $3,34$ , $3,85$ y $1,46 \, cal \cdot mol^{-1} \cdot K^{-1}$ , a $T=20^{\circ} C$ ; y también falla al no reproducir el hecho observado de que, para todos los sólidos, a bajas temperaturas, el calor específico disminuye bruscamente, tendiendo a cero en el límite $T \rightarrow 0$ .
En 1907 Einstein señaló al principio de equipartición de la energía como el responsable del fracaso, desarrollando una teoría en la que la probabilidad de que un oscilador tenga la frecuencia $\nu$ viene dada por $f(\nu)= \frac{1}{e^{\frac{h\nu}{k_B T}} -1}$ (como luego establecería la estadística cuántica de Bose-Einstein para bosones, 1924), de forma que la energía media por oscilador de frecuencia $\nu$ es $\bar{E}= h\nu f(\nu)=\frac{h\nu}{e^{\frac{h\nu}{k_B T}}-1}$ , frente al valor clásico $K_{B}T$ del teorema de equipartición.
La energía interna de un mol de sólido, por tanto, resulta ser $E=3N_{A}\bar{E}=\frac{3N_{A}h\nu}{e^{\frac{h\nu}{k_B T}}-1}$ , que conduce al calor molar a volumen constante $C_V=(\frac{\partial E}{\partial T} )_{V_{cte}} = 3R ( \frac{h\nu}{k_B T})^2$ $\frac{e^{\frac{h\nu}{K_BT}}}{(e^{\frac{h\nu}{K_BT}}-1)^2}$ , fórmula que en el límite de altas temperaturas reproduce la ley de Dulong-Petit: como ya sucedía en el cuerpo negro, cuando $h\nu$ $\ll$ $k_B T$ el cuanto de energía se hace tan pequeño que un cálculo que considere la energía de los osciladores como una variable continua representa una aproximación válida. Ahora bien, al disminuir la temperatura $T$ , el carácter discreto de la energía no puede ser ignorado para explicar el decrecimiento observado en el valor del $C_V$ .
La ley de Einstein para el calor específico supuso un gran avance respecto a la de Dulong-Petit, pero tampoco lograba explicar la conducta observada para el calor específico en el límite $T \rightarrow 0$ , pues aunque sí acierta en el valor final nulo, no lo hace en la forma en que la función se aproxima al origen. Sí que reproduce bien la ley de Dulong-Petit en el límite de altas temperaturas, cuando $h\nu$ $\ll$ $k_B T$ y puede realizarse la aproximación $e^{\frac{h \nu}{K_{BT}}} \approx 1 + \frac{h\nu}{K_BT}$ , que lleva al valor clásico $\bar{E}=K_{B}T$ .
Sería P. Debye quien, en 1912, lograra el ajuste perfecto de los datos experimentales disponibles, al abandonar la suposición de Einstein de que cada átomo en el sólido vibraba independientemente de los vecinos, pasando a considerar al sólido como un medio elástico continuo, cuya energía interna no radicaba ya en las vibraciones de los átomos individuales, sino que consistía en ondas elásticas estacionarias, longitudinales y transversales, con rango de frecuencias entre $\nu=0$ y $\nu_{max}$ , y energía correspondiente cuantizada en unidades $h\nu$ (al cuanto de energía acústica en el sólido se le denominón como «fonón», con velocidad la del sonido).