Entrelazamiento a tres: estados y teorema GHZ

Entrelazamiento a 3 en Waterloo, Canadá (2014).) — Entrelazamiento a 3 en Waterloo, Canadá (2014).

Teorema GHZ (Greenberger-Horne-Zeilinger)

En 1989 Greenberger, Horne y Zeilinger mostraron como la consideración de sistemas de más de dos partículas involucraba violaciones del realismo local todavía mayores, y sin necesidad de involucrar ni desigualdades ni estadísticas hechas sobre muchas medidas: un test al realismo local del tipo denominado como AVN (All versus Nothing, o Always versus Never).

En palabras de D. Mermin:

En un experimento GHZ los elementos de realidad locales requieren unos resultados que han de ocurrir siempre, mientras en Mecánica Cuántica esos resultados no ocurren nunca.

D. M. Greengerber, M. A. Horne and A. Zeilinger, Going beyond Bell’s theorem, in Bell’s Theorem, Quantum Theory and Conception of the Universe, M. Kafatos ed., Kluwer, 1989, pp. 69-72.

D. M. Greengerber, M. A. Horne, A. Shimony and A. Zeilinger, Bell’s theorem without inequality, Am. J. Phys. 58 (1990) 1131-1143.

La siguiente exposición sigue la versión abreviada de Laloë,

F. Laloë, Do we really understand Quantum Mechanics?; American Journal of Physics 69 (2001) 655-701; http://arxiv.org/abs/quant-ph/0209123v2 ,

que a su vez sigue la presentación de N. D. Mermin, desarrollada en sus artículos:

N. D. Mermin, Quantum mysteries revisited, Am. J. Phys. 58 (1990) 731-734.

N. D. Mermin, Extreme Quantum Entanglement in a Superposition of Macroscopically Distinct States, Phys. Rev. Lett. 65 (1990) 1838.

Cálculo mecano-cuántico:

-Sea un sistema de tres partículas de espín $1/2$ , preparado en un estado cuántico normalizado (norma unidad):

$|\Phi>=\frac{1}{\sqrt{2}}(|+_1 +_2 +_3> - |-_1 -_2 -_3>)$ ,

un estado entrelazado del tipo que se denomina «estado GHZ«,

donde $\{ |+>\,,\,|->\}$ representa la base de autoestados monoparticulares de espín, de manera que, considerado el operador de Pauli de tercera componente $\sigma_z =\frac{2}{\hbar}S_z$ , se satisface:

$\sigma_z |+>=+|+> \; ; \quad \sigma_z |->=-|->$ ,

teniéndose en consecuencia:

$\sigma_x= \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \Rightarrow \sigma_x |+>=|-> \,,\, \sigma_x |->=|+>$

$\sigma_y= \left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right) \Rightarrow \sigma_y |+>=i|-> \,,\, \sigma_y |->=-i|+>$

-A continuación, se calculan las probabilidades para los resultados de las medidas de determinados productos de tres operadores de espín compatibles (conmutan entre sí dos a dos, siempre que no compartan índice de partícula) de la forma general $\sigma_{i1}\sigma_{j2}\sigma_{k3}$ .

-Para ello, consideremos el estado $|\Psi>$ siguiente:

$\, \bullet |\Psi> \ =(|+_1 +_2 +_3> + \ \eta |-_1 -_2 -_3>)\;, \; \eta= \pm 1$ ,

que satisface:

$\bullet |\Phi>=\sqrt{2} \, | \Psi(\eta=-1)>$

$\bullet \, \sigma_{x1}|\Psi>\ = |\Psi '>\ =|-_1 +_2 +_3> + \ \eta \, |+_1 -_2 -_3>$

$\bullet \, \sigma_{y2}\sigma_{x1}|\Psi >\ =\sigma_{y2}|\Psi'>$

$= |\Psi ''>\ =i\, |-_1 -_2 +_3> - \ \eta \cdot i \, |+_1 +_2 -_3>$

$\bullet \, \sigma_{y3}\sigma_{y2}\sigma_{x1}|\Psi >\ =\sigma_{y3}|\Psi''>$

$=-|-_1 -_2 -_3> - \ \eta |+_1 +_2 +_3>=-\eta |\Psi>$

-Es decir, $|\Psi>$ es autofunción del operador $\sigma_{y3} \sigma_{y2} \sigma_{x1}$ con autovalor $-\eta$ .

-La norma de este estado es la raíz cuadrada positiva de:

$\, \bullet < \Psi | \Psi>=1 + \eta^2=2$

(recuérdese que $\eta=\pm 1$ , de modo que $\eta^2=1$ ).

Por tanto, para una medida del observable representado por el operador en cuestión, $\sigma_{x1}\sigma_{y2}\sigma_{y3}$ , sobre el estado $|\Psi>$ con valor $\eta=-1$ , hay certeza de obtener el resultado +1 (lo cual no significa en mecánica cuántica que para ninguna de las tres componentes individuales involucradas se tenga certeza de obtener un resultado dado de los dos posibles: sólo se establece que para el producto de los tres se predice una probabilidad 1: certeza teórica).

-Por simetría, lo mismo puede afirmarse para los operadores $\sigma_{y1} \sigma_{x2} \sigma_{y3}$ y $\sigma_{y1} \sigma_{y2} \sigma_{x3}$ .

-Por otro lado, también se tiene:

$\bullet \, \sigma_{x1}\sigma_{x2}\sigma_{x3}|\Psi >\ =\sigma_{x2}\sigma_{x3}|\Psi '>\ =\sigma_{x2}(|-_1 +_2 -_3> + \ \eta |+_1 -_2 +_3>)$
$= |\Psi '''>\ =|-_1 -_2 -_3> + \ \eta |+_1 +_2 +_3>$

$= \ \eta |\Psi>$

-Puesto que $|\Phi>=\sqrt{2} \, | \Psi(\eta=-1)>$ , se tiene para las cuatro probabilidades de obtener el resultado $+1$ en las medidas sobre el estado GHZ $|\Phi>$ de los sendos observables representados por los siguientes operadores:

$P(\sigma_{y1} \sigma_{y2} \sigma_{x3}\; ; \; +1) = 1$
$P(\sigma_{x1} \sigma_{y2} \sigma_{y3}\; ; \; +1) = 1$
$P(\sigma_{y1} \sigma_{x2} \sigma_{y3}\; ; \; +1) = 1$

$P(\sigma_{x1} \sigma_{x2} \sigma_{x3}\; ; \; -1) = 1$

(recuérdese que se tiene $< \Psi | \Psi>=1 + \eta^2=2$ y $< \Phi | \Phi>=1$ ).

Cálculo con elementos de realidad locales:

-Sean $A_x,A_y$ los resultados de las respectivas medidas de $\sigma_x,\sigma_y$ sobre la partícula 1; análogamente sean $B_x,B_y$ y $C_x,C_y$ los resultados para las partículas 2 y 3.

-Entonces, las primeras tres ecuaciones anteriores para las probabilidades establecen:

$A_yB_yC_x=+1$
$A_xB_yC_y=+1$
$A_yB_xC_y=+1$

-Si suponemos que las correspondientes medidas se realizan en regiones separadas (a la EPR: regiones del espacio-tiempo separadas por un intervalo de género espacio), el requisito de localidad implica que no puede haber influencia causal entre ellas: se trata de medidas por completo independientes, que en consecuencia apelan según EPR a la introducción de unos elementos de realidad a la EPR, objetivos y locales, correspondientes a las respectivas componentes y partículas.

-Ahora bien, para la cuarta ecuación anterior, la que predice mecanocuánticamente certeza de encontrar el resultado $-1$ en la medida del observable $\sigma_{x1} \sigma_{x2} \sigma_{x3}$ , puesto que se tiene siempre que

$A_i^2=+1=B_i^2=C_i^2\;,\; i=x,y,z$ ,

se deduce del producto de las tres ecuaciones anteriores que el resultado clásico ha de ser también, siempre, $+1$ :

$\bullet \, A_yB_yC_x\,A_xB_yC_y\,A_yB_xC_y=+1=A_y^2A_xB_y^2B_xC_xC_y^2=A_xB_xC_x=+1$

Resulta imposible obtener asumiendo realismo local el resultado mecano-cuántico que fijaría para los elementos de realidad clásicos $A_xB_xC_x=-1$ .

Si se compara esta discrepancia con la situación respecto a las desigualdades de Bell:

Con la situación GHZ se tiene una discrepancia que no involucra una estadística de resultados, sino la imposibilidad para el realismo local de dar cuenta del resultado de una medida sobre un sistema individual entrelazado de tres partículas.

F. Laloë, página 40 del artículo Do we really understand Quantum Mechanics? ; American Journal of Physics 69 (2001) 655 – 701; http://arxiv.org/abs/quant-ph/0209123v2:

Here we obtain a contradiction that looks even more dramatic than for the Bell inequalities: the two predictions do not differ by some significant fraction (about 40%), they are just completely opposite. In addition, all fluctuations are eliminated since all of the results (the products of the three components) are perfectly known before measurements: the 100% contradiction is obtained with 100% certainty! Unfortunately, this does not mean that, experimentally, tests of the GHZ equality are easy. Three particles are involved, which must be put in the GHZ state, surely a non-trivial task; moreover one has to design apparatuses that measure the product of three spin components.

La insuficiencia del realismo local queda tan radicalmente expuesta que Mermin, en otro de sus célebres artículos,

N. D. Mermin, What’s wrong with these elements of reality?, Phys. Today 43 (1990) 9-11, afirmó:

So farewell elements of reality! And farewell in a hurry. The compelling hypothesis that they exist can be refuted by a single measurement of the three x components: The elements of reality require the product of the three outcomes invariably to be +1; but invariably the product of the three outcomes is -1.
This is an altogether more powerful refutation of the existence of elements of reality than the one provided by Bell’s theorem for the two-particle EPR experiment. Bell showed that the elements of reality inferred from one group of measurements are incompatible with the statistics produced by a second group of measurements. Such a refutation cannot be accomplished in a single run, but is built up with increasing confidence as the number of runs increases. […] I recently declared in writing that no set of experiments, real or gedanken, was known that could produce such an all-or-nothing demolition of the elements of reality. With a bow of admiration to Greenberger, Home and Zeilinger, I hereby recant.

En resumen, el desarrollo GHZ establece un resultado imposible para el realismo local, y en una situación muy diferente a la planteada en EPR o en el teorema de Hardy: en GHZ los cuatro operadores de espín involucrados conmutan entre sí, de forma que las medidas concernidas son compatibles y por tanto realizables con el mismo aparato o dispositivo experimental. En este sentido, la respuesta de Bohr al argumento EPR no cabe aquí: no se trata de que no deban considerarse elementos de realidad locales cuando las correspondientes disposiciones experimentales de medida son incompatibles, sino de que, más dramáticamente:

Resulta imposible considerar elementos de realidad locales para observables compatibles.

Repárese que los cuatro observables compatibles manejados se expresan en términos de seis componentes de espín que, éstas sí, no son todas compatibles. En mecánica cuántica, la medida de un solo producto de tres operadores que conmutan es equivalente a la medida de esos tres operadores, puesto que puede realizarse a la vez con el mismo aparato (el orden en la medida de observables compatibles no afecta a los resultados).

-Pero cuando se involucran varios productos de operadores, y no todos los operadores involucrados en esos productos conmutan entre sí, aunque conmuten los involucrados en cada producto individual, que es el caso GHZ, la equivalencia no se mantiene, ya que no pueden determinarse todos en una sola medida, con una única disposición experimental. En cambio, en una teoría realista local se asocian elementos de realidad a las seis magnitudes, lo que conlleva la imposibilidad de satisfacer la igualdad GHZ.

Finalmente, señalemos que con posterioridad los tres autores GHZ publicaron una propuesta de experimento en la que, usando estados entrelazados de dos partículas producidos vía el mecanismo de conversión paramétrica a la baja (SPDC), probaban una nueva versión del resultado GHZ, ahora para dos sistemas y cada evento individual, como en la situación EPR original, e involucrando detectores con eficiencias teóricas del 100%:

D. Greenberger, M. Horne, and A. Zeilinger, 2005, A Bell Theorem Without Inequalities for Two Particles, Using Efficient Detectors.

-En este artículo afirman:

Our papers differ also in kind from the papers we quote above in that those papers are interested in showing that an experiment can rule out various types of theories built on local realism. We are interested in showing that the local, realistic theories themselves are internally inconsistent, in the sense that they cannot be constructed to reproduce the quantum results for all perfect correlations. These realistic theories are inconsistent and cannot reproduce the quantum results, even in just the perfect correlation cases, which are where the EPR elements of reality argument holds. All individual values of the hidden variables yield definite EPR elements of reality which, taken together, produce results that cannot be fitted together to explain the quantum results for perfect correlations. These inconsistent results occur at the level of the individual variables, and do not have to be integrated over. So there is no need for «random sampling» type assumptions. In this paper we consider only 100% efficient detectors.

Estados GHZ

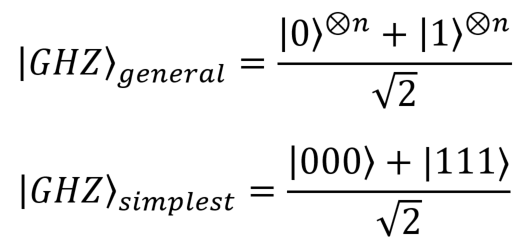
Un estado general GHZ es un estado mecano-cuántico entrelazado para más de dos subsistemas; para $n$ subsistemas de dos dimensiones (qubits) tiene la expresión general:

$|GHZ>=\frac{|0>^{\otimes n}+|1>^{\otimes n}}{\sqrt{2}}$

-Una expresión muy simple es la del estado GHZ de 3 partículas usado en el desarrollo anterior, que presenta además entrelazamiento máximamente no trivial, en el sentido de que, para muchas formas introducidas de cuantificación del entrelazamiento, resulta con un valor máximo:

$|\Phi>=\frac{1}{\sqrt{2}}(|000>-|111> )$ .

En general, para tres partículas son posibles 8 estados GHZ:

$|\Psi_{1\pm}> \ =\frac{1}{\sqrt{2}}(|+_1 +_2 +_3> \pm \ |-_1 -_2 -_3>)$

$|\Psi_{2\pm}> \ =\frac{1}{\sqrt{2}}(|+_1 +_2 -_3> \pm \ |-_1 -_2 +_3>)$

$|\Psi_{3\pm}> \ =\frac{1}{\sqrt{2}}(|+_1 -_2 +_3> \pm \ |-_1 +_2 -_3>)$

$|\Psi_{4\pm}> \ =\frac{1}{\sqrt{2}}(|-_1 +_2 +_3> \pm \ |+_1 -_2 -_3>)$

-Considerado el siguiente conjunto de observables compatibles dos a dos:

$A=\sigma_{y1} \sigma_{y2} \sigma_{x3}$

$B=\sigma_{x1} \sigma_{y2} \sigma_{y3}$

$C=\sigma_{y1} \sigma_{x2} \sigma_{y3}$

$D=\sigma_{x1} \sigma_{x2} \sigma_{x3}$

(que es redundante, ya que $D=-ABC$ ) , todos sus integrantes son diagonalizados por los 8 estados GHZ.

Los estados GHZ son estados entrelazados, y han sido ya creados en el laboratorio, a partir de fotones (las componentes de espín $\pm \frac{\hbar}{2}$ se sustituyen por polarizaciones: H/V si se elige la base Horizontal / Vertical, o + / – para polarización dextrógira / levógira).

-Los estados GHZ presentan diversas propiedades como, por ejemplo, la de que producen un estado mezcla cuando se toma la traza de uno de los subsistemas, por ejemplo:

$Tr_3((|000>+ \ |111>)(<000| \ +<111|))$

$=\frac{1}{2}(|00><00|+|11><11|)$

-Por lo tanto, admiten descomposición generalizada de Schmidt con número de Schmidt o rango mayor que la unidad.

Entrelazamiento GHZ a tres en el laboratorio

Conseguir el entrelazamiento a tres en el laboratorio llevó casi diez años a partir de la publicación del artículo en el que GHZ introdujeron su resultado. En el año 2000, se publicó la primera realización experimental del entrelazamiento a tres, un experimento realizado en Innsbruck , que se considera el primer test del realismo local sobre un estado entrelazado de tres partículas sin involucrar desigualdades:

J.-W. Pan, D. Bouwmeester, M. Daniell, H. Weinfurter & A. Zeilinger, Experimental test of quantum nonlocality in three -photon Greenberger±Horne±Zeilinger entanglement , Nature, 403 (2000) 515-519.

Abstract: Bell’s theorem states that certain statistical correlations predicted by quantum physics for measurements on two-particle systems cannot be understood within a realistic picture based on local properties of each individual particle -even if the two particles are separated by large distances. Einstein, Podolsky and Rosen first recognized the fundamental significance of these quantum correlations (termed ‘entanglement’ by Schrödinger) and the two-particle quantum predictions have found ever-increasing experimental support. A more striking conflict between quantum mechanical and local realistic predictions (for perfect correlations) has been discovered; but experimental verification has been difficult, as it requires entanglement between at least three particles. Here we report experimental confirmation of this conflict, using our recently developed method to observe three-photon entanglement, or ‘Greenberger±Horne±Zeilinger’ (GHZ) states. The results of three specific experiments, involving measurements of polarization correlations between three photons, lead to predictions for a fourth experiment; quantum physical predictions are mutually contradictory with expectations based on local realism. We find the results of the fourth experiment to be in agreement with the quantum prediction and in striking conflict with local realism.

El hecho es que, al igual que con la desigualdad de Bell, lo que se somete a test experimental es de hecho un resultado GHZ corregido: una igualdad GHSZ (A. Shimony también contribuyó a su desarrollo), que incorpora las inevitables vicisitudes experimentales. A resultas de todo ello, siempre se ha de corregir el resultado GHZ para su test en el laboratorio, de manera que se han presentado en la bibliografía correcciones diversas, algunas de las cuales, por ejemplo, convierten la igualdad GHZ en una desigualdad.

Otro problema que se presenta es que se debe de nuevo invocar la denominada hipótesis de «muestra correcta» (fair sampling), que tiene en cuenta que siempre se pierden sistemas de tres partículas del conjunto total (ensemble) sobre el que se mide. La hipótesis establece que el subconjunto de sistemas a tres sobre el que la medida culmina con éxito proporciona un resultado escalable al que proporcionarían unas condiciones experimentales ideales (no se pierde ningún sistema). Esto es, las ineficiencias no tienen conexión con los elementos de realidad (V.O.) ni con el diseño concreto del experimento (los operadores concretos elegidos para medir). Para un estudio a fondo de lo sólido de esta refutación del realismo local, pese a este inevitable ruido que podría considerarse un loophole (vía de escape), puede verse:

M. Zukowski, Violations of Local Realism in the Innsbruck GHZ experiment.

Pero siempre habrá heterodoxos por convencer:

L. E. Szabó and A. Fine, A local hidden model for the GHZ experiment , Phys. Lett. A295, 5-6 (2002) 229-240 :

Abstract: A recent analysis by de Barros and Suppes of experimentally realizable GHZ correlations supports the conclusion that these correlations cannot be explained by introducing local hidden variables. We show, nevertheless, that their analysis does not exclude local hidden variable models in which the inefficiency in the experiment is an effect not only of random errors in the detector equipment, but is also the manifestation of a pre-set, hidden property of the particles («prism models»). Indeed, we present an explicit prism model for the GHZ scenario; that is, a local hidden variable model entirely compatible with recent GHZ experiments.

Otras realizaciones experimentales relacionadas con estados GHZ:

A. Cabello, Stronger Two-Observer All-Versus-Nothing Violation of Local Realism, Phys. Rev. Lett. 95 (2005) 210401.

http://www.nature.com/srep/2012/121210/srep00942/full/srep00942.html

Experimental three-photon quantum nonlocality under strict locality conditions

Experimental realization of a concatenated Greenberger-Horne-Zeilinger state for macroscopic quantum superpositions

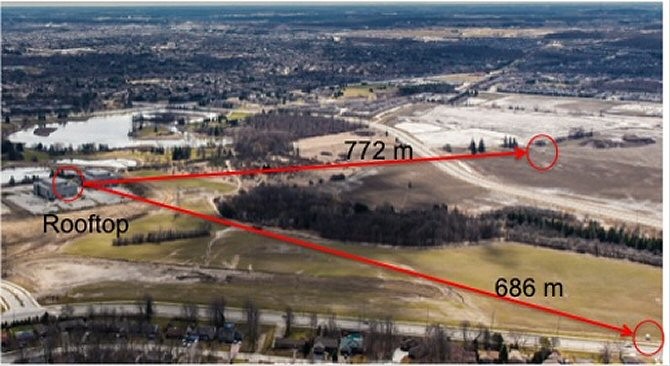
Una noticia más reciente (Universidad de Waterloo, Canadá, 2014): producción de un estado entrelazado de tres fotones con la misma polarización, y aplicación en otro test del realismo local con separaciones de más de medio kilómetro: