La ecuación general de Schrödinger y sus soluciones para un sistema conservativo. Evolución temporal.

Solución general de la ecuación de Schrödinger para un potencial $V(\vec{r})$ (independiente del tiempo)

Teorema (forma 1): La solución general $\Psi(\vec{r};t)$ de la ecuación de Schrödinger para un sistema conservativo,
$i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=H\Psi(\vec{r};t)=[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})] \Psi(\vec{r};t)$
admite expresión en desarrollo en serie de autofunciones de energía:
$\Psi(\vec{r};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\psi_{E,l}(\vec{r})$ , donde $c_{E,l}(t)$ representa los coeficientes del desarrollo, escalares que pueden depender de la variable tiempo $t$ :
$c_{E,l}(t)= \int \psi_{E,l}^*(\vec{r})\Psi(\vec{r};t) \ d\vec{r}$
$= \left\langle \psi_{E,l}(\vec{r}) | \Psi(\vec{r};t) \right\rangle$
Esta forma 1 del teorema corresponde al caso en se han normalizado los estados del continuo procediendo a su discretización.
Teorema (forma 2): La solución general $\Psi(\vec{r};t)$ de la ecuación de Schrödinger para un sistema conservativo,
$i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=H\Psi(\vec{r};t)=[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})] \Psi(\vec{r};t)$
admite expresión en desarrollo en serie de autofunciones de energía:
$\Psi(\vec{r};t)=\sum_{E\in \sigma_p(H)} \sum_{l=1}^{d_E} \left\langle \psi_{E,l} (\vec{r}) | \Psi(\vec{r};t) \right\rangle \psi_{E,l}(\vec{r})$
$+\int_{E \in \sigma_c(H)} \sum_{l=1}^{d_E} \ \left\langle \psi_{E,l}(\vec{r}) | \Psi(\vec{r};t) \right\rangle \psi_{E,l}(\vec{r}) \ dE$
Esta forma 2 del teorema corresponde al caso en se han normalizado los estados del continuo vía la delta de Dirac.
Sustituyendo el anterior desarrollo en serie (forma 1) para $\Psi(\vec{r};t)$ en la ecuación de Schrödinger se obtiene:
$i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=H\Psi(\vec{r};t)$
$i\hbar\frac{\partial [\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\psi_{E,l}]}{\partial t}=H\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\psi_{E,l}$
$i\hbar\frac{\partial}{\partial t} \sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\psi_{E,l}=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)E\psi_{E,l}$
ya que $H \ne H(t)$ (sistema conservativo).
A continuación, proyectamos a la izquierda sobre $\psi_{E',l'}^*$ ( $E'\in \sigma(H)$ fijo) e integramos sobre la región de confinamiento:
$i\hbar\frac{\partial}{\partial t} \sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\int_V \psi_{E',l'}^*(\vec{r}) \psi_{E,l}(\vec{r})\ d\vec{r}$
$=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)E \int_V \psi_{E',l'}^*(\vec{r})\psi_{E,l}(\vec{r}) \ d\vec{r}$
Aplicando la relación de ortonormalidad de las autofunciones:
$\Rightarrow i\hbar\frac{d}{d t} c_{E',l'}(t)= c_{E',l'}(t)E' \Rightarrow c_{E',l'}(t)=cte \ e^{-iE't/\hbar}$
Incorporando la condición inicial
$c_{E,l}(t=t_o)=cte \ e^{-iEt_o/\hbar}= c_{E,l}(t_o)$
$\Rightarrow cte=c_{E,l}(t_o)e^{+iEt_o/\hbar}=C_{E,l}$
donde $C_{E,l} \in \mathbb{C}$ no depende del tiempo $t$ y
$c_{E,l}(t)=c_{E,l}(t_o)e^{-iE(t-t_o)/\hbar}=C_{E,l}e^{-iEt/\hbar}$
Por tanto (sistema conservativo): la solución general de la ecuación de Schrödinger, en el caso de un potencial real $V(\vec{r})$ , independiente del momento $\vec{p}$ y del tiempo, admite expresión como superposición de estados estacionarios de energía $\Psi_{E,l}(\vec{r};t)$ :
$\Psi(\vec{r};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\psi_{E,l}(\vec{r})=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ C_{E,l}e^{-iEt/\hbar}\psi_{E,l}(\vec{r})$
$=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ C_{E,l}\Psi_{E,l}(\vec{r};t)$
donde $C_{E,l} \in \mathbb{C}$ y $\psi_{E,l}(\vec{r})$ son las soluciones del problema de autovalores de la energía, o autofunciones de energía,
$H \psi_{E,l}(\vec{r})=E \psi_{E,l}(\vec{r}) \ \forall l$
cumpliéndose también (¡sistema conservativo!)
$H \Psi_{E,l}(\vec{r};t)=He^{-iEt/\hbar}\psi_{E,l}(\vec{r})=Ee^{-iEt/\hbar}\psi_{E,l}(\vec{r})=E \Psi_{E,l}(\vec{r};t)$

Evolución temporal en un sistema conservativo: Función propagadora $\mathscr{K}$

Partimos del desarrollo en serie de la función de onda solución general de la ecuación de Schrödinger, en términos de las autofunciones de energía:
$\Psi(\vec{r};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\psi_{E,l}(\vec{r})$ ,
donde los coeficientes $c_{E,l}(t)$ del desarrollo, dados por
$c_{E,l}(t)= \int_V \psi_{E,l}^*(\vec{r})\Psi(\vec{r};t)\ d\vec{r}$ ,
satisfacen también:
$c_{E,l}(t)=c_{E,l}(t_o)e^{-iE(t-t_o)/\hbar}=C_{E,l}e^{-iEt/\hbar}$ , expresión en la que los $C_{E,l}$ son escalares (complejos) sin dependencia temporal.
Las constantes sin dependencia temporal $C_{E,l}$ pueden determinarse a partir del conocimiento de la función de onda en un instante $t=t_o$ , tomado como inicial:
$C_{E,l}= e^{+iEt_o/\hbar}c_{E,l}(t_o)=e^{+iEt_o/\hbar} \int_V \psi_{E,l}^*(\vec{r})\Psi(\vec{r};t_o)\ d\vec{r}$
$\Rightarrow \Psi(\vec{r};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ C_{E,l} \ e^{-iEt/\hbar}\psi_{E,l}(\vec{r})$
$=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ [e^{+iEt_o/\hbar} \int_V \psi_{E,l}^*(\vec{r'})\Psi(\vec{r'};t_o)\ d\vec{r'}] \ e^{-iEt/\hbar}\psi_{E,l}(\vec{r})$
$=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E} \ [ \int_V \psi_{E,l}^*(\vec{r'})\Psi(\vec{r'};t_o)\ d\vec{r'}] \ e^{-iE(t-t_o)/\hbar} \psi_{E,l}(\vec{r})$
$=\int_V \mathscr{K}(\vec{r},t;\vec{r'},t_o)\Psi(\vec{r'};t_o)\ d\vec{r'}$ ,
donde se ha definido el propagador o función propagadora
$\mathscr{K}(\vec{r},t;\vec{r'},t_o)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E} \ \psi_{E,l}^*(\vec{r'}) \psi_{E,l}(\vec{r})\ e^{-iE(t-t_o)/\hbar}$ .
El propagador $\mathscr{K}$ permite obtener la función de ondas en cualquier instante $t$ , conocido un valor inicial $\Psi(\vec{r};t_o)$ en un instante arbitrario dado $t_o$ :
$\Psi(\vec{r};t)=\int_V \mathscr{K}(\vec{r},t;\vec{r'},t_o)\Psi(\vec{r'};t_o)\ d\vec{r'}$
En efecto: la ecuación de Schrödinger es una ecuación diferencial en derivadas parciales, de primer orden en la variable temporal. Consecuentemente, establecida una condición inicial, o valor de la función de onda en un instante inicial $t_o$ , esto es, dada $\Psi(\vec{r};t=t_o)=\Psi_o$ , la función $\Psi(\vec{r};t)$ queda determinada $\forall t$ .

Operador evolución temporal en un sistema general con Hamiltoniano $H(t)$
(no necesariamente conservativo)

La ecuación de Schrödinger es una ecuación diferencial en derivadas parciales, de primer orden en la variable temporal. Consecuentemente, establecida una condición inicial, es decir, especificado el vector ket en un instante inicial $t_o$ , $| \left.\Psi(t=t_o)\right\rangle =|\left.\Psi_o\right\rangle$ , queda determinada la evolución temporal del ket, es decir, $\forall t$ .
Se puede introducir entonces un operador de evolución temporal $U(t,t_o)$ , definido según la ecuación
$|\left. \Psi(t)\right\rangle =U(t,t_o)|\left.\Psi_o\right\rangle$
y que habrá de satisfacer las condiciones:
$U(t_o,t_o)=I$
$|\left.\Psi(t)\right\rangle =U(t,t_o)|\left.\Psi_o\right\rangle=U(t,t')|\left.\Psi(t') \right\rangle=U(t,t')U(t',t_o)|\left.\Psi_o\right\rangle$
$\Rightarrow U(t,t_o)=U(t,t')U(t',t_o)$
$|\left.\Psi_o\right\rangle=U^{-1}(t,t_o) |\left.\Psi(t)\right\rangle=U(t_o,t)|\left.\Psi(t)\right\rangle \Rightarrow U^{-1}(t,t_o)=U(t_o,t)$
Además, el operador de evolución temporal ha de ser unitario:
-Por conservación de la probabilidad, debe tenerse:
$\left\langle \Psi(t) | \Psi(t) \right\rangle= \left\langle \Psi(t_o) | \Psi(t_o) \right\rangle = \left\langle \Psi_o | \Psi_o \right\rangle$
de forma que el operador debe ser isométrico, esto es, conservar las normas.
-Y de ello se deriva:
$\left\langle \Psi(t) | \Psi(t) \right\rangle=\left\langle U(t,t_o)\Psi_o | U(t,t_o)\Psi_o \right\rangle$ $=\left\langle \Psi(t_o)\left| U^+(t,t_o)U(t,t_o) \right| \Psi(t_o) \right\rangle$
$\Rightarrow U^+(t,t_o)U(t,t_o)=I=U^+(t,t_o)U^{-1}(t_o,t)$
-Y también: el operador evolución transforma todo el espacio de Hilbert (su dominio es todo $\mathscr{H}$ ) sobre todo $\mathcal{H}$ (suprayectivo) (véase [Gal-89], p. 103).
En resumen: $U(t,t_o)=U^{-1}(t_o,t)=U^{+}(t_o,t)$
-O sea: isométrico, no singular e invertible: se trata de un isomorfismo isométrico: es unitario.
Ecuación para el operador evolución a partir de la ecuación de Schrödinger para un Hamiltoniano general $H(t)$ :
$i\hbar\frac{\partial |\left.\Psi(t)\right\rangle}{\partial t}=H(t)|\left.\Psi(t)\right\rangle \Rightarrow i\hbar\frac{\partial U(t,t_o)|\left. \Psi_o\right\rangle}{\partial t}=H(t)U(t,t_o)|\left.\Psi_o\right\rangle$
$\Rightarrow i\hbar\frac{\partial U(t,t_o)}{\partial t}=H(t)U(t,t_o)$
-A esta ecuación diferencial debe añadirse la condición inicial $U(t_o,t_o)=I$ , que permite obtener la ecuación final:
$\Rightarrow U(t,t_o)=I-\frac{i}{\hbar}\int_{t_o}^{t} H(t')U(t',t_o)dt'$
En el caso particular de un sistema conservativo:
1. En el caso de un sistema conservativo, caso en el que $H \ne H(t)$ , la anterior ecuación
  $U(t,t_o)=I-\frac{i}{\hbar}\int_{t_o}^{t} HU(t',t_o)dt'$
  donde $H$ es autoadjunto, puede comprobarse por simple derivación que posee la solución:
  $U(t,t_o)=e^{-\frac{i}{\hbar}H(t-t_o)}$ .
2. Procediendo a la expansión en serie
  $U(t,t_o)=e^{-\frac{i}{\hbar}H(t-t_o)}=\sum_{n=0}^{+\infty}\frac{1}{n!}(\frac{-i}{\hbar})^nH^n(t-t_o)^n$
  y haciendo uso de la expresión de la función de onda en la base de autofunciones de energía,
  $\Psi(\vec{r};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\psi_{E,l}(\vec{r})$
  es inmediato obtener (recordar la propiedad 5 en la lista I, entrada ecuación autovalores de la energía):
  $\Psi(\vec{r};t)=U(t,t_o)\Psi_o=e^{-\frac{i}{\hbar}H(t-t_o)}\Psi(\vec{r};t_o)$
  $=\sum_{n=0}^{+\infty}\frac{1}{n!}(\frac{-i}{\hbar})^nH^n(t-t_o)^n[\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t_o)\psi_{E,l}(\vec{r})]$
  $=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t_o) [ \sum_{n=0}^{+\infty}\frac{1}{n!}(\frac{-i}{\hbar})^nE^n(t-t_o)^n \psi_{E,l}(\vec{r})]$
  $=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t_o) e^{-\frac{i}{\hbar}E(t-t_o)} \psi_{E,l}(\vec{r})$
  $=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ C_{E,l} e^{-\frac{i}{\hbar}Et} \psi_{E,l}(\vec{r})$ ,
  expresión que proporciona la evolución temporal de una combinación lineal de estados estacionarios.
3. Nota: obsérvese que a partir de la identidad (válida para un sistema conservativo)
  $\Psi(\vec{r};t)=U(t,t_o)\Psi_o=e^{-\frac{i}{\hbar}H(t-t_o)}\Psi(\vec{r};t_o)$
  $=\int e^{-\frac{i}{\hbar}H(t-t_o)}\delta(\vec{r}-\vec{r}\ ')\Psi(\vec{r}\ ';t_o)d\vec{r}\ '$
  e incorporando la relación de clausura
  $\delta(\vec{r}-\vec{r}\ ')= \sum_{E \in \sigma(H)} \sum_{l=1}^{d_E} \psi^*_{E,l}(\vec{r}\ ') \psi_{E,l}(\vec{r})$
  se recupera la anterior expresión general para el propagador $\mathscr{K}$ :
  $\Psi(\vec{r};t)=\sum_{E \in \sigma(H)} \sum_{l=1}^{d_E} \int e^{-\frac{i}{\hbar}H(t-t_o)} \psi^*_{E,l}(\vec{r}\ ') \psi_{E,l}(\vec{r}) \Psi(\vec{r}\ ';t_o)d\vec{r}\ '$
  $=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E} \ [ \int \psi_{E,l}^*(\vec{r'})\Psi(\vec{r'};t_o)\ d\vec{r'}] \ e^{-iE(t-t_o)/\hbar} \psi_{E,l}(\vec{r})$
  $=\int \mathscr{K}(\vec{r},t;\vec{r'},t_o)\Psi(\vec{r'};t_o)\ d\vec{r'}$

Propiedades de la solución de la ecuación de Schrödinger para un sistema conservativo

Una solución de la ecuación de Schrödinger para un sistema conservativo posee las siguientes propiedades:
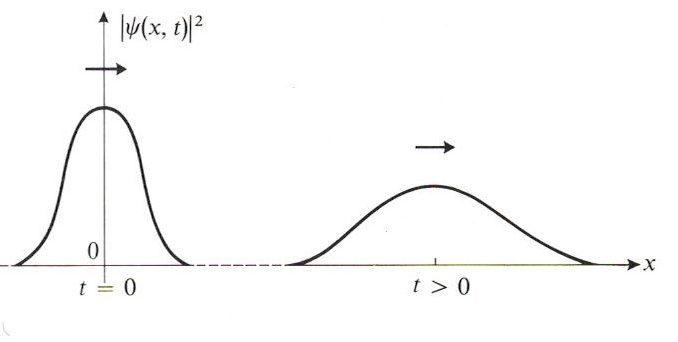
1. Dependencia temporal de la densidad de probabilidad:
  La densidad de probabilidad correspondiente a una superposición lineal de estados estacionarios depende del tiempo (a diferencia de lo que sucede para cada estado estacionario individual):
  $P(\vec{r};t)=\left|\Psi(\vec{r};t)\right|^2=\Psi^*(\vec{r};t)\Psi(\vec{r};t)$
  $=\sum_{E,E'}\sum_{l,l'}C^*_{E',l'}C_{E,l}\psi^*_{E',l'}(\vec{r})\psi_{E,l}(\vec{r})e^{-i(E-E')t/\hbar}$
  $=\sum_{l,l'}|C_{E,l}|^2$
  $+\sum_{E\ne E'}\sum_{l,l'}C^*_{E',l'}C_{E,l}\psi^*_{E',l'}(\vec{r})\psi_{E,l}(\vec{r})e^{-i(E-E')t/\hbar}=f(t)$
  a diferencia de la correspondiente expresión para un estado estacionario individual:
  $P(\vec{r};t)=\left|\Psi_{E,l}(\vec{r};t)\right|^2=\Psi^*_{E,l}(\vec{r};t)\Psi_{E,l}(\vec{r};t)$
  $=| \psi_{E,l}(\vec{r})e^{-iEt/\hbar}|^2=| \psi_{E,l}(\vec{r})|^2\ne f(t)$ .
  En otras palabras: la superposición de estados estacionarios no es, en general, un estado estacionario.
2. Normalización de $\Psi(\vec{r};t)$ y coeficientes del desarrollo:
  $\Psi(\vec{r};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ C_{E,l}e^{-iEt/\hbar}\psi_{E,l}(\vec{r})$
  $\Psi^*(\vec{r};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ C^*_{E,l}e^{+iEt/\hbar}\psi^*_{E,l}(\vec{r})$
  $\Rightarrow \int \Psi^*(\vec{r};t)\Psi(\vec{r};t)\ d\vec{r} \ =1$
  $=\sum_{E, E'\, \in \sigma(H)} \sum_{l=1}^{d_E} \sum_{l'=1}^{d_E'}\ C^*_{E',l'}C_{E,l}e^{-i(E-E')t/\hbar}\int \psi^*_{E',l'}(\vec{r})\psi_{E,l}(\vec{r})\ d\vec{r}$
  $\Rightarrow \sum_{E \in \sigma(H)} \sum_{l=1}^{d_E}\ |C_{E,l}|^2=1$
3. Dependencia temporal del valor esperado de un operador arbitrario:
  El hecho de que la densidad de probabilidad presente una dependencia temporal tiene como consecuencia que, en general, el valor esperado de un operador arbitrario $A$ también es una función del tiempo:
  $\left\langle A \right\rangle_\Psi=\left\langle \Psi(\vec{r};t)\left|A \right| \Psi(\vec{r};t)\right\rangle$
  $=\int \Psi^*(\vec{r};t) A \Psi(\vec{r};t)\ d\vec{r}=f(t)$ .

Ley de dependencia temporal del valor esperado de un operador
(repetición: ver entrada sobre el principio de indeterminación, antes de la relación E-t, y también tras teoremas de Ehrenfest)

Para un sistema físico general (conservativo o no):
1. La ecuación de Schrödinger y su conjugada se expresan:
  $i\hbar\frac{\partial}{\partial t}\Psi(\vec{r};t)=H\Psi(\vec{r};t)$
  $-i\hbar\frac{\partial}{\partial t}\Psi^*(\vec{r};t)=(H\Psi(\vec{r};t))^*$
  (recuérdese que $H$ es autoadjunto y, por lo tanto, hermítico).
2. Evolución temporal de un valor esperado:
  $\left\langle A \right\rangle_\Psi=\left\langle \Psi(\vec{r};t) \left|A \right|\Psi(\vec{r};t) \right\rangle =\int \Psi^*(\vec{r};t) A \Psi(\vec{r};t)\ d\vec{r}=f(t)$
  $\Rightarrow \frac{\partial}{\partial t}\int \Psi^*(\vec{r};t) A \Psi(\vec{r};t)\ d\vec{r}$
  $=\int (\frac{\partial}{\partial t}\Psi^*(\vec{r};t)) A \Psi(\vec{r};t)\ d\vec{r} +\int \Psi^*(\vec{r};t) A (\frac{\partial}{\partial t}\Psi(\vec{r};t))\ d\vec{r}$
  $+\int \Psi^*(\vec{r};t) \frac{\partial A}{\partial t} \Psi(\vec{r};t)\ d\vec{r}$
  $=\frac{-1}{i\hbar}\int (H\Psi(\vec{r};t))^* A \Psi(\vec{r};t)\ d\vec{r} + \frac{1}{i\hbar}\int \Psi^*(\vec{r};t) A H\Psi(\vec{r};t)\ d\vec{r}$
  $+\int \Psi^*(\vec{r};t) \frac{\partial A}{\partial t} \Psi(\vec{r};t)\ d\vec{r}$
  $=\frac{1}{i\hbar}\int \Psi(\vec{r};t))^* [A,H] \Psi(\vec{r};t)\ d\vec{r}\$
  $+\int \Psi^*(\vec{r};t) \frac{\partial A}{\partial t} \Psi(\vec{r};t)\ d\vec{r}$
  $\Rightarrow \frac{\partial}{\partial t}\left\langle A \right\rangle_\Psi =\frac{1}{i\hbar}\left\langle \Psi(\vec{r};t)\left| [A,H] \right| \Psi(\vec{r};t)\right\rangle + \left\langle \Psi(\vec{r};t)\left| \frac{\partial A}{\partial t} \right| \Psi(\vec{r};t)\right\rangle$

Constantes del movimiento

Para un sistema físico general (conservativo o no):
1. Un observable $C$ se define como constante del movimiento cuando cumple la ecuación (cf. [GAL-89], pp. 106ss.):
  $i\hbar\frac{\partial C}{\partial t}+[C,H]=0$
  -Nota: en la línea anterior, aparece una ecuación de igualdad entre operadores. Conviene recordar que este tipo de igualdad requiere no sólo igual regla de actuación, sino también coincidencia en los respectivos dominio y recorrido. En general, es suficiente con que la igualdad se satisfaga sobre una base común a los dominios involucrados.
2. Teorema: Para un observable que es constante del movimiento, el valor medio, sobre cualquier estado $\Psi(\vec{r};t)$ , es independiente del tiempo:
  $\frac{\partial}{\partial t}\left\langle C(t)\right\rangle_\Psi =0$ $\Rightarrow \left\langle C(t) \right\rangle_\Psi \ne f(t)$
En particular, para un sistema conservativo:
1. Para un sistema conservativo, el Hamiltoniano es una constante del movimiento.
  Nota: recordemos una vez más que, en Física Clásica, suele denominarse «sistema conservativo» aquel sistema para el que $H \ne H(t)$ y representa la energía total del sistema.
2. En un sistema conservativo, considerado en particular un estado estacionario $\Psi_E(\vec{r};t)$ , se tiene para cualquier observable $A$ que
  $\left\langle \Psi_E(\vec{r};t)\left| [A,H] \right| \Psi_E(\vec{r};t)\right\rangle$
  $=\left\langle \Psi_E(\vec{r};t)\left| A(t) \ H \right| \Psi_E(\vec{r};t)\right\rangle - \left\langle \Psi_E(\vec{r};t)\left| H\ A(t) \right| \Psi_E(\vec{r};t)\right\rangle =0$
  por lo que:
  $\frac{\partial}{\partial t}\left\langle A \right\rangle_{\Psi_E}=\frac{\partial}{\partial t} \left\langle \Psi_E(\vec{r};t) \left|A \right|\Psi_E(\vec{r};t) \right\rangle = \left\langle \Psi_E(\vec{r};t)\left| \frac{\partial A}{\partial t} \right| \Psi_E(\vec{r};t)\right\rangle$ .
  (Nota: adviértase que decir que $A$ y $B$ conmutan sobre una función de onda específica NO es decir que $[A,B]=0$ , esto es, que «conmutan», o sea, no es decir que son compatibles. Para que esto último suceda, se requiere que el conmutador sea nulo sobre un dominio denso en el Hilbert).
  -Si, en particular $A \ne A(t)$ , entonces su valor esperado no presenta dependencia temporal,
  $\frac{\partial}{\partial t}\left\langle A \right\rangle_{\Psi_E}=0 \Rightarrow \left\langle A \right\rangle_{\Psi_E} \ne f(t)$ ,
  permaneciendo constante en la evolución temporal.
3. En un sistema conservativo, un observable $C$ que sea constante del movimiento y no presente dependencia temporal, $C \ne C(t)$ , necesariamente conmuta con el Hamiltoniano, $[C, H] =0$ , es decir, es siempre compatible con el Hamiltoniano del sistema. Por tanto, ambos pueden formar parte simultáneamente de un C.C.O.C. (conjunto completo de observables compatibles), y admiten diagonalización simultánea. En otras palabras: es posible tomar una base ortonormal constituida por autofunciones simultáneas de ambos operadores.
4. Teorema: En un sistema conservativo, la distribución de probabilidad para los resultados de la medida de un observable que sea constante del movimiento y no presente dependencia temporal explícita se mantiene constante en el tiempo. Es obvio que, en consecuencia, el valor medio de dicha distribución también permanece constante.

Dependencia temporal del valor esperado del Hamiltoniano en un sistema conservativo y amplitudes de probabilidad

Puesto que para un sistema conservativo el Hamiltoniano es una constante del movimiento, según el apartado anterior su valor esperado es independiente del tiempo.
En efecto:
$\left\langle H \right\rangle_\Psi=\left\langle i\hbar \frac{\partial}{\partial t} \right\rangle_\Psi$
$=\left\langle \Psi(\vec{r};t)\left|H \right| \Psi(\vec{r};t)\right\rangle$
$=\int \Psi^*(\vec{r};t) H \Psi(\vec{r};t)\ d\vec{r}$
$=\sum_{E, E'\, \in \sigma(H)} \sum_{l=1}^{d_E} \sum_{l'=1}^{d_E'}\ C^*_{E',l'}C_{E,l}e^{-i(E-E')t/\hbar}\int \psi^*_{E',l'}(\vec{r})H \psi_{E,l}(\vec{r})\ d\vec{r}$
$=\sum_{E, E'\, \in \sigma(H)} \sum_{l=1}^{d_E} \sum_{l'=1}^{d_E'}\ C^*_{E',l'}C_{E,l}e^{-i(E-E')t/\hbar}\int \psi^*_{E',l'}(\vec{r})E \psi_{E,l}(\vec{r})\ d\vec{r}$
$=\sum_{E, E'\, \in \sigma(H)} \sum_{l=1}^{d_E} \sum_{l'=1}^{d_E'}\ C^*_{E',l'}C_{E,l}e^{-i(E-E')t/\hbar}\ E\ \delta_{E,E'}\delta_{l,l'}$
$=\sum_{E \in \sigma(H)} \sum_{l=1}^{d_E}\ |C_{E,l}|^2\ E \ne f(t)$
El anterior resultado permite interpretar la cantidad $\sum_{l=1}^{d_E}\ |C_{E,l}|^2$ como la probabilidad de que al realizar una medida de la energía total del sistema se encuentre como resultado el valor $E$ , de degeneración $d_E$ . Es decir, esta cantidad es interpretable como la correspondiente amplitud de probabilidad.
La ecuación
$\left\langle H \right\rangle_\Psi=\sum_{E \in \sigma(H)} \sum_{l=1}^{d_E}\ |C_{E,l}|^2\ E \ne f(t)$
proporciona el promedio de los valores obtenidos al realizar la medida de la energía total en un gran número de sistemas (conservativos) idénticos e idénticamente preparados en el mismo estado cuántico representado o al que se le asocia la función de onda
$\Psi(\vec{r};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\psi_{E,l}(\vec{r})$
$=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ C_{E,l}e^{-iEt/\hbar}\psi_{E,l}(\vec{r})$ .
En general, este valor medio o esperado, cuyo significado es simplemente el de un valor promedio de un gran número de resultados de medida de la energía total del sistema, no tiene por qué coincidir con alguno de los autovalores de energía $E$ (aunque a veces puede hacerlo).
Otro caso particular sucede cuando el sistema se encuentra:
-bien en el estado representado por la función de onda de un estado estacionario de la energía no degenerado, $\Psi_{E_n}(\vec{r};t)$ , es decir, el caso en que se tenga:
$\Psi(\vec{r};t)=c_n(t)\Psi_{E_n}(\vec{r};t)=C_ne^{-iE_nt/\hbar}\psi_{E_n}(\vec{r})$ ,
-bien en el estado representado por una función de onda combinación lineal de estados estacionarios degenerados con la misma energía $E_n$ , autovalor que suponemos con degeneración $m$ :
$\Psi(\vec{r};t)=\sum_{l=1}^{m} c_{E_n,l}(t) \Psi_{E_n,l}(\vec{r};t)=e^{-iE_nt/\hbar}\sum_{l=1}^{m} C_{E_n,l}\psi_{E_n,l}(\vec{r})$ ;
en ambos casos sucede que $\left\langle H \right\rangle_\Psi \in \sigma(H)$ y, además:
$\Rightarrow \left\langle H \right\rangle_\Psi=\left\langle i\hbar\frac{\partial}{\partial t} \right\rangle_\Psi=E_n$ ,
esto es, el valor promedio de la energía, su valor medio o esperado, coincide con el autovalor $E_n$ .
En efecto: el primer caso es trivial; para el segundo:
$\left\langle H \right\rangle_\Psi=\sum_{E \in \sigma(H)} \sum_{l=1}^{d_E}\ |C_{E,l}|^2\ E$
$=\sum_{l=1}^{m}\ |C_{E_n,l}|^2\ E_n=E_n$ ,
ya que, por normalización de la función de onda se ha de tener que
$\int \Psi^*(\vec{r};t)\Psi(\vec{r};t)\ d\vec{r}=1=\sum_{l=1}^{m}\ |C_{E_n,l}|^2$ .

Nota: en todo este apartado, en general la notación se corresponde con la normalización por confinamiento; las modificaciones para que las fórmulas sean válidas en caso de normalización a la delta de Dirac son directas.

Espacio de momentos

En el espacio de momentos se tienen resultados análogos a los dados anteriormente en el espacio de configuración. En particular, consideradas las funciones , soluciones de la ecuación de Schrödinger independiente del tiempo en el espacio de momentos (cuya forma general es la de una ecuación integro-diferencial):
1. Postulado: Cada conjunto ortonormal de funciones
  $\{\phi_{E,l}(\vec{p})\} \,,\,l=1,\ldots,d_E , E \in \sigma(H)$ ,
  considerados todos los autovalores de energía del sistema y aportando cada uno de ellos un número de autofunciones igual a su degeneración, constituye una base ortonormal (en rigor, base generalizada: incluye funciones que no son del Hilbert: los estados de difusión) del correspondiente subespacio del Hilbert asociado al sistema físico que está generado por todas las funciones en el dominio de los Hamiltonianos de expresión general $H=\frac{\vec{p}^2}{2m} + V(\vec{r})$ .
2. Consecuentemente, la solución general $\Phi(\vec{p};t)$ de la ecuación de Schrödinger en el espacio de momentos, en el caso de un potencial independiente del tiempo, de expresión
  $i\hbar\,\frac{\partial \Phi(\vec{p}\ ;t)}{\partial t}=\frac{\vec{p}^2}{2m} \ \Phi(\vec{p}\ ;t)\ +\ \int \mathscr{V}_{op}(\vec{p}\ -\vec{p}\ ')\Phi(\vec{p}\ ';t)\ d\vec{p}\ '$ ,
  donde
  $\mathscr{V}_{op}(\vec{p}\ - \vec{p}\ ')=\frac{1}{(2\pi \hbar)^3}\int V(\vec{r})\ e^{-i(\vec{p}\ -\vec{p}\ ')\cdot \vec{r} /\hbar}\,d\vec{r}$ ,
  admite expresión en desarrollo en serie de funciones $\phi_{E,l}(\vec{p})$ :
  $\Phi(\vec{p};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ c_{E,l}(t)\phi_{E,l}(\vec{p})$ ,
  donde $c_{E,l}(t)$ representa los coeficientes del desarrollo, escalares que pueden depender de la variable tiempo $t$ :
  $c_{E,l}(t)= \int \phi_{E,l}^*(\vec{p})\Phi(\vec{p};t) \ d\vec{p}= \left\langle \phi_{E,l}(\vec{p}) | \Phi(\vec{p};t) \right\rangle$ .
3. También: la solución general de la ecuación de Schrödinger en el espacio de momentos, en el caso de un sistema conservativo, admite expresión como superposición de estados estacionarios de energía:
  $\Phi(\vec{p};t)=\sum_{E\in \sigma(H)} \sum_{l=1}^{d_E}\ C_{E,l}e^{-iEt/\hbar}\phi_{E,l}(\vec{p})$ ,
  donde los coeficientes $C_{E,l} \ne C_{E,l}(t)$ , esto es, no presentan dependencia temporal .