Los paquetes de onda

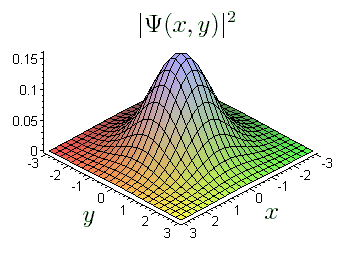
paquete-ondas-densidad_de_probabilidad_en_dos_dimensiones_la-mc-blogspot-com

Ondas planas y su normalización

Consideremos una partícula de masa $m_o \ne 0$ , moviéndose a lo largo del eje $OX$ en el sentido positivo, con energía $E$ y momento $\vec{p}=p_x\hat{i}$ bien definido ( $p_x>0$ ).
Le asociamos una onda plana que viaja en la misma dirección, con número de ondas $k=\frac{2\pi}{\lambda}$ fijo, de expresión $\Psi(x;t)=Ae^{i[kx-\omega(k)t]}$ , donde $A$ es una constante (real o compleja); el número de ondas $k$ y la frecuencia vienen dados por la relación de de Broglie, $k=\frac{2\pi}{\lambda}=\frac{p_x}{\hbar}$ y $\omega=2\pi\nu=\frac{E}{\hbar}$ .
Para una onda distinguimos entre la velocidad de fase, $v_f=\frac{\omega(k)}{k}$ , que es la velocidad a la cual la fase de cualquier componente en frecuencia de la onda se propaga (puede ser distinta para cada frecuencia), y la velocidad de grupo, $v_g=\frac{\partial \omega (k)}{\partial k}$ , que es la velocidad a la que se desplaza la energía contenida en la onda.
Para una partícula material libre no relativista, $E=\frac{p_x^2}{2m}=\frac{\hbar^2 k^2}{2m}$ , por lo que $\omega(k)=\frac{E(p_x)}{\hbar}=\frac{E(k)}{\hbar}=\frac{ \hbar k^2}{2m}$ , resultando pues $v_f=\frac{\hbar k}{2m}=\frac{h}{2m\lambda}$ y $v_g=\frac{\hbar k}{m}=\frac{p_x}{m}$ .
Puede escribirse pues $\Psi(x;t)=Ae^{i[p_xx-E(p_x)t]/ \hbar}$ , que satisface el par de ecuaciones diferenciales $-i\hbar\frac{\partial }{\partial x}\Psi(x;t)=p_x\Psi(x;t)$ y $i\hbar\frac{\partial }{\partial t}\Psi(x;t)=E\Psi(x;t)$ .
La generalización al caso tridimensional, para una partícula no relativista de masa $m$ , es la onda plana $\Psi(\vec{r};t)=Ae^{i[\vec{k}\cdot\vec{r}-\omega(k)t]}=Ae^{i[\vec{p}\cdot\vec{r}-E(p)t]/ \hbar}$ , donde $\vec{p}=\hbar\vec{k}$ , $\omega(k)=\frac{\hbar k^2}{2m}$ , satisfaciendo el par de ecuaciones diferenciales $-i\hbar\nabla\Psi(\vec{r};t)=\vec{p}\Psi(\vec{r};t)$ y $i\hbar\frac{\partial}{\partial t}\Psi(\vec{r};t)=E\Psi(\vec{r};t)$ .
El examen de las ecuaciones anteriores muestra que, para una partícula libre de masa $m$ , la energía y el momento pueden representarse por sendos operadores diferenciales $E_{op}=i\hbar\frac{\partial}{\partial t}$ y $\vec{p}_{op}= -i\hbar\nabla$ , actuando sobre la función de onda $\psi(\vec{r};t)$ .
La asociación anterior constituye un postulado de la Mecánica Cuántica, que se establece para toda partícula, libre y no libre.
La condición de normalización para la anterior función de onda, la onda plana, se encuentra con el problema de que es imposible satisfacer el requisito $\int_{\mathbb{R}^3}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=1$ , $\int_{-\infty}^{\infty}\left|\Psi(x;t)\right|^2dx=1$ en el caso monodimensional, ya que las correspondientes integrales resultan ser divergentes. Para salvar esta dificultad, y dado que $\left|\Psi(\vec{r};t)\right|^2=|A|^2$ , esto es, hay igual probabilidad de encontrar a la partícula en cualquier punto del espacio, optamos por asociar esta onda plana con el estado de preparación de la partícula en que ésta tiene un momento perfectamente definido y está completamente deslocalizada.
Nota: otra posibilidad será restringir la integral a una región muy extensa, pero finita: integrar sobre un volumen $V \subset \mathbb{R}^3$ , muy grande pero finito, sobre cuya frontera se impone la condición de contorno de anulación de la función de onda. De esta forma, la condición de normalización pasa a ser $\int_{V}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=1$ . Este tipo de funciones de onda se usará, por ejemplo, en teoría de colisiones, y aparecerán al discutir la parte continua del espectro.

Consecuentemente, para una partícula que presente alguna localización, tendremos que introducir alguna indeterminación en su momento: superponer ondas elementales, ondas planas, correspondientes a distintos valores del momento de la partícula: formar un «paquete de ondas», localizado ya espacialmente y, por tanto, admitiendo normalización a la unidad vía una integración a todo el espacio $\mathbb{R}^3$ .

Paquetes de onda

Concepto

Una onda plana se extiende por todo el espacio. Por ejemplo, en el caso monodimensional, la onda plana armónica de ecuación $E_C(x;t)=E_0\,cos(kx - \omega t )$ ,
Onda armónica (imagen del blog la-mecanica-cuantica.blogspot.com).

no puede representar la onda de de Broglie asociada a una partícula dada, ya que ésta debe responder a la forma:

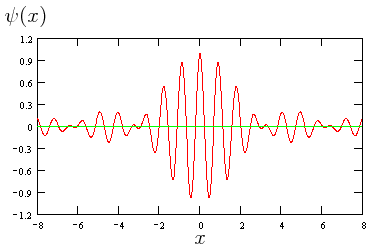
Paquete de ondas (imagen del blog la-mecanica-cuantica.blogspot.com).
La forma anterior responde a lo que se denomina un «paquete de ondas», o grupo de ondas, y que no es sino el resultado de la superposición de muchas ondas planas con diferentes números de ondas.
Un ejemplo trivial lo proporciona la superposición de dos ondas planas de igual amplitud, $E_1=E_0cos(k_1x - \omega_1 t)$ y $E_2=E_0cos(k_2x - \omega_2 t )$ : $E=E_1 + E_2 = 2E_0cos(k_+x - \omega_+ t)cos(k_- x - \omega_- t)$ , con $k_{\pm}=\frac{1}{2}(k_1 \pm k_2)$ y $\omega_{\pm}=\frac{1}{2}(\omega_1 \pm \omega_2)$ ; suponemos $k_1$ y $k_2$ muy próximos:
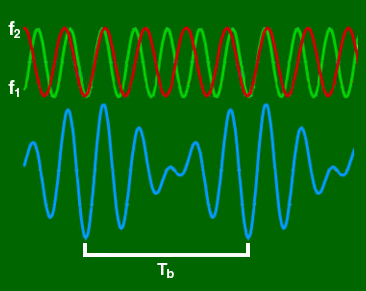
Suma de dos ondas con igual amplitud y frecuencias levemente diferentes (imagen del blog la-mecanica-cuantica.blogspot.com).
Es decir, la onda suma resultante resulta ser el producto de una onda portadora (la de mayor frecuencia) de longitud de onda $\lambda_+=\frac{4\pi}{|k_1 + k_2|}=\frac{2\pi}{k_+}$ y un factor que modula la amplitud en forma de otra onda envolvente (la de menor frecuencia) de longitud $\lambda_-=\frac{4\pi}{\left|k_2 - k_1\right|}=\frac{2\pi}{k_{-}}$ . El resultado es que la intensidad se ha concentrado en ciertas regiones del espacio, frente a otras en que se ha amortiguado.
Las siguientes figuras nos representan, respectivamente, los resultados de sumar tres ondas ( $\sin x + \sin1.1x + \sin1.2 x$ ) y cinco ondas( $\sin x + \sin 1.05x + \sin 1.1x + \sin 1,15x + \sin 1.2x$ ), sinusoidales:

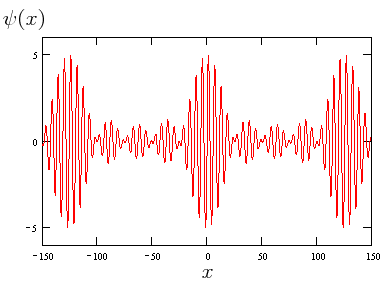
Imágenes del blog: http://la-mecanica-cuantica.blogspot.com.es/2009/08/la-particula-libre-i.html
Conforme aumenta el número de ondas elementales que se van sumando, cada una con diferentes números de ondas dentro de un intervalo estrecho de valores, las interferencias entre ellas (las ondas componentes empiezan a desfasarse entre sí, cancelándose al alejarse del punto en torno al cual se concentra al paquete) hace que se vayan espaciando las regiones de refuerzo, hasta que, con un número de sumandos infinito, se obtiene el caso límite correspondiente a un único grupo central: un paquete de ondas:
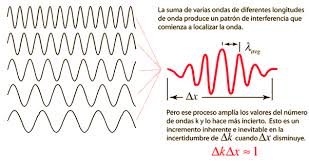
Obtención de un paquete de ondas (imagen de http://hyperphysics.phy-astr.gsu.edu/hbasees/waves/wpack.html).

Imagen del blog: http://la-mecanica-cuantica.blogspot.com.es/2009/08/la-particula-libre-i.html
Matemáticamente, la formación de tal paquete o grupo de ondas corresponde a la integración $E_C(x,t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}f(k)e^{i(kx-\omega (k) t)}dk$ , donde la función $f(k)$ da cuenta de la amplitud de cada onda de número de ondas respectivo $k$ , con las característica de ser una función que presenta un máximo muy acusado en el valor $k=k_0$ y valores apreciables sólo en un entorno $\Delta k$ estrecho en torno a $k_0$ . Obsérvese que el paquete de ondas en $t=0$ viene dado por la transformada de Fourier inversa de la función de amplitud: $E_C(x;0)=\mathscr{F}^{-1}\{f\}$ ( $f=\mathscr{F}\{E_C\}$ ).

Ejemplos

Ejemplo 1: paquete de ondas gaussiano para una suma de ondas todas con igual velocidad de fase :
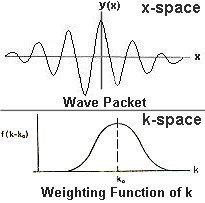
Paquete de ondas gaussiano (y=E_c(x;t=0) .
1. Sea $f(k)$ dado por $f(k)=\frac{1}{\pi^{\frac{1}{4}}\Delta_k^{\frac{1}{2}}}e^{\frac{-(k-k_0)^2}{2\Delta_k^{2}}}$ , es decir, una gaussiana centrada en $k_0$ y de anchura $\Delta_k$ , normalizada a la unidad, $\int_{-\infty}^{+\infty}\left|f(k)\right|^2dk=1$ :
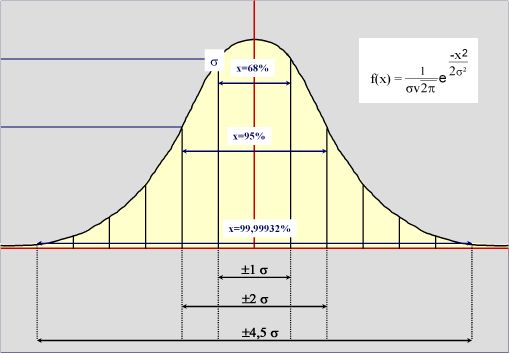
2. La anchura $\Delta_k$ de la gaussiana representa el valor para el que en $k=k_0 \pm \Delta_k$ la función $\left|f(k)\right|^2$ cae a $\frac{1}{e}$ de su valor máximo o valor en el punto central $k_0$ : $f(k_0 \pm \Delta_k)=\frac{1}{\sqrt{e}}f(k_0)$ .
3. Sea $\beta(k)=kx-\omega t=k(x-v_ft)$ , de forma que se tiene
  $E_C(x;t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}f(k)e^{i\beta (k)}dk$ . Esta integral tendrá un valor no despreciable sólo cuando $\beta (k) \approx$ constante en la vecindad de $k=k_0$ , donde $f(k)$ es máximo. Esto constituye la denominada «condición de fase estacionaria», $\frac{d\beta (k)}{dk}|_{k=k_0}=0\, \Rightarrow \, x=x_0=ct$ , que define el centro del paquete y su velocidad de desplazamiento $v_g$ , que resulta ser $v_g=c$ . Si esta condición no se cumple, la fase $e^{i\beta (k)}$ oscila rápidamente en la vecindad de $k=k_0$ , única zona donde $f(k)$ no es despreciable, y la integral resulta nula.
4. $E_C(x;t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}f(k)e^{i\beta (k)}dk$
  $=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}\frac{1}{\pi^{\frac{1}{4}}\Delta_k^{\frac{1}{2}}}e^{\frac{-(k-k_0)^2}{2\Delta_k^{2}}}e^{i\beta (k)}dk$ ,
  expresión desde la que vía el cambio de variable $u=k-k_0$ se llega a la
  $E_C(x,t)=\frac{1}{\sqrt{2\pi}}\frac{1}{\pi^{\frac{1}{4}}\Delta_k^{\frac{1}{2}}}e^{ik_0(x-v_ft)}\int_{-\infty}^{+\infty}e^{\frac{-u^2}{2\Delta_k^{2}}}e^{iu(x-v_ft)}du$ ;
  usando el resultado $\int_{-\infty}^{+\infty}e^{-p^2x^2 \pm qx}dx=\frac{\sqrt{\pi}}{p}e^{\frac{q^2}{4p^2}}$ (válido para cualquier $p$ con $Re (p)\, > 0$ , se obtiene a continuación
  $E_C(x;t)=\frac{1}{\sqrt{2\pi}}\frac{1}{\pi^{\frac{1}{4}}\Delta_k^{\frac{1}{2}}}e^{ik_0(x-v_ft)}\sqrt{2\pi}\Delta_ke^{-(x-v_ft)^2 \cdot \frac{\Delta_k^2}{2}}$
  $=\frac{\Delta_k^{\frac{1}{2}}}{\pi^{\frac{1}{4}}}e^{-(x-v_ft)^2\frac{\Delta_k^2}{2}}e^{ik_0(x-ct)}$ .
5. En $t=0$ se tiene, introduciendo $\Delta_x=1/ \Delta_k$ :
  $E_C(x;t=0)=\frac{1}{\pi^{\frac{1}{4}}\Delta_x^{\frac{1}{2}} }e^{\frac{-x^2}{2\Delta_x^2 }}e^{ik_0x}$ ,
  producto de una gaussiana de anchura $\Delta_x$ por un factor de fase.
6. Encontramos que $E_C$ representa una onda plana, propagándose con velocidad $v_g=\frac{d\omega (k)}{dk}=c$ en el sentido positivo del eje $OX$ , con una amplitud concentrada en una región espacial de amplitud o anchura $\Delta_x=\frac{1}{\Delta_k}$ , centrada alrededor del punto $x=v_gt=ct$ .
7. Las siguientes imágenes muestran, para una gaussiana (nuestro $f(k)$ ),
  Gaussiana: la representada en la figura corresponde a la normalización que integra en toda la recta real directamente f; en el texto se normaliza integrando |f|^2.
  
  el correspondiente paquete de ondas $E_C(x;0)$ (la representación se ha hecho para una mejor visualización en dos dimensiones, $E_C(x,y;t=0)$ , suponiendo $x=y$ ) :
  
  Paquete de ondas gaussiano en dos dimensiones (imagen procedente de: http://phy.ntnu.edu.tw/ ~moe89/GH/g4/myweb3/gau-fun.html).
8. Puesto que se satisface $\Delta_x \cdot \Delta_k=1$ , cuánto más estrecha se haga la función $f(k)$ , más ancha se hará $\Delta_x$ , esto es, más ancha será la región en que el paquete de ondas posee intensidad apreciable.
9. En este ejemplo, tanto el paquete como todas las ondas parciales que se suman comparten la misma velocidad de fase, establecida como $c$ , de forma que el paquete mantiene su forma en el tiempo y no sufre dispersión o desparramamiento en la evolución temporal, desplazándose con velocidad de grupo $v_g=c$ :
  Paquete de ondas sin dispersión (imagen de Wiki, licencia GNU).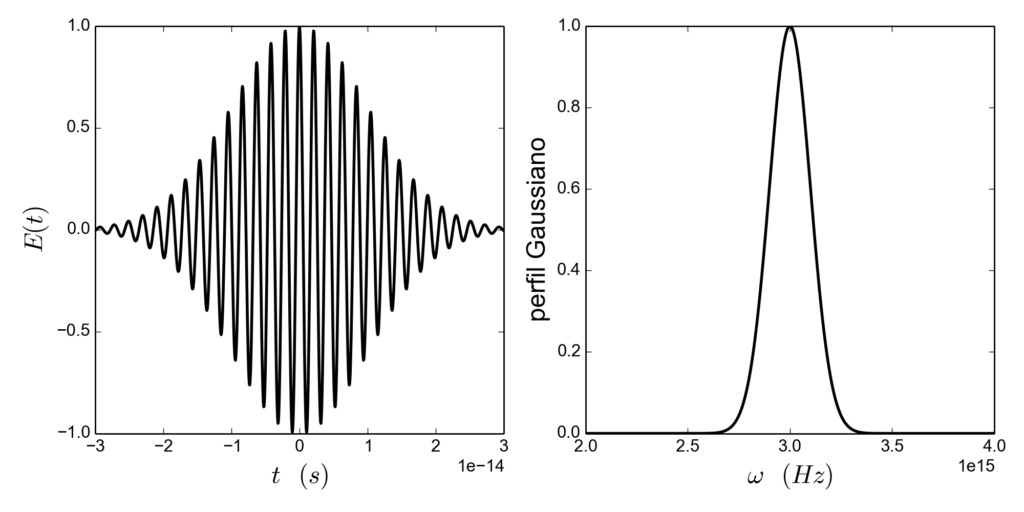
  
  Pulso de luz plano gaussiano (fuente: http://pendientedemigracion.ucm.es/info/aocg/python/optica/pulsos/index.html).
10. ¿Hemos construido una «función de onda fotónica«?
  Imagen: http://www.nist.gov/pml/div684/fcdc/quantum-physicstheory.cfm.
  
  -Sobre la tentación de considerar el anterior paquete de ondas como la función de onda de un fotón, de un cuanto de luz normalizado de frecuencia angular media $\omega_0$ y energía $\hbar \omega_0$ , vale la pena recordar que no existe hoy una función de onda aceptada para el fotón, constituyendo un tema de investigación abierto en que han sido publicados numerosos y diferentes enfoques… Lo que está claro es que la interpretación probabilística para la anterior función de onda como una densidad de probabilidad de posición (para $\left|E_C\right|^2$ ) no es aplicable al fotón, aunque quizás resultaría más plausible la de $\left|f(k)\right|^2$ como una densidad de probabilidad para el número de ondas $k$ fotónico (cf. [BOH-89], cap. 4, pp. 81ss.). Feynman dijo que a la pregunta «¿Dónde está el fotón?», la respuesta es «nadie lo sabe, y lo mejor es que no se intente pensar sobre ello». Desde luego, si acudimos al concepto de fotón como un modo de excitación normal del campo, y no como una partícula, la pregunta se difumina… Información amplia sobre todo esto puede encontrarse en la referencia ¿qué es un fotón?
  -Introducida la cuantización del campo electromagnético, los denominados estados coherentes o cuasi-clásicos, estados Glauber (1963), se consideran los estados de radiación más clásicos (límite clásico), y se identifican con los autoestados del operador destrucción $\hat{a}$ , en los que las fluctuaciones del campo electromagnético son mínimas. La expresión de un estado Glauber en representación de posiciones es, precisamente, una gaussiana cuyo centro se comporta como el del paquete asociado a una partícula material sometida a un potencial de oscilador armónico.
Ejemplo 2: paquete de ondas para una partícula material (cf. [BRA-00], pp. 60 ss.):
1. Consideremos una partícula material libre, masa $m_o \ne 0$ y moviéndose a lo largo del eje $OX$ , con energía (tomamos caso no relativista, $m=m_o$ ) $E=\frac{p_x^2}{2m}$ y momento $\vec{p}=p_x\hat{i}$ ( $|\vec{p}|=|p_x|$ ).
2. El paquete de onda asociado tendrá la expresión general
  $\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i(p_xx-E(p_x) t)/\hbar}dp_x$ , donde ahora cada onda plana individual $j$ -ésima tendrá una velocidad de fase distinta, dada por $(v_{f})_j=(\frac{x}{t})_j=\frac{\omega (k_j)}{k_j}=\frac{E_j(p_{xj})}{p_{xj}}=\frac{p_{xj}}{2m}=\frac{\hbar k_j}{2m}$ .
3. Supongamos ahora que la función $\phi (p_x)$ presenta un pico muy acusado en torno a algún valor $p_{xo}$ , presentando valores despreciables fuera del intervalo de anchura $\Delta p_x$ centrado en el valor $p_{xo}$ (por ejemplo, podría ser una gaussiana).
  Dos funciones peso y sus correspondientes paquetes de onda (imagen procedente de: http://www.met.reading.ac.uk/pplato2/h-flap/phys10_3.html).
4. El paquete de ondas general para una función con tal característica (anchura $\Delta p_x$ estrecha en torno a un pico acusado $p_{xo}$ ) resulta ser:
  $\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i\beta (p_x)/\hbar}dp_x$ ,
  donde $\beta (p_x)=p_xx-E(p_x)t$ .
5. Si $\beta (p_x)$ varía significativamente sobre el intervalo $(p_{xo}-\Delta p_{xo}\,,\,p_{xo}+\Delta p_{xo})$ , entonces el factor de fase $e^{i\beta (p_x)}$ oscilará fuertemente y la integral que representa el paquete de ondas se anulará. Así que la intensidad del paquete de ondas, $\left|\psi(x;t)\right|^2$ , sólo será significativa cuando $\beta (p_x)$ se mantenga constante en el entorno de $p_{xo}$ .
6. La condición de fase estacionaria,
  $\frac{d\beta (p_x)}{dp_x}|_{p_x=p_{xo}}=0=x-\frac{dE(p_x)}{dp_x}|_{p_x=p_{xo}} \, t$ ,
  define el centro del paquete, un punto distinguido $x_o(t)$ para el que $x_o =v_g \,t$ , esto es, que se desplaza con la velocidad de grupo
  $v_g=\frac{dE(p_x)}{dp_x}|_{p_x=p_{xo}}=\frac{d\omega (k)}{dk}|_{k=k_o}=\frac{p_{xo}}{m}$ ,
  siendo $k_o=\frac{p_{xo}}{\hbar}$ .
7. La velocidad de grupo $v_g$ debe coincidir en el límite macroscópico, cuando $\Delta p_x \rightarrow 0$ , con la velocidad clásica de la partícula, cuando el movimiento de la partícula sigue la ley clásica (principio de correspondencia) : la anchura del paquete $\Delta p_x$ se hace despreciable y $v=\frac{p_{xo}}{m}$ .
8. De la expresión para $v_g$ se deduce que $\frac{dE(p_x)}{dp_x}=\frac{p_x}{m}$ , de forma que se obtiene la ecuación para la energía $E(p_x)=\frac{p_x^2}{2m}\,+\,constante$ , donde la constante de integración se toma nula (elección arbitraria de origen de energía), puesto que sólo tienen interés físico las diferencias de energía (y de ahí también que las frecuencias absolutas $\nu=\frac{E}{h}$ carezcan de interpretación física para la partícula material).
9. Para la onda parcial correspondiente al momento $p_x=p_{xo}$ se tiene una velocidad de fase $v_f|_{p_x=p_{xo}}=\frac{E(p_{xo})}{p_{xo}}=\frac{p_{xo}}{2m}=\frac{v_g}{2}$ .
10. Procedamos a desarrollar la energía $E(p_x)$ en serie de potencias en torno a $p_x=p_{xo}$ , esto es,
  $E(p_x)=\frac{p_x^2}{2m}=\frac{p_{xo}^2}{2m}+\frac{p_{xo}}{m}(p_x-p_{xo})+\frac{(p_x-p_{xo})^2}{2m}$ ;
  despreciando el término de segundo orden se obtiene
  $E(p_x) \approx \frac{p_{xo}^2}{2m}+v_g(p_x-p_{x0})$ .
11. Despreciar el término de segundo orden tiene sentido cuando el tiempo $t$ se considera lo suficientemente pequeño como para que $\frac{1}{2}E^{"}(p_{x0})(p_x-p_{x0})^2\frac{t}{\hbar}=\frac{(p_x-p_{x0})^2t}{2m\hbar} \ll 1$ , esto es, $t \ll \frac{2m\hbar}{(\Delta p_x)^2}=t_2$ , de forma que $e^{\frac{-i(p_x-p_{x0})^2t}{2m\hbar}} \approx 1$ .
12. Introduciendo lo anterior en la expresión del paquete $\Psi(x;t)$ , se llega a:
  $\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i[p_xx - E(p_x)t]/\hbar}dp_x$
  $\approx \frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i[p_xx -E(p_{x0})t - v_g(p_x-p_{x0})t]/\hbar}dp_x$
  $=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i[(p_x - p_{x0})(x - v_gt)]/\hbar}e^{i[p_{x0}x - E(p_{x0})t]/\hbar} dp_x$
  $= e^{i[p_{x0}x - E(p_{x0})t]/\hbar} \cdot F(x;t)$ ,
  donde
  $F(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{i[(p_x - p_{x0})(x - v_gt)]/\hbar}\phi(p_x) dp_x$ .
13. El paquete de ondas $\Psi(x;t)$ anterior resulta por tanto ser el producto de una onda plana monocromática, de longitud de onda $\lambda_o=\frac{h}{|p_{xo}|}$ y frecuencia angular $\omega_o=E(p_{xo})/\hbar =\frac{p_{xo}^2}{2m\hbar}$ , por una función envolvente portadora, o factor modulante $F(x;t)$ tal que $\left|\Psi(x;t)\right|^2=\left|F(x;t)\right|^2$ , es decir, proporcionando la correspondiente densidad de probabilidad; la figuras siguientes representas su aspecto para la partícula libre:
  Paquete de ondas para la partícula libre, con dispersión (imagen de Wiki, licencia GNU).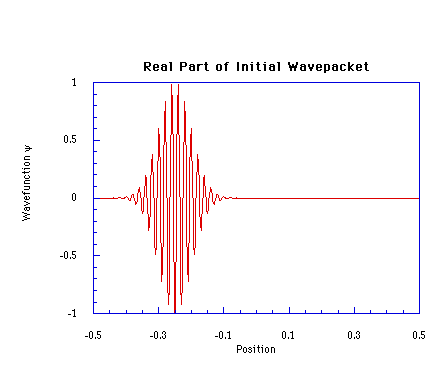
  
  Imagen de: http://www.nat.vu.nl/~jo/hovo/InitialWavepacket.html
14. Puesto que se satisface $F(x'=x+v_gt;t')=F(x;\Delta t=t'-t)$ , la onda envolvente se propaga aparentemente sin cambio de forma y con la velocidad de grupo $v_g$ , pero recuérdese que esto es sólo cierto para un intervalo de tiempo transcurrido $\Delta t$ tal que $\frac{1}{2}E^{"}(p_{x0})(p_x-p_{x0})^2\frac{\Delta t}{\hbar}=\frac{(p_x-p_{x0})^2\Delta t}{2m\hbar} \ll 1$ . Es decir, en el transcurso del tiempo, a la larga la forma del paquete cambiará durante su propagación: se produce un efecto de dispersión, debido a la diferente velocidad de fase $v_f=\frac{\omega (k)}{k}=\frac{p_x}{2m}=\frac{h}{2m\lambda}$ de cada onda parcial sumada:
Ejemplo 3: paquete de ondas gaussiano para una partícula material (cf. [BRA-00], pp. 64 ss.):
1. Consideremos una partícula material libre, masa $m_o \ne 0$ y moviéndose a lo largo del eje $OX$ , con energía (tomamos caso no relativista, $m=m_o$ ) $E=\frac{p_x^2}{2m}$ y momento $\vec{p}=p_x\hat{i}$ .
2. El paquete de onda asociado tendrá la expresión general
  $\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i(p_xx-E(p_x) t)/\hbar}dp_x$ , donde ahora cada onda plana individual tendrá una velocidad de fase distinta, dada por $v_{fi}=(\frac{x}{t})_i=\frac{\omega (k_i)}{k_i}=\frac{E_i(p_{xi})}{p_{xi}}=\frac{p_{xi}}{2m}=\frac{\hbar k_i}{2m}$ .
3. Supongamos ahora que la función $\phi (p_x)$ es una gaussiana de expresión $\phi (p_x)=\frac{1}{\pi^{\frac{1}{4}}(\Delta p_x)^{\frac{1}{2}}}e^{\frac{-(p_x-p_{xo})^2}{2(\Delta p_x)^2}}$ , función que en efecto presenta un pico muy acusado en torno al valor $p_{xo}$ y valores despreciables fuera del intervalo de anchura $\Delta p_x$ centrado en el valor $p_{xo}$ ; la función está normalizada a la unidad, $\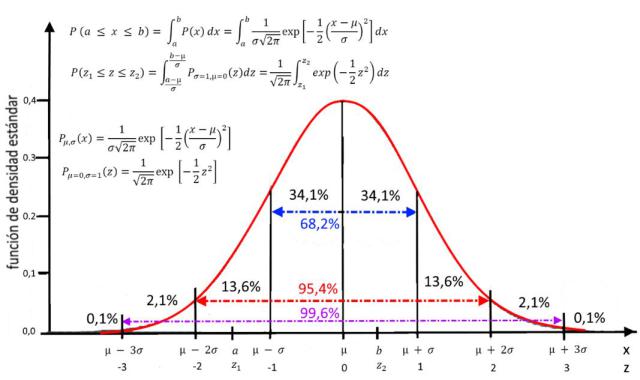int_{-\infty}^{+\infty}\left|\phi(p_x)\right|^2dp_x=1$ :
  Distribución de probabilidad gaussiana; obsérvese que la nuestra se define como el cuadrado de la considerada en la figura, que es la usual en matemáticas. Imagen de: https://analisisdecircuitos1.wordpress.com/parte-1-circuitos-resistivos/capitulo-5-cifras-significativas/capitulo-05b-tratamiento-de-las-incertidumbres-y-la-teoria-de-probabilidades/.
4. El paquete de ondas resulta ser (según resultados del apartado anterior y tras un laborioso cálculo):
  $\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i(p_xx - \frac{p_x^2}{2m}t)/\hbar}dp_x$
  $=\frac{1}{\pi^{\frac{1}{4}}(\Delta p_x)^{\frac{1}{2}}}\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{\frac{-(p_x-p_{xo})^2}{2(\Delta p_x)^2}} e^{i(p_xx - \frac{p_x^2}{2m}t)/\hbar}dp_x$
  $=\frac{1}{\pi^{\frac{1}{4}}}\sqrt{\frac{\Delta p_x}{\hbar}}$ $\sqrt{\frac{1}{1+it(\Delta p_x)^2/m\hbar}}$
  $e^{-\frac{p_{xo}^2}{2(\Delta p_x)^2}}$ $e^{\frac{-(\Delta p_x)^4x^2 + p_{xo}^2 \hbar^2 + 2ix (\Delta p_x)^2 p_{xo}\hbar}{\frac{\hbar}{m}(\Delta p_x)^22[(\Delta p_x)^2it + m\hbar]}}$ ,
  donde se ha usado $\int_{-\infty}^{+\infty}e^{-\alpha x^2 -\beta x}dx=(\frac{\pi}{\alpha})^{\frac{1}{2}}e^{\frac{\beta ^2}{4\alpha}}$ , siempre que $Re(\alpha)>0$ .
5. Simplificando la expresión anterior se llega a
  $\Psi(x;t)= \frac{1}{\pi^{\frac{1}{4}}}\sqrt{\frac{\Delta p_x}{\hbar}}\sqrt{C}e^{-C\frac{x^2}{2}(\frac{\Delta p_x}{\hbar})^2}e^{i[p_{xo}x - \frac{p_{xo}^2}{2m}t]\frac{C}{\hbar}}$ ,
  donde $C=\frac{1}{1 + it(\Delta p_x)^2/m\hbar}$ .
6. La correspondiente densidad de probabilidad viene dada por (obtenible tras otra larga manipulación):
  $\left|\Psi(x;t)\right|^2=\frac{1}{\sqrt{\pi}}\frac{\Delta p_x}{\hbar}\frac{1}{\sqrt{1 + t^2(\Delta p_x)^4/m^2\hbar^2}}e^{-\frac{(\frac{\Delta p_x}{\hbar})^2(x - v_gt)^2}{1 + t^2(\Delta p_x)^4/m^2\hbar^2}}$ .
7. Las expresiones anteriores en $t=0$ proporcionan:
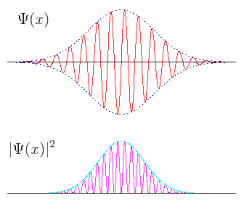
  $\psi(x)=\Psi(x;t=0)= \frac{1}{\pi^{\frac{1}{4}}}\sqrt{\frac{\Delta p_x}{\hbar}}e^{-\frac{x^2}{2}(\frac{\Delta p_x}{\hbar})^2}e^{ip_{xo}x/\hbar}$ ,
  $\left|\psi(x)\right|^2=\left|\Psi(x;t=0)\right|^2=\frac{1}{\sqrt{\pi}}\frac{\Delta p_x}{\hbar}e^{-x^2(\frac{\Delta p_x}{\hbar})^2}$ .
  
  Imagen del blog: http://la-mecanica-cuantica.blogspot.com.es/2010/07/el-espacio-posicion-y-el-espacio.html
8. Ante los resultados obtenidos, vemos que:
  1. $\Psi(x;0)$ es también una gaussiana, y es una función tal que la densidad de probabilidad asociada, $\left|\Psi(x;t=0)\right|^2$ , presenta un máximo en el punto $x=0$ , y cae a $\frac{1}{e}$ de su valor máximo en los puntos $x=\pm \Delta x$ , donde $\Delta x=\frac{\hbar}{\Delta p_x}$ es la anchura de la distribución de valores de la variable posición $x$ . Para este paquete se tiene pues la relación $\Delta x \cdot \Delta p_x=\hbar$ y, consecuentemente: si disminuimos $\Delta p_x$ , de forma que la función $\phi(p_x)$ presente un pico aún más acusado en el valor $p_x=p_{xo}$ , entonces $\Delta x$ aumenta y $\Psi(x;t)$ se vuelve más deslocalizado. Recíprocamente, si $\Delta p_x$ aumenta, o sea, deslocalizamos $\phi(p_x)$ , entonces $\Psi(x;t)$ se localiza más en torno al punto $x=x_o=x(t=0)$ .
  2. Considerando la evolución temporal, expresión $\Psi(x;t)$ , el centro del paquete de ondas se mueve uniformemente con la velocidad de grupo $v_g=\frac{p_{xo}}{m}$ , y su anchura, dada la anchura $\Delta p_x$ de $\phi(p_x)$ , puede obtenerse imponiendo la condición $\left|\Psi(x=v_gt\pm \Delta x;t)\right|^2=\frac{1}{e}\left|\Psi(x=v_gt;t)\right|^2$ , que conduce a
    $\Delta x(t)=\frac{\hbar}{\Delta p_x}\frac{1}{\sqrt{\left|C\right|}}=\frac{\hbar}{\Delta p_x}[1+\frac{(\Delta p_x)^4}{m^2\hbar^2}t^2]^{\frac{1}{2}}$ ,
    expresión que establece el fenómeno de dispersión del paquete de ondas: su anchura $\Delta x(t)$ aumenta con el tiempo:
    
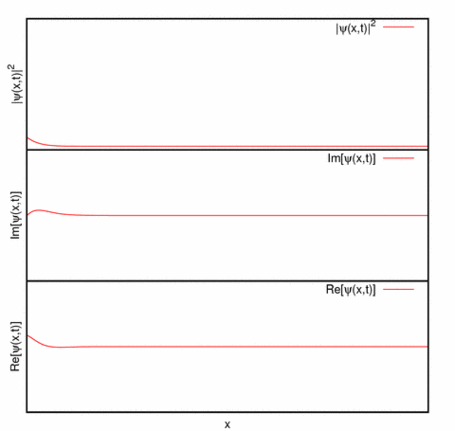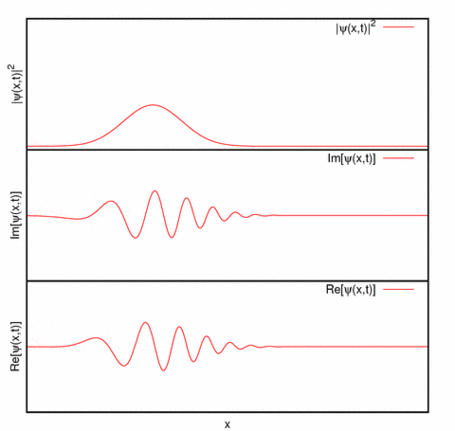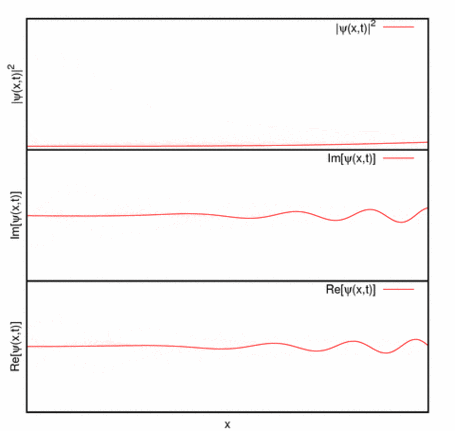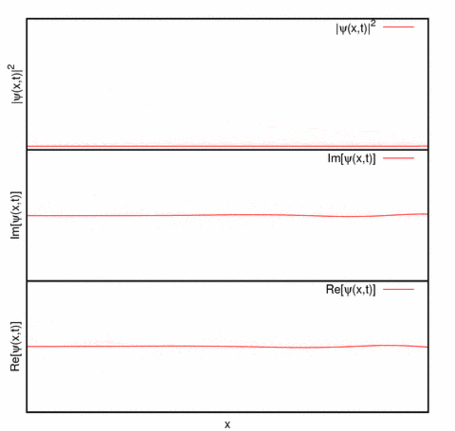
    Imagen de la Wikipedia.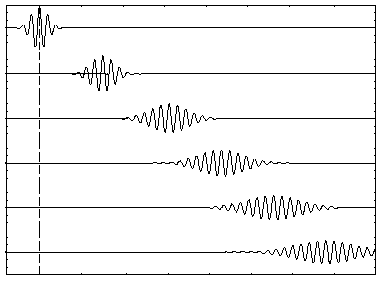
    
    Paquete de ondas con dispersión (imagen del blog la-mecanica-cuantica.blogspot.com).
    
    -Sólo para intervalos de tiempo transcurridos del orden $\Delta t$ , con $\Delta t \ll t_1=\frac{m\hbar}{(\Delta p_x)^2}$ (esto es, valores de tiempo que hacen $C \approx 1$ ; $C=1 \; \Leftrightarrow \;t=0$ ), el paquete de ondas mantiene su anchura.
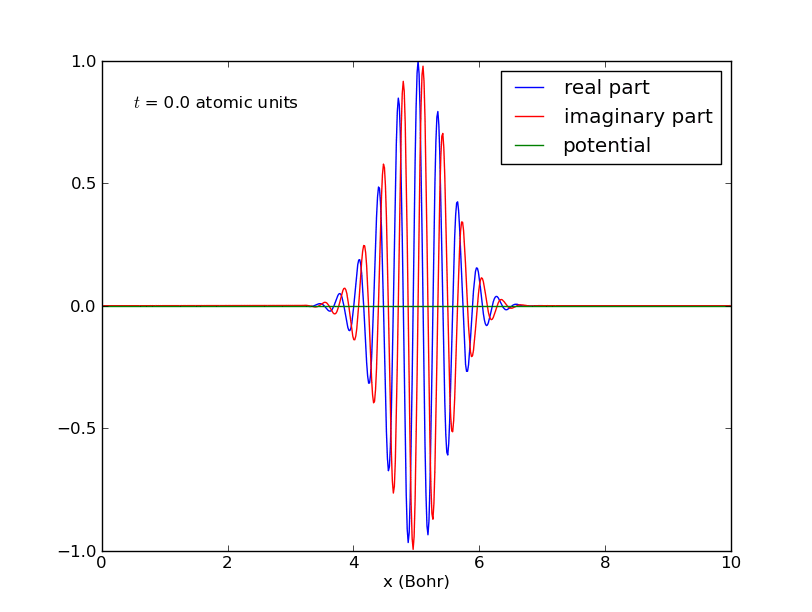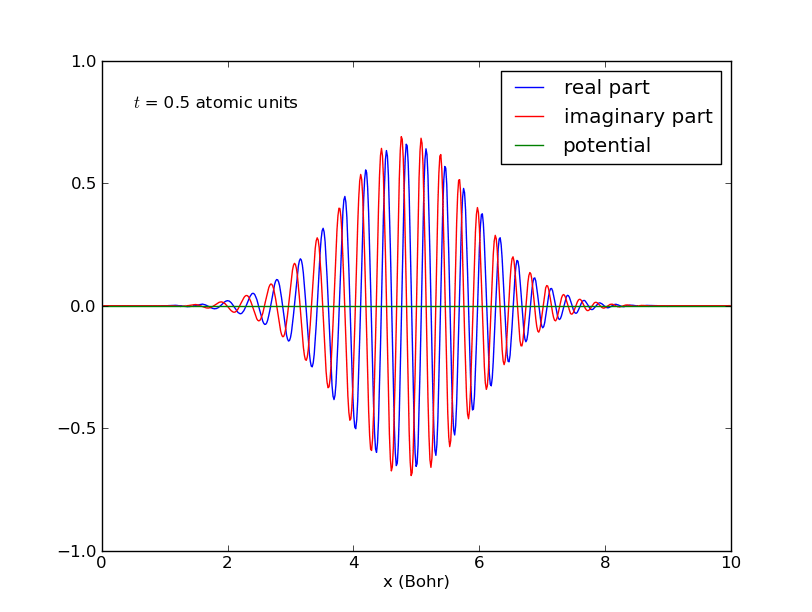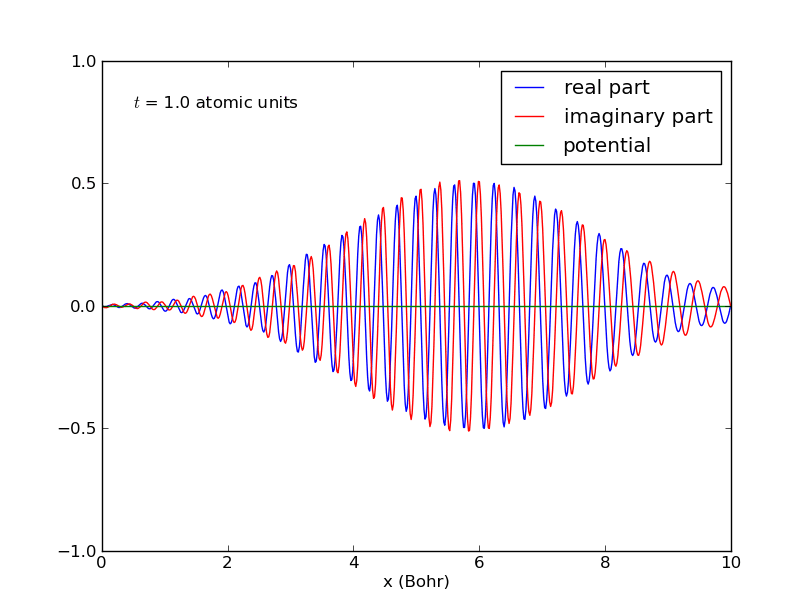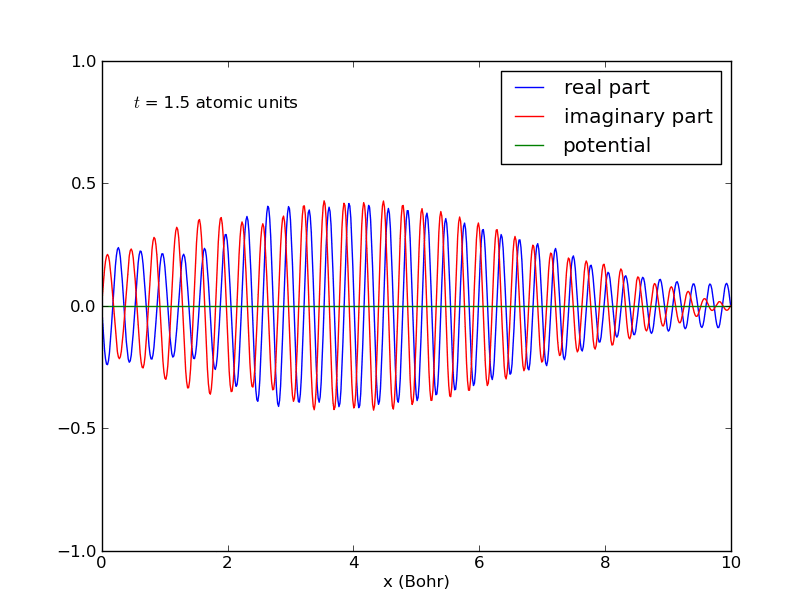
    -Universidad de St. Andrews: evolución temporal de un paquete de ondas gaussiano: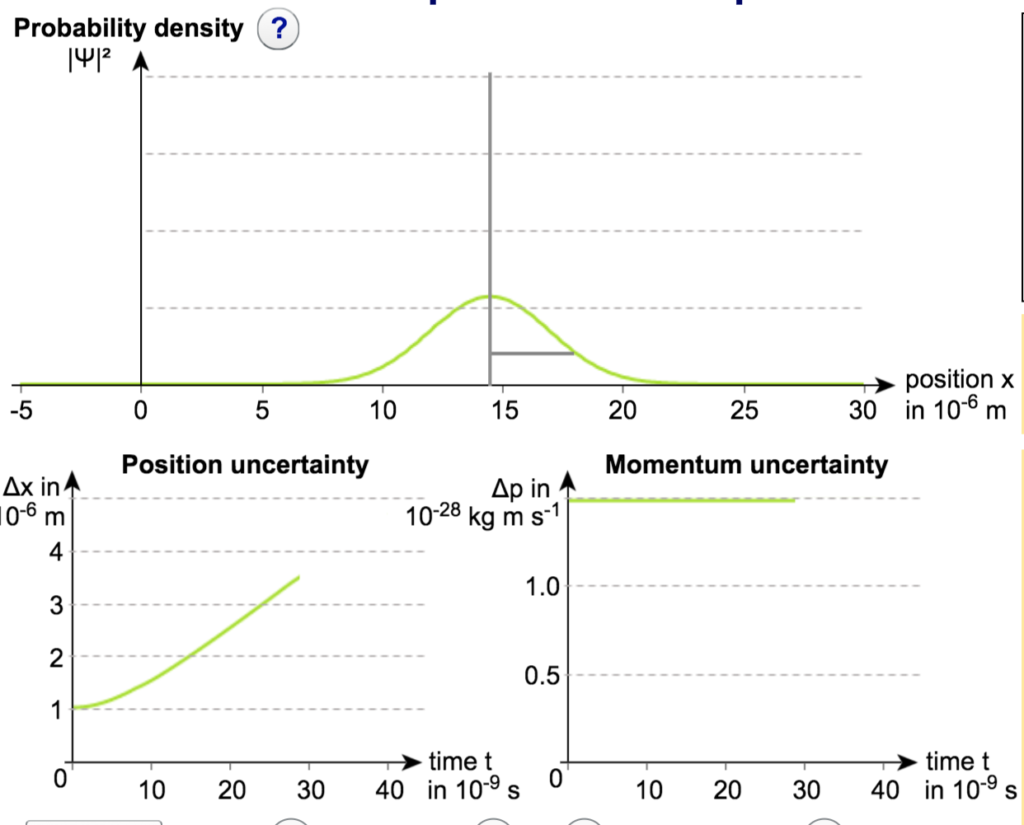
    
    Universidad de St. Andrews: evolución temporal de un paquete de ondas gaussiano.
  3. Obsérvese que, además, la forma del paquete $\Psi(x;t)$ es sólo aparentemente la de una gaussiana, pues en la expresión el factor que correspondería a la fase de la gaussiana, por la presencia de $C$ , no constituye en general un verdadero factor de fase (no se expresa como $e^{ia}\,,\,a\in \mathbb{R}$ ; sí lo es cuando $t \ll t_1 \Rightarrow C \approx 1$ ).
  4. Para un valor dado de la anchura $\Delta p_x$ , cuando $\Delta t \ll t_1=\frac{m\hbar}{(\Delta p_x)^2}$ , esto es , $C\approx 1$ , se cumple la relación la relación $\Delta x \cdot \Delta p_x \approx \hbar$ , pero ahora sólo aproximadamente.
  5. En resumen, el paquete de ondas asociado a una partícula material, masa $m\ne 0$ , modifica su altura y anchura con el tiempo, es decir, se produce un fenómeno de deslocalización de la partícula, debido a que hay muchas velocidades de fase distintas, pues $v_f=\frac{\omega}{k}=\frac{E(p_x)}{p_x}=\frac{p_x}{2m}=\frac{h}{2m\lambda}$ depende de la $\lambda$ de la onda parcial, y en general hay numerosas $\lambda$ diferentes presentes en el paquete.
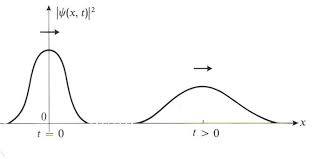
    Deslocalización progresiva de la partícula.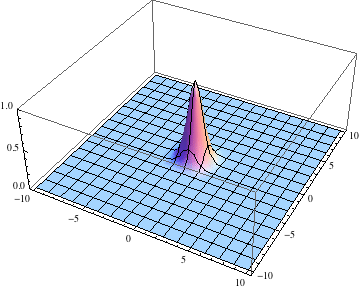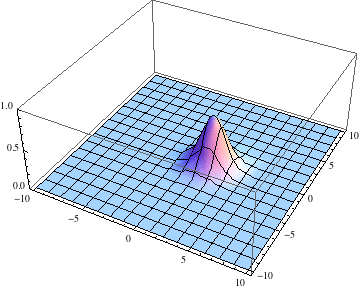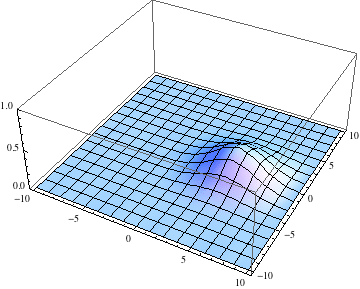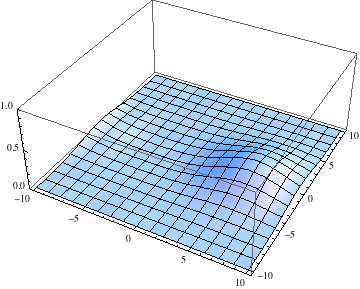
    
    Dispersión del paquete de ondas de la partícula material (imagen procedente de: http://mathematica.stackexchange.com/questions/27842/complex-valued-21d-pde-schr%C3%B6dinger-equation-numerical-method-for-ndsolve).
    
    -Mientras que se cumpla $t \ll t_1=\frac{m\hbar}{(\Delta p_x)^2}$ , el paquete de ondas no se deforma (salvo quizás la fase), acompañando a su centro que se desplaza con la velocidad de grupo, coincidente con la velocidad clásica. Pero en el transcurso temporal, el paquete comienza a deformarse, ensanchándose asintóticamente sin límite, de forma que la imagen clásica de partícula pierde sentido por completo.
  6. Ejemplos:
    -Un protón, $M_0=938,280\,Mev/c^2$ , supuesta una velocidad de $v=c/30$ , con una indeterminación en su momento $\Delta k \approx 10\,cm^{-1}$ , $\Delta x \approx 0,1\,cm$ , recorrerá una distancia de $3,2 \times 10^{10}\,cm$ hasta que se haga $\left|\frac{t\hbar}{2m(\Delta x)^2}\right| \approx 1$ , esto es, $t\approx 2t_1$ (cf. [GAL-89], p. 57).
    -Para un electrón, $m_0=0,511\,MeV/c^2$ , supuesta en $t=0$ una localización $\Delta x=10^{-10}\, m$ (característica del rango atómico), se tendrá $\Delta p_x \approx \frac{\hbar}{\Delta x}\approx 10^{-24}\,kg\cdot m\cdot s^{-1}$ , y el paquete doblará su anchura en $t\approx \sqrt{3}t_1 \approx 10^{-16}\,s$ .
    -Para una partícula macroscópica, $m=1\,g$ , localizada inicialmente con $\Delta x \approx 10^{-6}\,m$ , el tiempo en que el paquete duplica su anchura resulta de $t\approx 10^{+19}\,s$ .
    (los dos últimos ejemplos en [BRA-00], p. 66).
Por tanto, el paquete de onda asociado a una partícula material libre de masa $m\ne 0$ tiene la expresión general (caso no relativista):
$\Psi(x,t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{i(p_xx-E(p_x) t)/\hbar}\phi(p_x)dp_x$ , con $E(p_x)=\frac{p_x^2}{2m}$ ,
pudiendo expresarse
$\Psi(x,t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{ip_xx/\hbar}e^{-iE(p_x) t/\hbar}\phi(p_x)dp_x=\mathscr{F}^{-1}\{\Phi (p_x;t) \}$ ,
es decir: el paquete se expresa como la transformada de Fourier inversa de la función $\Phi (p_x;t)=e^{-iE(p_x)t/\hbar}\phi(p_x)$ . Esta última función se asocia a lo que se denomina un «estado estacionario de energía«.
Las anteriores expresiones son también válidas para un sistema físico constituido por una partícula material de masa $m \ne 0$ cuyo Hamiltoniano se exprese como $H=K+V(x) \ne H(t)$ , donde $K$ y $V$ representan, respectivamente, las energías cinética y potencial; $V$ ha de ser un potencial de variación suave en una longitud del orden de la longitud de onda de de Broglie asociada a la partícula, $\lambda=\frac{h}{\sqrt{[2m(E-V(x)]}}$ , siendo $p_x=|\vec{p}|=+\sqrt{[2m(E-V(x)]}$ el módulo del momento clásico de la partícula.
-Por ejemplo, la figura siguiente nos presenta el aspecto del paquete de onda correspondiente a una partícula material confinada en una caja unidimensional de paredes impenetrables:

Imagen de: physics.oregonstate.edu.
En general, (cf. [GAL-89], p. 141) «para que el movimiento de un paquete de ondas pueda asimilarse al de una partícula clásica, es necesario que: a) los valores medios de los observables posición y momento satisfagan en buena aproximación las leyes clásicas (teorema de Ehrenfest); y b) las dimensiones del paquete sean lo suficientemente pequeñas y se mantengan así en su evolución temporal«.
Dimensiones de $\Psi$ : las dimensiones de la función de onda del paquete monodimensional para una partícula son $L^{-\frac{1}{2}}$ , donde $L$ simboliza longitud.

Paquetes de ondas y relaciones de indeterminación

Según los resultados obtenidos en los anteriores ejemplos:
1. Para el paquete de ondas del anterior ejemplo 1, en que se suman ondas parciales todas con igual velocidad de fase $c$ , las sendas anchuras del paquete $E_C(x;t)$ y de la función de distribución de momentos $f(k)$ satisfacen la relación $\Delta x \cdot \Delta k=1\,\Rightarrow \,\Delta x \cdot \Delta p_x=\hbar$ : cuánto más estrecha se haga la función $f(k)$ , más ancha se hará $E_C(x;t)$ , esto es, más ancha será la región en que el paquete de ondas posee intensidad apreciable; y viceversa.
2. Para el paquete de ondas gaussiano asociado con una partícula material, de masa $m\ne 0$ , las sendas anchuras del paquete $\Psi(x;t)$ y de la función de distribución de momentos $\phi(p_x)$ satisfacen la relación $\Delta x(t)=\frac{\hbar}{\Delta p_x}\frac{1}{\sqrt{\left|C\right|}}=\frac{\hbar}{\Delta p_x}[1+\frac{(\Delta p_x)^4}{m^2\hbar^2}t^2]^{\frac{1}{2}}$ , de forma que, en general, la relación puede expresarse como $\Delta x (t) \cdot \Delta p_x \ge \hbar$ .
3. Cuando $\Delta t \ll t_1=\frac{m\hbar}{(\Delta p_x)^2}$ , esto es , $C=\frac{1}{1+it(\Delta p_x)^2/(m\hbar)} \approx 1$ , se cumple la relación $\Delta x\,(t) \cdot \Delta p_x \gtrsim \hbar$ . Obsérvese que para el paquete $\Delta x$ resulta ser una función de $t$ , mientras que $\Delta p_x$ se considera constante, puesto que aquí simboliza la anchura de la función de distribución de momentos $\phi(p_x)$ tomada.
4. Sea un paquete de ondas asociado con una partícula material, de masa $m\ne 0$ , y sean dadas las condiciones tales que se cumple $\Delta x \cdot \Delta p_x \approx \hbar$ . Entonces se implica que, si se requiere determinar la posición de la partícula con precisión $\Delta x$ , sólo se podrá determinar simultáneamente su momento con una precisión $\Delta p_x\approx \frac{\hbar}{\Delta x}$ , un resultado que no es sino un caso particular del denominado Principio de indeterminación de Heisenberg.
5. Relaciones del tipo $\Delta x \cdot \Delta p_x \approx \hbar$ se derivan de una propiedad general de la transformada de Fourier para las correspondientes anchuras en los dos espacios involucrados (vía la desigualdad de Cauchy-Schwarz y la identidad de Parseval), pero no fue éste su origen en el histórico artículo de Heisenberg de 1927.
6. Si se estima el orden de magnitud del tiempo en que el paquete recorre su propia anchura, $\Delta t \approx\frac{\Delta x}{v_g}=\frac{m\Delta x}{p_{xo}}$ , y admitiendo una anchura o indeterminación en la energía dada por $\Delta E\approx \frac{p_{xo}\Delta p_x}{m}$ , se concluye que $\Delta E \cdot \Delta t \approx \hbar$ , un caso de la relación de indeterminación energía-tiempo.

Espacio tridimensional

Ondas planas en tres dimensiones

Sea una partícula no relativista de masa $m$ , con onda plana asociada $\Psi(\vec{r};t)=Ae^{i[\vec{k}\cdot\vec{r}-\omega(k)t]}=Ae^{i[\vec{p}\cdot\vec{r}-E(p)t]/ \hbar}$ , donde $\vec{p}=\hbar\vec{k}$ , $\omega(k)=\frac{\hbar |\vec{k}|^2}{2m}=\frac{E}{\hbar}$ y $E(\vec{p})= \frac{|\vec{p}|^2}{2m}$ .
Se satisfacen el par de ecuaciones diferenciales:
$-i\hbar\nabla\Psi(\vec{r};t)=\vec{p}\, \Psi(\vec{r};t)$ ;
$i\hbar\frac{\partial}{\partial t}\Psi(\vec{r};t)=E\, \Psi(\vec{r};t)$ .
La energía y el momento se representan (postulado) por los sendos operadores diferenciales $E_{op}=i\hbar\frac{\partial}{\partial t}$ y $\vec{p}_{op}= -i\hbar\nabla$ ,
actuando sobre la función de onda $\Psi(\vec{r};t)$ .

Paquetes tridimensionales

El paquete de ondas tridimensional para una partícula material libre no relativista, de masa $m=m_o \ne 0$ , tiene la expresión:
$\Psi(\vec{r};t)=\frac{1}{(2\pi \hbar)^{\frac{3}{2}}}\int_{\mathbb{R}^3}e^{i(\vec{p}\cdot \vec{r}-E(\vec{p}) t)/\hbar}\phi(\vec{p})d\vec{p}$ , donde ahora cada onda plana individual tendrá una velocidad de fase distinta.
En el caso de que la función $\phi (\vec{p})$ presente un pico muy acusado en torno a algún valor $\vec{p_o}$ , y valores despreciables fuera del intervalo de anchura $\Delta \vec{p}$ centrado en el valor $\vec{p_o}$ , denominando $\beta(\vec{p})=\vec{p}\cdot \vec{r}-E(\vec{p}) t$ , la condición de fase estacionaria $\nabla_{\vec{p}}\beta(\vec{p})|_{\vec{p}=\vec{p_o}}=0$ define el centro del paquete $\vec{r_o}$ , para el que $\vec{r_o}=\vec{v_g}t$ , proporcionando la velocidad de desplazamiento del paquete: la velocidad de grupo $\vec{v_g}$ , que se establece igual en el límite clásico a la velocidad de la partícula $\vec{v}=\frac{\vec{p_o}}{m}$ (de donde se infiere $E(\vec{p})=\frac{p^2}{2m}$ , más una constante arbitraria que se fija como nula).
Las anteriores expresiones son también válidas para un sistema físico constituido por una partícula material de masa $m \ne 0$ cuyo Hamiltoniano se exprese como $H=K+V(\vec{r}) \ne H(t)$ , donde $K$ y $V$ representan, respectivamente, las energías cinética y potencial; $V$ ha de ser un potencial de variación suave en una longitud del orden de la longitud de onda de de Broglie asociada a la partícula, $\lambda=\frac{h}{\sqrt{[2m(E-V(\vec{r})]}}$ , siendo $p=|\vec{p}|=+\sqrt{[2m(E-V(\vec{r})]}$ el módulo del momento clásico de la partícula.
Dimensiones de $\Psi$ : la dimensión de la función de onda del paquete tridimensional para una partícula es de $L^{-\frac{3}{2}}$ , donde $L$ simboliza longitud.
-En general, la función de onda en el espacio de posiciones o configuración, para un sistema de $N$ partículas, caso $d-$ dimensional, tiene dimensiones $L^{-\frac{d\,N}{2}}$ .

Espacio de momentos y conservación de la probabilidad

Caso monodimensional

Si consideramos el anterior paquete de ondas de expresión
$\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i(p_xx-E(p_x) t)/\hbar}dp_x$ ,
el cual se desplaza con velocidad $v_g=\frac{dE(p_x)}{dp_x}|_{p_xo}=\frac{p_{xo}}{m}$ , donde $p_{xo}$ es el valor donde la función de distribución de momentos $\phi(p_x)$ presenta un máximo acusado, es inmediato reparar en que en $t=0$ el paquete representa la transformada de Fourier inversa de la función de distribución de momentos:
$\psi(x)=\Psi(x;t=0)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{ip_xx/\hbar}\phi(p_x)dp_x=\mathscr{F}^{-1}\{\phi (p_x) \}$ ,
mientras que la relación inversa establece
$\phi(p_x)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{-ip_xx/\hbar}\psi(x)dx=\mathscr{F}\{\psi (x) \}$ .
Generalizando: Sea un sistema físico constituido por una partícula material de masa $m \ne 0$ cuyo Hamiltoniano se exprese como $H=K+V(x) \ne H(t)$ , donde $K$ y $V$ representan, respectivamente las energías cinética y potencial, siendo $V$ un potencial de variación suave en una longitud del orden de la longitud de onda de de Broglie asociada a la partícula, $\lambda=\frac{h}{\sqrt{[2m(E-V(x))]}}$ , siendo $p=\sqrt{[2m(E-V(x))]}$ el momento clásico de la partícula. Se introduce entonces una función $\Phi(p_x;t)$ tal que satisfaga que ella y una función de ondas $\Psi(x;t)$ son mutua transformada de Fourier la una de la otra:
$\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{ip_xx/\hbar}\Phi(p_x;t)dp_x=\mathscr{F}^{-1}\{\Phi (p_x;t) \}$ ,
$\Phi(p_x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{-ip_xx/\hbar}\Psi(x;t)dx=\mathscr{F}\{\Psi (x;t) \}$ .
La función $\Phi(p_x;t)$ se denomina función de ondas en el espacio de momentos (caso monodimensional), y su definición como transformada de Fourier $\mathscr{F}\{\Psi (x;t) \}$ es válida para cualquier función de ondas $\Psi(x;t)$ (es decir, no sólo para un paquete de ondas).
Su interpretación es: $\left|\Phi(p_x;t)\right|^2$ define una densidad de probabilidad de momento, por unidad de volumen:
Postulado: El cuadrado del valor absoluto de la función de onda en el espacio de momentos, $\left|\Phi(p_x;t)\right|^2$ , representa la densidad de probabilidad de que el resultado de un experimento de determinación del momento de la partícula sea: «momento $\vec{p_x}=p_x \hat{i}$ en el instante t».
Según la identidad o teorema de Parseval, si la función $\phi(p_x)=\Phi(x;t=0)$ está normalizada a la unidad, $\int_{-\infty}^{\infty}\left|\phi(p_x)\right|^2dp_x=1$ , se implica que la función $\psi(x)=\Psi(x;t=0)$ también lo está, y además permanece normalizada durante su evolución temporal:
$\int_{-\infty}^{\infty}\left|\Psi(x;t)\right|^2dx=1 \; \forall t$ .
Este hecho establece la conservación de la probabilidad, que se produce también en el espacio de momentos,
$\int_{-\infty}^{\infty}\left|\Phi(p_x;t)\right|^2dp_x=1 \; \forall t$ .
En efecto, sea por ejemplo el paquete de ondas para una partícula material de masa $m \ne 0$ :
$\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i(p_xx-E(p_x) t)/\hbar}dp_x$ ,
para el que suponemos que $\phi(p_x)$ está normalizado, de forma que, por el teorema de Parseval, su transformada de Fourier $\psi(x)=\Psi(x;t=0)$ también lo está,
$\int_{-\infty}^{\infty}\left|\psi(x)\right|^2dx=1$ .
Entonces:
$\int_{-\infty}^{\infty}\left|\Psi(x;t)\right|^2dx$
$=\int_{-\infty}^{\infty}\Psi^*(x;t)\Psi(x;t)dx$
$=\frac{1}{2\pi \hbar}\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{-i(p^{'}_xx-E(p^{'}_x) t)/\hbar}e^{i(p_xx-E(p_x) t)/\hbar}\phi^{*}(p^{'}_x)\phi(p_x)dp^{'}_xdp_xdx$
$=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}e^{i(E(p^{'}_x)-E(p_x))t/\hbar}\delta(p_xx-p^{'}_xx)\phi^{*}(p^{'}_x)\phi(p_x)dp^{'}_xdp_x$
$=\int_{-\infty}^{+\infty}\phi^{*}(p_x)\phi(p_x)dp_x=1$ ,
donde ha aparecido la distribución Delta de Dirac,
$\delta(p_xx-p^{'}_xx)=\frac{1}{2\pi \hbar}\int_{-\infty}^{+\infty}e^{-i(p^{'}_xx-p_xx)/\hbar}dx$ , de propiedades que se suponen conocidas (en particular, recuérdese que $\int_a^bf(x)\delta(x-x_0)dx=f(x_0)$ cuando $a<x_0<b$ , cero en otro caso).

Caso tridimensional

Sea un sistema físico constituido por una partícula material de masa $m \ne 0$ cuyo Hamiltoniano se exprese como $H=K+V(\vec{r}) \ne H(t)$ , donde $K$ y $V$ representan, respectivamente, las energías cinética y potencial; siendo $V$ un potencial de variación suave en una longitud del orden de la longitud de onda de de Broglie asociada a la partícula, $\lambda=\frac{h}{\sqrt{[2m(E-V(\vec{r})]}}$ , siendo $p=|\vec{p}|=+\sqrt{[2m(E-V(\vec{r})]}$ el módulo del momento clásico de la partícula.
La función de ondas en el espacio de posiciones $\Phi(\vec{p};t)$ y la función de ondas en el espacio de momentos $\Psi(\vec{r};t)$ son mutua transformada de Fourier la una de la otra:
$\Psi(\vec{r};t)=\frac{1}{(2\pi \hbar)^{\frac{3}{2}}}\int_{\mathbb{R}^3}e^{i\vec{p}\cdot \vec{r}/\hbar}\Phi(\vec{p};t)d\vec{p}=\mathscr{F}^{-1}\{\Phi (\vec{p};t) \}$ ,
$\Phi(\vec{p};t)=\frac{1}{(2\pi \hbar)^{\frac{3}{2}}}\int_{\mathbb{R}^3}e^{-i\vec{p} \cdot \vec{r}/\hbar}\Psi(\vec{r};t)d\vec{r}=\mathscr{F}\{\Psi (\vec{r};t) \}$ .
La función $\Phi(\vec{p};t)$ se denomina función de ondas en el espacio de momentos, y su definición como transformada de Fourier $\mathscr{F}\{\Psi (\vec{r};t) \}$ es válida para cualquier función de ondas $\Psi(x;t)$ (es decir, no sólo para un paquete de ondas).
Su interpretación es: $\left|\Phi(\vec{p};t)\right|^2$ define una densidad de probabilidad de momento, por unidad de volumen:
Postulado: El cuadrado del valor absoluto de la función de onda en el espacio de momentos, $\left|\Phi(\vec{p};t)\right|^2$ , representa la densidad de probabilidad de que el resultado de un experimento de determinación del momento de la partícula sea: «momento $\vec{p}$ en el instante t». Esto es, $| \Phi(\vec{p},t)|^2$ como densidad de probabilidad de momento, por unidad de volumen.
Consecuentemente, la probabilidad de encontrar a la partícula en un elemento de volumen $d\vec{p}$ en el instante t viene dada por $| \Phi(\vec{p},t)|^2d\vec{p}$ ; la de encontrarla en una región V del espacio en t es $\int_V|\Phi(\vec{p},t)|^2d\vec{p}$ , supuesta la normalización $\int_{\mathbb{R}^3}\left|\Phi(\vec{p};t)\right|^2d\vec{p}=1$ (la probabilidad de determinar su momento situándola en algún punto de todo el espacio de momentos ha de ser la unidad).
Dimensiones de $\Phi$ : según la anterior condición de normalización, las dimensiones de la función de onda en el espacio de momentos, en el caso de un sistema compuesto por una sola partícula, deben ser de (momento) $^{-\frac{3}{2}}$ (esto es, $(MLT^{-1})^{-\frac{3}{2}}$ ), donde $L$ simboliza longitud, $M$ masa y $T$ tiempo. En general, la función de onda para un sistema de $N$ partículas, caso $d-$ dimensional, tiene dimensiones (momento) $^{-\frac{d\,N}{2}}$ .
Según el teorema de Parseval, si la función $\phi(\vec{p})=\Phi(\vec{r};t=0)$ está normalizada a la unidad, $\int_{\mathbb{R}^3}\left|\phi(\vec{p})\right|^2d\vec{p}=1$ , se implica que la función $\psi(\vec{r})=\Psi(\vec{r};t=0)$ también lo está, y además permanece normalizada durante su evolución temporal:
$\int_{\mathbb{R}^3}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=1 \; \forall t$ .
Este hecho establece la conservación de la probabilidad, que se produce también en el espacio de momentos,
$\int_{\mathbb{R}^3}\left|\Phi(\vec{p};t)\right|^2d\vec{p}=1 \; \forall t$ .

Referencias

[BOH-89] Bohm, D.; Quantum Theory; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; Quantum Mechanics; 2nd ed., Pearson; Dorchester, 2000.

[GAL-89] Galindo, A. y Pascual, P.; Mecánica Cuántica, Eudema, 1989.

[JAM-74] Jammer, M.; The philosophy of Quantum Mechanics, Wiley, 1974.

[MEH-82] Mehra, J., Rechenberg, H.; The Historical Development of Quantum Mechanics, 6 vol., Springer-Verlag, Nueva York, 1982.

[NEU-91] Neumann, J. von; Fundamentos matemáticos de la Mecánica Cuántica, CSIC, Raycar, Madrid, 1991.

[WHE-83] Wheeler, J.A. y Zurek, W.H., ed.; Quantum Theory and measurement, Princeton Univ., Princeton, 1983.

Páginas complementarias

Velocidad de grupo y de fase; el índice de refracción no tiene que ser siempre mayor que 1

http://physics.oregonstate.edu/~roundyd/COURSES/ph365x/366.html

http://la-mecanica-cuantica.blogspot.com.es/2009/08/la-particula-libre-i.html

http://la-mecanica-cuantica.blogspot.com.es/2009/08/la-particula-libre-ii.html

https://eva.fing.edu.uy/pluginfile.php/49091/mod_resource/content/0/materiales/PaquetesDeOndas.pdf

http://www.met.reading.ac.uk/pplato2/h-flap/phys10_3.html

http://scientificsentence.net/Waves/index.php?key=yes&Integer=wave_packets

Ondas en un medio dispersivo

Sobre el «Zitterbewegung»: https://cuentoscuanticos.com/2011/12/03/zitterbewegung/

APPS

Velocidad de fase y velocidad de grupo

The red dot moves with the phase velocity, and the green dots propagate with the group velocity. In this deep-water case, the phase velocity is twice the group velocity. The red dot overtakes two green dots when moving from the left to the right of the figure. For surface gravity waves, the water particle velocities are much smaller than the phase velocity, in most cases. (Texto e imagen de: http://armanhayetasanoee.blogfa.com/post/7).

Simulación para la velocidad de grupo (mit.ocw.universia.net).

Universidad de St. Andrews: evolución temporal de un paquete de ondas gaussiano.

Wave packet spreading en mathematica.stackexchange.com

http://www.uco.es/hbarra/index.php/fc/appletsfc/77-gauss

http://www.uco.es/hbarra/index.php/fc/appletsfc/78-particula-libre

Wavepacket for a Free Particle from the Wolfram Demonstrations Project by Andrés Santos

Evolution of a Gaussian Wave Packet from the Wolfram Demonstrations Project by S. M. Blinder