Representaciones de posiciones y momentos

763px-quantum_mechanics_travelling_wavefunctions-604x270

El vector de estado y la función de onda

A cada sistema físico que se pretenda describir en el marco de la MC, se le hace corresponder un espacio de Hilbert $\mathscr{H}$ complejo y separable. Cada estado puro del sistema en un instante $t$ , en el que el sistema ha sido preparado de forma que el conocimiento predictivo sobre el mismo es máximo, se representa por un rayo unidad $\left|\Psi(t)\right\rangle_R \subset \mathscr{H}$ , o conjunto de vectores de norma unidad, integrado por diferentes vectores de estado o kets $\left| \psi(t)\right\rangle \in \mathscr{H}$ que difieren entre sí únicamente en factores de fase (escalares de norma unidad).
-El que la preparación del sistema en un estado puro sea maximal refiere al hecho de que se ha controlado el mayor número posible de observables compatibles: en el sentido de que la medida del correspondiente número máximo de magnitudes físicas compatibles independientes, sobre una colección de sistemas idénticos en ese mismo estado (puro) en ese instante $t$ , dará con certeza un resultado para cada uno; las medidas para los restantes observables sí presentarán dispersión.
-Nota: la recíproca no es cierta: no siempre los vectores de norma unidad del Hilbert representan un estado puro del sistema, ya que pueden existir reglas de superselección que restrinjan (véase [GAL-89]). Y es que, dado un vector del Hilbert combinación lineal arbitrario de otros, representativos éstos de estados puros del sistema, no siempre está asegurada la existencia de un C.C.O.C. que posibilite la preparación del sistema en un estado puro asociado a esa combinación lineal.
Cada estado puro, correspondiente a una preparación maximal del sistema físico, es autoestado de un C.C.O.C. o «conjunto completo de observables compatibles», integrado por observables que conmutan entre sí dos a dos: $[A,B]=AB-BA=0$ , donde $A$ y $B$ son los operadores autoadjuntos que representan a los dos observables en el formalismo. Se trata, en consecuencia, de observables medibles simultáneamente sobre el sistema con precisión arbitraria, por no estar ligados por una relación de indeterminación. La reunión de todos estos autoestados, bajo determinadas condiciones, permite construir una base ortonormal del espacio:
–Definición de conjunto completo de observables compatibles (C.C.O.C.): Dado un sistema físico al que, en el marco teórico de la mecánica cuántica en el espacio de Hilbert, se le ha asociado para su descripción un espacio de Hilbert $\mathcal{H}$ complejo y separable (postulado 1), se define como un C.C.O.C. un conjunto de observables $A_1,A_2\ldots$ , representados por los sendos operadores autoadjuntos $\hat{A}_1,\hat{A}_2\ldots$ (postulado 2), tales que:
1. Los operadores son todos compatibles entre sí, es decir, conmutan dos a dos: $[A_1,A_2]=0$ , al menos sobre un conjunto denso en el espacio.
2. La diagonalización simultánea de todos ellos produce una base de autofunciones comunes que es única en el espacio, es decir, cada elemento de la base queda fijado, salvo fase.
3. El sistema no es redundante, es decir, si se elimina cualquiera de los observables, el sistema pierde la condición de C.C.O.C.
-Cada vector $|\psi>$ de la base queda completamente caracterizado por el conjunto de todos los valores propios con que satisface que la ecuación de autovalores para todos los observables del C.C.O.C., por lo que suele recurrirse a la notación:
$|\psi> \equiv |a_1,a_2\ldots > \quad, \quad A_i |a_1,a_2 \ldots> =a_i |a_1,a_2 \ldots> \; i=1,2\ldots$ .
La función de onda: dado un sistema físico y un C.C.O.C., $\{ A,B,C\ldots \}$ , la base ortonormal asociada, $\{|a,b,c\ldots >\}$ , integrada por los correspondientes vectores propios comunes (las soluciones de $A\, |a,b,c\ldots >=a \,|a,b,c\ldots >$ , etc.), permite expresar la «función de onda en la representación asociada a esa base»,
$\psi(a,b,c\ldots;t) \, \doteq \, < a,b,c\ldots| \psi(t) >$ ,
conjunto de escalares (complejos) obtenidos cuando las variables $a,b,c\ldots$ recorren los sendos espectros de los operadores del C.C.O.C.:
$| \psi(t) >=\sum_{a,b,c\ldots} \psi(a,b,c\ldots;t)|a,b,c\ldots >$
donde $\psi(a,b,c\ldots;t) \in \mathbb{C} \, ; \, a \in \sigma(A)\, , \, b \in \sigma(B)\, , \, c \in \sigma(C) \ldots$ .
-Nota: obsérvese que, conocido el C.C.O.C. y su base ortonormal asociada, construir una función de onda específica requiere fijar las fases de los vectores de la base.

Representaciones de posiciones y momentos

Consideremos una partícula sin espín. Los tres operadores lineales autoadjuntos $\{x_{op},y_{op},z_{op}\}$ , componentes del operador posición $\vec{r}_{op}$ , conmutan entre sí dos a dos y forman un conjunto completo de observables compatibles (C.C.O.C.), ya que determinar la posición de la partícula determina su estado (y el conjunto no es redundante pues eliminar cualquiera de los tres operadores le hace perder su carácter de completo).
Puesto que integran un C.C.O.C., los tres operadores pueden ser diagonalizados simultáneamente, esto es, existe una base ortonormal del espacio formada por vectores propios comunes a todos ellos, caracterizables de forma única salvo fase como $\left. \left| x,y,z \right.\right\rangle$ , donde se han simbolizado los respectivos valores propios, es decir:
$x_{op} \left. \left| x,y,z \right.\right\rangle = x \left. \left| x,y,z \right.\right\rangle$ ,
$y_{op} \left. \left| x,y,z \right.\right\rangle = y \left. \left| x,y,z \right.\right\rangle$ ,
$z_{op} \left.\left| x,y,z \right.\right\rangle =z \left. \left| x,y,z \right.\right\rangle$ ,
teniéndose debido a la completitud del conjunto que la dimensión del subespacio asociado a cada valor propio es la unidad (partícula sin espín).
Estos kets $\left. \left| x,y,z \right.\right\rangle$ representan estados en los que se prepara al sistema de forma que se tiene información maximal sobre el C.C.O.C., y se denominan estados puros. En definitiva, representan estados sobre los que es posible medir simultáneamente sin dispersión en los resultados todos los observables del C.C.O.C.
Nota: para una discusión rigurosa, puede verse [GAL-89], pp. 86ss.; el hecho es que, en pleno rigor matemático, la base ortonormal común a dos observables compatibles puede afirmarse como libre de dispersión para ambos sólo para operadores acotados y con espectro puramente puntual; por otra parte, por razones experimentales prácticas, así resultan ser los observables en los laboratorios. Además, para operadores autoadjuntos generales la base ortonormal podrá incluir funciones generalizadas.
La función de onda en representación de posiciones corresponde a la expresión del estado puro $\left|\Psi (t)\right>\in \mathscr{H}$ en la anterior base ortonormal, constituida por todos los autovectores simultáneos $\{\left|\vec{r}\right>\}$ (fases por fijar) del operador posición $\vec{r}_{op}$ .
-Recordemos que el espectro de cada componente $r_{iop}$ es continuo y llena $\mathbb{R}$ :
$\vec{r}_{op} \ | \vec{r} > = \vec{r} \ | \vec{r} > \; ; \; \vec{r}_{op} : \mathscr{H} \rightarrow \mathscr{H} \; ; \; \sigma(\vec{r}_{op})=\mathbb{R}^3 \; ; \;| \vec{r} > \in \mathcal{H}\; ; \; \vec{r} \in \mathbb{R}^3$
-Por tanto: la función de onda representativa del estado puro $\left|\Psi (t)\right>$ en la anterior base ortonormal, o función de onda en representación de posiciones, $\Psi (\vec{r};t)$ , viene dada por:
$\Psi (\vec{r};t)=\left\langle \vec{r} \left|\Psi(t)\right.\right\rangle \quad , \; \left\langle \vec{r} \left|\Psi(t)\right.\right\rangle \in \mathbb{C}$ ,
donde $\left. \left| \vec{r}\right.\right\rangle$ representa los autoestados del operador posición y $\vec{r}$ representa los distintos puntos del espacio $\mathbb{R}^3$ , que son los autovalores del operador posición.
-Es decir, la función de onda en representación de posiciones «es» («queda definida por») el conjunto de escalares $\{\Psi (\vec{r};t)=\left\langle \vec{r} \left|\Psi(t)\right.\right\rangle \} \subset \mathbb{C}$ ,
que constituyen el recorrido de una función compleja $\Psi$ definida sobre $\mathbb{R}^3$ , función que denominaremos como la función de onda en representación o espacio de posiciones.
-El conjunto de escalares $\{ \left\langle \vec{r} \left|\Psi(t)\right.\right\rangle \} \subset \mathbb{C}$ , esto es, de los coeficientes del anterior desarrollo en la base ortonormal del espacio integrada por las autofunciones comunes a todos los operadores del C.C.O.C. $\{ \vec{r}_{op.} \}$ (partícula sin espín), definen (constituyen el recorrido de) la función de onda, cuyo dominio en esta representación es $\mathbb{R}^3$ :
$\Psi \ : \ \mathbb{R}^3 \rightarrow D(\Psi) \subset \mathbb{C}$ ,
función tal que, en cada punto de su dominio, asocia el valor según:
$\Psi(\vec{r},t) \, = \, \left\langle \vec{r} \left|\Psi(t)\right.\right\rangle$
( $t$ representa un parámetro temporal, que no es formalizado como observable).
-En definitiva:
$\left. \left|\Psi(t)\right.\right\rangle \in \mathscr{H}\quad ; \; \Psi (\vec{r};t)=\left\langle \vec{r} \left|\Psi(t)\right.\right\rangle \quad ; \; \{\Psi (\vec{r};t)=\left\langle \vec{r} \left|\Psi(t)\right.\right\rangle \;\,$ , $\vec{r} \in \mathbb{R}^3 \} \subset \mathbb{C} \; ; \; \Psi \in L^2(\mathbb{R}^3)$
-En otras palabras, el espacio de Hilbert $\mathscr{H}$ queda realizado en representación de posiciones como el Hilbert de las funciones complejas (recorrido en $\mathbb{C}$ ) definidas (con dominio) en $\mathbb{R}^3$ y de cuadrado integrable Lebesgue, el espacio de Hilbert funcional $L^2(\mathbb{R}^3)$ .
Propiedades e interpretación de la función de onda :
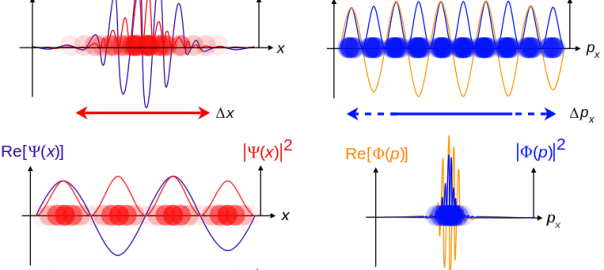
1. La densidad de probabilidad $\rho(\vec{r};t)=\left|\Psi(\vec{r};t)\right|^2$ se interpreta:
  $\rho(\vec{r};t)\,d\vec{r} =\left|\Psi(\vec{r};t)\right|^2\,d\vec{r}$
  representa la probabilidad de que al medir la posición de la partícula en el instante $t$ se encuentre como resultado su localización en un volumen $d\vec{r}$ alrededor de la posición $\vec{r}$ .
2. Normalización: $\int_{\mathbb{R}^3}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=1$ .
3. En representación de posiciones, la actuación de los operadores $r_{iop}$ , $\vec{r}_{op}$ , consiste simplemente en realizar una multiplicación:
  $(r_{iop}\Psi)(\vec{r};t)=r_i\Psi(\vec{r};t)$ ,
  $(\vec{r}_{op}\Psi)(\vec{r};t)=\vec{r}\,\Psi(\vec{r};t)$ .
4. El dominio de actuación de cada operador $r_{iop}$ está formado (cf. [GAL-89], vol. I, p. 126) por todas las funciones de $L^2(\mathbb{R}^3)$ tales que $\int_{\mathbb{R}^3} |r_i|^2\ | \Psi (\vec{r}) |^2 d \vec{r} <\infty$ .
5. En una dimensión, la ecuación de autovalores $r_{iop} \left. \left| r_i \right.\right\rangle = \lambda \left. \left| r_i \right.\right\rangle$ , esto es, $(r_{iop}\Psi)(r_i)=r_i\Psi(r_i)$ , donde $\Psi (r_i) \in D(r_{iop})$ , tiene la solución (en sentido de distribuciones): $\Psi_{\lambda}(r_i)=N\ \delta (r_i-\lambda)$ , donde $\lambda$ representa los autovalores de posición y $r_i=x, y, z$ .
Dimensiones de $\Psi$ : según la anterior condición de normalización, las dimensiones de la función de onda en el espacio de posiciones o configuración, en el caso de un sistema compuesto por una sola partícula, deben ser $L^{-\frac{3}{2}}$ , donde $L$ simboliza longitud. En general, la función de onda para un sistema de $N$ partículas, caso $d-$ dimensional, tiene dimensiones $L^{-\frac{d\,N}{2}}$ .
La función de ondas no es en general una función $f(\vec{r})$ sobre el espacio usual tridimensional: es una función sobre el espacio de configuración, que resulta ser isomorfo al espacio usual tridimensional sólo en el caso del sistema constituido por una partícula (espín aparte). En general, para un sistema de $N$ partículas, la función de ondas $\Psi(\vec{r}_1,\ldots,\vec{r}_N)$ posee un dominio de definición que se incluye en un espacio de $3\,N$ dimensiones.
Además, ha de tenerse en cuenta que, contra lo que se creyó en el inicio del desarrollo del formalismo cuántico, en realidad el C.C.O.C. integrado por los tres operadores lineales autoadjuntos $\{x_{op},y_{op},z_{op}\}$ , componentes del operador posición $\vec{r}_{op}$ , debe ser completado con el correspondiente operador adicional de espín, observable independiente a los tres antes considerados. Es decir, que para el caso de una partícula, en realidad la dimensión del subespacio asociado a cada valor propio del conjunto de componentes no es la unidad, sino $2$ , algo que queda manifiesto en fenómenos experimentales como el efecto Zeeman no clásico o el Stern-Gerlach, y un verdadero C.C.O.C. para una partícula será (por ejemplo) el conjunto $\{x_{op},y_{op},z_{op},S_z\}$ o, en notación vectorial, $\{ \vec{r}_{op},S_z\}$ , donde $S_z$ representa la tercera componente del operador espín de la partícula, un momento angular intrínseco sin análogo clásico.
Alternativamente, para una partícula sin espín puede considerarse el C.C.O.C. integrado por los tres operadores lineales autoadjuntos $\{p_{xop},p_{yop},p_{zop}\}$ , componentes del operador momento $\vec{p}_{op}$ , puesto que también conmutan entre sí dos a dos y forman un conjunto completo de observables compatibles (C.C.O.C.), ya que determinar el momento de la partícula determina su estado (y el conjunto no es redundante pues eliminar cualquiera de los tres operadores le hace perder su carácter de completo).
Puesto que integran un C.C.O.C., los tres operadores pueden ser diagonalizados simultáneamente, esto es, existe una base ortonormal del espacio formada por vectores propios comunes a todos ellos, caracterizables de forma única salvo fase como $\left. \left| p_x,p_y,p_z \right.\right\rangle$ , donde se han simbolizado los respectivos valores propios, es decir:
$p_{xop} \left. \left| p_x,p_y,p_z \right.\right\rangle = p_x \left. \left| p_x,p_y,p_z \right.\right\rangle$ ,
$p_{yop} \left. \left| p_x,p_y,p_z \right.\right\rangle = p_y \left. \left| p_x,p_y,p_z \right.\right\rangle$ ,
$p_{zop} \left.\left| p_x,p_y,p_z \right.\right\rangle =p_z \left. \left| p_x,p_y,p_z \right.\right\rangle$ ,
teniéndose debido a la completitud del conjunto que la dimensión del subespacio asociado a cada valor propio es la unidad (partícula sin espín).
Estos kets $\left. \left| p_x,p_y,p_z \right.\right\rangle$ representan estados en los que se prepara al sistema de forma que se tiene información maximal sobre el C.C.O.C., y se denominan estados puros. En definitiva, representan estados sobre los que es posible medir simultáneamente (idealmente) sin dispersión en los resultados todos los observables del C.C.O.C.
La función de onda en representación de momentos corresponde a la expresión del estado puro $\left|\Psi (t)\right>\in \mathscr{H}$ en la anterior base ortonormal, constituída por todos los autovectores simultáneos $\{\left|\vec{p}\right>\}$ (fases por fijar) del operador momento $\vec{p}_{op}$ (el espectro de cada $p_{iop}$ es continuo y llena $\mathbb{R}$ ).
Por tanto: la función de onda representativa del estado puro en la anterior base ortonormal, o función de onda en representación de momentos, , viene dada por () , donde representa los autoestados del operador momento y representa los distintos puntos del espacio . Es decir, la función de onda en representación de momentos es el conjunto de escalares . En otras palabras, el espacio de Hilbert queda realizado en representación de momentos como el Hilbert .
1. La densidad de probabilidad $\rho(\vec{p};t) =\left|\Phi(\vec{p};t)\right|^2$ se interpreta de modo que $\rho(\vec{p};t)\,d\vec{p} =\left|\Phi(\vec{p};t)\right|^2\,d\vec{p}$ representa la probabilidad de que al medir el momento de la partícula en el instante $t$ se encuentre como resultado su localización en un volumen $d\vec{p}$ alrededor del valor $\vec{p}$ .
2. Normalización: $\int_{\mathbb{R}^3}\left|\Phi(\vec{p};t)\right|^2d\vec{p}=1$ .
3. En representación de momentos, la actuación de los operadores $p_{iop}$ , $\vec{p}_{op}$ , consiste simplemente en realizar una multiplicación:
  $(p_{iop}\Phi)(\vec{p};t)=p_i\Phi(\vec{p};t)$ ,
  $(\vec{p}_{op}\Phi)(\vec{p};t)=\vec{p}\,\Phi(\vec{p};t)$ .
4. El dominio de actuación de cada operador $p_{iop}$ está formado (cf. [GAL-89], vol. I, p. 126) por todas las funciones de $L^2(\mathbb{R}^3)$ tales que la $-i\hbar \nabla_i \Psi \in L^2(\mathbb{R}^3)$ (distribución), es decir, $\int_{\mathbb{R}^3} |\nabla_i \Psi (\vec{r}) |^2 d \vec{r} <\infty$ .
5. La ecuación de autovalores $(p_x\psi)(x)=-i\hbar \frac{\partial \psi(x)}{\partial x} =\lambda \psi(x)$ , donde $\psi (x) \in D(p_x)$ , tiene la solución (en sentido de distribuciones): $\psi_{\lambda}(x)=N\ e^{i \lambda \frac{x}{\hbar}}$ , donde $\lambda$ representa los autovalores de momento.
6. Como antes se comentó para la representación de posiciones, para el caso de una partícula, en realidad la dimensión del subespacio asociado a cada valor propio del conjunto de componentes del momento no es la unidad, sino $2$ : un verdadero C.C.O.C. para una partícula será (por ejemplo) el conjunto $\{p_{xop},p_{yop},p_{zop},S_z\}$ o, en notación vectorial, $\{ \vec{p}_{op},S_z\}$ , donde $S_z$ representa la tercera componente del operador espín de la partícula, un momento angular intrínseco sin análogo clásico.
7. Dimensiones de $\Phi$ : según la anterior condición de normalización, las dimensiones de la función de onda en el espacio de momentos, en el caso de un sistema compuesto por una sola partícula, deben ser de $(momento)^{-\frac{3}{2}}$ ( $(MLT^{-1})^{-\frac{3}{2}}$ ), donde $L$ simboliza longitud, $M$ masa y $T$ tiempo. En general, la función de onda en representación de momentos para un sistema de $N$ partículas, caso $d-$ dimensional, tiene dimensiones $(momento)^{-\frac{d\,N}{2}}$ .
La relación entre las funciones de onda en cada una de las dos bases la da la matriz del cambio de base, de elementos $\left\langle \vec{r} \left|\vec{p}\right.\right\rangle$ ; una vez determinados se establece que la relación entre las dos funciones de onda, en el espacio de posiciones $\Psi(\vec{r};t)$ y en el espacio de momentos $\Phi(\vec{p};t)$ , viene dada por la transformada de Fourier:
$\Psi(\vec{r};t)=\frac{1}{(2\pi \hbar)^{\frac{3}{2}}}\int_{\mathbb{R}^3}e^{i\vec{p}\cdot \vec{r}/\hbar}\Phi(\vec{p};t)d\vec{p}=\mathscr{F}^{-1}\{\Phi (\vec{p};t) \}$ ,
$\Phi(\vec{p};t)=\frac{1}{(2\pi \hbar)^{\frac{3}{2}}}\int_{\mathbb{R}^3}e^{-i\vec{p} \cdot \vec{r}/\hbar}\Psi(\vec{r};t)d\vec{r}=\mathscr{F}\{\Psi (\vec{r};t) \}$ .

APÉNDICE A: ESPACIO DUAL Y NOTACIÓN DE DIRAC

Espacio dual; funcionales; notación de Dirac; distribuciones.

APÉNDICE B: TEORÍA ESPECTRAL

Introducción a la teoría espectral.

Espectro de operadores

Familia de operadores $T - \lambda I$ : Dado un operador lineal $T$ en un espacio de Hilbert $\mathscr {H}$ , se define la familia no numerable de operadores $T - \lambda I$ , donde $\lambda$ es un número complejo arbitrario e $I$ es el operador identidad; es evidente que $D(T) = D(T-\lambda I)$ .
Esta familia de operadores $T_{\lambda}\equiv (T-\lambda I)$ permitirá la clasificación de los diferentes valores $\lambda$ del plano complejo ${\mathbb C}$ , en función de la existencia y características del operador lineal inverso $T_{\lambda}^{-1}\equiv(T - \lambda I)^{-1}$ , cuyo dominio es el rango o recorrido del correspondiente operador directo $T_{\lambda}$ .
Resolvente de un operador lineal: Todos los valores $\lambda \in {\mathbb C}$ para los que existe el operador lineal inverso $T_{\lambda}^{-1}$ , su dominio es denso en $\mathscr {H}$ y, además, es operador acotado, se dice que pertenecen al conjunto resolvente del operador $T$ , $\rho(T)$ , y se definen como valores o puntos regulares.
Espectro de un operador lineal: Todos los números complejos que no pertenecen al resolvente de $T$ se dice que pertenecen a su espectro, $\sigma(T)$ , denominándose valores o puntos espectrales.
Se tiene pues:
${\mathbb C} = \rho(T) \cup \sigma(T) \,$ .
Topológicamente, el resolvente $\rho(T)$ es un conjunto abierto, mientras que el espectro $\sigma(T)$ es un conjunto cerrado.
Partes puntual, continua y residual del espectro de un operador lineal:
El espectro de un operador lineal se compone de tres conjuntos, disjuntos dos a dos:
1. Espectro puntual: Se dice que el escalar $\lambda$ pertenece al espectro puntual de $T$ , $\lambda \in \sigma_p(T)$ , si no existe el operador lineal inverso del $T-\lambda I$ . Esto implica que $\exists ~f \in D(T), ~f \neq 0$ , que cumple
  $(T- \lambda I) f = 0 \Rightarrow Tf = \lambda f, ~~f \in D(T), ~~f \neq 0 \,$ .
  A $\lambda$ se le llama autovalor o valor propio y a $f$ autovector, autofunción o vector propio, con valor propio $\lambda$ . La ecuación $Tf = \lambda f$ se denomina ecuación de autovalores.
2. Puede ocurrir que para un autovalor $\lambda$ existan diferentes vectores propios linealmente independientes, $f_{\lambda,k}, \ k=1,\ldots,n_\lambda$ ; se dice entonces que $\lambda$ tiene multiplicidad $n_\lambda$ o, equivalentemente, que es un autovalor degenerado con degeneración $n_\lambda$ .
3. Espectro continuo: Se dice que el escalar $\lambda$ pertenece al espectro continuo de $T$ , $\lambda \in \sigma_c(T)$ , si existe el operador lineal inverso del $T-\lambda I$ , su dominio es denso en $\mathscr {H}$ y no es operador acotado.
4. Espectro residual: Se dice que el escalar $\lambda$ pertenece al espectro residual de $T$ , $\lambda \in \sigma_r(T)$ , si existe el operador lineal inverso del $T-\lambda I$ y su dominio no es denso en $\mathscr {H}$ .
El espectro del operador $T$ es la unión del espectro puntual, continuo y residual:
$\sigma(T) = \sigma_p(T)\cup \sigma_c(T) \cup \sigma_r(T)\,$ .
Autovalor o valor propio generalizado: Dado $\lambda \in \mathbb {C}$ , se define como autovalor o valor propio generalizado cuando existe en el dominio de $T$ una sucesión de vectores unitarios $g_n$ , $\left\|g_n \right\| =1$ , que cumplen la ecuación:
$\lim_{n \rightarrow \infty} (T - \lambda I) g_n ~=~ 0 \,$ .
Todo autovalor es un valor propio generalizado caracterizado por una sucesón constante, $g_n=f$ , donde $f$ es un vector propio unitario, pero el recíproco no tiene por qué ser cierto.
En un espacio de Hilbert:
1. Todo valor propio generalizado de un operador pertenece a una parte de su espectro (puntual, continuo o residual).
2. Pueden existen valores del espectro de un operador que no sean caracterizables como valores propios generalizados; si existen, pertenecen al espectro residual.
3. Todos los puntos del espectro puntual y del continuo, $\lambda \in \sigma_p(T)\cup \sigma_c(T)$ , son valores propios generalizados, es decir, siempre puede encontrarse una sucesión de vectores $g_n$ que cumple la definición.

Espectro de operadores especiales

En un espacio de Hilbert (recuérdese que siempre estamos considerando operadores con dominio denso en un $\mathscr{H}$ complejo y separable):

El espectro de un operador lineal acotado, que es no vacío, está formado por valores $\lambda$ tales que $\left|\lambda \right| \leq \left\| T \right\|$ .
Si el espacio es de dimensión finita, los operadores lineales, que son todos acotados, sólo tienen espectro puntual, $\sigma(T) = \sigma_p(T)$ .
El espectro de un operador cerrado está relacionado con el espectro de su operador adjunto. Se cumplen las siguientes implicaciones:
1. $\lambda \in \rho(T) \Leftrightarrow \lambda^* \in \rho(T^+)$
2. $\lambda \in \sigma_p(T) \Rightarrow \lambda^* \in \sigma_p (T^+) \cup \sigma_r(T^+)$
3. $\lambda \in \sigma_r(T) \Rightarrow \lambda^* \in \sigma_p (T^+)$
4. $\lambda \in \sigma_c(T) \Leftrightarrow \lambda^* \in \sigma_c (T^+)$
Si dos operadores son unitariamente equivalentes (es decir, existe un operador unitario, $U$ , tal que $B= U^+AU$ ), entonces el espectro puntual, el espectro continuo y el espectro residual de $B$ coinciden con los de $A$ . En particular, cualquier autovalor generalizado de $B$ también lo es de $A$ .
El espectro residual de un operador hermítico acotado, nomal acotado, unitario o autoadjunto es vacío.
El espectro de un operador unitario está integrado por números complejos de módulo unidad.
El espectro de un proyector ortogonal sólo tiene parte puntual, teniéndose para $P \neq 0,I$ que $\sigma (P)=\sigma_p (P)=\left\{0,1\right\}$ , de forma que todos los restantes números complejos son puntos regulares.
Un operador hermítico tiene su espectro puntual y continuo confinados en la recta real pero, sin embargo, puede tener un espectro residual no vacío, aunque siempre con valores no reales. En este caso, bien el semiplano superior, bien el inferior, bien los dos simultáneamente pertenecen al espectro residual.
Para un operador hermítico (y, por serlo, válido también para operadores esencialmente autoadjuntos y autoadjuntos), se tiene:
1. $\sigma_p(T) \cup \sigma_c(T) \subset \mathbb{R}$ .
2. Definidos
  $m(T)={\mbox{inf}}_{\left\|x\right\|=1}\left\langle x,Tx\right\rangle \geq -\infty \;$ ,
  $M(T)={\mbox{sup}}_{\left\|x\right\|=1}\left\langle x,Tx\right\rangle \leq +\infty \;$ ,
  entonces $m(T)\leq \lambda \leq M(T)\;$ $\forall \lambda \in \sigma_p(T)$ .
3. Para operadores hermíticos acotados, $m(T)$ y $M(T)$ son siempre finitos y pertenecen al espectro.
Para un operador autoadjunto en un espacio de Hilbert:
1. El espectro residual es vacío; por tanto, su espectro sólo posee partes puntual y continua: $\sigma(T) = \sigma_p(T) \cup \sigma_c(T)$ .
2. El espectro está confinado en la recta real: $\sigma(T) \subset \mathbb{R}$ .
3. Todo punto espectral bien es autovalor, $\lambda \in \sigma_p(T)$ , bien pertenece a la parte continua del espectro, $\lambda \in \sigma_c(T)$ , siendo entonces valor propio generalizado.
Para un operador en un espacio de Hilbert , respecto al espectro puntual (valores que resuelven la ecuación de autovalores):
1. Sea $\lambda$ un valor propio $\in \sigma_p(T)$ ; consideradas todas las autofunciones $f_{\lambda,k}$ linealmente independientes asociadas a $\lambda$ , se demuestra que la variedad lineal formada por combinación lineal de estas autofunciones, $M_\lambda <H$ , tiene estructura de subespacio de Hilbert, $M_\lambda \triangleleft H$ , y se denomina subespacio propio.
2. Dentro de un subespacio propio $M_\lambda \triangleleft H$ , las autofunciones linealmente independientes $f_{\lambda,k}, ~ k=1,...,n_\lambda$ , pueden ortonormalizarse, dando lugar a un conjunto de funciones $g_{\lambda,k}\ , \, k=1,...,n_\lambda$ , que constituyen una base ortonormal numerable (b.o.n.) de dicho subespacio ( $\left\langle g_{\lambda,k} \, | \, g_{\lambda,k^{\prime}} \right\rangle= \delta_{k,k^{\prime}}$ )
  (requiere espacio de Hilbert separable, uno de los supuestos aquí).
3. Si $\lambda$ y $\lambda^{\prime}$ son valores propios distintos de $T$ ( $\lambda \neq\lambda^{\prime}$ ), entonces $M_\lambda \bot M_{\lambda^{\prime}}$ , es decir, autofunciones asociadas a valores propios distintos son ortogonales entre sí.
Para un operador autoadjunto en un espacio de Hilbert, el conjunto de funciones propias asociadas a los autovalores del espectro puntual constituye un conjunto ortonormal, donde cada función está asociada a un autovalor:
$\left\langle \,g_{\lambda ,k} \right. \left| \left. \,g_{\lambda^{ \prime},k^{\prime}} \right\rangle \right. \,=\, \delta_{\lambda,\lambda^{\prime}} \delta_{k,k^{\prime}}$
Si el espacio es de dimensión finita, el conjunto anterior constituye una base ortonormal del mismo.
Para un operador $A \in {\cal A}(\mathscr {H})$ que sea compacto, autoadjunto y no singular (es decir, $0 \notin \sigma_p(A)$ ), el conjunto ortonormalizado de vectores propios de $A$ es base ortonormal de $\mathscr {H}$ .
El especial interés de los operadores autoadjuntos reside en que representan a los observables de un sistema físico en el formalismo matemático de la Mecánica Cuántica en espacios de Hilbert.