FÍSICA MATEMÁTICA
Introducción
- Las Matemáticas son “el lenguaje de la ciencia”, un lenguaje que es esencialmente de naturaleza relacional: sus objetos son símbolos abstractos que se agrupan en conjuntos y se relacionan. Es fundamental, pues, el estudio de las diversas estructuras:
- Algebraicas (y su composición).
- Analíticas: como las analíticas (concepto básico: el entorno) y medibles (concepto básico: la extensión).
- Ejemplo: dado
, podemos considerarlo:
- estructura algebraica: espacio lineal conmutativo, con división de primer orden…
- estructura topológica: espacio métrico completo, separable, local y simplemente conectado, localmente compacto…(1-espacio euclídeo).
- estructura con medida: espacio medible completo, totalmente σ-finito….
- Disponemos de posibilidades variadas de combinación de los distintos tipos de estructuras:
- componer algebraicamente estructuras topológicas: Topologías algebraicas.
- superponer estructuras topológica y/o de medida a un sistema algebraico: Álgebras topológicas ( Análisis Funcional).
- Lo que haremos: superponer una estructura topológica a un sistema algebraico, estudiando:
- El Álgebra topológica o Análisis Funcional.
- Las aplicaciones (maps) sobre espacios con estructuras algebraicas y analíticas combinadas: Teoría de Operadores.
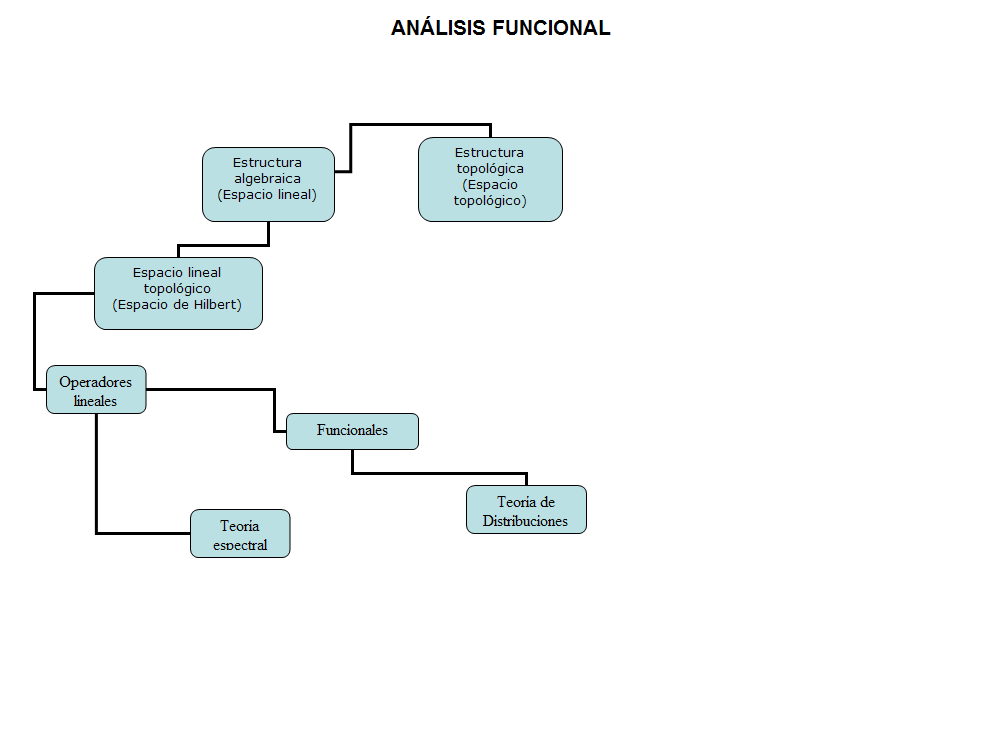
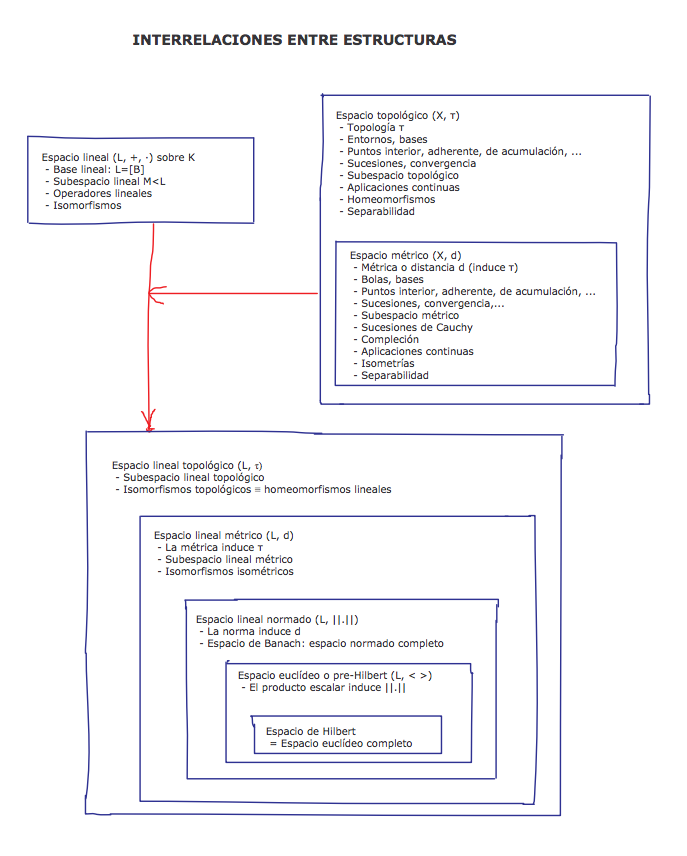
- La siguiente figura nos presenta las interrelaciones entre los temas que vamos a estudiar:
Espacios de Hilbert
-
Introducción
-
Espacios topológicos y métricos. Espacios lineales normados. Espacios de Banach.
- Espacios topológicos y métricos.
- Norma y espacio lineal normado.
- Operadores lineales continuos. Norma de un operador.
- Espacio de Banach.
-
Espacios euclídeos y de Hilbert.
- Producto escalar.
- Ortogonalidad y ortonormalidad.
- Separabilidad.
- Espacios de Hilbert:
- Teorema de proyección ortogonal. Aproximación óptima.
- Teorema de Riesz-Fisher.
- Separabilidad.
-
Espacios funcionales.
- La integral de Lebesgue.
- Espacios
.
- Bases ortonormales.
-
Operadores lineales.
- Operadores continuos; cerrados.
- Funcionales.
- Topologías.
- Adjunto de un operador.
- Proyectores.
- Operadores positivos; normales; compactos.
-
Funcionales y Distribuciones.
-
Teoría espectral. Mecánica Cuántica.
Bibliografía
- L. Abellanas y A. Galindo, Espacios de Hilbert, Eudema, 1987.
- S. K. Berberian, Introducción al espacio de Hilbert, Teide, 1977.
- P. García González, J. E. Alvarellos Bermejo y J. J. García Sanz, Introducción al formalismo de la mecánica cuántica, U.N.E.D., Madrid, 2001.
- G. Helmberg, Introduction to spectral theory in Hilbert space, North Holland, 1969.
- R. P. Kanwall, Generalized functions (theory and technique), Academic Press, 1983.
- N. Kolmogórov y S,V, Fomín, Elementos de la teoría de funciones y del análisis funcional, M.I.R., 1975.
- E. Romera Gutiérrez, M. C. Boscá Díaz-Pintado, F. Arias de Saavedra Alías, F. J. Gálvez Cifuentes, J. I. Porras Sánchez; Métodos Matemáticos: Problemas de Espacios de Hilbert, Operadores lineales y Espectros; Paraninfo; 2013.
- R.D. Richtmyer, Principles of Advanced Mathematical Physics, vol. 1, Springer-Verlag, 1978.
- Roman, Some modern mathematics for physicists and other outsiders, vol. 2, Pergamon, 1975.
- A. Vera López y P. Alegría Ezquerra, Un curso de Análisis Funcional. Teoría y problemas, AVL, 1997.
Enlaces
- Una referencia histórica: F. Bombal, Los espacios abstractos y el Análisis Funcional:
http://www.mat.ucm.es/~bombal/Personal/Historia/espacios.pdf
Gracias por existir…