Momento angular de espín

El espín electrónico: bases experimentales

El modelo atómico de Sommerfeld, desarrollado en 1916 y que incorporaba correcciones relativistas, logró un acuerdo excelente en la justificación de la estructura fina observada de los niveles del espectro del átomo de Hidrógeno, ya descrita por Michelson en 1891 y que consiste en unos desdoblamientos observados para las líneas espectrales cuando se realizaban medidas espectroscópicas con creciente precisión. Sin embargo, la multiplicidad de los niveles en el modelo resultaba incorrecta, y tampoco logró explicar porque no se observaban todas las transiciones posibles, ni justificó correctamente las intensidades y polarizaciones de las líneas sí observadas. En cualquier caso, se ha llegado a calificar este éxito como de fortuito, en el sentido de que la fórmula correcta necesita incorporar el espín electrónico, un momento angular intrínseco sin análogo clásico postulado por S. Goudmit y G.E. Uhlenbeck en 1925, para explicar el efecto Zeeman anómalo (desdoblamiento de niveles atómicos en campos magnéticos débiles). Tras su desarrollo teórico-matemático riguroso por Pauli en 1927, Dirac formularía en 1928 en su ecuación mecánico-cuántica relativista para el electrón, en la que emerge del propio desarrollo el espín.
-Nota histórica: parece que la primicia de la concepción del espín, por meses, se debiera en realidad a R. Kronig, quien desistiera sin embargo de desarrollar su idea por la desfavorable opinión inicial de Pauli.
El modelo de Sommerfeld contenía también la predicción del fenómeno de la cuantización espacial, que consiste en que la dirección de $\vec{L}$ debe formar con el eje $OZ$ (en general, con cualquier dirección prefijada) sólo determinados ángulos (esto es: bajo medida, su proyección sobre una dirección arbitraria sólo puede proporcionar determinados resultados, fenómeno de la cuantización espacial). Puesto que el espacio es isótropo, esta cuantización que surge en el modelo carece de sentido físico hasta que no se marque experimentalmente una dirección en el espacio, por ejemplo aplicando un campo magnético. Esta predicción quedó confirmada experimentalmente en 1922 por O. Stern y W. Gerlach, vía la medida de momentos magnéticos atómicos, pero las observaciones experimentales sólo serían justificadas teóricamente por completo con la aplicación del concepto de espín, que resultaría ser la pieza ausente con la que se lograría entender por fin el resultado observado en el experimento. En efecto, al incorporar en el cálculo del momento angular total los espines de todos los electrones del átomo de Plata, añadiéndolos a los momentos angulares orbitales, resultaba que el momento angular total dependía sólo del espín del electrón de valencia. Introducida su adecuada cuantización, se justificó el resultado experimental observado.
Como se comentó anteriormente, el concepto de espín electrónico surgió en el contexto experimental del denominado efecto Zeeman «anómalo», o desdoblamientos de las líneas espectrales observados al situar los átomos en el seno de campos magnéticos de intensidades débiles, caso, en que se producen desdoblamientos de naturaleza diferente (efecto Paschen-Back para campos medios y Zeeman anómalo para campos débiles, éste descubierto por T. Preston) a los correspondientes a campos intensos, o efecto Zeeman normal, el único que logró ser explicado por la teoría clásica y los modelos pre-cuánticos como el de Sommerfeld. En el efecto Zeeman anómalo, cada línea espectral se desdobla de una manera que sólo encontrarían justificación en la teoría plenamente cuántica moderna, en que se incorpora el espín electrónico, nueva magnitud cuántica sin análogo clásico y para cuyo descubrimiento la experimentación relacionada con los distintos efectos Zeeman fue decisiva: tras su postulación en 1925, por Uhlenbeck y Goudmit, su incorporación al Hamiltoniano de interacción del momento magnético atómico con el campo magnético permitió por fin explicar teóricamente las correspondientes observaciones experimentales.
El espín finalizó conceptualizado como una propiedad más de la materia, no sólo de los electrones, de modo que las partículas se clasifican en dos grandes grupos:
1.Fermiones: partículas con espín semi-impar, como los hadrones protón y neutrón; los electrones, los quarks (todos ellos con espín $s=\frac{1}{2}$ )… Su comportamiento estadístico sigue la distribución de Fermi-Dirac y están sujetos al principio de exclusión de Pauli (1925): dos fermiones no pueden poseer todos sus números cuántico idénticos en el mismo sistema; sus funciones de onda son anti-simétricas bajo el intercambio de dos partículas. Por ejemplo, en el átomo de Helio neutro, que tiene dos electrones ligados, si el sistema está en el estado fundamental o más bajo en energía, los dos electrones tienen que ocupar los estados de menor energía (n=1, l=0: 1s), pero entonces han de tener espines (tercera componente) opuestos.
2. Bosones: partículas con espín nulo o entero: bosón de Higgs ( $s=0$ ), fotones ( $s=1$ ), partículas alpha (núcleos de He, $s=0$ ) , piones ( $s=0$ ), gravitón ( $s=2$ )… Su comportamiento estadístico sigue la distribución de Bose-Einstein; no están sujetos al principio de exclusión de Pauli y sus funciones de onda son simétricas bajo el intercambio de dos partículas.

El espín electrónico: definición y propiedades

El espín de un electrón es una magnitud física, un observable, representado en el formalismo matemático por el operador de momento angular $\vec{S}$ , un operador vectorial cuyo módulo vale $\hbar\sqrt{s(s+1)}=\hbar \frac{\sqrt{3}}{2}$ , ya que el número cuántico de espín $s$ tiene el valor $s=\frac{1}{2}$ para el electrón; sus dimensiones son pues las de un momento angular (es decir, momento lineal por distancia); es usual medirlo en unidades de la constante de Dirac o $h$ barrada, $\hbar=\frac{h}{2\pi}$ . 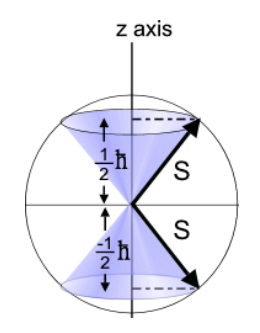Como momento angular que es, presenta un fenómeno de cuantización espacial, consistente para él ( $s=\frac{1}{2}$ ) en que, fijada una dirección arbitraria $\vec{n}$ en el espacio, que suele tomarse como eje $OZ$ , la medida de su proyección sobre esa dirección, o componente $S_z$ , sólo produce dos resultados:

Magnitud $+\frac{\hbar}{2}$ , apuntando en el sentido creciente del eje $OZ$ ; este resultado por convención se refiere como «hacia arriba» y se nota como $\uparrow$ . Se corresponde con las orientaciones del vector $\vec{S}$ con origen en $O$ y situadas sobre la superficie de un cono con vértice también en $O$ y eje a lo largo de la dirección positiva $OZ$ (según dirección $\vec{d}$ ). Algunas de estas posibles orientaciones se muestran dibujadas en la figura adjunta, cono superior.
Resultado análogo, de igual magnitud, pero correspondiente a la proyección apuntando en el sentido decreciente, $-\frac{\hbar}{2}$ , «hacia abajo», $\downarrow$ . En este caso, se corresponde con las orientaciones de $\vec{S}$ con origen en $O$ y sobre la superficie de otro cono similar al anterior, también con vértice $O$ y eje a lo largo de $OZ$ , pero ahora en sentido decreciente: enfrentado al anterior. Corresponde al cono inferior en la figura siguiente:

Únicas posibles orientaciones para el espín electrónico respecto a una dirección arbitraria d, marcada como eje OZ; se corresponden con las direcciones con origen en O y sobre la superficie de dos conos enfrentados por su vértice común en O. Todas proporcionan en su proyección sobre un eje OZ una longitud de magnitud $\hbar /2$ , pero una mitad con signo positivo (sentido creciente del eje) y la otra negativo (sentido decreciente); $\hbar$ representa la constante de Planck reducida o constante de Dirac, $\hbar=h/(2\pi)$ (imagen del libro «La realidad cuántica», de RBA ediciones, colección «Un paseo por el cosmos», núm. 32).

Únicas posibles orientaciones para el espín electrónico respecto a una dirección arbitraria d, marcada como eje OZ; se corresponden con las direcciones con origen en O y sobre la superficie de dos conos enfrentados por su vértice común en O. Todas proporcionan en su proyección sobre un eje OZ una longitud de magnitud $\hbar /2$ , pero una mitad con signo positivo (sentido creciente del eje) y la otra negativo (sentido decreciente); $\hbar$ representa la constante de Planck reducida o constante de Dirac, $\hbar=h/(2\pi)$ (imagen del libro «La realidad cuántica», de RBA ediciones, colección «Un paseo por el cosmos», núm. 32).

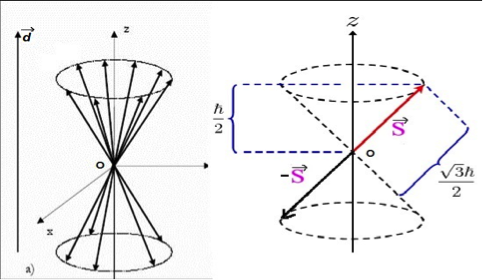
Así pues, en el formalismo cuántico, el electrón se describe como un «fermión», o partícula con un número cuántico de espín $s$ semi-impar (1/2, 3/2, etc.); en particular, al electrón le corresponde el valor $s=\frac{1}{2}$ .
Conforme al Principio de superposición aplicado al espín de un electrón, y dado que la ausencia de determinación de su proyección sobre una dirección cualquiera, marcada como OZ, conlleva que en la correspondiente función de onda se superponen todas las orientaciones con origen en O que se sitúan sobre la superficie de dos conos enfrentados por su vértice común en O (las únicas compatibles con el hecho de que, bajo medida de la componente $S_z$ , el resultado sea bien $+\frac{\hbar}{2}$ ( $\uparrow$ , «hacia arriba»), bien $-\frac{\hbar}{2}$ ( $\downarrow$ , «hacia abajo»). Es decir, que cuando se dice que «la tercera componente del espín tiene uno de los dos valores posibles $\hbar m_s=\pm \frac{\hbar}{2}$ , o, equivalentemente, que $\vec{S}$ es «paralelo» o «antiparalelo» al eje $OZ$ , lo que se está indicando es que ése es el valor promedio de una serie de medidas, sin que de ninguna manera se pueda suponer una orientación espacial fija de $\vec{S}$ . Por ello, una «representación figurativa» del espín electrónico nos lo podría mostrar en general como la siguiente figura borrosa:
El espín es una propiedad sin análogo clásico, es decir, no hay correlato en Física Clásica; para ella, simplemente, no existe. Así que, si lo ha leído alguna vez, olvídelo: el espín no tiene nada que ver con un momento angular de rotación de una partícula, aparte de compartir unidades.
La siguiente figura nos indica lo que sucede experimentalmente si hacemos pasar electrones por varios artilugios de tipo Stern-Gerlach de forma sucesiva:
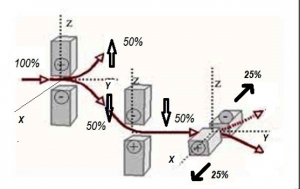
Medidas Stern-Gerlach sucesivas sobre electrones (imagen del libro «La realidad cuántica», de RBA ediciones, colección «Un paseo por el cosmos», número 32).
Tarea formal 1: ampliar el formalismo matemático para incluir en la descripción del sistema físico el observable espín. Esta tarea se culminará sustituyendo el espacio de Hilbert asociado (postulado primero) $\mathcal{H}$ en el caso sin espín por un espacio que pasa a tener la expresión matemática $L^2(\mathbb{R}^3) \otimes \mathbb{C}^{2s+1}$ , que es con frecuencia ejemplificada en las expresiones equivalentes:
$L^2(\mathbb{R}^3) \otimes \mathbb{C}^{2s+1} \backsimeq L^2(\mathbb{R}^3 \ , \ \mathbb{C}^{2s+1} )\backsimeq L^2(\mathbb{R}^3) \oplus L^2(\mathbb{R}^3) \oplus \cdots \oplus L^2(\mathbb{R}^3)$ ,
donde la última expresión nos ilustra que cada función de onda en el Hilbert asociado a un sistema sin espín va a ser reemplazada por un conjunto de $(2s+1)$ funciones, una entidad matemática que denominaremos como espinor.

Tarea formal 2: representar en el formalismo matemático las componentes del espín según los tres ejes coordenados ( $\vec{S}=\frac{\hbar}{2}\vec{\sigma}$ , donde $\vec{\sigma}$ representa las matrices de Pauli), y sumar vectorialmente los momentos angulares cuantizados orbital $\vec{L}$ y espín $\vec{S}$ (necesitaremos operar con los coeficientes de Clebsch-Gordan para el cambio entre vectores de las correspondientes bases).
Imagen de la Wikipedia.
Nota histórica: el espín sería justificado teóricamente por primera vez en 1928, cuando Dirac formuló la hoy conocida como «ecuación de Dirac», que surge en origen como una ecuación relativista para el electrón, desarrollada a partir de la ecuación de Klein-Gordon, la generalización relativista para la ecuación de Schrödinger de una partícula libre. Y ello porque la ecuación de Schrödinger, por sí sola, es incapaz de predecir un momento angular intrínseco, mientras que en el desarrollo que acometió Dirac en pos de alcanzar la compatibilidad del formalismo cuántico con el relativista, el espín, esto es, el desdoblamiento de la función de onda en partes relacionadas con un espectro discreto, va a emerger de forma natural. Y, como resultado de ello, se abrió el camino hacia la teoría de campos cuánticos (la segunda cuantización), pasando a ser la misma función de onda considerada como un campo, un campo cuántico.

El espín: operadores, autofunciones y autovalores

Sea un sistema elemental poseyendo un grado de libertad intrínseco de espín, observable representado en el formalismo de espacios de Hilbert por el operador autoadjunto de espín $\vec{S}\equiv (S_1\,,\,S_2\,,\,S_3)$ , que satisface por tanto las reglas de conmutación:
$[S_i\,,\,S_j]=i\hbar \, \epsilon_{ijk}\,S_k\,;\, i,j,k=1,2,3 \;\equiv \, \vec{S} \times \vec{S}=i\hbar \,\vec{S}$ .
Dado el operador autoadjunto de momento angular $\vec{S} \equiv (S_1\,,\,S_2\,,\,S_3)$ , actuando en un espacio de Hilbert $\mathcal{H}^{(S)}$ de dimensión finita, los tres operadores autoadjuntos componentes ${S_1\,,\,S_2\,,\,S_3}$ constituyen un conjunto irreducible de operadores en $\mathcal{H}^{(S)}$ , en el sentido de que todo operador lineal que conmuta con ellos es necesariamente un múltiplo de la identidad (cf. [GAL-89], pp. 247 y 329).
El operador cuadrado del momento angular espín, operador $\vec{S}^2$ , se define según:
$\vec{S}^2=\sum_i\,S_i^2$ .
-el operador cuadrado del momento angular $\vec{S}^2$ es un operador autoadjunto que satisface las relaciones de conmutación
$[\vec{S}^2\,,\,S_i]=0\,,\,i=1,2,3$ ,
esto es, es un operador escalar.
-el operador cuadrado del momento angular $\vec{S}^2$ es un operador autoadjunto que, en la representación irreducible $\vec{S}^2 \,,\, S_i$ , espacio de Hilbert $\mathcal{H}^(S)$ , de dimensión finita, admite expresión como múltiplo del operador identidad:
$\vec{S}^2\,=\,\hbar^2 \, s(s+1)\,I$ .
Puesto que los operadores $\vec{S}^2$ y $S_i \,,\,i=x,y,z$ , conmutan entre sí, son diagonalizables simultáneamente, esto es, existe una base ortonormal común en el Hilbert $\mathcal{H}^{(S)}$ , de dimensión finita.
-Es usual elegir el eje $OZ$ para señalar una dirección de cuantización arbitraria en el espacio, en cuyo caso la notación estándar que se adopta en términos de los números cuánticos de momento angular, $s$ , y de momento angular de tercera componente, $m_s$ es:
$\left. \begin{array}{l} \vec{S}^2 \, |s\, m_s\, > \,=\,\hbar^2s(s+1) \, |s\, ms\, >\\ S_z \,|s\, m_s\, > \,=\, \hbar \, m_s \, |s\, m_s\, > \end{array} \right\}$
-El correspondiente conjunto de autovectores simultáneos de los operadores $\vec{S}^2$ y $S_z$ ,
$\{| s\, m_s > \}_{m_s=-s,m_s=-s+1,\ldots,s}$ ,
para cada valor fijo de $s$ , constituye una base ortonormal en el espacio de Hilbert $\mathcal{H}^{(S)}$ , de dimensión $dim(\mathcal{H}^{(S)})=2s+1$ .
-relación de ortonormalidad:
$\left\langle s'\, m_s'\, | s\, m_s\, \right\rangle$ $=\,\delta_{s,\,s'} \,\delta_{m_s,\,m_s'}$ .
Los vectores integrantes de la base ortonormal común a $\vec{S}^2$ y $S_z$ se suelen notar como $|s\, m_s > \, \doteq \,\chi_{sm_s}$ y $< s\, m_s| \, \doteq \,\chi_{sm_s}^+$ , y la expresión general para un vector $|\chi_S> \in \mathcal{H^{(S)}}$ se representa entonces como la «función del espacio de espín» $\chi_S$ , de expresión en la base según
$\chi_S \,= \, \sum_{m_s=-s}^{s} \, c_{m_s} \chi_{s,m_s} \quad , \quad c_{m_s} \, \in \mathbb{C}$
$\chi_S \, \doteq \, \begin{pmatrix} c_{m_s=s} \\ c_{m_s=s-1} \\ \cdots \\ c_{m_s=-s} \end{pmatrix} \quad , \quad \chi^+_S \chi_S \,=\,1 \,=\,\sum_{m_s=+s}^{m_s=-s} | c_{m_s} |^2$
-Cada coeficiente en la combinación lineal se interpretará (supuesta cumplida la condición de normalización indicada) de modo que $| c_{m_s} |^2$ representa la probabilidad de encontrar a la partícula en el estado de espín $\chi_{s,ms}$ , es decir, en un estado en el que la predicción para el resultado de la medida para la proyección del espín según una dirección OZ del espacio es el valor $\hbar m_s$ con probabilidad $| c_{m_s} |^2$ , siendo $m_s$ es el número cuántico de tercera componente.
-Advertencia: en estos apuntes, no denominaremos espinor a una función $\chi_S \in \mathcal{H^{(S)}}$ , aunque este uso está muy extendido; aquí lo reservamos para los elementos del espacio $L^2(\mathbb{R}^3 , \mathbb{C}^{2s+1} )\backsimeq L^2(\mathbb{R}^3) \oplus L^2(\mathbb{R}^3) \oplus \cdots \oplus L^2(\mathbb{R}^3)$ .
Según la teoría general de momento angular, los valores de los números cuánticos de espín pueden tomar los valores:
$s\,=0\,,\,\frac{1}{2}\,,1\,,\frac{3}{2}\,,2\,,\frac{5}{2}\,\ldots$ ,
para el número cuántico de espín; para cada valor $s$ , el número cuántico de tercera componente $m_s$ toma entonces los valores reales
$m_s\,=\,-s\,,\,-s+1\,,\,-s+2\,,\,\ldots \,, \,s$ ,
positivos o negativos.
El subespacio de Hilbert $\mathcal{H}^{(S)})$ es invariante bajo los operadores $\vec{S}^2$ , $S_z$ , y también bajo $S_x$ , $S_y$ , $S_+=S_x\,+\,i\, S_y$ y $S_- =S_x\,- \,i\, S_y$ , de manera que estos operadores no conectan estados pertenecientes a subespacios con distinto valor del número cuántico $s$ . Por tanto, la representación matricial de todos ellos tendrá la forma de una matriz cuadrada.

Funciones de onda para sistemas con espín: los espinores

Consideremos un sistema constituido por una partícula en un estado representado por el ket $| \Psi(t)>$ del correspondiente espacio de Hilbert $\mathcal{H}$ asociado al sistema en el formalismo cuántico. En representación de posiciones, esto es, relativa al C.C.O.C. $\{ \vec{r} \}$ , la función de onda de la partícula, supuesta sin espín, es $\Psi(\vec{r},t)= < \vec{r} \, | \Psi(t) >$ . Pero si la partícula posee espín, tenemos que ampliar la dependencia funcional de esta función, incorporando la variable de espín, que en general se suele representar como $\sigma$ .
En definitiva: el que una partícula posea espín implica que es necesario completar el conjunto de observables (usualmente conteniendo posición o momento) que integran un C.C.O.C., y la elección frecuente es el observable tercera componente del espín, $S_z$ , que posee un espectro discreto y finito.
-Dado el C.C.O.C. $\{ \vec{r} \, , S_z \}$ , la base ortonormal asociada, integrada por autofunciones comunes, habrá de incorporar en su notación para la partícula con espín $S$ una variable de espín, $\sigma$ , pasando a notarse los correspondientes kets como $| \vec{r} \ , \ \sigma= \hbar m_s>$ , de modo que, en representación de posiciones, las funciones de onda de la b.o. común pasarán a ser:
$\psi_{m_s}(\vec{r},t) \equiv < \vec{r} \ , \ \sigma= \hbar m_s | \psi(t) > \quad , \quad m_s=-s, -s+1,\cdots,+s$
-Es decir: para cada ket $|\psi(t)>$ del Hilbert, su función de onda en representación o espacio de posiciones $|\psi(\vec{r} , t)>$ en el formalismo sin espín va a ser desdoblada y reemplazada por un conjunto de $2s+1$ funciones.
-Ejemplo: si $s=\frac{1}{2}$ , entonces la función de onda en representación de posiciones adquiere ahora la siguiente expresión ordenada de dos elementos, o función espinor:
$| \psi(t) > \rightarrow \psi(\vec{r},\sigma,t)\, \doteq \,\begin{pmatrix} \psi_{m_s=+\frac{1}{2}}(\vec{r},t) \\ \psi_{m_s=-\frac{1}{2}}(\vec{r},t) \end{pmatrix}\,\doteq\,\sum_{m_s=\pm \frac{1}{2}} \, \psi_{m_s}(\vec{r},t)\, \chi_{s,m_s}$
con
$\psi_{m_s}(\vec{r},t)\,\equiv \,< \vec{r} \,\sigma=\hbar m_s | \psi(t) > \quad , \;< \vec{r} \,\sigma=\hbar m_s | \psi(t) > \in \mathbb{C}$
y donde se ha usado introducido también la notación funcional $\chi_{s,m_s} \doteq |s \ m_s>$ para el ket $|s \ m_s> \in \mathcal{H}^{(S)}$ .
-Cada componente del espinor $\psi_{m_s=\pm \frac{1}{2}}$ se va a interpretar en el formalismo como la amplitud de probabilidad de hallar a la partícula en el punto $\vec{r}$ , con proyección del espín $\vec{S}$ sobre el eje OZ con valor $\pm \hbar \frac{1}{2}$ .
Considerando la nueva expresión matemática introducida para el Hilbert, , y en rigor, el observable que se añade al C.C.O.C. debería en consecuencia expresarse como $S_z=I \otimes (\hat{k} \cdot \vec{S})$ , donde $\hat{k}$ es el vector unitario según el eje OZ, puesto que con la ampliación de variables de espín en realidad se está realizando el espacio de Hilbert $\mathcal{H}$ del sistema como $L^2(\mathbb{R}^3) \otimes \mathbb{C}^{2s+1}$ , de modo que cada estado del sistema viene ahora a representarse por $2s+1$ funciones complejas de cuadrado integrable Lebesgue, actuando los operadores de espín sobre el Hilbert a través de su factor en $\mathbb{C}^{2s+1}$ (cf. [GAL-89]pp. 131,245-246).
-De forma más general, se puede incorporar una componente $S_n$ del espín $\vec{S}$ , componente o proyección en la dirección y sentido señalados por un vector unitario $\hat{n}=\frac{\vec{n}}{|\vec{n}|} \in \mathbb{R}^3$ , de manera que el correspondiente operador que se añade en este caso para completar el C.C.O.C. es el $S_n=I \otimes (\hat{n} \cdot \vec{S})$ , actuando el segundo factor en el espacio de espín.
En resumen: dado el C.C.O.C. (representación) $\{\vec{r}, S_z \}$ , para cada ket $| \Psi(t)>\in \mathcal{H}$ la función de onda general en representación de posiciones, $\Psi(\vec{r},\sigma,t)$ , admite desarrollo en serie en términos de las autofunciones de espín:
$| \Psi(t) > \rightarrow \Psi(\vec{r},\sigma,t)\,=\,\sum_{m_s=-s}^{s} \, \psi_{m_s}(\vec{r},t)\, \chi_{s,m_s} \quad ,\; \psi_{m_s}(\vec{r},t)\,=\,< \vec{r} \,\sigma | \Psi(t) >$
-Por tanto, una partícula de espín $S$ es descrita por una función de onda $\Psi(\vec{r},\sigma,t)$ con $2s+1$ componentes $\psi_{m_s}(\vec{r},t)$ , cada una de ellas asociada a un valor particular de los $2s+1$ valores para el número cuántico de tercera componente $m_s$ , o sea , equivalentemente, para la variable $\sigma=\hbar m_s$ , la cual, a diferencia de $\vec{r}$ , es una variable discreta.
Este tipo de funciones de onda, con componentes, se denominan espinores, y es un postulado adicional del formalismo cuántico que todos los axiomas fundacionales y definiciones desarrollados para funciones sin espín les son también aplicables a los espinores (con las modificaciones requeridas en cada caso en su expresión matemática).
-Por ejemplo, supuesta la normalización a la unidad de la función de onda :
1. El postulado sobre la interpretación probabilística de la función de onda quedaría como:
  $| \psi_{m_s}(\vec{r},t) |^2 \, d \vec{r}$ representa la probabilidad de encontrar a la partícula, en el instante $t$ , dentro de un elemento de volumen espacial $d\vec{r}$ y con su componente de espín a lo largo de una dirección fijada en el espacio con valor $\hbar m_s$ .
2. La definición de valor esperado o medio se generalizaría:
  $< \Psi \, | A | \, \Psi > \, = \, \int \Psi^+(\vec{r},\sigma,t) \, A \, \Psi(\vec{r},\sigma,t) \, d \vec{r}$
  $= \, \sum_{m_s}\sum_{m_s'}\, \int \psi_{m_s}^*(\vec{r},t)\, \chi_{s,m_s}^+ \, A \, \psi_{m_s'}(\vec{r},t)\, \chi_{s,m_s'}\, d \vec{r}$ .
Notación: pueden usarse diferentes tipos de notaciones para los espinores:
-Como ecuación que muestra una combinación lineal:
$\Psi(\vec{r},\sigma ;t) \ \doteq \,\sum_{m_s=-s}^{s} \, \psi_{m_s}(\vec{r},t)\, \chi_{s,m_s}$ ,
donde
$\psi_{m_s}(\vec{r},t) =\, < \vec{r},\sigma=\hbar m_s | \Psi(t) >$ .
-En términos matriciales:
$\Psi(\vec{r},\sigma; t) \ \doteq \, \begin{pmatrix} \psi_{m_s=s}(\vec{r},t) \\ \psi_{m_s=s-1}(\vec{r},t) \\ \cdots \\ \psi_{m_s=-s}(\vec{r},t) \end{pmatrix}$ $=\,\begin{pmatrix} < \vec{r} \,\sigma=\hbar s | \Psi(t) > \\ < \vec{r} \,\sigma=\hbar (s-1) | \Psi(t) > \\ \cdots \\ < \vec{r} \,\sigma=-\hbar s | \Psi(t) > \end{pmatrix}$
La generalización a sistemas de $N$ partículas, con espines respectivos $\vec{S_i}\, , \, i=1,\ldots,N$ :
$\Psi(\vec{r}_1,\sigma_1=\hbar m_{s1} ; \ldots ; \vec{r}_N,\sigma_N=\hbar m_{sN}; t)$
$\doteq \,\sum_{m_{s1}=s_1}^{-s_1} \ldots \sum_{m_{sN}=s_N}^{-s_N} \, \psi_{m_{s1},\ldots,m_{sN}}(\vec{r}_1, \ldots , \vec{r}_N ;t)\, \chi_{s,m_{s1}} \dots \chi_{s,m_{sN}}$ ,
donde
$\psi_{m_{s1},\ldots,m_{sN}}(\vec{r}_1, \ldots , \vec{r_N} ; t) =\, < \vec{r}_1,\sigma_1=\hbar m_{s1} ; \ldots ; \vec{r}_N,\sigma_N=\hbar m_{sN} \ | \ \Psi(t) >$
Por ejemplo, para una partícula de espín $S=1$ se tendría:
$\Psi(\vec{r},\sigma ;t) \, = \,\sum_{m_s=1,0,-1} \, \psi_{m_s}(\vec{r},t)\, \chi_{s,m_s}$
$=\,\psi_{1}(\vec{r};t)\, \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \,+\, \psi_{0}(\vec{r};t)\, \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\,+ \,\psi_{-1}(\vec{r};t)\, \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$
$=\, \begin{pmatrix} \psi_{1}(\vec{r};t) \\ \psi_{0}(\vec{r};t) \\ \psi_{-1}(\vec{r};t) \end{pmatrix} \; = \, \begin{pmatrix} < \vec{r} \,\sigma =\hbar \, | \, \Psi(t) > \\ < \vec{r} \,\sigma =0 \, | \, \Psi(t) > \\ < \vec{r} \,\sigma =-\hbar \, | \, \Psi(t) > \end{pmatrix}$
$\Psi^+(\vec{r},\sigma ;t) \, = \, \begin{pmatrix} \psi^*_{1}(\vec{r};t) & \psi^*_{0}(\vec{r};t) & \psi^*_{-1}(\vec{r};t) \end{pmatrix}$ .
Si el sistema se encuentra en un autoestado de espín $\chi_{s,m_s}$ , entonces todas las componentes del espinor serán nulas, menos la que corresponde al valor determinado del número cuántico de tercera componente $m_s$ . Así, en el ejemplo anterior de la partícula de espín 1, si está en el estado de espín con proyección nula sobre el eje $OZ$ , el espinor se convierte en:
$\Psi(\vec{r},\sigma=0\, ;t) \, =\, \begin{pmatrix} 0 \\ \psi_{0}(\vec{r};t) \\ 0 \end{pmatrix}$
Un caso particular ocurre cuando la expresión de la función de onda general es de la forma
$\Psi(\vec{r},\sigma ;t)\,= \, \psi(\vec{r};t)\,\chi_S \,= \, \psi(\vec{r};t)\,\sum_{m_s=-s}^{s} \, c_{m_s} \chi_{s,m_s} \quad , \quad \chi_S \, \in \mathcal{H}^{(S)}$ ,
es decir, la función admite separación en variables espacio-temporales, de un lado, y de espín, de otro.
-En este caso, se ha introducido la función de espín
$\chi_S \,= \, \sum_{m_s=-s}^{s} \, c_{m_s} \chi_{s,m_s} \quad , \quad c_{m_s} \, \in \mathbb{C}$
$\chi_S \, \doteq \, \begin{pmatrix} c_{m_s=s} \\ c_{m_s=s-1} \\ \cdots \\ c_{m_s=-s} \end{pmatrix} \quad , \quad \chi^+_S \chi_S \,=\,1 \,=\,\sum_{m_s=-s}^{s} | c_{m_s} |^2$ ,
interpretándose cada coeficiente en la combinación lineal (supuesta cumplida la condición de normalización indicada) de modo que $| c_{m_s} |^2$ representa la probabilidad de encontrar a la partícula en el estado de espín $\chi_{s,ms}$ , es decir, en un estado en el que la predicción para el resultado de la medida para la proyección del espín según una dirección OZ del espacio es el valor $\hbar m_s$ con probabilidad $| c_{m_s} |^2$ , siendo $m_s$ es el número cuántico de tercera componente.
-De esta forma, y sólo en este caso particular, la función de onda general resulta normalizada a la unidad en ambas partes por separado, espacial y de espin:
$|| \Psi(\vec{r},\sigma ;t) ||^2 = 1$
$\Rightarrow < \Psi \, | \, \Psi > \, = \, \int | \Psi(\vec{r} ;t) |^2 d \vec{r} \; \chi^+_{S} \chi_{S} = \int | \Psi(\vec{r} ;t)|^2 d \vec{r}=1 \cdot 1 \,=\,1$
-Este caso ocurre sucede, por ejemplo, cuando las interacciones presentes en el sistema son independientes de espín, esto es, el Hamiltoniano no contiene dependencia alguna en las variables de espín; también, cuando aun conteniendo partes operatoriales de espín todos los operadores actúan separadamente sobre los sendos espacios orbital y de espín.
En resumen: elegida la base ortonormal común al C.C.O.C. $\{\vec{r}, S_z \}$ , el espacio de Hilbert global asociado al sistema es realizable como
$L^2(\mathbb{R}^3) \otimes \mathbb{C}^{2s+1} \backsimeq L^2(\mathbb{R}^3 \ , \ \mathbb{C}^{2s+1} )\backsimeq L^2(\mathbb{R}^3) \oplus L^2(\mathbb{R}^3) \oplus \cdots \oplus L^2(\mathbb{R}^3)$ ,
es decir, cada estado viene representado por $2s+1$ funciones complejas de cuadrado integrable Lebesgue.
-O sea, en representación de posiciones, a cada ket $| \Psi(t) >$ del Hilbert le corresponde como función de onda un espinor:
$\Psi(\vec{r},\sigma ;t) \ \doteq \,\begin{pmatrix} < \vec{r} \,\sigma=\hbar s | \Psi(t) > \\ < \vec{r} \,\sigma=\hbar (s-1) | \Psi(t) > \\ \cdots \\ < \vec{r} \,\sigma=-\hbar s | \Psi(t) > \end{pmatrix}$
( $\{ \psi_{m_s}(\vec{r} ;t) \equiv < \vec{r} \ , \ \sigma= \hbar m_s | \psi(t) > \; , \; m_s=+s, +s-1,\cdots,-s \; \} \ \subset \mathbb{C}^{(2s+1)}$ ).

Espín $\frac{1}{2}$ : las matrices de Pauli

El caso del espín $\frac{1}{2}$ es muy importante, ya que tanto los electrones como los nucleones (protones y neutrones), así como los quarks, partículas componentes de los átomos, poseen este valor de espín.
Bosones, hadrones, fermiones, quarks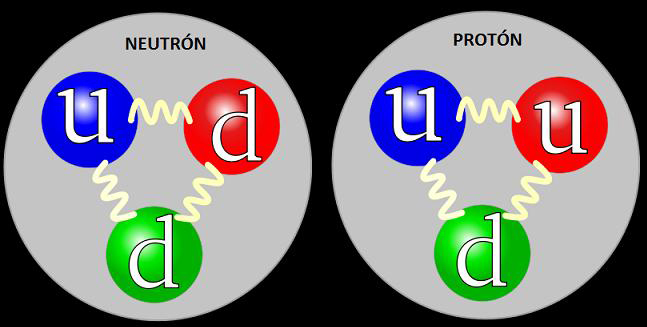

En una aproximación extremadamente simplificada se suele considerar que los nucleones (protones y neutrones) están formados por 3 quarks denominados quarks de valencia (dos quarks down y un quark up en el caso del neutrón, y dos quarks up y uno down para el protón).
No obstante, desde un punto de vista más profundo, más del 50% de la masa propia de los nucleones viene de la energía de enlace debida a la interacción fuerte y a un sinfín de quarks y gluones que se están constantemente produciendo y desintegrando en su interior. De manera general, las partículas formadas por quarks unidos mediante la interacción fuerte se conocen con el nombre de hadrones. (imagen y pie de la web https://www.i-cpan.es/).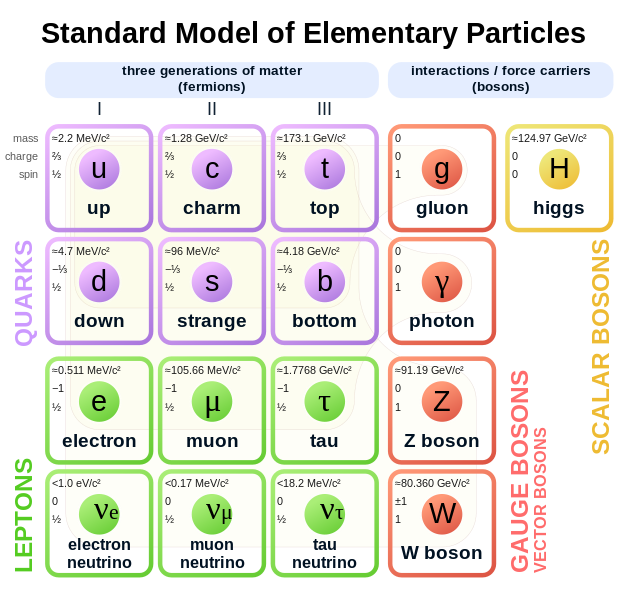

Modelo estándar de partículas (imagen de la Wikipedia by Cush).
En el caso de espín , puesto que el número cuántico de tercera componentes sólo puede tomar dos valores, , se tienen las siguientes ecuaciones (que no son nuevas, sino sólo casos particulares de fórmulas anteriores, cuyo interés radica sobre todo en introducir nuevas notaciones muy comunes en los diversos manuales):
1. Base común ortonormal en $\mathcal{H}^{(S)}$ de los operadores $\vec{S}^2$ y $S_z$ :
  $\{ \alpha \equiv \chi_{\frac{1}{2} , \frac{1}{2}} \equiv | \frac{1}{2}\,\frac{1}{2}\, > \equiv \chi_{\frac{1}{2}} \equiv \chi_{\uparrow} \equiv \chi_+ \equiv \left(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\right)\; ;$
  $\; \beta \equiv \chi_{\frac{1}{2} , -\frac{1}{2}} \equiv |\frac{1}{2}\,-\frac{1}{2}\, > \equiv \chi_{-\frac{1}{2}} \equiv \chi_{\downarrow} \equiv \chi_- \equiv \left(\begin{smallmatrix} 0 \\ 1 \end{smallmatrix}\right) \}$ ,
  el par de funciones de espín a las que se suele referir (induciendo frecuentes errores conceptuales) como estado «hacia arriba», up, y estado «hacia abajo», down.
  -Ortonormalidad:
  $< \frac{1}{2} , m_{\frac{1}{2}} \ | \ \frac{1}{2} , m_{\frac{1}{2}}' \ > \, \doteq \, \chi_{\frac{1}{2} , m_{\frac{1}{2}}}^+ \ \chi_{\frac{1}{2} , m_{\frac{1}{2}}'} \,=\, \delta_{m_{\frac{1}{2}} , \ m_{\frac{1}{2}}'}$
  $< \alpha | \alpha > = < \beta | \beta > =1 \equiv \alpha^+ \alpha= \beta^+ \beta =1$
  $< \alpha | \beta > = < \beta | \alpha > =0 \equiv \alpha^+ \beta= \beta^+ \alpha =0$
2. Ecuaciones de autovalores:
  $\vec{S}^2 \chi_{\frac{1}{2},\pm \frac{1}{2}}= \frac{3}{4}\hbar^2\chi_{\frac{1}{2},\pm \frac{1}{2}}$
  $\vec{S}^2\chi_{\downarrow}= \frac{3}{4}\hbar^2 \chi_{\downarrow}$
  $\vec{S}^2\chi_{\uparrow}=\frac{3}{4} \hbar^2 \chi_{\uparrow}$
  $S_z \chi_{\frac{1}{2},\pm \frac{1}{2}}= \pm \frac{\hbar}{2} \chi_{\frac{1}{2},\pm \frac{1}{2}}$
  $S_z \chi_{\downarrow}=-\frac{\hbar}{2} \chi_{\downarrow}$
  $S_z \chi_{\uparrow}=+\frac{\hbar}{2} \chi_{\uparrow}$
3. Expresión matricial de los distintos operadores de espín $\vec{S}^2$ y $S_z$ :
  $\vec{S}^2 = \frac{3}{4} \hbar^2 \left(\begin{smallmatrix}1 & 0 \\ 0 & 1 \end{smallmatrix}\right)$
  $S_z= \frac{\hbar}{2} \left(\begin{smallmatrix}1 & 0 \\ 0 & -1 \end{smallmatrix}\right)$
  $S_x= \frac{\hbar}{2} \left(\begin{smallmatrix}0 & 1 \\ 1 & 0 \end{smallmatrix}\right)$
  $S_y= \frac{\hbar}{2} \left(\begin{smallmatrix}0 & -i \\ i & 0 \end{smallmatrix}\right)$
  $S_+= S_x+iS_y=\hbar \left(\begin{smallmatrix}0 & 1 \\ 0 & 0 \end{smallmatrix}\right)$
  $S_-= S_x-iS_y=\hbar \left(\begin{smallmatrix}0 & 0 \\ 1 & 0 \end{smallmatrix}\right)$
4. Actuación de algunos operadores sobre la base:
  $\left. \begin{array}{l} \vec{S}^2 \alpha = \frac{3}{4} \hbar^2 \alpha \\ S_z \alpha = \frac{\hbar}{2} \alpha \\ S_+ \alpha = 0 \\ S_- \alpha = \hbar \beta \\ S_x \alpha = \frac{\hbar}{2} \beta \\S_y \alpha = \frac{i\hbar}{2} \beta \end{array} \right\} \quad \quad \quad \left. \begin{array}{l} \vec{S}^2 \beta = \frac{3}{4} \hbar^2 \beta \\ S_z \beta =-\frac{\hbar}{2} \beta \\ S_+ \beta =\hbar \alpha \\ S_- \beta =0 \\ S_x \beta =\frac{\hbar}{2} \alpha \\ S_y \beta =-\frac{i\hbar}{2} \alpha \end{array} \right\}$
5. Algunas propiedades de los operadores de espín $\frac{1}{2}$ actuando sobre los espinores:
  $\vec{S}^2 \Psi \,=\, \frac{3}{4} \hbar^2 \Psi \leftrightarrow \vec{S}^2 \,=\, \frac{3}{4} \hbar^2 \, I$
  $S_z^2 \Psi \,=\,S_x^2 \Psi \,=\,S_y^2 \Psi \,=\, \frac{\hbar^2}{4} \Psi \leftrightarrow S_z^2 \,=\,S_x^2 \,=\,S_y^2 \,=\, \frac{\hbar^2}{4} \, I$
6. Conmutación y anticonmutación de los operadores de espín $\frac{1}{2}$ :
  $[S_i\,,\,S_j] \, = \, S_iS_j\ ,- \, S_jS_i \, = \, i\hbar \, \epsilon_{ijk}\,S_k\,;\, i,j,k=x,y,z$
  $\equiv \, \vec{S} \times \vec{S}=i\hbar \,\vec{S}$
  (¡la ecuación que lo establece como operador de momento angular!)
  $\{ S_i\,,\,S_j \} \equiv [S_i\,,\,S_j]_+ \, = \, S_iS_j\ + \, S_jS_i \, = \,\frac{\hbar^2}{2}\, \delta_{i,j}\,I$
  -De ambas ecuaciones anteriores se deriva la siguiente :
  $S_iS_j \, = \,\frac{\hbar^2}{4}\, \delta_{i,j}\,I \, + \, \frac{i\hbar}{2}\, \epsilon_{ijk}\,S_k\,;\, i,j,k=x,y,z$ ,
  que es muy útil para reducir un producto arbitrario de operadores de espín $\frac{1}{2}$ bien a un término independiente de espín, bien a un término lineal en componentes de $\vec{s}$ , por ejemplo:
  $A=S_x S_y S_z S_y S_z S_x = -\frac{\hbar^6}{64} I$
  $B=S_x S_y S_x S_y S_z S_x = -i\frac{\hbar^5}{32} S_y$
7. Dado el operador autoadjunto de momento angular $\vec{S} \equiv (S_1\,,\,S_2\,,\,S_3)$ , actuando en un espacio de Hilbert $\mathcal{H}^{(S)}$ de dimensión finita, los tres operadores autoadjuntos componentes ${S_1\,,\,S_2\,,\,S_3}$ constituyen un conjunto irreducible de operadores en $\mathcal{H}^{(S)}$ , en el sentido de que todo operador lineal que conmuta con ellos es necesariamente un múltiplo de la identidad (cf. [GAL-89], pp. 247 y 329).
  -Por tanto, la expresión general de un operador de espín $\frac{1}{2}$ que sea producto arbitrario de componentes del operador $\vec{S}$ es:
  $A(\sigma)= A_o + A_xS_x + A_y S_y + A_z S_z = A_o + \vec{A} \cdot \vec{S}$ ,
  donde $A_i\, , \, i=0,x,y,z$ , son independientes de espín.
8. Algunos valores medios o esperados:
  $\left. \begin{array}{l} < \frac{1}{2}\, \pm \frac{1}{2}\, | \, \vec{S}^2\, | \, \frac{1}{2}\, \pm \frac{1}{2}> \, = \, \frac{3}{4}\hbar^2\\ < \frac{1}{2}\, \pm \frac{1}{2}\, | \, S_z^2\, | \, \frac{1}{2}\, \pm \frac{1}{2}> \, = \, < \frac{1}{2}\, \pm \frac{1}{2} \, | \, S_x^2\, |\, \frac{1}{2}\, \pm \frac{1}{2}> \, = \, < \frac{1}{2}\, \pm \frac{1}{2} \, | \, S_y^2\, | \, \frac{1}{2}\, \pm \frac{1}{2}> \, = \, \frac{\hbar^2}{4} \\ < \frac{1}{2}\, \pm \frac{1}{2} \, | \, S_z\, | \, \frac{1}{2}\, \pm \frac{1}{2}> \, = \, \pm \frac{\hbar}{2} \\ < \frac{1}{2}\, \pm \frac{1}{2} \, | \, S_x\, | \, \frac{1}{2}\, \pm \frac{1}{2}> \, = \, < \frac{1}{2}\, \pm \frac{1}{2} \, | \, S_y\, | \, \frac{1}{2}\, \pm \frac{1}{2}> \, = \, 0 \end{array} \right\}$
9. Función de ondas general en el espacio $L^2(\mathbb{R}^3 , \mathbb{C}^{2} )\backsimeq L^2(\mathbb{R}^3) \oplus L^2(\mathbb{R}^3)$ :
  $\Psi(\vec{r},\sigma,t) \, = \,\sum_{m_s=\frac{1}{2},-\frac{1}{2}} \, \psi_{m_s}(\vec{r},t)\, \chi_{s,m_s}$ ,
  un espinor de dos componentes:
  $=\,\psi_{\frac{1}{2}}(\vec{r},t)\, \begin{pmatrix} 1 \\ 0 \end{pmatrix} \,+\, \psi_{-\frac{1}{2}}(\vec{r},t)\, \begin{pmatrix} 0 \\ 1 \end{pmatrix} \, \equiv \, \psi_{\frac{1}{2}}(\vec{r},t)\,\alpha \, + \,\psi_{-\frac{1}{2}}(\vec{r},t)\,\beta$
  $\Psi(\vec{r},\sigma,t) \,=\, \begin{pmatrix} \psi_{\frac{1}{2}}(\vec{r},t) \\ \psi_{-\frac{1}{2}}(\vec{r},t) \end{pmatrix} \, = \,\begin{pmatrix} < \vec{r} \,\sigma =\frac{\hbar}{2} \, | \, \Psi(t) > \\ < \vec{r} \,\sigma =-\frac{\hbar}{2} \, | \, \Psi(t) > \end{pmatrix}$
  $\Psi^+(\vec{r},\sigma ,t) \, = \, \begin{pmatrix} \psi^*_{\frac{1}{2}}(\vec{r},t) & \psi^*_{-\frac{1}{2}}(\vec{r},t) \end{pmatrix}$
10. Normalización: el anterior espinor (expresado en la base canónica) estará normalizado cuando satisfaga:
  $| \Psi > \rightarrow \begin{pmatrix} \psi_{\frac{1}{2}}(\vec{r}) \\ \psi_{-\frac{1}{2}}(\vec{r}) \end{pmatrix}$
  $< \Psi | \Psi > \ = \ 1 \rightarrow \Psi^+(\vec{r},\sigma) \ \Psi(\vec{r},\sigma) \, = \, 1$
  $\Rightarrow \begin{pmatrix} \psi^*_{\frac{1}{2}}(\vec{r}) & \psi^*_{-\frac{1}{2}}(\vec{r}) \end{pmatrix} \, \begin{pmatrix} \psi_{\frac{1}{2}}(\vec{r}) \\ \psi_{-\frac{1}{2}}(\vec{r}) \end{pmatrix} \, = \, 1$
  $\rightarrow \ \int ( |\psi_{\frac{1}{2}}(\vec{r})|^2 \, + \, |\psi_{-\frac{1}{2}}(\vec{r})|^2) \ d \vec{r} \, = \, 1$
  -Caso particular: si, por ejemplo, el Hamiltoniano no depende de espín, o,
  aun conteniendo partes operatoriales de espín todos los operadores actúan separadamente sobre los sendos espacios orbital y de espín, la función de ondas general se factoriza y las dos partes se normalizan independientemente introduciendo los escalares requeridos:
  $\Psi(\vec{r},\sigma;t)\, = \, \psi(\vec{r};t)\, \chi_S\, = \, \psi(\vec{r};t) \, \sum_{+\frac{1}{2}, -\frac{1}{2}} c_{m_s} \chi_{m_s}$
  $=\,\psi(\vec{r};t)\,(c_{+\frac{1}{2}} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \,+\,c_{-\frac{1}{2}}\begin{pmatrix} 0 \\ 1 \end{pmatrix} )\, \equiv \, \psi(\vec{r};t)\,(c_{+\frac{1}{2}} \alpha \, + \, c_{-\frac{1}{2}} \beta )$ ;
  donde se ha introducido el desarrollo de la función de espín $\chi_S$ en la base ortonormal común a $\vec{S}^2$ y $S_z$ :
  $\chi_{S}\, = \, \sum_{+\frac{1}{2}, -\frac{1}{2}} c_{m_s} \chi_{m_s} \, \equiv \, c_{\uparrow} \alpha \,+ \, c_{\downarrow} \beta \, \equiv \, \begin{pmatrix} c_{\uparrow} \\ c_{\downarrow} \end{pmatrix}$
  que se normaliza exigiendo
  $\sum_{+\frac{1}{2}, -\frac{1}{2}} | c_{m_s} |^2 \, = \, |c_{\uparrow}|^2 \,+ \, |c_{\downarrow}|^2 \, = \,1$ ,
  por lo que la normalización global se expresa como:
  $\Psi^+(\vec{r},\sigma;t) \ \Psi(\vec{r},\sigma;t) \, = \, 1$
  $\Rightarrow 1 \, = \, \int | \psi(\vec{r};t) |^2 d \vec{r} \; \chi_S^+ \chi_S \, = \, \int | \psi(\vec{r};t) |^2 d \vec{r} \; \sum_{-\frac{1}{2}, \frac{1}{2}} | c_{m_s} |^2 =1 \cdot 1$

Matrices de Pauli.

En el caso de espín $s=\frac{1}{2}$ es conveniente introducir el operador vectorial $\vec{\sigma}$ , u operador de Pauli, definido según:
$\vec{\sigma}=\frac{2}{\hbar}\, \vec{S}$ ,
cuyas componentes poseen en la base
$\{ \alpha \equiv | \frac{1}{2}\,\frac{1}{2}\, > \equiv \chi_{\frac{1}{2}} \equiv \chi_{\uparrow} \equiv \left(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\right)\; ; \; \beta \equiv |\frac{1}{2}\,-\frac{1}{2}\, > \equiv \chi_{-\frac{1}{2}} \equiv \chi_{\downarrow} \equiv \left(\begin{smallmatrix} 0 \\ 1 \end{smallmatrix}\right) \}$
las expresiones:
$\sigma_x= \begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix} \quad \quad \sigma_y= \begin{pmatrix}0 & -i \\ i & 0 \end{pmatrix} \quad \quad \sigma_z= \begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix}$
conocidas como las matrices de Pauli
Propiedades:
1. $[\sigma_i,\sigma_j]\,=\, 2i\, \epsilon_{ijk}\,\sigma_k\,;\quad i,j,k=x,y,z \;(\equiv \, \vec{\sigma} \times \vec{\sigma}=i\hbar \,\vec{\sigma})$
2. $\{ \sigma_i,\sigma_j \} \,=\,2\, \delta_{i,j}$
3. $\sigma_i \, \sigma_j \,=\, \delta_{i,j}\, + \, i \ \epsilon_{ijk}\,\sigma_k$
4. $Tr(\sigma_i)=0$
5. $det(\sigma_i)=-1$
6. $\sigma_x^2 =\sigma_y^2 =\sigma_z^2=I$
7. El conjunto de las tres matrices de Pauli más el operador identidad constituye una base en el espacio de las matrices 2X2: cualquier matriz arbitraria 2×2 admite expresión como combinación lineal de estos cuatro elementos:
  $\forall A \in \mathcal{M}^{2x2} \; : \, A=C_o\,I + C_x\, \sigma_x + C_y\, \sigma_y +C_z\, \sigma_z \; , \; C_i \, \in \mathbb{C} \; \forall i=0,x,y,z$
Otras propiedades: dados dos operadores vectoriales y que conmutan con (pero no necesariamente entre sí):
1. $\vec{\sigma} \,( \vec{A} \cdot \vec{\sigma}) \,=\, \vec{A} \, + i \, (\vec{A} \times \vec{\sigma})$
2. $(\vec{A} \cdot \vec{\sigma}) \, \vec{\sigma} \,=\, \vec{A} \, - i \, (\vec{A} \times \vec{\sigma})$
3. $(\vec{\sigma} \cdot \vec{A}) \,(\vec{\sigma} \cdot \vec{B}) \,=\, \vec{A} \cdot \vec{B} \,+ i \, \vec{\sigma} \cdot (\vec{A} \times \vec{B})$
4. $(\vec{\sigma} \cdot \vec{A}) \, \vec{\sigma} \, (\vec{\sigma} \cdot \vec{B}) \,=\,\vec{A}(\vec{\sigma} \cdot \vec{B}) \, + \, (\vec{A} \cdot \vec{\sigma}) \vec{B} - \,(\vec{A} \cdot \vec{B})\, \vec{\sigma} \, -\,i(\vec{A} \times \vec{B})$
5. $\sigma_i (\vec{\sigma} \cdot \vec{A}) \ \sigma_i \,=\,-\vec{\sigma} \cdot \vec{A}$

Espín $\frac{1}{2}$ : autofunciones y autovalores de una componente

Sea $\hat{n}=\frac{\vec{r}}{|r|}$ un vector unitario en la dirección especificada por los ángulos polares $(\theta,\varphi)$ .
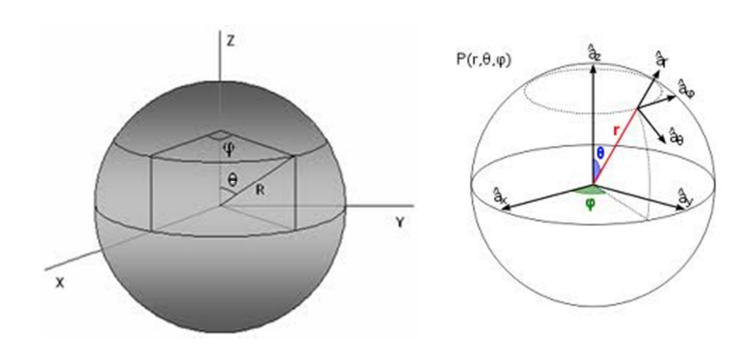
Coordenas esféricas (imagen del archivo: www.uv.mx/personal/aherrera/files/2014/05/03-Sistemas-de-Coordenadas-en-3D-AHE.pdf).
La componente del operador $\vec{S}$ en la dirección $\hat{n}$ es $S_n=\hat{n} \cdot \vec{S}$ , y su ecuación de autovalores:
$S_n \chi^n_{\nu} \,=\,\hbar \, \nu\, \chi^n_{\nu}$
Las componentes del vector unitario $\hat{n}$ se expresan como:
$\hat{n}=(\sin \theta\cos \varphi, \sin \theta \sin \varphi, \cos \theta)$
de donde se implica
$S_n=S_x \, \sin \theta\cos \varphi \,+\, S_y \, \sin \theta \sin \varphi \,+\, S_z \, \cos \theta$
$\; =\, \frac{\hbar}{2} \, \begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix}\, \sin \theta\cos \varphi \,+\,\frac{\hbar}{2} \, \begin{pmatrix}0 & -i \\ i & 0 \end{pmatrix}\,\sin \theta \sin \varphi \,+\,\frac{\hbar}{2} \, \begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix}\,\, \cos \theta)$
$\; =\, \frac{\hbar}{2} \, \begin{pmatrix} \cos \theta & \sin \theta e^{-i\varphi} \\ \sin \theta e^{i\varphi} & -\cos \theta \end{pmatrix}$
A partir de la expresión de la función de espín $\chi^n_{\nu} \in \mathcal{H}^{(S)}$ en la base estándar,
$\chi^n_{\nu}\, = \, \sum_{-\frac{1}{2}, \frac{1}{2}} c_{m_s} \chi_{m_s} \, \equiv \, c_{\uparrow} \alpha \,+ \, c_{\downarrow} \beta \, \equiv \, \begin{pmatrix} c_{\uparrow} \\ c_{\downarrow} \end{pmatrix}$ ,
condición de normalización
$\chi^{n+}_{\nu}\,\chi^n_{\nu}\, = \,\sum_{-\frac{1}{2}, \frac{1}{2}} | c_{m_s} |^2 \, = \, |c_{\uparrow}|^2 \,+ \, |c_{\downarrow}|^2 \, = \,1$ ,
la ecuación de autovalores
$S_n \, \chi^n_{\nu} \, =\, \frac{\hbar}{2} \, \begin{pmatrix} \cos \theta & \sin \theta e^{-i\varphi} \\ \sin \theta e^{i\varphi} & -\cos \theta \end{pmatrix} \,\begin{pmatrix} c_{\uparrow} \\ c_{\downarrow} \end{pmatrix} \,=\, \hbar \nu \,\begin{pmatrix} c_{\uparrow} \\ c_{\downarrow} \end{pmatrix}$
se transforma en el sistema de ecuaciones:
$S_n \, \chi ^n_{\nu}\, =\, \frac{\hbar}{2} \, \begin{pmatrix} c_{\uparrow} \, \cos \theta \, + \, c_{\downarrow} \, \sin \theta e^{-i\varphi} \\ c_{\uparrow} \, \sin \theta e^{i\varphi} \,- \, c_{\downarrow} \, \cos \theta \end{pmatrix} \, = \, \hbar \, \nu \, \begin{pmatrix} c_{\uparrow} \\ c_{\downarrow} \end{pmatrix}$
$\Rightarrow \left. \begin{array}{l} c_{\uparrow} \, ( \cos \theta \,-\, 2\nu ) \, + \, c_{\downarrow} \, \sin \theta e^{-i\varphi} \,= \, 0 \\ c_{\uparrow} \, \sin \theta e^{i\varphi} \, - \,c_{\downarrow} \, ( \cos \theta \,+\, 2\nu ) \, = \, 0 \end{array} \right\}$
sistema que posee solución no trivial si y sólo si
$\begin{vmatrix} \cos \theta \,-\, 2\nu & \sin \theta \, e^{-i\varphi} \\ \sin \theta \, e^{i\varphi} & -(\cos \theta \,+\, 2\nu) \end{vmatrix} \,=\, 0\,=\, 4\nu^2 \,-\,\sin^2 \theta \,-\,\cos^2 \theta \,=\, 4\nu^2 \,-\, 1$
$\quad \Rightarrow \; \nu^2 \,=\, \frac{1}{4} \quad \Rightarrow \; \nu \,=\, \pm \frac{1}{2}$
A cada autovalor de los dos obtenidos le corresponden las autofunciones de :
1. Autovalor $\hbar\nu \,=\, + \hbar \frac{1}{2}$ :
  $\Rightarrow \left. \begin{array}{l} c^+_{\uparrow} \, ( \cos \theta \,-\, 1 ) \, + \, c^+_{\downarrow} \, \sin \theta e^{-i\varphi} \,= \, 0 \\ c^+_{\uparrow} \, \sin \theta e^{i\varphi} \, - \,c^+_{\downarrow} \, ( \cos \theta \,+\, 1 ) \, = \, 0 \end{array} \right\}$
  $\Rightarrow \frac{c^+_{\downarrow}}{c^+_{\uparrow}} \,= \, \frac{ \sin \theta e^{i\varphi}}{\cos \theta \, + \,1} \,= \, \frac{ 2 \, \sin (\frac{\theta}{2})\, \cos (\frac{\theta}{2})}{1\,+\,\cos^2 (\frac{\theta}{2}) \,-\,\sin^2 (\frac{\theta}{2})} \,e^{i\varphi}\,=\,\tan(\frac{\theta}{2}) \,e^{i\varphi}$ ,
  pudiendo tomar el par de valores
  $\left. \begin{array}{l} c^+_{\uparrow} \,=\, \cos (\frac{\theta}{2}) \\ c^+_{\downarrow} \,= \, \sin (\frac{\theta}{2})\, e^{i\varphi} \end{array} \right\}$
  para los que la correspondiente autofunción de espín es (salvo fase):
  $\Rightarrow \, \chi^n_{\nu = +\frac{1}{2}} \, \equiv \, \chi^n_{+\frac{1}{2}} \,=\, \begin{pmatrix} \cos (\frac{\theta}{2})\\ \sin (\frac{\theta}{2})\, e^{i\varphi}\end{pmatrix}$
2. Autovalor $\hbar \nu \,=\, - \hbar \frac{1}{2}$ :
  $\Rightarrow \left. \begin{array}{l} c^-_{\uparrow} \, ( \cos \theta \,+ \, 1 ) \, + \, c^-_{\downarrow} \, \sin \theta e^{-i\varphi} \,= \, 0 \\ c^-_{\uparrow} \, \sin \theta e^{i\varphi} \, - \,c^-_{\downarrow} \, ( \cos \theta \,-\, 1 ) \, = \, 0 \end{array} \right\}$
  $\Rightarrow \frac{c^-_{\downarrow}}{c^-_{\uparrow}} \,= \, \frac{ \sin \theta e^{i\varphi}}{\cos \theta \, - \,1} \,= \, \frac{ 2 \, \sin (\frac{\theta}{2})\, \cos (\frac{\theta}{2})}{-1\,+\,\cos^2 (\frac{\theta}{2}) \,-\,\sin^2 (\frac{\theta}{2})} \,e^{i\varphi}\,=\,-\cot(\frac{\theta}{2}) \,e^{i\varphi}$ ,
  pudiendo tomar el par de valores
  $\left. \begin{array}{l} c^-_{\uparrow} \,=\, \sin (\frac{\theta}{2}) \\ c^-_{\downarrow} \,= \, -\cos (\frac{\theta}{2})\, e^{i\varphi} \end{array} \right\}$
  para los que la correspondiente autofunción de espín es (salvo fase):
  $\Rightarrow \, \chi^n_{\nu = -\frac{1}{2}} \, \equiv \, \chi^n_{-\frac{1}{2}} \,=\, \begin{pmatrix} \sin (\frac{\theta}{2})\\ -\cos (\frac{\theta}{2})\, e^{i\varphi}\end{pmatrix}$
Relaciones de ortonormalidad:
$< \,\chi^n_{\nu} \, | \, \chi^n_{\nu'} \,> \,\equiv \,\chi^{n+}_{\nu} \, \chi^n_{\nu '}\,=\,\delta_{\nu,\nu'}$
Valores medios o esperados:
$< S_z >_{n \uparrow} \,=\, < \, \chi^n_{+\frac{1}{2}} \, | \, S_z \, | \, \chi^n_{+\frac{1}{2}} \,>$
$=\, \begin{pmatrix} \cos (\frac{\theta}{2})\;,\; \sin (\frac{\theta}{2})\,e^{-i\varphi} \end{pmatrix}\, \frac{\hbar}{2} \, \begin{pmatrix} \cos (\frac{\theta}{2}) \\ -\sin (\frac{\theta}{2})\,e^{i\varphi} \end{pmatrix} \, =\, \frac{\hbar}{2}\, \cos \theta$
$< S_z >_{n \downarrow}\,=\, < \, \chi^n_{-\frac{1}{2}} \, | \, S_z \, | \, \chi^n_{-\frac{1}{2}} \,>\,=\,-\frac{\hbar}{2}\, \cos \theta$
$< S_x >_{n \uparrow}\,=\,\frac{\hbar}{2}\, \sin \theta \cos \varphi$
$< S_x >_{n \downarrow}\,=\,-\frac{\hbar}{2}\, \sin \theta \cos \varphi$
$< S_y >_{n \uparrow}\,=\,\frac{\hbar}{2}\, \sin \theta \sin \varphi$
$< S_y >_{n \downarrow}\,=\,-\frac{\hbar}{2}\, \sin \theta \sin \varphi$
–Podría decirse que los ángulos polares $(\theta,\varphi)$ marcan la dirección de $\vec{S}$ como genetratriz de una superficie cónica cuando la partícula está en el estado propio $\chi^n_{\nu = +\frac{1}{2}}$ («estado up«), y los ángulos $(\pi - \theta,\varphi + \pi)$ para el autoestado $\chi^n_{\nu = -\frac{1}{2}}$ («estado down«).
Probabilidades:
1. Probabilidad de obtener el espín «hacia arriba» (up: autovalor $+\hbar \frac{1}{2}$ ) al realizar una medida de la tercera componente de espín, $S_z$ , sobre una partícula de espín $\frac{1}{2}$ preparada («medida de primera especie») en el autoestado de espín $\chi^n_{+\frac{1}{2}}$ , donde $\hat{n}$ indica una dirección arbitraria en el espacio señalada por los ángulos polares $(\theta,\varphi)$ :
  $P_{S_z,\chi^n_{+\frac{1}{2}}}(\sigma = +\frac{\hbar}{2}) \,=\, |< \, \chi_{+\frac{1}{2}} \, | \, \chi^n_{+\frac{1}{2}} \,>|^2\,\equiv\, |< \, \alpha \, | \, \chi^n_{+\frac{1}{2}} \,>|^2$
  $=\, |< \,\begin{pmatrix} 1\;,\; 0 \end{pmatrix}\, \begin{pmatrix} \cos (\frac{\theta}{2}) \\ \sin (\frac{\theta}{2})\,e^{i\varphi} \end{pmatrix}\,>|^2\,=\,|\cos (\frac{\theta}{2})|^2 \,=\,\cos^2 (\frac{\theta}{2}) (\,=\, |c^+_{\uparrow}|^2)$
  -Cuando $\theta$ varía entre $0$ y $\pi$ , esta probabilidad varía entre $1$ y $0$ :
  $P_{S_z,\chi^n_{+\frac{1}{2}}}(\sigma = +\frac{\hbar}{2}) \vert_{\theta=0}\,=\,1 \, \leftrightarrow \, \hat{n}\,=\,\hat{k} \, \equiv \,\hat{z} \, \leftrightarrow \, \chi^n_{+\frac{1}{2}}\,= \,\chi_{+\frac{1}{2}} \, \equiv \left(\begin{smallmatrix} 1 \\ 0 \end{smallmatrix}\right) \, \equiv \alpha$ $P_{S_z,\chi^n_{+\frac{1}{2}}}(\sigma = +\frac{\hbar}{2}) \vert_{\theta=\pi}\,=\,0 \, (\leftrightarrow \, \hat{n}\,=\,-\hat{k} \, \equiv \,-\hat{z} \; si \; \varphi=0)$
  $\leftrightarrow \, \chi^n_{+\frac{1}{2}}\,= \, \left(\begin{smallmatrix} 0 \\ e^{i\varphi} \end{smallmatrix}\right) \, \equiv e^{i\varphi}\, \beta$
2. Probabilidad de obtener el espín «hacia abajo» (down: autovalor $-\hbar \frac{1}{2}$ ) al realizar una medida de la tercera componente de espín, $S_z$ , sobre una partícula de espín $\frac{1}{2}$ preparada («medida de primera especie») en el autoestado de espín $\chi^n_{+\frac{1}{2}}$ , donde $\hat{n}$ indica una dirección arbitraria en el espacio señalada por los ángulos polares $(\theta,\varphi)$ :
  $P_{S_z,\chi^n_{+\frac{1}{2}}}(\sigma = -\frac{\hbar}{2}) \,=\, |< \, \chi_{-\frac{1}{2}} \, | \, \chi^n_{+\frac{1}{2}} \,>|^2\,\equiv\, |< \, \beta \, | \, \chi^n_{+\frac{1}{2}} \,>|^2$
  $=\, |< \,\begin{pmatrix} 0\;,\; 1 \end{pmatrix}\, \begin{pmatrix} \cos (\frac{\theta}{2}) \\ \sin (\frac{\theta}{2})\,e^{i\varphi} \end{pmatrix}\,>|^2\,=\,|\sin (\frac{\theta}{2})|^2 \,=\,\sin^2 (\frac{\theta}{2}) (\,=\, |c^+_{\downarrow}|^2)$ ,
  de modo que, cuando $\theta$ varía entre $0$ y $\pi$ , esta probabilidad varía entre $0$ y $1$ .
3. Probabilidad de obtener el espín «hacia arriba» (up: autovalor $+\hbar \frac{1}{2}$ ) al realizar una medida de la tercera componente de espín, $S_z$ , sobre una partícula de espín $\frac{1}{2}$ preparada («medida de primera especie») en el autoestado de espín $\chi^n_{-\frac{1}{2}}$ , donde $\hat{n}$ indica una dirección arbitraria en el espacio señalada por los ángulos polares $(\theta,\varphi)$ :
  $P_{S_z,\chi^n_{-\frac{1}{2}}}(\sigma = +\frac{\hbar}{2}) \,=\, |< \, \chi_{+\frac{1}{2}} \, | \, \chi^n_{-\frac{1}{2}} \,>|^2\,\equiv\, |< \, \alpha \, | \, \chi^n_{-\frac{1}{2}} \,>|^2$
  $=\, |< \,\begin{pmatrix} 1\;,\; 0 \end{pmatrix}\, \begin{pmatrix} \sin (\frac{\theta}{2}) \\ -\cos (\frac{\theta}{2})\,e^{i\varphi} \end{pmatrix}\,>|^2\,=\,|\sin (\frac{\theta}{2})|^2 \,=\,\sin^2 (\frac{\theta}{2}) (\,=\, |c^-_{\uparrow}|^2)$ ,
  de modo que, cuando $\theta$ varía entre $0$ y $\pi$ , esta probabilidad varía entre $0$ y $1$ .
4. Probabilidad de obtener el espín «hacia abajo» (down: autovalor $-\hbar \frac{1}{2}$ ) al realizar una medida de la tercera componente de espín, $S_z$ , sobre una partícula de espín $\frac{1}{2}$ preparada («medida de primera especie») en el autoestado de espín $\chi^n_{-\frac{1}{2}}$ , donde $\hat{n}$ indica una dirección arbitraria en el espacio señalada por los ángulos polares $(\theta,\varphi)$ :
  $P_{S_z,\chi^n_{-\frac{1}{2}}}(\sigma = -\frac{\hbar}{2}) \,=\, |< \, \chi_{-\frac{1}{2}} \, | \, \chi^n_{-\frac{1}{2}} \,>|^2\,\equiv\, |< \, \beta \, | \, \chi^n_{-\frac{1}{2}} \,>|^2$
  $=\, |< \,\begin{pmatrix} 0\;,\; 1 \end{pmatrix}\, \begin{pmatrix} \sin (\frac{\theta}{2}) \\ -\cos (\frac{\theta}{2})\,e^{i\varphi} \end{pmatrix}\,>|^2\,=\,|\cos (\frac{\theta}{2})|^2 \,=\,\cos^2 (\frac{\theta}{2}) (\,=\, |c^-_{\downarrow}|^2)$ ,
  de modo que, cuando $\theta$ varía entre $0$ y $\pi$ , esta probabilidad varía entre $1$ y $0$ .