Potenciales separables

Potencial de Morse (https://es.wikipedia.org/wiki/Potencial_de_Morse). — Potencial de Morse (imagen del blog http://la-mecanica-cuantica.blogspot.com; para su resolución, puede verse la Wikipedia: https://es.wikipedia.org/wiki/Potencial_de_Morse).

Ecuación de Schrödinger para sistemas tridimensionales
Nota previa: antes de abordar esta serie de entradas, agrupadas bajo el epígrafe «potenciales tridimensionales», conviene tener bien trabajado los anteriores epígrafes, especialmente el de «potenciales monodimensionales» (y, por supuesto, ¡previo a los dos!, el general «Física cuántica no relativista»).

1. Ecuación de Schrödinger tridimensional

Consideremos el caso particular de la ecuación de Schrödinger para el siguiente sistema conservativo: una partícula material (no relativista) de masa $m$ y sin espín, moviéndose en el seno de un potencial real $V(\vec{r})$ (independiente de $\vec{p}$ y de $t$ ); bajo estas condiciones, el Hamiltoniano clásico $H\,=\, \frac{\vec{p}^2}{2m}+V(\vec{r})\;$ es independiente del tiempo y representa la energía total de la partícula, constituyendo una constante del movimiento.
La correspondiente ES tiene la siguiente forma:
,
ecuación en derivadas parciales de segundo orden que, en los casos en que la forma particular del potencial lo permita, admite resolución por el método de separación de variables, de forma que el problema original tridimensional se reduce a inferior dimensión.
Comenzamos la resolución con una primera separación de variables, la espacio-temporal ( ):
1. $\Psi(\vec{r};t)=\psi(\vec{r})\tau(t)$
2. $i\hbar\frac{\partial [\psi(\vec{r})\tau(t)]}{\partial t}=H_{op}\psi(\vec{r})\tau(t)=[-\frac{\hbar^2 }{2m}\nabla^2\psi(\vec{r})+V(\vec{r})\psi(\vec{r})] \tau(t)$
3. $i\hbar\psi(\vec{r})\frac{d \tau(t)}{d t}=[-\frac{\hbar^2}{2m}\nabla^2\psi(\vec{r})+V(\vec{r})\psi(\vec{r})] \tau(t)$
4. $i\hbar\frac{1}{\tau(t)}\frac{d\tau(t)}{d t}=[-\frac{\hbar^2}{2m}\nabla^2\psi(\vec{r})+V(\vec{r})\psi(\vec{r})] \frac{1}{\psi(\vec{r})}=E$
  donde $E$ simboliza una constante de separación, que tiene dimensiones de energía.
5. Separando variables se obtiene el par de ecuaciones:
  Ecuación 1: $i\hbar\frac{d\tau(t)}{d t}=E\tau(t)$
  Ecuación 2: $H\psi_E(\vec{r})=[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})]\psi_E(\vec{r})=E\psi_E(\vec{r})$
6. La ecuación diferencial 1 anterior es una ecuación diferencial ordinaria lineal y homogénea, de primer orden en el tiempo $t$ , cuya solución general tiene la forma: $\tau(t)=C\,e^{-iEt/\hbar}$ , donde $C$ representa una constante arbitraria.
7. Por lo tanto: para un sistema conservativo como el presente, la ES posee soluciones de la forma separable general:
  $\Psi_E(\vec{r};t)=C\,e^{-iEt/\hbar}\ \psi_E(\vec{r})$ , donde $C$ representa una constante arbitraria.
  -Nota: un sistema es conservativo cuando el Hamiltoniano es independiente del tiempo y representa la energía total del sistema.
8. Es usual normalizar también a la unidad la función de onda independiente del tiempo:
  -definimos $\psi_E^N(\vec{r})=\frac{1}{C}\psi_E(\vec{r})$ , de modo que:
  $\Psi_E(\vec{r};t)=C\,e^{-iEt/\hbar}\ \psi_E(\vec{r})=e^{-iEt/\hbar}\ \psi_E^N(\vec{r})$ ,
  teniéndose así la normalización común:
  $\left\langle \Psi_E \left|\Psi_E\right.\right\rangle =\left\langle \psi_E^N \left|\psi_E^N\right.\right\rangle=1$ .
  -En lo que sigue, usualmente se notará $\psi_E \equiv \psi_E^N$ .
La ecuación diferencial 2 anterior constituye la ecuación de Schrödinger para los estados estacionarios de energía, a menudo denominada también como ecuación de Schrödinger independiente del tiempo:
$H\psi_E(\vec{r})=[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})]\psi_E(\vec{r})=E\psi_E(\vec{r})$ ,
cuya expresión es la de una ecuación de autovectores o valores propios:
$H\psi_E(\vec{r})=E\psi_E(\vec{r})$ ;
la función $\psi_E(\vec{r})$ se denomina función de onda independiente del tiempo.
-En la resolución de esta ecuación diferencial ordinaria será esencial en Física determinar para qué potenciales $V(\vec{r})$ el correspondiente operador Hamiltoniano es autoadjunto en el dominio de interés o, al menos, esencialmente autoadjunto (cf. [GAL-89]p. 276) , esto es, es hermítico y posee una única extensión autoadjunta o, de forma equivalente, su adjunto es autoadjunto, lo que garantiza que representa un observable del sistema (la energía total para sistemas conservativos). Con este fin, la resolución de la ecuación diferencial ha de incorporar las adecuadas condiciones de contorno. El tema es peliagudo, pero, por fortuna para estos apuntes, los potenciales que se van a discutir, los de mayor interés físico, serán fáciles de tratar. Una discusión completa sobre las complicaciones matemáticas generales del asunto puede encontrase, cómo no, en el magnífico texto a qué tanto debemos los estudiantes de Física: [GAL-89]pp. 276ss.
Las funciones de onda de expresión separable $\Psi_E(\vec{r};t)=C\,e^{-iEt/\hbar}\ \psi_E(\vec{r})$ se denominan estados estacionarios de energía, y representan soluciones de la ES
$i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=H_{op}\Psi(\vec{r};t)$
en el caso de un sistema conservativo que son autofunciones del operador Hamiltoniano correspondientes a los valores propios $E$ :
$H\,\Psi_E(\vec{r};t)=E\,\Psi_E(\vec{r};t)$ .
Los estados estacionarios de energía satisfacen también la ecuación:
$i\hbar\frac{\partial}{\partial t}\Psi_E(\vec{r};t)=E\,\Psi_E(\vec{r};t)$ ,
de manera que son autofunciones del operador energía $i\hbar \frac{\partial}{\partial t}$ para los valores propios o autovalores $E$ .
Nota importante: ¡Los autovalores $E$ son los únicos valores de energía accesibles o permitidos al sistema como resultados de las medidas de la energía, pero las autofunciones de energía $\Psi_E(\vec{r};t)$ NO son los únicos estados accesibles o posibles para el sistema!

2. Ecuación de Schrödinger para dos partículas y separación de variables centro de masas y relativa

El problema de dos cuerpos sometidos a una interacción dependiente sólo de sus posiciones mutuas se reduce a un problema de un cuerpo cuya masa es la reducida del sistema. Este resultado fundamental en mecánica clásica puede consultarse por ahora desarrollado en el caso atómico en la siguiente web:
https://ocw.uniovi.es/pluginfile.php/3237/mod_resource/content/1/slides2009-L03.pdf
En estos apuntes, la reducción, ya empleada en los modelos atómicos precuánticos, se desarrollará con detalle más adelante, en la entrada correspondiente al tratamiento mecano-cuántico del átomo de Hidrógeno.
Así pues, en el caso de dos partículas interaccionado bajo un potencial que sólo depende de sus posiciones, de forma que, por simetría traslacional ha de ser de la forma particular $V(\vec{r}_1,\vec{r}_2)=V(\vec{r}=\vec{r}_1-\vec{r}_2)$ , por lo que la transformación canónica
$\left. \begin{array}{l} \vec{r}= \vec{r}_1 - \vec{r}_2 \\ \vec{R}=\frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{M} \end{array} \right\}$ $\left. \begin{array}{l} \vec{p}=\frac{m_2 \vec{p}_1 - m_1 \vec{p}_2}{m_1+m_2} \\ \vec{P}= \vec{p}_1 + \vec{p}_2 \end{array} \right\} \;\;, M=m_1+m_2\;,$

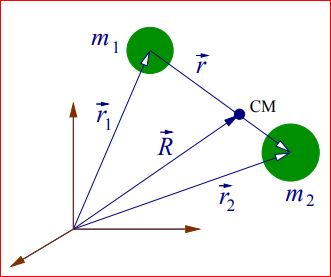
que permite derivar las expresiones
$\left. \begin{array}{l} \nabla_1=(\nabla_1 \vec{R})\nabla_R + (\nabla_1 \vec{r})\nabla_r = \frac{m_1}{M} \nabla_R + \nabla_r \\ \nabla_2=(\nabla_2 \vec{R})\nabla_R + (\nabla_2 \vec{r})\nabla_r = \frac{m_2}{M} \nabla_R - \nabla_r \end{array} \right\} \Rightarrow \frac{\nabla_1^2}{m_1} + \frac{\nabla_2^2}{m_2} =\frac{\nabla_R^2}{M} + \frac{\nabla_r^2}{\mu}$
tiene el efecto de conseguir reducir el estudio del problema de los dos cuerpos a la resolución de la anterior ecuación de Schrödinger independiente del tiempo, sin más que sustituir la masa $m$ de la partícula por la masa reducida $\mu$ del sistema de las dos partículas,
$\mu=\frac{m_1 \cdot m_2 }{m_1 + m_2 }$ ,
y la posición $\vec{r}$ de la partícula individual por la coordenada relativa,
$\vec{r}= \vec{r_1} - \vec{r_2}$ .
Las variables $\vec{R}$ y $\vec{P}$ representan, respectivamente, la posición y momento del centro de masas de las dos partículas, mientras que $\vec{r}$ y $\vec{p}$ representan la posición y el momento relativos.
En resumen: dado un sistema aislado de dos partículas sin espín, con masas respectivas $m_1$ y $m_2$ , interaccionado entre sí a través de un potencial $V(\vec{r}_1,\vec{r}_2)\equiv V(\vec{r}=\vec{r}_1-\vec{r}_2)$ , la ecuación de Schrödinger para los estados estacionarios (sistema conservativo) del sistema es
$H\psi_E(\vec{r}_1,\vec{r}_2)=[-\frac{\hbar^2}{2m_1}\nabla_1^2 -\frac{\hbar^2}{2m_2}\nabla_2^2 + V(\vec{r}_1,\vec{r}_2 )]\psi_E(\vec{r}_1 , \vec{r}_2 )=E\psi_E(\vec{r}_1 , \vec{r}_2 )$ ,
ecuación que introduciendo las variables relativa y de centro de masas pasa a ser
$H\psi_E(\vec{r},\vec{R})=[-\frac{\hbar^2}{2M}\nabla_R^2 -\frac{\hbar^2}{2\mu}\nabla_{r}^2 + V(\vec{r},\vec{R} )]\psi_E(\vec{r} , \vec{R} )=E\psi_E(\vec{r} , \vec{R} )$ .
La correspondiente ecuación de Schrödinger dependiente del tiempo es por su parte:
$i\hbar\frac{\partial}{\partial t}\Psi(\vec{r},\vec{R};t)=H(\vec{r},\vec{R};\vec{p},\vec{P}; t ) \,\Psi(\vec{r},\vec{R};t)$ ,
cuyas soluciones estacionarias son de la forma:
$\Psi(\vec{r},\vec{R};t) \, = \, \psi_E(\vec{r},\vec{R}) \, e^{-\frac{iEt}{\hbar}}$ ,
donde
$H\, \psi_E(\vec{r},\vec{R}) \, = \, [ -\frac{\hbar^2}{2M}\nabla_R^2 -\frac{\hbar^2}{2\mu}\nabla_{r}^2 + V(\vec{r},\vec{R} ) ]\, \psi_E(\vec{r},\vec{R}) \, = \, E\, \psi_E(\vec{r},\vec{R})$ .
-Al ser el sistema aislado, ha de ser invariante bajo traslaciones (y rotaciones); por lo tanto, el potencial $V$ no puede depender de la coordenada centro de masas $\vec{R}$ , por lo que la ecuación es separable:
$H\, \psi_E(\vec{r},\vec{R}) \, = \, [ -\frac{\hbar^2}{2M}\nabla_R^2 -\frac{\hbar^2}{2\mu}\nabla_{r}^2 + V(\vec{r}) ]\, \psi_E(\vec{r},\vec{R}) \, = \, E\, \psi_E(\vec{r},\vec{R})$
$\Rightarrow \left\{ \begin{array}{l} H(\vec{r},\vec{R}) \, = \, H_R(\vec{R})+H_r(\vec{r}) \, = \, [ -\frac{\hbar^2}{2M} \nabla_R^2] + [ -\frac{\hbar^2}{2\mu} \nabla_{r}^2 + V(\vec{r}) ] \\ \psi_E(\vec{r},\vec{R}) \, = \, \psi_{E_r}(\vec{r}) \ \phi_{E_R}(\vec{R}) \end{array} \right\} \Rightarrow$
$\Rightarrow H(\vec{r},\vec{R}) \ \psi_E(\vec{r},\vec{R}) \, = \, H_R(\vec{R}) \ \psi_{E_r}(\vec{r}) \ \phi_{E_R}(\vec{R}) \, + \, H_r(\vec{r}) \ \psi_{E_r}(\vec{r}) \ \phi_{E_R}(\vec{R})$
$= \, E\,\psi_{E_r}(\vec{r}) \ \phi_{E_R}(\vec{R} )$
$\Rightarrow \frac{1}{\psi_{E_r}} H_r \ \psi_{E_r}(\vec{r}) \ + \ \frac{1}{\phi_{E_R}} H_R \ \phi_{E_R}(\vec{R}) \, = \, E \, = \, E_r \, + \, E_R$
$\Rightarrow \left\{ \begin{array}{l} H_R(\vec{R}) \ \phi_{E_R}(\vec{R} ) \,= \, -\frac{\hbar^2}{2M}\nabla_R^2 \ \phi_{E_R}(\vec{R} ) \, = \, E_R \ \phi_{E_R}(\vec{R} ) \\ H_r(\vec{r}) \ \psi_{E_r}(\vec{r} ) \,= \,[ -\frac{\hbar^2}{2\mu}\nabla_r^2 \, + \, V(\vec{r})] \ \psi_{E_r}(\vec{r} ) \, = \, E_r \ \psi_{E_r}(\vec{r} ) \end{array} \right\} \, E_R \, + \, E_r \, = \, E$
La ecuación del movimiento del centro de masas no es sino la ecuación de Schrödinger para el movimiento de una partícula libre, cuyas soluciones son las ondas planas,
$\phi_{E_R}(\vec{R})\, = \, \frac{1}{(2 \pi \hbar)^{\frac{3}{2}}}\ e^{i \vec{P} \cdot \vec{R}/ \hbar}$ ,
$E_R \, = \, \frac{\vec{P}^2}{2M}$ ,
ecuación que describe el movimiento libre del centro de masas del sistema; $E_R$ representa la denominada como «energía del centro de masas».
La ecuación del movimiento relativo,
$H_r \ \psi_{E_r}(\vec{r})\, = \, [ -\frac{\hbar^2}{2\mu} \nabla_{r}^2 + V(\vec{r}) ] \ \psi_{E_r}(\vec{r})\, = \,E_r \ \psi_{E_r}(\vec{r})\, = \,(E-E_R) \ \psi_{E_r}(\vec{r})$ ,
da cuenta del movimiento relativo o intrínseco de las dos partículas; representa el movimiento en el seno del potencial $V(\vec{r})$ de una partícula de masa la reducida del sistema.
En conclusión, la solución general de la ES inicialmente planteada es superposición lineal continua de funciones del tipo
$\psi_E(\vec{r},\vec{R}) \, = \,\frac{1}{(2 \pi \hbar)^{\frac{3}{2}}}\ e^{i \vec{P} \cdot \vec{R}/ \hbar} \,\psi_{E_r}(\vec{r})$ ,
representando cada una estados en los que el centro de masas tiene un movimiento bien determinado por $\vec{P}$ y $\psi_{E_r}(\vec{r})$ es solución de la denominada «ecuación de Schröndiger del movimiento relativo», de expresión general
$H_r \ \psi_{E_r}(\vec{r})\, = \, [ -\frac{\hbar^2}{2\mu} \nabla_{r}^2 + V(\vec{r}) ] \ \psi_{E_r}(\vec{r})\, = \,E_r \ \psi_{E_r}(\vec{r})\, = \,(E-E_R) \ \psi_{E_r}(\vec{r})$ ,
donde $\mu$ representa la masa reducida del sistema de las dos partículas y la energía total del sistema viene dada por la suma
$E_{Tot.} \equiv E= E_r + \frac{\vec{P}^2}{2M}$ .
-Eligiendo un sistema de referencia con origen en el centro de masas del sistema se anula el momento del centro de masas, $\vec{P}=0$ , lo que lleva a la identificación de la energía total con la energía relativa, $E_{Tot.} \equiv E= E_r$ , de forma que la solución de la ES del movimiento relativo proporciona, vía las autofunciones y autovalores aceptables físicamente, la descripción completa del sistema.

3. Ecuación de Schrödinger independiente del tiempo para potenciales aditivos en coordenadas cartesianas y separación de variables

Sea un potencial $V(\vec{r})$ que admita expresión aditiva en coordenadas cartesianas de la forma:
$V(\vec{r})=V_x(x) + V_y(y)+ V_z(z)$ ,
de modo que el operador Hamiltoniano resulta ser
$H=-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})=H_x(x) + H_y(y)+ H_z(z)$ ,
donde cada sumando $H_i(r_i)$ tiene la expresión
$H_i(r_i)=-\frac{\hbar^2}{2m} \ \frac{\partial^2}{\partial r_i^2} \ + \ V_i(r_i) \quad ; \; i=x,y,z \; ; \; r_i \equiv i$ ,
y la ecuación de Schrödinger independiente del tiempo es:
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2}\, + \, \sum_i V_i(r_i) \} \psi_E(\vec{r})=E \ \psi_E(\vec{r})$
Esta expresión del Hamiltoniano permite la búsqueda de soluciones por el método de separación de variables, esto es, sustituir la solución expresándola según
$\psi_E(\vec{r}=(x,y,z)) = X(x) \ Y(y) \ Z(z) \equiv \prod_{x,y,z} R_i(r_i)$
y realizar el procedimiento habitual:
1. Sustitución en la ecuación:
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2}\, + \, \sum_i V_i(r_i) \} \prod_{x,y,z} R_i(r_i)=E \ \prod_{x,y,z} R_i(r_i)$
2. División por la función:
$\sum_i \{ (-\frac{\hbar^2}{2m}) \frac{1}{R_i(r_i)} \frac{d^2 R_i(r_i)}{d r_i^2}\, + \, V_i(r_i) \} =E$
3. Igualación de cada sumando de dependencia exclusiva en cada coordenada $r_i$ a una constante con dimensiones de energía, $E_i$ :
$\{ (-\frac{\hbar^2}{2m}) \ \frac{d^2}{d r_i^2}\, + \, V_i(r_i) \} R_i(r_i)=E_i \ R_i(r_i)$ ,
con la condición
$E=\sum_i E_i=E_x+E_y+E_z$ .
Por tanto, se ha conseguido convertir el problema tridimensional en la resolución de tres problemas monodimensionales.

3.1. Ejemplo: Partícula confinada en una caja de paredes impenetrables

Sea una partícula de masa $m$ , sin espín, en interior de una caja prismática rectangular de lados $L_i \, , \, i=x,y,z$ y paredes impenetrables, de tal forma que la partícula está sometida al siguiente potencial:
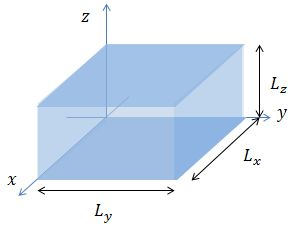
$V(\vec{r}) \,= \, \left\{ \begin{array}{l} 0 \quad 0 \le r_i \le L_i \\ \infty \quad r_i < 0 \, , \, r_i > L_i \end{array} \right.$
La anterior ES independiente del tiempo contiene en este caso un potencial $V(\vec{r})$ que en el interior de la caja y sobre sus caras admite expresión aditiva en coordenadas cartesianas de la forma:
$V(\vec{r})=V_x(x) + V_y(y)+ V_z(z)=0+0+0$ ,
de modo que el operador Hamiltoniano resulta ser
$H=-\frac{\hbar^2}{2m}\nabla^2+0=H_x(x) + H_y(y)+ H_z(z)$ ,
donde cada sumando $H_i(r_i)$ tiene la expresión
$H_i(r_i)=-\frac{\hbar^2}{2m} \ \frac{\partial^2}{\partial r_i^2} \quad ; \; i=x,y,z \; ; \; r_i \equiv i$ ,
y la ecuación de Schrödinger independiente del tiempo en coordenadas cartesianas toma la forma en la región $0 \le r_i \le L_i$ :
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2} \} \psi_E(\vec{r})=E \ \psi_E(\vec{r})$ ,
ecuación a la que se añade la condición de frontera de anulación de la función de onda sobre las paredes de la caja.
Esta expresión del Hamiltoniano permite la búsqueda de soluciones por el método de separación de variables, esto es, sustituir la solución expresándola según
$\psi_E(\vec{r}=(x,y,z)) = X(x) \ Y(y) \ Z(z) \equiv \prod_{x,y,z} R_i(r_i)\; , \; i=x,y,z$ ,
junto con las condiciones de frontera
$R_i(r_i)=0 \quad \forall r_i \le 0 \, , \, \forall r_i \ge L_i \; , \; i=x,y,z$
y a continuación realizar el procedimiento habitual:
1. Sustitución en la ecuación:
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2} \ \} \prod_{x,y,z} R_i(r_i)=E \ \prod_{x,y,z} R_i(r_i)$
2. División por la función:
$\sum_i \{ (-\frac{\hbar^2}{2m}) \frac{1}{R_i(r_i)} \frac{d^2 R_i(r_i)}{d r_i^2} \ \} =E$
3. Igualación de cada sumando de dependencia exclusiva en cada coordenada $r_i$ a una constante con dimensiones de energía, $E_i$ :
$\{ (-\frac{\hbar^2}{2m}) \ \frac{d^2}{d r_i^2} \ \} R_i(r_i)=E_i \ R_i(r_i)$ ,
con la condición
$E=\sum_i E_i=E_x+E_y+E_z$ .
Por tanto, se ha conseguido convertir el problema tridimensional en la resolución de tres problemas monodimensionales.
4. Resolución monodimensional:
$0 \le r_i \le L_i \rightarrow -\frac{\hbar^2}{2m} \ \frac{d^2 R_i(r_i)}{d r_i^2}\,=\,E_i \ R_i(r_i)$
$\Rightarrow \frac{d^2 R_i(r_i)}{d r_i^2} \,+\, \frac{2m}{\hbar^2} E_i \ R_i(r_i) \, = \, 0$
-La EDO lineal homogénea $u'' \mp k^2u=0 \, , \, k \in \mathbb{R} \, , \, k>0$ tiene por solución general la combinación lineal de soluciones particulares:
a) signo (-) : $u(r)=C_1 \ e^{kr} + C_2\ e^{-kr}$
con $C_1,C_2$ escalares arbitrarios.
b) signo (+) : $u(r)=C_1 \ e^{+ikr} + C_2\ e^{-ikr}=C'_1 \ cos\ kr + C'_2\ sen \ kr$
con $C_1,C_2,C'_1,C'_2$ escalares arbitrarios.
-Buscamos soluciones que se anulen sobre las paredes de la caja, por tanto, ha de ser cada constante de separación $E_i$ positiva, para que las soluciones se correspondan con las funciones oscilatorias, siendo directo obtener la solución general para valores $E>0$ :
$R_{i,E_i}(r_i)=C_1 \ cos\ k_ir_i + C_2\ sen \ k_ir_i$ ,
donde $C_1,C_2$ son escalares arbitrarios y
$k_i=\frac{+\sqrt{2mE_i}}{\hbar}>0 \, , \, E_i > 0\, , \, k_i > 0 \, , \, k_i \in \mathbb{R}\, , \, i=x,y,z$
-Puesto que la solución ha de anularse en el origen y en $L_i$ , las soluciones particulares adecuadas, las que satisfacen las condiciones de frontera impuestas, son las que presentan dependencia sinusoidal:
$R_{i,E_i}(0)=0=C_1 \Rightarrow R_{i,E_i}(r_i) \, = \, C_2 \ sen \ k_ir_i$ ,
$R_{i,E_i}(L_i)=0=C_1 \ sen \ k_iL_i \Rightarrow k_iL_i = n_i \pi \, , \, n_i=1,2,3\ldots (k_i \ne 0)$
-Finalmente, pues, la solución queda:
$R_{i,E_i}(r_i)\, =\, C_2 \ sen \ k_ir_i \, =\, C_2 \ sen \ (\frac{n_i \pi}{L_i}r_i)$
$E_i \, = \, \frac{\hbar^2}{2m} \ \frac{\pi^2}{L_i^2} \ n_i^2 \, , \, n_i=1,2,3\ldots$ ,
soluciones que, una vez normalizadas,
$\int_{-\infty}^{+\infty} \ |N|^2 | R_{i,E_i}(r_i) |^2 dr_i\, =\, 1$
$|N|^2 \int_{-\infty}^{+\infty} \ |sen (\frac{n_i \pi}{L_i}r_i) |^2 dr_i\, =\,|N|^2 [\frac{r_i}{2} -(\sin (\frac{2n_i \pi}{L_i}r_i) )\frac{L_i}{4n_i\pi}]|_0^{L_i}\,=\, |N|^2 \ \frac{L_i}{2}$
$|N|=(\frac{2}{L_i})^{\frac{1}{2}}$ ,
toman la forma normalizada:
$R_{i,E_i}(r_i)\, =\, (\frac{2}{L_i})^{\frac{1}{2}} \ sen \ (\frac{n_i \pi}{L_i}r_i)$ ,
que representa una onda estacionaria, con nodos sobre la superficie de la caja.
Reuniendo las tres dimensiones, las autofunciones y autovalores resultan:
$\psi_{E(n_x,n_y,n_z)}(\vec{r}) \equiv \psi_{n_x,n_y,n_z}(x,y,z) \, = \, (\frac{8}{L_xL_yL_z})^{\frac{1}{2}} \ sen \ (\frac{n_x \pi}{L_x}x) \ sen \ (\frac{n_y \pi}{L_y}y) \ sen \ (\frac{n_z \pi}{L_z}z)$
$E(n_x,n_y,n_z) \, =\, \frac{\hbar^2\pi^2}{2m} \ [(\frac{n_x}{L_x})^2 + (\frac{n_y}{L_y})^2 + (\frac{n_z}{L_z})^2 ]$
$n_x,n_y,n_z=1,2,3\ldots$ .

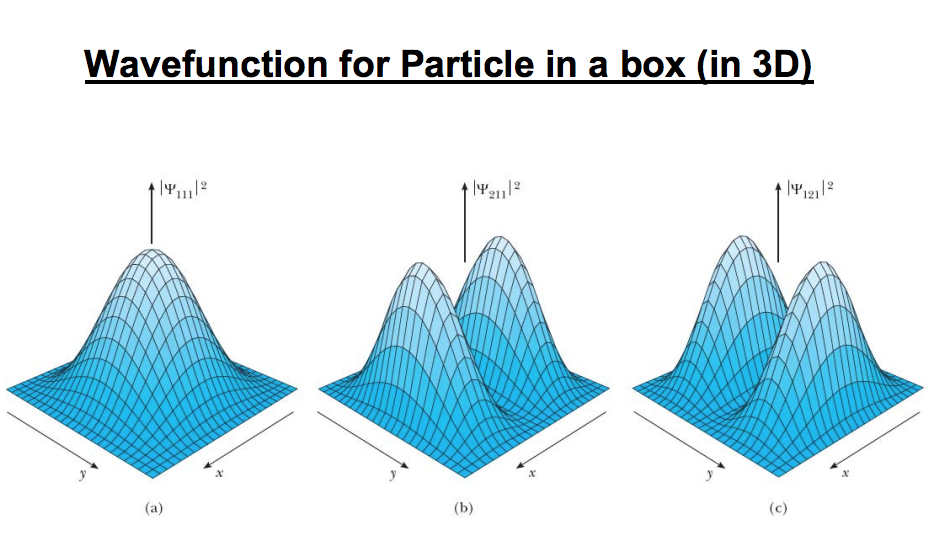
Funciones de onda en una caja cúbica tridimensional (imagen: https://web.iitd.ac.in/~pramitc/Lecture%20review%207_Particle%20in%20a%20box%20%283D&2D%29.pdf).
En particular, para una caja cúbica, $L_x=L_y=L_z\equiv L$ , se obtiene:
$\Rightarrow \psi_{E(n_x,n_y,n_z)}(\vec{r}) \equiv \psi_{n_x,n_y,n_z}(x,y,z) \, = \, (\frac{8}{L^3})^{\frac{1}{2}} \ sen (\frac{n_x \pi}{L}x) \ sen (\frac{n_y \pi}{L}y) \ sen (\frac{n_z \pi}{L}z)$
$E(n_x,n_y,n_z) \equiv E_n\, =\, \frac{\hbar^2\pi^2}{2mL^2} \ n^2$
$n_x,n_y,n_z=1,2,3\ldots \quad , \quad n^2=n_x^2 + n_y^2 + n_z^2 =3,6,9\ldots$ .
-El estado fundamental, pues, es el estado $\psi_{E(1,1,1)}$ de energía
$E_{GS}=E_{1,1,1}\, = \, 3 \ \frac{\hbar^2\pi^2}{2mL^2}$ ,
un estado no degenerado; el primer estado excitado es de energía
$E_{exc.1}\, = \,6 \ \frac{\hbar^2\pi^2}{2mL^2}=2E_{GS}$ ,
con degeneración 3, correspondiente a los tres conjuntos de valores de los tres números cuánticos $n_i$ que comparten autovalor:
$n_x=2,n_y=n_z=1;n_x=1,n_y=2,n_z=1;n_x=1,n_y=n_y=1,n_z=2$
-La siguiente figura ilustra la sucesión de niveles:

Niveles de energía en una caja cúbica y su degeneración.

4. Potenciales centrales: separación de variables en coordenadas esféricas

Sea la ecuación de Schrödinger independiente del tiempo para el movimiento de una partícula de masa $m$ en el seno de un potencial $V(\vec{r})$ :
$H\psi(\vec{r})=[-\frac{\hbar^2}{2 \mathsf{m}}\nabla^2+V(\vec{r})]\psi(\vec{r})=E\psi(\vec{r})$ ,
ecuación que, según ha quedado establecido anteriormente, coincide en su expresión con la ecuación para el movimiento relativo de un sistema aislado de dos partículas de sendas masas $m_1$ y $m_2$ , interaccionando a través de un potencial $V(\vec{r}_1,\vec{r}_2)$ , sin más que realizar las sustituciones:
a) masa $m$ de la partícula individual por la masa reducida $\mu=\frac{m_1 \cdot m_2 }{m_1 + m_2 }$ del sistema de las dos partículas,
y b) la posición $\vec{r}$ de la partícula individual por la coordenada relativa $\vec{r}= \vec{r_1} - \vec{r_2}$ .
En el caso particular de un potencial central, , situación asociada a la invariancia rotacional, la ecuación es directamente resoluble introduciendo las coordenadas esféricas para proceder a continuación a la separación de variables:
1. Introduzcamos las coordenadas esféricas, $\vec{r},\theta,\varphi$ :
  $\left. \begin{array}{l} x=r \sin \theta \cos \varphi \,,\; 0 \leq r=|\vec{r}| < \infty \\ y=r \sin \theta \sin \varphi \,,\; 0 \leq \theta \le \pi \\ z=r \cos \theta \,,\; 0 \le \varphi \leq 2\pi \end{array} \right\}$ $\left. \begin{array}{l} r=+\sqrt{x^2+y^2+z^2} \,,\; 0 \leq x < \infty \\ \theta = \arccos \frac{z}{r} \,,\; 0 \leq z < \infty \\ \varphi = \arctan \frac{y}{x} \,,\; 0 \leq y < \infty \end{array} \right\}$
  
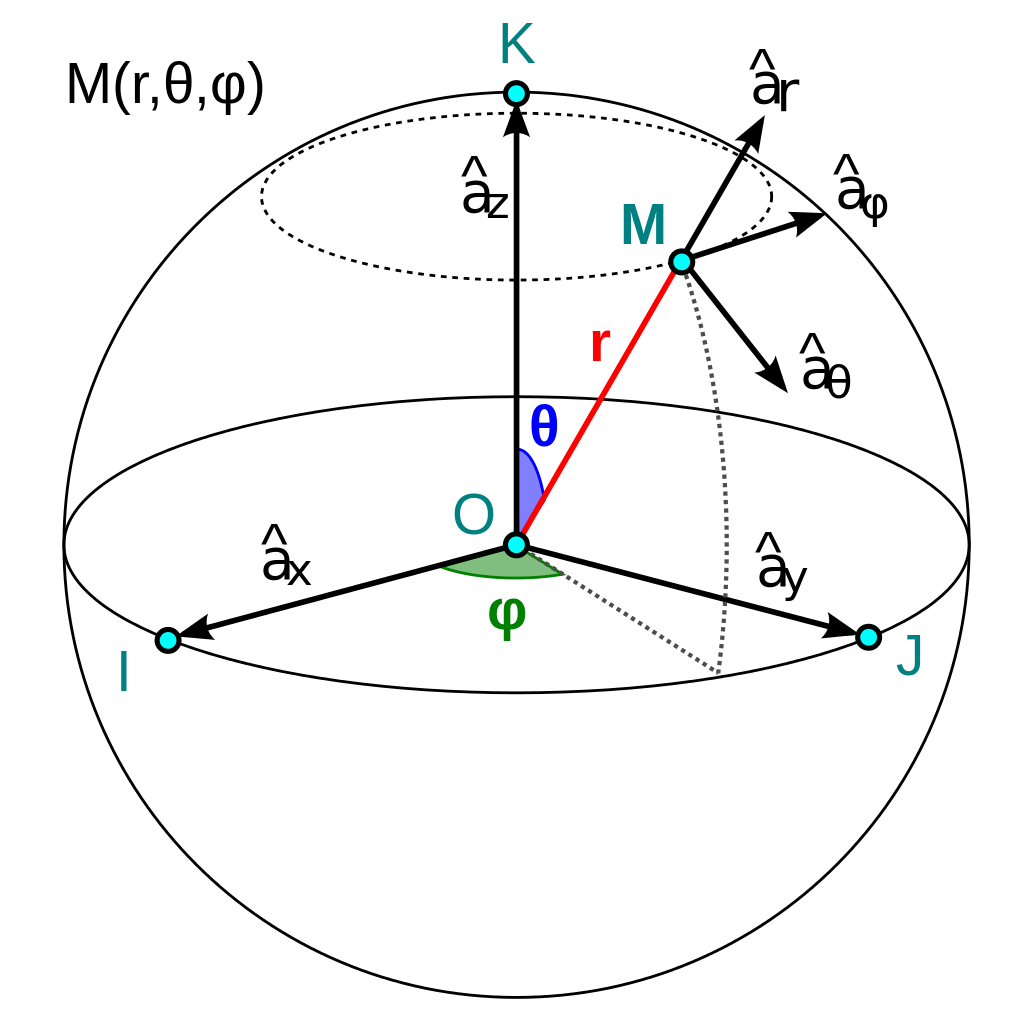
  Coordenadas esféricas de un punto M, imagen de la Wikipedia (derivative work by Josemontero9, from the original
  Coordenadas_eséricas_figura , by Romero Schmidtke).
  
  -En estas coordenadas, un elemento de volumen $dV$ y el operador $\nabla^2$ se expresan, respectivamente:
  $dV \, = \, d^3r \equiv d \vec{r} \, = \, dx \, dy \, dz=r^2 \sin \theta \, dr \, d \theta \, d \varphi$
  $\nabla^2 \, = \, \frac{1}{r^2 \sin \theta} \{ \sin \theta \, \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, + \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin \theta}(\frac{\partial^2}{\partial \varphi^2}) \}$ ,
  de manera que el momento angular orbital y su cuadrado en esféricas resultan ser:
  $L_x\,=\, yp_z-zp_y\,=\,-i\hbar \,(y\frac{\partial}{\partial z} - \,z \frac{\partial}{\partial y}) \, = \, -i\hbar \, (-\sin \varphi \, \frac{\partial}{\partial \theta} \, - \, \cot \theta \, \cos \varphi \, \frac{\partial}{\partial \varphi})$
  $L_y\,=\, zp_x-xp_z\,=\,-i\hbar \,(z\frac{\partial}{\partial x} - x \frac{\partial}{\partial z}) \, = \, -i\hbar \, (\cos \varphi \, \frac{\partial}{\partial \theta} \, - \, \cot \theta \, \sin \varphi \, \frac{\partial}{\partial \varphi})$
  $L_z\,=\, xp_y-yp_x\,=\,-i\hbar \,(x\frac{\partial}{\partial y} - y \frac{\partial}{\partial x}) \, = \, -i\hbar \, \frac{\partial}{\partial \varphi}$
  $\vec{L}^2 \,=\, \vec{L} \cdot \vec{L}\, = \,L_x^2 \,+\, L_y^2 \, +\, L_z^2$ $= \,-\hbar^2 \, [ \,\frac{1}{\sin \theta} \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2} \, ]$
  $= \,-\hbar^2 \, [ \,\frac{\partial^2}{\partial \theta^2} \,+ \, \cot \theta \, \frac{\partial}{\partial \theta} \, + \, \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2} \, ]$ .
2. Ecuación de Schrödinger independiente del tiempo en coordenadas esféricas:
  $H\psi(\vec{r})$
  $= \, \{-\frac{\hbar^2}{2m}[ \ \frac{1}{r^2 \sin \theta} \{ \sin \theta \, \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, + \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin \theta}(\frac{\partial^2}{\partial \varphi^2}) \ ] \, + \, V(r) \ \} \ \psi(\vec{r})$
  $= \, \{-\frac{\hbar^2}{2m}[ \ \frac{1}{r^2} \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2} \ ] \, + \, V(r) \} \psi(\vec{r})$
  $= \, E \ \psi(\vec{r})$
3. Autofunciones: ondas parciales:
  Tanto $\vec{L}$ como $\vec{L}^2$ son operadores puramente angulares, es decir, que no contienen dependencia explícita de la coordenada radial $r=|\vec{r}|$ . Por tanto, para cualquier potencial central (esféricamente simétrico) se satisfacen las conmutaciones:
  $[\vec{L},V(r)]=[\vec{L}^2,V(r)]=0$ .
  Además,
  $[\vec{L}^2,L_i]=0\,, \, i=x,y,z$ ,
  y también ambos operadores $\vec{L}$ y $\vec{L}^2$ conmutan con el operador energía cinética, $T$ , de expresión en esféricas
  $T\, = \, -\frac{\hbar^2}{2m}\nabla^2 \, = \, -\frac{\hbar^2}{2m} [ \ \frac{1}{r^2} \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2} \ ]$ .
  Por todo ello, considerado el operador Hamiltoniano del sistema (conservativo), $H=T+V$ , que representa la energía total del sistema, satisface:
  $[H, \vec{L}]=[H,\vec{L}^2]=0$ ,
  derivándose que el conjunto de operadores $\{ H,\vec{L}^2,L_z \}$ puede ser diagonalizado simultáneamente: integran un C.C.O.C. (en ausencia de grados de libertad adicionales, como pudiera ser el espín) y existe en el espacio una base integrada por autofunciones comunes a los tres operadores, que denominaremos como ondas parciales $\psi_{Elm}$ y cuya expresión, como vamos a demostrar a continuación, involucrará los armónicos esféricos, las autofunciones comunes de los operadores de momento angular orbital, expresándose como (a demostrar):
  Onda parcial $l$ : $\psi_{Elm}(\vec{r})=R_{El}(r) \ Y_{lm}(\theta,\varphi)$ ,
  donde $R_{El}(r)$ es la denominada función radial, de expresión a determinar por separación de variables, y las funciones $Y_l^m$ son los armónicos esféricos:
  $\vec{L}^2 \,Y_{lm}(\theta, \varphi) \, =\, \hbar^2 \, l(l+1)\, Y_{lm}(\theta, \varphi)$
  $L_z \,Y_{lm}(\theta, \varphi) \, =\, \hbar \, m\, Y_{lm}(\theta, \varphi)$ .
4. En efecto, por separación de variables:
  Sea la solución de la anterior ES independiente del tiempo poseyendo la forma separada
  $\psi(\vec{r})\, = \, R(r) \ Y(\Omega)$ ;
  entonces, sustituyendo en la ES,
  $H \, \psi(\vec{r}) \, = H\, R(r) \ Y(\Omega)$
  $= \, \{-\frac{\hbar^2}{2m}[ \ \frac{1}{r^2} \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2} \ ] \, + \, V(r) \} \, R(r) \ Y(\Omega)$
  $= \, E \, R(r) \ Y(\Omega)$ ;
  multiplicamos por $-2mr^2/\hbar^2$ y dividimos por $RY$ :
  $\Rightarrow \, [ \ \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, - \, \frac{2mr^2}{\hbar^2} ( V(r) \, - \, E)\, - \, \ \frac{\vec{L}^2}{\hbar^2} \ ] \ R(r) \ Y(\Omega) \, = \, 0$
  $\Rightarrow \, \{ \ \frac{1}{R(r)} \ [\frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, - \, \frac{2mr^2}{\hbar^2} ( V(r) \, - \, E) ] \,R(r) \ \} \, + \, \{ \ - \frac{1}{Y(\Omega)} \ \frac{\vec{L}^2}{\hbar^2} \ Y(\Omega) \} \, = \, 0$
  de donde se derivan las dos ecuaciones ( $\beta$ es la constante de separación):
  1. $-\beta = \, -\frac{1}{\hbar^2 Y(\Omega)} \ \vec{L}^2 \ Y(\Omega)$
  $\Rightarrow \, \vec{L}^2 \ Y(\Omega) \, = \, \beta \ \hbar^2 \, Y(\Omega) \$
  $\Rightarrow \, \left\{ \begin{array}{l} Y(\Omega) \ \equiv \ Y_{lm}(\Omega) \\ \beta \, = \, l(l+1) \, , \, l=0,1,2,\ldots \end{array} \right.$
  (¡no confundir la masa con el número cuántico de tercera componente de momento angular orbital!)
  2. $\{ \ \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, - \, \frac{2mr^2}{\hbar^2} [ V(r) \, - \, E] \, \} \, R(r) \, = \, \beta \, R(r)\, = \, l(l+1) \, R(r)$
  $\Rightarrow \, \{ \ \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, - \, \frac{2mr^2}{\hbar^2} V(r) \, - \, l(l+1) \} \, R(r) = -\frac{2mr^2}{\hbar^2} E \, R(r)$
  $\Rightarrow \, \{ \ -\frac{\hbar^2}{2mr^2} \, \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, + \, V(r) \,+ \frac{\hbar^2}{2mr^2} \, l(l+1) \} \, R(r) \, = \,E \, R(r)$
  $\Rightarrow \, \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, V(r) \ \} \, R(r) \, = \,E \, R(r)$ ,
  que es la denominada como ecuación radial, y en la que es común incluir en la notación los parámetros $\{ E,l\}$ como subíndices de la función incógnita:
  $\Rightarrow \, \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, V(r) \ \} \, R_{El}(r) \, = \,E \, R_{El}(r)$
Degeneración de la energía:
Como consecuencia de la invariancia rotacional, existe una degeneración energética: ya que para cada valor dado del número cuántico de momento angular orbital $l$ existen $2l + 1$ autofunciones $\psi_{El \mathsf{m}}=R_{El}Y_{l \mathsf{m}}$ , correspondientes a los $2l+1$ valores posibles del número cuántico $\mathsf{m}$ de tercera componente de momento angular orbital, $\mathsf{m} =l,l-1,l-2,\ldots,-l$ , todas ellas satisfaciendo la misma ecuación de ES para un autovalor dado de energía E.
-Es decir, fijada una dirección arbitraria en el espacio, debido a su isotropía, el Hamiltoniano correspondiente a un potencial central es invariante bajo rotaciones, de modo que los niveles de energía no pueden depender del número cuántico de tercera componente o magnético $\mathsf{m}$ .

4.1. Potenciales centrales y ondas parciales l

Ondas parciales:
La expresión de cada función de ondas $\psi(\vec{r})$ como suma de funciones $\psi_{Elm}=R_{El}Y_{lm}$ , autofunciones simultáneas de los operadores $\{ H,\vec{L}^2,L_z \}$ , se denomina «descomposición en ondas parciales» , siendo usual, siguiendo la tradición espectroscópica, referir a los sumandos correspondientes a los valores $l=0,1,2,3,4\ldots$ como sendas ondas o estados s(harp), p(rincipal), d(ifusivo), f(undamental), g … (a partir de aquí, orden alfabético).
Propiedades de las ondas parciales:
1. Densidad de probabilidad:
  $| \psi_{Elm}=R_{El}Y_{lm} |^2 \, = \, |R_{El}(r) |^2\, |Y_{lm}(\theta, \varphi) | ^2 \, = \, |R_{El}(r) |^2 \, | [\frac{(2l+1)(l-m)!}{4\pi (l+m)!}]^{\frac{1}{2}} \,P_l^m(\cos \theta)\, e^{im\varphi}|^2$
  $= \,|R_{El}(r) |^2 \, | [\frac{(2l+1)(l-m)!}{4\pi (l+m)!}]^{\frac{1}{2}} \,P_l^m(\cos \theta)|^2$ ,
  independiente de $\varphi$ , donde los armónicos esféricos dictan el comportamiento de la densidad de probabilidad en cada dirección $\Omega=(\theta,\varphi)$ y la función radial $R(r)$ marca, a partir de cada potencial central particular $V(r)$ , el comportamiento radial.
2. Normalización:
  a) Si el estado es ligado, la normalización será a la unidad:
  $\int_V \ | \psi_{Elm}=R_{El} \ Y_{lm} |^2 \, d \vec{r} \, = \,1$ ,
  es decir, $\psi_{Elm}(\vec{r}) \in L^2(\mathbb{R}^3)$ , función de cuadrado integrable Lebesgue.
  Puesto que los armónicos esféricos están normalizados sobre la esfera unidad, se deriva la condición de normalización para la parte radial:
  $1\, = \, \int_0^{\infty} \ | R_{El} |^2 \,r^2 \, d r \ \int_0^{\pi} \ \sin \theta \ d \theta \int_0^{2 \pi} \ \ d \varphi \ |Y_{lm} |^2$
  $\Rightarrow \, \int_0^{\infty}\ | R_{El} |^2 \,r^2 \, d r \, = \, 1$ .
  b) Si el estado es de difusión (estado de colisión o «scattering»), es decir, un estado no ligado o solución del problema de autovalores en sentido generalizado, que estrictamente no pertenece al Hilbert $\mathscr{H}=L^2(\mathbb{R})$ , entonces representa un sistema que no está ni localizado ni confinado, una función matemáticamente oscilante que no se anula a largas distancias (o que se anula tan lentamente que no es normalizable). Para trabajar con esta clase de estados se requerirá de la introducción de formas especiales de normalización efectiva, como, por ejemplo, el confinamiento en una región de gran volumen delimitada por fronteras infranqueables, sobre las que se impondrá su anulación, de donde se derivará una discretización «fina» del espetro continuo. Otra posibilidad es recurrir a la delta de Dirac.
3. Paridad:
  En coordenadas esféricas la operación de paridad $\vec{r} \, \rightarrow \, -\vec{r}$ corresponde a la tríada de cambios $(r,\theta,\varphi )\, \rightarrow \,(r,\pi -\theta,\pi + \varphi )$ . Puesto que el Hamiltoniano de una partícula en un campo central es invariante bajo la operación de paridad, $[H,P]=0$ , pueden encontrarse autofunciones simultáneas de ambos operadores, esto es, autofunciones de energía (sistema conservativo) con paridad bien definida:
  $P \ \psi_{Elm}(\vec{r}) \,= \, P \ R_{El}(r) \ Y_{lm}(\theta, \varphi)\,= \, R_{El}(r) \ P \ Y_{lm}(\theta, \varphi)$
  $= \, R_{El}(r) \ Y_{lm}(\pi - \theta, \pi +\varphi)$
  $= \, R_{El}(r) \ (-1)^l Y_{lm}(\theta,\varphi)$
  $= \, (-1)^l \ \psi_{Elm}(\vec{r})$ .
  Por tanto, las ondas parciales tienen paridad definida: son funciones pares para valores del número cuántico orbital pares, e impares si $l$ impar.
  -Caso particular: la onda s presenta simetría esférica y paridad par:
  $\psi_{E0m}(\vec{r}) \, \equiv \, \psi_{E00} \,= \,R_{E0}(r) \ Y_{00} \,= \,R_{E0}(r) \ \sqrt{\frac{1}{4\pi}}$

4.2. Ecuación radial reducida para potenciales centrales y sus condiciones de contorno

Sea la ecuación radial
$\Rightarrow \, \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, V(r) \ \} \, R_{El}(r) \, = \,E \, R_{El}(r)$ ;
se realiza el cambio de función incógnita
$R_{El}(r)=\frac{1}{r} \ u_{El}(r)$ ,
siendo $u(r)$ la función radial reducida, que ha de satisfacer la ecuación radial reducida en onda parcial l:
$\{ -\frac{\hbar^2}{2m} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \, + \, V(r) \ \} \, u_{El}(r) \, = \,E \, u_{El}(r)$
$\equiv \, H_l u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2m} \ \frac{d^2}{d r^2} \,+ \, V_{ef_l}(r) \ \} \ u_{El}(r)\, = \,E \, u_{El}(r)$ ,
donde se ha introducido un potencial efectivo de onda $l$ ,
$V_{ef_l}(r) \,= \, \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \, + \, V(r) \quad , \; l=0,1,2\ldots$ .
El término adicional al potencial $V(r)$ se denomina barrera centrífuga, constituyendo un potencial repulsivo que tiende a alejar a las partículas (tiende a $+\infty$ cuando $r \rightarrow 0$ ) y que se suma al original $V(r)$ .
-Es interesante el observar que esta ecuación es la misma que ya se resolvió en el estudio de los distintos casos monodimensionales.
-Las figuras siguientes representan el aspecto general de los dos sumandos en el caso general de potenciales $V(r)$ atractivos, y de su suma, esto es, de los potenciales efectivos usuales de ondas parciales $l$ (la segunda figura, para el caso particular de un potencial culombiano $V(r)=-\frac{1}{r}$ ):

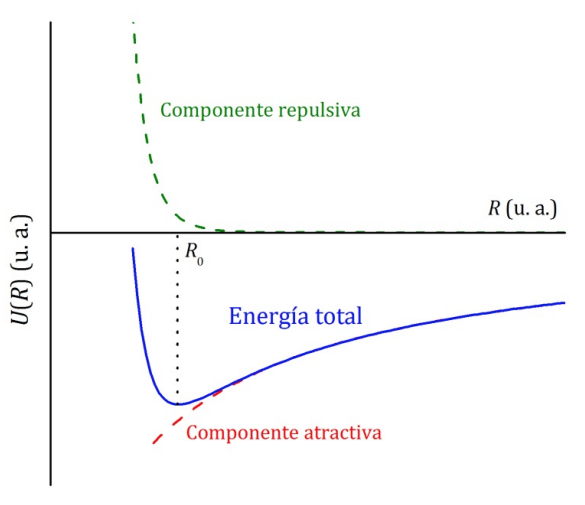
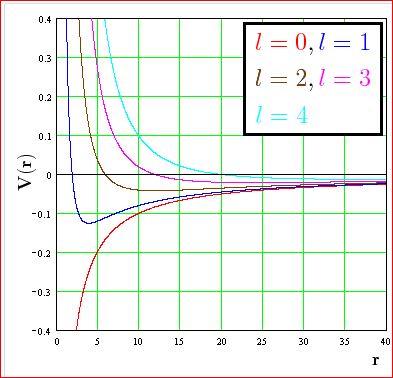
Representación de la función [-1/r + l(l+1)/r^2 ] (imagen de la web: http://la-mecanica-cuantica.blogspot.com/2009/08/la-funcion-de-onda-radial.html).
En definitiva, se ha reducido el problema de valores propios original a la resolución del conjunto de los sendos problemas reducidos asociados a cada onda parcial $l$ .
Se plantea a continuación el problema de determinar las condiciones que garanticen que cada Hamiltoniano de onda parcial, $H_l$ , sea autoadjunto en $L^2(0, \infty)$ o, por lo menos, esencialmente autoadjunto (posee una única extensión autoadjunta, o, equivalentemente su adjunto es autoadjunto), debiéndose también satisfacer que la suma de los correspondientes espacios $\tilde{\mathcal{H}_l}$ proporcione el espacio total asociado al sistema físico, esto es, $\mathcal{H}= \oplus \tilde{\mathcal{H}}_l$ , donde $\tilde{\mathcal{H}}_l=\mathcal{H}_l \otimes I_l$ , siendo $I_l$ el operador identidad sobre la parte angular de momento $l$ .
Se demuestra (cf. [GAL-89], pp. 282ss.) que el problema de encontrar los autoestados ligados solución de la ecuación de Schrödinger independiente del tiempo es equivalente a buscar las soluciones de la ecuación radial reducida en onda parcial $l$ que satisfagan el siguiente par de condiciones:
1. Condición de integrabilidad:
$\int_0^{\infty} \ |u_{El} |^2 \ dr \, < \, \infty$
2. Condición de regularidad:
$u_{El}(0)\, = \, 0 \, , \, \forall l$ , con $u_{El}(r) \ \xrightarrow{r\rightarrow 0} \ 0$ más rápido que $r^l \xrightarrow{r\rightarrow 0} \ 0$ , pudiendo demostrarse que debe ser $lim_{r\rightarrow 0}u_{El}(r) \approx \ r^{l+1}$ (por lo que $lim_{r\rightarrow 0}R_{El}(r) \approx \ r^l$ ) , ya que $R_{El}(r)=u(r)_{El} /r$ debe ser continua (finita) en el origen para todos los valores $l$ .
-La actuación de la condición de regularidad puede ilustrarse considerando la ecuación diferencial
$H_l u_{El}(r) \, = \, -\frac{d^2 u_{El}(r)}{d r^2} \,+ \,[\frac{l(l+1)}{r^2}\, + \, U(r)] \ u_{El}(r)\, = \, \epsilon \, u_{El}(r)$ ,
donde
$\epsilon = \frac{2m}{\hbar^2} E$ y $U(r)= \frac{2m}{\hbar^2}V(r)$ ; $U_{ef_l}(r)= \frac{l(l+1)}{r^2}\, + \, U(r)$ ,
convirtiéndose la ecuación en:
$\frac{d^2 u_{El}(r)}{d r^2} \,- \,[\frac{l(l+1)}{r^2}\, + \, U(r) \, - \, \epsilon] \ u_{El}(r)\, = \, 0$
Si ahora se toma un potencial $U(r)$ cuyo comportamiento a cortas distancias sea $U(r) \ \xrightarrow{r\rightarrow 0} \ \lambda r^{-s} \; , \, \lambda \ne 0 \;, \; s \in \mathbb{Z} \, , \, s < 2$ , esto es, un potencial no más singular que el culombiano en el origen (cf. [BRA-00] p. 339; [GAL-89] I, p. 282), como es el caso de muchas interacciones de interés en Física, en un entorno del origen la parte predominante de la función $(U_{ef_l}(r)-\epsilon)$ la proporcionará la barrera centrífuga, esto es, en ese entorno
$u_{El}'' \equiv \frac{d^2 u_{El}(r)}{d r^2} \approx \frac{l(l+1)}{r^2}u_{El}(r)$ , de forma que la ecuación se convierte en la
$u_{El}'' - \frac{l(l+1)}{r^2}u_{El}(r) \approx 0$ .
Ésta es una EDO (ecuación diferencial ordinaria) cuya solución general es una combinación lineal con constantes arbitrarias de dos soluciones particulares con sendos comportamientos asintóticos $u_{El}(r) \ \xrightarrow{r\rightarrow 0} \ r^{l+1}$ y $u_{El}(r) \ \xrightarrow{r\rightarrow 0} \ r^{-l}$ .
Nota: se trata de una EDO resoluble en series de potencias en torno al origen (véase, por ejemplo, [RAI-72]): una EDO tipo general $u'' +p(r)u'+q(r)=0$ con $p(r)$ regular en el origen y $q(r)$ con un polo doble en el origen; la ecuación indicial tiene por raíces
$c^2 +[\lim_{r\rightarrow 0}rp(r) -1]c+\lim_{r\rightarrow 0}r^2q(r)=c^2-c-l(l+1)=0$
$\Rightarrow c_1=l+1,c_2=-l \quad \Rightarrow \, u=\sum_{n=0}^{\infty} \ a_n \ r^{n+c_i}$ .
-Pero si $l \ne 0$ , la potencia $a_0 r^{-l}$ viola la condición de integrabilidad, quedando pues como candidata a solución físicamente aceptable, o solución al problema de contorno planteado, sólo la correspondiente a la raíz $l+1$ , que satisface la condición de regularidad.
-Si $l= 0$ , entonces para la solución $r^{-l}$ se tiene que $u_{E0}(r) \sim 1$ , que conduce a $R_{E0} \sim r^{-1}$ , que tras aplicar el operador $-\nabla^2$ hace aparecer una $\delta(\vec{r})$ , imposible de contrarrestar con los restantes términos del Hamiltoniano. De nuevo, pues, sólo queda la solución $r^{l+1}$ , regular en el origen: $u_{E0}(0)=0$ .
Una vez incorporada a la resolución la condición de regularidad, en la forma
$u_{El}(r) \ \xrightarrow{r\rightarrow 0} \ \sim r^{l+1}$ ,
la función radial tendrá que comportarse en el entorno del origen según
$R_{El}(r) \ \xrightarrow{r\rightarrow 0} \ \sim r^{l}$ .
En consecuencia, conforme $l$ aumenta tanto $u_{El}(r)$ como $R_{El}(r)$ se van haciendo más pequeñas en ese entorno. Este hecho es una consecuencia de la presencia de la barrera centrífuga, la cual para $l \ne0$ «bloquea» la región próxima al origen, tanto más cuanto mayor es el número cuántico orbital $l$ .
Por lo tanto, para los distintos sistema físicos se plantea resolver el problema de hallar los autoestados del potencial pozo efectivo monodimensional $V_{ef_l}$ , que debe ser definido según:
$V_{ef_l}(x) \,= \, \left\{ \begin{array}{l} \frac{\hbar^2}{2m} \ \frac{l(l+1)}{x^2} \, + \, V(x) \quad x >0 \\ +\infty \quad x \le 0 \end{array} \right. \; , \; l=0,1,2\ldots$ ,
con las condiciones de integrabilidad y regularidad (anulación en el origen) para los estados ligados; para los estados de difusión cambiará la normalización y, a menudo, también bastará exigir $u_{El}$ finita en el origen, aunque muchas veces se tendrá su anulación.
Nota: (cf. [BRA-06], p.131, cita casi textual): existen ejemplos de funciones de onda que son suavemente singulares en el origen; por ejemplo, en la teoría relativista de Dirac para átomos hidrogenoides. En estos casos, la condición de frontera correcta se obtiene requiriendo que todos los estados físicos posibles se describan mediante un conjunto completo ortogonal de funciones de onda. Pero para la mayoría de los potenciales, incluyendo al potencial de Coulomb, esta condición lleva a la de regularidad (anulación $u(r=0)=0$ ) .
En la siguiente figura se muestran las formas típicas de potenciales importantes en Física:
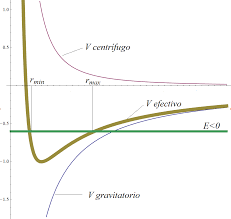
Formas típicas de los potenciales en Física.
En las siguientes entradas, se discutirán algunos casos importantes de potenciales básicos cuyo comportamiento a cortas distancias sea el adecuado para que se garantice el cumplimiento la condición de regularidad, $u_{El}(0)=0$ , teniéndose además que:
$u(r) \ \xrightarrow{r\rightarrow 0} \sim r^{l+1} \ \Rightarrow \ R_{El}(r) \ \xrightarrow{r\rightarrow 0} \sim r^{l}$ .
-Según el tipo de potencial, podrán aparecer, dependiendo del rango de valores de la energía, tanto estados ligados, correspondientes a valores de energía discretos, como estados de difusión, en un rango continuo de energías.
Resultados adicionales para potenciales centrales tridimensionales (véase [GAL-89] vol. I, pp. 286-290): bajo las condiciones matemáticas apropiadas, que satisfarán los potenciales de mayor interés en Física:
-El teorema de Sturm sigue siendo válido en los casos tridimensionales, de forma que los estados ligados se ordenan en función de sus nodos.
-El estado fundamental, de existir, es una onda s, por tanto, presenta simetría esférica.
-El número de estados ligados en onda l+1 no es nunca superior al de estados ligados en onda l.
-Para potenciales centrales que cumplen
$\int_o^{\infty} |V(r)| r^2 dr < \infty$ y $\int_o^{\infty} |V(r)| r dr < \infty$
existe siempre un valor del número cuántico de momento angular l tal que para valores superiores ya no hay estados ligados, por lo que para estos potenciales el número total de estados ligados es siempre finito.

4.3. Ejemplo: El pozo cuadrado finito tridimensional central

Sea el potencial de pozo cuadrado central (esféricamente simétrico) finito definido según:
$V(r)=\left\{ \begin{array}{l} -V_0 \quad 0 \le r \le a \\ 0 \quad r >a \end{array} \right. ; \quad V_0>0 \, , \, a>0$ ,
al que corresponde el potencial efectivo de onda parcial $l$
$V_{ef_l}(r) \,= \, \left\{ \begin{array}{l} \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \, - \, V_0 \quad 0 \le r \le a \\ \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \quad r >a \end{array} \right. \; , \; l=0,1,2\ldots$ ,
un potencial para el que
$V_+=\lim_{r \rightarrow \infty} V_{efl}(r) =0$ .

-Si el valor mínimo del potencial ( $-V_0$ ) se desplaza en una cantidad constante , $-V_0 + \lambda$ , las autofunciones no cambian, ocurriendo tan sólo un desplazamiento constante, de valor $\lambda$ , en los autovalores de energía. Es decir, la adición de una constante (¡con las dimensiones correctas!) al potencial carece de efecto físico: equivale a un mero corrimiento del origen de la escala de la energía. A este respecto, es frecuente, cuando el potencial es acotado para todo el intervalo de valores, escoger el mínimo del potencial en todas la direcciones como el origen de energías, de forma que, como consecuencia, la parte puntual del espectro, sobre la que reposan los autovalores de los estados ligados, esté sobre la semirrecta real negativa, mientras que la parte continua del espectro, compuesta por los autovalores de los estados de difusión, se extienda sobre la semirrecta real positiva, $\mathbb{R}^+=(0,\infty)$ .

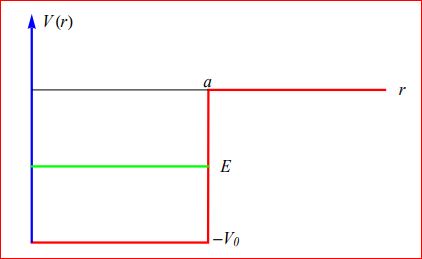
$Pozo cuadrado central o esféricamente simétrico. Si el valor mínimo $latex -V_0$ se desplaza en una cantidad constante , $latex -V_0 + \lambda$ , las autofunciones no cambian, ocurriendo tan sólo un desplazamiento constante, de valor $latex \lambda$ , en los autovalores de energía.$
Pozo cuadrado central o esféricamente simétrico. Si el valor mínimo $-V_0$ se desplaza en una cantidad constante , $-V_0 + \lambda$ , las autofunciones no cambian, ocurriendo tan sólo un desplazamiento constante, de valor $\lambda$ , en los autovalores de energía.

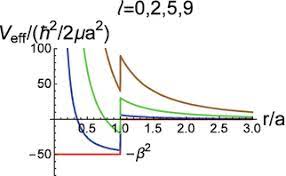
Aspecto del potencial efectivo para algunas ondas parciales (ejemplo general, $\beta^2 \equiv V_0$ y $\mu=m$ ).
Expresada la función de ondas como
$\psi_{Elm}=R_{El}(r)Y_{lm}(\Omega)=\frac{1}{r}u_{El}(r)Y_{lm}(\Omega)$ ,
las ecuaciones radial y reducida son:
$\left. \begin{array}{l} \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, - \, V_0 \ \} \, R_{El}(r) \, = \,E \, R_{El}(r) \quad 0 \le r \le a \\ \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \} \, R_{El}(r) \, = \,E \, R_{El}(r)\quad r >a \end{array} \right\}$
$\left. \begin{array}{l} \{ -\frac{\hbar^2}{2m} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \, - \, V_0 \ \} \, u_{El}(r) \, = \,E \, u_{El}(r) \quad 0 \le r \le a \\ \{ -\frac{\hbar^2}{2m} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \ \} \, u_{El}(r) \, = \,E \, u_{El}(r) \quad r >a \end{array} \right\}$
$\equiv \, H_l u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2m} \ \frac{d^2}{d r^2} \,+ \, V_{ef_l}(r) \ \} \ u_{El}(r)\, = \,E \, u_{El}(r)$ ;
las soluciones buscadas han de satisfacer la condición de regularidad,
$u_{El}(0)\, = \, 0 \, , \, \forall l$ ,
con $u_{El}(r) \ \xrightarrow{r\rightarrow 0} \ 0$ más rápido que $r^l \xrightarrow{r\rightarrow 0} \ 0$ , ya que $R_{El}(r)=u(r)_{El} /r$ debe ser continua (finita) en el origen para todos los valores $l$ ; adicionalmente, los estados ligados (no así los estados de difusión) han de de cumplir también la condición de integrabilidad, que permitirá normalizarlos:
$\int_0^{\infty} \ |u_{El} |^2 \ dr \, = \, 1$ .
En la resolución se encuentran los resultados:
a) Si $\frac{2ma^2|V_0|}{\hbar^2} < \frac{\pi^2}{4}$ :
–No existen estados ligados, sólo estados de difusión, correspondientes a valores $E \ge 0$ , integrando la parte continua del espectro, $\sigma_c(H) = [0,\infty)$ , con autofunciones que presentan conducta oscilatoria a largas distancias y satisfacen la condición de regularidad pero no así la condición de integrabilidad.
b) Si $\frac{2ma^2|V_0|}{\hbar^2} \ge \frac{\pi^2}{4}$ :
-Se presentan tanto estados de difusión, para $E \ge 0$ , como estados ligados en algunas ondas l, teniéndose para la parte discreta del espectro que $\sigma_p(H) \subset (-|V_{0}| ,0]$ , con autofunciones que satisfacen tanto la condición de regularidad como la de integrabilidad.
c) El valor $E=0$ puede ser, dependiendo del caso, o bien un estado ligado, o bien un estado de difusión.
A diferencia de lo que sucede en los casos monodimensional y bidimensional, donde hay siempre al menos un estado ligado, en tres dimensiones un pozo, por ejemplo si es demasiado estrecho o poco profundo, o ambas cosas, puede carecer de estados ligados. Además, los estados ligados en el caso tridimensional sí pueden presentar degeneración: aunque estados de energía correspondientes a distintas ondas parciales (distintos valores de $l$ ) no suelen estar degenerados, la degeneración en el número cuántico de tercera componente está presente: cada nivel de energía de onda parcial $E_{l}$ es $(2l+1)$ veces degenerado (algo común a todos los potenciales centrales).

Referencias

[ABR-65] Abramowitz, Milton; Stegun, Irene A., eds.; “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables”; Dover; New York, 1965; ISBN 978-0-486-61272-0.

[BAL-98] Ballentine, L.E.; “Quantum Mechanics: A Modern Development”; World Scientific; Singapore, 1998.

[BER-18] Berman, P.R.; “ Introductory Quantum Mechanics: ”; Springer, 2018; https://doi.org/10.1007/978-3-319-68598-4_10.

[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.

[BRA-06] Bransden, B.H. and Joachain, C.J.; «Physics of Atoms & Molecules»; Longman, New York, 1983 (2nd ed.: Pearson; Dorchester, 2000).

[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.

[NEU-91] Neumann, J. von; «Fundamentos matemáticos de la Mecánica Cuántica», CSIC, Raycar, Madrid, 1991.

[RAI-72] Rainville, E.D., «Intermediate Differential Equations», Chelsea Pub. Co.; N.Y., 1972.

[SCH-68] Schiff, L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.

Páginas complementarias

La función de onda radial en el blog lamecanicacuantica.blogspot.com
Wolfram: https://demonstrations.wolfram.com/ParticlesIn1DAnd3DBoxes/
Particle in 2D y 3D boxes: https://web.iitd.ac.in/~pramitc/Lecture%20review%207_Particle%20in%20a%20box%20%283D&2D%29.pdf
La caja de potencial: http://www.sc.ehu.es/sbweb/fisica3/cuantica/separacion/separacion.html
Partícula en una caja tridimensional: https://web.iitd.ac.in/~pramitc/Lecture.pdf
Estados ligados en un pozo de potencial esféricamente simétrico: https://quantummechanics.ucsd.edu/ph130a/130_notes/node227.html
Finite spherical square well potential: deuteron, with the use of Mathematica, by Masatsugu Sei Suzuki and Itsuko S. Suzukhttps; Department of Physics, SUNY at Binghamton: https://bingweb.binghamton.edu/~suzuki/QuantumMechanicsII/5-4_Finite_spherical_well.pdf
Página interactiva para, a partir de las funciones esféricas de Bessel y de Hankel, encontrar las soluciones a la ecuación de Schrödinger en el pozo cuadrado 3D (un átomo): https://support.ptc.com/help/mathcad/r9.0/es/index.html#page/PTC_Mathcad_Help/example_bessel_functions.html
Funciones especiales: https://es.mathworks.com/help/matlab/special-functions.html?s_tid=CRUX_lftnav
NIST Digital Library of Mathematical Functions
Funciones de Bessel: http://www.sc.ehu.es/sbweb/fisica3/especial/bessel/bessel.html
Funciones de Bessel en la Wikipedia en inglés:
https://en.wikipedia.org/wiki/Bessel_function#Spherical_Bessel_functions
Funciones de Bessel en la Wikipedia en español: https://es.wikipedia.org/wiki/Funci%C3%B3n_de_Bessel
Modelos para pozos tridimensionales: http://www.fisica.unlp.edu.ar/materias/expcuani/2019-centros-f/centros%20F%20pozos%20de%20potencial%20-%20Leo.pdf
Wolfram:
-Particle in an Infinite Circular Well: https://demonstrations.wolfram.com/ParticleInAnInfiniteCircularWell/
-Particle in an Infinite Spherical Well: https://demonstrations.wolfram.com/ParticleInAnInfiniteSphericalWell/

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

Potenciales separables

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta