Autofunciones de energía
(repetición)
- El problema general de autovalores de energía para un sistema conservativo,
,
dondees una función potencial satisfaciendo determinados requisitos matemáticos, es equivalente a la resolución de la ecuación de Schrödinger independiente del tiempo, o ecuación diferencial ordinaria (EDO)
,
con la incorporación de las adecuadas condiciones de contorno que permitan extraer de la solución general las soluciones físicamente aceptables: soluciones que cumplan quesea una función continua
; para su derivada primera
se exigirá también continuidad, salvo en el caso de potenciales que presenten discontinuidades de segunda especie. Además, para que una solución matemática del problema sea físicamente aceptable, habrá de satisfacer, alternativamente:
- En el caso de funciones
, que representan estados ligados del sistema, se requerirá
.
- En el caso de funciones
, que representan estados no ligados o de difusión del sistema, se impondrá sólo
,
.
- En el caso de funciones
- Aparecen pues dos tipos de soluciones físicamente aceptables:
- Estados ligados:
-
- Son las soluciones que existen asociadas sólo a algunos valores discretos específicos del parámetro de energía
(fenómeno de cuantización de la energía), para los cuales el problema tiene solución físicamente aceptable
no nula. Es decir, existe una función
que puede ser tomada como función de onda (independiente del tiempo) del problema de autovalores planteado, ya que satisface la ecuación
y, además, cumplen
continua
,
.
Un ejemplo de una autofunción de energía de este tipo se representa en la siguiente figura:
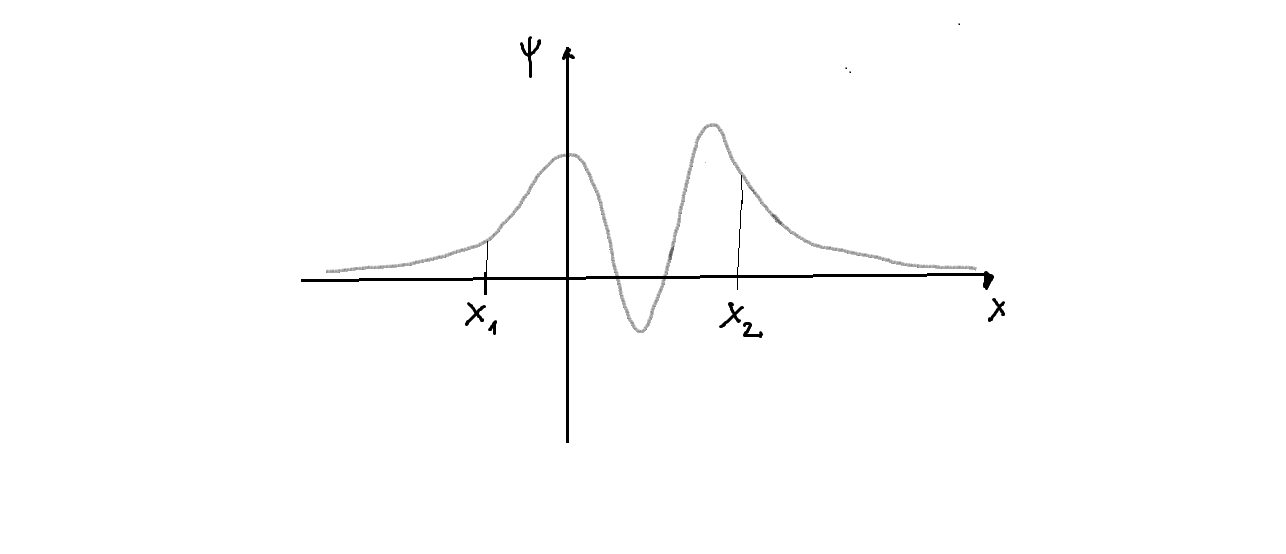
- Son las soluciones que existen asociadas sólo a algunos valores discretos específicos del parámetro de energía
- Estas autofunciones de energía se dice que representan estados ligados (bound-states), y a los valores discretos de
para los que existen esas soluciones se les denomina energías de estados ligados.
- Para los estados ligados:
, donde
es autovalor en sentido estricto (no sólo generalizado).
continuas
(siempre que la función
sea finita
).
.
- Son funciones de cuadrado integrable Lebesgue, es decir,
, y lo mismo para
siempre que
sea continuo o continuo a trozos, es decir, finito
.
.
-
- Estados de difusión:
- Son las soluciones que existen asociadas a valores del parámetro de energía
que se sitúan en la parte continua del espectro del Hamiltoniano y para los cuales el problema tiene solución físicamente aceptable
no nula. Es decir, existe una función
que puede ser tomada como función de onda (independiente del tiempo) del problema de autovalores planteado, ya que satisface la ecuación
y, además, se tiene
continua
. Estas autofunciones no se anulan en general a largas distancias,
, aunque sí permanecen acotadas,
,
.
-Un ejemplo de una autofunción de energía de este tipo se representa en la siguiente figura:
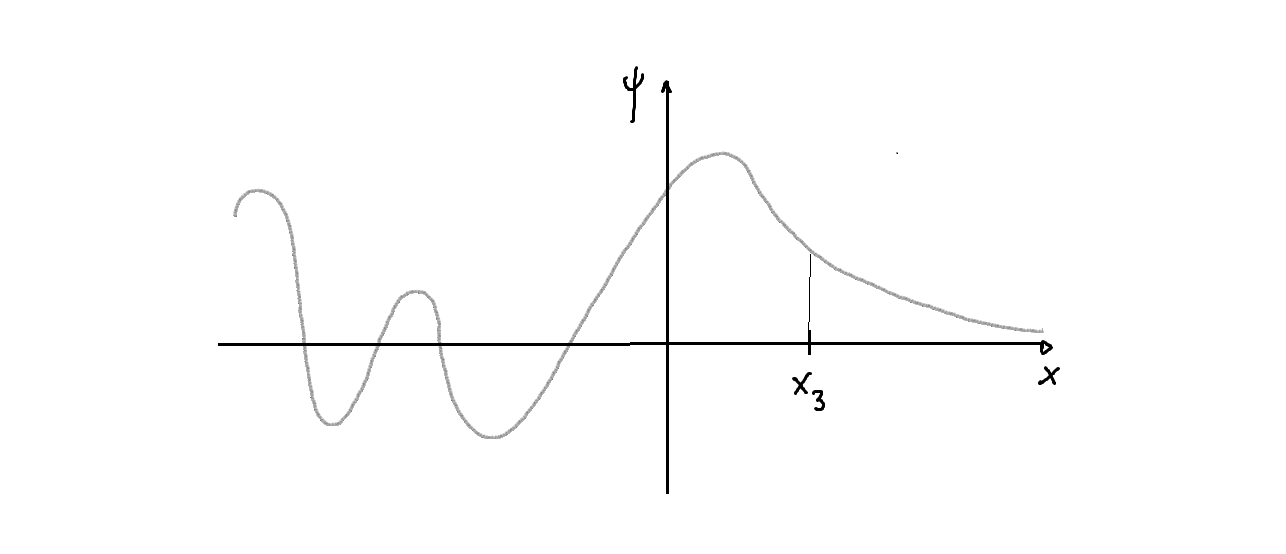 Estas autofunciones de energía se dice que representan estados de difusión.
Estas autofunciones de energía se dice que representan estados de difusión.
-Nota: pueden existir también estados de difusión que se anulen a largas distancias, es decir, que cumplan: son estados oscilatorios que tienden a cero a largas distancias y que sin embargo no son de cuadrado integrable, pues se mantienen oscilando demasiado lejos; un ejemplo de estos estados aparece para el potencial coulombiano.
- Las soluciones de este tipo, que surgen asociadas a autovalores (en sentido sólo generalizado) de energía en la parte continua del espectro del operador, cumplen pues las condiciones de contorno:
,
,
y no son funciones de cuadrado integrable Lebesgue,.
- Son las soluciones que existen asociadas a valores del parámetro de energía
- Estados ligados:
- Dimensiones de
: recuérdese que las dimensiones para una función de onda en el espacio de configuración son:
(1 partícula, espacio tridimensional
), donde
simboliza longitud (en general,
, donde
simboliza el número de partículas y
la dimensión espacial).
Normalización de las autofunciones de energía
- Normalización de los estados ligados:
Los estados ligados son funciones del Hilbert, de forma que para normalizarlos basta dividirlos por su norma: dado un estado ligado
no normalizado,
,
la funciónestará siempre normalizada, esto es, su norma es la unidad:
.
- Normalización de los estados de difusión:
- Puesto que estas funciones no son de cuadrado integrable Lebesgue, surge el problema de que es imposible satisfacer el requisito
,
ya que la correspondiente integral resulta divergente. Así que, en ausencia de una normalización, no se les podría interpretar asociándoles (a su módulo al cuadrado) una densidad de probabilidad, ni calcular valores esperados sobre ellas. - Para su normalización usualmente se recurre a dos procedimientos alternativos:
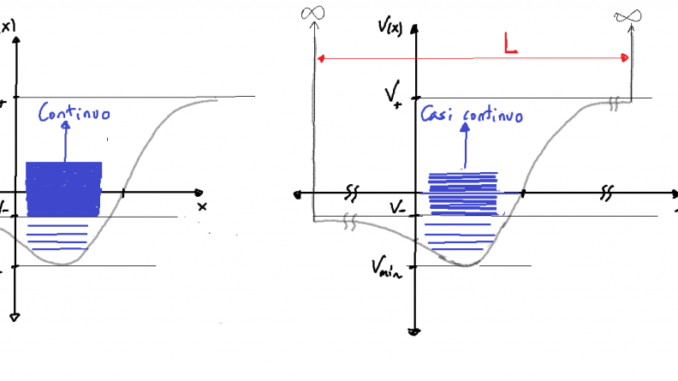
- Confinamiento en una región muy extensa, pero de volumen
finito:
- En una dimensión, este procedimiento restringe el movimiento de la partícula a un intervalo de longitud dada
de la recta real, y la condición de normalización de la densidad de probabilidad adquiere entonces la expresión
.
- En este procedimiento, se supone que la partícula no puede salirse de ese intervalo especificado, lo cual suele conllevar asumir que en los extremos del intervalo se sitúan barreras de potencial infinito. Consecuentemente, la función de onda debe anularse en los extremos del intervalo, y de esta manera se fuerza a los estados de energía en el continuo a convertirse en estados ligados: se introduce una discretización del espectro continuo de energía. Pero, si la dimensión
del intervalo se toma lo suficientemente grande, esta discretización será prácticamente inapreciable: el efecto sobre el espectro energético se puede despreciar, habiéndose sin embargo superado la dificultad matemática de normalizar a las funciones, de manera que ya se les puede asociar la correspondiente densidad de probabilidad y, por lo mismo, calcular sobre ellas valores esperados de operadores.
Nota: pero, por ejemplo, para ondas planas, que son las autofunciones en el problema de la partícula libre, se han de imponer condiciones del tipo periódico:)
- Gráficamente, el proceso corresponde a la transición entre las dos gráficas en la figura siguiente:
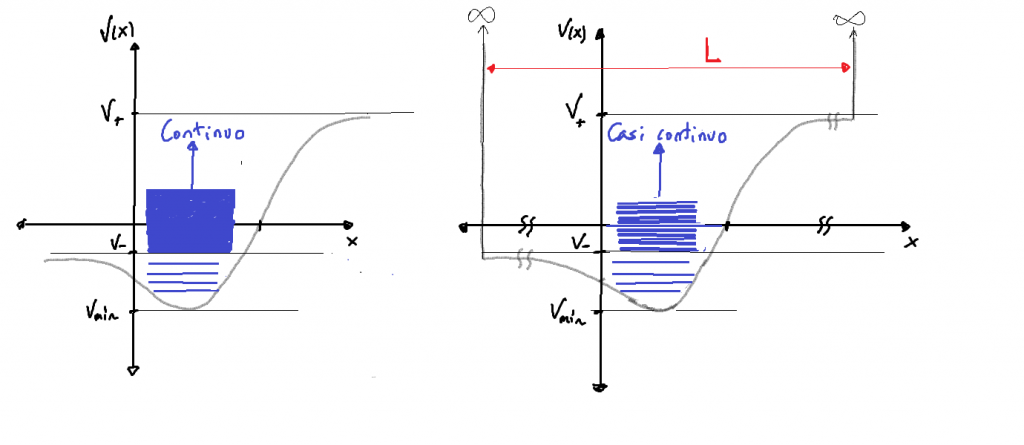
- Estrictamente hablando, no todos los valores
integrantes del espectro energético se habrán conservado, pues se ha sustituido un intervalo continuo por uno casi-continuo (es decir, discreto en realidad, por muy cercanos que estén estos valores discretos). Pero si
es suficientemente grande, en la práctica puede ignorarse esta pérdida.
- En tres dimensiones se procede análogamente: los estados de difusión se normalizan confinando al sistema en una región muy extensa, pero de volumen
finito: una caja de paredes que usualmente se fijan como impenetrables, en cuyo caso sobre las superficies que la delimitan se impone la anulación de la función de onda.
La correspondiente condición de normalización es:
.
- En una dimensión, este procedimiento restringe el movimiento de la partícula a un intervalo de longitud dada
- Normalización a la delta de Dirac:
.
-En tres dimensiones:
.
- Confinamiento en una región muy extensa, pero de volumen
- Puesto que estas funciones no son de cuadrado integrable Lebesgue, surge el problema de que es imposible satisfacer el requisito
Propiedades de las autofunciones y autovalores de energía (II)
- Las autofunciones de energía
, soluciones para un cierto autovalor de energía
del problema de autovalores de la energía o ecuación de Schrödinger independiente del tiempo,
, poseen las siguientes propiedades:
(Nota: en lo siguiente, se supondrá que todas las autofunciones han sido sometidas a un proceso de normalización de entre los expuestos anteriormente, y de ello dependerá a qué zona concreta se extiendan las integrales involucradas, región que en algunos casos no se indicará expresamente).- Autofunciones correspondientes a distintos autovalores son ortogonales entre sí:
Es decir, dadas
, solución de
,
, solución de
,
y siendo, se implica:
.
En efecto:
(anulación debida al carácter autoadjunto y, por tanto, hermítico, del operador) .
- Autofunciones linealmente independientes correspondientes al mismo autovalor de energía pueden elegirse como ortogonales entre sí:
Sean, un conjunto (finito o infinito numerable) de autofunciones linealmente independientes correspondientes al autovalor
, que presenta por tanto degeneración
.
De entrada estas autofunciones pudieran no ser ortogonales entre sí, pero por la aplicación de un método de ortonormalización adecuado (como, por ejemplo, el método de Gram-Schmidt), pueden convertirse en un conjunto alternativo, ya ortonormal, de autofunciones (la elección no única), que genera como su envolvente lineal cerrada el mismo subespacio del Hilbert,,
, que el conjunto original primero.
- Ortonormalidad:
El conjunto de autofunciones de energía puede elegirse siempre de manera que constituya un sistema ortonormal (la elección no es única): existe un conjunto de autofunciones de energía,
,
tal que satisface:
,
es decir, que constituye un conjunto ortonormal.
-Nota 1: recuérdese que un conjunto ortonormal es siempre linealmente independiente.
-Nota 2: si se hubiera optado por normalizar los estados del continuo mediante la delta de Dirac, las correspondientes deltas de Kronecker enen la expresión anterior pasarían a ser deltas de Dirac.
- Autofunciones correspondientes a distintos autovalores son ortogonales entre sí:
Postulados fundamentales
- Considerado el problema de autovalores de energía
,
dondees el operador Hamiltoniano de un sistema conservativo, independiente del tiempo y que representa la energía total,
,
entonces:-
- Postulado sobre los autovalores de energía:
«El espectro de energíasobtenido al resolver dicho problema de autovalores (ecuación de Schrödinger independiente del tiempo) representa todas las energías posibles para el correspondiente sistema físico».
- Postulado sobre las autofunciones de energía:
«Cada conjunto ortonormal de autofunciones
,
considerados todos los autovalores (propios y generalizados) de energía del Hamiltoniano y aportando cada uno de ellos un número de autofunciones igual a su degeneración, constituye una base ortonormal del correspondiente espacio de Hilbert asociado al sistema físico constituido por una partícula material no relativista en el seno de un potencial conservativo» .
-Nota: en rigor, se trata pues, en general, de una base ortonormal generalizada: incluye funciones que no son del Hilbert, los estados de difusión.
- Postulado sobre los autovalores de energía:
-
Solución general de la ecuación de Schrödinger para un potencial (independiente del tiempo)
- Teorema (forma 1): La solución general
de la ecuación de Schrödinger para un sistema conservativo,
,
admite desarrollo en serie en términos de un conjunto ortonormal de autofunciones de energía según la expresión:
, donde
representa los coeficientes del desarrollo, escalares que pueden depender de la variable tiempo
:
-Esta forma 1 del teorema corresponde al caso en se han normalizado los estados del continuo procediendo a su discretización.
-La correspondiente relación de cierre o clausura toma la expresión (en notación de Dirac):
donderepresenta el operador identidad.
- Teorema (forma 2): La solución general
de la ecuación de Schrödinger para un sistema conservativo,
admite desarrollo en serie en términos de un conjunto ortonormal de autofunciones de energía según la expresión:
;
que en notación de Dirac toma la expresión:
-Esta forma 2 del teorema corresponde al caso en se han normalizado los estados del continuo vía la delta de Dirac, tomando ahora la relación de cierre o clausura la expresión:
- Nota: si no se adopta la notación de Dirac, la relación de cierre o clausura se escribe:
-Forma 1:
-Forma 2:
Referencias
[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.
[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.
[SCH-68] Schiff, L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.
Páginas complementarias
http://la-mecanica-cuantica.blogspot.com.es/2009/08/solucion-matematica-de-la-ecuacion-de.html
http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-espacio-de-hilbert-ii.html
http://la-mecanica-cuantica.blogspot.com.es/2009/08/evolucion-temporal-de-las-ondas-de.html
APPS
Dejar una contestacion