Método variacional

Introducción

Existen muy pocos sistemas de interés físico para los que la resolución pueda realizarse de forma exacta, tanto en la mecánica cuántica como en la clásica. En consecuencia, los métodos aproximados van a ser muy importantes en la mayoría de las aplicaciones, y en su desarrollo serán muy útiles como recurso los escasos sistemas que admiten resolución analítica: sus soluciones se usarán a menudo como punto de partida para la resolución aproximada.
Los principales métodos aproximados en mecánica cuántica se clasifican en:
a) Métodos perturbativos, de un lado, para aquellos problemas en que sea posible descomponer el Hamiltoniano $H$ de la forma
$H=H_0+\lambda H' \; , \; \lambda \in \mathbb{R}$ ,
donde el sumando $H_0$ es el «Hamiltoniano no perturbado» y $\lambda H'$ representa el «Hamiltoniano de perturbación», que es supuesto cumpliendo las condiciones tanto de que la ecuación de Schrödinger a orden cero correspondiente,
$H_0 \ \psi_n^{(0)} \, = \,E_n^{(0)} \ \psi_n^{(0)}$
admita resolución sencilla, analítica o numérica, como de que la perturbación «sea pequeña», en el sentido de que la magnitud de la corrección no altere el orden energético establecido en el estadio sin perturbación.
b) Métodos variacionales, útiles en aquellos problemas en que se disponga, por razones de tipo físico o matemático, de una idea previa aproximada sobre la forma de la función de onda buscada.

Método variacional para estados ligados estacionarios

El método variacional para estados estacionarios ligados o teoría de Rayleigh-Ritz se aplica al caso de un sistema conservativo, con un Hamiltoniano $H$ independiente del tiempo, que supondremos de espectro
$\sigma(H)= \sigma_p(H) \cup \sigma_c(H) \doteq \{ E_0,E_1,E_2,\ldots , E_i, \ldots \}$ , y con $\sigma_p(H) \ne \varnothing$ , no vacío, de manera que unificamos la notación para las dos partes del espectro, debiendo entenderse la diferencia de significado en las distintas fórmulas en que intervengan estados ligados y de difusión.
-Los autovalores se supondrán ordenados en orden creciente de energía ( $E_{GS} \doteq E_0$ ya que la parte dicreta del espectro no es vacía), y las autofunciones se representarán como $\{ \psi_{i \alpha_i} \, , \, \alpha_i=1,2,\ldots,g_i=deg(E_i) \}$ .
La fundamentación teórica del método es el principio variacional de Rayleigh-Ritz, cuyo enunciado establece que la resolución del problema de autovalores $H |\psi>=E|\psi>$ equivale a la resolución del problema variacional
$\delta E(\psi)=0 \; , \; E(\psi)=\frac{\left< \psi | H |\psi \right>}{\left< \psi | \psi \right>}$ ,
esto es:
$H |\psi>=E|\psi> \ \Leftrightarrow \ \delta E(\psi)=0$ .
-En efecto:
$\left< \psi | \psi \right> E(\psi) \, = \, \left< \psi | H |\psi \right>$
$\Rightarrow \left< \psi | \psi \right> \delta E(\psi) \, + \, E (\delta \left< \psi | \psi \right>) \, = \, \delta (\left< \psi | H |\psi \right>)$
$\Rightarrow \delta E(\psi) \, = \, \frac{1}{\left< \psi | \psi \right>} \ \delta(\left< \psi | H - E|\psi \right>)$ ,
de donde se deriva la expresión inicial,
$H |\psi>=E|\psi> \ \Leftrightarrow \ \delta E(\psi)=0$ .
Puesto que $H$ es un operador autoadjunto, sus autofunciones $\{ \psi_{i \alpha_i} \}$ constituyen una base ortonormal (un conjunto ortonormal completo) del espacio, en el cual se podrán integrar, por lo dicho y en su caso, funciones generalizadas.
-Si el espectro del hamiltoniano es puramente discreto, $\sigma(H)=\sigma_p(H)$ , la relación de ortonormalidad de los estados de la base se expresa:
a) Para estados ligados:
$\left< \psi_n \ | \ \psi_m \right> \, = \, \delta_{n,m} \;$ ,
si ningún estado es degenerado, o
$\left< \psi_{n,k} \ | \ \psi_{m,k'} \right> \, = \, \delta_{n,m} \ \delta_{k,k'}$
si la base integra autoestados ligados degenerados;
b) Para estados generalizados: en este casos la relación de ortonormalización pasa a escribirse en términos de la delta de Dirac:
$\left< \psi_{E, k} \ | \ \psi_{E', k'} \right> \, = \, \delta (E-E') \ \delta_{k,k'}$
-Por simplicidad de la notación, se suele considerar que la primera notación, en término de dos deltas de Kronecker, recoge todas las posibilidades.
Cualquier estado del sistema, esto es, cualquier estado del Hilbert asociado al sistema, admite pues expresión en la base:
$\psi \, = \, \sum_i \sum_{\alpha =1}^{g_i} c_{i\alpha} | \psi_{i\alpha} >$
(donde se ha unificado la notación para estados ligados y del continuo, de forma que la sumatoria representa tanto una suma discreta para los puntos discretos del espectro energético como una integral sobre la parte continua; además, al ser en la expresión $\alpha$ un índice mudo, no fijo, es superfluo usar en la notación $\alpha_i$ y se ha suprimido el subíndice $i$ ).
-Esta expresión permite el cálculo del valor medio del Hamiltoniano sobre cada estado, esto es, el correspondiente elemento de matriz del Hamiltoniano:
$< \psi | H | \psi > \, = \, \sum_i \sum_{\alpha =1}^{g_i} \sum_{i'} \sum_{\alpha' =1}^{g_i'} c_{i\alpha}^* c_{i'\alpha'} < \psi_{i\alpha} | H | \psi_{i'\alpha'} >$
$= \, \sum_i \sum_{\alpha =1}^{g_i} | c_{i\alpha}|^2 E_i \ge E_0 \sum_i \sum_{\alpha =1}^{g_i} | c_{i\alpha}|^2 =E_0 < \psi | \psi >$ ,
de donde se deriva la desigualdad:
$\Rightarrow E_0 \le E(\psi) = \frac{< \psi | H | \psi >}{< \psi | \psi >}$
-Es decir, para cualquier estado $\psi$ del sistema, el valor medio de la energía proporciona una cota superior a la energía del estado fundamental.
-Caso particular: sea $M_i$ el subespacio generado por el subconjunto de la base integrado por las autofunciones degeneradas en energía correspondientes al autovalor $E_i$ , conjunto $\{ \psi_{i \alpha_i} \}_{\alpha_i=1}^{g_i}$ , de modo que se satisface:
$| \psi > \in M_0 \Rightarrow H | \psi > = E_0 \ |\psi> \Rightarrow E( \psi )= E_0$ ,
esto es, la cota coincide con el valor exacto.
Para aplicar el método variacional, es obvio que es imposible probar todas las funciones del espacio, por lo que es usual arrancar considerando una familia de estados, denominados como los estados o funciones prueba, que dependen de $n$ parámetros $\lambda_1,\ldots,\lambda_n$ ; a partir de ellos, se calcula el valor
$E(\psi)= \frac{< \psi(\lambda_1,\ldots,\lambda_n) | H | \psi(\lambda_1,\ldots,\lambda_n) >}{< \psi | \psi >}$ ,
procediendo a continuación a minimizar respecto a los parámetros:
$\frac{\partial E(\psi)}{\partial \lambda_i} =0 \, , \, i=1,\ldots,n$ .
-Se logra obtener así la mejor cota y el mejor estado de toda la familia de prueba.

Estado fundamental

Cualquier estado normalizado $| \psi>$ puede escribirse en la forma
$| \psi> \, = \, P_{M_0} | \psi> \ + \ \epsilon | \varphi>$ ,
donde $| \varphi>$ es el estado normalizado que satisface $| \varphi> \perp M_0$ y $P_{M_0}$ representa el proyector ortogonal sobre el subespacio $M_{0}$ . De este hecho se deriva que:
$< \psi | \psi > = 1 = ||P_{M_0} |\psi> ||^2 \ + \ |\epsilon|^2$
$\Rightarrow E_0 \le \; < \psi | H | \psi > = < P_{M_0} \psi + \epsilon \varphi | H |P_{M_0}\psi + \epsilon \varphi>$
$= E_0 < P_{M_0} \psi | H |P_{M_0}\psi > +|\epsilon|^2 < \varphi | H | \varphi > = E_0( 1-|\epsilon|^2) + |\epsilon|^2< \varphi | H | \varphi >$
$= E_0 + |\epsilon|^2 \ [ < \varphi | H | \varphi > - E_0]$ ,
de modo que $E(\psi)$ difiere de $E_0$ en un término de orden 2 en $\epsilon$ .
-Conclusión: si el estado $\psi$ difiere de un elemento del subespacio $M_0$ en términos de orden 1 en $\epsilon$ , la cota de la energía que suministra difiere del valor de la energía $E_0$ en términos de orden 2 en $\epsilon$ . Aunque también puede suceder que el término que multiplica a $|\epsilon|^2$ fuese demasiado grande…

Estados excitados

Si se conoce cuál es el espacio $M_{0}$ , es posible elegir $|\psi>$ de manera que $|\psi> \perp M_{0}$ y proceder como anteriormente:
$|\psi> \perp M_{0} \Rightarrow |\psi> \, = \, \sum_{i\ne 0} \sum_{\alpha =1}^{g_i} c_{i\alpha} | \psi_{i\alpha} >$
$\Rightarrow < \psi | H | \psi > \, = \, \sum_{i \ne 0} \sum_{\alpha =1}^{g_i} \sum_{i'\ne 0} \sum_{\alpha' =1}^{g_i'} c_{i\alpha}^* c_{i'\alpha'} < \psi_{i\alpha} | H | \psi_{i'\alpha'} >$
$= \, \sum_{i\ne 0} \sum_{\alpha =1}^{g_i} | c_{i\alpha}|^2 E_i \ge E_1 \sum_{i\ne 0} \sum_{\alpha =1}^{g_i} | c_{i\alpha}|^2 =E_1 < \psi | \psi >$ ,
de donde se deriva la desigualdad para la energía del primer estado excitado:
$\Rightarrow E_1 \le E(\psi) = \frac{< \psi | H | \psi >}{< \psi | \psi >} \,, \, |\psi> \perp M_{0}$
De forma análoga se obtiene una cota superior a cada nivel excitado sucesivo $E_i$ , siempre que la correspondiente $|\psi>$ se elija de manera que $|\psi> \perp (M_{0} \oplus M_1 \oplus \ldots \oplus M_{i-1})$ .
La incorporación de las condiciones adicionales que se vayan imponiendo (normalizaciones, ortogonalidad, etc.) puede hacerse también mediante los correspondientes multiplicadores de Lagrange, desarrollando así un método variacional condicionado.

Aplicación práctica del método

En la práctica, es difícil conocer cuáles son en cada caso los distintos subespacios $M_i$ asociados a cada valor propio, pero a veces sucede que sí se conoce una información previa que facilita el proceso. Por ejemplo, se conocen algunas propiedades del estado fundamental (número de nodos, comportamientos asintóticos…); una serie de números cuánticos, asociados con sendas constantes del movimiento, cuyas correspondientes funciones de ondas poseen estructura conocida; etc. En estos casos, basta tomar funciones prueba con ese comportamiento, que se correspondan con valores fijos de determinados números cuánticos, para tener garantizado de que los valores medios de la energía en esos estados no son inferiores al menor valor de energía correspondiente a un nivel con esas propiedades.
-Por ejemplo, si el momento angular es una constante del movimiento, por tenerse simetía esférica en el problema, se pueden tomar funciones prueba con momento angular $J$ y tercera componente $M$ fijos, que permitirán obtener una cota superior a la energía del nivel fundamental en cada onda $JM$ .

Ejemplos

A. Partícula en un pozo cuadrado infinito monodimensional

Sea el potencial de pozo cuadrado infinito
$V(x) = \left \{ \begin{matrix} V_o & \mbox{si } |x| < a\;:\; zona \;\; I \\ +\infty & \mbox{si } |x| \ge a\;: \; zona \;\; II \; \end{matrix}\right.$
donde $V_o$ es un número real, con dimensiones de energía y que puede ser positivo o negativo.

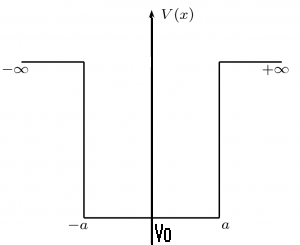
-Se trata de una función con discontinuidades de segunda especie en los puntos $x=\pm a\; \; ,\;a\in \mathbb{R}\;,\; a > 0$ , puntos en los que se sitúan sendas barreras impenetrables de potencial; por lo tanto, en ellos se debe imponer la condición de frontera de anulación de la función de onda $\psi(x)$ : se produce el confinamiento o ligadura de la partícula en el interior del intervalo $(-a,a)$ de la recta real, de longitud $L=2a$ .
Aparece pues el fenómeno de cuantización de la energía, ya que sólo hay solución físicamente aceptable del problema de autovalores para los valores discretos de energía
$E_n=\frac{\hbar^2k_{n}^2}{2m}+V_o=\frac{\hbar^2\pi^2n^2}{2mL^2}+V_o=\frac{\hbar^2\pi^2n^2}{8ma^2}+V_o$ ,
asociados respectiva y alternadamente a los dos tipos de autofunciones:
$\psi_n^+(x)=Acos(\frac{n\pi}{2a}x)\;,\;n=1,3\ldots$
$\psi_n^-(x)=Bsen(\frac{n\pi}{2a}x)\;,\;n=2,4\ldots$
-Normalizadas,
$\int_{-\infty}^{+\infty} |\psi_n^{\pm}(x)|^2dx=1 \Rightarrow |A|^2=\frac{1}{a} \Rightarrow |A|=\frac{1}{\sqrt{a}}$
las autofunciones normalizadas se expresan:
$\psi_n^+(x)=\frac{1}{\sqrt{a}} \ cos(\frac{n\pi}{2a}x)\;,\;n=1,3\ldots$
$\psi_n^-(x)=\frac{1}{\sqrt{a}} \ sen(\frac{n\pi}{2a}x)\;,\;n=2,4\ldots$
en la zona I; fuera de esta zona siempre $\psi_n^{\pm}(x)=0$ .
-El conjunto de autofunciones $\{ \psi_n^{\pm} \}_{n=1}^{+\infty}$ constituye un conjunto ortonormal.
-Como corresponde a las autofunciones ligadas de un potencial unidimensional simétrico, $V(x)=V(-x)$ , todas las autofunciones tienen paridad definida: cada $\psi_n^{+}$ es par, cada $\psi_n^{-}$ es impar.
-El estado fundamental posee una energía:
$E_{GS}=E_1+V_o=\frac{\hbar^2k_{1}^2}{2m}+ V_o =\frac{\hbar^2 \pi^2}{8ma^2}+V_o \ne V_o$ ,
denominada energía del punto cero; la correspondiente autofunción par es:
$\psi_{GS}^+(x)=\frac{1}{\sqrt{a}} \ cos(\frac{\pi}{2a}x)$ .
Como ilustración sencilla del método variacional, supondremos desconocida la solución exacta $\psi_0(x)$ del problema, aunque sí se asume que conocemos algunas de sus propiedades:
-Que debe ser una función par.
-Que debe anularse $\forall \ |x| >a$ .
A partir de esta información, escogemos como función prueba para la aplicación del método variacional, para el estado fundamental, la función:
$\psi_0(x,c) = \left \{ \begin{matrix} (a^2-x^2) \ (1+ cx^2) & \mbox{si } |x| < a\;:\; zona \;\; I \\ 0 & \mbox{si } |x| \ge a\;: \; zona \;\; II \; \end{matrix}\right.$ ,
donde $c$ representa el correspondiente parámetro variacional.
El paso siguiente es calcular el funcional:
$E(\psi) = \frac{< \psi | H | \psi >}{< \psi | \psi >}$
$= \frac{-\frac{\hbar^2}{2m} \int_{-a}^{a}(a^2-x^2) (1+ cx^2) \frac{d^2}{dx^2}[(a^2-x^2) \ (1+ cx^2)] \ dx}{\int_{-a}^{a}(a^2-x^2) (1+ cx^2) \ dx}$
$=(\frac{3\hbar^2}{4ma^2}) \frac{11a^4c^2 +14 a^2 c +35}{a^4c^2 +6a^2c+21} \equiv E(c) \ge E_0$
-A continuación, se minimiza respecto al parámetro $c$ :
$\frac{dE(\psi(c))}{dc}=0=26a^4c^2 +196 a^2 c +42$
$\Rightarrow \left\{ \begin{matrix} c_1=-0.22075 \frac{1}{a^2} \Rightarrow E(\psi(c_1))=1,23372 \frac{\hbar^2}{ma^2}\\ c_2=-7,31771 \frac{1}{a^2} \Rightarrow E(\psi(c_2))=12,7663 \frac{\hbar^2}{ma^2} \end{matrix}\right\}$ ,
de modo que la mejor cota superior, para el tipo de función de prueba elegido, es el correspondiente al valor $c_1=-0.22075 \frac{1}{a^2}$ , teniéndose:
$E_0^{ex.} \le E(\psi(c_1))= 1,23372 \frac{\hbar^2}{ma^2}$ .
-Y en efecto, la aproximación es muy buena:
$E_0^{ex.}= \frac{\hbar^2 \pi^2}{8ma^2}= 1,23370 \frac{\hbar^2}{ma^2} \le E(\psi(c_2))=1,23372 \frac{\hbar^2}{ma^2}$
Respecto a la función de onda del estado fundamental, en la zona $|x| < a$ :
$\psi_{GS}^+(x)=\frac{1}{\sqrt{a}} \ cos(\frac{\pi}{2a}x) = \frac{1}{\sqrt{a}} \ [ \ 1- \frac{1}{2!}(\frac{\pi}{2a}x)^2 + \frac{1}{4!} (\frac{\pi}{2a}x)^4 - \cdots ]$
$\psi(c_1))=(a^2-x^2) \ (1 - 0.22075 \frac{x^2}{a^2}) = a^2-(1 + 0.22075) x^2 + 0.22075 \frac{x^4}{a^2}$ ,
la segunda por normalizar y ambas sin nodos (la solución para $c_2$ sí presenta nodos en $x=\pm (-\frac{1}{c_2})^{\frac{1}{2}}\approx \pm 0,37 a$ , además de proporcionar una energía muy superior).
En el estudio de los estados excitados, puesto que, ordenados los autovalores de energía en orden creciente de energía, las correspondientes autofunciones excitadas presentan paridad alternativa, empezando la primera de ellas por la impar, se deberían probar funciones con este requisito incorporado. Por ejemplo, una función de prueba para el primer estado excitado podría ser:
$\psi_1(x,c) = \left \{ \begin{matrix} (a^2-x^2) \ (x+ cx^3) & \mbox{si } |x| < a\;:\; zona \;\; I \\ 0 & \mbox{si } |x| \ge a\;: \; zona \;\; II \; \end{matrix}\right.$

B. Átomo hidrogenoide

Consideremos un átomo hidrogenoide, esto es, un sistema atómico ligado formado por un núcleo con carga positiva $Ze$ ( $Z=1$ para el Hidrógeno) y un solo electrón cortical, de carga negativa $-e$ , interaccionando mutuamente a través del potencial central de Coulomb,
$V(\vec{r})=V(r=|\vec{r}_1 -\vec{r}_2|)= -\frac{1}{4\pi \epsilon_0}\frac{Ze^2}{r}$
(expresión en el sistema internacional de unidades, donde $\epsilon_0$ representa la constante dieléctrica del vacío).
El estudio del problema de los dos cuerpos inicial se reduce a la resolución de la ecuación de Schrödinger independiente del tiempo para el movimiento relativo, de expresión:
$H_r \ \psi_{E_r}(\vec{r})\, = \, [ -\frac{\hbar^2}{2\mu} \nabla_{\mu}^2 + V(\vec{r}) ] \ \psi_{E_r}(\vec{r})\, = \,E_r \ \psi_{E_r}(\vec{r})$ ,
que da cuenta del movimiento intrínseco de las dos partículas y que representa un problema de un cuerpo: el movimiento en el seno del potencial $V(\vec{r})$ de una partícula de masa la reducida del sistema de las dos partículas,
$\mu=\frac{m_1 \cdot m_2 }{m_1 + m_2 }$ ;
los autovalores y las autofunciones de los estados ligados resultan (en la aproximación de estructura gruesa):
-Autovalores:
$\Rightarrow E\equiv E_{n} \, = \, (\frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ (-\frac{\mu}{2}) \ \frac{1}{n^2} \,=\, -\frac{e^2}{4\pi \epsilon_0} \ \frac{1}{a_0} \ \frac{\mu}{m} \ \frac{Z^2}{2} \ \frac{1}{n^2}$
$=\,(Z\alpha)^2 \ (-\frac{1}{2}\mu c^2) \ \frac{1}{n^2} \quad , \quad n=1,2\ldots$ ,
donde $m$ es la masa del electrón; $\mu$ , su masa reducida; $c$ la velocidad de la luz en el vacío y $a_0$ el radio de Bohr,
$a_0 \, = \, \frac{4\pi \epsilon_0 \hbar^2}{m e^2} \, = \, \frac{\hbar}{m (\alpha c)}$
que reducido (corrección de masa reducida) se expresa como:
$a_{\mu} \, = \, \frac{4\pi \epsilon_0 \hbar^2}{\mu e^2} \, = \, a_0 \ \frac{m}{\mu}\, = \, \frac{\hbar}{\mu (\alpha c)}$ ;
el parámetro $\alpha$ es la constante de estructura fina, $\alpha \approx 1/137.035999084$ (valor 2018), adimensional,
$\alpha=\frac{e^2}{4\pi \epsilon_0 \hbar c} \approx \frac{1}{137}$ .
-Autofunciones normalizadas de energía (sin parte de espín):
$\psi_{nlm}(\vec{r}) \, = \, \frac{2} {n^2} \ (\frac{Z}{a_{\mu}})^{\frac{3}{2}} \ [\frac{(n-l-1)!}{(n+l)!}]^{\frac{1}{2}} \ (\frac{2 Z r}{n a_{\mu}})^l \ e^{-\frac{Z}{na_{\mu}}r} \ L_{n-l-1}^{2l+1}(\frac{2 Z r}{n a_{\mu}})\ Y_{lm}(\theta,\varphi)$ ,
donde $a_{\mu}$ representa el radio de Bohr reducido,
$a_{\mu}= a_0\frac{m}{\mu}$ ,
y el símbolo $(a)_n$ representa la función factorial generalizada, $(a)_n=a(a+1)(a+2) \ldots (a+n-1)$ ; por ejemplo: $n!\equiv (1)_n$ .
-Los valores para los número cuánticos involucrados son:
$\left\{ \begin{array}{l} n_r \, = \, n - l -1 \; , \quad n_r=0,1,2\ldots \; , \quad n_r < n \\ n = n_r+l+1= \lambda \; , \quad n=1,2,3\ldots \, (capas \, K,L,M \ldots) \; , \quad n > n_r \, , \, n > l \\ l \, = \, n- n_r -1 \; , \quad l=0,1,2, \ldots , n-1 \ (s,p,d \ldots) \; , \quad l < n \\ m \, = \, 0, \pm 1 , \pm 1 , \ldots , \pm l \end{array} \right\}$
-Algunas expresiones y propiedades para los polinomios generalizados de Laguerre:
$L_{n}^{k}(x)=\sum_{r=0}^{n} \frac{(-1)^r (n+k)!}{(n-r)! (k+r)! r!} x^r$
$L_{n}^{k}(x)=\frac{e^x}{n! x^k} \frac{d^n}{dx^n} (x^{n+k} e^{-x})$ (fórmula de Rodrigues)
$L_0^k(x)=1$
$L_1^1(x)=2-x \quad ; \quad L_2^1(x)=3-3x + \frac{1}{2}x^2$
$L_1^3(x)=4-x \quad ; \quad L_3^1(x)=4-6x + 2x^2 - \frac{1}{6}x^3$
$L_2^3(x)=10-5x + \frac{1}{2}x^2 \quad ; \quad L_1^5(x)=6-x$
En particular:
a) Para el estado fundamental o estado más bajo en energía del átomo de Hidrógeno, $Z=1$ :
$E_{GS} \equiv E_0\, = \, E_{n=1} \, = \,(-\frac{\mu}{2}) \ (\frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ \frac{1}{n^2} \,=\,-13,6 \ eV$ ,
$\psi_0 \equiv \psi_{100}(\vec{r}) = \frac{1}{\sqrt{\pi}} (\frac{Z}{a_{\mu}})^{\frac{3}{2}} e^{-\frac{Zr}{2a_{\mu}}}$
b) Para el primer estado excitado del átomo de Hidrógeno, $Z=1$ :
$E_1\, = \, E_{n=2} \, = \,(-\frac{\mu}{2}) \ (\frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ \frac{1}{4} \,=\,-\frac{13,6}{4} \ eV=-3,4 \ eV$ ,
$\psi_1 \equiv \psi_{2lm}(\vec{r})$

B.1 Estudio variacional para el estado fundamental

Expresiones exactas:
$E_0=E_{n=1}=-\frac{1}{2} \mu c^2 (Z \alpha)^2$
$\psi_0(\vec{r})=\psi_{100}(\vec{r})=\frac{1}{\sqrt{\pi}} (\frac{Z}{a_{\mu}})^{\frac{3}{2}} e^{-\frac{Zr}{a_{\mu}}}$
Tomamos como función de pueba:
1. :
  1. Normalización:
    $<\psi | \psi > = |A|^2 \int_0^{+\infty}r^4 \ e^{-2br} \ dr =|A|^2 \frac{4!}{(2b)^5} \Rightarrow |A|= \sqrt{\frac{(2b)^5}{ 4!}}$
  2. Se calcula el funcional:
    $E(\psi) = \frac{< \psi | H | \psi >}{< \psi | \psi >}$ :
    $H \psi(r,b)=[T+V] \ \psi(r,b) =[ -\frac{\hbar^2}{2\mu} \nabla_{\mu}^2-\frac{1}{4\pi \epsilon_0}\frac{Ze^2}{r}] \ \psi(r,b)$
    $=[-\frac{\hbar^2}{2\mu} ( \frac{d^2}{dr^2} + \frac{2}{r}\frac{d}{dr} -\frac{\vec{L}^2}{\hbar^2r^2} )-\frac{1}{4\pi \epsilon_0}\frac{Ze^2}{r}] \sqrt{\frac{(2b)^5}{ 4!}} \ r \ e^{-br} \ Y_{00}$ ;
    $\left\{ \begin{array}{l} \frac{d}{dr}(r \ e^{-br})= (1 -br) e^{-br}\\ \frac{d^2}{dr^2}(r \ e^{-br})= (b^2 r -2b) e^{-br} \\ (\frac{d^2}{dr^2} + \frac{2}{r}\frac{d}{dr})(r \ e^{-br})= (b^2 r + \frac{2}{r} -2b) e^{-br} \end{array}\right\}$
    $\Rightarrow \left\{ \begin{array}{l} < T >_{\psi(r,b)} =-\frac{\hbar^2}{2\mu} \frac{(2b)^5}{ 4!} \int_0^{+\infty}r^3 \ (b^2 r + \frac{2}{r} -2b) \ e^{-2br} \ dr = \frac{\hbar^2}{2\mu} \frac{b^2}{3}\\ < V >_{\psi(r,b)} = -\frac{Ze^2}{4\pi \epsilon_0} \frac{(2b)^5}{ 4!}\int_0^{+\infty}r^3 \ e^{-2br} \ dr = -\frac{Ze^2}{4\pi \epsilon_0} \frac{b}{ 2} \end{array} \right\}$
    $\Rightarrow E(\psi(b,r)=\frac{\hbar^2}{2\mu} \frac{b^2}{3}-\frac{Ze^2}{4\pi \epsilon_0} \frac{b}{ 2}$
  3. Minimizando respecto al parámetro variacional $b$ :
    $\frac{d}{db}E(\psi(b,r))= \frac{\hbar^2}{3\mu} b-\frac{Ze^2}{4\pi \epsilon_0} \frac{1}{ 2}=0$
    $\Rightarrow b_m= \frac{Ze^2}{4\pi \epsilon_0}\frac{3\mu}{2\hbar^2}$
  4. Por lo tanto, se obtiene la mejor cota superior:
    $E(\psi(b_m,r)= -\frac{3}{8} \mu c^2 (Z\alpha)^2=\frac{3}{4}(-\frac{1}{2} \mu c^2 Z^2 \alpha^2 ) \approx 0,75 E_0^{ex.}$ ,
    esto es, un 75% del valor exacto.
2. :
  1. Normalización:
    $< \psi | \psi > =1 \Rightarrow \psi(r,b)= \sqrt{\frac{b^2}{\pi}}\frac{1}{1+b^2r^2}$
  2. Se calcula el funcional:
    $E(\psi) =< \psi | H=T+V | \psi > = \frac{\hbar^2 b^2}{4\mu} -\frac{Ze^2}{4\pi \epsilon_0}\frac{2b}{\pi}$
  3. Minimizando:
    $\frac{dE(\psi)}{db}=0 \Rightarrow b_m=\frac{4Z}{\pi a_{\mu}}$
  4. Por lo tanto, se obtiene la mejor cota superior:
    $E(\psi(b_m))=-\frac{4}{\pi^2} \mu c^2(Z \alpha)^2 \approx 0,81 E_0^{ex.}$
3. (que es la función exacta):
  1. Normalización:
    $< \psi | \psi > =1 \Rightarrow \psi(r,b)= 2b^{\frac{3}{2}}\ e^{-br} \ Y_{00}$
  2. Se calcula el funcional:
    $E(\psi) = < \psi | H=T+V | \psi > =\frac{\hbar^2 b^2}{2\mu} -\frac{Ze^2}{4\pi \epsilon_0}b$
  3. Minimizando:
    $\frac{dE(\psi)}{db}=0 \Rightarrow b_m=\frac{Ze^2}{4\pi \epsilon_0}\frac{\mu}{\hbar^2}$
  4. Por lo tanto, se obtiene la mejor cota superior:
    $E(\psi(b_m))=-\frac{1}{2} \mu c^2 (Z \alpha)^2 = E_0^{ex.}$
Puede observarse a partir de la comparación entre los resultados anteriores, para las tres funciones de prueba distintas usadas para el cálculo variacional del estado fundamental, que la función de prueba usada en segundo lugar proporciona mejor aproximación al valor energético del estado fundamental que la primera, que es, sin embargo, más próxima a la exacta.
-En efecto, si se analiza para cada función de prueba $\psi_i$ el valor del parámetro
$\epsilon_i = 1-|< \psi_0^{ex.} | \psi_i > |^2$ , que resulta ser para cada una de las tres funciones usadas:
$\psi_i=\sum_{m=0}^{\infty} \ c_m \psi_m \Rightarrow < \psi_0^{ex.} | \psi_i > =c_0 \Rightarrow \epsilon_i = 1-|c_0|^2$ ,
por lo que
$\psi_1(r,b)=A \ r \ e^{-br} \ Y_{00} \Rightarrow \epsilon_1=0,0445$
$\psi_2(r,b)= A \ \frac{1}{1+b^2r^2} \ Y_{00}\Rightarrow \epsilon_2=0,20$
$\psi_3(r,b)= A \ e^{-br} \ Y_{00}\Rightarrow \epsilon_1=0$ ,
es decir, $\psi_1$ está más próxima a la función de onda exacta que $\psi_2$ y, de hecho, proporciona mejor información. Por ejemplo, si calculamos el valor medio $< r >$ :
$< r >_{\psi_1}= \int r |\psi_1|^2 dr = \frac{5}{3}a_{\mu}$
$< r >_{\psi_2}= \int r |\psi_1|^2 dr \rightarrow \infty$
$< r >_{\psi_3}= \int r |\psi_1|^2 dr = \frac{3}{2}a_{\mu}$ (exacto).
-Puede concluirse entonces que el que una función de prueba proporcione una mejor estimación para el correspondiente valor de energía, por ejemplo, no implica que sea la mejor aproximación también para la determinación de la predicción de resultados de la medida de otras magnitudes físicas sobre el sistema.

B.2 Estudio variacional para estados excitados

Un estudio para los estados excitados del átomo hidrogenoide podría iniciarse a partir del hecho de que el estado fundamental presenta simetría esférica, de modo que es conveniente comenzar con funciones prueba que incorporen la ortogonalidad al estado fundamental, es decir, funciones prueba con $l \ne 0$ de expresión:
$\psi_l=R(r) \ Y_{lm} \; , \; < \psi_0 | \psi_l > =0$ ,
teniéndose también que las funciones para distintos valores de $l$ serán ortogonales entre sí.
Un estudio variacional para el primer estado excitado de un átomo hidrogenoide podría entonces comenzar con la función de prueba
$\psi_{lm}=R(r)Y_{lm}(\Omega)= \sqrt{\frac{(2b)^{2l+3}}{(2l+2)!}} Y_{lm}(\Omega)$ ,
una función normalizada que conduce al resultado
$< \psi_{lm} | H | \psi_{lm} > = \frac{\hbar^2b^2}{2\mu} - \frac{Ze^2}{4\pi \epsilon_0} \frac{b}{l+1}$ ,
que tiene un mínimo del correspondiente funcional $E(\psi_{lm})$ en el valor $b_m= \frac{1}{(l+1)a_{\mu}}$ , el cual proporciona el valor para la cota a la energía del primer estado excitado:
$E_1=-\frac{1}{2(l+1)^2} \mu c^2 (Z \alpha)^2 |_{l=0}=E_{n=2}$ ,
que no es sino el correspondiente valor exacto, ya que la familia de funciones prueba contiene la función exacta.

Funciones de prueba con parámetros variacionales lineales: Teorema de Hylleraas-Undheim

Un tipo de funciones de onda de prueba muy empleado para aplicar el método variacional es el que se construye a partir de un conjunto de funciones linealmente independientes,
$\phi_1, \phi_2,\ldots,\phi_N$ ,
no necesariamente ortogonales entre sí, mediante la combinación lineal
$\Phi=\sum_{m=1}^N c_m \phi_m \; , \; c_m \in \mathbb{R}$ ,
donde se han tomado coeficientes variacionales $c_m$ reales.
La anterior elección conduce al funcional
$E(\Phi)=\frac{< \Phi | H | \Phi >}{< \Phi | \Phi >}=\frac{\sum_{m'} \sum_{m} c_{m'} c_{m} H_{m'm}}{\sum_{m'} \sum_{m} c_{m'} c_{m} \Delta_{m'm}}$ ,
donde
$H_{m'm}=< \phi_{m'} | H | \phi_{m} >$
$\Delta_{m'm}=< \phi_{m'} | \phi_{m} >$
-Operando:
$E(\Phi) \ \sum_{m'} \sum_{m} c_{m'} c_{m} \ \Delta_{m'm}=\sum_{m'} \sum_{m} c_{m'} c_{m} \ H_{m'm}$ ;
derivando respecto a cada parámetro variacional e igualando a cero:
$\frac{\partial}{\partial c_{m'}} E(\Phi)=0 \; , \; m'=1,2,\ldots,N$ ,
se obtiene el siguiente sistema lineal y homogéneo de N ecuaciones en las N incógnitas $c_m$ :
$\sum_{m=1}^N c_m (H_{m'm} \ - \ E \Delta_{m'm})=0$ ,
que tendrá solución no trivial si y sólo si el determinante de los coeficientes se anula:
$det|H_{m'm} \ - \ E \Delta_{m'm}|=0 \; , \; m',m=1,2,\ldots,N$ ,
una ecuación polinómica de grado $N$ en la energía $E$ que proporcionará las N raíces $E_o^{(N)},\ldots, E_{N-1}^{(N)}$ , no necesariamente todas distintas (posible presencia de degeneraciones) y que supondremos ordenadas en orden creciente.
Por el principio de mínimo, base del método variacional, habrá de tenerse
$E_0^{ex.}\doteq E_0 \le E_0^{(N)}$ ,
y la sustitución de la raíz $E_0^{(N)}$ en el sistema de ecuaciones conducirá a la colección de coeficientes
$c_1,\ldots,c_{N}$ ,
expresados en términos de uno de ellos, que se podrá fijar arbitrariamente ya que $E(\Phi)$ no depende de la normalización de $\Phi$ .
-Se ha obtenido por tanto la correspondiente aproximación variacional $\Phi_0$ a la función exacta $\psi_o$ del estado fundamental.
A continuación, siguiendo un método inductivo, se puede establecer que las restantes raíces $E_1^{(N)},\ldots, E_{N-1}^{(N)}$ son respectivas cotas superiores a las sendas energías exactas $E_1, \ldots, E_{N-1}$ de los sucesivos estados excitados en orden creciente energético:
$E_1 \le E_1^{(N)}, E_2 \le E_2^{(N)},\ldots,E_{N-1} \le E_{N-1}^{(N)}$ ,
donde pueden aparecer valores repetidos de cotas.
-Las correspondientes funciones variacionales óptimas $\phi_i \; , \; i=1,2 , \ldots,N$ se obtendrán a su vez de forma similar a como se generó para el estado fundamental: sustituyendo cada raíz $E_i^{(N)}$ en el sistema de ecuaciones y resolviendo para los coeficientes $c_m^{(i)} \; , \; m=1,2 , \ldots,N$ , para formar la combinación $\Phi_i=\sum_{m=1}^N c_m^{(i)} \phi_m$ .

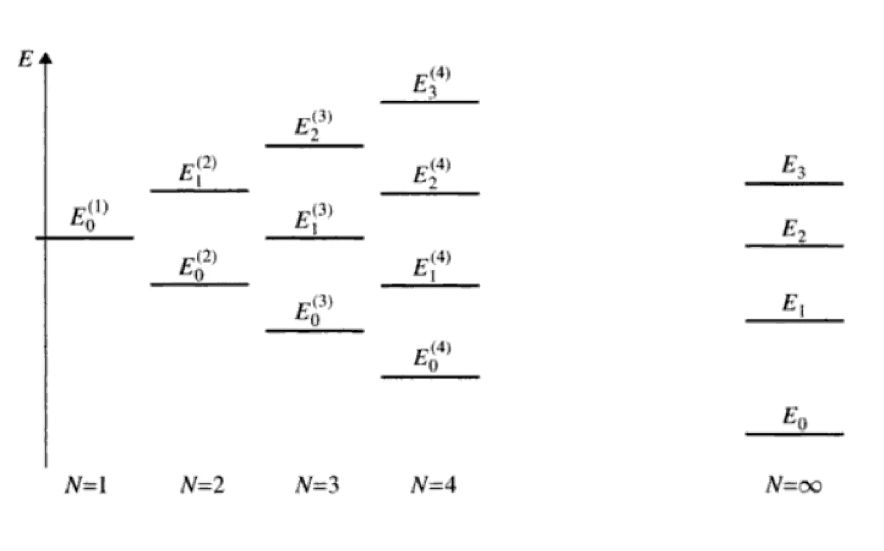
El teorema de Hylleraas-Undheim

El teorema de Hylleraas-Undheim establece:
Construida la función de prueba $\Phi^+$ ,
$\Phi^+=\sum_{m=1}^{N+1} c_m \phi_m \; , \; c_m \in \mathbb{R}$ ,
que contiene un parámetro variacional más que la función de prueba $\Phi$ ,
$\Phi=\sum_{m=1}^N c_m \phi_m \; , \; c_m \in \mathbb{R}$ ,
donde
$\phi_1, \phi_2,\ldots,\phi_N , \phi_{N+1}$
constituyen un conjunto de funciones linealmente independientes, no necesariamente ortogonales entre sí y se han tomado coeficientes variacionales $c_m \; , \; m=1,2,\ldots,m,m+1$ reales, entonces se tiene:
Las nuevas $N+1$ raíces $E_i^{(N+1)}$ de la ecuación determinamental
$det|H_{m'm} \ - \ E \Delta_{m'm}|=0 \; , \; m',m=1,2,\ldots,N,N+1$
se encuentran intercaladas entre los raíces $E_i^{(N)}$ de la ecuación determinamental correspondiente a una dimensión N inferior en una unidad, ecuación
$det|H_{m'm} \ - \ E \Delta_{m'm}|=0 \; , \; m',m=1,2,\ldots,N$ .
-La siguiente figura ilustra el significado del teorema:
Como se indicó anteriormente, en el caso particular de que el Hamiltoniano posea determinadas simetrías conocidas, esto es, conmute con algún operador autoadjunto $A$ dado, $[H,A]=0$ , el problema variacional se debe resolver por separado para cada autovalor $a$ de $A$ , de modo que las funciones prueba $\Phi$ se construirán para conjuntos de funciones $\phi_i\; , \; i=1,2, \ldots,N$ integrados por autofunciones de $A$ para el mismo autovalor $a$ , y la correspondiente ecuación determinamental proporcionará N raíces que serán cotas superiores a los primeros N niveles de energía asociados a ese autovalor $a$ de A.

Ejemplo
Partícula en un pozo cuadrado infinito monodimensional

Retomemos el ejemplo anterior de una partícula en un potencial de pozo cuadrado infinito:
$V(x) = \left \{ \begin{matrix} 0 & \mbox{si } |x| < a\;:\; zona \;\; I \\ +\infty & \mbox{si } |x| \ge a\;: \; zona \;\; II \; \end{matrix}\right.$
-Tomemos en la zona I una función de prueba
$\Phi=c_1 \phi_1 + c_2 \phi_2$ ,
donde $\phi_1 , \phi_2$ son las funciones pares
$\phi_1=a^2-x^2$ ,
$\phi_2=x^2(a^2-x^2)$ ,
y de los dos parámetros variacionales se fija $c_1=1$ (ya que uno de ellos siempre puede fijarse de forma arbitraria).
-Se tiene entonces:
$\Phi=\phi_1 + c_2 \phi_2 \Rightarrow$
$E_0^{(2)}\le E_1^{(2)}$
$E_0 \le E_0^{(2)}$
$E_2 \le E_1^{(2)}$