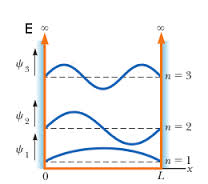
El pozo cuadrado infinito
- Función potencial
:
Pozo infinito (caja de paredes impenetrables); simétrico en torno al origen.
dondees un número real, con dimensiones de energía y que puede ser positivo o negativo.
-Se trata de una función con discontinuidades de segunda especie en los puntos, puntos en los que se sitúan sendas barreras impenetrables de potencial; por lo tanto, en ellos se debe imponer la condición de frontera de anulación de la función de onda
: se produce el confinamiento o ligadura de la partícula en el interior del intervalo
de la recta real, de longitud
.
- Problema de autovalores de energía:
,
y buscamos solucionesque sean funciones continuas y con derivada primera
también continua allí donde
es finito: en el intervalo
; las funciones
tendrán sendos nodos en los puntos extremos
:
(donde
presentará una discontinuidad de primera especie).
- La solución general de una EDO
,
donde,
, tiene la expresión:
-Signo (-) :
conescalares arbitrarios.
-Signo (+) :
conescalares arbitrarios.
- En la región espacial considerada I,
, la forma concreta de la EDO planteada es:
Zona I : - Cuantización de la energía:
:
- -Zona I:
:
,
cony
escalares arbitrarios.
-Zona II::
.
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulación
-Anulación
-Puesto que este conjunto de condiciones conduce a la solución trivial, la conclusión es que no existen soluciones físicamente aceptables del problema de autovalores de energía para valores del parámetro de separación.
- -Zona I:
:
- Expresión de la función de onda:
-Zona I :,
con
yescalares arbitrarios.
-Zona II::
- Imponiendo las condiciones de contorno:
-Anulación
-Anulación
-De las dos ecuaciones anteriores se llega al par equivalente:
Nota:se excluye pues conduce a la solución trivial (
).
- Aparece pues el fenómeno de cuantización de la energía, ya que sólo hay solución físicamente aceptable del problema de autovalores para los valores discretos de energía
,
asociados respectiva y alternadamente a los dos tipos de autofunciones:
-Normalizadas,
las autofunciones normalizadas se expresan:
en la zona I; fuera de esta zona siempre.
-El conjunto de autofuncionesconstituye un conjunto ortonormal.
-Como corresponde a las autofunciones ligadas de un potencial unidimensional simétrico,, todas las autofunciones tienen paridad definida: cada
es par, cada
es impar.
- En términos de la longitud de onda de de Broglie, las autofunciones se corresponden con los números de onda
tales que un número entero o semientero de longitudes de onda caben en la anchura
del pozo:
.
- El estado fundamental posee una energía:
,
denominada energía del punto cero; la correspondiente autofunción par es:
.
- Principio de indeterminación:
-En una rápida estimación:
.
-En rigor, estadísticamente:
;
por tanto:
- La forma general característica que presentan las funciones y densidades de probabilidad para la partícula confinada en la caja de potencial se representa en las siguientes figuras:
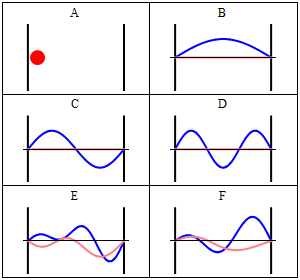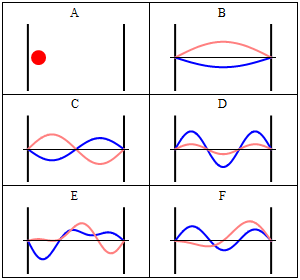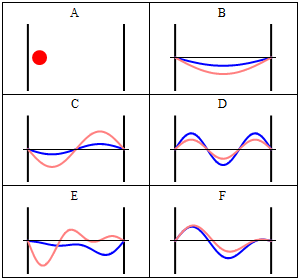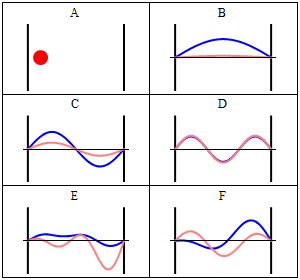
Trajectories of a particle in a box (also called an infinite square well) in classical mechanics (A) and quantum mechanics (B-F). In (A), the particle moves at constant velocity, bouncing back and forth. In (B-F), wavefunction solutions to the Time-Dependent Schrodinger Equation are shown for the same geometry and potential. The horizontal axis is position, the vertical axis is the real part (blue) or imaginary part (red) of the wavefunction. (B,C,D) are stationary states (energy eigenstates), which come from solutions to the Time-Independent Schrodinger Equation. (E,F) are non-stationary states, solutions to the Time-Dependent but not Time-Independent Schrodinger Equation. Both (E) and (F) are randomly-generated superpositions of the four lowest-energy eigenstates, (B-D) plus a fourth not shown (imagen y texto de la Wikipedia, por Sbyrnes321). 
Densidades de probabilidad (imagen de: http://www.amarketplaceofideas.com/category/science/physics/quantum-mechanics).
- Expresión de la función de onda:
- NOTA: recuérdese que, si bien es cierto que los autovalores de energía son los únicos valores de energía permitidos al sistema, las autofunciones de energía constituyen una base: cualquier combinación lineal de ellas, que no genera en general una autofunción, representa no obstante un estado posible para el sistema.
- En el problema estudiado, Hamiltoniano del pozo cuadrado infinito, o caja de paredes impenetrables, resulta por tanto:
: infinitos estados ligados, con paridad definida y sin degeneración; se satisface el teorema de oscilación.
El pozo cuadrado infinito (bis)
- Función potencial
:
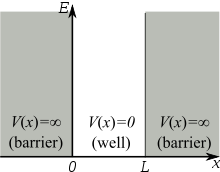
Imagen de la Wikipedia.
-Se trata de una función con discontinuidades de segunda especie en los puntosy
, puntos en los que se sitúan sendas barreras impenetrables de potencial; por lo tanto, en ellos se debe imponer la condición de frontera de anulación de la función de onda
: se produce el confinamiento o ligadura de la partícula en el interior del intervalo
de la recta real.
- Problema de autovalores de energía:
,
y buscamos solucionesque sean funciones continuas y con derivada primera
también continua allí donde
es finito: en el intervalo
; las funciones
tendrán sendos nodos en los puntos extremos
y
:
(donde
presentará una discontinuidad de primera especie).
- La solución general de una EDO
,
donde,
, tiene la expresión:
-Signo (-) :
conescalares arbitrarios.
-Signo (+) :
conescalares arbitrarios.
- En la región espacial considerada I,
, la forma concreta de la EDO planteada es:
Zona I : - Cuantización de la energía:
:
- -Zona I:
:
,
cony
escalares arbitrarios.
-Zona II:y
:
.
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulación
-Anulación
-Puesto que este conjunto de condiciones conduce a la solución trivial, la conclusión es que no existen soluciones físicamente aceptables del problema de autovalores de energía para valores del parámetro de separación.
- -Zona I:
:
- Expresión de la función de onda:
Zona I :
con
yescalares arbitrarios.
- Imponiendo las condiciones de contorno:
-Anulación
-Anulación
- Aparece pues el fenómeno de cuantización de la energía, ya que sólo hay solución físicamente aceptable del problema de autovalores para los valores discretos de energía
cuyas autofunciones asociadas tienen la expresión
.
-Una vez normalizadas,
,
las autofunciones se expresan:
-El conjunto de autofuncionesconstituye un conjunto ortonormal.
- En términos de la longitud de onda de de Broglie, las autofunciones se corresponden con los números de onda
tales que un número entero o semientero de longitudes de onda caben en la anchura
del pozo:
.
- El estado fundamental posee una energía:
,
denominada energía del punto cero; se satisface el principio de indeterminación:
.
-Le corresponde la autofunción:
.
- La forma general característica que presentan las funciones y densidades de probabilidad para la partícula confinada en la caja de potencial se representa en las siguientes figuras:

Trajectories of a particle in a box (also called an infinite square well) in classical mechanics (A) and quantum mechanics (B-F). In (A), the particle moves at constant velocity, bouncing back and forth. In (B-F), wavefunction solutions to the Time-Dependent Schrodinger Equation are shown for the same geometry and potential. The horizontal axis is position, the vertical axis is the real part (blue) or imaginary part (red) of the wavefunction. (B,C,D) are stationary states (energy eigenstates), which come from solutions to the Time-Independent Schrodinger Equation. (E,F) are non-stationary states, solutions to the Time-Dependent but not Time-Independent Schrodinger Equation. Both (E) and (F) are randomly-generated superpositions of the four lowest-energy eigenstates, (B-D) plus a fourth not shown (imagen y texto de la Wikipedia, por Sbyrnes321). 
Densidades de probabilidad (imagen de: http://www.amarketplaceofideas.com/category/science/physics/quantum-mechanics). - NOTA: recuérdese que, si bien es cierto que los autovalores de energía son los únicos valores de energía permitidos al sistema, las autofunciones de energía constituyen una base: cualquier combinación lineal de ellas, que no genera en general una autofunción, representa no obstante un estado posible para el sistema.
- Expresión de la función de onda:
Autovalores y espectro del pozo cuadrado infinito
- Para un pozo finito de anchura
y fondo
aparece el fenómeno de cuantización de la energía, ya que sólo hay solución físicamente aceptable del problema de autovalores para los valores discretos de energía:
,
es decir, estos son los únicos valores de energía accesibles al sistema. - Recuérdese que, si bien es cierto que los autovalores de energía son los únicos valores de energía permitidos al sistema, las correspondientes autofunciones de energía constituyen una base: cualquier combinación lineal de ellas, que no genera en general una autofunción (no es solución de la ecuación de autovalores de la energía o ecuación de Schrödinger independiente del tiempo), representa no obstante un estado posible para el sistema (sí es solución de la ecuación de Schrödinger).
- Un ejemplo de valores numéricos de las energías de los estados ligados:

Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/; tomada también de http://en.wikibooks.org/wiki/Materials_in_Electronics/Confined_Particles/1D_Finite_Wells; los números se corresponden con la elección .
- En el problema estudiado, Hamiltoniano del pozo cuadrado infinito, o caja de paredes impenetrables, resulta por tanto:
: infinitos estados ligados, sin degeneración; se satisface el teorema de oscilación.
Referencias
[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.
[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.
[SCH-68] Schiff,L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.
Páginas complementarias
http://en.wikipedia.org/wiki/Particle_in_a_box
http://www.uco.es/hbarra/index.php/fc/apuntesfc/334-fc0303
http://eltamiz.com/2008/05/15/cuantica-sin-formulas-el-pozo-de-potencial-infinito/
APPS
http://www.sc.ehu.es/sbweb/fisica/cuantica/pozo/caja.htm
http://www.uco.es/hbarra/index.php/fc/appletsfc/70-pozo-infinito
http://www.uco.es/hbarra/index.php/fc/appletsfc/71-paquete-pozo-infinito
http://www.st-andrews.ac.uk/physics/quvis/embed_item_3.php?anim_id=24&file_sys=index_phys
Probability Density in an Infinite Square Well from the Wolfram Demonstrations Project by Carlos Anton Solanas
Quantum Particles in an Infinite Square Potential Well from the Wolfram Demonstrations Project by Jeff Bryant
Dejar una contestacion