Teoría de perturbaciones (estados ligados estacionarios)

Teoría de perturbaciones para estados ligados

Introducción

Existen muy pocos sistemas de interés físico para los que la resolución pueda realizarse de forma exacta, tanto en la mecánica cuántica como en la clásica. En consecuencia, los métodos aproximados van a ser muy importantes en la mayoría de las aplicaciones, y en su desarrollo serán muy útiles como recurso los escasos sistemas que admiten resolución analítica: sus soluciones se usarán a menudo como punto de partida para la resolución aproximada.
Los principales métodos aproximados en mecánica cuántica se clasifican en dos grupos distintos, según sean aplicables a los estados ligados del sistema o a los estados de difusión; en esta entrada nos limitaremos a exponer los primeros, que a su vez se clasifican dependiendo de si son válidos para sistemas con hamiltonianos dependientes o no del parámetro temporal, y si se aplican a estados de energía degenerados o no.

Teoría de perturbaciones para estados ligados de Hamiltonianos sin dependencia temporal

La teoría de perturbaciones independiente del tiempo para estados ligados o teoría de Rayleigh-Schrödinger se aplica al caso de un sistema conservativo, con un Hamiltoniano $H$ independiente del tiempo que admite expresión de la forma
$H=H_0+\lambda H' \; , \; \lambda \in \mathbb{R}$ ,
donde el sumando $H_0$ representa un operador autoadjunto que se va a denominar como el «Hamiltoniano no perturbado», mientras que $\lambda H'$ va a representar el «Hamiltoniano de perturbación», que es supuesto cumpliendo las condiciones de que: a) la ecuación de Schrödinger correspondiente,
$H_0 \ \psi_n^{(0)} \, = \,E_n^{(0)} \ \psi_n^{(0)}$ ,
admite resolución sencilla, analítica o numérica, de un lado; y b) la perturbación «sea pequeña», de otro (en el sentido que se especificará más adelante); el parámetro real $\lambda$ permitirá entonces realizar una expansión en potencias que marcarán los distintos órdenes del cálculo aproximado.
Puesto que $H_0$ es un operador autoadjunto, sus autofunciones $\{ \psi_n^{(0)} \}$ constituyen una base ortonormal (un conjunto ortonormal completo) del espacio, en el cual se podrán integrar, en su caso, funciones generalizadas.
-Si el espectro del hamiltoniano es puramente discreto, $\sigma(H_0)=\sigma_p(H_0)$ , la relación de ortonormalidad de los estados de la base se expresa:
$\left< \psi_n^{(0)} \ | \ \psi_m^{(0)} \right> \, = \, \delta_{n,m} \;$
si ningún estado es degenerado, o
$\left< \psi_{n,k}^{(0)} \ | \ \psi_{m,k'}^{(0)} \right> \, = \, \delta_{n,m} \ \delta_{k,k'}$
si la base integra autoestados degenerados; si el espectro contiene parte continua, la base contiene estados generalizados y la relación de ortonormalización para ellos pasa a escribirse en términos de la delta de Dirac (se conserva la delta de Kronecker para la posible degeneración de los autovalores de energía):
$\left< \psi_{E,k}^{(0)} \ | \ \psi_{E',k'}^{(0)} \right> \, = \, \delta (E-E') \ \delta_{k,k'}$
-Por simplicidad de la notación, se suele considerar que la primera notación, en términos exclusivos de la delta de Kronecker, recoge todas las posibilidades.
Para la resolución del problema de autovalores de la energía,
$H \ \psi_n \, = \,E_n \ \psi_n$ ,
se comienza resolviendo el problema para el Hamiltoniano no perturbado $H_0$ ,
$H_0 \ \psi_n^{(0)} \, = \,E_n^{(0)} \ \psi_n^{(0)}$ ,
en la que aparecerán en general estados ligados $E_n^{(0)}$ sin y con degeneración, requiriendo sendos métodos distintos de tratamiento.

Estados ligados no degenerados

Sea $E_n^{(0)}$ un autovalor de energía de $H_0$ no degenerado, siendo $\psi_n^{(0)}$ la correspondiente autofunción. Se define una perturbación como «suficientemente pequeña», tanto como para que el tratamiento perturbativo sea adecuado y proporcione resultados correctos, cuando, tras la perturbación de cada nivel $E_n^{(0)}$ , el nivel menos próximo a él que resulta al corregir ese valor de orden cero, en términos energéticos, está más próximo a él que cualquier otro nivel $E_m^{(0)}\, , \, m \ne n$ .
-Es decir, la perturbación puede alterar el valor de $E_n^{(0)}$ , o, en su caso, desdoblarlo, y el tratamiento perturbativo hecho se considerará correcto si la magnitud de la corrección no altera el orden energético establecido en el estadio sin perturbación; es decir, tras la perturbación, un estado que ha surgido a partir de $E_n^{(0)}$ no puede estar más lejos de él que cualquier otro de los iniciales no perturbados. En términos matriciales, esto equivale a que los elementos de la matriz perturbativa no pueden ser mayores en magnitud que el espaciado entre los niveles no perturbados (véase al respecto, por ejemplo, la discusión en: https://physics.stackexchange.com/questions/169877/energy-levels-in-close-proximity-of-each-other-in-time-independent-degenerate-pe).
La hipótesis matemática que subyace a la consideración de una perturbación como suficientemente pequeña es la suposición de que autofunciones y autovalores del Hamiltoniano $H$ admiten desarrollo en serie de potencias del parámetro $\lambda$ :
$E_n \, = \, \sum_{i=0}^{\infty} \lambda^i \ E_n^{(i)}$
$\psi_n \, = \, \sum_{i=0}^{\infty} \lambda^i \ \psi_n^{(i)}$ ,
donde cada valor del índice $i$ establece el orden perturbativo en que se van a proporcionar las correcciones.
-Sustituyendo ambos desarrollos en la ecuación de Schrödinger:
$H \ \psi_n \, = \,E_n \ \psi_n$
$(H_0 \ + \ \lambda H') \ \sum_{i=0}^{\infty} \lambda^i \ \psi_n^{(i)} \, = \,( \sum_{i=0}^{\infty} \lambda^i \ E_n^{(i)} ) \ (\sum_{i=0}^{\infty} \lambda^i \ \psi_n^{(i)})$ ;
igualando coeficientes de igual potencia de $\lambda$ en ambos lados de la igualdad:
$\left. \begin{array}{l} i=0 \, , \, \lambda^0 \Rightarrow H_0 \ \psi_n^{(0)} \, = \, E_n^{(0)} \ \psi_n^{(0)}\\ i=1 \, , \, \lambda^1 \Rightarrow H_0 \ \psi_n^{(1)} \,+ \, H' \ \psi_n^{(0)} = \, E_n^{(0)} \ \psi_n^{(1)} \, + \, E_n^{(1)} \ \psi_n^{(0)} \\ i=2 \, , \, \lambda^2 \Rightarrow H_0 \ \psi_n^{(2)} \,+ \, H' \ \psi_n^{(1)} = \, E_n^{(0)} \ \psi_n^{(2)} \, + \, E_n^{(1)} \ \psi_n^{(1)} \, + \, E_n^{(2)} \ \psi_n^{(0)} \\ \ldots \\ i \, , \, \lambda^i \Rightarrow H_0 \ \psi_n^{(i)} \,+ \, H' \ \psi_n^{(i-1)} = \, E_n^{(0)} \ \psi_n^{(i)} \, + \, E_n^{(1)} \ \psi_n^{(i-1)} \, + \ldots + \, E_n^{(i)} \ \psi_n^{(0)} \end{array} \right\}$
Este conjunto de ecuaciones permite encontrar la solución al problema, proporcionando autofunciones y autovalores en los sucesivos órdenes de la corrección perturbativa.
Corrección en orden cero:
$H_0 \ \psi_n^{(0)} \, = \, E_n^{(0)} \ \psi_n^{(0)}$
-Es el caso no perturbado, de solución sencilla según lo presupuesto. La correspondiente resolución proporcionará los autovalores $E_n^{(0)}$ y las autofunciones $\psi_n^{(0)}$ , que integrarán una base ortonormal $\{ \psi_n^{(0)} \}$ del espacio (que podrá contener o no funciones del continuo).
Corrección a la energía en primer orden:
$H_0 \ \psi_n^{(1)} \,+ \, H' \ \psi_n^{(0)} = \, E_n^{(0)} \ \psi_n^{(1)} \, + \, E_n^{(1)} \ \psi_n^{(0)}$
-Multiplicando a la izquierda por el estado de la base $\psi_n^{(0)*}$ e integrando:
$\left< \psi_n^{(0)} | H_0 | \psi_n^{(1)} \right> \,+ \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right> \, = \, \left< \psi_n^{(0)} | E_n^{(0)} | \psi_n^{(1)} \right> \,+ \, \left< \psi_n^{(0)} | E_n^{(1)} | \psi_n^{(0)} \right>$
$\Rightarrow \left< \psi_n^{(0)} | H_0 | \psi_n^{(1)} \right> \,+ \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right> \, = \, E_n^{(0)} \left< \psi_n^{(0)} | \psi_n^{(1)} \right> \, + \, E_n^{(1)}$ ;
usando el hecho de que $H_0$ es autoadjunto, por lo que cumple
$\left< \psi_n^{(0)} \ | H_0 | \ \psi_n^{(1)} \right> \, = \, \left< H_0 \ \psi_n^{(0)} \ | \ \psi_n^{(1)} \right> \, = \, E_n^{(0)} \, \left< \psi_n^{(0)} \ | \ \psi_n^{(1)} \right>$ ,
se obtiene finalmente la corrección a la energía en primer orden de perturbaciones $(O(\lambda^1), \lambda=1)$ :
$\Rightarrow E_n^{(1)} \, = \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right>$
$\Rightarrow E_n \, \approx \, E_n^{(0)} \, + \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right>$
Corrección a la función de onda en primer orden:
-Se parte del desarrollo de $\psi_n^{(1)}$ en la base ortonormal $\{ \psi_n^{(0)} \}$ :
$\psi_n^{(1)} \, = \, \sum_{k} a_{nk}^{(1)} \ \psi_k^{(0)}$ ,
donde la suma sobre el índice $k$ debe entenderse como una suma sobre las autofunciones correspondientes a la parte discreta del espectro y una integral para las contribuciones de las funciones generalizadas:
$\psi_n^{(1)} \, = \, \sum_{E_k\in \sigma_p(H_0)} a_{nk}^{(1)} \ \psi_k^{(0)} \, + \, \int_{E_k \in \sigma_c(H_0)} a_{nk}^{(1)} \ \psi_{E_k}^{(0)} \ dE_k$ ;
los escalares complejos $a_{nk}^{(1)}$ representan los correspondientes coeficientes del desarrollo.
-A continuación, sustituimos este desarrollo (utilizaremos la forma simple válida para espectros puramente discretos):
$H_0 \ \psi_n^{(1)} \,+ \, H' \ \psi_n^{(0)} = \, E_n^{(0)} \ \psi_n^{(1)} \, + \, E_n^{(1)} \ \psi_n^{(0)}$
$\Rightarrow (H_0 \, - \, E_n^{(0)}) \psi_n^{(1)} \,+ \, (H' \, - \, E_n^{(1)}) \psi_n^{(0)} \, = \, 0$
$\Rightarrow (H_0 \, - \, E_n^{(0)}) \, \sum_{k} a_{nk}^{(1)} \ \psi_k^{(0)} \,+ \, (H' \, - \, E_n^{(1)})\, \psi_k^{(0)} \, = \, 0$
-Proyectamos sobre $< \psi_m^{(0)} |$ , con $m$ fijo:
$\left< \psi_m^{(0)} | (H_0 \, - \, E_n^{(0)}) | \sum_{k} a_{nk}^{(1)} \ \psi_k^{(0)} \right> \,+ \, \left< \psi_m^{(0)} | (H' \, - \, E_n^{(1)} )| \psi_n^{(0)} \right> \, = \, 0$
$\Rightarrow \sum_{k} a_{nk}^{(1)} \ ( E_m^{(0)} \, - \, E_n^{(0)}) \ \delta_{m,k} \,+ \, \left< \psi_m^{(0)} |H' | \psi_n^{(0)} \right> \,- \, E_n^{(1)}) \ \delta_{m,n} \, = \, 0$
$\left. \begin{array}{l} m=n \Rightarrow 0 \cdot a_{nn}^{(1)} \, + \, E_n^{(1)} \, - \, E_n^{(1)} \, = \, 0 \cdot a_{nn}^{(1)} \, = \,0 \\ \forall m \ne n \Rightarrow a_{nm}^{(1)} \, = \, \frac{ \left< \psi_m^{(0)} |H' | \psi_n^{(0)} \right> }{ E_n^{(0)} \, - \, E_m^{(0)} } \, = \, \frac{ H'_{mn}}{ E_n^{(0)} \, - \, E_m^{(0)} } \end{array} \right\}$
-El coeficiente
$a_{nn}^{(1)} \, = \,\left< \psi_n^{(0)} | \psi_n^{(1)} \right>$
resulta sin determinar, pudiendo escogerse como nulo (sin efecto físico), de modo que se obtiene la expresión final para la corrección a la función de onda en primer orden de perturbaciones $(O(\lambda^1), \lambda=1)$ :
$\psi_n^{(1)} \, = \, \sum_{k \ne n} \frac{ H'_{kn}}{ E_n^{(0)} \, - \, E_k^{(0)} } \, \psi_k^{(0)}$
$\Rightarrow \psi_n \approx \psi_n^{(0)} \, + \, \sum_{k \ne n} \frac{ H'_{kn}}{ E_n^{(0)} \, - \, E_k^{(0)} } \, \psi_k^{(0)} \, = \, \psi_n^{(0)} \, + \, \sum_{k \ne n} \frac{ \left< \psi_k^{(0)} |H' | \psi_n^{(0)} \right> }{ E_n^{(0)} \, - \, E_k^{(0)} } \, \psi_k^{(0)}$ ,
expresión a normalizar.
Validez/aplicabilidad de la teoria de perturbaciones estacionarias: a la vista de las anteriores expresiones para $E_n^{(1)}$ y $\psi_n^{(1)}$ , la condición para que la corrección que proporciona el desarrollo perturbativo sea válida es:
-En términos energéticos:
$|E_n^{(1)}| \, = \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right> << |E_{n\pm 1}^{(0)} \, - \, E_n^{(0)}|$ ;
-Para la expresión en la corrección a la función de onda:
$| \sum_{k \ne n} \frac{ \left< \psi_k^{(0)} |H' | \psi_n^{(0)} \right> }{ E_n^{(0)} \, - \, E_k^{(0)} } | << 1 \quad \forall k \ne n$
Corrección a la energía en segundo orden:
$\lambda^2 \Rightarrow H_0 \ \psi_n^{(2)} \,+ \, H' \ \psi_n^{(1)} = \, E_n^{(0)} \ \psi_n^{(2)} \, + \, E_n^{(1)} \ \psi_n^{(1)} \, + \, E_n^{(2)} \ \psi_n^{(0)}$
$(H_0 \, - \, E_n^{(0)}) \ \psi_n^{(2)} \,+ \, (H' \, - \, E_n^{(1)}) \ \psi_n^{(1)} \, - \, E_n^{(2)} \ \psi_n^{(0)} \, + \, 0$
-Multiplicando a la izquierda por el estado de la base $\psi_n^{(0)*}$ e integrando:
$\left< \psi_n^{(0)} | (H_0 \, - \, E_n^{(0)}) | \psi_n^{(2)} \right> \,+ \, \left< \psi_n^{(0)} | (H' \, - \, E_n^{(1)}) | \psi_n^{(1)} \right> \, - \, E_n^{(2)} \left< \psi_n^{(0)} | \psi_n^{(0)} \right> \,= \, 0$ ,
expresión en la que el primer sumando es nulo por ser $H_0$ autoadjunto, resultando:
$\Rightarrow E_n^{(2)} \, = \, \left< \psi_n^{(0)} \ | \ H' \, - \, E_n^{(1)} \ | \ \psi_n^{(1)} \right>$ ,
donde se sustituyen las expresiones anteriores para $E_n^{(1)}$ y $\psi_n^{(1)}$ :
$E_n^{(2)} \, = \, \sum_{k \ne n} \left< \psi_n^{(0)} \ | \ H' \, - \, H'_{nn} \ | \ \frac{ H'_{kn}}{ E_n^{(0)} \, - \, E_k^{(0)} } \, \psi_k^{(0)} \right>$
$= \, \sum_{k \ne n} \, \frac{1}{E_n^{(0)} \, - \, E_k^{(0)}} \, [ \ H'_{kn} \ \left< \psi_n^{(0)} \ | \ H' \ | \psi_k^{(0)} \right> \, - \, H'_{nn} \ H'_{kn} \ \left< \psi_n^{(0)} \ | \ \psi_k^{(0)} \right> \ ]$ ;
expresión en la que el segundo sumando a la derecha se anula (por ser $k\ne n$ ) quedando el resultado final para la corrección a la energía en segundo orden de perturbaciones $(O(\lambda^2), \lambda=1)$ :
$\Rightarrow E_n^{(2)} \, = \, \sum_{k \ne n} \, \frac{ | \ H'_{kn} \ |^2 }{E_n^{(0)} \, - \, E_k^{(0)}}$
$\Rightarrow E_n \, \approx \, E_n^{(0)} \, + \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right> \, + \, \sum_{k \ne n} \, \frac{ | \ H'_{kn} \ |^2 }{E_n^{(0)} \, - \, E_k^{(0)}}$
-Obsérvese que una elección no nula para el coeficiente $a_{nn}^{(1)}$ no habría tenido repercusión en el cálculo: la suma podría haberse extendido (¡antes de la división por el término en la diferencia en energías!) a $k=n$ sin consecuencias:
$E_n^{(2)} \, = \, \left< \psi_n^{(0)} | H' \, - \, E_n^{(1)} | \psi_n^{(1)} \right> \, = \, \left< \psi_n^{(0)} | H' \, - \, E_n^{(1)} | \sum_k a_{nk}^{(1)} \ \psi_k^{(0)} \right>$
$= \, \sum_k a_{nk}^{(1)} \ (H'_{nk} - H'_{nn} \delta_{kn}) \, = \, \sum_{k \ne n} a_{nk}^{(1)} \ H'_{nk}$
-Y obsérvese también que la corrección a la energía en segundo orden para el estado fundamental, $E_{n=0}^{(2)}$ , resulta siempre negativa, para toda perturbación $H'$ :
$\forall \ k>0 \ : \ E_{k}^{(0)} > E_{0}^{(0)} \Rightarrow \ E_{0}^{(2)} < 0$
-Cada término de la suma en la corrección a la energía en segundo orden $E_n^{(2)}$ puede interpretarse como una sucesión de transiciones de primer orden en las que el sistema abandona el estado $\psi_n^{(0)}$ y se propaga a diferentes estados intermedios $\psi_k^{(0)} \, , \, k \ne 0$ , para regresar posteriormente al estado $\psi_n^{(0)}$ , viniendo cada transición asociada a un factor de ponderación $[E_{n}^{(0)} \ - \ E_{k}^{(0)}]^{-1}$ .
Corrección a la función de onda en segundo orden (inicio):
-Se parte del desarrollo de $\psi_n^{(2)}$ en la base ortonormal $\{ \psi_n^{(0)} \}$ :
$\psi_n^{(2)} \, = \, \sum_{k} a_{nk}^{(2)} \ \psi_k^{(0)}$ ,
donde la suma sobre el índice $k$ debe entenderse como una suma sobre las autofunciones correspondientes a la parte discreta del espectro y una integral para las contribuciones de las funciones generalizadas:
$\psi_n^{(2)} \, = \, \sum_{E_k\in \sigma_p(H_0)} a_{nk}^{(2)} \ \psi_k^{(0)} \, + \, \int_{E_k \in \sigma_c(H_0)} a_{nk}^{(2)} \ \psi_{E_k}^{(0)} \ dE_k$ ;
los escalares complejos $a_{nk}^{(2)}$ representan los correspondientes coeficientes del desarrollo.
-A continuación, sustituimos este desarrollo (utilizaremos la forma simple válida para espectros puramente discretos):
$\lambda^2 \Rightarrow H_0 \ \psi_n^{(2)} \,+ \, H' \ \psi_n^{(1)} = \, E_n^{(0)} \ \psi_n^{(2)} \, + \, E_n^{(1)} \ \psi_n^{(1)} \, + \, E_n^{(2)} \ \psi_n^{(0)}$
$(H_0 \, - \, E_n^{(0)}) \ \psi_n^{(2)} \,+ \, (H' \, - \, E_n^{(1)}) \ \psi_n^{(1)} \, - \, E_n^{(2)} \ \psi_n^{(0)} \, + \, 0$
-Proyectamos sobre $< \psi_m^{(0)} |$ , con $m$ fijo, e integramos:
$\sum_k a_{nk}^{(2)} \left< \psi_m^{(0)} | H_0 - E_n^{(0)} | \psi_k^{(0)} \right> + \sum_k a_{nk}^{(1)} \left< \psi_m^{(0)} | H' - E_n^{(1)} | \psi_k^{(0)} \right>$
$- E_n^{(2)} \ \left< \psi_m^{(0)} | \psi_n^{(0)} \right> \, = \, 0$
$\Rightarrow \sum_k a_{nk}^{(2)} \ (E_m^{(0)}\, - \, E_n^{(0)}) \ \delta_{km} + \sum_k a_{nk}^{(1)} \ (H_{mk}' \, - \, H_{nn}' \ \delta_{km} ) \, - \, E_n^{(2)} \ \delta_{mn} \, = \, 0$ ,
separando ahora de nuevo las expresiones para $m=n$ y $m \ne n$ :
a) Expresiones para $m=n$ :
$\left. \begin{array}{l} m=n \ \Rightarrow 0 \cdot a_{nn}^{(2)} \, + \, \sum_k a_{nk}^{(1)} \ H'_{nk} \, - \, H'_{nn} \ a_{nn}^{(1)} \, - \,E_n^{(2)} \, = 0 \\ \Rightarrow E_n^{(2)} \, = \, \sum_k a_{nk}^{(1)} \ H_{nk}' \, - \, H_{nn}' \ a_{nn}^{(1)} \, = \, \sum_{k \ne n } a_{nk}^{(1)} \ H_{nk}' \\ \Rightarrow E_n^{(2)} \, = \, \sum_{k \ne n } \frac{H_{kn}' \ H_{nk}'}{ E_n^{(0)} \, - \, E_k^{(0)}} \end{array} \right\}$ ,
recuperándose el resultado anterior; también ahora, no se involucra el valor elegido de forma arbitraria para $a_{nn}^{(1)}$ y, de modo análogo a lo que se encontró en el orden 1, el coeficiente $a_{nn}^{(2)}$ del desarrollo de $\psi_n^{(2)}$ en la base $\{ \psi_k^{(0)} \}$ resulta indeterminado y no interviene en el valor de la corrección a la energía en segundo orden de perturbaciones (aunque sí intervendrá en la constante de normalización para la función de onda en ese orden).
b) Expresiones para $m \ne n$ :
$\left. \begin{array}{l} \forall \ m \ne n \Rightarrow a_{nm}^{(2)} \ ( E_m^{(0)} \, - \, E_n^{(0)} ) \, + \, \sum_k a_{nk}^{(1)} \ H'_{mk} \, - \, a_{nm}^{(1)} \ H'_{nn} \, = 0 \\ \Rightarrow a_{nm}^{(2)} \, = \,\frac{1}{ E_n^{(0)} \, - \, E_m^{(0)}} \ [ \sum_{k} a_{nk}^{(1)} \ H_{mk}' \, - \, a_{nm}^{(1)} \ H_{nn}' ] \\ \Rightarrow a_{nm}^{(2)} \, = \, \frac{1}{ E_n^{(0)} \, - \, E_m^{(0)} } \ [ \sum_{k \ne n} \frac{H_{kn}'}{ E_n^{(0)} \, - \,E_k^{(0)} } \ H_{mk}' \, - \, \frac{H_{mn}'}{ E_n^{(0)} \, - \,E_m^{(0)} } \ H_{nn}' \, + \, a_{nn}^{(1)} \ H_{mn}' ] \end{array} \right\}$

Normalizaciones para la función de onda

Recuperemos las siguientes expresiones para la función de onda:
-Desarrollo perturbativo:
$\psi_n \, = \, \sum_{i=0}^{\infty} \lambda^i \ \psi_n^{(i)}$
-Corrección a la función de onda en orden r, $\psi_n^{(r)}$ , en la base ortonormal $\{ \psi_n^{(0)} \}$ :
$\psi_n^{(r)} \, = \, \sum_{k} a_{nk}^{(r)} \ \psi_k^{(0)}$ ,
a partir de las cuales se obtiene:
Ecuación A):
$\left< \psi_n^{(0)} | \psi_n \right> \, = \, \left< \psi_n^{(0)} | \sum_{i=0}^{\infty} \lambda^i \ \psi_n^{(i)} \right> \, = \, \sum_{i=0}^{\infty} \lambda^i \ \left< \psi_n^{(0)} | \psi_n^{(i)} \right>$
$= \, \left< \psi_n^{(0)} | \psi_n^{(0)} \right> \, + \, \sum_{i=1}^{\infty} \lambda^i \ \left< \psi_n^{(0)} | \psi_n^{(i)} \right>$
$= \, 1 \, + \, \sum_{i=1}^{\infty} \lambda^i \ \left< \psi_n^{(0)} | \psi_n^{(i)} \right> \, = \, 1 \, + \, \sum_{i=1}^{\infty} \lambda^i \ a_{nn}^{(i)}$
Ecuación B):
$\left< \psi_n | \psi_n \right> \, = \, \left< \sum_{i=0}^{\infty} \lambda^i \ \psi_n^{(i)} | \sum_{i=0}^{\infty} \lambda^j \ \psi_n^{(j)} \right>$
$= \, \left< \psi_n^{(0)} | \psi_n^{(0)} \right> \, + \, \sum_{j=1}^{\infty} \lambda^j \left< \psi_n^{(0)} | \sum_{k} a_{nk}^{(j)} \ \psi_k^{(0)} \right> \, + \, \sum_{i=1}^{\infty} \lambda^i \left< \sum_{k} a_{nk}^{(i)} \ \psi_k^{(0)} | \psi_n^{(0)} \right>$
$+ \, \sum_{i,j \ge 1} \lambda^{i+j} \left< \sum_{k} a_{nk}^{(i)} \ \psi_k^{(0)} | \sum_{k'} a_{nk'}^{(j)} \ \psi_{k'}^{(0)} \right>$
$= \,1 \, + \, \sum_{j=1}^{\infty} \lambda^j \ a_{nn}^{(j)} \, + \, \sum_{i=1}^{\infty} \lambda^i \ a_{nn}^{(i)*} \, + \, \sum_{i,j \ge 1} \sum_k \lambda^{i+j} \ a_{nk}^{(i)*} \ a_{nk}^{(j)}$
$= \,1 \, + \, \lambda \ [a_{nn}^{(1)} \, + \, a_{nn}^{(1)*}] \, + \, \lambda^2 \ [a_{nn}^{(2)} \, + \, a_{nn}^{(2)*} \, + \, \sum_k | a_{nk}^{(1)} |^2 ]$
$+ \, \lambda^3 \ \{ a_{nn}^{(3)} \, + \, a_{nn}^{(3)*} \, + \, \sum_k [a_{nk}^{(2)*} \ a_{nk}^{(1)} \, + \, a_{nk}^{(1)*} \ a_{nk}^{(2)} ] \}$
$+ \, \lambda^4 \ \{ a_{nn}^{(4)*} \, + \, a_{nn}^{(4)} \, + \, \sum_k [a_{nk}^{(2)*} \ a_{nk}^{(2)} \, + \, a_{nk}^{(3)*} \ a_{nk}^{(1)} \, + \, a_{nk}^{(1)*} \ a_{nk}^{(3)} ] \}$
$+ \, \ldots$
-Dos formas posibles de normalizar la función de onda son:
N1) Escoger $a_{nn}^{(r)} \, = \,\left< \psi_n^{(0)} | \psi_n^{(r)} \right> \, = \, 0 \ \forall \ r \ge 1$
$\Rightarrow \left< \psi_n^{(0)} | \psi_n \right> \, = \, 1$ ,
de forma que se obtiene una función de onda que sólo está normalizada hasta orden $r=1$ :
$r=0 \rightarrow \left< \psi_n | \psi_n \right> \approx \left< \psi_n^{(0)} | \psi_n^{(0)} \right> \, = \, 1$
$r=1 \rightarrow \left< \psi_n | \psi_n \right> \approx \left< \psi_n^{(0)} | \psi_n^{(0)} \right>$
$+ \lambda \ [ \left< \psi_n^{(0)} | \psi_n^{(1)} \right> + \left< \psi_n^{(1)} | \psi_n^{(0)} \right> ]= 1 + \lambda \ [ a_{nn}^{(1)} + a_{nn}^{(1)*}] = 0$
$r=2 \rightarrow \left< \psi_n | \psi_n \right> \approx 1 \, + \, 0 \, + \, \lambda^2 \ [ a_{nn}^{(2)} \ + \ a_{nn}^{(2)*} \ + \ \left< \psi_n^{(1)} | \psi_n^{(1)} \right> ]$
$= \, 1\, + \, \lambda^2 \ \left< \psi_n^{(1)} | \psi_n^{(1)} \right> \, = \, 1\, + \, \lambda^2 \ \sum_{k \ne n} |a_{nk}^{(1)}|^2$
$= \, 1 \, + \,O(\lambda^{2})$
$\cdots$
$\Rightarrow \left< \psi_n | \psi_n \right> \, = \, 1 \, + \, O(\lambda^{k \ge 2})$
-Con esta elección, en cada aproximación de orden $r \ge 2$ hay que renormalizar la función obtenida, introduciendo la adecuada constante adicional de normalización:
$\psi_n^{(r)} \, = \, \sum_{k} a_{nk}^{(r)} \ \psi_k^{(0)} \rightarrow N^{(r)}(\lambda) \psi_n^{(r)}$ tal que
$\left< N^{(r)}(\lambda) \psi_n^{(r)} | N^{(r)}(\lambda) \psi_n^{(r)}\right> \, = \, 1$
$\Rightarrow \left< \psi_n | \psi_n \right> \, = \, 1 \, + \, O(\lambda^{k > r})$ ,
teniéndose ( $\lambda=1$ ):
$\psi_n = \psi_n^{(0)} \ + \ \psi_n^{(1)} \ + \ \cdots \ + \ \psi_n^{(r)} \Rightarrow \left< \psi_n | \psi_n \right> \, = \, 1$
-Ésta es, por ejemplo, la elección que realiza el manual [GAL-89].
N2) Imponer de partida $\left< \psi_n | \psi_n \right> \, = \, 1$ , para todo orden en $\lambda$ .
-En este caso se tiene:
$r=0 \rightarrow \left< \psi_n | \psi_n \right> \approx \left< \psi_n^{(0)} | \psi_n^{(0)} \right> \, = \, 1$
$r=1 \rightarrow \left< \psi_n | \psi_n \right> \approx \left< \psi_n^{(0)} | \psi_n^{(0)} \right>$
$+ \lambda \ [ \left< \psi_n^{(0)} | \psi_n^{(1)} \right> + \left< \psi_n^{(1)} | \psi_n^{(0)} \right> ]= 1 + \lambda \ [ a_{nn}^{(1)} + a_{nn}^{(1)*}] \, = \, 1 \, + \, \lambda \ 2 \ Re(a_{nn}^{(1)} )$
$\Rightarrow Re(a_{nn}^{(1)} ) \, = \, 0$ ,
quedando $Im(a_{nn}^{(1)})$ sin determinar, pudiendo tomarse como nulo, por lo que se fija $a_{nn}^{(1)}=0$ .
$r=2 \rightarrow \left< \psi_n | \psi_n \right> \approx 1 \, + \, 0 \, + \, \lambda^2 \ [ a_{nn}^{(2)} \ + \ a_{nn}^{(2)*} \ + \ \left< \psi_n^{(1)} | \psi_n^{(1)} \right> ]$
$= \, 1\, + \, \lambda^2 \ ^[ a_{nn}^{(2)} \ + \ a_{nn}^{(2)*} \ + \ \sum_{k \ne n} |a_{nk}^{(1)}|^2] \, = \, 1$
$\Rightarrow Re(a_{nn}^{(2)} ) \, = \, -\frac{1}{2} \ \sum_{k \ne n} |a_{nk}^{(1)}|^2$ ,
quedando $Im(a_{nn}^{(2)})$ sin determinar.
-Esta arbitrariedad que permanece se corresponde con el hecho de que un factor de fase arbitrario en $\psi_n$ no afecta a su normalización, por lo que, como antes, y sin pérdida de generalidad, puede tomarse $Im(a_{nn}^{(2)}) = 0$
-Para órdenes superiores se obtienen resultados análogos, de forma que se impone $Im(a_{nn}^{(r)}) = 0$ en cada orden r-ésimo, mientras que $Re(a_{nn}^{(r)})$ se obtiene de la condición de normalización en cada potencia de $\lambda$ .
-Ésta es, por ejemplo, la elección que realiza el manual [BRA-00].
Corrección a la función de onda en segundo orden (final):
$\lambda=1 \rightarrow \psi_n \approx \psi_n^{(0)} \ + \ \psi_n^{(1)} \ + \ \psi_n^{(2)}$
N1) Normalizando según la elección $a_{nn}^{(r)} \, = \,\left< \psi_n^{(0)} | \psi_n^{(r)} \right> \, = \,0 \, , \, r=1,2$ :
$a_{nn}^{(1)} \ = \ a_{nn}^{(2)} \ = \ 0 \ \Rightarrow$
$\psi_n \approx \psi_n^{(0)} \ + \ \sum_{k \ne n } \frac{H_{kn}'}{ E_n^{(0)} \ - \ E_k^{(0)}} \ \psi_k^{(0)}$
$+ \ \sum_{k \ne n } [ \sum_{m \ne n} \frac{H_{mn}' \ H_{km}'}{ (E_n^{(0)} \ - \ E_k^{(0)}) \ (E_n^{(0)} \ - \ E_m^{(0)}) } \ - \ \frac{H_{kn}' \ H_{nn}'}{ (E_n^{(0)} \ - \ E_k^{(0)})^2 } ] \ \psi_k^{(0)}$
-Esta función no está normalizada, por lo que habrá que hacerlo mediante la adecuada constante de normalización $N(\lambda)$ ;
$\psi_n \rightarrow N(\lambda)\psi_n \rightarrow \left< N(\lambda)\psi_n \ | \ N(\lambda)\psi_n \ \right> \, = \, 1$
N2) Normalizando según la elección $\left< \psi_n \ | \ \psi_n \ \right> \, = \, 1$ para cada orden en $\lambda$ :
$\left. \begin{array}{l} a_{nn}^{(1)} \ = \ 0 \\ Re(a_{nn}^{(2)}) \ = \ -\frac{1}{2}\sum_{k \ne n} |a_{nk}^{(1)}|^2 \\ Im(a_{nn}^{(2)}) \ = \ 0 \end{array} \right\} \Rightarrow$
$\psi_n \approx \psi_n^{(0)} \ + \ \sum_{k \ne n } \frac{H_{kn}'}{ E_n^{(0)} \ - \ E_k^{(0)}} \ \psi_k^{(0)}$
$+ \ \sum_{k \ne n } [ \sum_{m \ne n} \frac{H_{mn}' \ H_{km}'}{ (E_n^{(0)} \ - \ E_k^{(0)}) \ (E_n^{(0)} \ - \ E_m^{(0)}) } \ - \ \frac{H_{kn}' \ H_{nn}'}{ (E_n^{(0)} \ - \ E_k^{(0)})^2 } ] \ \psi_k^{(0)}$
$-\frac{1}{2} \sum_{k \ne n} \frac{|H_{kn}'|^2}{ |E_n^{(0)} \ - \ E_k^{(0)}|^2 } \ \psi_n^{(0)}$ ,
función normalizada a la unidad: $\left< \psi_n \ | \ \psi_n \ \right> \, = \, 1$
Las fórmulas para las correcciones de orden superior se van derivando sucesivamente; pueden encontrase en la bibliografía. Por ejemplo:
–Corrección a la energía en tercer orden:
$E_n^{(3)}\, = \, \left< \psi_n^{(0)} \ | \ H' \ | \ \psi_n^{(2)} \ \right> \, = \, \left< \psi_n^{(1)} \ | \ H' - E_n^{(1)} \ | \ \psi_n^{(1)} \ \right>$
(válida para ambas formas de normalización).

Ejemplo: el potencial del oscilador armónico monodimensional con perturbación

El oscilador armónico monodimensional es un potencial de expresión general:
$V_{HO} \equiv V(x)\, = \, \frac{1}{2} k \ x^2 \, + \, V_0$ ,
donde
$k= m\omega^2 \leftrightarrow \omega=+\sqrt{\frac{k}{m}} \leftrightarrow \alpha=+\sqrt{\frac{m\omega}{\hbar}}$ ;
se suele tomar $V_0=0$ , una elección arbitraria del origen de energías que conduce a que todos los estados ligados, en número infinito numerable, pertenezcan a autovalores positivos de energía, extendiéndose sobre la recta real positiva, $\sigma (H)=\sigma_p(H) \subset \{ \mathbb{R}^+ - 0\}$ .
Las correspondientes autofunciones y autovalores son:
$\psi_n(x)=C_n\ e^{-\alpha^2x^2/2}\ H_n(\alpha x)\;,\;n=0,1,2\ldots$
$=C_n\ e^{-\alpha^2x^2/2} \left \{ \begin{matrix} (-1)^{\frac{n}{2}}\frac{n!}{(\frac{n}{2})!}\ M(-\frac{n}{2},\frac{1}{2};\alpha^2x^2)\;,\;n=0,2,4\ldots \\ (-1)^{\frac{n-1}{2}}\frac{n!}{(\frac{n-1}{2})!}\ 2\alpha x\ M(-\frac{n-1}{2},\frac{3}{2};\alpha^2x^2)\;,\;n=1,3,5\ldots \end{matrix}\right.$
-Normalización:
$\int_{-\infty}^{+\infty}|\psi_n(x)|^2dx=1$
$=|C_n|^2\ \int_{-\infty}^{+\infty}e^{-\alpha^2x^2}\ H_n^2(\alpha x)dx$
$=|C_n|^2\frac{1}{\alpha} \int_{-\infty}^{+\infty}e^{-z^2}\ H_n^2(z)dz=|C_n|^2\ \frac{\sqrt{\pi}}{\alpha}2^nn!$
$\Rightarrow |C_n|=\frac{\sqrt{\alpha}}{\pi^{\frac{1}{4}}\sqrt{2^nn!}}$
$\Rightarrow \psi_n(x)=(\frac{\alpha}{\sqrt{\pi}2^nn!})^{\frac{1}{2}}e^{-\alpha^2x^2/2}\ H_n(\alpha x)\;,\;n=0,1,2\ldots$
$=(\frac{\alpha}{\sqrt{\pi}2^nn!})^{\frac{1}{2}}\ e^{-\alpha^2x^2/2} \left \{ \begin{matrix} (-1)^{\frac{n}{2}}\frac{n!}{(\frac{n}{2})!}\ M(-\frac{n}{2},\frac{1}{2};\alpha^2x^2)\;,\;n=0,2,4\ldots \\ (-1)^{\frac{n-1}{2}}\frac{n!}{(\frac{n-1}{2})!}\ 2\alpha x\ M(-\frac{n-1}{2},\frac{3}{2};\alpha^2x^2)\;,\;n=1,3,5\ldots \end{matrix}\right.$
donde
$\alpha=(\frac{mk}{\hbar^2})^{\frac{1}{4}}=(\frac{m\omega}{\hbar})^{\frac{1}{2}}$ ( $[\alpha]=L^{-1}$ ).
-Estas autofunciones constituyen un sistema ortonormal:
$\int_{-\infty}^{+\infty}\psi_n^*(x)\psi_m(x)dx=\delta_{n,m}$
-Cada autofunción $\psi_n(x)$ corresponde al autovalor de energía:
$E_n=(n+\frac{1}{2})\hbar \omega=(n+\frac{1}{2})h \nu \;,\;n=0,1,2\ldots$
donde
$\nu=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$

A. Perturbación cuadrática

Para ilustrar la aplicación del método perturbativo, se considera en primer lugar el Hamiltoniano adicional:
$H'=\lambda \frac{1}{2} k' \ x^2$ ,
(es evidente que el Hamiltoniano total $H=H_0+H'$ es resoluble de forma exacta, sustituyendo la constante $k$ del oscilador en las fórmulas por $k \rightarrow (k+k')$ ).
a) Corrección a la energía en primer orden de teoría perturbaciones $(O(\lambda^1), \lambda=1)$ :
$\Rightarrow E_n^{(1)} \, = \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right> \, = \, \left< \psi_n^{(0)} | \frac{1}{2} k' x^2| \psi_n^{(0)} \right>$
$= \frac{1}{2} k' \ \left< \psi_n^{(0)} | \ x^2 \ | \psi_n^{(0)} \right> =\frac{1}{2} \frac{2k'}{k} \ \left< \psi_n^{(0)} | \frac{1}{2} x^2 \ | \psi_n^{(0)} \right> = \frac{1}{2} \frac{k'}{k} \ (n+\frac{1}{2})\hbar \omega$
$\Rightarrow E_n \, \approx \, E_n^{(0)} \, + \,E_n^{(1)} \, = \, (n+\frac{1}{2})\hbar \omega_0 \, + \, \frac{1}{2} \frac{k'}{k} \ (n+\frac{1}{2})\hbar \omega_0$
$= \,(n+\frac{1}{2}) \hbar \omega_0 [1 +\frac{1}{2} \frac{k'}{k}]$ ,
donde $\omega_0=\omega$ y el resultado coincide con los primeros términos del desarrollo en serie de potencias del valor exacto, ya que:
$(1 + \frac{k'}{k})^{\frac{1}{2}} \, = \, 1 + \frac{1}{2} \frac{k'}{k} -\frac{1}{8} (\frac{k'}{k})^2 - \cdots \, , \, -1 \le \frac{k'}{k} \le 1$ ,
a comparar con la resolución exacta, que proporciona:
$E_n= (n+\frac{1}{2})\hbar \omega' =(n+\frac{1}{2})\hbar \sqrt{\frac{k+k'}{m}} =(n+\frac{1}{2})\hbar \sqrt{\frac{k}{m}} \sqrt{1+\frac{k'}{k}}=(n+\frac{1}{2})\hbar \omega_0 \sqrt{1+\frac{k'}{k}}$
b) Corrección a la energía en segundo orden de teoría perturbaciones $(O(\lambda^2), \lambda=1)$ :
$\Rightarrow E_n^{(2)} \, = \, \sum_{m \ne n} \, \frac{ | \ H'_{mn} \ |^2 }{E_n^{(0)} \, - \, E_m^{(0)}}\, = \, \sum_{m \ne n} \, \frac{ | \ \left< \psi_m^{(0)} |\frac{1}{2} k' x^2 | \psi_n^{(0)} \right> \ |^2 }{E_n^{(0)} \, - \, E_m^{(0)}}$ .
-Usando los resultados:
$\left\langle x^2 \right\rangle_n=\int_{-\infty}^{+\infty}\psi_n^*(x)(x^2)\psi_n(x)dx=\frac{2n+1}{2\alpha^2}=(n+\frac{1}{2})\frac{\hbar}{m\omega}$
$\left\langle \psi_n |x^2| \psi_m \right\rangle \left \{ \begin{matrix} =\frac{1}{2\alpha^2}[(m+1)(m+2)]^{\frac{1}{2}}\quad \mbox{si}\quad n=m+2 \\ =\frac{1}{2\alpha^2}[2m+1]\quad \mbox{si}\quad n=m \\ =\frac{1}{2\alpha^2}[m(m-1)]^{\frac{1}{2}}\quad \mbox{si}\quad n=m-2 \\ =0 \quad \mbox{otro caso} \end{matrix}\right.$ ,
se obtiene:
$E_n^{(2)} \, = \, \frac{|\frac{k'}{2} \frac{1}{2\alpha_0^2}[(n+1)(n+2)]^{\frac{1}{2}}|^2}{E_n^{(0)} \, - \, E_{n+2}^{(0)}} \ (\delta_{m, n+2}) \, + \, \frac{| \frac{k'}{2} \frac{1}{2\alpha_0^2}[(n)(n-1)]^{\frac{1}{2}}|^2}{E_n^{(0)} \, - \, E_{n-2}^{(0)}} \ (\delta_{m, n-2})$ ;
$\left. \begin{array}{l} n=0 \, , \, E_0^{(2)}= \, \frac{ | \frac{k'}{4} \frac{\sqrt{2}}{\alpha_0^2}|^2}{ -2 \hbar \omega_0} \, = \, -\frac{\hbar \omega_0}{16} (\frac{k'}{k})^2\\ n=1 \, , \, E_1^{(2)}= \, \frac{ | \frac{k'}{4} \frac{\sqrt{6}}{\alpha_0^2}|^2}{ -2 \hbar \omega_0} \, = \, -\frac{3\hbar \omega_0}{16} (\frac{k'}{k})^2\\ n \ge 2 \, , \, E_n^{(2)} \, = \, \frac{|\frac{k'}{4} \frac{1}{2\alpha_0^2}[(n+1)(n+2)]^{\frac{1}{2}}|^2}{-2 \hbar \omega_0} \, + \, \frac{| \frac{k'}{4} \frac{1}{2\alpha_0^2}[(n)(n-1)]^{\frac{1}{2}}|^2}{2 \hbar \omega_0} \, = \, (n + \frac{1}{2}) \hbar \omega_0 (-\frac{(-k')^2}{8k^2}) \end{array} \right\} \, ,$
esto es, de nuevo los primeros términos del desarrollo en potencias que proporciona el valor exacto,
$(1 + \frac{k'}{k})^{\frac{1}{2}} \, = \, 1 + \frac{1}{2} \frac{k'}{k} -\frac{1}{8} (\frac{k'}{k})^2 - \cdots \, , \, -1 \le \frac{k'}{k} \le 1$
La corrección en segundo orden queda pues finalmente:
$\Rightarrow E_n \, \approx \, E_n^{(0)} \, + \,E_n^{(1)} \, + \,E_n^{(2)}$
$= \, E_n^{(0)} \, + \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right> \, + \, \sum_{m \ne n} \, \frac{ | \ H'_{mn} \ |^2 }{E_n^{(0)} \, - \, E_m^{(0)}}$
$\Rightarrow E_n \, \approx \,(n+\frac{1}{2}) \hbar \omega_0 [1 +\frac{1}{2} \frac{k'}{k} - \frac{1}{8} (\frac{k'}{k})^2]$
Observaciones:
1. Sobre la condición de «pequeña perturbación»: según esta condición, tras la perturbación de cada nivel $E_n^{(0)}$ , el nivel menos próximo a él que resulta al corregir ese valor de orden cero, en términos energéticos, debe de estar más próximo a él que cualquier otro nivel $E_k^{(0)}\, , \, k \ne n$ . Es decir, la perturbación puede alterar el valor de $E_n^{(0)}$ , o incluso, en su caso, desdoblarlo, y el tratamiento perturbativo hecho se considerará correcto si la magnitud de la corrección no altera el orden energético establecido en el estadio sin perturbación; es decir, tras la perturbación, un estado que ha surgido a partir de $E_n^{(0)}$ no puede estar más lejos de él que cualquier otro de los iniciales no perturbados. En términos matriciales, esto equivale a que los elementos de la matriz perturbativa no pueden ser mayores en magnitud que el espaciado entre los niveles no perturbados.
  -Pero el ejemplo anterior es un caso particular: sucede que la condición de pequeña perturbación se viola para valores grandes de $n$ ,
  $\hbar \omega_0 > >(n+\frac{1}{2})\frac{1}{2}\frac{k'}{k} \hbar \omega_0 \Leftrightarrow (n+\frac{1}{2})\frac{k'}{k} < < 1$ ,
  y, sin embargo, la corrección sigue siendo válida:
  a) valor exacto:
  $E_n=\hbar \omega_0 (n+\frac{1}{2}) \sqrt{1+\frac{k'}{k}}$
  b) valor perturbado en $O(\lambda^1)$ :
  $E_n \approx \hbar \omega_0 (n+\frac{1}{2}) (1+\frac{1}{2}\frac{k'}{k})$ ,
  válido $\forall n$ siempre que $\frac{k'}{k} < < 1$ .
2. En un problema general real, en el que se usa teoría de perturbaciones porque se desconoce la solución exacta, si se viola la condición de «pequeña perturbación»… ¡no hay manera de tener seguridad sobre la convergencia del método!

B. Perturbaciones anharmónicas
Fuente: [BRA-00] cap. 8, pp. 382-384.

B1. Perturbación cuártica

Sea ahora el caso de una perturbación anharmónica cuártica,
$H'=\lambda \ K x^4$ ,
frecuente, por ejemplo, en el estudio vibracional de las moléculas.
Correcciones a la energía en primer y segundo orden de teoría perturbaciones:
$O(\lambda^1), \lambda=1)$ :
$\Rightarrow E_n^{(1)} \, = \, \left< \psi_n^{(0)} | H' | \psi_n^{(0)} \right> \, = \, \left< \psi_n^{(0)} | K x^4| \psi_n^{(0)} \right>$
$= K \frac{3}{4} (\frac{\hbar}{m\omega_0})^2 (2n^2 +2n+1)$
$O(\lambda^2), \lambda=1)$ :
$\Rightarrow E_n^{(2)} \, = \, -\frac{1}{8}\frac{K^2}{\hbar \omega_0} \frac{1}{8} (\frac{\hbar}{m\omega_0})^4 (34n^3 + 51n^2 +59n+21)$
En este caso, conforme $n$ aumenta, crece el valor de las correcciones a la energía en los sucesivos órdenes. Por tanto, habrá que considerar que el método perturbativo dejará de ser válido para los estados más excitados, y tanto más cuanto más grande sea la constante $K$ , algo esperable dado que, cuanto más por encima del estado fundamental se encuentra un estado excitado, debido a la presencia de la potencia cuarta de la variable de longitud $x$ , más lejos del origen se extiende la parte no nula de la correspondiente función de onda.

B2. Perturbación cúbica

Perturbación anharmónica cúbica,
$H'=\lambda \ K x^3$
Correcciones a la energía en primer y segundo orden de teoría perturbaciones:
$O(\lambda^1), \lambda=1)$ :
$\Rightarrow E_n^{(1)} \, = \, 0$
$O(\lambda^2), \lambda=1)$ :
$\Rightarrow E_n^{(2)} \, = \, -\frac{15}{4}\frac{K^2}{\hbar \omega_0} (\frac{\hbar}{m\omega_0})^4 (n^2 +n+\frac{11}{30})$

Estados ligados degenerados

Fuente: [BRA-00] cap. 8, pp. 386ss.

Sea ahora el caso en que el nivel de energía no perturbado $E_n^{(0)}$ , autovalor del Hamiltoniano no perturbado $H_0$ , posee una degeneración $\alpha_n > 1$ , esto es, la dimensión del correspondiente subespacio $M_{E_n^{(0)}}$ es $\alpha_n >1$ : existen $\alpha_n$ autofunciones de $H_o$ linealmente independientes en el subespacio y ortonormales (algo siempre conseguible con métodos como el de ortonormalización de Gram-Schmidt), que representaremos como $\{ \psi_{ns}^{(0)} \} \; , \; s=1,2,\ldots,\alpha_n$ , y que suponemos pues elegidas de modo que integren una base ortonormal del subespacio, $< \psi_{ns}^{(0)} | \psi_{ns'}^{(0)}> = \delta_{s,s'}$ .
-Estas funciones cumplirán todas:
$H_o \psi_{ns}^{(0)} = E_n^{(0)} \psi_{ns}^{(0)} \; , \; s=1,2,\ldots,\alpha_n$ .
En el caso previo, estados ligados no degenerados, se asumió la hipótesis matemática de perturbaciones pequeñas, considerando una perturbación como suficientemente pequeña cuando autofunciones y autovalores del Hamiltoniano $H$ admiten desarrollo en serie de potencias del parámetro $\lambda$ :
$E_n \, = \, \sum_{i=0}^{\infty} \lambda^i \ E_n^{(i)}$
$\psi_n \, = \, \sum_{i=0}^{\infty} \lambda^i \ \psi_n^{(i)}$ ,
donde cada valor del índice $i$ establece el orden perturbativo en que se van a proporcionar las correcciones.
-En el caso con degeneración, seguiremos trabajando en la hipótesis de perturbaciones pequeñas, esto es, el caso en que la corrección a la energía no perturbada $E_n^{(0)}$ es menor que el espaciado $\Delta E_n^{(0)}=$ mínimo $\{ |E_{n-1}^{(0)} - E_n^{(0)},E_{n+1}^{(0)} - E_n^{(0)} | \}$ .
-La diferencia en este caso es que, mientras cuando no hay degeneración el límite no perturbativo está claro,
$\lim_{\lambda \rightarrow 0} \psi_n=\psi_n^{(0)}$ ,
pero al considerarse un nivel degenerado existen $\alpha_n$ funciones candidatas, por lo que se requiere un tratamiento matemático distinto.
Sea pues la base ortonormal del Hilbert asociada a $H_0$ ,
$\{ \psi_{ks}^{(0)} \; , \; \forall k \ : \ \ E_k^{(0)} \in \sigma(H_o) \, , \, s=1,2,\ldots,\alpha_k=deg(E_k^{(0)}) \ \}$ ,
esto es, constituida por autofunciones del Hamiltoniano no perturbado:
$H_o \psi_{ks}^{(0)}=E_k^{(0)} \psi_{ks}^{(0)} \quad \forall s=1,2,\ldots , \alpha_k$ ,
$< \psi_{ks}^{(0)} | \psi_{k's'}^{(0)}> = \delta_{k,k'}\delta_{s,s'}$ ,
donde la primera $\delta_{k,k'}$ engloba notacionalmente los casos de la parte continua (delta $\delta(k-k')$ de Dirac) y discreta (delta $\delta_{k,k'}$ de Kronecker) del espectro de $H_0$ , mientras que la segunda $\delta_{s,s'}$ posee subíndices que refieren siempre a un conjunto discreto.
Se considera a continuación el conjunto de $\alpha_n$ autofunciones ortonormales del Hamiltoniano del sistema $H=H_0 + \lambda H'$ (¡las autofunciones exactas!):
$\{ \psi_{nr} \; , \; r=1,2, \ldots, \alpha_n=deg(E_{n}^{(0)}) \}$ ,
funciones del Hilbert elegidas de manera que cumplan:
a) son autoestados de $H$ con autovalor $E_{nr}$ :
$H \psi_{nr} \, = \, E_{nr}\psi_{nr} \quad , \,E_{nr} \in \sigma(H)$
b) constituyen un conjunto ortonormal:
$< \psi_{nr} | \psi_{nr'}> = \delta_{r,r'} \, , \, r=1,2, \ldots , \alpha_n$
c) en el límite no perturbado satisfacen:
$\lim_{\lambda \rightarrow 0} \psi_{nr}= \chi_{nr}^{(0)} =\sum_{s=1}^{\alpha_n} C_{nrs}\psi_{ns}^{(0)}$ , donde $H_0 \chi_{nr}^{(0)} = E_n^{(0)} \chi_{nr}^{(0)}$ ,
es decir, cada función exacta $\psi_{nr}$ tiende a una combinación lineal de funciones del subespacio $M_{E_n^{(0)}}$ . Esta combinación lineal vendrá especificada por el conjunto de coeficientes $\{ c_{nrs} \}$ , incógnitas a determinar.

Observaciones:
1. El conjunto anterior es siempre construible, ya que el que existan $\alpha_n$ funciones $\chi_{nr}^{(0)}$ garantiza que existan esas $\alpha_n$ funciones $\psi_{nr}$ linealmente independientes entre sí.
2. Pero, a priori, es imposible determinar si estas $\alpha_n$ funciones $\psi_{nr}$ estarán degeneradas en energía entre sí o no, y de ahí que el autovalor $E_{nr}$ posea los dos índices $n$ y $r$ ; sólo sabemos que, por construcción, sí están degenerados en el límite $\lambda \rightarrow 0$ , y que el número máximo de valores $E_{nr}$ distintos, es decir, el número de valores distintos de $r$ para cada $n$ fijo, ha de ser menor o igual que $\alpha_n$ . Será el cálculo perturbativo, en los sucesivos órdenes, el que, a un orden dado, proporcionará las correcciones al valor $E_n^{(0)}$ que rompan, total o parcialmente, o no rompan, la correspondiente degeneración.
3. Las $\alpha_n$ funciones $\chi_{nr}^{(0)}$ sí están degeneradas en energía: $H_0 \chi_{nr}^{(0)} = E_n^{(0)} \chi_{nr}^{(0)}$ , ya que son combinación lineal de autofunciones de $H_0$ para el mismo autovalor $E_n^{(0)}$ .
4. La notación que se está usando entonces es:
4.1. El conjunto $\{ \psi_{ns}^{(0)} \; , \; s=1,2, \ldots, \alpha_n=deg(E_{n}^{(0)}) \}$ está integrado por funciones que satisfacen:
$H_0 \psi_{ns}^{(0)} =E_{n}^{(0)}\psi_{ns}^{(0)}$
4.2. El conjunto $\{ \psi_{nr} \; , \; r=1,2, \ldots, \alpha_n=deg(E_{n}^{(0)}) \}$ está integrado por funciones que satisfacen:
$H \psi_{nr} =E_{nr}\psi_{nr}$ ,
donde el número de autovalores $E_{nr}$ distintos es siempre menor o igual a $\alpha_n$ .

Como en el caso no degenerado, la hipótesis matemática básica que se adopta a continuación es la asunción de la perturbación como lo suficientemente pequeña para que autofunciones y autovalores del Hamiltoniano $H$ admitan desarrollo en serie de potencias del parámetro $\lambda$ :
$E_{nr} \, = \, E_n^{(0)} + \sum_{i=1}^{\infty} \lambda^i \ E_{nr}^{(i)}$
$\psi_{nr} \, = \, \chi_{nr^{(0)}} + \sum_{i=1}^{\infty} \lambda^i \ \psi_{nr}^{(i)}$ ,
donde cada valor del índice $i$ establece el orden perturbativo en que se van a proporcionar las correcciones.
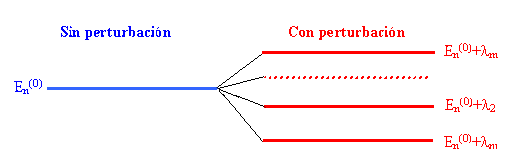
-El esquema de niveles de energía correspondiente sería:
$\{ \xrightarrow[(H_o)]{E_n^{(0)} \ , \ deg(E_n^{(0)})=\alpha_n > 1 } \} \longmapsto \left\{ \begin{array}{l} \xrightarrow{E_{n \alpha} \; \quad} \\ \cdots \\ \xrightarrow[(H_0+H')]{E_{n1}} \end{array} \right\} \quad ; \; \alpha \le \alpha_n \; , \; \sum_{i=1}^{\alpha} deg(E_{ni})= \alpha_n$
Sustituyendo ambos desarrollos anteriores en la ecuación de Schrödinger:
$H \ \psi_{nr} \, = \,E_{nr} \ \psi_{nr}$
$(H_0 \ + \ \lambda H') \ (\chi_{nr}^{(0)} + \sum_{i=1}^{\infty} \lambda^i \ \psi_{nr}^{(i)}) \, = \,( E_{n}^{(0)} + \sum_{i=1}^{\infty} \lambda^i \ E_{nr}^{(i)} ) \ (\chi_{nr}^{(0)} + \sum_{i=1}^{\infty} \lambda^i \ \psi_{nr}^{(i)})$ ;
igualando coeficientes de igual potencia de $\lambda$ en ambos lados de la igualdad:
$\left. \begin{array}{l} i=0 \, , \, \lambda^0 \Rightarrow H_0 \ \chi_{nr}^{(0)} \, = \, E_n^{(0)} \ \chi_{nr}^{(0)}\\ i=1 \, , \, \lambda^1 \Rightarrow H_0 \ \psi_{nr}^{(1)} \,+ \, H' \ \chi_{nr}^{(0)} = \, E_n^{(0)} \ \psi_{nr}^{(1)} \, + \, E_{nr}^{(1)} \ \chi_{nr}^{(0)} \\ i=2 \, , \, \lambda^2 \Rightarrow H_0 \ \psi_{nr}^{(2)} \,+ \, H' \ \psi_{nr}^{(1)} = \, E_n^{(0)} \ \psi_{nr}^{(2)} \, + \, E_{nr}^{(1)} \ \psi_{nr}^{(1)} \, + \, E_{nr}^{(2)} \ \chi_{nr}^{(0)} \\ \ldots \\ i \, , \, \lambda^i \Rightarrow H_0 \ \psi_{nr}^{(i)} \,+ \, H' \ \psi_{nr}^{(i-1)} = \, E_n^{(0)} \ \psi_{nr}^{(i)} \, + \, E_{nr}^{(1)} \ \psi_{nr}^{(i-1)} \, + \ \ldots \, + \ E_{nr}^{(i-1)} \ \psi_{nr}^{(1)} + \, E_{nr}^{(i)} \ \chi_{nr}^{(0)} \end{array} \right\}$
Este conjunto de ecuaciones permite encontrar la solución al problema, proporcionando autofunciones y autovalores en los sucesivos órdenes de la corrección perturbativa.
Corrección en orden cero:
$H_0 \ \chi_{nr}^{(0)} \, = \, E_n^{(0)} \ \chi_{nr}^{(0)}$
-Es el caso no perturbado, de solución sencilla según lo presupuesto. Pero lo que queremos ahora es encontrar unas expresiones particulares específicas para las funciones en orden cero, unas determinadas combinaciones lineales $\chi_{nr}^{(0)}$ de las autofunciones degeneradas $\psi_{ns}^{(0)} \; , \;s=1,2,\ldots,\alpha_n=deg(E_n^{(0)})$ , construidas de manera que constituyan el límite de las soluciones exactas cuando la constante perturbativa $\lambda$ tienda a cero:
$\chi_{nr}^{(0)} = \lim_{\lambda \rightarrow 0} \psi_{nr}$
-De hecho, a tales funciones $\chi_{nr}^{(0)}$ , por determinar, se les suele denominar como las aproximaciones en primer orden perturbativo, aunque son de orden cero.

Corrección a la energía en primer orden:
$H_0 \ \psi_{nr}^{(1)} \,+ \, H' \ \chi_{nr}^{(0)} = \, E_n^{(0)} \ \psi_{nr}^{(1)} \, + \, E_{nr}^{(1)} \ \chi_{nr}^{(0)}$
$(H' \ - \ E_{nr}^{(1)}) \ \psi_{nr}^{(1)} \ \chi_{nr}^{(0)} \, + \, (H_0 \ - \ E_n^{(0)}) \ \psi_{nr}^{(1)} \, = \, 0$ ,
insertando los desarrollos
$\chi_{nr}^{(0)} \, = \, \sum_{s=1}^{\alpha_n} c_{nrs} \ \psi_{ns}^{(0)}$
$\psi_{nr}^{(1)} \, = \,\sum_{k} \sum_{s=1}^{\alpha_k} a_{nrks}^{(1)} \psi_{ks}^{(0)}$ :
$(H' \ - \ E_{nr}^{(1)}) \ \sum_{s=1}^{\alpha_n} c_{nrs} \ \psi_{ns}^{(0)} \, + \, (H_0 \ - \ E_n^{(0)}) \ \sum_{k} \sum_{s=1}^{\alpha_k} a_{nrks}^{(1)} \psi_{ks^{(0)}}\, = \, 0$
-Multiplicando a la izquierda sobre el estado $\psi_{nu}^{(0)*}$ , con $u \in \{ 1, \ldots , \alpha_n \}$ fijo, e integrando:
$\sum_{s=1}^{\alpha_n} c_{nrs} \ \left< \psi_{nu}^{(0)} | H' - E_{nr}^{(1)} | \psi_{ns}^{(0)} \right>$
$+ \, \sum_{k} \sum_{s=1}^{\alpha_k} a_{nrks}^{(1)} \ \left< \psi_{nu}^{(0)} | H_0 - E_n^{(0)} | \psi_{ks}^{(0)} \right> \, = \, 0$ ,
$\sum_{s=1}^{\alpha_n} c_{nrs} \ [ H'_{nu,ns} \ - \ E_{nr}^{(1)} \ \delta_{us} ] \, + \, \sum_{k} \sum_{s=1}^{\alpha_k} a_{nrks}^{(1)} \ [ E_n^{(0)} \ \delta_{nk} \ \delta_{us} \, - \, E_{n}^{(0)} \ \delta_{nk} \ \delta_{us} ] \, = \, 0$
$\Rightarrow \sum_{s=1}^{\alpha_n} c_{nrs} \ [ H'_{nu,ns} \ - \ E_{nr}^{(1)} \ \delta_{us} ] \, = \, 0 \quad ; \; u=1, \ldots, \alpha_n$
-Es decir se obtiene un sistema lineal y homogéneo de $\alpha_n$ ecuaciones, en las $\alpha_n$ incógnitas $c_{nrs} \, , \ s=1, \ldots, \alpha_n$ , que tendrá solución no trivial si y sólo si el determinante de los coeficientes es nulo:
$det [ H'_{nu,ns} \ - \ E_{nr}^{(1)} \ \delta_{us} ] \, = \, 0$
En definitiva, se ha obtenido la siguiente ecuación secular, de grado $\alpha_n$ en la incógnita $E_{nr}^{(1)}$ , cuya resolución proporcionará las correcciones a la energía en primer orden de perturbaciones para el nivel degenerado $E_{n}^{(0)}$ , correcciones que, dependiendo de cuántos valores distintos afloren, romperán, parcial o totalmente, o no romperán en absoluto, su degeneración $\alpha_n$ :
$\begin{vmatrix} \left< \psi_{n1}^{(0)} | H'| \psi_{n1}^{(0)} \right> - E_{nr}^{(1)} & \left< \psi_{n1}^{(0)} | H'| \psi_{n2}^{(0)} \right> & \ldots & \left< \psi_{n1}^{(0)} | H'| \psi_{n \alpha_n}^{(0)} \right> \\ \left< \psi_{n2}^{(0)} | H'| \psi_{n1}^{(0)} \right> & \left< \psi_{n2}^{(0)} | H'| \psi_{n2}^{(0)} \right> - E_{nr}^{(1)} & \ldots & \left< \psi_{n2}^{(0)} | H'| \psi_{n \alpha_n}^{(0)} \right> \\ \cdots & \cdots & \cdots & \cdots \\ \left< \psi_{n \alpha_n}^{(0)} | H'| \psi_{n1}^{(0)} \right> & \left< \psi_{n \alpha_n}^{(0)} | H'| \psi_{n2}^{(0)} \right> & \ldots & \left< \psi_{n \alpha_n}^{(0)} | H'| \psi_{n \alpha_n}^{(0)} \right> - E_{nr}^{(1)}\\ \end{vmatrix}$
$= \, 0$ .
-En resumen: hay que diagonalizar el Hamiltoniano perturbativo $H'$ en el subespacio del Hilbert $M_{E_n^{(0)}}$ , de dimensión $\alpha_n$ , generado por el conjunto de funciones $\{ \psi_{ns}^{(0)} \, , \ s=1, \ldots, \alpha_n \}$ . Las raíces de la ecuación proporcionarán las correcciones a la energía en primer orden $(O(\lambda^1), \lambda=1)$ de teoría de perturbaciones:
$E_{nr} \approx E_n^{(0)} + E_{nr}^{(1)} \, , \, r=1, \ldots, \alpha_n$ .
-El correspondiente esquema de niveles de energía queda pues:
$\{ \xrightarrow[(H_o)]{E_n^{(0)} \ , \ deg(E_n^{(0)})=\alpha_n > 1 } \} \longmapsto \left\{ \begin{array}{l} \xrightarrow{E_{n \alpha}=E_n^{(0)} + E_{nr}^{(1)_{\alpha}}} \\ \cdots \\ \xrightarrow[(H_0+H')]{E_{n1}=E_n^{(0)} + E_{nr}^{(1)_1}} \end{array} \right\}$ ,
teniéndose que
$\alpha \le \alpha_n \; , \; \sum_{i=1}^{\alpha} deg(E_{ni})= \alpha_n$ ,
y donde $E_{nr}^{(1)_m} \, , \, m=1, \ldots, \alpha$ representa las distintas raíces de la ecuación determinamental.
En la resolución de la anterior ecuación secular aparecen dos posibilidades:
1. Caso en que se obtienen $\alpha_n$ raíces distintas $E_{nr}^{(1)} \, , \, r=1, \ldots, \alpha_n$ .
  -corresponde al caso en que la degeneración del nivel $E_n^{(0)}$ queda completamente removida en primer orden por la perturbación, y el nivel no perturbado se desdobla en $\alpha_n$ niveles distintos, representando los autovalores del Hamiltoniano $H$ , no degenerados ya en primer orden de teoría de perturbaciones.
2. Caso en que alguna(s), o todas, de las $\alpha_n$ raíces poseen multiplicidad mayor a la unidad. En este caso la degeneración es sólo parcialmente removida, y podrá o no ser removida ya en órdenes superiores del cálculo perturbativo (algo que dependerá de las propiedades de simetría que presenten $H_0$ y $H'$ ).
Expresión de la función de onda en orden cero:
-Una vez determinadas las raíces $E_{nr}^{(1)_m} \, , \, m=1, \ldots, \alpha$ , para cada una de ellas el sistema lineal homógeneo
$\Rightarrow \sum_{s=1}^{\alpha_n} c_{nrs}^m \ [ H'_{nu,ns} \ - \ E_{nr}^{(1)_m} \ \delta_{us} ] \, = \, 0 \quad ; \; u=1, \ldots, \alpha_n$
$\equiv \sum_{s=1}^{\alpha_n} c_{nrs}^m \ [ \left< \psi_{nu}^{(0)} | H'| \psi_{ns}^{(0)} \right> \ - \ E_{nr}^{(1)_m} \ \delta_{us} ]\, = \, 0 \quad ; \; u=1, \ldots, \alpha_n$
permitirá calcular los coeficiente $c_{nrs}^m$ que proporcionan el desarrollo de la función $\chi_{nr}^{(0)_m}$ en términos de las funciones del subespacio $M_{E_n^{(0)}}$ :
$\chi_{nr}^{(0)_m} =\sum_{s=1}^{\alpha_n} c_{nrs}^m\psi_{ns}^{(0)} = \lim_{\lambda \rightarrow 0} \psi_{nr}$ ,
donde $H_0 \chi_{nr}^{(0)_m} = E_n^{(0)} \chi_{nr}^{(0)_m}$ .
-Al ser el sistema homogéneo, todos los coeficientes $c_{nrs}^m$ se obtendrán en la resolución en términos de uno de ellos, un parámetro arbitrario que se puede fijar mediante la correspondiente condición de normalización de la función $\chi_{nr}^{(0)_m}$ .
-En cualquier caso, si hay raíces $E_{nr}^{(1)_m}$ múltiples, el procedimiento no producirá un resultado único, ya que la degeneración $\alpha_n$ de $E_n^{(0)}$ no será en este caso completamente removida.
-A las funciones $\chi_{nr}^{(0)_m}$ se les suele denominar como «funciones de onda en primer orden de teoría de perturbaciones», ¡aunque en realidad son de orden cero!.
Observaciones:
1. Si todos los elemento no diagonales de la ecuación determinamental son nulos,
  $\left< \psi_{nu}^{(0)} | H'| \psi_{ns}^{(0)} \right> \propto \delta_{us} \, ; \, u,s=1,\ldots, \alpha_n$ ,
  es decir, los estados degenerados
  $\psi_{nr} \, , \, r=1,\ldots,\alpha_n$
  no están conectados en primer por la perturbación, entonces la ecuación determinamental general
  $det [ H'_{nu,ns} \ - \ E_{nr}^{(1)} \ \delta_{us} ] \, = \, 0$
  toma la forma
  $det ([ H'_{nu,ns} \ - \ E_{nr}^{(1)}] \ \delta_{us}) \, = \, 0$
  $\Rightarrow E_{nr}^{(1)} \, = \, H'_{nr,nr}\, = \,\left< \psi_{nr}^{(0)} | H'| \psi_{nr}^{(0)} \right>\, , \, r=1,\ldots,\alpha_n$ ,
  por lo que la degeneración no viene a desempeñar ninguna consecuencia en el análisis: las funciones $\psi_{nr} \, , \, r=1,\ldots,\alpha_n$ son directamente las funciones correctas en orden primero (orden cero en realidad) para la perturbación $H'$ :
  $\chi_{nr}^{(0)} \, = \,\psi_{nr} \, , \, r=1,\ldots,\alpha_n$ .
  -En consecuencia, en los problemas en que se quiera aplicar la teoría de perturbaciones a niveles de energía ligados con degeneración, es muy conveniente elegir una base en la que la perturbación sea diagonal, esto es, una base ortonormal asociada con un conjunto de operadores que conmuten entre sí (un C.C.O.C.) y que sean tales que todos conmuten con $H'$ , lo que garantizará que los estados no perturbados puedan especificarse unívocamente.
2. Si tras aplicar la teoría de perturbaciones para un estado degenerado se consigue remover la degeneración por completo, entonces se tienen determinadas las funciones de onda no perturbadas $\chi_{nr}^{(0)} \ , \ r=1,\ldots,\alpha_n$ , a través de los coeficientes $c_{nrs}$ , que represntan las combinaciones lineales adecuadas de las funciones originales en orden cero $\psi_{nr}^{(0)}$ para las que la matriz
  $H_{nr,ns}^{' \chi} \, = \, \left< \chi_{nr}^{(0)} | H'| \chi_{ns}^{(0)} \right> \, ; \, r,s=1,\ldots,\alpha_n$
  es diagonal:
  $H_{nr,ns}^{' \chi} \, = \,\left< \chi_{nr}^{(0)} | H'| \chi_{ns}^{(0)} \right> \, \propto \delta_{rs}$ ,
  teniéndose
  $E_{nr}^{(1)} \, = \, H_{nr,nr}^{' \chi} \, = \, \left< \chi_{nr}^{(0)} | H'| \chi_{nr}^{(0)} \right> \, , \, r=1,\ldots,\alpha_n$ .
  -En este caso, las correcciones a la energía en segundo orden, $E_{nr}^{(2)}$ , y a la función de onda en primero, la auténtica, $\psi_{nr}^{(1)}$ , pueden ya calcularse aplicando la teoría de perturbaciones para estados sin degeneración.

Ejemplo: nivel no perturbado con doble degeneración

Sea un sistema conservativo, con un Hamiltoniano $H$ independiente del tiempo que admite expresión de la forma
$H=H_0+\lambda H' \; , \; \lambda \in \mathbb{R}$ ,
donde el sumando $H_0$ representa el Hamiltoniano no perturbado y $\lambda H'$ el Hamiltoniano de perturbación, que es supuesto cumpliendo las condiciones de que la ecuación de Schrödinger correspondiente,
$H_0 \ \psi_n^{(0)} \, = \,E_n^{(0)} \ \psi_n^{(0)}$
admite resolución sencilla, analítica o numérica, y de que la perturbación es «pequeña».
Sea $E^{(0)}$ un autovalor de $H_0$ con degeneración $\alpha=2$ y sean $\psi_i^{(0)} \, , \, i=1,2$ dos autofunciones linealmente independientes y ortonormales correspondientes a dicho autovalor; se efectúan los desarrollos en en serie de potencias del parámetro perturbativo $\lambda$ de las autofunciones y autovalores del Hamiltoniano $H$ :
$E_r \, = \, E^{(0)} \, + \, \sum_{i=0}^{\infty} \lambda^i \ E_r^{(i)} \, \ \, i=1,2$
$\psi_n \, = \, \chi_r^{(0)} \, + \, \sum_{i=1}^{\infty} \lambda^i \ \psi_r^{(i)} \, \ \, i=1,2$ ,
donde
$\chi_r^{(0)} \, = \, \sum_{s=1}^{2} c_{rs} \ \psi_s^{(0)} \quad ; \; \lim_{\lambda \rightarrow 0} \psi_r \, = \, \chi_r^{(0)}$
y cada valor del índice $i$ establece el orden perturbativo en que se van a proporcionar las correcciones.
Resolución del problema de valores propios:
Schrödinger:
$H \ \psi_{r} \, = \,E_{r} \ \psi_{r}$
$(H_0 \ + \ \lambda H') \ (\chi_{r}^{(0)} + \sum_{i=1}^{\infty} \lambda^i \ \psi_{r}^{(i)}) \, = \,( E^{(0)} + \sum_{i=1}^{\infty} \lambda^i \ E_{r}^{(i)} ) \ (\chi_{r}^{(0)} + \sum_{i=1}^{\infty} \lambda^i \ \psi_{r}^{(i)})$ ;
igualando coeficientes de igual potencia de $\lambda$ en ambos lados de la igualdad:
$\left. \begin{array}{l} i=0 \, , \, \lambda^0 \Rightarrow H_0 \ \chi_{r}^{(0)} \, = \, E^{(0)} \ \chi_{r}^{(0)} \\ i=1 \, , \, \lambda^1 \Rightarrow H_0 \ \psi_{r}^{(1)} \,+ \, H' \ \chi_{r}^{(0)} = \, E^{(0)} \ \psi_{r}^{(1)} \, + \, E_{r}^{(1)} \ \chi_{r}^{(0)} \\ \ldots \end{array} \right\}$
Corrección en orden cero:
$H_0 \ \chi_{r}^{(0)} \, = \, E^{(0)} \ \chi_{r}^{(0)}$
Corrección a la energía en primer orden:
$H_0 \ \psi_{r}^{(1)} \,+ \, H' \ \chi_{r}^{(0)} = \, E^{(0)} \ \psi_{r}^{(1)} \, + \, E_{r}^{(1)} \ \chi_{r}^{(0)}$
$(H' \ - \ E_{r}^{(1)}) \ \psi_{r}^{(1)} \ \chi_{r}^{(0)} \, + \, (H_0 \ - \ E^{(0)}) \ \psi_{r}^{(1)} \, = \, 0$ ,
insertando los desarrollos
$\chi_{r}^{(0)} \, = \, \sum_{s=1}^{2} c_{rs} \ \psi_{s}^{(0)}$
$\psi_{r}^{(1)} \, = \,\sum_{k} \sum_{s=1}^{\alpha_k} a_{rks}^{(1)} \psi_{ks}^{(0)}$ :
$(H' \ - \ E_{r}^{(1)}) \ \sum_{s=1}^{2} c_{rs} \ \psi_{s}^{(0)} \, + \, (H_0 \ - \ E^{(0)}) \ \sum_{k} \sum_{s=1}^{\alpha_k} a_{rks}^{(1)} \psi_{ks^{(0)}}\, = \, 0$
Multiplicando a la izquierda sobre el estado $\psi_{u}^{(0)*}$ , con $u=1,2$ fijo, e integrando:
$\sum_{s=1}^{2} c_{rs} \ \left< \psi_{u}^{(0)} | H' - E_{r}^{(1)} | \psi_{s}^{(0)} \right>$
$+ \, \sum_{k} \sum_{s=1}^{\alpha_k} a_{rks}^{(1)} \ \left< \psi_{u}^{(0)} | H_0 - E^{(0)} | \psi_{ks}^{(0)} \right> \, = \, 0$ ,
$\sum_{s=1}^{2} c_{rs} \ [ H'_{u,s} \ - \ E_{r}^{(1)} \ \delta_{us} ] \, + \, \sum_{k} \sum_{s=1}^{\alpha_k} a_{rks}^{(1)} \ [ E^{(0)} \ \delta_{us} \, - \, E^{(0)} \ \delta_{us} ] \, = \, 0$
$\Rightarrow \sum_{s=1}^{2} c_{rs} \ [ H'_{u,s} \ - \ E_{r}^{(1)} \ \delta_{us} ] \, = \, 0 \quad ; \; u=1, 2$ ,
se obtiene un sistema lineal y homogéneo de dos ecuaciones, en las incógnitas $c_{rs} \, , \ s=1, 2$ :
$\begin{pmatrix} \left< \psi_{1}^{(0)} | H'| \psi_{1}^{(0)} \right> - E_{r}^{(1)} & \left< \psi_{1}^{(0)} | H'| \psi_{2}^{(0)} \right> & \\ \left< \psi_{2}^{(0)} | H'| \psi_{1}^{(0)} \right> & \left< \psi_{2}^{(0)} | H'| \psi_{2}^{(0)} \right> - E_{r}^{(1)} & \end{pmatrix} \ \begin{pmatrix} c_{r1} \\ c_{r2} \end{pmatrix} \, = \, 0$
que tendrá solución no trivial si y sólo si el determinante de los coeficientes es nulo:
$det [ H'_{u,s} \ - \ E_{r}^{(1)} \ \delta_{us} ] \, = \, 0$
En definitiva, se ha obtenido la siguiente ecuación secular, de grado 2 en la incógnita $E_{r}^{(1)}$ , cuya resolución proporcionará las correcciones a la energía en primer orden de perturbaciones para el nivel degenerado $E^{(0)}$ , correcciones que romperán o no su degeneración:
$\begin{vmatrix} \left< \psi_{1}^{(0)} | H'| \psi_{1}^{(0)} \right> - E_{r}^{(1)} & \left< \psi_{1}^{(0)} | H'| \psi_{2}^{(0)} \right> & \\ \left< \psi_{2}^{(0)} | H'| \psi_{1}^{(0)} \right> & \left< \psi_{2}^{(0)} | H'| \psi_{2}^{(0)} \right> - E_{r}^{(1)} & \end{vmatrix} \, = \, 0$ .
En resumen: la diagonalización del Hamiltoniano perturbativo $H'$ en el subespacio del Hilbert $M_{E^{(0)}}$ , de dimensión 2 , generado por el conjunto de autofunciones $\{ \psi_{s}^{(0)} \, , \ s=1,2 \}$ , linealmente independientes, ortonormales y degeneradas en energía, proporciona la ecuación cuyas raíces constituyen las correcciones a la energía en primer orden $(O(\lambda^1), \lambda=1)$ de teoría de perturbaciones:
$(E_{r}^{(1)})^2 - E_{r}^{(1)} \ (H'_{11} + H'_{22} ) \ + \ ( H'_{11} H'_{22} - H'_{12} H'_{21} ) \ = \ 0$ ,
$H'_{21} = (H'_{12})^*$
$\Rightarrow (E_{r}^{(1)})^2 - E_{r}^{(1)} \ (H'_{11} + H'_{22} ) \ + \ ( H'_{11} H'_{22} - |H'_{12}|^2 ) \ = \ 0$ ,
$\Rightarrow (E_{r}^{(1)})_{\pm} \ = \ \frac{1}{2} [(H'_{11} + H'_{22} ) \ \pm \ \sqrt{(H'_{11} + H'_{22} )^2 \ - \ 4 ( H'_{11} H'_{22} - |H'_{12}|^2 )}]$
$= \ \ \frac{1}{2} (H'_{11} + H'_{22} ) \ \pm \ \frac{1}{2} \sqrt{(H'_{11} - H'_{22} )^2 \ + \ 4 |H'_{12}|^2}]$ ,
ecuación cuadrática cuyas dos soluciones $E_{r}^{(1)}$ (que pueden ser iguales) proporcionan la aproximación buscada:
$E_{r} \approx E^{(0)} + E_{r}^{(1)} \, , \, r=1,2$ .
-Estas soluciones también permiten obtener las correspondiente funciones de onda $\chi$ , resolviendo para cada raíz el sistema de ecuaciones para los coeficientes:
$\left. \begin{array}{l} r=1 \rightarrow E_{1}^{(1)} = (E_{r}^{(1)})_{+} \Rightarrow \\ ( \ H'_{11} - \frac{1}{2} ( H'_{11} + H'_{22} ) \ - \frac{1}{2} \ \sqrt{(H'_{11} - H'_{22} )^2 \ + \ 4 |H'_{12}|^2 } \ ) \ \ c_{11} \, + \, H'_{12} \ c_{12} \, = \, 0 \\ \left< \chi_{1}^{(0)} | \chi_{1}^{(0)} \right> \, = \, |c_{11}|^2 \, + \, |c_{12}|^2 \, = \, 1 \end{array} \right\}$
$\left. \begin{array}{l} r=2 \rightarrow E_{2}^{(1)} = (E_{r}^{(1)})_{-} \Rightarrow \\ ( H'_{11} - \frac{1}{2} ( H'_{11} + H'_{22} ) \ + \frac{1}{2} \ \sqrt{(H'_{11} - H'_{22} )^2 \ + \ 4 |H'_{12}|^2 } ) \ \ c_{21} \, + \, H'_{12} \ c_{22} \, = \, 0 \\ \left< \chi_{2}^{(0)} | \chi_{2}^{(0)} \right> \, = \, |c_{21}|^2 \, + \, |c_{22}|^2 \, = \, 1 \end{array} \right\}$
El correspondiente esquema de niveles de energía queda pues:
,
teniéndose que si no se habrá roto la degeneración.
-Algunos casos que se pueden presentar:
1. Valores de los elementos de la matriz perturbativa satisfaciendo:
  $\left. \begin{array}{l} H'_{11} = H'_{22}=0 \\ H'_{12} = (H'_{21})* \ne 0 \end{array} \right\} \Rightarrow \left. \begin{array}{l} E_{1}^{(1)} = | H'_{12}| \\ E_{2}^{(1)} = -| H'_{12}| \end{array} \right\} \Rightarrow \frac{c_{11}}{c_{12}} = - \frac{c_{21}}{c_{22}} = \frac{H'_{12} }{ | H'_{12}| }$
  -En este caso, los dos estados originales inicialmente degenerados, $\psi_1^{(0)}$ y $\psi_2^{(0)}$ se mezclan al 50%, ya que $|c_{r1}| = |c_{r2}|$ .
2. Valores de los elementos de la matriz perturbativa satisfaciendo:
  $H'_{12} = (H'_{21})* = 0 \Rightarrow \left. \begin{array}{l} E_{1}^{(1)} = | H'_{11}| \\ E_{2}^{(1)} = -| H'_{22}| \end{array} \right\}$
  -En este caso, los dos estados originales inicialmente degenerados, $\psi_1^{(0)}$ y $\psi_2^{(0)}$ , no están conectados por la perturbación en primer orden.
3. Valores de los elementos de la matriz perturbativa satisfaciendo:
  $( H'_{11} + H'_{22} )^2 \ = \ 4 ( H'_{11} H'_{22} - |H'_{12}|^2 ) \Rightarrow E_{r}^{(1)} = \frac{1}{2}( H'_{11}| + H'_{22})$ , raíz doble.
  -En este caso, la degeneración original de los dos estados $\psi_1^{(0)}$ y $\psi_2^{(0)}$ no se rompe por la perturbación en primer orden.

Referencias

[BAL-98] Ballentine, L.E.; “Quantum Mechanics: A Modern Development”; World Scientific; Singapore, 1998.

[BOH-79] Bohm, D.; “Quantum Theory”; Dover; New York, 1979.

[BRA-00] Bransden, B.H. and Joachain, C.J.; Quantum Mechanics, 2nd ed.; Pearson, Dorchester, 2000.

[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.

[NEU-91] Neumann, J. von; «Fundamentos matemáticos de la Mecánica Cuántica», CSIC, Raycar, Madrid, 1991.

[SCH-68] Shiff, L.I. ; Quantum Mechanics, 3º ed; McGraw-Hill, 1968.

Páginas complementarias

-Métodos aproximados en el blog la-mecanica-cuantica.blogspot.com:
67. Técnicas de aproximación I
68. Técnicas de aproximación II
69. Técnicas de aproximación III
70. Técnicas de aproximación IV
71. Perturbación y estados degenerados I
72. Perturbación y estados degenerados II
73. Modelos perturbativos para átomos hidrogenoides
74. El efecto Stark I
75. El efecto Stark II
76. Corrección perturbativa relativista
77. La estructura fina del hidrógeno
78. Perturbaciones dependientes del tiempo I
79. Perturbaciones dependientes del tiempo II
80. Perturbaciones dependientes del tiempo III

–Teoría de perturbaciones estacionarias, archivo UNED.

-Apuntes de J.P. Paz (teoría de perturbacioners independiente del tiempo): http://materias.df.uba.ar/ft2a2020c1/files/2020/06/cuantica_paz_c17_2020.pdf

-Seminario sobre Teoría de perturbaciones por R. Fernández Ruiz.

–Teoría de perturbaciones dependiente del tiempo, archivo de N. Fernández. Univ. Autónoma de Madrid.

-archivo pdf en libretexts.org:
https://espanol.libretexts.org/Fisica/Mec%C3%A1nica_Cu%C3%A1ntica/Mec%C3%A1nica_Cu%C3%A1ntica_(Fowler)/09%3A_Teor%C3%ADa_de_la_perturbaci%C3%B3n/9.01%3A_Teor%C3%ADa_de_la_perturbaci%C3%B3n_independiente_del_tiempo

APPS
Wolfram demostrations project:
Perturbation Theory Applied to the Quantum Harmonic Oscillator

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

Teoría de perturbaciones (estados ligados estacionarios)

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta