Momento angular orbital

Operadores de momento angular orbital: definición y propiedades

Sea una partícula de masa $m$ , sin espín; sean $\vec{p}$ y $\vec{r}$ , respectivamente, los operadores autoadjuntos que representan su momento lineal y posición respecto a un sistema de coordenadas cartesiano $OXYZ$ , actuando en el espacio de Hilbert asociado a la descripción mecano-cuántica del sistema. El momento angular orbital de la partícula, con respecto al origen $O$ , se representa en el formalismo cuántico por el siguiente operador autoadjunto $\vec{L}$ , de acuerdo con la cuantización postulada en representación de posiciones:
$\vec{L}=(L_x,L_y,L_z)\,=\,\vec{r} \times \vec{p} \,=\, -i\hbar \, \vec{r} \times \nabla_r$ ,
de componentes cartesianas en representación de coordenadas:
$L_i=\sum_{jk} \epsilon_{ijk}r_jp_k$ , $i=x,y,z$ ,
esto es:
$L_x\,=\, yp_z-zp_y\,=\,-i\hbar \,(y\frac{\partial}{\partial z} - z \frac{\partial}{\partial y})$
$L_y\,=\, zp_x-xp_z\,=\,-i\hbar \,(z\frac{\partial}{\partial x} - x \frac{\partial}{\partial z})$
$L_z\,=\, xp_y-yp_x\,=\,-i\hbar \,(x\frac{\partial}{\partial y} - y \frac{\partial}{\partial x})$
Las componentes de $\vec{L}$ satisfacen las reglas de conmutación definitorias de un momento angular:
$[L_i\,,\,L_j]=i\hbar \, \epsilon_{ijk}\,L_k\,;\, i,j,k=1,2,3$ ,
o, en notación compacta equivalente:
$\vec{L} \times \vec{L}\,=\,i\hbar \,\vec{L}$ :
$\vec{L} \times \vec{L}\,=\, \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\L_x & L_y & L_z \\ L_x & L_y & L_z \end{vmatrix}$
$=\,\hat{i}\,(L_yL_z-L_zL_y) \,+\, \hat{j}\,(L_zL_x-L_xL_z) \,+\, \hat{k}\,(L_xL_y-L_yL_x)$
$=\, i\hbar \, (\hat{i}L_x+\hat{j}L_y+\hat{k}L_z) \,=\, i\hbar \,\vec{L}$
(se trata de un operador vectorial en $\mathcal{H}$ , no de un vector en $\mathbb{R}^3$ como lo es el análogo clásico).
-Por su no conmutación, dos componentes de $\vec{L}$ no pueden diagonalizarse simultáneamente, esto es, no existe en el Hilbert un conjunto completo de autofunciones comunes o base común libre de dispersión a la vez para dos componentes distintas (¡lo que no excluye que sí puedan existir autofunciones comunes, sin formar base en el espacio!). Estos dos operadores no pueden, por tanto, formar parte a la vez de un C.C.O.C.
El operador momento angular orbital al cuadrado, $\vec{L}^2$ ,
$\vec{L}^2 \,=\, \vec{L} \cdot \vec{L}\, = \,L_x^2 \,+\, L_y^2 \, +\, L_z^2$ ,
posee las siguientes propiedades:
$[\vec{L}^2,L_i]=0\,, \, i=x,y,z$ .
-Ejercicio:
$[\vec{L}^2,L_z]=[L_x^2 \,+\, L_y^2 \, +\, L_z^2,L_z]=[L_x^2 \,+\, L_y^2 \,,L_z]$
$= L_x[L_x,L_z]+[L_x,L_z]L_x+L_y[L_y,L_z]+[L_y,L_z]L_y$
$= L_x(-i\hbar L_y)+(-i\hbar)L_yL_x+L_y(i\hbar L_x)+(i\hbar)L_xL_y=0$
donde se ha hecho uso de la propiedad
$[AB,C]=A[B,C]+[A,C]B$
-Por su conmutación, $\vec{L}^2$ y cualquier componente de $\vec{L}$ pueden diagonalizarse simultáneamente, esto es, existe en el correspondiente Hilbert un conjunto completo de autofunciones comunes o base común libre de dispersión a la vez para los dos operadores. Ambos operadores pueden, por tanto, formar parte a la vez de un C.C.O.C.

Expresión de $\vec{L}$ en coordenadas esféricas

Introduzcamos las coordenadas esféricas, $\vec{r},\theta,\varphi$ :
$\left. \begin{array}{l} x=r \sin \theta \cos \varphi \,,\; 0 \leq r=|\vec{r}| < \infty \\ y=r \sin \theta \sin \varphi \,,\; 0 \leq \theta \le \pi \\ z=r \cos \theta \,,\; 0 \le \varphi \leq 2\pi \end{array} \right\}$ $\left. \begin{array}{l} r=+\sqrt{x^2+y^2+z^2} \,,\; 0 \leq x < \infty \\ \theta = \arccos \frac{z}{r} \,,\; 0 \leq y < \infty \\ \varphi = \arctan \frac{y}{x} \,,\; 0 \leq z < \infty \end{array} \right\}$

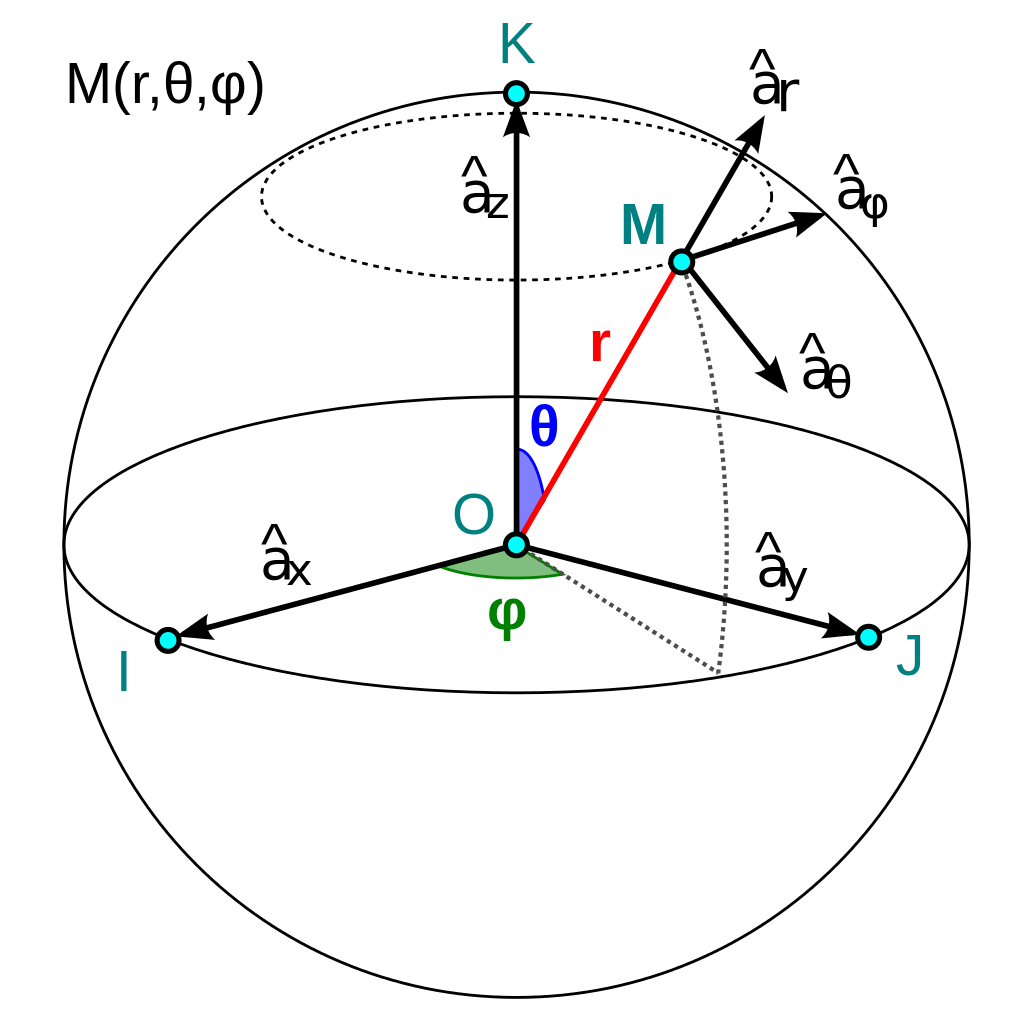
Coordenadas esféricas de un punto M, imagen de la Wikipedia (derivative work by Josemontero9, from the original
Coordenadas_eséricas_figura , by Romero Schmidtke).

-En estas coordenadas, un elemento de volumen $dV$ y el operador $\nabla^2$ se expresan, respectivamente:
$dV \, = \, d^3r \equiv d \vec{r} \, = \, dx \, dy \, dz=r^2 \sin \theta \, dr \, d \theta \, d \varphi$
$\nabla^2 \, = \, \frac{1}{r^2 \sin \theta} \{ \sin \theta \, \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, + \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin \theta}(\frac{\partial^2}{\partial \varphi^2}) \}$
El momento angular orbital de la partícula, en representación de coordenadas, respecto al origen $O$ de un sistema cartesiano $OXYZ$ , esto es, el operador autoadjunto
$\vec{L}=(L_x,L_y,L_z) = -i\hbar \, \vec{r} \times \nabla$ ,
$L_i=\sum_{jk} \epsilon_{ijk}r_jp_k$ , $i=x,y,z$ ,
posee las siguientes componentes en coordenadas esféricas:
$L_x\,=\, yp_z-zp_y\,=\,-i\hbar \,(y\frac{\partial}{\partial z} - \,z \frac{\partial}{\partial y})$
$= \, -i\hbar \, (-\sin \varphi \, \frac{\partial}{\partial \theta} \, - \, \cot \theta \, \cos \varphi \, \frac{\partial}{\partial \varphi})$
$L_y\,=\, zp_x-xp_z\,=\,-i\hbar \,(z\frac{\partial}{\partial x} - x \frac{\partial}{\partial z})$
$= \, -i\hbar \, (\cos \varphi \, \frac{\partial}{\partial \theta} \, - \, \cot \theta \, \sin \varphi \, \frac{\partial}{\partial \varphi})$
$L_z\,=\, xp_y-yp_x\,=\,-i\hbar \,(x\frac{\partial}{\partial y} - y \frac{\partial}{\partial x}) \, = \, -i\hbar \, \frac{\partial}{\partial \varphi}$
-Para la deducción de estas expresiones, puede consultarse, por ejemplo: https://www.uco.es/hbarra/; también en: https://www.quimicafisica.com
–Nota: recuérdese que el postulado de cuantización se aplica sólo para coordenadas generalizadas cartesianas. Por lo tanto, se cuantiza en cartesianas, componentes $\vec{L}=(L_x,L_y,L_z) = -i\hbar \, \vec{r} \times \nabla$ , y después se cambia a coordenadas esféricas, pero no al revés.
El momento angular orbital al cuadrado en esféricas es:
$\vec{L}^2 \,=\, \vec{L} \cdot \vec{L}\, = \,L_x^2 \,+\, L_y^2 \, +\, L_z^2$ $= \,-\hbar^2 \, [ \,\frac{1}{\sin \theta} \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2} \, ]$
$= \,-\hbar^2 \, [ \,\frac{\partial^2}{\partial \theta^2} \,+ \, \cot \theta \, \frac{\partial}{\partial \theta} \, + \, \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2} \, ]$
–Nota: utilizando la anterior ecuación, obsérvese que el operador $\nabla^2$ puede expresarse como:
$\nabla^2 \, = \, \frac{1}{r^2} \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2}$
Los operadores $\vec{L}$ y $\vec{L}^2$ son puramente angulares: no contienen dependencia explícita de la coordenada radial $r=|\vec{r}|$ . En consecuencia, conmutarán con cualquier función con exclusiva dependencial radial, $f(r)$ , y cualquier función de esta clase será autofunción simultánea de los cuatro operadores $\vec{L}^2 \;,\; L_i\,,\,i=1,2,3$ :
$[\vec{L}^2,f(r)]=[L_i \ ,f(r)] =0$
$\Rightarrow \vec{L}^2\,f(r)=L_i\,f(r) =0\;,\; i=1,2,3$ .
Dado un operador vectorial momento angular orbital, su componente $L_n$ a lo largo de una dirección arbitraria en el espacio, determinada por el vector unitario $\hat{n}=\frac{\vec{r}}{|r|}$ en la dirección especificada por los ángulos polares $(\theta,\varphi)$ ,
$\hat{n}=(\sin \theta\cos \varphi, \sin \theta \sin \varphi, \cos \theta)$ ,
se expresa:
$L_n \,=\, \hat{n} \cdot \vec{L} \,=\,\sum_{i=x,y,z} \,n_i \,L_i$
$\Rightarrow L_n \, = \, L_x \, \sin \theta\cos \varphi \,+\, L_y \, \sin \theta \sin \varphi \,+\, L_z \, \cos \theta$
Los operadores escalón se definen:
$\left. \begin{array}{l} L_+=L_x + iL_y \\ L_-=L_x - iL_y \end{array} \right\}$ $\left. \begin{array}{l} L_x=\frac{1}{2}(L_+ + L_-) \\ L_y=\frac{1}{2i}(L_+ - L_-) \end{array} \right\}$ ,
siendo sus expresiones en coordenadas esféricas:
$L_{\pm}\,=\,\hbar \, exp^{\pm i \varphi}\,[\pm \, \frac{\partial}{\partial \theta } \, + \, i \, \cot \theta \, \frac{\partial}{\partial \varphi}]$
Propiedades:
1. Los operadores $L_+$ y $L_-$ no son autoadjuntos:
  $(L_+)^+=L_- \;,\; (L_-)^+=L_+$
2. $\vec{L}^2\,=\, \frac{1}{2}\, (L_+L_- \,+\, L_-L_+)\,+\,L_z^2$
3. $L_-L_+\,=\,\vec{L}^2\,-\,L_z\,(L_z\,+\,\hbar)$
4. $L_+L_-\,=\,\vec{L}^2\,-\,L_z\,(L_z\,-\,\hbar)$
5. $L_{\pm} \ L_{\mp} \,=\,\vec{L}^2 - L_z^2 \pm \hbar \, L_{z} \,=\,\vec{L}^2 - L_z\,( L_z \mp \hbar)$
6. $[L_+ \,,\, L_{-} ]\,=\, 2 \hbar \, L_{z}$
7. $[\vec{L}^2 \,,\, L_{\pm} ]=0$
8. $[L_z \,,\, L_{\pm} ]\,=\, \pm \, \hbar \, L_{\pm}$

Momento angular orbital $\vec{L}$ para sistemas de varias partículas

Para un sistema físico compuesto de $N$ partículas de masa $m_i$ , con respectivos coordenadas de posición $\vec{r_i}$ y momentos lineales $\vec{p_i}$ , $i=1,2,\ldots , N$ , la variable dinámica momento angular orbital total $\vec{L}$ del sistema se define como:
$\vec{L}\,=\, \sum_{j=1}^{N} \, \vec{L}^{\,(j)}\,=\, \sum_{j=1}^{N} \,\vec{r}^{\,(j)} \times \vec{p}^{\,(j)}$ , cuantizado en representación de posiciones según el postulado correspondiente como
$\vec{L}\, = \, -i\hbar \,\sum_{j=1}^{N} \,\vec{r}^{\,(j)} \times \nabla_r^{\,(j)}$ ,
cumpliéndose las reglas de conmutación $\vec{L} \times \vec{L}=i\hbar \, \vec{L}$ :
$[L_i^{\,(n)}\, ,\, L_j^{\,(m)} ]\,=\,\delta_{n,m} \, i\hbar \, \epsilon_{ijk}\, L_k \, ; \, i,j=1,2,3 \,;\, n,m=1,2,\ldots , N$

Autofunciones y valores propios de momento angular orbital: los armónicos esféricos

Por su conmutación, $\vec{L}^2$ y la componente $L_z$ pueden diagonalizarse simultáneamente, esto es, existe en el Hilbert $\mathcal{H}^{(l)}$ un conjunto completo de autofunciones comunes $\{ |lm> \} \subset \mathcal{H}^{(l)}$ , esto es, una base común libre de dispersión a la vez para los dos operadores ${\vec{L}^2\ , \, L_z}$ y cuyos vectores satisfacen:
$\vec{L}^2\, |lm >\, =\, \hbar^2 \, l(l+1)\, |lm>$
$L_z\, |lm >\, =\, \hbar \, m\, |lm>$
Para establecer la forma matemática de estos autovectores $|lm>$ en representación de posiciones, y coordenadas esféricas, notaremos estas funciones de onda como $Y_{lm}(\theta, \varphi)$ , las funciones incógnitas con dependencia angular exclusiva a determinar resolviendo las dos ecuaciones de autovalores:
$\vec{L}^2 \,Y_{lm}(\theta, \varphi) \, =\, \hbar^2 \, l(l+1)\, Y_{lm}(\theta, \varphi)$
$L_z \,Y_{lm}(\theta, \varphi) \, =\, \hbar \, m\, Y_{lm}(\theta, \varphi)$ ,
donde
$Y_{lm}(\theta, \varphi) \, =\, < \vec{r} (r,\theta , \varphi) \, | \, lm>$
$=\, \int Y_{lm}(\theta ', \varphi ') \,\delta(\vec{r}-\vec{r}' )\, d \vec{r}' \,= \, \int Y_{lm}(\theta', \varphi ') \,\delta(\Omega-\Omega ' )\, d \Omega'$
( $\delta$ representa la distribución «delta de Dirac»).
-Anticipando el resultado final de la resolución, indicamos ya que vamos a establecer, tras resolver el sistema de las dos ecuaciones de autovalores anteriores, que las funciones incógnitas $Y_{lm}(\theta, \varphi)$ van a coincidir con unas determinadas funciones especiales de la Física Matemática, los denominados «armónicos esféricos«, por lo que así las llamaremos en lo que sigue.
Resolución por separación de variables:
$L_z \, Y_{lm}(\theta, \varphi) \, =\, -i\hbar \, \frac{\partial}{\partial \varphi} \,Y_{lm}(\theta, \varphi)\, =\, \hbar \, m\, Y_{lm}(\theta, \varphi)$
$\Rightarrow \, \frac{\partial}{\partial \varphi} \,Y_{lm} \, - \, im \,Y_{lm} \,=0 \Rightarrow \, Y_{lm}(\theta, \varphi) \, = \, C(\theta)\, e^{im\varphi}$ ;
es decir, cada armónico esférico se factoriza según la siguiente separación de variables:
$Y_{lm}(\theta, \varphi) \, =\, \Theta (\theta) \, \Phi(\varphi)$ ,
Propiedades de la función :
1. Univocidad:
  $\Phi_m(\varphi)\, = \, \Phi_m(\varphi + 2\pi)\, \Rightarrow e^{im\varphi} \, = \, e^{im (\varphi + 2\pi)}$
  $\Rightarrow \, e^{im \, 2\pi} \, = \,+1 \, \Rightarrow \, m=0,\pm 1,\pm 2\ldots$
  -Consecuentemente, puesto que los valores del número cuántico de tercera componente de momento angular orbital (o número cuántico magnético orbital) $m$ deben abarcar, para cada valor determinado $l$ del número cuántico de momento angular orbital, desde el valor $-l$ hasta el valor $+l$ , variando de uno en uno, se implica que $l$ está restringido a valores enteros:
  $l=0, 1, 2,3\ldots$
2. Se elige la normalización convencional:
  $\Phi(\varphi)\, = \, \frac{1}{\sqrt{2 \pi}}\, e^{im\varphi} \equiv \Phi_m(\varphi)$
  -Con esta elección de constante:
  $\int_0^{2\pi}\, \Phi_{m'}^*(\varphi) \, \Phi_m(\varphi) \, d\varphi \, =\, \frac{1}{2\pi}\, \int_0^{2\pi}\,e^{i(m-m')\varphi }d\varphi$
  $=\, \left\{ \begin{array}{l} 1 \; si \; m=m' \\ \frac{e^{i(m-m')\varphi }}{2\pi i(m-m')} \lvert_o^{2\pi} \,=\, 0 \; si \; m \, \ne \, m' \end{array} \right\} \, = \, \delta_{m,m'}$
3. Sistema completo: el conjunto de autofunciones
  $\left\{ \Phi_m(\varphi)\,=\, \frac{1}{\sqrt{2 \pi}}\, e^{im\varphi} \right\}_{m=-\infty}^{\infty}$
  constituye una base ortonormal en el espacio $L^2(0,2\pi)$ .
4. Toda función $f(\varphi)\, \in L^2(0,2\pi)$ admite desarrollo en serie:
  $\forall f\,:\,[0,2\pi]\, \rightarrow \, \mathbb{C}\,,\, f \, \in \, L^2(0,2\pi)$
  se tiene que
  $f(\varphi) \,=\, \sum_{m=-\infty}^{+\infty}\, a_m \, \Phi_m(\varphi)$
  $\quad \leftrightarrow \, a_m= \int_0^{2\pi} \,\Phi_{m}^*(\varphi) \,f(\varphi)\, d\varphi \; , \; a_m \, \in \,\mathbb{C}$
5. Relación de clausura:
  $f(\varphi) \,=\, \sum_{m=-\infty}^{+\infty}\, a_m \, \Phi_m(\varphi)$
  $= \, \sum_{m=-\infty}^{+\infty}\, [ \int_0^{2\pi} \,\Phi_{m}^*(\varphi') \,f(\varphi')\, d\varphi'] \,\Phi_m(\varphi)$
  $= \,\int_0^{2\pi} \,f(\varphi') \,[ \sum_{m=-\infty}^{+\infty} \,\Phi_{m}^*(\varphi') \,\Phi_m(\varphi) \,] d\varphi'$
  $\Rightarrow \, \sum_{m=-\infty}^{+\infty}\,\Phi_{m}^*(\varphi') \,\Phi_m(\varphi) \,=\, \delta(\varphi' - \varphi)$
Resolución de la ecuación para la función $\Theta (\theta)$ :
$\vec{L}^2 \,Y_{lm}(\theta, \varphi) \, =\, \hbar^2 \, l(l+1)\, Y_{lm}(\theta, \varphi)$
$\Rightarrow \vec{L}^2 \Theta (\theta) \, \Phi(\varphi) \, =\, \hbar^2 \, l(l+1)\, \Theta (\theta) \, \Phi(\varphi)$
$\Rightarrow -\hbar^2 \, [ \,\frac{1}{\sin \theta} \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2}] \, \Theta (\theta) \, \Phi(\varphi)$
$=\, \hbar^2 \, l(l+1)\, \Theta (\theta) \, \Phi(\varphi)$
$\Rightarrow - \, [ \,\frac{1}{\sin \theta} \, \frac{\partial }{\partial \theta}(\sin \theta \, \frac{\partial (\Theta (\theta) \, \Phi(\varphi) ) }{\partial \theta}) \, + \, \frac{1}{\sin^2 \theta}\frac{\partial^2 (\Theta (\theta) \, \Phi(\varphi) ) }{\partial \varphi^2}]$
$= \, l(l+1)\, \Theta (\theta) \, \Phi(\varphi)$
$=- \, [ \,\frac{1}{\sin \theta} \, \frac{\partial }{\partial \theta}(\sin \theta \, \frac{\partial \Theta (\theta) }{\partial \theta}) \,\Phi (\varphi) \, + \, \frac{1}{\sin^2 \theta}\frac{\partial^2 (\Phi(\varphi) ) }{\partial \varphi^2} \, \Theta (\theta) ]$ ;
dividiendo por $\Theta \Phi$ y multiplicando por $\sin^2\theta$ : $\frac{\sin \theta}{\Theta( \theta)} \, \frac{\partial }{\partial \theta}(\sin \theta \, \frac{\partial \Theta (\theta) }{\partial \theta}) \, + \, \frac{1}{\Phi(\varphi)}\frac{\partial^2 (\Phi(\varphi) ) }{\partial \varphi^2} \, + \, l(l+1)\, \sin^2 \theta\,=\,0$ ,
ecuación que permite separar a los dos lados de la igualdad la dependencia en cada variable:
$\frac{\sin \theta}{\Theta( \theta)} \, \frac{\partial }{\partial \theta}(\sin \theta \, \frac{\partial \Theta (\theta) }{\partial \theta}) \, + \, l(l+1)\, \sin^2 \theta\,=\,K\,=\, -\frac{1}{\Phi(\varphi)}\frac{\partial^2 (\Phi(\varphi) ) }{\partial \varphi^2}$ ,
donde la constante $k$ tiene el valor:
$K\,=\, -\frac{1}{\Phi(\varphi)}\frac{\partial^2 (\Phi(\varphi) ) }{\partial \varphi^2}\,=\, -\sqrt{2\pi}\,e^{-im\varphi} \,\frac{(im)^2}{\sqrt{2\pi}} e^{im\varphi} \,=\, m^2$ ,
lo que conduce a la ecuación diferencial ordinaria para la función $\Theta$ :
$\frac{1}{\sin \theta} \, \frac{d }{d \theta}(\sin \theta \, \frac{d \Theta (\theta) }{d \theta}) \, + \, [ l(l+1)\, -\frac{m^2}{ \sin^2 \theta}] \, \Theta(\theta)=\,0$
-A continuación, se realiza el cambio de variable
$\xi = \cos \theta \quad (0 \le \theta \le \pi \, \Rightarrow \, 1 \le \xi \le -1 )$ ,
que transfoma hacia la nueva ecuación
$\frac{d}{d \xi}\, [(1\, - \, \xi^2)\, \frac{d \Theta(\xi)}{d \xi}] \, + \, [l(l+1) \, - \,\frac{m^2}{1-\xi^2} ]\, \Theta (\xi)\, = \, 0$ ,
esto es, una ecuación asociada de Legendre, una fuchsiana con tres singularidades, las tres regulares, en los puntos $\xi=-1, +1, \infty$ .
La solución general de la ecuación asociada de Legendre anterior es:
$\Theta(\theta)\, =\, K_1 \, P_l^m(\xi)\,+\,K_2\, Q_l^m(\xi)$ ,
donde $K_1$ y $K_2$ son constantes arbitrarias y $P$ y $Q$ representan, respectivamente, las funciones asociadas de Legendre de primera y de segunda especie, siendo las funciones $P$ las únicas soluciones regulares de la ecuación para $\xi \in [-1,+1]$ .
Puesto que se tiene establecido, en la teoría general de momento angular, tanto que los valores del número cuántico de momento angular orbital $l$ han de ser enteros, $l=0,1,2\ldots$ , como la relación $l \ge |m|$ ( $m=l,l-1 \cdots , -l$ ) las únicas soluciones particulares aceptables para la ecuación, las funciones asociadas de Legendre de primera especie $P_l^m(\xi)$ , se expresan en este caso, $l$ y $m$ cero o enteros, en términos de los polinomios de Legendre, funciones $P_l(\xi)$ :
$\left. \begin{array}{l} P_l^m(\xi)\,=\, (-1)^m\, (1-\xi^2)^{m/2}\,\frac{d^{m}}{d\xi^{m}}P_l(\xi) \; ,\; m \ge 0 \\ P_l^{-m}(\xi)\,=\,(-1)^m\, \frac{(l\,-\,m)!}{(l\,+\,m)!} \,P_l^{m}(\xi) \; , \; m \ge 0 \end{array} \right\}$ .
Nota: aunque es frecuente leer la denominación de «polinomios asociados» para estas funciones asociadas de Legendre, éstas sólo son polinomios cuando, siendo $l$ entero, $m$ es cero o par. Si $l$ es entero y $m=0$ , entonces funciones asociadas y polinomios de Legendre coinciden.
-Expresiones de las primeras funciones asociadas de Legendre: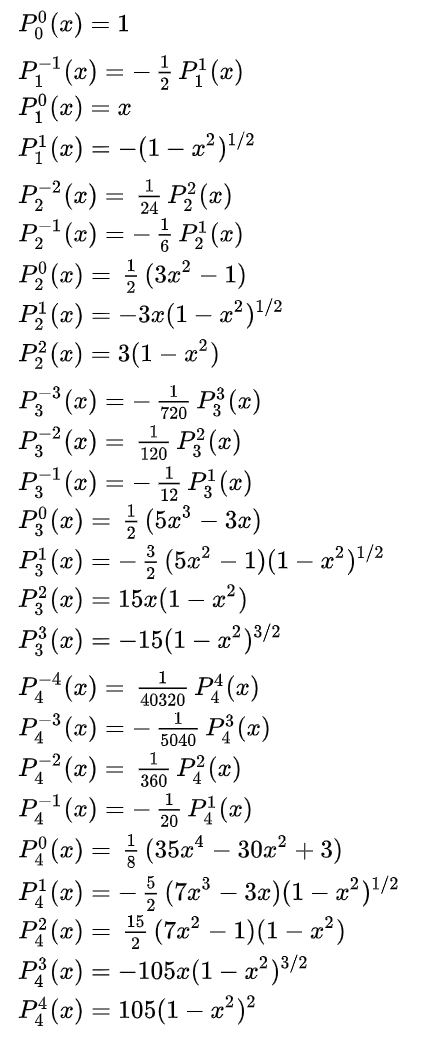

Primeras funciones asociadas de Legendre (fuente: Wikipedia). Obsérvese que cuando $m$ es par $P_l^m$ es un polinomio de grado $l$ .
Expresión estándar de los polinomios de Legendre de grado $l$ : $P_l(\xi)\, \equiv \,P_l^{m=0}(\xi) \,= \, F(-l\,,\, l+1\,,\, 1\,;\, \frac{1-\xi}{2})$ $=\,2^{-l}\, \sum_{n=0}^{[l/2]}\,\frac{(-1)^n\, (2l-2n)!}{n!\,(l-n)!\, (l-2n)!}\,\xi^{l-2n}$ ,
donde $F$ representa la función hipergeométrica.
-Puede encontrarse más información sobre los polinomios de Legendre en el blog lamecanicacuantica.blogspot.com.
Reuniendo resultados, los armónicos esféricos, autofunciones simultáneas de los operadores $\vec{L}^2$ y $L_z$ , tienen la expresión:
$Y_{lm}(\theta, \varphi)\,=\,C\,P_l^m(\cos \theta)\,\frac{1}{\sqrt{2\pi}}\, e^{im\varphi}$ ,
donde la constante $C$ se determina imponiendo la normalización a la unidad:
$Y_{lm}(\theta, \varphi)\,=\, [\frac{(2l+1)(l-m)!}{4\pi (l+m)!}]^{\frac{1}{2}} \,P_l^m(\cos \theta)\, e^{im\varphi}$ ,
teniéndose:
$\left. \begin{array}{l} 0 \le \theta \le \pi \\ 0 \le \varphi < 2\pi \\ (n=1,2,3\ldots) \\ l=0,1,2,3,\ldots,(n-1) \\ m=-l,-l+1,\ldots ,l-1,l \end{array} \right\}$ $\leftrightarrow \left\{ \begin{array}{l} 0 \le \theta \le \pi \\ 0 \le \varphi < 2\pi \\ |m|\,=\,0,1,2,3\ldots \\ l\,=\, |m|,|m|+1,|m|+2,\ldots \\ (n=l+1,l+2,l+3,\ldots) \end{array} \right.$
Propiedades:
1. $Y_{l,m}^*(\theta, \varphi)\,=\,(-1)^m\, Y_{l,-m}(\theta, \varphi)$
2. Poseen paridad definida: bajo inversión espacial, $\vec{r} \rightarrow -\vec{r}$ , se transforman según:
  $Y_{l,m}(\pi - \theta, \varphi + \pi)\,=\,(-1)^l\, Y_{l,m}(\theta, \varphi)$
3. Ortonormalización:
  $\int \, Y_{l',m'}^*(\theta, \varphi)\,Y_{l,m}(\theta, \varphi)\,d\Omega\,=\,\delta_{l,l'}\,\delta_{m,m'}$
4. Los armónicos esféricos constituyen una base ortonormal en el espacio $L^2(S_2)$ , donde $S_2=\{ |\vec{r}|=1 \}$ , la esfera de radio unidad (nota: con medida $d\Omega_r$ , véase [GAL-89]) , satisfaciendo el convenio de Condon-Shortley.
5. Regla de acoplamiento:
  $Y_{l_1,m_1}(\Omega)\,Y_{l_2,m_2}\,(\Omega)$
  $\,=\, \sum_{l=0}^{\infty} \,[\frac{(2l_1+1)(2l_2+1)}{4\pi\,(2l+1)}]^\frac{1}{2} \,C(l_1\,l_2\,l\,|\,m_1\,m_2\,m) \, C(l_1\,l_2\,l\,|\,0\,0\,0) \,Y_{l,m=m_1+m_2}(\Omega)$
  $\Rightarrow \, \int \, Y_{l_3,m_3}^*(\Omega) \, Y_{l_2,m_2}(\Omega)\,Y_{l_1,m_1}(\Omega)\,d\Omega$
  $\,=\, [\frac{(2l_1+1)(2l_2+1)}{4\pi\,(2l_3+1)}]^\frac{1}{2} \,C(l_1\,l_2\,l_3\,|\,m_1\,m_2\,m_3) \, C(l_1\,l_2\,l_3\,|\,0\,0\,0)$ ,
  donde cada $C(l_1\,l_2\,l_3\,|\,m_1\,m_2\,m_3)$ representa el correspondiente coeficiente de Clebsch-Gordan.
6. $\sum_m \,Y_{l,m}^*(\Omega)\,Y_{l,m}\,(\Omega)\,=\,\frac{(2l+1)}{4\pi}$
7. $Y_{l,m}(0,\varphi)\,=\,\delta_{m,0}\,\sqrt{\frac{(2l+1)}{4\pi}}$
8. $Y_{l,0}(\Omega)\,=\,\sqrt{\frac{(2l+1)}{4\pi}}\,P_l(\cos \theta)$
9. $Y_{l,l}(\Omega)\,=\,(-1)^l \, \biggl[ \sqrt{\frac{(2l+1)(2l)!}{4\pi 2^{2l}(l!)^2}} \biggr] ^{\frac{1}{2}}\,(\sin \theta)^l \, e^{il\varphi}$
10. Satisfacen el convenio de Condon-Shortley:
  $<L_+>\,\ge 0 \;,\; <L_->\,\ge 0$
11. Dado el operador $\vec{r}$ y definidos
  $\left. \begin{array}{l} r_{+1}\,=\,-\frac{1}{\sqrt{2}} \ (x\, +\, iy) \\ r_0 \,=\,z \\ r_{-1}\,=\,\frac{1}{\sqrt{2}} \ (x\, -\, iy) \end{array} \right\}$ ,
  se tiene:
  $Y_{1,m}(\Omega)\,=\,\frac{1}{r}\,\sqrt{\frac{3}{4\pi}}\,r_{1,m} \;, \; m=0,\pm 1$
12. Puesto que $[ \vec{L}^2,L_{\pm}]=0$ y $[L_z \,,\, L_{\pm} ]\,=\, \pm \, \hbar \, L_{\pm}$ :
  $\left. \begin{array}{l} \vec{L}^2L_{\pm} \, Y_l^m \,=\, L_{\pm} \vec{L}^2 \, Y_l^m \,=\, \hbar^2 \,l(l+1) \,L_{\pm} \, Y_l^m \\ L_z L_{\pm} \, Y_l^m \,=\, \pm \hbar \, L_{\pm} \, Y_l^m \, + \,L_{\pm} L_z \, Y_l^m \,=\, \hbar \, (m \pm 1)\, L_{\pm} \, Y_l^m\end{array} \right\}$ $\Rightarrow \, L_{\pm} \, Y_l^m \,=\, C_{lm}^{(\pm)}\, Y_{l}^{m \pm 1}$ ,
  donde las constantes $C_{lm}^{(\pm)}$ se pueden determinar a partir de la condición de normalización:
  $|| L_{\pm}\, Y_l^m ||^2 \,=\,| C_{lm}^{(\pm)} |^2 \, || Y_l^{m\pm 1} ||^2 \,=\,| C_{lm}^{(\pm)}|^2$
  $=\,< L_{\pm} Y_l^m | L_{\pm} Y_l^m >\,=\,< Y_l^m |L_{\mp}L_{\pm} | Y_l^m >$
  $=\,< Y_l^m | \vec{L}^2 - L_z^2 \mp \hbar L_z | Y_l^m > \,=\, \hbar^2 \, [l(l+1)-m^2 \mp m]$
  $\Rightarrow \, C_{lm}^{(\pm)} \, =\, \hbar \, \sqrt{l(l+1)-m(m \pm 1)}$
13. Algunos valores esperados:
  $<Y_l^m | L_x | Y_l^m >\,=\,<Y_l^m | L_y | Y_l^m >\,=\, 0$
  $<Y_l^m | L_x^2 | Y_l^m >\,=\, <Y_l^m | L_y^2 | Y_l^m >\,=\,\frac{1}{2}\,\hbar^2 \, [l(l+1)-m^2]$
Primeros armónicos esféricos $Y_l^m$ y gráficos de sus densidades $|Y_l^m|^2$ asociadas (para mayor detalle, puede consultarse la correspondiente entrada del blog de Armando Martínez Téllez):
Primeros armónicos esféricos.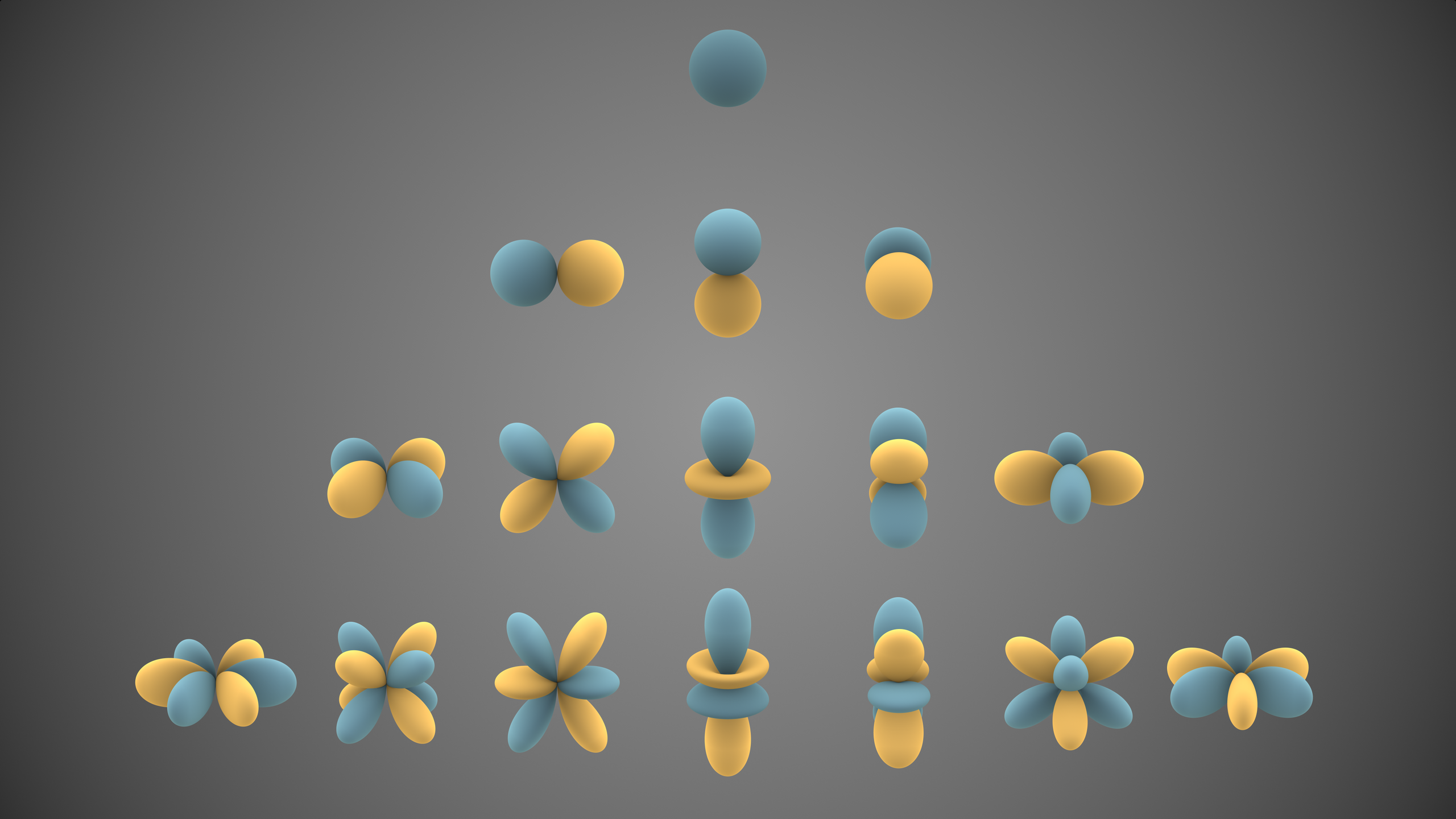

Representaciones visuales de los primeros armónicos esféricos reales. Las porciones azules representan regiones donde la función es positiva, y las amarillas, donde es negativa. La distancia de la superficie al origen indica el valor absoluto de $|Y_{\ell,m}^2(\theta,\varphi)|$ en dirección angular $(\theta,\varphi)$ (pie e imagen por De Inigo.quilez – Trabajo propio, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=32782753).

Superficies para las cuales la cantidad $|Y_{lm}^2(\theta,\varphi)|$ es igual a una constante (figura y pie tomados del blog lamecanicacuantica.blogspot.com).
Notación espectroscópica: según la notación usual en Espectroscopía, es frecuente designar los estados correspondientes a los valores sucesivos del numéro cuántico de momento angular orbital, $l=0,1,2,3,4,5\ldots$ , por la serie de sendas letras minúsculas (caso de una partícula) $s,p,d,f,g,h\ldots$ ; mayúsculas para más de una partícula.

Representación vectorial de $\vec{L}$

Lenguaje: de una partícula en el estado $|lm \alpha>$ , esto es, con función de onda en representación de coordenadas de expresión
$\Psi(\vec{r},t) \,=\,\psi_{\alpha}(r,t) \, Y_l^m(\theta,\varphi)$ ,
se dice que «tiene momento angular orbital $l$ con tercera componente $m$ » (en unidades $\hbar$ ); entonces, adoptado el convenio de Condon-Shortley, satisface el conjunto de ecuaciones:
$\left. \begin{array}{l} \vec{L}^2 \, |lm> \,=\,\hbar^2 \,l(l+1) \,|lm> \\ L_{z} \, |lm> \,=\,\hbar \,m \,|lm> \\ L_{\pm} \, |lm> \,=\,\hbar \,\sqrt{l(l+1)-m(m \pm 1)} \,|lm \pm 1> \\ L_{x} \, |lm> \,=\,\frac{\hbar}{2} \, [\sqrt{l(l+1)-m(m + 1)}|lm +1> + \sqrt{l(l+1)-m(m - 1)} \,|lm - 1>] \\ L_{y} \, |lm> \,=\,\frac{-i\, \hbar}{2} \, [\sqrt{l(l+1)-m(m + 1)}|lm +1> - \sqrt{l(l+1)-m(m - 1)} \,|lm - 1>] \end{array} \right\}$
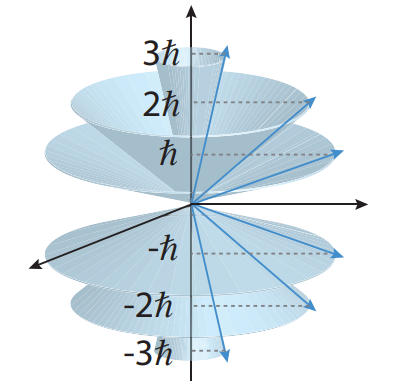
Figura: se suele visualizar el momento angular de un estado propio simultáneo de $\vec{L}^2$ y $L_z$ , con autovalores respectivos $\hbar^2l(l+1)$ y $\hbar m$ , como un vector (¡sin dirección fija!) de módulo $\hbar \ \sqrt{l(l+1)}$ y proyección sobre el eje $OZ$ de valor $\hbar m$ (siempre se tiene $|m| \le l$ ):
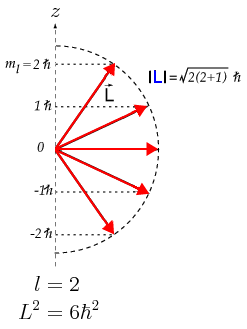
Diagrama vectorial para un momento angular orbital l=2 (figura del blog lamecanicacuantica.blogspot.com).
Puesto que los valores esperados de $L_x$ y $L_y$ son nulos, se pudiera imaginar al vector $\vec{L}$ realizando un movimiento de precesión alrededor del eje $OZ$ , viniendo dadas las $(2l+1)$ proyecciones permitidas del vector sobre el eje $OZ$ por los valores $\hbar m \,,\, m=-l,-l+1,\ldots,l-1,l$ ; el vector $\vec{L}$ , con origen en el origen de coordenadas, coincidiría con una de las generatrices sobre la superficie de un cono de altura en cada caso $\hbar m$ , teniéndose simetría axial en torno al eje y siendo todas las orientaciones posibles sobre esta superficie igualmente probables:
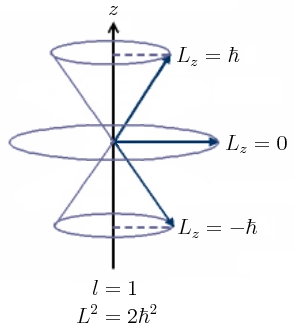
Proyecciones para la precesión de un momento angular orbital l=1 (figura del blog lamecanicacuantica.blogspot.com).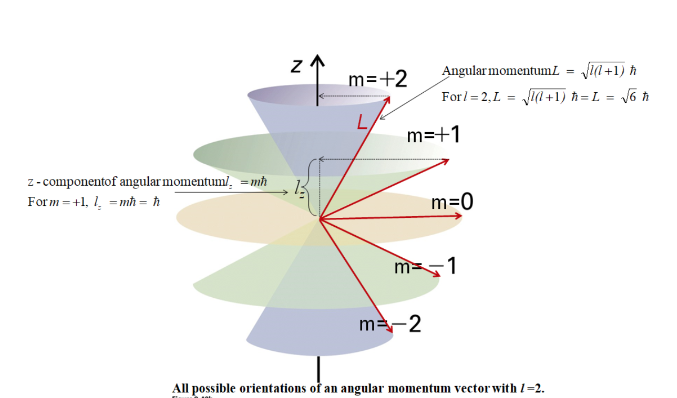

Modelo vectorial para el momento angular orbital , caso l=2 (imagen de: https://www.chegg.com/homework-help/).

-Obsérvese como en estas figuras queda patente que la variable ángulo $\theta$ entre $\vec{L}$ y sus proyecciones sobre el eje OZ, componente $L_z$ , resulta cuantizada según:
$\theta \, = \, \arccos (\frac{m}{\sqrt{l(l+1)}})$
En particular, para los valores $m=+l$ y $m=-l$ se dice que «el momento angular es paralelo al eje OZ» y «el momento angular es anti-paralelo al eje OZ» , respectivamente. Es importante señalar que estas expresiones no indican, en ningún caso, que la componente $L_z$ del vector $\vec{L}$ esté fija: aunque se tenga
$<Y_l^m | L_x | Y_l^m >\,=\,<Y_l^m | L_y | Y_l^m >\,=\, 0$ ,
también se tiene
$<Y_l^{m=\pm l } | L_x^2 | Y_l^{m=\pm l } >\, \ne \,0$ y $<Y_l^m | L_y^2 | Y_l^m >\, \ne \,0$ .
-Es decir, $<Y_l^{m=\pm l} | L_z | Y_l^{m=\pm l} >\,=\,\pm \hbar l$ en sentido promedio: no se trata de que el vector ${L}$ tenga una dirección fijada en el espacio, lo que implicaría una violación del principio de indeterminación (¡no se pueden medir simultáneamente dos componentes cualesquiera de $\vec{L}$ con precisión ilimitada!).
-Así pues, podemos dibujar una imagen borrosa para representar esta conceptualización: según el Principio de superposición, aplicado al momento angular de una partícula, en ausencia de determinación de su proyección sobre una dirección cualquiera, marcada como OZ, en la correspondiente función de onda se superponen todas las orientaciones, con origen en O y sobre la superficie de conos enfrentados por su vértice común en O, tales que sean compatibles con el hecho de que, bajo medida de la componente $L_z$ , el resultado sea $\hbar m \,,\, m=0,\,,\pm 1 \,,\,\ldots \,,\,\pm l$ .
La predicción del fenómeno de la cuantización espacial, que ya aparecía en el modelo atómico de Sommerfeld de 1916, quedó confirmada experimentalmente en 1922 por O. Stern y W. Gerlach, vía la medida de momentos magnéticos atómicos, aunque sólo sería justificada teórica y correctamente por completo con la aplicación del concepto de espín, un momento angular intrínseco sin análogo clásico postulado en 1925 por S. Goudmit y G.E. Uhlenbeck para explicar el efecto Zeeman anómalo.