
Principio de indeterminación
Enunciado y demostración
- Definiciones y resultados previos:
- Conmutador: Dados dos operadores lineales
y
, con dominios de definición respectivos
y
, se define el operador conmutador de ambos,
, como el operador
tal que
.
- Operadores que conmutan: Dados dos operadores lineales
y
, con dominios de definición respectivos
y
, se dice que conmutan, lo que se representa como
, cuando
.
- Álgebra de conmutadores:
(identidad de Jacobi).
- Teorema: Dados dos operadores autoadjuntos
y
sobre
, entonces:
es un operador autoadjunto
.
es un operador autoadjunto.
- Dado un vector propio
de A (o de B),
, entonces
.
- Valor medio (o «esperado») del observable representado por el operador lineal autoadjunto
en el estado asociado al ket
normalizado (
, notación de Dirac), se define como la media de los resultados obtenidos al efectuar un gran número
de medidas de este observable en sendos
sistemas idénticos, todos ellos preparados en el mismo estado
. Es decir:
.
-Este valor esperado es un concepto estadístico: es la media de los resultados obtenidos, y en general no tiene por qué pertenecer siquiera al espectro del operador. Es decir, siendo siempre real, no tiene por qué coincidir con el resultado de una de las medidas realizadas (aunque pueda suceder, en particular); tampoco tiene por qué coincidir con el valor más probable.
-Sies normalizable, pero no está normalizado, la expresión para el valor esperado es:
.
- Indeterminación fundamental en la medida del observable
sobre el sistema en el estado
:
- Definición general rigurosa:
-Para todo estadonormalizado,
- Definición usual:
Nota: obsérvese que esta segunda definición es válida sólo para estados que, además de pertenecer a, están en
, ya que pertenecer a
es requisito suficiente y necesario para pertenecer a
, pero no al revés.
- Definición general rigurosa:
- Conmutador: Dados dos operadores lineales
- Principio de indeterminación (Robertson, 1929): Dado el ket
normalizado (
), y dados dos operadores autoadjuntos
y
, tales que
,
y
, esto es,
, entonces:
,
dondees el conmutador de los dos operadores y
representa la indeterminación fundamental en la medida del observable
sobre el sistema en el estado
.
- Demostración:
- Sean los operadores
,
ambos autoadjuntos por serloy
, y tales que
.
- Se construye la familia de operadores
, donde
es una constante real,
. Obsérvese que
no es autoadjunto:
.
- Entonces, se tiene:
;
;
introduciendo
,
y
,
se deriva:
.
- Ahora bien,
es un operador autoadjunto, por serlo
y
, de forma que se cumple
, y su valor esperado ha de ser real,
, por lo que
representa una ecuación de segundo grado en
con coeficientes reales y siempre positiva (
). Se implica, en consecuencia, que el discriminante debe ser negativo o nulo:
,
ecuación de la que se obtiene, finalmente, el principio de indeterminación:
.
- Sean los operadores
Interpretación
- Principio de indeterminación (expresión de Robertson, 1929): Como acabamos de exponer, el formalismo matemático del Espacio de Hilbert permite demostrar el teorema:
-Dado un sistema físico en un estado caracterizado por el ket (normalizado), y dados dos observables representados por sendos operadores autoadjuntos
y
, entonces
, donde
es el conmutador de los dos operadores y
representa la desviación típica o raíz cuadrada positiva de la varianza del conjunto de medidas del observablerealizadas sobre una colección de sistemas, idénticos entre sí e igualmente preparados en el mismo estado puro
, denominada usualmente como indeterminación fundamental en la medida del observable
sobre el sistema en el estado
.
- Los observables posición
y momento
vienen representados en el formalismo por dos operadores autoadjuntos que no conmutan entre sí,
, de forma que cada dos componentes en la misma dirección están ligadas por una relación matemática de indeterminación:
.
- La interpretación del símbolo
es: representa la indeterminación mínima con que un valor puede ser adscrito al correspondiente observable. Es decir, si la indeterminación del observable
es
en un estado dado
de un sistema físico, entonces es imposible realizar un experimento que sea capaz de asignar un valor a ese observable, sobre el sistema, con precisión superior a
.
- El principio de indeterminación enunciado no es un axioma o postulado de la teoría, sino un teorema, esto es, una consecuencia matemática de los postulados que conforman la base axiomática establecida para la teoría. Por lo tanto, una violación del mismo conllevaría la renuncia a alguno de sus postulados (o su modificación).
- Como hemos visto en el estudio de los paquetes de onda, también desde el momento que queda establecida la descripción de las partículas por medio de funciones de onda, siendo la transformada de Fourier la relación matemática entre los espacios de posiciones y de momentos, las anchuras de las respectivas funciones de onda quedan matemáticamente ligadas por una relación de indeterminación.
- Interpretación estadística: imaginemos un gran número
de sistemas idénticos e idénticamente preparados, en las mismas condiciones, compuestos cada uno por una partícula de masa
; sea
la función asociada, que ha de ser la misma para todos ellos si la preparación está bien diseñada y ejecutada.
- Si realizamos un experimento de determinación o medida simultánea de dos observables
y
, en cada una de estas copias idénticas del mismo sistema, obtendremos una colección de resultados que, estadísticamente, presentarán sendas desviaciones típicas
y
, las cuales satisfacen siempre la desigualdad
.
- Las relaciones de indeterminación no restringen la precisión con que un solo observable puede medirse, sino las precisiones con que pueden medirse simultáneamente dos observables no compatibles (esto es, que no conmutan). Establecen la imposibilidad de preparar un sistema físico en un estado en que los resultados de la medida conjunta de cualesquiera dos observables complementarios presenten distribuciones estadísticas cuyas desviaciones típicas violen el principio de indeterminación.
- Si sobre una colección de sistemas idénticos se realiza la misma medida de primera especie, convirtiéndola en una colección de sistemas idénticos e idénticamente preparados en un estado puro dado
, y si se tiene una indeterminación
(esto es, la medida del observable
sobre la colección de copias idénticas ha producido una serie de resultados con esta desviación típica), la medida de cualquier segundo observable
tal que
(complementario al primero):
a) Habría producido una serie de resultados con una desviación típica satisfaciendo; y
b) producirá una serie de resultados con una desviación típica satisfaciendodonde
.
- Es decir, por ejemplo, si sobre un sistema (monodimensional) constituido por una partícula (
) se tiene en un instante totalmente determinado el momento (vía la preparación del sistema en un estado dado
, por la realización de una medida de primera especie sobre él o, estrictamente hablando, sobre la colectividad de muchos
sistemas idénticos), de forma que
, entonces en ese instante la posición estará totalmente indeterminada, reflejando una deslocalización total:
. Supongamos que, a continuación, se realiza una medida de la posición, que arroja resultados (sobre la correspondiente subcolectividad, que pasa a estar preparada en un segundo estado dado
por dicha segunda medida de primera especie realizada, «filtrante») con indeterminación
finita; entonces, la distribución de probabilidades asociada al observable complementario momento presentará, en ese instante y sobre esa subcolectividad, una desviación típica
no nula, tal que
. Es decir, la actualización del observable posición por su medida se ve instantáneamente acompañada de una alteración de la distribución de probabilidad de los observables complementarios al operador posición, alteración que está sujeta al principio de indeterminación que liga las indeterminaciones en la medida simultánea de dos observables complementarios.
 La relación de indeterminación
La relación de indeterminación expresa la alteración que en la potencialidad de los valores de una de las dos magnitudes
y
en un estado
produce la actualización de los valores de la otra a través de su medida, y viceversa. (cf. [GAL-89], I, p. 86).
- Dados dos observables complementarios, el hecho matemático de su no conmutación representa el hecho experimental de que el resultado de su medida depende del orden en que se acometa. En cambio, el resultado de la medida de dos observables compatibles sobre un mismo estado es independiente del orden en que se realicen las respectivas medidas.
- En definitiva, hacer una medida, realizar un experimento, es en Física Cuántica algo conceptualmente diferente por completo a lo que significa en Física Clásica. Hacer un experimento en Física Cuántica significa, en general, cambiar el estado del sistema de una forma que se refleja en general en una modificación instantánea e impredecible de la función de onda que contiene la información maximal posible sobre el sistema.
- Si realizamos un experimento de determinación o medida simultánea de dos observables
- Nota: en la literatura sobre el tema, coexisten dos interpretaciones fundamentales:
- La estadística (Robertson, 1929): es la que se ha adoptado antes. En ella,
se interpreta como un concepto estadístico, el de desviación típica (raíz cuadrada positiva de la varianza o dispersión cuadrática media) de una colección de medidas. En esta interpretación, el Principio establece que el producto de las desviaciones típicas en la medida simultánea de dos observables complementarios ha de ser mayor o igual que la mitad del valor absoluto del valor medio de su conmutador, y es un auténtico principio o teorema, en el sentido de que se deriva matemáticamente de los postulados de la teoría.
- La no estadística: es la que refiere a un sistema individual, estableciendo que es imposible determinar sobre el sistema, simultáneamente, los valores de dos observables complementarios con precisiones respectivas cuyo producto sea inferior a una cota dada (que depende del conmutador de los dos observables en cuestión). Esta es la versión original de Heisenberg del Principio (1927, ver apartado sobre fundamentos),

Pre-publication proof sheet of the first paper in which Heisenberg advanced his famous uncertainty principle. Includes the Pauling annotation: «Given to me in Göttingen by Born.» Texto e imagen en: http://scarc.library.oregonstate.edu/coll/pauling/bond/papers/corr155.1-01-large.html derivada a partir de diversos experimentos conceptuales (como el «microscopio de rayos
«), y resulta problemática como planteamiento inicial a la hora de definir o dotar de sentido a
. En la actualidad, se prefiere denominar a esa formulación inicial como el «principio de indeterminación de Heisenberg error-perturbación» («error-disturbance«), y experimentos recientes parece que comienzan a sugerir para algunos que su expresión quizás no es todo lo exigente que debiera, en el sentido en que necesitaría ser reformulada a efectos de prevenir su violación (una tarea acometida por M. Ozawa en 2003). Una referencia recomendable (comprensible) sobre esta especializada cuestión puede ser: Neutrons revive Heisenberg’s first take on uncertainty (2012); la polémica está servida y también hay autores que no aceptan de ninguna manera que los mencionados experimentos indiquen que haya que reformular la expresión original de Heisenberg: véase Uncertainty reigns over Heisenberg’s measurement analogy (2013).
-Nota: Además, comentan otros, la formulación original del principio de incertidumbre de Heisenberg en 1927 sólo es válida para pulsos gaussianos: en la formulación matemática original, Heisenberg formuló su principio utilizando el error cuadrático medio en las medidas experimentales, asumiendo que el error en las medidas experimentales sigue una distribución gaussiana, una hipótesis que de hecho se viola en general. En el siguiente enlace puede encontrarse amplia información sobre ello a raíz de algún reciente revuelo mediático relacionado:
http://francis.naukas.com/2013/06/10/francis-en-trending-ciencia-el-principio-de-incertidumbre-de-heisenberg/ - Ahora bien, introducida la versión estadística (que es la consolidada y que predomina en los textos modernos), se acepta (mayoritaria, que no unánimemente) inferida la no estadística: basta considerar sólo medidas ideales (medidas que afectan mínimamente al estado, esto es, que no alteran los observables compatibles con los medidos, véase [GAL-89], I, p. 96). De no cumplirse el principio para el sistema individual, sería preparable siempre un subconjunto con un número grande de sistemas individuales en que se violaría el principio. Es decir, «No interpretación no-estadística» implica «No interpretación estadística», por lo que, según las reglas lógicas, ha de ser «interpretación estadística» implica «interpretación no-estadística».
- La interpretación estadística establece sin ambigüedad el sentido para la indeterminación cuántica que representamos por el símbolo
.
- La estadística (Robertson, 1929): es la que se ha adoptado antes. En ella,
- Ejemplo: según los resultados expuestos en el apartado de paquetes de onda, hemos visto como, para el paquete de ondas asociado con una partícula material de masa
, caso monodimensional, las anchuras del paquete
y de la función de distribución de momentos
satisfacen la relación (expresión de Kennard, 1927)
:
- Cuánto más estrecha se haga la función de distribución de momentos, más ancha se hará
, esto es, más ancha será la región en que el paquete de ondas posee intensidad apreciable; y viceversa. Y, para tiempos suficientemente cortos,
, entonces se cumple la relación la relación
(donde
significa «no puede ser menor que un numero del orden de
«).
- Así pues, dadas las condiciones tales que se cumple
, entonces se implica que, si se requiere determinar la posición de la partícula con precisión
, sólo se podrá determinar su momento con una precisión
.
- La relación
no es sino una propiedad general de la transformada de Fourier (propiedad de escalado) para las correspondientes anchuras en los espacios involucrados, posición y momento en este caso.
- Cuánto más estrecha se haga la función de distribución de momentos, más ancha se hará
Consecuencias
- Consecuencias fundamentales del principio de indeterminación:
- Pérdida del determinismo clásico: Como consecuencia inmediata de la imposibilidad de conocer el presente con precisión ilimitada (restricción fundamental o de principio, no práctica o asociada a errores experimentales mejorables), se establece la pérdida del determinismo clásico. La descripción inherente a la Mecánica Cuántica es probabilística, consistente en general en el abanico de probabilidades de un conjunto de posibles resultados para cada medida, sin indicar qué resultado concreto va a producirse. En palabras de Heisenberg, «no podemos predecir el futuro porque es imposible conocer el presente»:
 Heisenberg, W.; “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik”, Zeitschrift für Physik 43 (1927) 172-198; “The physical content of Quantum Kinematics and Mechanics”, trad. al inglés en [WHE-83]:
Heisenberg, W.; “Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik”, Zeitschrift für Physik 43 (1927) 172-198; “The physical content of Quantum Kinematics and Mechanics”, trad. al inglés en [WHE-83]:
 Cita ampliada: «But what is wrong in the sharp formulation of the law of causality, ‘When we know the present precisely, we can predict the future’, is not the conclusion but the assumption. Even in principle we cannot know the present in all detail. For that reason everything observed is a selection from a plenitude of possibilities and a limitation on what is possible in the future. As the statistical character of quantum theory is so closely linked to the inexactness of all perceptions, one might be led to the presumption that behind the perceived statistical world there still hides a ‘real’ world in which causality holds. But such speculations seem to us, to say it explicitly, fruitless and senseless. Physics ought to describe only the correlation of observations. One can express the true state of affairs better in this way: Because all experiments are subject to the laws of quantum mechanics, and therefore to equation
Cita ampliada: «But what is wrong in the sharp formulation of the law of causality, ‘When we know the present precisely, we can predict the future’, is not the conclusion but the assumption. Even in principle we cannot know the present in all detail. For that reason everything observed is a selection from a plenitude of possibilities and a limitation on what is possible in the future. As the statistical character of quantum theory is so closely linked to the inexactness of all perceptions, one might be led to the presumption that behind the perceived statistical world there still hides a ‘real’ world in which causality holds. But such speculations seem to us, to say it explicitly, fruitless and senseless. Physics ought to describe only the correlation of observations. One can express the true state of affairs better in this way: Because all experiments are subject to the laws of quantum mechanics, and therefore to equation , it follows that quantum mechanics establishes the final failure of causality«.
-El concepto clásico de causalidad está ausente de la Física Cuántica: no hay conexión causal entre las configuraciones del sistema cuántico antes y después de una observación. - Trabazón de los sistemas físicos con los medios de observación: asociada a cada medida hay una ineludible correlación establecida entre el aparato con que se mide y el sistema sobre el que se mide. Estas correlaciones se manifiestan en la alteración de las distribuciones de probabilidad de los observables complementarios a los medidos, y quedan incorporadas en las relaciones de indeterminación. Por tanto, es imposible (a diferencia de lo que ocurre en Física Clásica) elaborar una teoría correctiva que tenga en cuenta la intervención del aparato de medida y permita establecer lo medido como propiedad inherente sólo al sistema sobre el que se mide. Es decir, el resultado de una medida en Física Cuántica no es concebible como la revelación de un valor poseído por la correspondiente magnitud en el sistema antes de la medida («contextualidad cuántica«), ni es legítimo inferir que ése es el valor de la magnitud en el sistema tras la medida. La interacción aparato-sistema puede perturbar al sistema de forma incontrolable.
-Un fenómeno, por lo tanto, no puede ser descrito científicamente de manera independiente o al margen de los medios de observación aplicados. - Concepción relacional de estado: elaborada por Bohr tras la publicación del teorema EPR, en ella el objeto bajo observación y el aparato de medida forman un sistema indivisible, no susceptible de separación en partes para su análisis.
-La descripción del estado de un sistema, por tanto, no se puede restringir al sistema bajo observación, puesto que ha de expresar una relación entre el sistema y el montaje experimental involucrado en la medida.
-El sistema cuántico y el aparato de medida u observación forman un todo indivisible.
-Para determinar las propiedades de los objetos debemos, tanto en Física Clásica como en Física Cuántica, hacer experimentos, pero en la segunda, peculiarmente, las propiedades, en último término, están definidas por los experimentos que realizamos. - Consecuentemente: supongamos que se realiza un mismo experimento de determinación o medida del observable A en un gran número de copias idénticas del mismo sistema, obteniéndose una colección de resultados que, estadísticamente, presentarán en general una desviación típica
; se hace algo similar para un observable
complementario con el
, que es obvio involucra un montaje experimental diferente al anterior. Estamos antes sendas colecciones de resultados de medidas hechas en el mismo instante sobre sendas subcolecciones de gran número de sistemas individuales de una misma colección inicial, todos ellos asociados al mismo ket
; en cada caso, sobre cada sistema individual o copia sólo se ha medido uno de los dos observables, y todos en el mismo momento. En este caso, no es legítimo inferir una violación del principio de indeterminación: esas dos sendas colecciones de medidas de los observables
y
son el resultado de dos contextos experimentales diferentes, de forma que no constituyen una medida simultánea de ellos. Según establece la contextualidad de los observables cuánticos, no está legitimado inferir que, a partir de las dos colecciones separadas de resultados, si se hubieran medido conjuntamente (en un tercer montaje experimental, que sería necesariamente distinto a los dos anteriores), se hubieran producido los mismos resultados y, por tanto, una violación del principio de indeterminación.
- Principio de Complementariedad: En palabras de Bohr, versión de d’Espagnat (cf. [ESP-76], p. 252):
 «The nonseparable whole constituted by the quantum system and a definite instrument can be described by using a simplification of our language, according to which some of the properties that the system and the instrument share with one another are conventionally attributed to the system. However, other properties, which in our classical experience leads us to think of, cannot then be attributed to the system. They are said to be complementary to the first ones. They can also be attributed to a quantum system similar in type to the one considered so far, but this is possible only if that system builds up an indivisible whole with some new instrument, which is appropiate for a measurement of the new quantities.»
«The nonseparable whole constituted by the quantum system and a definite instrument can be described by using a simplification of our language, according to which some of the properties that the system and the instrument share with one another are conventionally attributed to the system. However, other properties, which in our classical experience leads us to think of, cannot then be attributed to the system. They are said to be complementary to the first ones. They can also be attributed to a quantum system similar in type to the one considered so far, but this is possible only if that system builds up an indivisible whole with some new instrument, which is appropiate for a measurement of the new quantities.» - Observables complementarios: En el formalismo cuántico (un formalismo matemático), existen observables representados por operadores autoadjuntos que no conmutan entre sí, denominándose entonces como observables complementarios.
-Dos operadores complementarios no pueden proporcionar una base de autofunciones comunes: es imposible encontrar un conjunto completo de funciones que sean propias de ellos a la vez. En otras palabras, no pueden formar parte juntos de un Conjunto Completo de Observables Compatibles (C.C.O.C.), lo que se traduce en general en la imposibilidad de diseñar un montaje experimental que los determine sobre un sistema dado con precisión ilimitada (refiere a «precisión» conceptualmente no relacionada con la asociada a errores experimentales).
-Obsérvese que el hecho de que sobre un estado particularse tenga
no significa que
(como se verá al estudiar momento angular, el armónico esférico correspondiente a
es autofunción simultánea de pares de observables complementarios).
-Por lo tanto, cuando dos observablesy
son complementarios, la determinación exacta de uno de ellos en un estado del sistema físico
,
, implica que en dicho estado todos los posibles resultados del otro observable
tienen la misma probabilidad. En general, ello conlleva que
(existen excepciones, como el caso del antes mencionado esférico armónico
para los operadores de momento angular orbital).
- Pérdida de la trayectoria clásica: Un ejemplo de observables complementarios lo proporcionan la posición y el momento de una partícula material (con masa
), ya que vienen representados en el formalismo por dos operadores autoadjuntos que no conmutan entre sí,
, de forma que cada dos componentes en la misma dirección están ligadas por una relación matemática de indeterminación:
. Consecuentemente, y puesto que si, por ejemplo, preparamos la partícula en un estado en que determinamos por completo su posición, tendremos por completo indeterminado su momento, por lo que el concepto de trayectoria clásico pierde su sentido en Física Cuántica.
-Por ejemplo (cf. [GAL-89], I, pp.59-60): consideremos la órbita precuántica de un electrón en el átomo de Hidrógeno en un estado de Bohr. Si suponemos un radio de la órbita de alrededor de, una medida significativa de la posición del electrón requeriría una determinación del orden de
, que provocará una indeterminación en su momento del orden
. Como la velocidad del electrón es del orden
, por lo que el momento del orden
, la indeterminación en la energía resulta
, que es a su vez del orden de unas cien veces la energía de ionización del átomo de Hidrógeno (
). Es imposible, pues, determinar en la teoría algo semejante o en correspondencia con la órbita precuántica del electrón; surge el concepto cuántico de «orbital«.
-Para trazar el recorrido o camino de una partícula, necesitamos recurrir a sucesivas determinaciones de posición, en una serie discreta de observaciones:
 Heisenberg, W.; “Reminiscences from 1926 and 1927″, en [FRE-85], pp. 163-171:
Heisenberg, W.; “Reminiscences from 1926 and 1927″, en [FRE-85], pp. 163-171:
 «We had always said so glibly that the path of the electron in the cloud chamber could be observed. But perhaps what we really observed was something much less. Perhaps we merely saw a serie of discrete and ill-defined spots through which the electron had passed. In fact, all we do see in the cloud chamber are individual droplets which must certainly be much larger than the electron» (cf. Heisenberg, 1927).
«We had always said so glibly that the path of the electron in the cloud chamber could be observed. But perhaps what we really observed was something much less. Perhaps we merely saw a serie of discrete and ill-defined spots through which the electron had passed. In fact, all we do see in the cloud chamber are individual droplets which must certainly be much larger than the electron» (cf. Heisenberg, 1927).
(un fragmento más amplio puede leerse en el apartado sobre fundamentos).
- Pérdida del determinismo clásico: Como consecuencia inmediata de la imposibilidad de conocer el presente con precisión ilimitada (restricción fundamental o de principio, no práctica o asociada a errores experimentales mejorables), se establece la pérdida del determinismo clásico. La descripción inherente a la Mecánica Cuántica es probabilística, consistente en general en el abanico de probabilidades de un conjunto de posibles resultados para cada medida, sin indicar qué resultado concreto va a producirse. En palabras de Heisenberg, «no podemos predecir el futuro porque es imposible conocer el presente»:
- Descripción completa: Junto a todo lo anterior, la teoría se arroga y postula como completa, en el sentido de que es imposible ir más allá de la predicción probabilista o estadística. Es decir, algunos fenómenos naturales son de naturaleza fundamental probabilista (el azar como propiedad esencial), por lo que es imposible (axioma) concebir una teoría que, conservando toda la corrección predictiva de la Mecánica Cuántica, establezca un determinismo absoluto que excluya el azar de las predicciones sobre la Naturaleza.
Doble rendija y Principio de indeterminación
- Consideremos de nuevo el experimento de la doble rendija, incorporando al análisis el principio de indeterminación a la Heisenberg, es decir, considerando «perturbaciones incontroladas por el acto de la medición».
- En ausencia de un dispositivo de determinación de rendija atravesada, el resultado del experimento con partículas materiales es que, con las condiciones apropiadas, se produce un fenómeno de interferencia por completo similar al que se produce cuando el experimento se realiza con radiación.
- Es decir, que en vez de observarse el resultado esperable clásicamente,
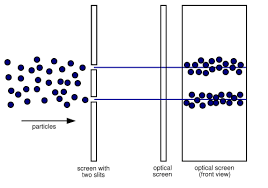
Imagen procedente de: http://scienceblogs.com/startswithabang/2009/06/01/a-tale-of-two-slits/. lo que se observa es un patrón de franjas de interferencia, característico de los fenómenos clásicos ondulatorios:
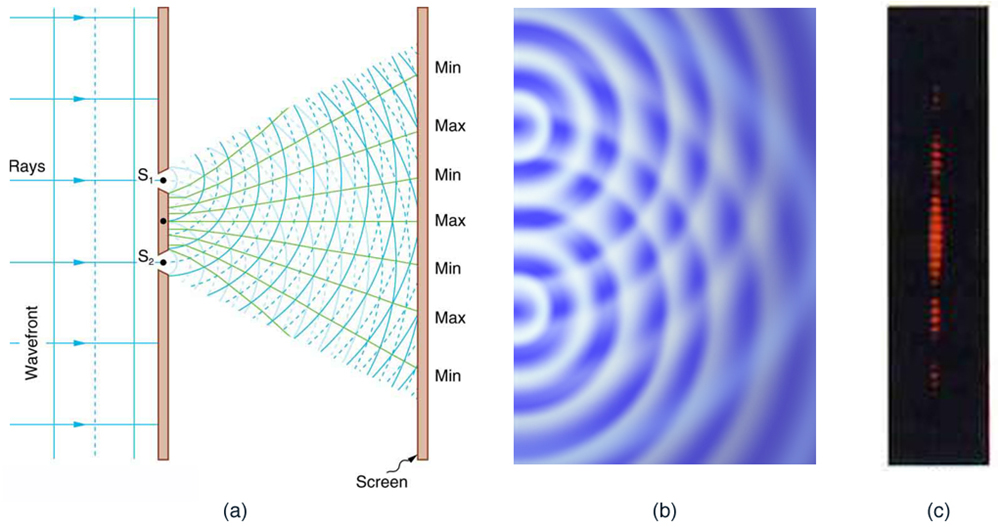
Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@8.9@8.9 (licencia Creative Commons). - La explicación del fenómeno de interferencia radica en la diferencia de caminos cuando las ondas llegan a un punto dado sobre la pantalla: si se superponen en fase, se da una interferencia constructiva, produciendo un máximo de intensidad; caso contrario, se produce interferencia destructiva, con resultado nulo (se dan todos los caso intermedios):
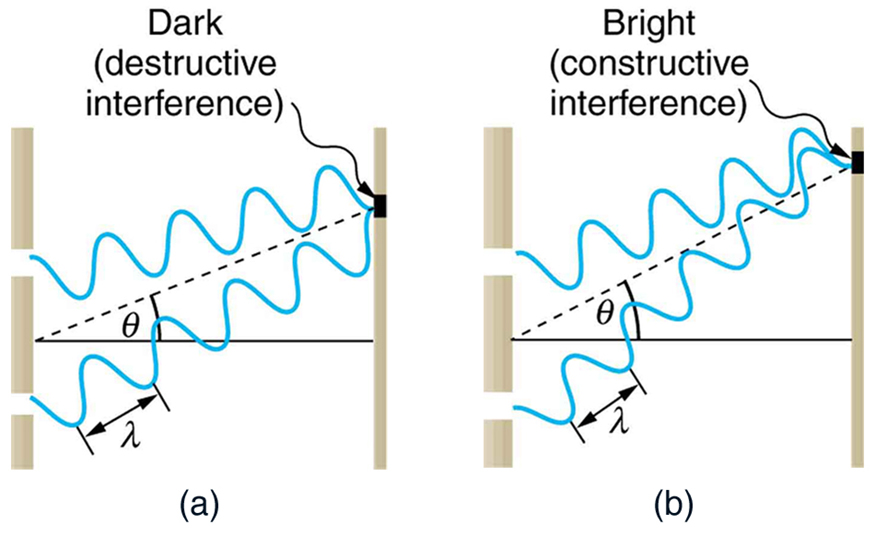
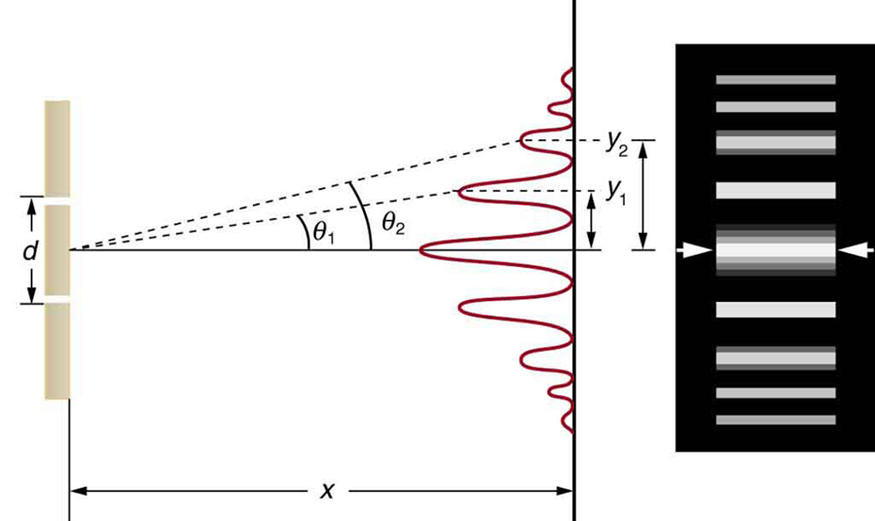
Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@8.9@8.9 (licencia Creative Commons 4.0). - La diferencia de camino recorrido
desde el plano de las dos rendijas hasta un punto dado sobre la pantalla, cuando la distancia
entre ambos planos es grande comparada con la distancia
entre rendijas, viene dada aproximadamente por
, según se desprende de la siguiente figura:
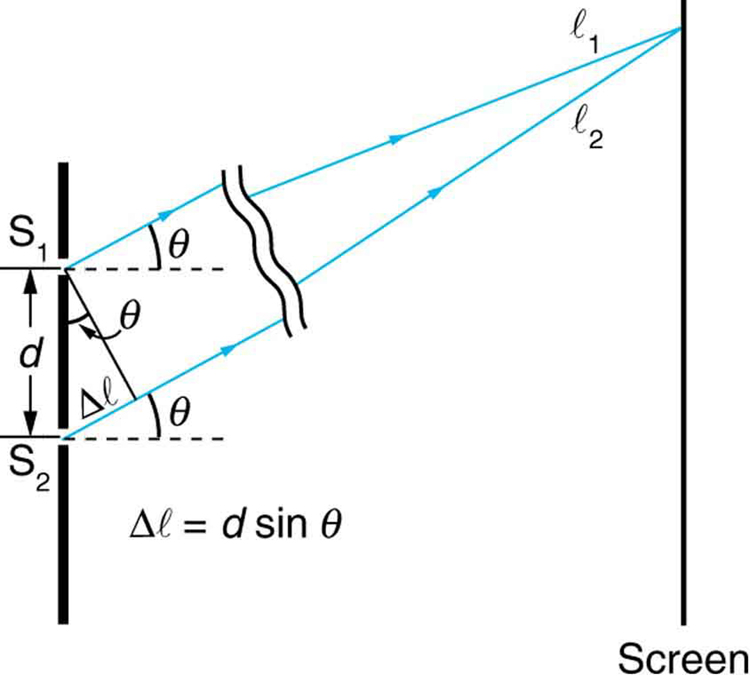
Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@8.9@8.9 (licencia Creative Commons). - Para que la interferencia sea constructiva (destructiva), la diferencia de caminos debe ser un múltiplo entero (semientero) de la longitud de onda:
-condición de interferencia constructiva:,
-condición de interferencia destructiva:, donde
marca el orden del máximo (mínimo) correspondiente.
- Supongamos ahora que se incluye en el dispositivo experimental un procedimiento de determinación de rendija atravesada por cada partícula, de forma que se puede determinar la coordenada posición vertical
la partícula, en el instante en que atraviesa el plano de las dos rendijas, con una precisión al menos
. Por ejemplo, podemos concebir observar el proceso con un microscopio cuyo poder de resolución
debe ser menor que esta semidistancia entre rendijas, es decir,
. Por ello, la longitud de onda iluminadora que emplee el microscopio debe ser
; si se trata de un microscopio óptico, entonces el momento de los correspondientes fotones será
.
- La componente
de la posición de cada partícula se determinará con una precisión
dada por el poder de resolución
del microscopio. Se produce una colisión Compton entre la partícula y el fotón de iluminación, de manera que la partícula retrocede con un momento
del orden de magnitud del momento del fotón,
, determinable tan sólo con indeterminación cumpliendo
, es decir,
.
- Ahora bien, esta indeterminación del momento se traduce en un indeterminación
en la dirección vertical del movimiento de la partícula, teniéndose
, de forma que, para ángulos pequeños,
, es decir,
, donde
es la longitud de onda de de Broglie de la partícula.
- La indeterminación
infiere finalmente una indeterminación
sobre la posición en que llegará a la pantalla.
- Para ángulos pequeños,
, por lo que la distancia entre dos máximos consecutivos es
, que es del mismo orden de magnitud que
, por lo que el intento de determinación de la rendija que fue atravesada produce la desaparición del patrón de interferencia.
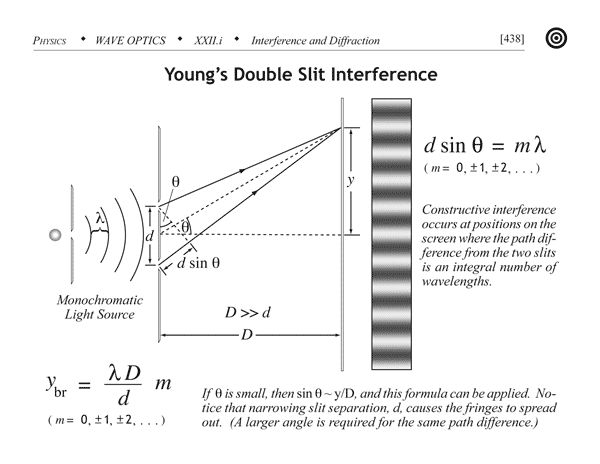
Imagen de http://www.wikipremed.com/01physicscards.php?card=876, licencia Creative Commomns. - Nota 1: Respecto al papel del principio de indeterminación, en el contexto de análisis como el que acabamos de realizar para la doble rendija, es frecuente escuchar expresiones del tipo: «La medición concreta de la rendija atravesada, esto es, las perturbaciones introducidas al realizar dicha medición, es lo que destruye las interferencias». Pero hay que ser conscientes de que no siempre es así: en rigor, es la propia distinguibilidad de los estados cuánticos correspondientes a las diversas trayectorias, las correlaciones que se establecen entre el aparato de medida y el sistema medido, lo que destruye las interferencias. Y por ello se requiere revisar expresiones como la popular «cada fotón (o partícula) interfiere consigo mismo»…
- Dos buenas lecturas al respecto:
1) G. García Alcaine; «Complementaridad, coherencia, dualidad», Revista Española de Física 6,3 (1993) 8-9:
G. García Alcaine; «Complementaridad, coherencia, dualidad», Revista Española de Física 6,3 (1993) 8-9:
 «La imposibilidad de determinar el camino seguido sin destruir la coherencia entre los distintos caminos posibles (y con ello los fenómenos de interferencia), no exige invocar alteraciones incontrolables del sistema en su interacción con un aparato de medida. La distinguibilidad en principio de las diversas trayectorias basta para destruir la coherencia«.
«La imposibilidad de determinar el camino seguido sin destruir la coherencia entre los distintos caminos posibles (y con ello los fenómenos de interferencia), no exige invocar alteraciones incontrolables del sistema en su interacción con un aparato de medida. La distinguibilidad en principio de las diversas trayectorias basta para destruir la coherencia«.
2) B-G Englert, M.O. Scully and H. Walther; «La dualidad en la materia y en la luz», Misterios de la Física Cuántica, Investigación y Ciencia, Temas 10, 1997, pp. 68-74: sobre como es imposible observar, en un experimento de doble rendija, la figura interferencial y, al mismo tiempo, determinar la rendija atravesada, pero no por nada semejante a «perturbaciones incontrolables introducidas por el acto de observar», sino porque basta con que la trayectoria sea distinguible en principio, sin llegar a realizar una medida que la especifique, para que se destruya la coherencia entre las diversas amplitudes y desaparezca la figura interferencial, como consecuencia, pues, de las correlaciones entre el aparato de medida y el sistema medido.
B-G Englert, M.O. Scully and H. Walther; «La dualidad en la materia y en la luz», Misterios de la Física Cuántica, Investigación y Ciencia, Temas 10, 1997, pp. 68-74: sobre como es imposible observar, en un experimento de doble rendija, la figura interferencial y, al mismo tiempo, determinar la rendija atravesada, pero no por nada semejante a «perturbaciones incontrolables introducidas por el acto de observar», sino porque basta con que la trayectoria sea distinguible en principio, sin llegar a realizar una medida que la especifique, para que se destruya la coherencia entre las diversas amplitudes y desaparezca la figura interferencial, como consecuencia, pues, de las correlaciones entre el aparato de medida y el sistema medido.
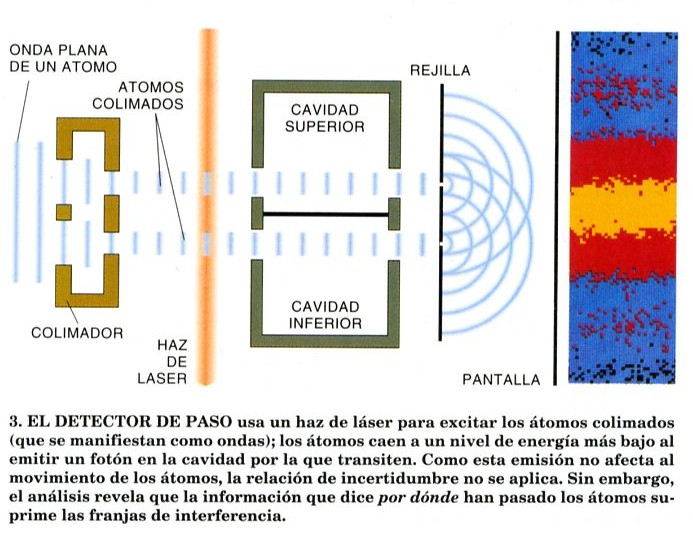
Imagen del artículo por B-G Englert, M.O. Scully and H. Walther, «La dualidad en la materia y en la luz», Misterios de la Física Cuántica, Investigación y Ciencia, Temas 10, 1997, pp. 68-74. - Recuérdese: dos funciones de onda
y
, con
, esto es, dos funciones de onda que difieran entre sí sólo en un factor de fase, proporcionan la misma densidad de probabilidad: son equivalentes. Ahora bien, a la hora de producir interferencias, las fases relativas entre funciones de onda son muy importantes y han de tenerse en cuenta.
-Por ejemplo: dadas dos funciones de onday
, con
y
reales, su combinación lineal con coeficientes escalares arbitrarios
, complejos, representa otra función de onda
(por el principio de superposición, que rige debido a la linealidad del espacio), que proporciona la densidad de probabilidad
.
-El tercer sumando, que provoca que las distribuciones de probabilidad asociadas a las funcionesy
no se sumen directamente, justifica los fenómenos observados de interferencia (por ejemplo, en el experimento de la doble rendija).
- Referencias interesantes:
 The two Slit Experiment
The two Slit Experiment
 Controlled double-slit electron diffraction
Controlled double-slit electron diffraction - Nota 2: Considérese la pregunta: «¿Por cuál rendija ha tenido lugar el paso?» Respuesta: «Sólo tienen sentido físico aquellas cuestiones que se contestan experimentalmente» (de forma equivalente: «los experimentos no realizados no tienen resultados«). Así que:
-Si los caminos son indistinguibles, la pregunta es metafísica.
-Interpretación ortodoxa: no tiene sentido afirmar que «aunque no pueda determinarse cuál es la rendija atravesada, cada partícula tiene que haber pasado por una sola de ellas».
-La teoría predice correctamente todos los resultados experimentales: !suficiente¡ (interpretación ortodoxa: instrumentalismo).
Principio de indeterminación y valores medios
- (Recapitulación) Principio de indeterminación (expresión de Robertson, 1929): Rigurosamente, en Teoría de Espacios de Hilbert puede demostrarse el siguiente teorema:
Dado un sistema físico en un estado caracterizado por el ket, y dados dos observables representados por sendos operadores autoadjuntos
y
, entonces:
,
dondees el conmutador de los dos operadores y
representa la desviación típica del conjunto de medidas realizadas sobre una colección de sistemas idénticos entre sí e igualmente preparados en el mismo estado puro, o indeterminación en la medida del observable
sobre el sistema en el estado
.
- La interpretación del símbolo
es que representa la indeterminación mínima con que un valor puede ser adscrito al correspondiente observable: si la indeterminación del observable
es
, en un estado representado por el vector de estado normalizado
, sognifica que es imposible realizar un experimento que sea capaz de asignar un valor a ese observable, sobre el sistema, con precisión superior a
.
- Demostración de la igualdad entre las dos expresiones equivalentes en la definición de la indeterminación
de un operador autoadjunto
:
(recuérdese que se está suponiendo que el estadoestá normalizado a la unidad).
- Dado el carácter autoadjunto de
, se tiene siempre
; además
:
.
- Consecuentemente:
,
es decir, cuando, y sólo cuando,es un vector propio de
, con valor propio su valor esperado
.
- Así pues, en general, dado un sistema físico preparado en el estado descrito o asociado al vector de estado normalizado
, la distribución estadística de los resultados obtenidos por la medida de un observable
, representado por el correspondiente operador autoadjunto
, presenta una dispersión
, excepto en el caso particular de que se haya preparado al sistema en un estado propio del operador
con valor propio
, en cuyo caso se satisface
, es decir:
.
- Repárese en que, si se prepara un sistema físico en un estado que es propio de un observable dado, se tiene certeza del resultado que se va a obtener al medir ese observable sobre el sistema (siempre que se preserve el sistema entre la preparación inicial y la medida posterior sin alterar su estado, esto es, a resguardo de cualquier interacción ): el correspondiente valor propio.
-Al respecto, quizás sea interesante recordar las palabras de Heisenberg:
 Heisenberg, W.; “Die Rolle der Unbestimmtheitsrelationen in der modernen Physik”, Monatshefte für Mathematik und Physik 38 (1931) 365-372:
Heisenberg, W.; “Die Rolle der Unbestimmtheitsrelationen in der modernen Physik”, Monatshefte für Mathematik und Physik 38 (1931) 365-372:
 «If at a certain time all data are known for a given system then there exist, at any later time, experiments the results of which can be exactly predicted, provided the system is subjected to no other disturbances than those necessary for the performance of the experiment. Whether a regularity of this kind may be still regarded as causality or not is purely a question of taste».
«If at a certain time all data are known for a given system then there exist, at any later time, experiments the results of which can be exactly predicted, provided the system is subjected to no other disturbances than those necessary for the performance of the experiment. Whether a regularity of this kind may be still regarded as causality or not is purely a question of taste».
Ley de dependencia temporal del valor medio de un operador
- La ecuación de Schrödinger y su conjugada tienen las expresiones respectivas:
,
,
dondees el Hamiltoniano del sistema, cuyo operador representativo
es autoadjunto y, por lo tanto, hermítico (recuérdese que un operador $A$ es hermítico si y sólo si
);
es el ket del correspondiente Hilbert que describe el estado (puro) del sistema.
- Evolución temporal de un valor medio o esperado:
-Seaun observable cualquiera del sistema en el estado
; en general, la evolución del valor esperado
se deberá de una parte a la evolución del vector estado y, de otra, a la evolución del operador (en el caso en que efectivamente el operador
dependa explícitamente del tiempo). Así que, formalmente:
.
- En general, se define una constante del movimiento como un observable
que satisface la ecuación:
.
-Por tanto, cuando un observable es constante del movimiento, su valor medio se mantiene constante en el transcurso temporal. - Obsérvese que un caso particular de un observable que es constante del movimiento es el de un observable sin dependencia explícita temporal y que conmuta con el Hamiltoniano.
Indeterminación energía-tiempo
- Las expresiones del tipo
, o relaciones de indeterminación energía-tiempo, han conocido numerosas interpretaciones desde su primera formulación por Heisenberg. Actualmente, una de las interpretaciones más aceptada es la de Mandelstam-Tamm (1945), que escribe esta forma del principio de indeterminación, en el caso particular de un sistema conservativo (el Hamiltoniano representa la energía total del sistema y no depende del tiempo) en el estado puro
, como:
,
simbolizandoun intervalo de tiempo característico de la evolución del sistema, en el instante
, especificable en el formalismo bajo las condiciones indicadas a partir del principio de indeterminación.
- En concreto (cf. [GAL-89], I, pp. 109-110), el significado de
es:
- En el instante
, se mide un observable
, sin dependencia explícita temporal, en muchos sistemas idénticos e idénticamente preparados en el mismo estado
; buscamos la expresión de un intervalo de tiempo característico
de la evolución del sistema, en el instante
, tal que la distribución estadística de los resultados de las medidas de
sea esencialmente la misma que se obtendría al medir, de forma análoga, en otro instante
tal que
.
- Para ello, partimos de la relación de indeterminación
,
que, aplicando la fórmula anterior de evolución temporal de los valores esperados, para un operadorsin dependencia explícita temporal y un sistema conservativo (en el que el Hamiltoniano no depende del tiempo), se transforma en la expresión:
,
donderepresenta la velocidad con que se desplaza el valor medio de la distribución de probabilidad para los resultados de la medida del observable
sobre
.
- A continuación, definimos el intervalo de tiempo
,
que representa una estimación del tiempo que hay que dejar transcurrir para que la distribución estadística de resultados de la medida dese desplace en una cantidad
, según se refleja en la siguiente figura (tomada del excelente manual de A. Galindo y P. Pascual):
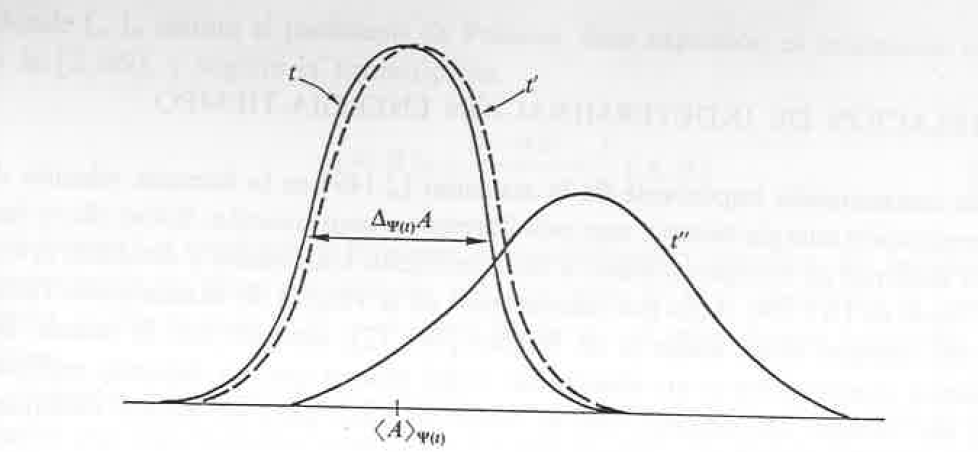
Evolución temporal de la distribución de probabilidad para resultados de la medida del observable A (cf. A. Galindo y P. Pascual, «Mecánica cuántica», volumen I, Eudema). - Entonces, si se considera el conjunto
de todos los observables
del sistema que no dependen explícitamente del tiempo, se tendrá en correspondencia un conjunto de sendos valores temporales característicos
, definiéndose finalmente:
ínf
.
- Este tiempo característico de la evolución temporal del sistema, en el instante
, es tal que, cualquiera que sea el observable
medido sobre el sistema, en dicho instante
, las distribuciones estadísticas de los resultados de su medida en dos instantes distintos, el considerado
y otro
, son esencialmente las mismas, siempre que
(algo que, en general, dejará de ser cierto si
, como ocurre, por ejemplo, para el
en la anterior figura).
- Relación de indeterminación energía-tiempo: Para un sistema físico conservativo, en un estado cualquiera
, la indeterminación en la energía y un tiempo característico
del sistema, definido de modo que, transcurrido ese intervalo de tiempo, las distribuciones de probabilidad de todos los observables del sistema sin dependencia explícita temporal se mantengan esencialmente iguales, han de satisfacer la relación
.
- Nota (cf. [GAL-89], I, p. 111): en un sistema conservativo, con la definición precisa
,
se deriva.
- En el instante
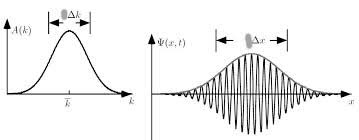
- Ejemplo en términos de análisis armónico: Considérese una función de onda
, asociada al estado cuántico de cierta partícula y centrada en torno a la posición
, y sea su expresión la de un paquete de ondas en el espacio de tiempos o pulso de anchura (duración)
.
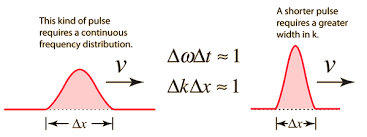
Véase: http://hyperphysics.phy-astr.gsu.edu/. - Su expresión en términos del análisis armónico o de Fourier es la superposición de ondas monocromáticas de frecuencia respectiva
(cf. [BRA-00], pp. 73-74), con fórmula matemática:
;
recíprocamente,
.
- Por las propiedades de la transformación de Fourier,
toma valores apreciables sólo en el rango de frecuencias
que satisface
, y puesto que
, se deriva que
, relación en la que la variable
, a diferencia de las restantes que han aparecido anteriormente en una relación de indeterminación, no representa un observable del sistema físico, sino un parámetro de la teoría. Por ello, no cabe la interpretación del símbolo
como una desviación típica cuando se yuxtapone al parámetro «tiempo» t.
- Su expresión en términos del análisis armónico o de Fourier es la superposición de ondas monocromáticas de frecuencia respectiva
Anchura natural y vida media de los niveles de energía
- Si se considera una transición (atómica, por ejemplo) entre dos niveles de energía, en una especie atómica concreta, en la que se emite un fotón con energía la diferencia energética entre ellos,
, la vida media
o duración promedio del estado inicial se define como el tiempo medio observado que tarda un átomo de esa especie, en ese estado excitado, en realizar la transición atómica señalada. Se trata, pues, de un concepto estadístico: ante un átomo individual concreto, la teoría sólo proporciona una probabilidad de que realice la transición, probabilidad conocida como resultado de la observación de un gran número de átomos de esa especie en ese estado de excitación.
- Dada la asociación de ese parámetro temporal vida media con cada estado excitado, la correspondiente función de onda asociada no debe tomar valores significativos fuera de un intervalo de tiempo de un orden de magnitud
, lo que, debido a la anteriormente establecida relación de indeterminación-tiempo, se traduce en una indeterminación
asociada al estado excitado en cuestión y conocida como anchura natural en energía del nivel. A más corta vida media, pues, se tendrá una mayor indeterminación o anchura energética en el nivel, y viceversa.
- Respecto al estado fundamental, puesto que es estable (esto es, los átomos en el estado fundamental no experimentan transiciones o excitaciones espontáneas), la vida media asociada es muy larga, infinita de hecho,
, por lo que la anchura energética asociada será
.
- Es evidente que las anchuras naturales de los niveles energéticos se verán acompañadas de unas anchuras en las energías (frecuencias) de los fotones emitidos en las transiciones, que ya no tendrán una frecuencia perfectamente definida
, sino que presentarán un ensanchamiento natural
, de expresión
, donde
.
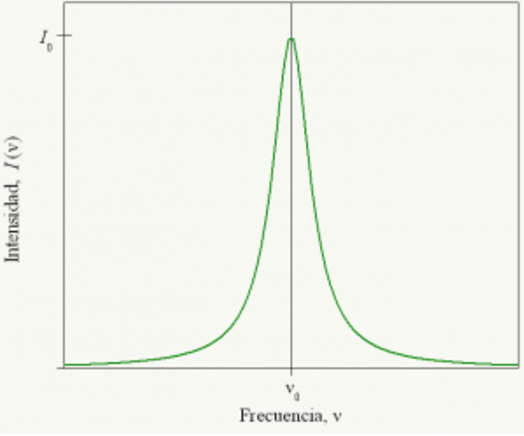
Ensanchamiento natural de una línea de emisión; la línea adquiere un perfil lorentziano (imagen por Gsrdzl, licencia GNU, de Wikipedia). -Estos ensanchamientos de líneas atómicas son típicamente de un orden de entre
y
, bastante inferiores a los debidos a otros efectos.
- Los ensanchamientos naturales relacionados con el principio de indeterminación energía-tiempo se observan tanto para estados atómicos como en otros sistemas, como moléculas y núcleos. Son especialmente significativos en la espectroscopía nuclear, y bastante menos importantes en la atómica.
- La siguiente figura muestra una comparativa entre las distribuciones estadísticas de Lorentz (también conocida como de Cauchy) y de Gauss:
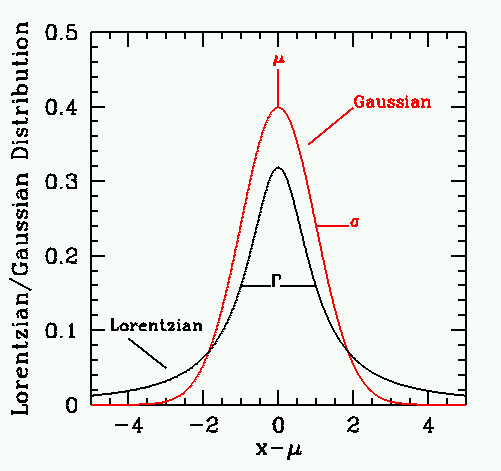
Imagen de: http://www.das.uchile.cl/~mhamuy/courses/AS750/tema1.html
Referencias
[BOH-89] Bohm, D.; Quantum Theory; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; Quantum Mechanics; 2nd ed., Pearson; Dorchester, 2000.
[ESP-76] Espagnat, B.D’; Conceptual Foundations of Quantum Mechanics, Benjamin, 1976.
[FRE-85] French, A.P. and Kennedy, P.J.; Niels Bohr: a centenary volume, Harvard Univ. Press, 1985.
[GAL-89] Galindo, A. y Pascual, P.; Mecánica Cuántica, Eudema, 1989.
[JAM-74] Jammer, M.; The philosophy of Quantum Mechanics, Wiley, 1974.
[MEH-82] Mehra, J., Rechenberg, H.; The Historical Development of Quantum Mechanics, 6 vol., Springer-Verlag, Nueva York, 1982.
[NEU-91] Neumann, J. von; Fundamentos matemáticos de la Mecánica Cuántica, CSIC, Raycar, Madrid, 1991.
[WHE-83] Wheeler, J.A. y Zurek,W.H., ed.; Quantum Theory and measurement, Princeton Univ., Princeton, 1983.
Páginas complementarias
http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-principio-de-incertidumbre-ii.html
http://cuentos-cuanticos.com/2013/05/08/prohibido-conmutar-i/
http://www2.math.umd.edu/~begue/Expository/Uncertainty.pdf
APPS
Dejar una contestacion