
https://www.youtube.com/watch?v=NUS6_S1KzC8
El experimento de la doble rendija
![]() Un experimento paradigmático, elegido en 2002, Physics World, como uno de los 10 más bellos experimentos en Física: http://physicsworld.com/cws/article/print/9745.
Un experimento paradigmático, elegido en 2002, Physics World, como uno de los 10 más bellos experimentos en Física: http://physicsworld.com/cws/article/print/9745.
![]() Realizaciones experimentales famosas de un experimento paradigmático:
Realizaciones experimentales famosas de un experimento paradigmático:
-
- Con luz: Young, 1899:
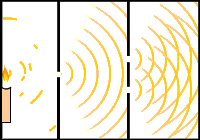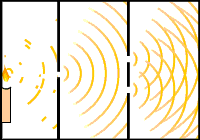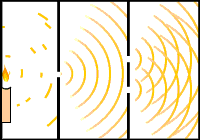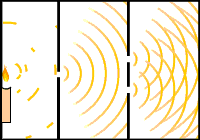
Experimento de Young, 1899. - Con electrones: Jönsson, Tübingen, 1961.
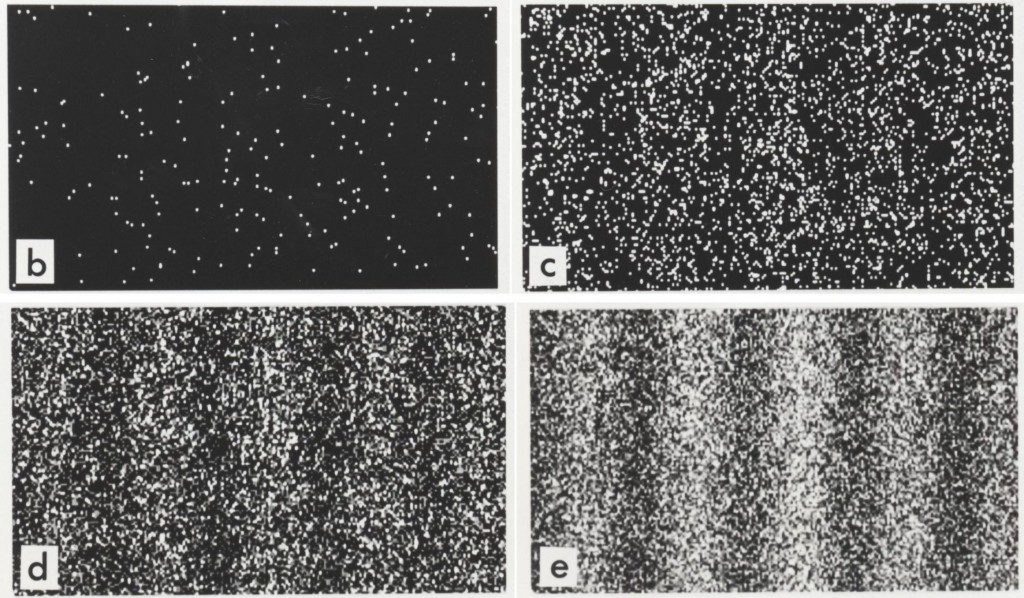
- Con electrones lanzados uno a uno:
 Merli, Missiroli and Pozzi, Bologna, 1974: On the statistical aspect of electron interference phenomena; American Journal of Physics 44 (1976) 306; https://doi.org/10.1119/1.10184.
Merli, Missiroli and Pozzi, Bologna, 1974: On the statistical aspect of electron interference phenomena; American Journal of Physics 44 (1976) 306; https://doi.org/10.1119/1.10184.
 A. Tonomura, J. Endo, T. Matsuda, and T. KawasakiH. Ezawa-Tonomura (laboratorios Hitachi, 1989); Demonstration of single-electron buildup of an interference pattern; American Journal of Physics 57 (1989) 117; doi: 10.1119/1.16104.
A. Tonomura, J. Endo, T. Matsuda, and T. KawasakiH. Ezawa-Tonomura (laboratorios Hitachi, 1989); Demonstration of single-electron buildup of an interference pattern; American Journal of Physics 57 (1989) 117; doi: 10.1119/1.16104.
- Con luz: Young, 1899:

- Con moléculas pesadas como los fullerenos, de en torno a 100 átomos: A. Zeilinger, 1999.
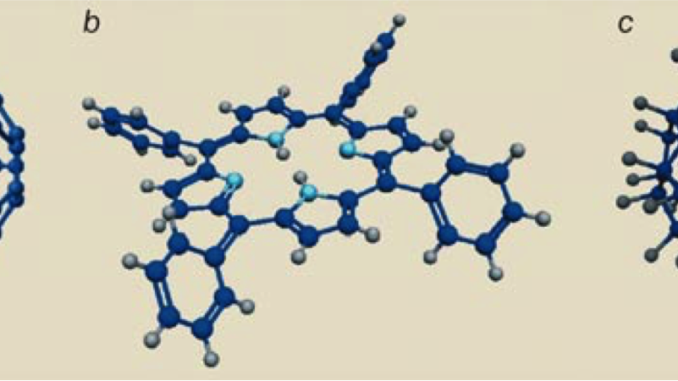
- Con moléculas de ftalocianina, una molécula de 16 átomos, ocho de nitrógeno y ocho de carbono:
 Thomas Juffmann, Adriana Milic, Michael Müllneritsch, Peter Asenbaum, Alexander Tsukernik, Jens Tüxen, Marcel Mayor, Ori Cheshnovsky, Markus Arndt, “Real-time single-molecule imaging of quantum interference,” Nature Nanotechnology, published online 25 March 2012:
Thomas Juffmann, Adriana Milic, Michael Müllneritsch, Peter Asenbaum, Alexander Tsukernik, Jens Tüxen, Marcel Mayor, Ori Cheshnovsky, Markus Arndt, “Real-time single-molecule imaging of quantum interference,” Nature Nanotechnology, published online 25 March 2012:
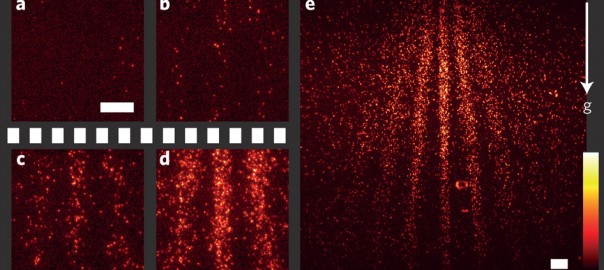
https://www.youtube.com/watch?v=wGkx1MUw2TU -Vídeo:
(subido por Francis Villatoro).
Doble rendija y principio de indeterminación
- Consideremos de el experimento de la doble rendija, incorporando al análisis el principio de indeterminación a la Heisenberg, es decir, considerando «perturbaciones incontroladas por el acto de la medición».
- En ausencia de un dispositivo de determinación de rendija atravesada, el resultado del experimento con partículas materiales es que, con las condiciones apropiadas, se produce un fenómeno de interferencia por completo similar al que se produce cuando el experimento se realiza con radiación.
- Es decir, que en vez de observarse el resultado esperable clásicamente,
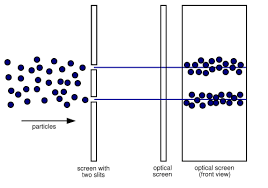
Imagen de http://scienceblogs.com/startswithabang/2009/06/01/a-tale-of-two-slits/. lo que se observa es un patrón de franjas de interferencia, característico de los fenómenos clásicos ondulatorios:
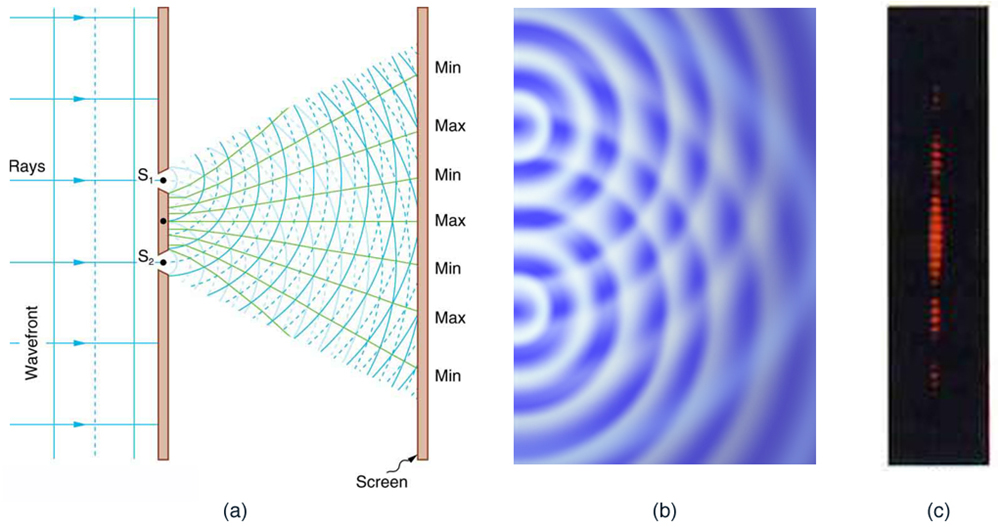
Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@8.9@8.9 (licencia Creative Commons). - La explicación del fenómeno de interferencia radica en la diferencia de caminos cuando las ondas llegan a un punto dado sobre la pantalla: si se superponen en fase, se da una interferencia constructiva, produciendo un máximo de intensidad; caso contrario, se produce interferencia destructiva, con resultado nulo (se dan todos los caso intermedios):
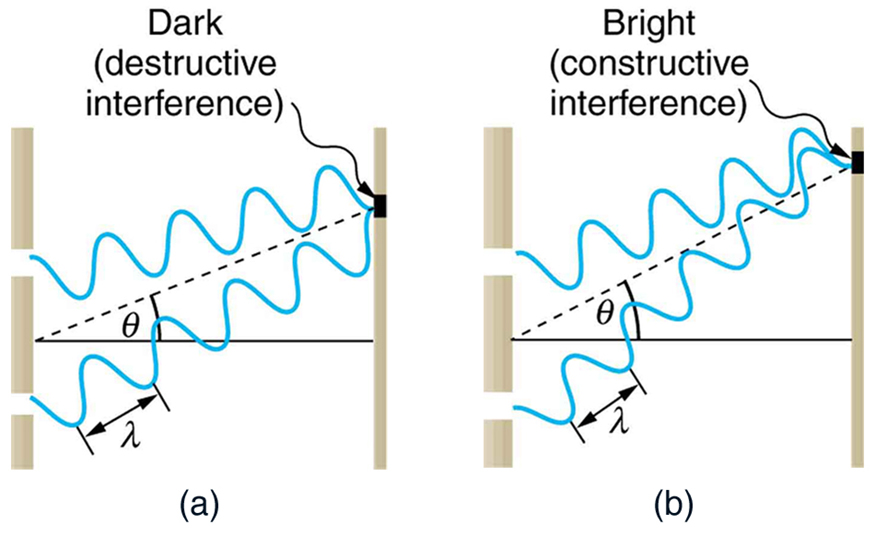
Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@8.9@8.9 (licencia Creative Commons 4.0). - La diferencia de camino recorrido
desde el plano de las dos rendijas hasta un punto dado sobre la pantalla, cuando la distancia
entre ambos planos es grande comparada con la distancia
entre rendijas, viene dada aproximadamente por
, según se desprende de la siguiente figura:
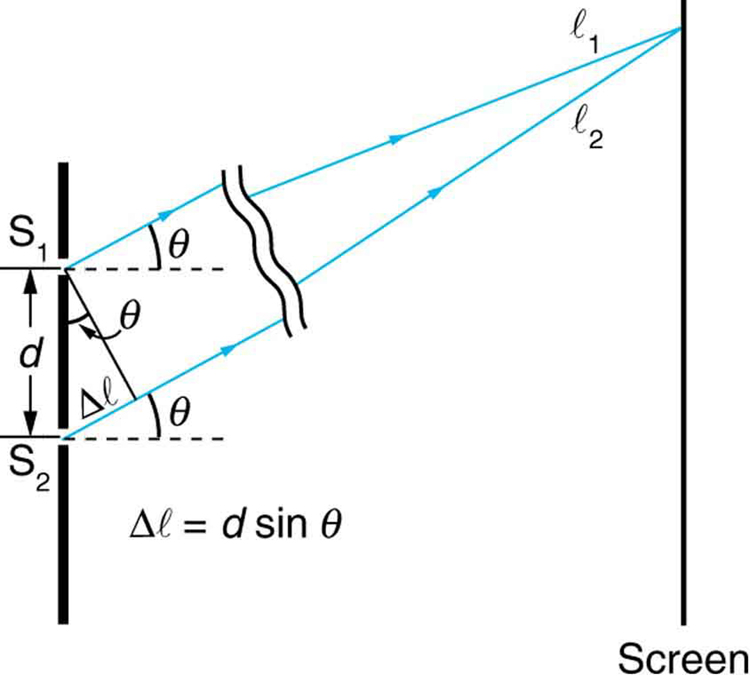
Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@8.9@8.9 (licencia Creative Commons). - Para que la interferencia sea constructiva (destructiva), la diferencia de caminos debe ser un múltiplo entero (semi-impar) de la longitud de onda:
-condición de interferencia constructiva:,
-condición de interferencia destructiva:,
dondemarca el orden del máximo (mínimo) correspondiente.
- Supongamos ahora que se incluye en el dispositivo experimental un procedimiento de determinación de rendija atravesada por cada partícula, de forma que se puede determinar la coordenada posición vertical
la partícula, en el instante en que atraviesa el plano de las dos rendijas, con una precisión al menos
. Por ejemplo, podemos concebir observar el proceso con un microscopio cuyo poder de resolución
debe ser menor que esta semidistancia entre rendijas, es decir,
. Por ello, la longitud de onda iluminadora que emplee el microscopio debe ser
; si se trata de un microscopio óptico, entonces el momento de los correspondientes fotones será
.
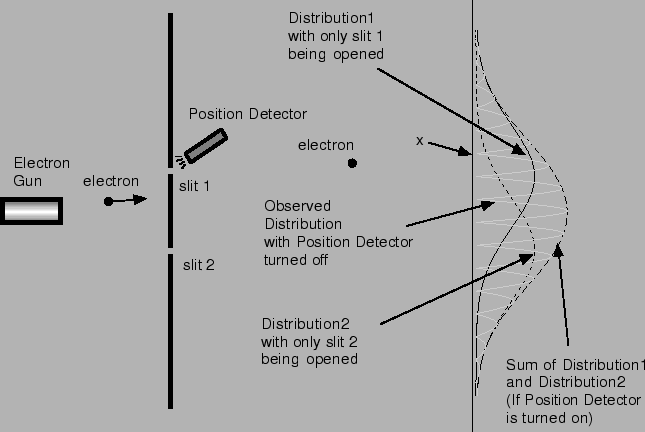
Montaje con determinación de la rendija atravesada por cada electrón en un experimento de doble rendija. - La componente
de la posición de cada partícula se determinará con una precisión
dada por el poder de resolución
del microscopio. Se produce una colisión Compton entre la partícula y el fotón de iluminación, de manera que la partícula retrocede con un momento
del orden de magnitud del momento del fotón,
, determinable tan sólo con indeterminación cumpliendo
, es decir,
.
- Ahora bien, esta indeterminación del momento se traduce en un indeterminación
en la dirección vertical del movimiento de la partícula, teniéndose
, de forma que, para ángulos pequeños,
, es decir,
, donde
es la longitud de onda de de Broglie de la partícula.
- La indeterminación
infiere finalmente una indeterminación
sobre la posición en que llegará a la pantalla.
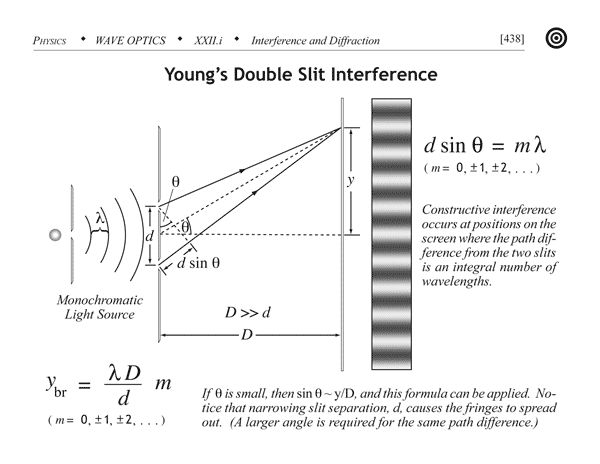
Imagen de http://www.wikipremed.com/01physicscards.php?card=876, licencia Creative Commomns. -Para ángulos pequeños,
, por lo que la distancia entre dos máximos consecutivos es
, que es del mismo orden de magnitud que
, por lo que el intento de determinación de la rendija que fue atravesada produce la desaparición del patrón de interferencia.
- Nota 1: Respecto al papel del principio de indeterminación, en el contexto de análisis como el que acabamos de realizar para la doble rendija, es frecuente escuchar expresiones del tipo «La medición concreta de la rendija atravesada, las perturbaciones introducidas al realizar dicha medición, son los que destruyen las interferencias«. Pero hay que ser conscientes de que no siempre es así: en rigor, es la propia distinguibilidad de los estados cuánticos correspondientes a las diversas trayectorias, las correlaciones que se establecen entre el aparato de medida y el sistema medido, lo que destruye las interferencias. Y ello convierte también en obsoletas formas de expresión como la archirrepetida «cada fotón (o partícula) interfiere consigo mismo»…
- Una buena lectura al respecto:
 1) G. García Alcaine; «Complementaridad, coherencia, dualidad», Revista Española de Física 6,3 (1993) 8-9: «La imposibilidad de determinar el camino seguido sin destruir la coherencia entre los distintos caminos posibles (y con ello los fenómenos de interferencia), no exige invocar alteraciones incontrolables del sistema en su interacción con un aparato de medida. La distinguibilidad en principio de las diversas trayectorias basta para destruir la coherencia«.
1) G. García Alcaine; «Complementaridad, coherencia, dualidad», Revista Española de Física 6,3 (1993) 8-9: «La imposibilidad de determinar el camino seguido sin destruir la coherencia entre los distintos caminos posibles (y con ello los fenómenos de interferencia), no exige invocar alteraciones incontrolables del sistema en su interacción con un aparato de medida. La distinguibilidad en principio de las diversas trayectorias basta para destruir la coherencia«.
 2) B-G Englert, M.O. Scully and H. Walther; «La dualidad en la materia y en la luz», Misterios de la Física Cuántica, Investigación y Ciencia, Temas 10, 1997, pp. 68-74: sobre como es imposible observar, en un experimento de doble rendija, la figura interferencial y, al mismo tiempo, determinar la rendija atravesada, pero no por las perturbaciones incontrolables introducidas por el acto de observar, sino porque basta con que la trayectoria sea distinguible en principio, sin llegar a realizar una medida que la especifique, para que se destruya la coherencia entre las diversas amplitudes y desaparezca la figura interferencial, como consecuencia, pues, de las correlaciones entre el aparato de medida y el sistema medido.
2) B-G Englert, M.O. Scully and H. Walther; «La dualidad en la materia y en la luz», Misterios de la Física Cuántica, Investigación y Ciencia, Temas 10, 1997, pp. 68-74: sobre como es imposible observar, en un experimento de doble rendija, la figura interferencial y, al mismo tiempo, determinar la rendija atravesada, pero no por las perturbaciones incontrolables introducidas por el acto de observar, sino porque basta con que la trayectoria sea distinguible en principio, sin llegar a realizar una medida que la especifique, para que se destruya la coherencia entre las diversas amplitudes y desaparezca la figura interferencial, como consecuencia, pues, de las correlaciones entre el aparato de medida y el sistema medido.
Complementaridad sin indeterminación
![]() M.O. Scully, B-G. Englert y H. Walther; Quantum optical tests of complementarity; Nature 351(1991)111-116.
M.O. Scully, B-G. Englert y H. Walther; Quantum optical tests of complementarity; Nature 351(1991)111-116.
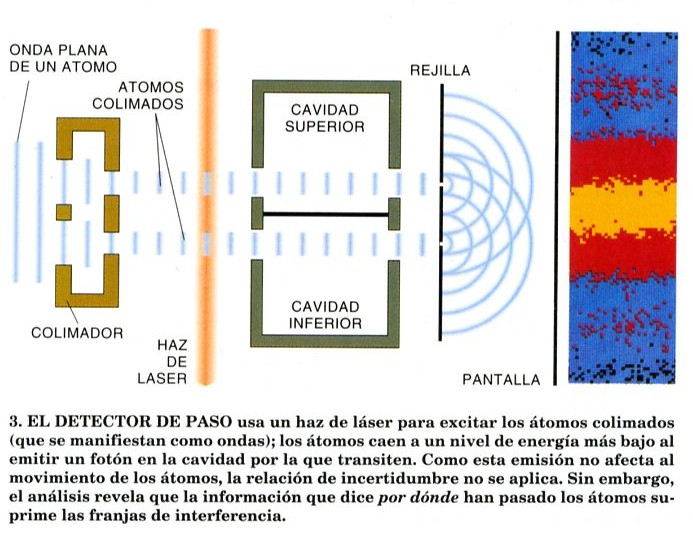
![]() Los autores presentan una variación del experimento de doble rendija tradicional, incorporando dos cavidades de micromáseres que actúan de detectores de camino o rendija atravesada, supuestamente sin afectar su movimiento.
Los autores presentan una variación del experimento de doble rendija tradicional, incorporando dos cavidades de micromáseres que actúan de detectores de camino o rendija atravesada, supuestamente sin afectar su movimiento.
![]() Experiencia ESW: Sobre como es imposible observar, en un experimento de doble rendija, la figura interferencial y, al mismo tiempo, determinar la rendija atravesada, pero no por nada semejante a “perturbaciones incontrolables introducidas por el acto de observar”, sino porque basta con que la trayectoria sea distinguible en principio, sin llegar a realizar una medida que la especifique, para que se destruya la coherencia entre las diversas amplitudes y desaparezca la figura interferencial, como consecuencia, pues, de las correlaciones entre el aparato de medida y el sistema medido.
Experiencia ESW: Sobre como es imposible observar, en un experimento de doble rendija, la figura interferencial y, al mismo tiempo, determinar la rendija atravesada, pero no por nada semejante a “perturbaciones incontrolables introducidas por el acto de observar”, sino porque basta con que la trayectoria sea distinguible en principio, sin llegar a realizar una medida que la especifique, para que se destruya la coherencia entre las diversas amplitudes y desaparezca la figura interferencial, como consecuencia, pues, de las correlaciones entre el aparato de medida y el sistema medido.
![]() Complementariedad sin perturbaciones incontroladas por transferencias de momento.
Complementariedad sin perturbaciones incontroladas por transferencias de momento.
![]() Descripción del experimento ESW:
Descripción del experimento ESW:
![]() D. Aleksandar, U. Princenton: The World of Quantum Physics.
D. Aleksandar, U. Princenton: The World of Quantum Physics.
-Sendas cavidades de micromáseres que actúan como detectores de camino o rendija atravesada se colocan delante de cada una de las dos rendijas, de manera que todos los átomos en tránsito las atraviesan antes de llegar a una rejilla.
-Se usa un láser para excitar los átomos que van a atravesar el montaje, cada átomo absorbe un fotón de corta λ del láser y salta a un estado excitado o de energía mayor; por la geometría de las cavidades, los átomos emiten un fotón, de mayor λ, cuya localización indica la cavidad, esto es, la rendija, atravesada por cada átomo.
-Y esta emisión no supone una perturbación en el movimiento del átomo (veáse nota a continuación), pero, pese a ello, en cuanto se ha obtenido la información de por dónde ha pasado el átomo, la figura interferencial de franjas desaparece.
-La complementariedad se preserva, explican los autores del experimento, porque descansa en las correlaciones existentes entre la libertad de movimientos del átomo y los fotones de la cavidad: el fotón chivato que queda en la cavidad preclude la interferencia, porque al hacerse disponible la información de por dónde ha pasado cada átomo el patrón interferencial se pierde.
![]() Nota: Esta afirmación ha sido muy discutida, pues ha habido autores que insistieron en que la destrucción de la figura interferencial es siempre consecuencia de la perturbación y la inherente transferencia de momento; véase por ejemplo:
Nota: Esta afirmación ha sido muy discutida, pues ha habido autores que insistieron en que la destrucción de la figura interferencial es siempre consecuencia de la perturbación y la inherente transferencia de momento; véase por ejemplo:
![]() E.P. Storey, S.M. Tan, M.J. Collett and D.F. Walls; Nature 367(1994)626-628;
E.P. Storey, S.M. Tan, M.J. Collett and D.F. Walls; Nature 367(1994)626-628;
-Resulta muy interesante consultar las siguientes aclaraciones:
![]() B.-G. Englert, M. O. Scully y H. Walther: Quantum erasure in double-slit interferometers with which-way detectors .
B.-G. Englert, M. O. Scully y H. Walther: Quantum erasure in double-slit interferometers with which-way detectors .
![]() H.M. Wiseman, and F.E. Harrison; Nature 377(1995)584.
H.M. Wiseman, and F.E. Harrison; Nature 377(1995)584.
-En otro contexto experimental, la observación de efectos interferenciales en luz dispersada por átomos atrapados, evidencia también la destrucción de la interferencia sin invocar la perturbación y el principio de indeterminación:
![]() U. Eichmann, J.C. Bergquist, J.J. Bollinger, J.M. Gilligan, W.M. Itano and D.J. Wineland; Young’s Interference Experiment with Light Scattered from Two Atoms: Phys. Rev. Let. 70(1993)2359-2362.
U. Eichmann, J.C. Bergquist, J.J. Bollinger, J.M. Gilligan, W.M. Itano and D.J. Wineland; Young’s Interference Experiment with Light Scattered from Two Atoms: Phys. Rev. Let. 70(1993)2359-2362.
-Otras referencias aclarativas al respecto:
![]() Jeff Lundeen; Does a which-way measurement kick the particle? Young’s double-slit revisited.
Jeff Lundeen; Does a which-way measurement kick the particle? Young’s double-slit revisited.
![]() A. Karlsson, G. Björk and E. Forsberg; ’Interaction’ (Energy Exchange) Free and Quantum Nondemolition Measurement; Phys. Rev. Let. 80,6(1998)1198-1201.
A. Karlsson, G. Björk and E. Forsberg; ’Interaction’ (Energy Exchange) Free and Quantum Nondemolition Measurement; Phys. Rev. Let. 80,6(1998)1198-1201.
![]() J. Volz et al; Measurement of the internal state of a single atom without energy exchange; Nature 475 (2011) 210–213.
J. Volz et al; Measurement of the internal state of a single atom without energy exchange; Nature 475 (2011) 210–213.
![]() Propuesto en 1991, el experimento al parecer no ha sido todavía realizado; sin embargo, otros dispositivos con el mismo propósito sí han sido ya implementados, en el contexto de elección retardada con incorporación del denominado borrado cuántico:
Propuesto en 1991, el experimento al parecer no ha sido todavía realizado; sin embargo, otros dispositivos con el mismo propósito sí han sido ya implementados, en el contexto de elección retardada con incorporación del denominado borrado cuántico:
![]() S. P. Walborn et al; Borrado cuántico; Investigación y Ciencia, febrero 2004.
S. P. Walborn et al; Borrado cuántico; Investigación y Ciencia, febrero 2004.
![]() S. P. Walborn et al; A double-slit quantum eraser; ArXiv.
S. P. Walborn et al; A double-slit quantum eraser; ArXiv.
![]() Yoon-Ho Kim, R. Yu, S.P. Kulik, Y.H. Shih and Marlon O. Scully, A Delayed Choice Quantum Eraser; Phys.Rev.Lett. 84 1-5 (2000) 1-5; el artículo en ArXiv.org:http://xxx.lanl.gov/pdf/quant-ph/9903047.pdf.
Yoon-Ho Kim, R. Yu, S.P. Kulik, Y.H. Shih and Marlon O. Scully, A Delayed Choice Quantum Eraser; Phys.Rev.Lett. 84 1-5 (2000) 1-5; el artículo en ArXiv.org:http://xxx.lanl.gov/pdf/quant-ph/9903047.pdf.
-Excerpts: http://www.bottomlayer.com/bottom/kim-scully/kim-scully-web.htm
![]() Dos funciones de onda
Dos funciones de onda y
, con
, esto es, dos funciones de onda que difieran entre sí sólo en un factor de fase, proporcionan la misma densidad de probabilidad: son equivalentes. Ahora bien, a la hora de producir interferencias, las fases relativas entre funciones de onda sí son importantes y han de tenerse en cuenta.
-Por ejemplo: dadas dos funciones de onda y
, con
y
reales, su combinación lineal con coeficientes escalares arbitrarios
, complejos, representa otra función de onda
(por el principio de superposición, que rige debido a la linealidad del espacio), que proporciona la densidad de probabilidad
.
-El tercer sumando, que provoca que las distribuciones de probabilidad asociadas a las funciones que se suman no se sumen directamente, justifica los fenómenos observados de interferencia (por ejemplo, en el experimento de la doble rendija).
![]() Siempre que haya vías alternativas de realización de la misma observación experimental (caminos o procesos de Feynman) indistinguibles, la amplitud de probabilidad total
Siempre que haya vías alternativas de realización de la misma observación experimental (caminos o procesos de Feynman) indistinguibles, la amplitud de probabilidad total para el evento es la suma de las amplitudes de probabilidad para cada proceso,
, de forma que en el cálculo de la probabilidad del evento,
,
pueden ocurrir cancelaciones entre las amplitudes: aparecen interferencias.
![]() Pero si hay distinguibilidad entre las vías alternativas, entonces las probabilidades se suman directamente
Pero si hay distinguibilidad entre las vías alternativas, entonces las probabilidades se suman directamente
y desaparecen las interferencias entre las amplitudes.
![]() Considérese la pregunta:
Considérese la pregunta:
«¿Por qué rendija ha tenido lugar el paso?»
![]() Respuesta:
Respuesta:
«Sólo tienen sentido físico aquellas cuestiones que se contestan experimentalmente» (equivalentemente: «los experimentos no realizados no tienen resultados«).
Así que:
-Si los caminos son indistinguibles, la pregunta es metafísica.
-Interpretación ortodoxa: no tiene sentido afirmar que «aunque no pueda determinarse cuál es la rendija atravesada, cada partícula tiene que haber pasado por una sola de ellas».
-La teoría predice correctamente todos los resultados experimentales: !suficiente¡ (interpretación ortodoxa: instrumentalismo).
![]() Referencias interesantes:
Referencias interesantes:
![]() The two Slit Experiment
The two Slit Experiment
![]() Controlled double-slit electron diffraction
Controlled double-slit electron diffraction
Observaciones intermedias en una doble rendija
![]() Situaciones observacionales intermedias en un experimento de doble rendija:
Situaciones observacionales intermedias en un experimento de doble rendija:
-En un experimento de doble rendija se observan a la vez características ondulatorias y corpusculares: no se conoce al 100% la rendija atravesada, pero las probabilidades asociadas son diferentes, observándose simultáneamente una figura de interferencia, aunque no perfecta. Realizados para fotones y partículas materiales como neutrones y átomos.
![]() L.S. Bartell; Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behaviour; Phys. Rev. D21, 6 (1980) 1698-1699.
L.S. Bartell; Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behaviour; Phys. Rev. D21, 6 (1980) 1698-1699.
![]() D.M. Greenberger and A. Yasin; Simultaneous wave and particle knowledge in a neutron interferometer; Phys. Lett. A128 (1988) 391-394.
D.M. Greenberger and A. Yasin; Simultaneous wave and particle knowledge in a neutron interferometer; Phys. Lett. A128 (1988) 391-394.
![]() F. Bardou; Transition between particle behavior and wave behavior; Am. J. of Phys. 59 (1991) 458-461.
F. Bardou; Transition between particle behavior and wave behavior; Am. J. of Phys. 59 (1991) 458-461.
![]() Resumiendo:
Resumiendo:
-Las situaciones intermedias pueden comprobarse en un experimento de doble rendija con fotones, modificación de la versión original de Einstein que permite controlar el balance de exhibición de las características patrón-interferencia/which-way, utilizando como detector una placa fotográfica cuya distancia al plano de las dos rendijas puede variarse.
-Entre las dos situaciones extremos usuales, desde cero (detección perfecta de la rendija atravesada) hasta una distancia para la cual la interferencia es total (con un máximo central y franjas bien definidas), se pueden realizar todas las intermedias en las que, teniéndose dos máximos frente a las rendijas, también se observan franjas de interferencia. En estas disposiciones no se puede asegurar cuál es la rendija atravesada, pero sí, por ejemplo, que las probabilidades respectivas son 89% y 11%, mientras que se dispone de una observabilidad difuminada de las franjas interferenciales (véase Tabla I en Bardou, op. cit., p. 461).
![]() Como advierten los autores, las observaciones en ningún modo permiten afirmar que se da una transición entre onda y partícula para el paquete de ondas involucrado: la transición entre aspectos ondulatorios y corpusculares afecta a la descripción interpretativa del experimento en términos de estos conceptos clásicos.
Como advierten los autores, las observaciones en ningún modo permiten afirmar que se da una transición entre onda y partícula para el paquete de ondas involucrado: la transición entre aspectos ondulatorios y corpusculares afecta a la descripción interpretativa del experimento en términos de estos conceptos clásicos.
-Además, en estos experimentos, sobre un paquete de ondas, esto es, sobre un fotón individual, no se pueden observar a la vez las dos situaciones extremas onda y partícula, en acuerdo con el resultado tradicional.
-Una situación similar se manifiesta en experimentos de interferometría de neutrones, si se coloca un absorbente parcial en uno de los dos caminos. La probabilidad de que los neutrones finalmente detectados hayan recorrido el otro camino puede aproximarse a la unidad, sin que la interferencia desaparezca del todo. El conocimiento del carácter onda frente al carácter corpúsculo viene gobernado por un parámetro que puede variar de forma continua entre las dos situaciones extremas usuales, cf.:
![]() D.M. Greenberger and A. Yasin; «Simultaneous wave and particle knowledge in a neutron interferometer»; Phys. Lett. A128(1988)391-394.
D.M. Greenberger and A. Yasin; «Simultaneous wave and particle knowledge in a neutron interferometer»; Phys. Lett. A128(1988)391-394.
La dualidad interferométrica
![]() La dualidad onda-corpúsculo, considerada por Bohr como el componente fundamental del nuevo formalismo mecánico-cuántico, debe ser replanteada incorporando los resultados de determinados experimentos realizados en las últimas décadas del siglo XX.
La dualidad onda-corpúsculo, considerada por Bohr como el componente fundamental del nuevo formalismo mecánico-cuántico, debe ser replanteada incorporando los resultados de determinados experimentos realizados en las últimas décadas del siglo XX.
-El concepto de complementariedad en Bohr establece las características de exclusión mutua y compleción conjunta para dos descripciones (clásicas) de los objetos cuánticos, en una concepción que sufrió una evolución y replantaemiento constantes en Bohr, si bien no aparece nunca clara e inambigüamente desarrollada en su obra escrita.
![]() Tras la publicación del argumento Einstein-Podolsky-Rosen, la complementariedad inicial enunciada en el artículo seminal de 1927,
Tras la publicación del argumento Einstein-Podolsky-Rosen, la complementariedad inicial enunciada en el artículo seminal de 1927,
![]() N. Bohr; Das Quantenpostulat und die neuere Entwicklung der Atomistik; Die Naturwissensenschaften 16 (1928) 245-257; en inglés The Quantum Postulate and the Recent Development of the Atomic Theory, Nature 121 (1928) 580-590; también en [WHE-83], pp. 87-126,
N. Bohr; Das Quantenpostulat und die neuere Entwicklung der Atomistik; Die Naturwissensenschaften 16 (1928) 245-257; en inglés The Quantum Postulate and the Recent Development of the Atomic Theory, Nature 121 (1928) 580-590; también en [WHE-83], pp. 87-126,
es reinterpretada y pasa a referir no tanto a las descripciones de los objetos atómicos, sino a montajes experimentales incompatibles: la dualidad onda corpúsculo, o complementariedad onda-corpúsculo, podría expresarse afirmando que no puede montarse un dispositivo experimental en que se manifiesten a la vez los aspectos ondulatorio y corpuscular que, en un experimento de doble rendija, se corresponderían, respectivamente, con la determinación de la rendija atravesada y la observación de figura interferencial.
![]() En el formalismo actual de la mecánica cuántica, la complementariedad establece dos observables como complementarios cuando el conocimiento exacto de uno de ellos en un estado de un sistema físico (es decir: se ha realizado una medida que ha ofrecido un resultado preciso) implica que en dicho estado todos los valores posibles del otro son igualmente probables.
En el formalismo actual de la mecánica cuántica, la complementariedad establece dos observables como complementarios cuando el conocimiento exacto de uno de ellos en un estado de un sistema físico (es decir: se ha realizado una medida que ha ofrecido un resultado preciso) implica que en dicho estado todos los valores posibles del otro son igualmente probables.
![]() Este enunciado riguroso, que se desprende de la relación matemática de incompatibilidad o no conmutación entre los operadores autoadjuntos que representan a los correspondientes observables en el formalismo, convierte en problemática su extensión a dos conceptos clásicos -y sin representación en el formalismo matemático cuántico- como los denominados carácter ondulatorio y corpuscular de un fenómeno.
Este enunciado riguroso, que se desprende de la relación matemática de incompatibilidad o no conmutación entre los operadores autoadjuntos que representan a los correspondientes observables en el formalismo, convierte en problemática su extensión a dos conceptos clásicos -y sin representación en el formalismo matemático cuántico- como los denominados carácter ondulatorio y corpuscular de un fenómeno.
![]() B-G. Englert ha propuesto una desigualdad con la que formalizar matemáticamente, en el contexto de un experimento de doble rendija, la noción de dualidad onda-corpúsculo, es decir, el grado de compatibilidad entre la visión parcial de la figura de interferencia y el conocimiento parcial del camino seguido (welcher Weg o which-way information: qué camino):
B-G. Englert ha propuesto una desigualdad con la que formalizar matemáticamente, en el contexto de un experimento de doble rendija, la noción de dualidad onda-corpúsculo, es decir, el grado de compatibilidad entre la visión parcial de la figura de interferencia y el conocimiento parcial del camino seguido (welcher Weg o which-way information: qué camino):
![]() B-G. Englert; Fringe Visibility and Which-Way information: An inequality; Phys. Rev. Let. 77, 11 (1996) 2154-2157.
B-G. Englert; Fringe Visibility and Which-Way information: An inequality; Phys. Rev. Let. 77, 11 (1996) 2154-2157.
-Sus argumentos identifican, en un experimento de doble rendija y como es usual, “manifestación del carácter ondulatorio” con presencia de interferencias y “manifestación del carácter corpuscular” con determinación de la rendija atravesada y detección individualizada.
-En la deducción de la desigualdad propuesta, inspirada en las ideas previas de:
![]() W.K. Looters and W.H. Zurich, Phys. Rev. D19 (1979) 473-484.
W.K. Looters and W.H. Zurich, Phys. Rev. D19 (1979) 473-484.
![]() D.M. Greenberger and A. Yasin; Simultaneous wave and particle knowledge in a neutron interferometer; Phys. Lett. A128(1988)391-394.
D.M. Greenberger and A. Yasin; Simultaneous wave and particle knowledge in a neutron interferometer; Phys. Lett. A128(1988)391-394.
no interviene el principio de indeterminación, y la desigualdad, a la que denominan dualidad interferométrica, tiene la expresión final:
![]() P.D. Schwindt, P.G. Kwiat and B-G. Englert; Quantitative wave-particle duality and non-erasing quantum erasure; Phys. Rev. A60 (1999) 4285-4290.
P.D. Schwindt, P.G. Kwiat and B-G. Englert; Quantitative wave-particle duality and non-erasing quantum erasure; Phys. Rev. A60 (1999) 4285-4290.
![]() Y. Abranyos, M. Jacob and J. Bergou; Interference and partial which-way information: A quantitative test of duality in two-atom resonance; Phys. Rev. A61 (1999) 013804.
Y. Abranyos, M. Jacob and J. Bergou; Interference and partial which-way information: A quantitative test of duality in two-atom resonance; Phys. Rev. A61 (1999) 013804.
Desigualdad propuesta:
donde simboliza la distinguibilidad del camino a través del interferómetro, esto es, la información which-way disponible, y
la visibilidad de las franjas de interferencia.
-Los símbolos y
vienen definidos por expresiones matemáticas cuyos valores pueden medirse, esto es, obtenerse experimentalmente.
![]() Los dos valores extremos en la anterior desigualdad (es decir, los dos casos
Los dos valores extremos en la anterior desigualdad (es decir, los dos casos y
) se corresponderían con la complementariedad bohriana, garantizada en aquellos experimentos de interferencia en ésta se origina por la correlación establecida entre los estados del sistema que van a interferir y los estados del correspondiente aparato o dispositivo experimental de medida:
![]() A. Ray and D. Home, Phys. Lett. A178 (1993) 33-37.
A. Ray and D. Home, Phys. Lett. A178 (1993) 33-37.
![]() El rango intermedio de valores entre esos dos extremos corresponde a observaciones intermedias del carácter ondulatorio-corpuscular, como las antes indicadas.
El rango intermedio de valores entre esos dos extremos corresponde a observaciones intermedias del carácter ondulatorio-corpuscular, como las antes indicadas.
![]() G. Brida, M. Genovese, M. Gramegna and E. Predazzi; A conclusive experiment to throw more light on ‘light’; Phys. Let. A328 (2004) 313-318, p. 313:
G. Brida, M. Genovese, M. Gramegna and E. Predazzi; A conclusive experiment to throw more light on ‘light’; Phys. Let. A328 (2004) 313-318, p. 313:
![]() [La dualidad onda-partícula] must be understood between interference and “welcher Weg” knowledge and not in a more general sense.
[La dualidad onda-partícula] must be understood between interference and “welcher Weg” knowledge and not in a more general sense.
![]() The extensión of complementarity to classical concepts of waves and particle in every situation (including, also, for example tunnel effect or birefringence) is nevertheless not contended in the mathematical formalism of quantum mechanics (and no tested by interference experiments) and can be questioned.
The extensión of complementarity to classical concepts of waves and particle in every situation (including, also, for example tunnel effect or birefringence) is nevertheless not contended in the mathematical formalism of quantum mechanics (and no tested by interference experiments) and can be questioned.
De acuerdo con la definición general propuesta por Englert para dualidad:
![]() B-G. Englert; Fringe Visibility and Which-Way information: An inequality; Phys. Rev. Lett. 77,11 (1996) 2154-2157, p. 2154:
B-G. Englert; Fringe Visibility and Which-Way information: An inequality; Phys. Rev. Lett. 77,11 (1996) 2154-2157, p. 2154:
![]() The observation of an interference pattern and the acquisition of which-way information are mutually exclusive.
The observation of an interference pattern and the acquisition of which-way information are mutually exclusive.
-Pero también:
![]() Existen situaciones intermedias en que aspectos corpusculares y ondulatorios coexisten.
Existen situaciones intermedias en que aspectos corpusculares y ondulatorios coexisten.
![]() A. Zeilinger: la complementariedad onda-corpúsculo es un concepto continuo:
A. Zeilinger: la complementariedad onda-corpúsculo es un concepto continuo:
![]() A. Zeilinger; Experiments and quantum physics; Rev. Mod. Phys. 71, 2 (1999) S292.
A. Zeilinger; Experiments and quantum physics; Rev. Mod. Phys. 71, 2 (1999) S292.
![]() Wave–particle duality quantified for the first time
Wave–particle duality quantified for the first time
![]() Existen además otras clase de experimentos interferenciales en los que la información welcher-Weg puede obtenerse sin que se involucre la correlación indicada antes, de forma que la interferencia no se produce entre las funciones de onda en el espacio de configuración. En estos casos, es posible una determinación precisa del camino asignado para la realización del suceso experimental (información welcher-Weg disponible) sin que resulte afectado en absoluto el patrón interferencial observado:
Existen además otras clase de experimentos interferenciales en los que la información welcher-Weg puede obtenerse sin que se involucre la correlación indicada antes, de forma que la interferencia no se produce entre las funciones de onda en el espacio de configuración. En estos casos, es posible una determinación precisa del camino asignado para la realización del suceso experimental (información welcher-Weg disponible) sin que resulte afectado en absoluto el patrón interferencial observado:
![]() A. Ray, D.D. Leach, R. Vandenbosch, K.T. Lesko and D. Shapira; Phys. Rev. Lett. 57 (1986) 815.
A. Ray, D.D. Leach, R. Vandenbosch, K.T. Lesko and D. Shapira; Phys. Rev. Lett. 57 (1986) 815.
![]() Además, también se han realizado experimentos en los que los aspectos corpusculares y ondulatorios (¡terminología clásica!) se muestran plena y simultáneamente, incluso sobre un solo sistema individual, como por ejemplo en el experimento del doble prisma de Bose y otros experimentos más recientes en interferometría cuántica:
Además, también se han realizado experimentos en los que los aspectos corpusculares y ondulatorios (¡terminología clásica!) se muestran plena y simultáneamente, incluso sobre un solo sistema individual, como por ejemplo en el experimento del doble prisma de Bose y otros experimentos más recientes en interferometría cuántica:
![]() Observaciones duales en un solo experimento.
Observaciones duales en un solo experimento.
![]() En resumen:
En resumen:
-Los resultados experimentales, totalmente integrables en el formalismo matemático mecano-cuántico, fuerzan a abandonar la afirmación original de Bohr respecto a la mutua exclusión de aspectos ondulatorios y corpusculares… si es que se pretende su descripción en esos términos clásicos.
-Consecuentemente, el significado original de la dualidad onda corpúsculo, que incluye la mutua exclusión de las descripciones clásicas correspondientes, a la hora de interpretar un resultado experimental, debe incorporar la posibilidad de su simultaneidad, trasladándose la mutua exclusión al nuevo concepto de la dualidad interferométrica, que es un concepto continuo.
-La complementariedad y la dualidad onda-corpúsculo se convierten, pues, en conceptos independientes, mientras que es la dualidad interferométrica la que sigue constituyendo un ejemplo de complementariedad, la cual por otra parte, también es independiente de las posibles perturbaciones incontroladas producidas en el acto de medición.
![]() Nota sobre una famosa controversia (puede saltarse):
Nota sobre una famosa controversia (puede saltarse):
-Controvertido: La polémica en torno al experimento de Afshar: una supuesta violación de la dualidad interferómetrica:
![]() http://en.wikipedia.org/wiki/Afshar_experiment
http://en.wikipedia.org/wiki/Afshar_experiment
-Y la respuesta que le dieron Grangier et al:
![]() V Jacques, N D Lai, A Dréau, D Zheng, D Chauvat, F Treussart, P Grangier and J.-F. Roch; Illustration of quantum complementarity using single photons interfering on a grating:
V Jacques, N D Lai, A Dréau, D Zheng, D Chauvat, F Treussart, P Grangier and J.-F. Roch; Illustration of quantum complementarity using single photons interfering on a grating:
http://iopscience.iop.org/1367-2630/10/12/123009/pdf/1367-2630_10_12_123009.pdf
¿Onda o corpúsculo?: ![]()
- El formalismo cuántico es suficiente para predecir correctamente todos los resultados observados hasta la fecha (óptica cuántica, QED, operadores de campo eléctrico y magnético, etc.).
- Sólo el requerir una comprensión que incorpore imágenes o representaciones mentales subyugadas a las percepciones cotidianas hace aparecer términos conceptuales ontológicos (onda, partícula), sin relevancia de orden predictivo. De hecho, en la moderna Teoría Cuántica de Campos se prescinde por completo de esos términos en su significado clásico: las partículas se convierten en excitaciones de los campos cuánticos, y estos en los componentes ontológicos de la realidad (en opinión de muchos).
- Por ejemplo, en un experimento de doble rendija, es hora de cambiar narrativas del tipo «cada partícula pasa por las dos rendijas e interfiere consigo mismo”, sustituyéndolas por, en este ejemplo, «cuando los dos caminos son indistinguibles, las amplitudes de probabilidad asociadas a cada uno (las
) interfieren entre sí”.
- En palabras de Bohr: “Is absolutely meaningless to ask whether light is ‘in reality’ waves or particles. We must never forget that ‘reality’ too is a human word just like ‘wave’ or ‘consciousness’. Our task is to learn to use these words correctly –that is, unambiguosly and consistently” (Bohr, 1967, cit. por Kalckar en [WHE-85], p. 5).
- Ya lo advirtió Heisenberg: “…the concept of complementarity introduced by Bohr into the interpretation of quantum theory has encouraged the physicists to use an ambiguous rather than an unambiguous language, to use the classical concepts in a somehow vague manner…”
(Heisenberg, 1958, cit. en Ghose and Home, Wave-Particle Duality of Single-Photon States, Foundations of Physics, 22-12, 1992, p. 1446). - Y concluía: “...when this vague and unsystematic use of the language leads into difficulties, the physicist has to withdraw into the matehmatical scheme and its unambiguous correlation with the experimental facts” (cf. Heisenberg, 1958, ibid.)
El experimento de la doble rendija: realizaciones experimentales famosas
![]() http://www.hitachi.com/rd/portal/research/em/doubleslit.html
http://www.hitachi.com/rd/portal/research/em/doubleslit.html
![]() http://rdg.ext.hitachi.co.jp/rd/moviee/doubleslite-n.wmv
http://rdg.ext.hitachi.co.jp/rd/moviee/doubleslite-n.wmv
![]() http://www.youtube.com/watch?v=_oWRI-LwyC4
http://www.youtube.com/watch?v=_oWRI-LwyC4


Bibliografía
- [BEI-87] Beiser, A.; Concepts of Modern Physics, McGraw-Hill, Singapore, 1987.
- [ESP-76] Espagnat, B.D’; Conceptual Foundations of Quantum Mechanics, Benjamin, 1976.
- [FRE-85] French, A.P. and Kennedy, P.J.; Niels Bohr: a centenary volume, Harvard Univ. Press, 1985.
- [JAM-74] Jammer, M.; The philosophy of Quantum Mechanics, Wiley, 1974.
- [MEH-82] Mehra,J., Rechenberg,H.; The Historical Development of Quantum Mechanics, 6 vol., Springer-Verlag, Nueva York, 1982.
- [WHE-83] Wheeler, J.A. y Zurek,W.H., ed.; Quantum Theory and measurement, Princenton Univ., Princenton, 1983.
Referencias y páginas complementarias
![]() García Alcaine, G.; “Complementaridad, coherencia, dualidad”, Revista Española de Física 6,3 (1993) 8-9.
García Alcaine, G.; “Complementaridad, coherencia, dualidad”, Revista Española de Física 6,3 (1993) 8-9.
![]() Tonomura, A., Endo, J., Matsuda, T., Kawasaki, T. and Ezawa, H.; “Demonstration of single-electron buildup of an interference pattern,” American Journal of Physics 57, 1989, pp. 117-120.
Tonomura, A., Endo, J., Matsuda, T., Kawasaki, T. and Ezawa, H.; “Demonstration of single-electron buildup of an interference pattern,” American Journal of Physics 57, 1989, pp. 117-120.
![]() Cálculos en el experimento de Young
Cálculos en el experimento de Young
![]() http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a:216/College_Physics
http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a:216/College_Physics
![]() http://www.physics.ohio-state.edu/~aubrecht/Faculty.pdf
http://www.physics.ohio-state.edu/~aubrecht/Faculty.pdf
![]() APPS:
APPS:
http://demonstrations.wolfram.com/WaveParticleDualityInTheDoubleSlitExperiment/
![]() Updating the wave-particle duality
Updating the wave-particle duality
![]() Welcher-Weg experiments:
Welcher-Weg experiments:
![]() http://philsci-archive.pitt.edu/4114/1/welcher-weg-experiment_Busch-Jaeger_philsci.pdf
http://philsci-archive.pitt.edu/4114/1/welcher-weg-experiment_Busch-Jaeger_philsci.pdf
![]() Sen; Complementarity controversy in wave–particle duality revisited: http://www.ias.ac.in/pramana/v72/p765/fulltext.pdf
Sen; Complementarity controversy in wave–particle duality revisited: http://www.ias.ac.in/pramana/v72/p765/fulltext.pdf
![]() Noticias relacionadas:
Noticias relacionadas:
y su divulgación y análisis:
![]() http://www.physics.ohio-state.edu/~aubrecht/Faculty.pdf
http://www.physics.ohio-state.edu/~aubrecht/Faculty.pdf
![]() http://wdb.ugr.es/~bosca/InformacionCuantica/?tag=complementariedad
http://wdb.ugr.es/~bosca/InformacionCuantica/?tag=complementariedad
![]() http://la-mecanica-cuantica.blogspot.com.es/2009/08/ondas-de-materia.html
http://la-mecanica-cuantica.blogspot.com.es/2009/08/ondas-de-materia.html
Para mí la forma que se observa no se justifica en que lo estamos observando o midiendo, sino desde un punto de vista mas natural con la ampliación del rango de vista a nivel de enfoque y periférico
https://images.app.goo.gl/68cMHeUaY2wHzBDh7
Por lo tanto, el electrón sabe a dónde ir antes de pasar debido a que tiene una visión periférica ampliada, al momentos de medir con sensores se piensa que al observarlo nuevamente vuelve a la imagen de dos concentraciones de puntos, pero no es asi, sino, volvemos a limitar el rango y dirigimos al electrón.