El átomo de Hidrógeno

El átomo hidrogenoide

Consideremos un átomo hidrogenoide, esto es, un sistema atómico ligado formado por un núcleo con carga positiva $Ze$ ( $Z=1$ para el Hidrógeno) y un solo electrón cortical, de carga negativa $-e$ , interaccionando mutuamente a través del potencial central de Coulomb,
$V(\vec{r})=V(r=|\vec{r}_1 -\vec{r}_2|)= -\frac{1}{4\pi \epsilon_0}\frac{Ze^2}{r}$
(expresión en el sistema internacional de unidades, donde $\epsilon_0$ representa la constante dieléctrica del vacío).
El problema de dos cuerpos sometidos a una interacción dependiente sólo de sus posiciones mutuas se reduce a un problema de un cuerpo cuya masa es la reducida del sistema. En efecto, en el caso de dos partículas interaccionado bajo un potencial que sólo depende de sus posiciones, por simetría traslacional el potencial ha de ser de la forma particular $V(\vec{r}_1,\vec{r}_2)=V(\vec{r}=\vec{r}_1-\vec{r}_2)$ ,
por lo que conviene realizar la transformación canónica
$\left. \begin{array}{l} \vec{r}= \vec{r}_1 - \vec{r}_2 \\ \vec{R}=\frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1+m_2} \end{array} \right\}$ $\left. \begin{array}{l} \vec{p}=\frac{m_2 \vec{p}_1 - m_1 \vec{p}_2}{m_1+m_2} \\ \vec{P}= \vec{p}_1 + \vec{p}_2 \end{array} \right\}$
donde las variables $\vec{R}$ y $\vec{P}$ representan, respectivamente, la posición y momento del centro de masas de las dos partículas, mientras que $\vec{r}$ y $\vec{p}$ representan la posición y el momento relativos.
-El anterior cambio de variables permite abordar la resolución aplicando el método de separación de variables para ambas variables (relativa y c.d.m.) introducidas, de modo que se consigue reducir el estudio del problema de los dos cuerpos inicial a la resolución de la ecuación de Schrödinger independiente del tiempo para el movimiento relativo, de expresión:
$H_r \ \psi_{E_r}(\vec{r})\, = \, [ -\frac{\hbar^2}{2\mu} \nabla_{\mu}^2 + V(\vec{r}) ] \ \psi_{E_r}(\vec{r})\, = \,E_r \ \psi_{E_r}(\vec{r})\, = \,(E-E_R) \ \psi_{E_r}(\vec{r})$ ,
que da cuenta del movimiento relativo o intrínseco de las dos partículas y que representa un problema de un cuerpo: el movimiento en el seno del potencial $V(\vec{r})$ de una partícula de masa la reducida del sistema de las dos partículas,
$\mu=\frac{m_1 \cdot m_2 }{m_1 + m_2 }$ .
-La anterior ES es una ecuación de autovectores o valores propios, donde la función incógnita, la función $\psi_E(\vec{r})$ , se denomina función de onda independiente del tiempo.
La ecuación del movimiento del centro de masas
$H_R(\vec{R}) \ \phi_{E_R}(\vec{R} ) \,= \, -\frac{\hbar^2}{2M}\nabla_R^2 \ \phi_{E_R}(\vec{R} ) \, = \, E_R \ \phi_{E_R}(\vec{R} )$
no es sino la ecuación de Schrödinger para el movimiento de una partícula libre, cuyas soluciones son las ondas planas,
$\phi_{E_R}(\vec{R})\, = \, \frac{1}{(2 \pi \hbar)^{\frac{3}{2}}}\ e^{i \vec{P} \cdot \vec{R}/ \hbar}$ ,
$E_R \, = \, \frac{\vec{P}^2}{2M}$ ,
ecuación que describe el movimiento libre del centro de masas del sistema; $E_R$ representa la denominada como «energía del centro de masas». Eligiendo un sistema de referencia con origen en el centro de masas del sistema se anula el momento del centro de masas, $\vec{P}=0$ , lo que lleva a la identificación de la energía total con la energía relativa, $E_{Tot.} \equiv E= E_r$ , de forma que la solución de la ES del movimiento relativo proporciona, vía las autofunciones y autovalores aceptables físicamente, la descripción completa del sistema.

Resolución de la ecuación relativa por separación de variables

Dada la ecuación de Schrödinger para un potencial central,
$H\psi_E(\vec{r})=[-\frac{\hbar^2}{2\mu}\nabla^2+V(r)]\psi_E(\vec{r})=E\psi_E(\vec{r})$ ,
como consecuencia de la simetría esférica del potencial es posible diagonalizar simultáneamente el conjunto de operadores $\{ H,\vec{L}^2,L_z \}$ ; recuperando los resultados generales de la resolución en coordenadas esféricas y separación de variables en el caso de un potencial central (véase apartado 4 de la entrada de potenciales separables), se tiene que las autofunciones toman la expresión general
$\psi_{Elm}=R_{El}(r)Y_{lm}(\Omega)=\frac{1}{r}u_{El}(r)Y_{lm}(\Omega)$ ,
donde $Y_{lm}$ representa los armónicos esféricos y $R_{nl}(r)$ y $u_{nl}(r)$ son, respectivamente, las funciones radial y radial reducida, soluciones de las sendas ecuaciones diferenciales radial y radial reducida para el átomo hidrogenoide:
$\{ -\frac{\hbar^2}{2 \mu} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, - \, \frac{1}{4\pi \epsilon_0}\frac{Ze^2}{r}\ \} \, R_{El}(r) \, = \,E \, R_{El}(r)$
$H_l \ u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2\mu} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \, - \, \frac{1}{4\pi \epsilon_0}\frac{Ze^2}{r} \ \} \, u_{El}(r) \, = \,E \, u_{El}(r)$
$H_l \ u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2\mu} \ \frac{d^2}{d r^2} \, + \, V_{efl}(r) \ \} \, u_{El}(r) \, = \,E \, u_{El}(r)$
$\Rightarrow \{ \ \frac{d^2}{d r^2} \,+ \, \frac{2\mu}{\hbar^2} \ (E \ - \ V_{ef_l}(r) \ ) \ \} \ u_{El}(r)\, = \,0$ ,
donde el potencial efectivo en onda parcial $l$ tiene la forma:
$V_{ef_l}(r) \,=\, -\frac{1}{4\pi \epsilon_0} \frac{Ze^2}{r} \, + \, \frac{\hbar^2 l (l+1)}{2 \mu r^2}$ ,
un potencial efectivo que, para todas las ondas parciales, se anula a largas distancias:
$V_{+}=\lim_{r \rightarrow +\infty} V_{efl}(r) =0$ .
-Las figuras siguientes ilustran la forma de estos potenciales de onda parcial, que en el caso de $l=0$ no es sino la del potencial de Coulomb:

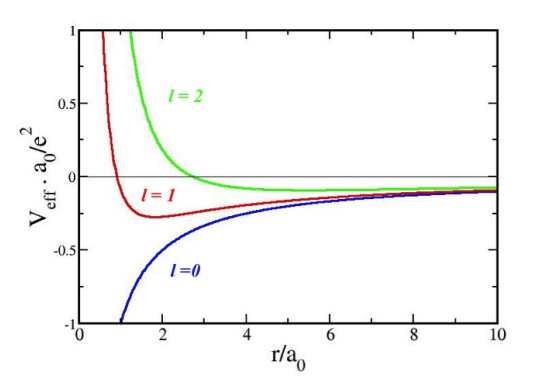
Primeros potenciales de onda parcial; $a_0$ representa el radio de Bohr.

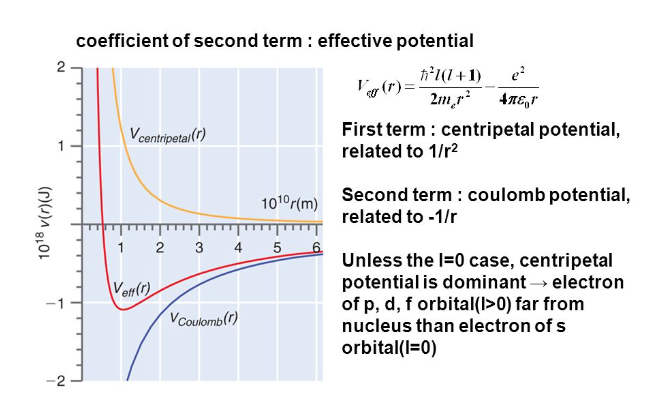
Potencial efectivo (fuente: Physics.Stackexchange.com).
Las soluciones buscadas, las autofunciones físicamente aceptables, han de satisfacer la condición de regularidad,
$u_{El}(0)\, = \, 0 \, , \, \forall l$ ,
con $u_{El}(r) \ \xrightarrow{r\rightarrow 0} \ 0$ más rápido que $r^l \xrightarrow{r\rightarrow 0} \ 0$ , ya que $R_{El}(r)=u(r)_{El} /r$ debe ser continua (finita) en el origen para todos los valores $l$ ; adicionalmente, los estados ligados (no así los de difusión) han de de cumplir también la condición de integrabilidad, que añadiendo la normalización a la unidad se expresa imponiendo:
$\int_0^{\infty} \ |u_{El} |^2 \ dr \, = \, 1$ .
En este caso, el espectro del correspondiente Hamiltoniano contendrá tanto parte continua como discreta, es decir, en la resolución se presentan dos casos:
a) Para los valores de energía $E>0$ , no existen estados ligados, sólo estados de difusión, correspondientes a valores que se integran en un espectro continuo, $\sigma_c(H)=(0,+\infty)$ , con autofunciones que presentan conducta oscilatoria a largas distancias y satisfacen la condición de regularidad pero no así la condición de integrabilidad. Estos estados se corresponden con un átomo disociado, es decir, cuando el electrón se ha alejado lo suficiente del núcleo como para que el sistema pase ser considerado como el de un ión hidrogenoide más un electrón libre.

Energía en términos de la distancia entre las dos partículas de un sistema atómico correspondiente a una molécula diatómica ( $H_2$ ).

b) Para los valores de energía $E<0$ , aparecen
estados ligados, constituyendo una parte discreta en el espectro, $\sigma_p(H) \subset (-\infty ,0)$ , con autofunciones que satisfacen tanto la condición de regularidad como la de integrabilidad.

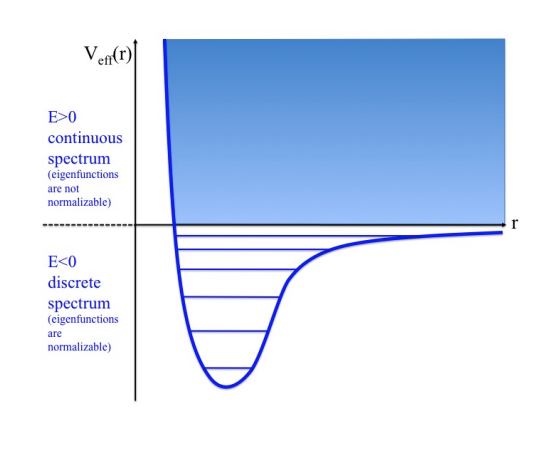
Espectro de energías en un átomo hidrogenoide (fuente: Cohen-Tannoudji, Chapter VII).

Estados ligados de un átomo hidrogenoide

La ecuación radial reducida del un átomo hidrogenoide es:
$H_l \ u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2\mu} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \, - \, \frac{1}{4\pi \epsilon_0}\frac{Ze^2}{r} \ \} \, u_{El}(r) \, = \,E \, u_{El}(r)$ ,
y buscamos las autofunciones de energía correspondientes a estados ligados, esto es, $-\infty < E < 0$ ( $\sigma_p(H) \subset (-\infty,o)$ ).
-Nota: una buena referencia para la resolución de este tipo de EDO y las funciones especiales que aparecen es: E. D. Rainville, Intermediate Differential Equations, Chelsea Pub. Co.; N.Y., 1972 (ref. [RAI-72]).
Realizando en la anterior EDO radial reducida el cambio de variable independiente
$\rho \, = \, (-\frac{8 \mu \ E}{\hbar^2})^{\frac{1}{2}} \ r \, = \, (+\frac{8 \mu \ |E|}{\hbar^2})^{\frac{1}{2}} \ r \quad , \quad (E<0)$ ,
e introduciendo el cambio de parámetro energético,
$\lambda \,=\, \frac{Ze^2}{(4\pi \epsilon_0)\hbar} (-\frac{\mu}{2E})^{\frac{1}{2}} \,=\, Z\alpha (-\frac{\mu c^2}{2E})^{\frac{1}{2}} \,=\, Z\alpha (+\frac{\mu c^2}{2|E|})^{\frac{1}{2}}$ ,
donde $\alpha$ es la constante de estructura fina, $\alpha \approx 1/137.035999084$ , adimensional,
$\alpha=\frac{e^2}{4\pi \epsilon_0 \hbar c} \approx \frac{1}{137}$ ,
se obtiene la nueva ecuación
$[\ \frac{d^2}{d \rho^2} \, - \, \frac{l(l+1)}{\rho^2} \, + \, \frac{\lambda}{\rho} \, - \,\frac{1}{4} \ \} \, u_{El}(\rho) \, = \, 0$ .
-Esta última ecuación nos proporciona a largas distancias el siguiente comportamiento asintótico: si $\rho \rightarrow +\infty$ , la ecuación en el límite se transforma a:
$[\ \frac{d^2}{d \rho^2} \, - \, \frac{1}{4} \ \} \, u_{El}(\rho) \, = \, 0$ ;
puesto que la EDO lineal homogénea $u'' - k^2u=0 \, , \, k \in \mathbb{R} \, , \, k>0$ tiene por solución general la combinación lineal de soluciones particulares $u(r)=C_1 \ e^{\frac{\rho}{2}} + C_2\ e^{-\frac{\rho}{2}}$ , con $C_1,C_2$ escalares arbitrarios, es obvio que para conseguir el comportamiento correcto a largas distancias, la acotación, se ha de seleccionar la solución particular que cumple
$u_{El}(\rho) \, \xrightarrow{\rho \rightarrow \infty} \ \sim e^{- \frac{\rho}{2}}$ .
En consecuencia, el comportamiento asintótico a largas distancias sugiere el primer cambio de función incógnita en la EDO
$u_{El}(\rho) \, = \, e^{- \frac{\rho}{2}} \ f_{El}(\rho)$ ,
tras el cual se obtiene la nueva EDO
$\{ \ \frac{d^2}{d \rho^2} \, - \, \frac{d}{d \rho} \, + \,[ \frac{\lambda}{ \rho} - \frac{l(l+1)}{\rho^2} ) \ ] \ \} \ f_{El}(\rho) \, = \, 0$ .
-Se trata de una ecuación diferencial con una singularidad regular en el origen y otra irregular en el punto del infinito. En el límite de las pequeñas distancias, si calculamos la ecuación indicial de la anterior EDO, $c^2 + (p_o-1)c + q_0=0$ , obtenemos:
$\left. \begin{array}{l} f_{El}''(\rho) - f_{El}'(\rho) + [ \frac{\lambda}{ \rho} - \frac{l(l+1)}{\rho^2} ] \} \ f_{El}(\rho) \, = \, 0 \\ \equiv f_{El}''(\rho) \, + \, p(\rho) \ f_{El}'(\rho)\, + \, q(\rho) \ f_{El}(\rho)\, = \, 0 \end{array} \right\}$
$\left. \begin{array}{l} p(\rho) = -1 \quad \text{anali'tica en} \quad \rho=0 \\ q(\rho) = \frac{\lambda}{ \rho}-\frac{l(l+1)}{\rho^2} \quad \text{polo doble en} \quad \rho=0 \end{array} \right\}$
$\Rightarrow \left\{ \begin{array}{l} p_0 \, = \, \lim_{\rho \rightarrow 0} \ \rho \ p(\rho) \, = \, 0 \\ q_0 =\lim_{\rho \rightarrow 0} \ \rho^2 \ q(\rho)\ = \ -l(l+1) \end{array} \right\} \Rightarrow c^2 - c -l(l+1)=0$
$\Rightarrow \left\{ \begin{array}{l} c=l+1 \rightarrow u_{El}(\rho)= \sum_k a_k\ \rho^{k+l+1} \quad \text{anali'tica en} \quad \rho=0\\ c=-l \rightarrow u_{El}(\rho)= \sum_k a_k\ \rho^{k-l} \quad \text{no anali'tica en} \quad \rho=0 \end{array} \right\}$ ,
lo que ahora lleva a seleccionar la solución regular en el origen, de comportamiento asintótico
$f_{El}(\rho) \, \xrightarrow{\rho \rightarrow 0} \, \rho^{l+1}$ .
La conducta asintótica a cortas distancias sugiere pues el nuevo cambio de función incógnita en la EDO
$f(\rho)\, = \, \rho^{l+1} \ g(\rho)$ ,
que produce finalmente una EDO hipergeométrica confluente:
$\{ \rho \ \frac{d^2}{d \rho^2} \, + \, (2l+2 \ - \ \rho \ ) \ \frac{d}{d \rho} \, + \, ( \ \lambda -l +1 \ ) \ \} \ g_{El}(\rho) \, = \, 0$ ,
siendo la solución regular en el origen la siguiente:
$g(\rho) \, = \, C \ M(l + 1 - \lambda,2l+2; \rho)$ ,
donde $C$ es una constante arbitraria y $M(a,b;z)$ representa la función hipergeométrica confluente.
Nota: La ecuación hipergeométrica confluente, o ecuación de Kummer-Laplace, de expresión general (véase [ABR] cap. 13, p. 504ss.):
$z\frac{d^2 \omega}{d z} + (c-z)\frac{d \omega}{d z} - a\omega=0$ ,
es una ecuación que posee dos singularidades, una regular en el origen y otra irregular en el infinito, obtenida a partir de la EDO fuchsiana general con sólo tres singularidades regulares en los puntos complejos $z=0$ , $z=b$ y $z=\infty$ , de expresión
$z(1-\frac{z}{b}) \ y'' +[(c-z) -\frac{(a+1)}{b}z ] \ y' -a \ y=0$ ,
mediante la confluencia de singularidades $b \rightarrow \infty$ .
-La resolución por series en torno al origen de la ecuación hipergeométrica confluente permite obtener su solución general, de expresión
$\omega(z)\, = \, C_1 \ M(a,c;z) \, + \, C_2 \ z^{1-c} \ M(1+a-c,2-c;z) \quad , \quad 0 < |z| < \infty$ ,
donde $C_1, C_2$ son constante arbitrarias; $M(a,c;z) \equiv _1F_1(a,c:z)$ es la función hipergeométrica confluente; las dos soluciones particulares son válidas, respectivamente, para:
a) solución $C_1 \ M(a,c;z)$ : validez en $|z| < \infty$ si y sólo si $c \ne 0 \,, \, c$ distinto de entero negativo;
b) solución $C_2 \ z^{1-c} \ M(1+a-c,2-c;z)$ : validez en $0 <|z| < \infty$ si y sólo si $c \ne 2 \,,\, c$ distinto de entero positivo.
-La función hipergeométrica confluente o función de Kummer se expresa:
$M(a,c;z)\, = \, 1 \, + \, \sum_{k=1}^{\infty} \ \frac{(a)_k z^k}{k! (c)_k} \quad |z| < \infty \quad, \quad c \ne 0 \,, \, c$ distinto de entero negativo.
–Estas funciones poseen numerosas aplicaciones en Física.
Las autofunciones de energía de los estados ligados de un átomo, además de satisfacer la condición de regularidad, deben ser normalizables en sentido estándar, esto es, pertenecer al Hilbert (espacio de las funciones de cuadrado integrable Lebesgue en la especificación funcional usual). Puesto que el comportamiento asintótico a largas distancias de la función hipergeométrica confluente es
$M(a,c;x) \, \xrightarrow{x \rightarrow \infty} \, x^{a-c} \ e^x$
$\Rightarrow M( l + 1 - \lambda,2l+2; \rho )\, \xrightarrow{\rho \rightarrow \infty} \, \rho^{ -l - \lambda -1 } \ e^{\rho}$ ,
se infiere que para evitar la divergencia de la solución hay que cortar la serie: sólo cuando conste de un número finito de términos la integrabilidad requerida de la solución se satisfará. Surge por tanto del formalismo matemático la
condición de cuantización: sólo para algunos valores de la energía, parámetro $E$ , habrá estado ligado: cuando se satisfaga:
$l + 1 - \lambda \, = \, -n_r \quad , \quad n_r=0,1,2\ldots$ ,
$\Rightarrow n \equiv \lambda \, = \, n_r + l + 1 \quad , \quad n=1,2\ldots$
$\leftrightarrow \quad n=l+1,l+2 \ldots \quad \leftrightarrow \quad l=0,1,2, \ldots , n-1$ ,
siendo $n_r$ el número cuántico denominado como el número cuántico radial , mientras que $n$ representa el número cuántico principal.
La condición de cuantización de la energía permite obtener los correspondientes autovalores o niveles de energía ligados para un átomo hidrogenoide:
$n \, = \, \lambda \, = \, \frac{Ze^2}{4\pi \epsilon_0 \hbar} (-\frac{\mu}{2E})^{\frac{1}{2}}$
$\Rightarrow E\equiv E_{n} \, = \, (\frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ (-\frac{\mu}{2}) \ \frac{1}{n^2} \,=\, -\frac{e^2}{4\pi \epsilon_0} \ \frac{1}{a_0} \ \frac{\mu}{m} \ \frac{Z^2}{2} \ \frac{1}{n^2}$
$=\,(Z\alpha)^2 \ (-\frac{1}{2}\mu c^2) \ \frac{1}{n^2} \quad , \quad n=1,2\ldots$ ,
que en unidades atómicas se expresa como
$E_n \, = \, \frac{Z^2}{2} \ \frac{\mu}{m} \ \frac{1}{n^2} \quad , \quad n=1,2\ldots$ ,
donde $m$ es la masa del electrón; $\mu$ , su masa reducida; $c$ la velocidad de la luz en el vacío y $a_0$ el radio de Bohr,
$a_0 \, = \, \frac{4\pi \epsilon_0 \hbar^2}{m e^2} \, = \, \frac{\hbar}{m (\alpha c)}$
que reducido (corrección de masa reducida) se expresa como:
$a_{\mu} \, = \, \frac{4\pi \epsilon_0 \hbar^2}{\mu e^2} \, = \, a_0 \ \frac{m}{\mu}\, = \, \frac{\hbar}{\mu (\alpha c)}$ ;
el parámetro $\alpha$ es la constante de estructura fina, $\alpha \approx 1/137.035999084$ (valor 2018), adimensional,
$\alpha=\frac{e^2}{4\pi \epsilon_0 \hbar c} \approx \frac{1}{137}$ .
-El estado fundamental o estado más bajo en energía del átomo de Hidrógeno, $Z=1$ , resulta ser (en la aproximación hecha):
$E_{GS} \equiv E_0\, = \, E_{n=1} \, = \, -13,6 \ eV \quad (-\frac{1}{2} \ u.a.)$ .
-Esquema de niveles de energía en este estadio del estudio: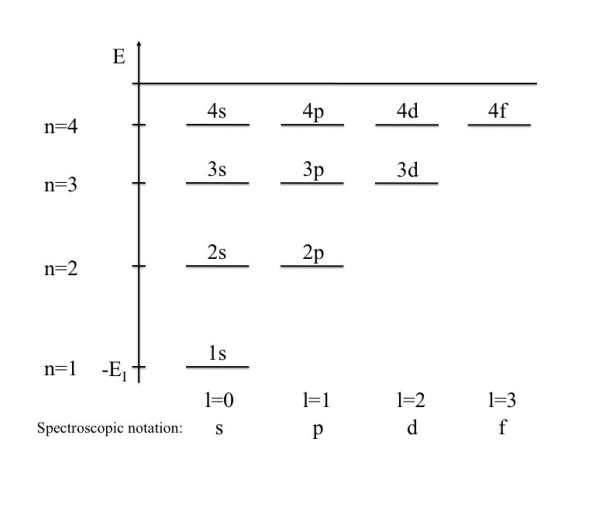

Niveles de energía en un átomo hidrogenoide(fuente: <a href=»http://www.thphys.nuim.ie/Notes/MP364/MP364_Ch2.pdf» target=»_blank» rel=»noopener»>Cohen-Tannoudji, Chapter VII</a>).
Degeneración energética: la energía de cada autoestado ligado, en el nivel de aproximación a que se ha realizado hasta aquí el cálculo, ha venido a depender sólo del número cuántico principal. Es por tanto evidente que los niveles de energía $E_n$ calculados tendrán una degeneración dada por la fórmula:
$D(E_n) \equiv D(n) \, = \, \sum_{l=0}^{n-1} \ (2l+1) \, = \, \frac{1+2(n-1)+1}{2} \ n \, = \, n^2$
-Al hecho de que, a este nivel de cálculo, la energía no dependa del número cuántico de momento angular orbital, $l$ , se le denomina como degeneración accidental, específica para sistemas como los atómicos hidrogenoideos (átomos con un solo electrón: el Hidrógeno y la serie de iones $He^{+}$ , $Li^{2+}$ …, mientras que al hecho de que no dependa del número cuántico de tercera componente de momento angular orbital, $m$ , o número cuántico magnético, se le denomina como degeneración bajo rotaciones, común para todos los potenciales centrales.
La estructura de niveles de energía, o espectro ligado, de un átomo hidrogenoide que hemos determinado se suele denominar como estructura gruesa, correspondiente al estudio asociado a la expresión del Hamiltoniano:
$H=H_0=-\frac{\hbar^2}{2\mu}\nabla^2+V(r)$ ,
donde $V(r)$ representa el potencial culombiano de interacción entre el núcleo atómico y el electrón. El siguiente paso en el estudio corresponde a incorporar en el problema el espín y las correcciones relativistas, lo que provocará una primera ruptura de la degeneración energética y hará surgir la denominada como estructura fina del espectro. El cálculo se puede desarrollar bien resolviendo la ecuación de Dirac para un electrón en un potencial central, bien recurriendo a métodos aproximados, como la teoría de perturbaciones.
-Un estudio perturbativo se realiza incorporando al anterior Hamiltoniano los términos adicionales:
a) Corrección relativista a la energía cinética:
$H_1=-\frac{p^4}{8m^3c^2}$
b) Interacción espín-órbita:
$H_2=\frac{1}{2m^2c^2} \ \frac{1}{r} \ \frac{dV(r)}{dr} \ \vec{L} \cdot \vec{S}$
c) Término de Darwin:
$H_3=\frac{\pi \hbar^2}{2m^2c^2} \ (\frac{Ze^2}{4 \pi \epsilon_0}) \ \delta(\vec{r})$
-La siguiente figura ilustra el efecto que este estudio tiene sobre el nivel $n=2$ :

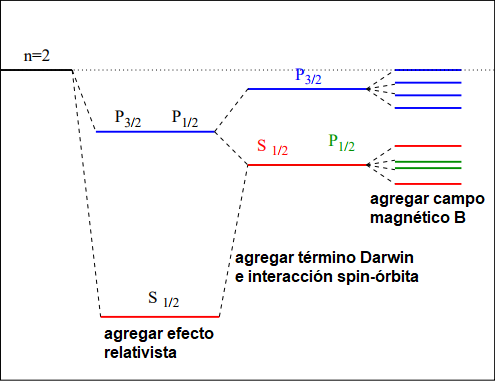
Estructura fina del nivel n=2 del átomo de Hidrógeno (fuente: https://la-mecanica-cuantica.blogspot.com/2009/08/la-estructura-fina-del-hidrogeno.html).
Relaciones, valores y significado de los distintos números cuánticos manejados:
$\left\{ \begin{array}{l} n_r \, = \, n - l -1 \; , \quad n_r=0,1,2\ldots \; , \quad n_r < n \\ n = n_r+l+1= \lambda \; , \quad n=1,2,3\ldots \, (capas \, K,L,M \ldots) \; , \quad n > n_r \, , \, n > l \\ l \, = \, n- n_r -1 \; , \quad l=0,1,2, \ldots , n-1 \ (s,p,d \ldots) \; , \quad l < n \\ m \, = \, 0, \pm 1 , \pm 2 , \ldots , \pm l \end{array} \right\}$
La notación usual para las tríadas de valores $n,l,m$ , que caracterizan cada orbital, es: $nl_m$ (para átomos de más de un electrón, se añade el número de electrones en cada orbital como supraíndice). El valor de $n$ identifica la capa; el par de valores $n,l$ , la subcapa; $n,l,m$ , el orbital.
-Nota: obsérvese que, a diferencia de lo que ocurre en el caso del oscilador armónico tridimensional, ha aparecido una restricción sobre el valor del número cuántico de momento angular orbital $l$ respecto al número cuántico principal: NO puede ser $l \ge n$ .
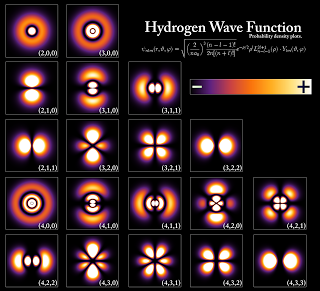
Algunas propiedades (puede consultarse la referencia «átomo de Hidrógeno» para una serie de figuras simples de las primeras funciones):
-Para los orbitales $s \, (l=0)$ , el número cuántico radial $n_r=n-l-1=n-1$ se corresponde con el número de nodos o ceros de la función radial $R_{n_r0}(r)$ en $(0,\infty)$ (a los que se añade el nodo en el punto del infinito). Estas funciones radiales, ondas $s$ , no se anulan en el origen.
-Las funciones radiales de los orbitales $2p$ , $(n=2,l=1)$ , carecen de nodos en $(0,\infty)$ ; poseen nodos en el origen y en el punto del infinito.
-El número de nodos radiales de las funciones $R_{np}$ en $(0,\infty)$ viene dado por $n-l-1$ ; se anulan en el origen y en el punto del infinito.
-En general: el número de nodos de las funciones radiales $R_{nl}$ , o nodos radiales, definidos como aquellos puntos en que la función cambia de signo, esto es, en $(0,\infty)$ , viene dado por $n-l-1$ .
-Cuando $l \ne 0$ , se tiene la dependencia funcional $R_{nl} \approx r^l$ , entrando en acción la barrera centrífuga, que actúa contra el acercamiento del electrón al núcleo atómico. Por contra, $R_{ns}(0) \ne 0$ .
-La carga electrónica se concentra en la región comprendida entre los dos últimos ceros de la función $R_{nl}(r)$ . Cuando $n$ aumenta; así lo hace también el radio de la distribución de carga eléctrica; en el límite $n \rightarrow \infty$ , el átomo se ioniza: toda la carga eléctrica se sitúa a distancia infinita del núcleo.
-Dado un valor de $n_r$ , sea $l=l_{max.}=n_r=n-1$ y sea la función $D_{n,l}=|rR_{nl}|^2=|u_{nl}(r)|^2$ , entonces:
$D_{n,l=n-1}(r) \approx r^{2n} \ e^{-\frac{2Zr}{na_{\mu}}}$
$\Rightarrow \frac{d \ D_{n,n-1}}{dr}=0=(2nr^{2n-1}-\frac{2Z}{na_{\mu}}r^{2n})\ e^{-\frac{2Zr}{na_{\mu}}} \Rightarrow r=\frac{n^2 a_{\mu}}{Z}$ ,
que para $n=1$ y $Z=1$ se convierte en el radior de Bohr reducido, $a_{\mu}$ , que es pues el valor más probable de $r$ en el estado $R_{10}$ (¡distinto del valor medio o esperado $< r >_{10}$ !).
Autofunciones normalizadas de energía: Una vez normalizadas, las autofunciones de energía de un átomo hidrogenoide tienen la expresión general:
$\psi_{nlm}(\vec{r}) \, = \, N_{nl} \ R_{nl}(r) \ Y_{lm}(\Omega) \, = \,N_{nl} \ \frac{1}{r} \ u_{nl}(r) \ Y_{lm}(\Omega)$
$= \, N_{nl} \ (-\frac{8 \mu \ E_n}{\hbar^2})^{\frac{1}{2}} \ \frac{1}{\rho} \ \rho^{l+1} \ e^{-\frac{\rho}{2}} \ M(l+1-n,2l+2;\rho) \ Y_{lm}(\theta,\varphi)$ ,
donde
$\rho = (-\frac{8 \mu \ E_n}{\hbar^2})^{\frac{1}{2}}\ r=br \quad , \quad E_n < 0$
$b=\frac{2Z}{na_{\mu}}=\frac{2Z}{na_0}\frac{\mu}{m} \quad , \quad E_n=(\frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ (-\frac{\mu}{2}) \ \frac{1}{n^2}$ ;
el parámetro $m$ es la masa del electrón y $\mu$ su masa reducida; $M(a,c;x)$ representa la correspondiente función hipergeométrica confluente y $N_{nl}$ es la correspondiente constante de normalización, de expresión
$|N_{nl}|^2\, = \, b \ \frac{(2l+1)_{n-l-1}^2}{2 \ (n-l-1)! (n+l)! \ n!}$
$\Rightarrow N_{nl}\, = \, [ \ \frac{2Z\mu}{na_0m} \ \frac{(2l+1)_{n-l-1}^2}{2 \ (n-l-1)! (n+l)! \ n!} ]^{\frac{1}{2}}$
salvo fase.
-Se obtiene así la expresión final de las autofunciones normalizadas de energía para un átomo hidrogenoide:
$\psi_{nlm}(\vec{r}) \, = \, [ \ \frac{2Z\mu}{na_0m} \ \frac{(2l+1)_{n-l-1}^2}{2 \ (n-l-1)! (n+l)! \ n!} ]^{\frac{1}{2}} \ (-\frac{8 \mu \ E_n}{\hbar^2})^{\frac{1}{2}} \ \frac{1}{\rho} \ \rho^{l+1}$
$e^{-\frac{\rho}{2}} \ M(l+1-n,2l+2;\rho)\ Y_{lm}(\theta,\varphi)$ .
La expresión también puede darse en términos de los polinomios generalizados de Laguerre ([GAL-89] , I, ap. A, pp. 378-380), haciendo uso de la relación
$M(-m,k+1;\rho)\, = \, \frac{m!}{(k+1)_m} \ L_{m}^{k}(\rho)$
$\Rightarrow M(l+1-n,2l+2;\rho=br) \, = \, L_{n-l-1}^{2l+1}(br)\ \frac{(n-l-1)!}{(2l+1)_{n-l-1}}$
obteniéndose:
$\psi_{nlm}(\vec{r}) \, = \, \frac{2} {n^2} \ (\frac{Z}{a_{\mu}})^{\frac{3}{2}} \ [\frac{(n-l-1)!}{(n+l)!}]^{\frac{1}{2}} \ (\frac{2 Z r}{n a_{\mu}})^l \ e^{-\frac{Z}{na_{\mu}}r} \ L_{n-l-1}^{2l+1}(\frac{2 Z r}{n a_{\mu}})\ Y_{lm}(\theta,\varphi)$ ,
donde $a_{\mu}$ representa el radio de Bohr reducido,
$a_{\mu}= a_0\frac{m}{\mu}$ .
-Nota: el símbolo $(a)_n$ representa la función factorial generalizada, $(a)_n=a(a+1)(a+2) \ldots (a+n-1)$
(por ejemplo: $n!\equiv (1)_n$ ).
-Algunas expresiones y propiedades para los polinomios generalizados de Laguerre:
$L_{n}^{k}(x)=\sum_{r=0}^{n} \frac{(-1)^r (n+k)!}{(n-r)! (k+r)! r!} x^r$
$L_{n}^{k}(x)=\frac{e^x}{n! x^k} \frac{d^n}{dx^n} (x^{n+k} e^{-x})$ (fórmula de Rodrigues)
$L_0^k(x)=1$
$L_1^1(x)=2-x \quad ; \quad L_2^1(x)=3-3x + \frac{1}{2}x^2$
$L_1^3(x)=4-x \quad ; \quad L_3^1(x)=4-6x + 2x^2 - \frac{1}{6}x^3$
$L_2^3(x)=10-5x + \frac{1}{2}x^2 \quad ; \quad L_1^5(x)=6-x$
Paridad: La paridad de las autofunciones ligadas del átomo hidrogenoide la marcan los armónicos esféricos, es decir, la proporciona el factor $(-1)^l$ . De modo que la paridad de cada estado de energía $E_n$ depende del valor del número cuántico de momento angular orbital.
Expresiones matemáticas de las primeras funciones radiales normalizadas y los primeros orbitales:
$\psi_{nlm}(\vec{r}) \, = \, R_{nl}^{(norm.)}(r) \ Y_{lm}(\theta,\varphi)$
$R_{nl}^{(norm.)}(r) \, = \, [ \ \frac{2Z\mu}{na_0m} \ \frac{(2l+1)_{n-l-1}^2}{2 \ (n-l-1)! (n+l)! \ n!} ]^{\frac{1}{2}} \ (-\frac{8 \mu \ E_n}{\hbar^2})^{\frac{1}{2}} \ \frac{1}{\rho} \ \rho^{l+1}$
$e^{-\frac{\rho}{2}} \ M(l+1-n,2l+2;\rho)$
$= \, \frac{2} {n^2} \ (\frac{Z}{a_{\mu}})^{\frac{3}{2}} \ [\frac{(n-l-1)!}{(n+l)!}]^{\frac{1}{2}} \ (\frac{2 Z r}{n a_{\mu}})^l \ e^{-\frac{Z}{na_{\mu}}r} \ L_{n-l-1}^{2l+1}(\frac{2 Z r}{n a_{\mu}})$ ;
las primeras funciones radiales normalizadas se proporcionan a continuación:

Primeras funciones radiales hidrogenoides (véase archivo de V. Luaña en las páginas complementarias).

Primeros orbitales hidrogenoides (véase archivo de V. Luaña en las páginas complementarias).

-Orbitales s en el átomo de Hidrógeno (figura de: Aron):

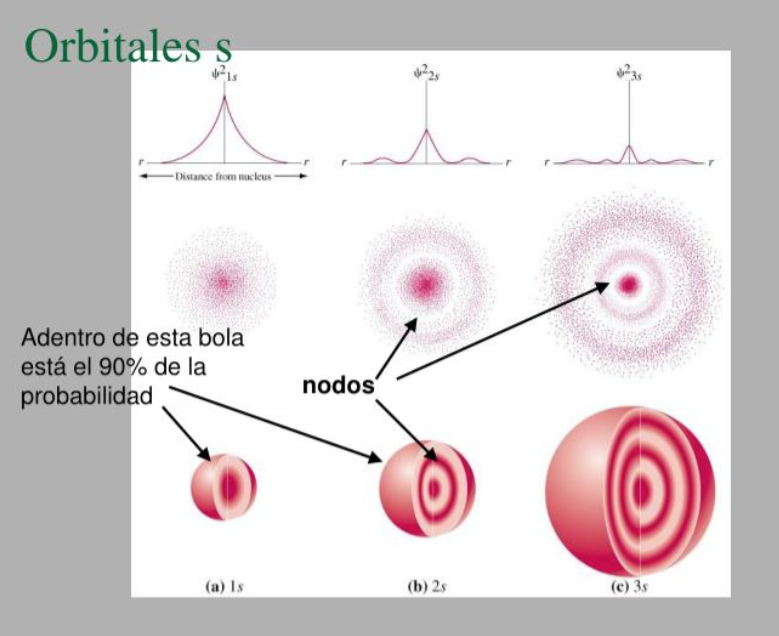
-Orbitales p en el átomo de Hidrógeno (figura de: Aron):
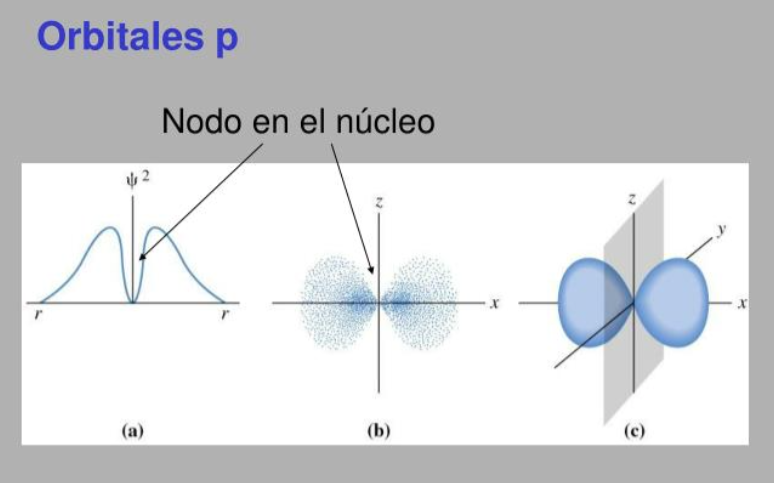-La siguiente figura ilustra las primeras funciones radiales del átomo de Hidrógeno: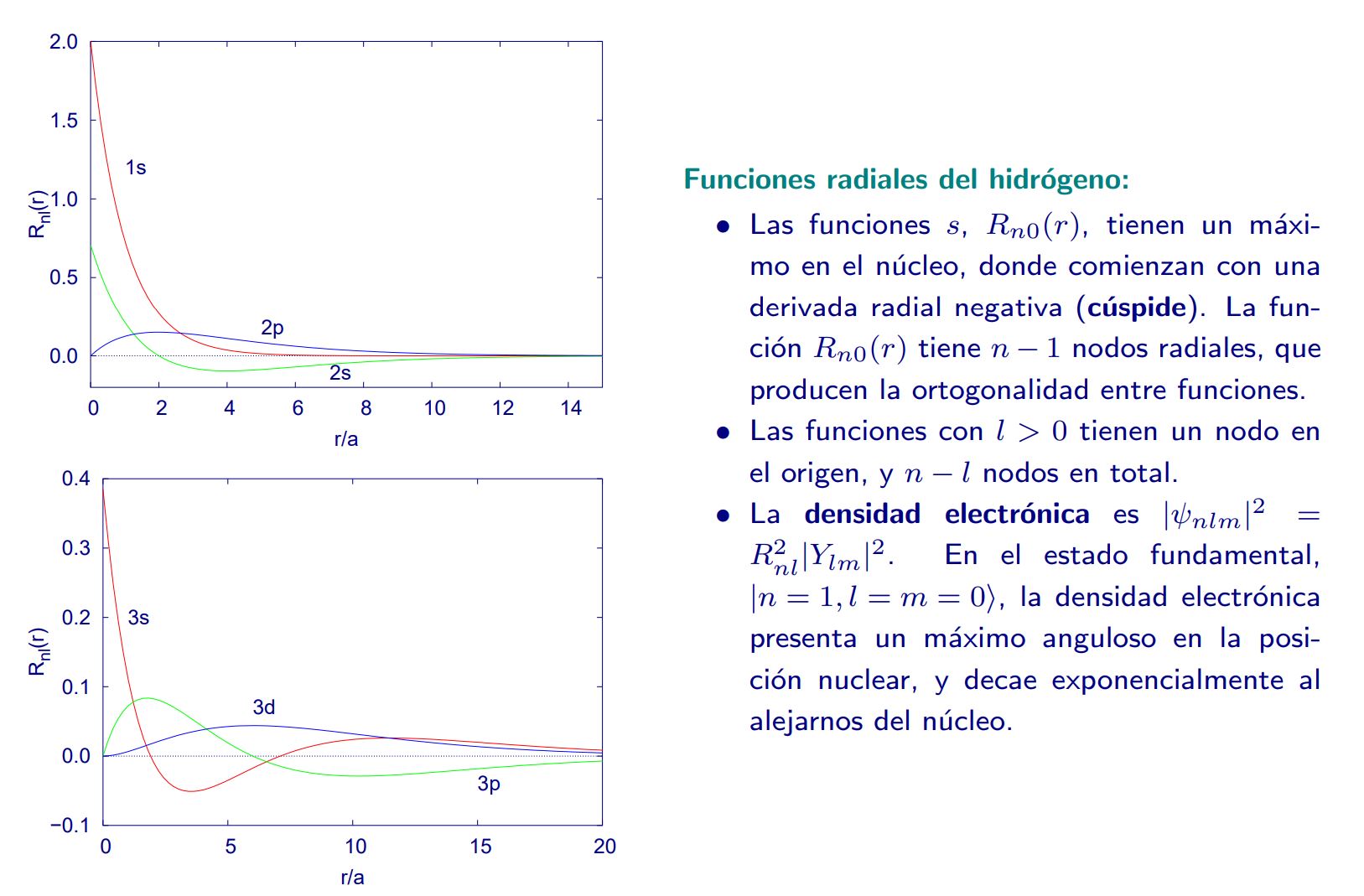

Primeras funciones radiales del átomo de Hidrógeno (véase archivo de V. Luaña en las páginas complementarias).
Densidades de probabilidad: Para una discusión muy interesante sobre las densidades de probabilidad asociadas a los primeros orbitales, funciones $|\psi_{nlm}|^2$ , acompañada de variadas ilustraciones, puede consultarse el archivo de J.J. Borrás:
https://www.uv.es/borrasj/EQEM_web_page/temas/tema_2/tema/tema_2_parte_II_red.pdf
Valor medio de las potencias de $|\hat{\vec{r}}|$ :
$< r^p >_{nl}=a^p \ I_{nl}^{(p)}$ ,
donde el símbolo $I_{nl}^{(p)}$ representa la siguiente integral de orden $p$ :
$I_{nl}^{(p)} \doteq \frac{n^{p-1}}{2^{p+1}} \frac{(n-l-1)!}{(n+l)!} \ \int_0^{+\infty} x^{2l+p+2} e^{-x} [L_{n-l-1}^{2l+1}(x)]^2 dx$ ,
la cual satisface la «relación de Kramers» (cf. [GAL-89] I, Ap. A, p. 380):
$\frac{p+1}{n^2}I_{nl}^{(p)} - (2p+1) I_{nl}^{(p-1)} + \frac{p}{4} [(2l+1)^2-p^2] I_{nl}^{(p-2)}=0 \quad ; \; p > -(2l+1)$ .
-Ejemplos:
$I_{nl}^{(p=0)}=1 \quad ; \quad I_{nl}^{(p=-1)}= \frac{1}{n^2} \quad ; \quad I_{nl}^{(p=-2)}= \frac{2}{(2l+1)n^3}$
$I_{nl}^{(p=1)}= \frac{1}{2} [3n^2 - l(l+1)] \quad ; \quad I_{nl}^{(p=2)}= \frac{n^2}{2} [5n^2 + 1 -3l(l+1)]$ ,
que permiten calcular la serie de valores medios:
$< r >_{nl}=a^{-1} I_{nl}^{(p=1)}= \frac{a}{2}[3n^2 - l(l+1)]$
$< r^{-1} >_{nl}=a^{-1} I_{nl}^{(p=-1)}= \frac{1}{an^2}$
$< r^{2} >_{nl}=a^{2} I_{nl}^{(p=2)}= \frac{a^2n^2}{2}[5n^2 + 1 -3l(l+1)]$
$< r^{-2} >_{nl}=a^{-2} I_{nl}^{(p=-2)}= \frac{1}{n^3a^2}\frac{1}{(l+\frac{1}{2})}$
$< r^{-3} >_{nl}=a^{-3} I_{nl}^{(p=-3)}= \frac{1}{a^3}\frac{1}{l(l+\frac{1}{2})(l+1)} \quad , \; l \ge 1$ .

El átomo hidrogenoide con interacción espín-órbita de coeficiente constante

Tomemos como punto de partida un átomo hidrogenoide, esto es, un sistema atómico ligado formado por un núcleo con carga positiva $Ze$ ( $Z=1$ para el Hidrógeno) y un solo electrón cortical, de carga negativa $-e$ , interaccionando mutuamente a través del potencial central de Coulomb, problema cuya resolución ha proporcionado la estructura de niveles de energía, o espectro ligado, denominada como estructura gruesa, correspondiente al estudio asociado a la expresión del Hamiltoniano:
$H=H_0=-\frac{\hbar^2}{2\mu}\nabla_r^2 -\frac{ Ze^2}{4\pi \epsilon_0 r}$ .
Sea ahora el problema de resolver la ecuación de Schrödinger independiente del tiempo con el Hamiltoniano
$H=H_0 + \alpha \ \vec{l} \cdot \vec{s} =-\frac{\hbar^2}{2\mu}\nabla_r^2 - \frac{ Ze^2}{4\pi \epsilon_0 r} + \alpha \ \vec{l} \cdot \vec{s}$ ,
donde se ha añadido un término de interacción espín-órbita adicional, con un coeficiente $\alpha$ constante, Hamiltoniano que puede expresarse como:
$H=-\frac{\hbar^2}{2\mu}\nabla_r^2 - \frac{ Ze^2}{4\pi \epsilon_0 r} + \frac{1}{2} \ \alpha \ (\vec{j}^2 - \vec{l}^2 - \vec{s}^2)$
en términos del momento angular total $\vec{j}=\vec{l} + \vec{s}$ .
Por la estructura separada en variables del Hamiltoniano, $H=H_1(r) + H_2(\theta, \varphi , \sigma)$ , las soluciones físicamente aceptables del correspondiente problema de autovalores tendrán la expresión:
$\psi_{Elsjm_j}(\vec{r}) = R_E(r) \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi;\sigma)$ ,
en términos de los armónicos esféricos vectoriales, o autofunciones angulares de espín, integrantes de la base acoplada en el correspondiente Hilbert, integrada por autofunciones simultáneas de los cuatro operadores $\vec{l}^2,\vec{s}^2,\vec{j}^2, j_z$ :
$\{ | l\, s \, j\, m_j > \}_{j \,;\,m_j=-j,-j+1,\ldots,j}$ , para cada valor posible de $j$ fijados el par $l,s$ ,
usándose también las notaciones alternativas en representación de posiciones:
$| l\, s \, j\, m_j > \, \rightarrow \, <\hat{r} \, | \,l\, s \, j\, m_j > \, \equiv \, \psi_{l s j m_j}(\hat{r}) \, \doteq \, \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi;\sigma)$
El problema de autovalores a resolver toma pues la expresión:
$H \ R_E(r) \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi , \sigma) = E \ R_E(r) \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi , \sigma)$
-Sustituyendo la expresión del Hamiltoniano y resolviendo:
$H \ R_E(r) \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi , \sigma) = [-\frac{\hbar^2}{2\mu}\nabla_r^2 - \frac{ Ze^2}{4\pi \epsilon_0 r} + \alpha \ \vec{l} \cdot \vec{s}] \ R_E(r) \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi , \sigma)$
$= [-\frac{\hbar^2}{2\mu}\nabla_r^2 - \frac{ Ze^2}{4\pi \epsilon_0 r} + \alpha \ \vec{l} \cdot \vec{s}] \ R_E(r) \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi , \sigma)$
$= \{ -\frac{\hbar^2}{2\mu} [\frac{1}{r^2} [ \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2} ] ] - \frac{ Ze^2}{4\pi \epsilon_0 r} + \frac{1}{2} \ \alpha \ (\vec{j}^2 - \vec{l}^2 - \vec{s}^2) \}\ R_E \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi , \sigma)$
$= E \ R_E(r) \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi , \sigma)$ ;
dividiendo ambos lados de la ecuación por la solución no trivial $\mathcal{Y}$ , y simplificando, se obtiene la EDO (ecuación diferencial ordinaria) para la función incógnita $R_E(r)$ :
$-\frac{\hbar^2}{2\mu r^2} \ \frac{d}{d r}(r^2 \ \frac{d R_E}{d r} ) \, + \, \frac{\hbar^2 l (l+1) }{ 2\mu r^2} \ R_E -\frac{ Ze^2}{4\pi \epsilon_0 r} \ R_E$
$= \, \{ E \, - \, \frac{\alpha \hbar^2}{2} \ [(j(j+1) - l(l+1) - s(s+1)] \} \ R_E$ ,
o ecuación diferencial radial para un átomo hidrogenoide con una interacción espin-órbita con coeficiente constante.
-Si comparamos esta ecuación con la correspondiente al Hamiltoniano de estructura gruesa $H_0$ , vemos que la ecuación radial es la misma, sin más que una modificación en el autovalor de energía, que ahora tiene la expresión modificada $E'(H_0)$ :
$E (H_0) \ \leftrightarrow E'(H_0)=E (H) \, - \, \frac{\alpha \hbar^2}{2} \ [(j(j+1) - l(l+1) - s(s+1)]$ .
Se obtienen pues los autovalores de energía ligados:

.
-Sustituyendo , como fijado hay dos posibilidades para , y , resulta la siguiente estructura de niveles ligados:
1. Caso $l=0$ : $j=s=\frac{1}{2}$ :
  $E_{n0j=\frac{1}{2}} \ = \ - \frac{\mu}{2} \ ( \frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ \frac{1}{n^2}$
2. Caso $l \ne 0$ : $j=l \pm \frac{1}{2}$ :
  A: $j=l + \frac{1}{2} \doteq j_+$ :
  $E_{nlj_+} \ = \ - \frac{\mu}{2} \ ( \frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ \frac{1}{n^2}$
  $+ \frac{\alpha \hbar^2}{2} \ [(j_+(j_++1) - l( l + 1) - \frac{1}{2}(\frac{1}{2}+1)]$
  $= \ - \frac{\mu}{2}\ ( \frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ \frac{1}{n^2} + \frac{\alpha \hbar^2}{2} \ l$
  B: $j=l - \frac{1}{2} \doteq j_-$ :
  $E_{nlj_-} \ = \ - \frac{\mu}{2} \ ( \frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ \frac{1}{n^2}$
  $+ \frac{\alpha \hbar^2}{2} \ [(j_-(j_-+1) -l (l + 1) - \frac{1}{2}(\frac{1}{2}+1)]$
  $= \ - \frac{\mu}{2}\ ( \frac{Ze^2}{4\pi \epsilon_0 \hbar})^{2} \ \frac{1}{n^2} - \frac{\alpha \hbar^2}{2} \ (l+1)$
-Obsérvese que los autovalores o energías de los estado ligados sólo dependen de $j$ , o $l$ , pero son diferentes para un mismo valor de $j$ (o sea, de un mismo valor $l \ge 1$ ), según sea $j=l+\frac{1}{2}$ o $j=l -\frac{1}{2}$ .
-La siguiente figura proporciona un esquema (¡no a escala energética real!) de los niveles del átomo hidrogenoide con y sin el término adicional de interacción espín-órbita (para el caso de coeficiente $\alpha$ constante):
$\left\{ \begin{array}{l} \cdots \\ \xrightarrow{E_{n}= -\frac{13,6}{n^2} \ eV \ , \ d=2n^2} \\ \cdots \\\xrightarrow{E_{n=3}= -1,51 \ eV \ , \ d=18}\\ \xrightarrow{E_{n=2}= -3,4 \ eV \ , \ d=8} \\ \xrightarrow[(H_0)]{E_{n=1}= -13,6 \ eV \ , \ d=2} \end{array} \right\} \longmapsto \left\{ \begin{array}{l} \cdots \\ \xrightarrow{E_{nlj}= (-\frac{13,6}{n^2} + \Delta E_{j(l)})\ eV \ , \ d} \\ \cdots \\ \xrightarrow{E_{n=3l=2 j=\frac{5}{2}}= (-1,51 -\alpha \hbar^2) \ eV \ , \ d=6}\\ \xrightarrow{E_{n=3l=2 j=\frac{3}{2}}= (-1,51 -\alpha \frac{3\hbar^2}{2}) \ eV \ , \ d=4}\\ \xrightarrow{E_{n=3l=1 j=\frac{3}{2}}= (-1,51 +\alpha \frac{\hbar^2}{2}) \ eV \ , \ d=4}\\ \xrightarrow{E_{n=3l=1 j=\frac{1}{2}}= (-1,51 -\alpha \hbar^2) \ eV \ , \ d=2}\\ \xrightarrow{E_{n=3l=0 j=\frac{1}{2}}= -1,51 \ eV \ , \ d=2}\\ \xrightarrow{E_{n=2l=0 j=\frac{1}{2}}= -3,4 \ eV \ , \ d=2} \\ \xrightarrow{E_{n=2l=1 j=\frac{3}{2}}= (-3,4+\alpha \frac{\hbar^2}{2}) \ eV \ , \ d=4} \\ \xrightarrow{E_{n=2l=1 j=\frac{1}{2}}= (-3,4-\alpha \hbar^2) \ eV \ , \ d=2} \\ \xrightarrow[(H_0+\alpha \vec{l} \cdot \vec{s})]{E_{n=1l=0j=\frac{1}{2}}= -13,6 \ eV \ , \ d=2}\end{array} \right\}$
Respecto a las autofunciones, basta recordar la expresión de los estados de la base acoplada vía los coeficientes de Clebsch-Gordon:
,
de modo que a partir de la tabla de coeficientes, la parte angular-espín o acoplada, incorporando las autofunciones de espín , se expresa como:
1. Caso $l=0$ :
  $\mathcal{Y}_{0 \ \frac{1}{2}}^{\frac{1}{2} \ m_j} \, =\,Y_{00} \ \chi_{ \frac{1}{2} \ m_j } \ \delta_{m_j, +\frac{1}{2} } \,+ \,Y_{00} \ \chi_{ \frac{1}{2} \ m_j }\ \delta_{m_j, -\frac{1}{2} }$
2. Caso $l \ne 0$ :
  $\mathcal{Y}_{l \ \frac{1}{2}}^{j \ m_j} \, =\,\sum_{m_l, m_s= \pm \frac{1}{2}} \, C(l\,\frac{1}{2}\,j\,|\,m_l\,m_s\,m_j)\, Y_{l \ m_l} \cdot \chi_{\frac{1}{2} \ m_s}$
  $=\,C(l\,\frac{1}{2}\,j\,|\,m_j - \frac{1}{2} \,\frac{1}{2} \, m_j)\,Y_{l \ m_j-\frac{1}{2}} \cdot \chi_{\frac{1}{2} \ \frac{1}{2}}$
  $+ \, C(l\,\frac{1}{2}\,j\,|\,m_j + \frac{1}{2} \,-\frac{1}{2} \, m_j)\,Y_{l \ m_j+\frac{1}{2}} \cdot \chi_{\frac{1}{2} \ -\frac{1}{2}}$
  $\Rightarrow \,\mathcal{Y}_{l \ \frac{1}{2}}^{l \pm \frac{1}{2} \ m_j} \, =\, \pm \sqrt{ \frac{l \pm m_j+\frac{1}{2}}{2l+1}} \,Y_{l \ m_j-\frac{1}{2}} \cdot \chi_{\frac{1}{2} \ \frac{1}{2}} \, + \,\sqrt{ \frac{l \mp m_j+\frac{1}{2}}{2l+1}} \,Y_{l \ m_j+\frac{1}{2}} \cdot \chi_{\frac{1}{2} \ -\frac{1}{2}}$ ,
  esto es, el espinor:
  $\mathcal{Y}_{l \ \frac{1}{2}}^{l \pm \frac{1}{2} \ m_j}\,\doteq \, \begin{pmatrix} \pm \sqrt{ \frac{l \pm m_j+\frac{1}{2}}{2l+1}} \,Y_{l \ m_j-\frac{1}{2}} \\ \sqrt{\frac{l \mp m_j+\frac{1}{2}}{2l+1}} \,Y_{l \ m_j+\frac{1}{2}} \end{pmatrix}$
-Estas funciones han de ser multiplicadas cada una por su correspondiente parte radial, según la ecuación:
$\psi_{Elsjm_j}(\vec{r}) = R_{E}(r) \ \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi;\sigma)$

Referencias

[ABR-65] Abramowitz, Milton; Stegun, Irene A., eds.; “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables”; Dover; New York, 1965; ISBN 978-0-486-61272-0.

[BAL-98] Ballentine, L.E.; “Quantum Mechanics: A Modern Development”; World Scientific; Singapore, 1998.

[BER-18] Berman, P.R.; “ Introductory Quantum Mechanics: ”; Springer, 2018; https://doi.org/10.1007/978-3-319-68598-4_10.

[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.

[BRA-06] Bransden, B.H. and Joachain, C.J.; «Physics of Atoms & Molecules»; Longman, New York, 1983 (2nd ed.: Pearson; Dorchester, 2000).

[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.

[NEU-91] Neumann, J. von; «Fundamentos matemáticos de la Mecánica Cuántica», CSIC, Raycar, Madrid, 1991.

[RAI-72] Rainville, E.D., «Intermediate Differential Equations», Chelsea Pub. Co.; N.Y., 1972.

[SCH-68] Schiff, L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.

Páginas complementarias

La función de onda radial en el blog lamecanicacuantica.blogspot.com
Estructura electrónica del átomo, archivo de la Universidad de Valencia: https://www.uv.es/borrasj/EQEM_web_page/temas/tema_2/tema/tema_2_parte_II_red.pdf
Problemas de dos partículas con solución analítica, un archivo de V. Luaña: https://ocw.uniovi.es/pluginfile.php/3237/mod_resource/content/1/slides2009-L03.pdf
NIST Digital Library of Mathematical Functions
La función hipergeométrica confluente:
-en Wolfram mathworld: https://mathworld.wolfram.com/ConfluentHypergeometricFunctionoftheFirstKind.html
-en la Wikipedia: https://en.wikipedia.org/wiki/Confluent_hypergeometric_function
Las funciones asociadas de Laguerre:
-en Wolfram mathworld: https://mathworld.wolfram.com/AssociatedLaguerrePolynomial.html
-en la Wikipedia: https://en.wikipedia.org/wiki/Laguerre_polynomials#Generalized_Laguerre_polynomials
Hydrogen Atom demostrations en Wolfram:
–Hydrogen Atom Radial Functions
–Hydrogen Atom: Fine Structure of Energy Levels
–hydrogen atomic spectrum
Applet which displays the wave functions (orbitals) of the hydrogen atom, by Paul Falstad: https://www.falstad.com/qmatom/
Hydrogen Atom Orbital Explorer, St. Olaf college: https://chemapps.stolaf.edu/jmol/unplugged/orbitals.htm

Ana María Gómez
21/06/2024 a las 19:27

tengo 13 años y escribo este comentario en este artículo por qué es el más nuevo en esta página web y por ende puede que alguien me responda a esta duda que tengo y sé que puede que nadie me responda pero es el único lugar donde puedo preguntar y dónde pueda que me respondan.
Sé que el mayor problema del cálculo en la teoría de cuerdas es, en resumen, la combinación de su complejidad matemática extrema, la falta de predicciones experimentales directas y la dificultad para unificar todas las fuerzas fundamentales en una teoría coherente y comprobable y mi pregunta va de La acción de Polyakov q es una formulación en la teoría de cuerdas que proporciona una manera conveniente de describir la dinámica de las cuerdas y ps esta acción se escribe en términos del mundo-hoja de la cuerda, que es la superficie bidimensional barrida por la cuerda al moverse en el espacio-tiempo

Y mis cálculos fueron:
– $ \alpha’ $ es la constante de Regge (relacionada con la tensión de la cuerda),
– $ \sigma^a $ (con $a, b = 0, 1$) son las coordenadas del mundo-hoja,
– $ h_{ab} $ es la métrica inducida en el mundo-hoja,
– $ X^\mu $ (con $ \mu = 0, 1, …, D-1 $) son las coordenadas de la cuerda en el espacio-tiempo de $ D $ dimensiones,
– $ \sqrt{-h} $ es la raíz cuadrada del determinante de la métrica $ h_{ab} $,
– $ h^{ab} $ es la métrica inversa de $ h_{ab} $,
– $ \partial_a $ denote la derivada parcial con respecto a $ \sigma^a $.

Para obtener las ecuaciones de movimiento a partir de la acción de Polyakov, utilize el principio de mínima acción, es decir, varie la acción con respecto a las variables $ X^\mu $ y $ h_{ab} $ y establece que la variación debe ser cero. Variación con respecto a $ X^\mu $

La variación de la acción con respecto a $ X^\mu $ medio las ecuaciones de movimiento:

\[ \partial_a (\sqrt{-h} h^{ab} \partial_b X^\mu) = 0. \]

Estas son las ecuaciones de onda bidimensionales para las coordenadas $ X^\mu $.

Variación con respecto a $ h_{ab} $

La variación de la acción con respecto a la métrica $ h_{ab} $ medio esto, que nos da las ecuaciones de movimiento que aseguran la conformidad de la teoría:

\[ T_{ab} = \partial_a X^\mu \partial_b X_\mu – \frac{1}{2} h_{ab} h^{cd} \partial_c X^\mu \partial_d X_\mu = 0. \]

(Quiero saber si hice el cálculo bien? Ojalá me entienda las notaciones, fue la única manera de representar los cálculos)

Responder

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

El átomo de Hidrógeno

1 comentario

Dejar una contestacion Cancelar la respuesta