Transformaciones unitarias de simetría y leyes de conservación

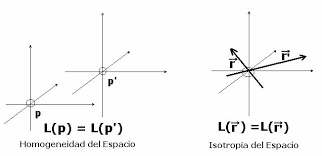
Las simetrías

Del Diccionario de la RAE:
La simetría es una propiedad del mundo natural tal y como lo percibimos, y es el hecho que su conceptualización matemática vertebra la estructura que la Física contemporánea modela para el Universo: existe una conexión entre las propiedades de simetría de un sistema y la leyes de conservación fundamentales en física para determinadas magnitudes físicas («observables»).
Por ejemplo:
-Asumamos que el espacio es homogéneo, esto es, presenta simetría translacional. La conclusión es que el momento lineal de un sistema aislado no cambia con los desplazamientos del sistema, lo que permite separar el movimiento en los correspondientes al centro de masas del sistema, de un lado, y el interno o intrínseco del mismo, del otro.
-Asumamos que el espacio es isótropo, esto es, posee simetría rotacional. Se implica entonces que el momento angular de un sistema aislado se mantendrá constante.
Se denominan simetrías geométricas las asociadas al desplazamiento de un sistema físico en el espacio-tiempo, o sea, con sus traslaciones, rotaciones y reflexiones o inversiones espaciales, y con la inversión temporal o cambio de sentido de la progresión temporal.
-Existen otros tipos de simetrías, como las dinámicas que provocan degeneración de los niveles de energía en determinados sistemas, como el átomo de hidrógeno o el oscilador armónico isotrópico; las simetrías en moléculas, cristales…; las que aparecen en Relatividad; las asociadas a permutaciones de partículas indistinguibles…
Consideradas dos clases de transformaciones unitarias en particular:
1. Las transformaciones unitarias (operadores lineales y unitarios) que efectúan cambios entre representaciones, esto es, producen rotaciones en el espacio de Hilbert, cambios de base, sin alterar los vectores ket o vectores estado.
2. Las transformaciones unitarias (en general, pero la inversión temporal en particular será antiunitaria: operador antilineal y unitario) que consisten en una rotación generalizada en el correspondiente espacio de Hilbert, que transforma el ket sin que se realice un cambio de ejes (base) asociado. Por ejemplo, la transformación que proporciona la evolución temporal de un sistema físico (operador unitario $U(t, t_o)$ ).
-Son las de este segundo tipo las que constituyen el objeto de esta entrada.
Existen dos «puntos de vista» a adoptar en su estudio:
1. El «activo»: se deja invariante el sistema de ejes en el espacio de coordenadas y se transforma el sistema.
2. El «pasivo»: se deja el estado invariante y se transforman los ejes de coordenadas.
Ambas formalizaciones son equivalentes: por ejemplo, se puede en una translación espacial dada por un vector $\vec{a}$ bien hacer esa translación sobre el sistema, bien realizar la translación $\vec{-a}$ sobre los ejes. En ambos casos, las nuevas coordenadas del sistema serán $\vec{r'}=\vec{r} + \vec{a}$ .
-En estos apuntes, se adoptará el activo, aunque en algunas deducciones se partirá del segundo (el pasivo, conviene mencionarlo, es frecuente en el estudio de las transformaciones de Lorentz homogéneas y, en general, cuando se prima el estudio del movimiento relativo, interviniendo dos observadores en movimiento mutuo).

Concepto matemático de transformación de simetría

(Cf. [GAL-89], p. 323ss.) Sea un sistema físico y sea $\mathcal{H}$ el espacio de Hilbert (coherente) asociado. Se denomina «transformación de simetría» $S$ en el espacio de Hilbert $\mathcal{H}$ , asociado a la descripción de un sistema físico en mecánica cuántica, a toda aplicación que establezca una correspondencia biyectiva entre los distintos rayos unidad del Hilbert, $| \psi >_R \subset \mathcal{H}$ , transformando entre sí rayos correspondientes a estados puros físicamente realizables y conservando sus probabilidades de transición:
$| \Psi >_R \xrightarrow{S} | \Psi' >_R \ \equiv \ S \ | \Psi >_R$ ,
conservándose los productos escalares:
$_R \left\langle \Phi | \Psi \right\rangle_{R} = _R \left\langle \Phi ' | \Psi ' \right\rangle_{R}$ ,
donde
$| \Phi' >_R = S \ | \Phi >_R\quad , \quad | \Psi' >_R = S \ | \Psi >_R$
y el producto escalar entre rayos unidad se define según:
$_R \left\langle \Phi | \Psi \right\rangle_{R} = | \left\langle \phi | \psi \right\rangle | \quad , \quad | \phi > \, \in \, | \Phi >_R$ y $| \psi > \, \in \, | \Psi >_R$ .
-Nota: un rayo unidad $\left|\Psi(t)\right\rangle_R \subset \mathcal{H}$ , se define como un conjunto de vectores de norma unidad, integrado por diferentes vectores de estado o kets $\left| \psi(t) \right\rangle \in \mathcal{H}$ que difieren entre sí únicamente en factores de fase (un factor de fase es un escalar de norma unidad).
El Hilbert se supone coherente:
-se asume la validez del principio de superposición sin restricciones y una correspondencia biunívoca entre los vectores ket del Hilbert y los estados puros del sistema, y entre los observables de este y los operadores autoadjuntos sobre el espacio.
Teorema 1: Todo operador unitario (un isomorfismo isométrico, $UU^+=U^+U=I$ ) o antiunitario que transforma vectores estado entre sí define una transformación de simetría S.
Teorema 2 (Wigner): Toda transformación de simetría S es implementable por un operador $U_S$ unitario (o antiunitario), único salvo fase, teniéndose:
$\left\langle \psi' | \varphi' \right\rangle = \left\langle \psi | \varphi \right\rangle$ , si $U_S$ es unitario, y
$\left\langle \psi' | \varphi' \right\rangle = \left\langle \psi | \varphi \right\rangle ^*$ , si $U_S$ es antiunitario,
donde:
$| \psi > \, \in \, | \psi >_R \, , \, | \psi' > \, \in \, | \psi' >_R$ , con $| \psi' > = U_S | \psi >$ ,
$| \varphi > \, \in \, | \varphi >_R \, , \, | \varphi' > \, \in \, | \varphi' >_R$ , con $| \varphi' > = U_S | \varphi >$ .
Dados un operador lineal $A: \mathcal{H} \rightarrow \mathcal{H}$ y una transformación de simetría $U_S$ en $\mathcal{H}$ , los vectores estado se transforman bajo $U_S$ según:
$U_S: \mathcal{H} \rightarrow \mathcal{H} \; : \; | \psi' > = U_S| \psi >$ ,
mientras que el operador se transforma según la definición:
$\left\langle \psi' | A' | \varphi' \right\rangle = \left\langle \psi | A | \psi \right\rangle \quad \forall \; | \varphi > \, , \, | \psi > \in \mathcal{H}$ ,
derivándose pues:
$\left\langle \psi' | A' | \varphi' \right\rangle = \left\langle U_S\psi | A' | U_S \varphi \right\rangle = \left\langle \psi | A | \varphi \right\rangle \quad \forall | \varphi > \, , \, | \psi > \in \mathcal{H}$ ,
$\Rightarrow A = U_S^+ A' U_S \quad ,\quad A' = U_S A U_S^+$ .
Propiedades (¡ya que $U_S$ es unitario!):
-Si $| \psi> = \sum_n \,c_n \, | \phi_n>$ , entonces $| \psi'> = \sum_n \, c_n'| \phi_n'>$ , donde $|c_n|^2=|c_n'|^2$ .
-si $A$ es un observable del sistema, su relación de transformación bajo $U_S$ conlleva que $A'$ es también un observable, y que poseen el mismo espectro, teniéndose:
$A\, |\psi_n>\,=\,a_n\,|\psi_n> \, \Rightarrow A'\, |\psi_n'>\,=\,a_n\,|\psi_n'>$ .
-el subespacio de $\mathcal{H}$ conformado por todos los vectores propios de $A'$ , para un valor propio determinado, es el transformado bajo $U_S$ del subespacio propio de $A$ asociado al mismo valor propio.
-toda relación algebraica entre los observables del sistema se mantiene bajo $U_S$ .
Un operador lineal $A: \mathcal{H} \rightarrow \mathcal{H}$ y se dice que es invariante bajo una trasformación de simetría $U_S$ en $\mathcal{H}$ cuando
$A = U_S^+ A'U_S= U_S A U_S^+ = A'$ .
-Propiedad: «Un operador $A$ es invariante bajo $U_S$ si y sólo si ambos operadores conmutan»:
$(\Rightarrow) A' = U_S A U_S^+ =A$ ; $[A, U_S]=AU_S - U_SA=U_SAU_S^+U_S-U_SA=0$ ,
$(\Leftarrow) [A, U_S]=0=AU_S-U_SA$ ; $A'=U_SAU_S^+=AU_SU_S^+=A$ .

Transformaciones unitarias infinitesimales

Una transformación unitaria $U_{\delta}$ se define como infinitesimal cuando se expresa según $U_{\delta} \equiv U(\delta)=I-i\delta F$ , donde $I$ es el operador identidad en el correpondiente espacio en el que se define $U$ ; $\delta$ es un escalar real arbitrario, de módulo suficientemente pequeño, de modo que el desarrollo de $U^+U$ pueda considerarse igual a la identidad en primer orden del parámetro $\delta$ ; $F$ un operador autoadjunto sobre el espacio de Hilbert $\mathcal{H}$ :
$I=U_{\delta}^+ U_{\delta}=(I+i\delta F^+)(I-i\delta F) + O(\delta ^2) \approx I-i\delta (F-F^+)=I$ .
-El operador $F$ se denomina «generador» de la correspondiente transformación unitaria infinitesimal.
-Obsérvese que, por ser la transformación unitaria: $I=U_{\delta}^+ U_{\delta}=I-i\delta (F-F^+)=U_{\delta} U_{\delta}^+= (I-i\delta F)(I+i\delta F^+)=I+i\delta (F-F^+) \Rightarrow F=F^+$
Ecuaciones de transformación de vectores y operadores bajo una tranformación unitaria infinitesimal $U_{\delta}$ :
-vectores: $| \psi' > = U_{\delta}| \psi > = (I-i\delta F) | \psi > =| \psi > + \Delta | \psi >$ , donde $\Delta | \psi > = i \delta F | \psi >$ (+ términos $O(\delta^2)$ ).
-operadores: $A'=U_{\delta}AU_{\delta}^+=(I-i\delta F)A(I+i\delta F^+)=A+\Delta A$ , donde $\Delta A=i\delta [A,F]$ (+ términos $O(\delta^2)$ ).

Transformaciones finitas continuas

Una transformación de simetría implementada por el operador (unitario o antiunitario) $U_S$ se denomina como «transformación finita continua» cuando el operador $U_S$ depende de un parámetro real finito $\epsilon$ y admite expresión como producto de transformaciones infinitesimales $U_S(\delta)$ :
$U_S(\epsilon)=\prod U_S(\delta)= \prod (I-i\delta F)$ .
Teorema: Toda transformación finita continua $U_S(\epsilon)$ admite la expresión general:
$U_S(\epsilon)=\lim_{n \to \infty} (I-i\frac{\epsilon}{n}F)^n=e^{-i\epsilon F}$ ,
donde se ha impuesto $\delta=\epsilon /n$ .
-esta expresión admite la generalización:
$U_S(\epsilon_1, \cdots , \epsilon_m)=e^{-i\sum_{j=1}^{m}\epsilon_j F_j}$ ,
donde cada $F_j$ es el generador de la transformación finita continua $U_S(\epsilon_j)$ .
-Ejercicio:
$U_S(\epsilon)| \psi >$ $= \lim_{n \to \infty} (I-i\frac{\epsilon}{n}F)^n| \psi >$ $= \sum_f \lim_{n \to \infty} (I-i\frac{\epsilon}{n}F)^n |f><f| \psi >$ $=\sum_f \lim_{n \to \infty} (I-i\frac{\epsilon}{n}f)^n |f><f| \psi >$ $= \sum_f e^{-i \epsilon f} |f><f| \psi >$ $= e^{-i \epsilon F} | \psi >$ , donde $F |f>=f|f>$ .
Una tranformación de simetría discreta es una transformación de simetría que no se puede generar por aplicación sucesiva de transformaciones infinitesimales: aquélla que no es continua.
-ejemplo: la inversión espacial.

Principales transformaciones geométricas y sus generadores

Translación temporal:
-se trata de una transformación finita continua (unitaria), asociada a la operación $t \rightarrow t+\tau$ , cuyo generador es el operador hamiltoniano $H$ , y que se liga al principio de conservación de la energía.
Translación espacial:
-se trata de una transformación finita continua (unitaria), asociada a la operación $\vec{r} \rightarrow \vec{r} + \vec{a}$ , cuyo generador es el operador momento lineal $\vec{P}$ , y que se liga al principio de conservación del momento lineal.
Rotación espacial:
-se trata de una transformación finita continua (unitaria), asociada a la operación rotación $\vec{r} \rightarrow \mathcal{R} \vec{r}$ , cuyo generador es el operador momento angular $\vec{J}$ , y que se liga al principio de conservación del momento angular.
Inversión espacial:
-se trata de una transformación finita discreta (unitaria), asociada a la operación $\vec{r} \rightarrow -\vec{r}$ , cuyo generador es el operador paridad y que se liga al principio de conservación de la paridad.
Inversión temporal:
-se trata de una transformación finita discreta (antiunitaria), asociada a la operación $t \rightarrow -t$ .
Nota histórico-biográfica: La conexión simetría-ley de conservación constituye el gran interés en Física del teorema de Noether, que data de 1916 y fue formulado por la gran matemática Emmy (Amalie) Noether (1882-1935). Una búsqueda en internet proporcionará múltiples enlaces con más información: blog casanchi.org, estudio sobre su impacto en la Física Teórica por S. Montero…

Sistemas físicos en MC, simetrías y leyes de conservación

La invariancia de un sistema bajo diversas simetrías geométricas conduce a leyes de conservación de determinados observables del sistema.
Definición: Invariancia de un sistema físico bajo una transformación de simetría $U_S$ :
Dado un sistema físico cuya descripción se realiza en el marco de la M.C., formalismo de espacios de Hilbert, y dada $U_S : \mathcal{H} \rightarrow \mathcal{H}$ una transformación de simetría en $\mathcal{H}$ , se dice que el sistema es invariante bajo $U_S$ cuando cada estado $| \psi> \in \mathcal{H}$ y su transformado bajo $U_S$ , $| \psi'> = U_S | \psi> \in \mathcal{H}$ satisfacen la misma ecuación de evolución temporal.
-Esto es, se satisfacen el par de ecuaciones:
$H(t) | \psi > = i\hbar \frac{d}{dt} | \psi>$
y
$H(t) | \psi' > = i\hbar \frac{d}{d t} | \psi'>$ ,
donde el Hamiltoniano que figura en la segunda ecuación es el original y no el transformado $H'(t)=U_S\,H(t)\,U_S^+$ .
NO invariancia de un sistema físico bajo una transformación de simetría dependiente del tiempo, $U_S = U_S(t)$ :
Dado un sistema físico cuya descripción (caso no relativista) se realiza en el marco de la M.C., formalismo de espacios de Hilbert, asumiéndose como postulado la correspondiente ecuación de Schrödinger,
$i\hbar \frac{d \, |\Psi(t)>}{d \, t}\,=\,H(t)\, |\Psi (t)>$ ,
donde $H(t)$ es el Hamiltoniano del sistema, entonces cada estado $| \psi> \in \mathcal{H}$ y su transformado bajo $U_S$ , estado $| \psi'> = U_S | \psi> \in \mathcal{H}$ , no satisfacen la misma ecuación de evolución temporal:
$i\hbar \frac{d \, |\Psi(t)'>}{d \, t}\,= \,i\hbar \frac{d }{d \, t}\, (U_S(t)\, |\Psi(t)>)\,=\, U_S\,i\hbar \, \frac{d | \psi(t)> }{d \,t}\,+\, i\hbar \,\frac{d\,U_S(t)}{d\, t} \,|\Psi(t)>$
$=\, U_S(t)\,H(t)\, |\Psi (t)> \,+\,i\hbar \frac{d \,U_S(t) }{d \,t}\,|\Psi(t)>$
$=\, ([U_S(t)\,,\,H(t)]\,|\Psi>\,+\,H(t)\,U_S(t))\, |\Psi(t)> \, + \, i\hbar \,\frac{d\,U_S(t)}{d\, t} \,|\Psi(t)>$
$=\,[U_S(t)\,,\,H(t)]\, |\Psi(t)> \, +\, H(t)\, |\Psi (t)'> \,+\,i\hbar \frac{d \,U_S(t) }{d \,t}\,|\Psi(t)$ ,
de manera que, aunque se tenga la invariancia de $H(t)$ bajo la transformación de simetría $U_S(t)$ , esto es,
$H'(t)=U_S(t)H(t)U_S(t)^+=H(t) \Leftrightarrow [H(t) \ , \ U_S(t)]=0$ ,
derivándose la conmutación entre $U_S(t)$ y $H(t)$ , cuando $\frac{d\,U_S}{d\,t} \ne 0$ los estados del Hilbert transformados bajo $U_S(t)$ , esto es, $|\Psi(t)'>\,=\,U_S\,|\Psi>$ , no obedecen la misma ecuación de Schrödinger que los estados originales $|\Psi>$ .
-De la ecuación anterior se desprende que sí ocurrirá la invariancia cuando, para un operador $Us(t)$ general, se cumpla que
$[U_S(t)\,,\,H(t)]\, + \, i\hbar \frac{d \,U_S(t) }{d \,t} \, = \, 0$
Invariancia de un sistema físico bajo una transformación de simetría independiente del tiempo, $U_S \ne U_S(t)$ :
Dado un sistema físico cuya descripción se realiza en el marco de la M.C., formalismo de espacios de Hilbert, y dada $U_S : H \rightarrow H$ una transformación de simetría independiente del tiempo en H, se tiene que el sistema es invariante bajo $U_S$ si y sólo si su Hamiltoniano es invariante bajo la transformación.
-Esto es:
$H'(t) = U_S H U_S^+ = H(t) \Leftrightarrow [H(t),U_S]=0$ ;
en particular, cuando $U_S$ sea una transformación finita continua, el Hamiltoniano ha de conmutar con su generador,
$H'(t) = U_S H U_S^+ = H(t) \Leftrightarrow [H(t),F]=0$ .
-En efecto, cuando $U_S \ne U_S(t)$ se tiene:
$(\Rightarrow) \quad i\hbar \frac{d}{d t} | \psi'(t)> = i\hbar \frac{d}{d t} U_S | \psi(t)> = U_S H(t) | \psi(t)>$
$= H(t) | \psi' (t)> = H(t) U_S | \psi(t)> \Rightarrow [H(t),U_S]=0$
$(\Leftarrow) \quad [H(t),U_S]=0 \Rightarrow i\hbar \frac{d}{d t} | \psi'(t)> = i\hbar \frac{d}{d t} U_S | \psi(t) >$
$= U_S H(t) | \psi(t)> = H(t) U_S | \psi(t) > \Rightarrow H(t) | \psi'(t)>$
Invariancia y leyes de conservación de observables :
Sea un sistema físico invariante bajo una transformación de simetría independiente del tiempo, $U_S \ne U_S(t)$ . Entonces se tiene:
$i\hbar \frac{d}{d t} | \psi'(t)> = H(t) | \psi'(t)> \Leftrightarrow H(t)=H'(t)\Leftrightarrow [H(t),U_S]=0$ .
Por lo tanto:
-si $U_S$ es un observable (sii es autoadjunto, ya que hemos supuesto el Hilbert coherente) representa una constante del movimiento, esto es:
$\frac{d t}{d t}U_S-\frac{i}{\hbar}[U_S,H(t)]=0$ $\Rightarrow \left\langle U_S \right\rangle_{\psi(t)} \ne f(t)$ .
-si la transformación de simetría es finita continua, con generador $F$ , $U_S\equiv U_S(\epsilon)=e^{-i\epsilon F}$ , se deriva que para $F$ también se aplica la misma ecuacion anterior y $F$ representa una constante del movimiento:
$[U_S=e^{-i\epsilon F}, H(t)]=0 \Leftrightarrow [F\,,\,H(t)]=0$ , siendo $F=F^+$ .
-Así, cuando $F \ne F(t)$ y $[F,H(t)]=0$ se implica que $F$ es una constante del movimiento: $\left\langle F \right\rangle_{\psi(t)} \ne f(t)$ .
Nota: recuérdese, sobre la definición de constante del movimiento:
Para un sistema físico general (tanto cuando es conservativo, esto es, su Hamiltoniano no depende del tiempo y es el observable energía total del sistema, como cuando no es el caso):
1. Definición: Un observable $C$ se define como constante del movimiento cuando cumple la ecuación (cf. [GAL-89], pp. 106ss.):
$i\hbar\frac{\partial C}{\partial t}+[C,H]=0$
(en la línea anterior, aparece una ecuación de igualdad entre operadores, y este tipo de igualdad requiere no sólo igual regla de actuación, sino también coincidencia en los respectivos dominio y recorrido; en general, es suficiente con que la igualdad se satisfaga sobre una base común a los dominios involucrados).
2. Teorema: Para un observable que es constante del movimiento, el valor medio, sobre cualquier estado $\Psi(\vec{r};t)$ , es independiente del tiempo:
$\frac{\partial}{\partial t}\left\langle C(t)\right\rangle_\Psi =0$ $\Rightarrow \left\langle C(t) \right\rangle_\Psi \ne f(t)$ .
En resumen: la invariancia de un sistema físico bajo una transformación de simetría conduce generalmente (¡ha de ser $U_S \ne U_S(t)$ y $U_S=e^{-i\epsilon F}\; , \: F=F^+$ !) a la existencia de una constante del movimiento, es decir, a una ley de conservación para un observable (el generador $F$ de la transformación finita continua independiente del tiempo) del sistema.
Ejemplo 1: consideremos el principio de conservación de la energía. Este principio fundamental de la Física se deriva a partir de la observación de que, para un sistema cerrado o aislado, es decir, sin interacción con su exterior (entre dos «medidas ideales»), se produce invariancia frente a translaciones temporales (lo mismo sucede para un sistema en un campo exterior constante). La consecuencia es que su Hamiltoniano $H$ es una constante del movimiento:
Invariancia frente a translaciones espaciales $\Rightarrow H \ne H(t)$ , y como un operador conmuta consigo mismo, la consecuencia es que el Hamiltoniano representa una constante del movimiento:
$\frac{\partial}{\partial t}\left\langle H\right\rangle_\Psi =0$ $\Rightarrow \left\langle H \right\rangle_\Psi \ne f(t)$ .
-Si el sistema es además conservativo (esto es, no sólo $H \ne H(t)$ , además de ser independiente del tiempo el Hamiltoniano representa la energía del sistema), lo que se ha derivado es la conservación de este observable.
-Nota: si el Hamiltoniano del sistema depende del tiempo, entonces lo hace también la correspondiente transformación de simetría, de forma que el sistema no presenta invariancia bajo translación espacial.
Ejemplo 2: consideremos el principio de conservación del momento angular. Este principio fundamental de la Física se deriva a partir de la observación de que, considerado un sistema físico aislado, y asumido que el espacio tridimensional es intrínsecamente isótropo, esto es, en su seno todas las direcciones son equivalentes, la física del sistema debe permanecer invariante bajo rotaciones en ese espacio. Por lo tanto, si el sistema no interacciona con su exterior, su momento angular total, que es el operador generador de las rotaciones espaciales, además de ser independiente del tiempo debe conmutar con el Hamiltoniano del sistema, por lo que se deriva que $\vec{J}$ es una constante del movimiento.
Invariancia y degeneración de autovalores :
Dados un sistema conservativo, $H \ne H(t)$ y representa la energía total del sistema; una transformación de simetría $U_S \ne U_S(t)$ bajo la que el sistema es invariante, $[H,U_S]=0$ ; y los estados propios de $H$ , estados estacionarios $| \psi_E>$ con autovalor $E$ , entonces se tiene que los estados transformados $U_S | \psi_E>$ , $F | \psi_E>$ son también estados propios del hamiltoniano $H$ con el mismo autovalor $E$ :
$H| \psi_E>=E | \psi_E>=U_S | \psi_E>=F | \psi_E>$ .
-En resumen:
a) Si $| \psi_E>$ y $F| \psi_E>$ son linealmente independientes entre sí, el valor propio $E$ es degenerado.
b) Si $H$ y $F$ , el generador (autoadjunto) de la simetría que representa un observable del sistema, conmutan, $[H,F]=0$ , existirá una base ortonormal común a ellos en el Hilbert.

Tensores irreducibles

Un operador tensorial irreducible o esférico de orden $J$ se define, para el grupo de rotaciones en $\mathbb{R}^n$ , como un operador combinación lineal de $(2J+1)$ operadores $T^{J}_{M} \, , \, M=+J,\, \ldots,-J$ que bajo la acción del grupo se transforman según la ley
$U_R(\alpha, \beta, \gamma)\, T_M^J\, U^+_R(\alpha, \beta, \gamma)=\sum_{M'}D^J_{M'M}(\alpha, \beta, \gamma)\, T_{M'}^J$
donde $D^J$ representa una matriz cuadrada de dimensión $(2J+1)$ .
Un operador tensorial se dice que es reducible cuando puede descomponerse en objetos que se transforman de manera diferente ante rotaciones. Todos los tensores esféricos son irreducibles.
Puesto que estos apuntes no exponen teoría de grupos, recurrimos a sustituir la definición general anterior por la formalmente equivalente (para los casos que consideraremos):
-Un operador tensorial irreducible o esférico de orden o rango $J$ se define como (una combinación lineal de) un conjunto de $(2J+1)$ operadores $T^{J}_{M} \, , \, M=+J,\, \ldots,-J$ que satisfacen las siguientes relaciones de conmutación:
$[J_{\pm}\,,\,T_M^J]=\hbar \, \sqrt{(J\mp M)(J\pm M+1)}\, T^J_{M\pm 1}$
$[J_{z}\,,\,T_M^J]=\hbar \, M\, T_M^J$ .
Estas relaciones caracterizan a ${T_M^J}$ como una base estándar (base esférica) del operador tensorial.
Ejemplos:
1. Operador escalar:
  El caso más sencillo de operador tensorial es el de un operador escalar, u operador tensorial de orden $J=0$ :
  Definición 1: Un operador tensorial de grado cero, $T^0_0 \equiv A$ , es un operador escalar si permanece invariante bajo rotaciones espaciales, esto es, $A'=U_{\mathcal{R}}\,A\, U^+_{\mathcal{R}}\,=A$ ,
  siendo $\mathcal{R}$ el operador que realiza una rotación espacial y $U_{\mathcal{R}}$ la correspondiente transformación de simetría.
  Definición 2: Un operador $A$ es escalar cuando satisface las siguientes relaciones de conmutación con el operador de momento angular $\vec{J}$ :
  $[J_i\,,\,A]=0\,;\, i=1,2,3$ .
  -ejemplos: los operadores energía cinética, energía potencial y cuadrado de momento angular son operadores escalares.
2. Operador vectorial, u operador tensorial de orden $J=1$ :
  Definición 1: Un operador $T^1_M\;, con \; M=-1,0,1$ , se define como operador vectorial cuando se transforma bajo rotaciones según:
  $\vec{A}'\, =\, U_{\mathcal{R}}\,\vec{A}\, U^+_{\mathcal{R}}\,=\, \mathcal{R}^{-1}(\phi \,,\, \hat{n})\,\vec{A}$ , donde $\mathcal{R}^{-1}$ representa la correspondiente matriz inversa de la matriz general de rotación (activa) en un ángulo $\phi$ en torno a la dirección espacial señalada por el vector unitario $\hat{n}$ .
  Definición 2: Un operador $\vec{A}$ es vectorial cuando satisface las siguientes relaciones de conmutación con el operador de momento angular $\vec{J}$ :
  $[J_i\,,\,A_j]=i\hbar \, \epsilon_{ijk}\,A_k\,;\, i,j,k=1,2,3$ .
  -Los operadores posición $\vec{r}$ , momento lineal $\vec{p}$ y momento angular $\vec{J}$ son operadores vectoriales.
Dado el operador autoadjunto de momento angular $\vec{J} \equiv (J_1\,,\,J_2\,,\,J_3)$ , actuando en un espacio de Hilbert $\mathcal{H}^{(J)}$ de dimensión finita, los tres operadores autoadjuntos componentes ${J_1\,,\,J_2\,,\,J_3}$ constituyen un conjunto irreducible de operadores en $\mathcal{H}^(J)$ , en el sentido de que todo operador lineal actuando en el espacio que conmuta con todos ellos es necesariamente un múltiplo de la identidad (cf. [GAL-89], pp. 247 y 329).
Los armónicos esféricos $Y_{lm}(\Omega)$ , como operadores multiplicativos, son base esférica de un tensor irreducible de orden $l$ .
Sean los estados de la denominada base acoplada, integrada por autofunciones simultáneas de los cuatro operadores $\vec{l}^2,\vec{s}^2,\vec{j}^2, j_z$ , donde $\vec{j}=\vec{l} + \vec{s}$ es el denominado momento angular total,
estados $\{| l\, s \, j\, m_j > \}_{j \,;\,m_j=-j,-j+1,\ldots,j}$ considerados para cada valor posible de $j$ fijados el par $l,s$ , o, en notación alternativa, estados
$| l\, s \, j\, m_j > \, \rightarrow \, <\hat{r} \, | \,l\, s \, j\, m_j > \, \equiv \, \psi_{l s j m_j}=\mathcal{Y}_{l s}^{j m_j}(\theta,\varphi;\sigma)$
$= \sum_{m_l,m_s} \ C(l \ s \ j \ | \ m_l \ m_s \ m_j=m_l + m_s) \ Y_{lm}(\Omega) \ \chi_{sm_s}$ ,
donde aparecen los coeficientes de Clebsch-Gordan $C(l \ s \ j \ | \ m_l \ m_s \ m_j=m_l + m_s)$ .
-En particular, en el caso $s=1$ , los $2j+1$ estados
$\mathcal{Y}_{l s=1}^{j m_j}(\theta,\varphi;\sigma) = \sum_{\mu=+1,0,-1} \ C(l \ 1 \ j \ | \ m_l-\mu \ \mu \ m_l) \ Y_{l \ m_l-\mu}(\Omega) \ \chi_{1 \mu}$
constituyen, para cada valor dado de $l$ , un tensor irreducible de orden $j$ , el denominado «armónico esférico vectorial».
Propiedades:
1. Dado un operador vectorial $\vec{A}$ con componentes cartesianas $\vec{A}=(A_1,A_2,A_3)$ , sus componentes estándar o esféricas $A_M^1$ son:
  $\left. \begin{array}{l} A_{+1}^{1}=\frac{1}{\sqrt{2}}(A_1\,+\,iA_2) \\ A_{+1}^{1}=A_3 \\ A_{-1}^{0}=\frac{1}{\sqrt{2}}(A_1\,-\,iA_2) \end{array} \right\}$ .
2. Dados dos operadores vectoriales $\vec{A}$ y $\vec{B}$ , con sendas componentes cartesianas $A_i\,y\,B_i\,,\, i=1,2,3$ , su producto escalar se puede expresar como: $\vec{A} \cdot \vec{B}\,=\,\sum_i\,A_iB_i=\,\sum_{M=-1,0,+1}\,(-1)^M\,A^1_M\,B_M^1\,=\,\sum_{M=-1,0,+1}\,A^{1+}_M\,B_M^1$ ,donde $A^{1}_M$ y $B_M^1$ simbolizan las respectivas componentes esféricas.
  -Dados dos tensores irreducibles de orden $J$ , $A_M^J$ y $B_M^J$ , la combinación lineal con escalares arbitrarios $\alpha A_M^J \,+\, \beta B_M^J$ , $\alpha , \beta \in \mathbb{C}$ , es un tensor irreducible del mismo orden $J$ .

Teorema de Wigner-Eckart

Sea $T_M^J$ un tensor irreducible de orden $J$ . Entonces sus elementos de matriz entre estados con momento angular bien definido satisfacen:
$< J_2 M_2 \alpha_2 | T_M^J | J_1 M_1 \alpha_1 > \, = C(J_1 J J_2 | M_1 M M_2) < J_2 \alpha_2 || T^J || J_1 \alpha_1 >$ ,
donde el elemento definido como $< || \quad || >$ por la expresión del teorema se denomina «elemento de matriz reducido», que es independiente pues de los valores de los números cuántico de tercera componente de los momentos angulares involucrados.
-En la expresión, los parámetros $\alpha_i$ simbolizan los números cuánticos adicionales que, en su caso, fuesen necesarios para especificar por completo cada estado cuántico.
El teorema resulta de gran importancia práctica, pues permite factorizar la dependencia en las terceras componentes de momento angular, encerrándola en el coeficiente de Clebsch-Gordan, derivándose el resultado de que el elemento de matriz es nulo a menos que se cumplan las condiciones:
$\left. \begin{array}{l} M=M_2-M_1 \\ \Delta (J_1J_2J)=1 \end{array} \right\}$ ,
donde $\Delta(J_1J_2J)=1$ simboliza que, elegidas las componentes de los tres operadores de momento angular involucrados en cualquier orden, han de cumplir
$J_i=J_j+J_k, \ldots , |J_j-J_k|$ .
-En efecto: para saber el valor de los $(2J_2+1)(2J+1)(2J_1+1)$ elementos de matriz a considerar, basta aplicando el teorema calcular el más sencillo de ellos; obtener el valor del correspondiente elemento de matriz reducido y, usándolo, calcular los restantes a partir de los valores de los coeficientes de Clebsch-Gordan requeridos.
Valores de algunos elementos de matriz reducidos:
$< J_2 \alpha_2 || T^J=J || J_1 \alpha_1 > = \delta_{\alpha_1,\alpha_2} \delta_{J_1,J_2}\hbar \sqrt{J(J+1)}$
$< L_2 \alpha_2 || T^J=Y^L || L_1 \alpha_1 > = \delta_{\alpha_1,\alpha_2} C(L-1 L_2 L | 0 0 0) \sqrt \frac{{(2L_1+1)(2L+1)}}{4 \pi (2L_2+1)}$
Dos propiedades, válidas sólo para los tensores irreducibles de primer orden:
$< J_1 M_2 \alpha_2 | T_M^1 | J_1 M_1 \alpha_1 > \, = \frac{1}{\hbar^2 J_1(J_1+1)} < J_1 M_2 \alpha_2 | J_M (\vec{J} \cdot \vec{T}) | J_1 M_1 \alpha_1 >$ ,
donde $T_M^1$ y $J_M$ simbolizan cualesquiera dos de las respectivas componentes de $T$ y $J$ , bien esféricas o bien euclídeas.
$< J_2 M_2 \alpha_2 | J_M (\vec{J} \cdot \vec{T}) | J_1 M_1 \alpha_1 > = \delta_{J_1,J_2} < J_1 M_2 | J_M | J_1 M_1 > < J_1 \alpha_2 || \vec{J} \cdot \vec{T} || J_1 \alpha_1 >$

Teorema de proyección

Sea $\vec{J}$ un operador de momento angular total, y sea $\vec{A}$ un tensor de rango 1, esto es, un operador vectorial, $[J_i , A_j]=i \hbar \epsilon_{ijk} A_k$ .Entonces, el teorema de proyección establece la identidad:
$< J' M' \alpha' | A_{\mu} | J M \alpha > \, = \,\frac{< J M' | J_{\mu} | J M >}{< J M | \vec{J}^2 | J M >} \ < J M \alpha' | \vec{A} \cdot \vec{J} | J M \alpha > \delta_{J,J'}$
$= \,\frac{< J M' | J_{\mu} | J M >}{\hbar^2 J (J+1) } \ < J M \alpha' | \vec{A} \cdot \vec{J} | J M \alpha > \delta_{J,J'}$
siendo $A_{\mu}$ la componente $\mu$ -ésima del tensor $\vec{A}$ .