Rotaciones y momento angular

simetría rotacional (imagen de F.J.E. Lagos)

Las rotaciones espaciales

La simetría rotacional juega un papel fundamental en el estudio de muchos sistemas de gran interés físico. Los operadores de momento angular en mecánica cuántica son los generadores de las rotaciones espaciales, y de ahí su papel esencial en el formalismo. El hecho observacional de partida es que, considerado un sistema físico aislado, y asumido que el espacio tridimensional es intrínsecamente isótropo, esto es, en su seno todas las direcciones son equivalentes, la física del sistema debe permanecer invariante bajo rotaciones en ese espacio.
El estudio riguroso de la simetría rotacional requiere la matemática de la teoría de grupos, pero en estos apuntes no se entrará en su desarrollo. En este apartado, se desarrolla sólo una introducción «ligera» al tema, con el fin primordial de introducir las matrices de rotación y establecer su conexión con los operadores cuánticos de momento angular, que descubriremos como los generadores de las rotaciones espaciales. Es oportuno recordar que, dado un sistema aislado, su Hamiltaniano es independiente del tiempo, $H \ne H(t)$ , en cuyo caso si el operador correspondiente a una simetría espacial es un operador (unitario) que es también independiente del tiempo, $U_{S}\ne U_S(t)$ , entonces se tiene que ambos operadores conmutan, $[H\,,\, U_S]=0$ , y se deriva una ley de conservación para el operador generador de la transformación (continua). En el caso de las rotaciones espaciales la conservación se va a aplicar para su correspondiente generador, el operador de momento angular $\vec{J}$ .
Se considera la operación de simetría «rotación en el espacio», a la cual asociamos el operador $\mathcal{R} : \mathbb{R}^3 \rightarrow \mathbb{R}^3$ , definido de forma que el transformado de cada vector $\vec{r}$ es el vector $\vec{r'}$ con
$\vec{r'}= \begin{pmatrix} x'\\ y'\\ z'\end{pmatrix} = \mathcal{R} \vec{r} = \mathcal{R} \begin{pmatrix} x\\ y\\ z\end{pmatrix}$ ,
que denominamos como una rotación del inicial o vector rotado.
Una rotación en el espacio euclídeo puede considerarse según dos «puntos de vista» para su formalización:
1. El «activo»: se deja invariante el sistema de ejes en el espacio de coordenadas y se transforma el sistema.
2. El «pasivo»: se deja el estado invariante y se transforman los ejes de coordenadas.
Ambas formalizaciones son equivalentes: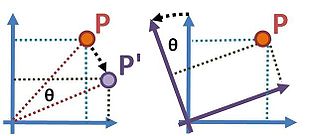

Rotaciones activa y pasiva: en la transformación activa (izquierda), un punto se mueve desde la posición P a P’ girándolo hacia la derecha en un ángulo θ sobre el origen del sistema de coordenadas. En la transformación pasiva (a la derecha), el punto P no se mueve, mientras que el sistema de coordenadas gira hacia la izquierda en un ángulo θ sobre su origen. Las coordenadas de P’ en el caso activo (es decir, en relación con el sistema de coordenadas original) son las mismas que las coordenadas de P en relación con el sistema de coordenadas girado (Fuente: Wikipedia).
Es conveniente representar el operador rotación en forma matricial:
$\vec{r}'=\mathcal{R} \vec{r}= \begin{pmatrix} R_{11}& R_{12}& R_{13}\\ R_{21}& R_{22}& R_{23}\\ R_{31}& R_{32}& R_{33}\end{pmatrix} \, . \,\begin{pmatrix} x\\ y\\z\end{pmatrix}$ ,
donde todos los elementos $R_{ij}$ deben ser reales, por serlo las componentes de los vectores $\vec{r}$ y $\vec{r}'$ .
-A continuación, se impone la condición de que el producto escalar entre cada dos vectores quede inalterado para una rotación arbitraria de ambos:
$\vec{r}_1 \cdot \vec{r}_2 =\vec{r}'_1 \cdot \vec{r}'_2 = (\mathcal{R} \vec{r}_1)\, . \, (\mathcal{R} \vec{r}_2)$ ,
ecuación que conduce a un sistema de nueve ecuaciones para los elementos de la matriz $\mathcal{R}$ :
$x_1 x_2 \rightarrow R_{xx}^2 + R_{yx}^2 + R_{zx}^2 = 1$ ,
y lo mismo para $y_1 y_2$ y $z_1 z_2$ ;
$x_1 y_2 \rightarrow R_{xx} R_{xy} + R_{yx} R_{yy} + R_{zx} R_{zy}=0$ ,
y lo mismo para $x_1 z_2$ , $y_1 x_2$ , $y_1 z_2$ , $z_1 x_2$ y $z_1 y_2$ .
Es decir: la matriz de rotación $\mathcal{R}$ es ortonormal: $\sum_i R_{ij}R_{ik}\,=\, \delta_{jk} \, ; \; i,j,k=1, 2, 3$ ( $1\equiv x\,,\, 2\equiv y\, , \,3\equiv z)$ , de modo que sus columnas representan sendos vectores en $\mathbb{R}^3$ mutuamente ortonormales.
A esta conclusión se puede llegar igualmente imponiendo la condición de que el módulo de cualquier vector arbitrario $\vec{r}$ se conserve bajo la rotación $\mathcal{R}$ ; también, a partir de la rotación de un triedro rectangular de vectores unitarios.
Los nueve elementos de la matriz de rotación $\mathcal{R}$ se identifican con nueve «cosenos directores» de un ángulo $\phi$ , a partir de la rotación en ese ángulo $\phi$ de un triedro de vectores unitarios $\hat{i}, \hat{j},\hat{k}$ (¡punto de vista pasivo!):
$\vec{r'}= \begin{pmatrix} x'\\ y'\\ z'\end{pmatrix} = \mathcal{R} \vec{r} = \mathcal{R} \begin{pmatrix} x\\ y\\ z\end{pmatrix}$
$\Rightarrow \left. \begin{array}{rcccl} x'& = & (\vec{r} \cdot \hat{i}') & = & R_{xx}x + R_{xy}y + R_{xz}z\\ y'&=&(\vec{r} \cdot \hat{j}')&=& R_{yx}x + R_{yy}y + R_{yz}z\\z'&=&(\vec{r} \cdot \hat{k}')&=& R_{zx}x + R_{zy}y + R_{zz}z\end{array} \right\}$ ;
en particular, para los vectores unitarios: $\left. \begin{array}{rcccl} \hat{i}' &=& (\hat{i}' \cdot \hat{i}) \hat{i} + (\hat{i}' \cdot \hat{j}) \hat{j} + (\hat{i}' \cdot \hat{k}) \hat{k}&=& R_{xx}\hat{i} + R_{xy}\hat{j} + R_{xz}\hat{k}\\ \hat{j}' &= &(\hat{j}' \cdot \hat{i}) \hat{i} + (\hat{j}' \cdot \hat{j}) \hat{j} + (\hat{j}' \cdot \hat{k}) \hat{k} &=& R_{yx}\hat{i} + R_{yy}\hat{j} + R_{yz}\hat{k} \\ \hat{k}' &=& (\hat{k}' \cdot \hat{i}) \hat{i} + (\hat{k}' \cdot \hat{j}) \hat{j} + (\hat{k}' \cdot \hat{k}) \hat{k} &=& R_{zx}\hat{i} + R_{zy}\hat{j} + R_{zz}\hat{k}\end{array} \right\}$ $\Rightarrow \mathcal{R}= \begin{pmatrix} R_{11}& R_{12}& R_{13}\\ R_{21}& R_{22}& R_{23}\\ R_{31}& R_{32}& R_{33}\end{pmatrix}= \begin{pmatrix} (\hat{i}' \cdot \hat{i})= \cos \widehat{(\hat{i}' \, ,\, \hat{i})}& (\hat{i}' \cdot \hat{j})= \cos \widehat{(\hat{i}' \, ,\, \hat{j})}& (\hat{i}' \cdot \hat{k})= \cos \widehat{(\hat{i}' \, ,\, \hat{k})}\\ (\hat{j}' \cdot \hat{i})= \cos \widehat{(\hat{j}' \, ,\, \hat{i})}& (\hat{j}' \cdot \hat{j})= \cos \widehat{(\hat{j}' \, ,\, \hat{j})}& (\hat{j}' \cdot \hat{k})= \cos \widehat{(\hat{j}' \, ,\, \hat{k})}\\ (\hat{k}' \cdot \hat{i})= \cos \widehat{(\hat{k}' \, ,\, \hat{i})}& (\hat{k}' \cdot \hat{j})= \cos \widehat{(\hat{k}' \, ,\, \hat{j})}& (\hat{k}' \cdot \hat{k})= \cos \widehat{(\hat{k}' \, ,\, \hat{k})}\end{pmatrix}$ .
-los cosenos directores han de satisfacer las seis ecuaciones de ligadura que se requieren por la ortogonalidad de la matriz, de modo que sólo tres de los nueve parámetros son independientes.
La rotación inversa a una dada, o rotación que transforma $\vec{r'}=\mathcal{R} \vec{r}$ en $\vec{r}$ , se definiría según la ecuación $\vec{r}=\mathcal{R}^{-1} \vec{r'}$ , donde queda por determinar la relación entre la nueva matriz $\mathcal{R}^{-1}$ y la $\mathcal{R}$ .
-Aplicando la condición $|\vec{r}\,|^2=|\mathcal{R}^{-1} \vec{r}\, ' |^2$ , e introduciendo la relación $r_i=\sum_j \mathcal{R}^{-1}_{ij} \vec{r_j}'$ , donde $\mathcal{R}^{-1}_{ij}$ representa el elemento en la fila i, columna j, de la matriz $\mathcal{R}^{-1}$ , se obtiene:
$\sum_i r_i^2 = \sum_i (\sum_j \mathcal{R}_{ij}^{-1} \,\vec{r}_j^{\,'})^2$ $= \sum_i (\sum_j \mathcal{R}_{ij}^{-1}\,\vec{r}_j^{\,'}) (\sum_k \mathcal{R}_{ik}^{-1} \,\vec{r}_k^{\,'})$ $= \sum_i \sum_{j,k} \mathcal{R}_{ij}^{-1}\, \mathcal{R}_{ik}^{-1}\,\,\vec{r}_j^{\,'} \, \vec{r}_k^{\;'}$ .
Puesto que las dos ecuaciones
$\left. \begin{array}{c}r_i=\sum_j \mathcal{R}^{-1}_{ij} r_j^{\,'} \\ r_k^{\,'}=\sum_i \mathcal{R}^{-1}_{ki} r_i \end{array} \right\}$
han de ser compatibles, eliminando $r_i$ entre los dos sistemas se obtiene:
$r_k^{\, '}\,=\, \sum_i \mathcal{R}_{ki} \, \sum_j \mathcal{R}_{ij}^{-1}\,r_j^{\,'} \,=\, \sum_j (\sum_i \mathcal{R}_{ki} \mathcal{R}_{ij}^{-1})r_j^{\,'}$ ,
ecuación que para ser correcta, dado que las componentes de $\vec{r}'$ son idependientes, conduce a la condición
$\sum_i \mathcal{R}_{ki} \mathcal{R}_{ij}^{-1}\,=\, \delta_{kj}$ ,
es decir, se ha de tener $\mathcal{R} \mathcal{R}^{-1}\,=\, I$ .
-Y, de forma análoga, variando el orden de los pasos en la anterior deducción, se llega a establecer finalmente la conmutación entre la matriz de rotación $\mathcal{R}$ y la que hemos notado como $\mathcal{R}^{-1}$ :
$\mathcal{R} \mathcal{R}^{-1}\,=\,\mathcal{R}^{-1}\mathcal{R}\,=\,I$ ,
estableciendo, de acuerdo con la notación usada, que $\mathcal{R}^{-1}$ es la matriz inversa de la $\mathcal{R}$ , y viceversa.
Por añadidura, a partir de la doble suma
$\sum_{k,i} \mathcal{R}_{kl}\mathcal{R}_{ki}\mathcal{R}_{ij}^{-1}\,=\sum_{i} (\sum_k \mathcal{R}_{kl}\mathcal{R}_{ki} ) \mathcal{R}_{ij}^{-1}\,=\, \sum_i \mathcal{R}_{lj}^{-1}$
$=\,\sum_{k} (\sum_i \mathcal{R}_{ki} \mathcal{R}_{ij}^{-1})\mathcal{R}_{kl}\,=\, \sum_k \delta_{kj}\mathcal{R}_{kj}^{-1}\,=\,\mathcal{R}_{jl}$
$\Rightarrow \mathcal{R}_{ij}^{-1} = \mathcal{R}_{ji}$ , esto es, $\mathcal{R}^{-1}=\mathcal{R}^{T}$ , un resultado general, inversa igual a transpuesta, que junto con la anterior relación de conmutación constituye una de las posibles condiciones necesarias y suficientes para la ortogonalidad de una matriz:
$\mathcal{R}\mathcal{R}^{T}=\mathcal{R}^T\mathcal{R}=I$ ,
como lo es también
$\sum_i \mathcal{R}_{ki} \mathcal{R}_{ij}^{-1}=\delta_{kj}=\sum_i \mathcal{R}_{ki}\mathcal{R}_{ji}$ .
En conclusión, $\mathcal{}$ es una matriz unitaria (toda matriz ortogonal real lo es):
$\left. \begin{array}{c} \mathcal{R}^{*}=\mathcal{R} \\ \mathcal{R}^{*}=\mathcal{R}\end{array} \right\} \Rightarrow \mathcal{R}^+=(\mathcal{R}^T)^*=\mathcal{R}^T=\mathcal{R}^{-1}$
$\Rightarrow \mathcal{R} \mathcal{R}^{+}\,=\,\mathcal{R}^{+}\mathcal{R}\,=\,I$ .
Puesto que $\mathcal{R}$ es una matriz ortogonal, su determinante ha de ser $det(\mathcal{R}) = \pm 1$ .
-se definen como rotaciones propias las rotaciones cuya matriz de rotación $\mathcal{R}$ asociada posee un determinante igual a la unidad, $det(\mathcal{R}) = + 1$ .
-se definen como rotaciones impropias las rotaciones cuya matriz de rotación $\mathcal{R}$ asociada posee un determinante $det(\mathcal{R}) = - 1$ . Una rotación de este tipo constituye en realidad una inversión, es decir, la conjunción de una rotación más una reflexión.

Las rotaciones espaciales y los ángulos de Euler

Toda rotación espacial puede configurarse como función de tres parámetros independientes (que son variables de variación continua, puesto que la rotación espacial se va a conformar como una transformación finita continua, unitaria). Una forma de fijar estos tres parámetros es elegirlos como los denominados «ángulos de Euler«, definidos, por ejemplo (múltiples posibilidades: véase vídeo conjuntos de ángulos Euler y conjuntos de Tait-Brian o náuticos; lo mismo en web U. de Sevilla), como:
-Sea un sistema de ejes cartesiano $OXYZ$ , dextrógiro, y sean las operaciones consecutivas sobre él:
1. Rotación pasiva positiva (sentido antihorario) de ángulo $\alpha$ , con $0 \leq \alpha < 2\pi$ , alrededor del eje $OZ$ : los ejes originales se transforman a los $OX'Y'Z'$ , con $Z'=Z$ .
2. Rotación pasiva positiva de ángulo $\beta$ , con $0 \leq \beta \le \pi$ , alrededor del eje $OY'$ : los ejes $OX'Y'Z'$ se transforman a los $OX''Y''Z''$ , con $Y''=Y'$ .
3.Rotación pasiva positiva (sentido antihorario) de ángulo $\gamma$ , con $0 \leq \alpha < 2\pi$ , alrededor del eje $OZ''$ : los ejes originales se transforman a los $OX''Y''Z''$ , con $Z'''=Z''$ .
-Recordemos que el punto de vista pasiva es aquel que deja inalterado cada vector $\vec{r}$ , actuando sobre el sistema coordenado. Las acción consecutiva de las tres rotaciones pasivas anteriores (cuyas respectivas matrices se obtienen a partir del adecuado conjunto de cosenos directores) se efectúa por la acción del operador rotación total pasiva (rotación pasiva positiva, sentido antihorario, de los ejes):
$\mathcal{R}_{pas}(\alpha, \beta,\gamma)=\mathcal{R}_{pas}(\gamma \, , \, OZ'') \mathcal{R}_{pas}(\beta \,,\,OY')\mathcal{R}_{pas}(\alpha \, , \, OZ)$
$=\begin{pmatrix} \cos \gamma & \sin \gamma & 0\\ -\sin \gamma & \cos \gamma & 0\\ 0 & 0 & 1 \end{pmatrix}$ $\begin{pmatrix} \cos \beta & 0 & - \sin \beta \\ 0 & 1 & 0\\ \sin \beta & 0 & \cos \beta \end{pmatrix}$ $\begin{pmatrix} \cos \alpha & \sin \alpha & 0\\ -\sin \alpha & \cos \alpha & 0\\ 0 & 0 & 1 \end{pmatrix}$ $= \begin{pmatrix} \cos\alpha \cos \beta \cos \gamma -\sin\alpha \sin\gamma & \sin\alpha \cos \beta \cos \gamma + \cos\alpha \sin\gamma & -\sin \beta \cos\gamma\\ -\cos\alpha \cos \beta \sin \gamma - \sin\alpha \cos\gamma & -\sin\alpha \cos \beta \sin \gamma + \cos\alpha\,\cos\gamma & \sin \beta \sin\gamma \\ \cos \alpha \sin \beta & \sin \alpha \sin\beta & \cos \beta \end{pmatrix}$
-Por tanto, el efecto final es una rotación activa positiva (sentido antihorario), rotación del sistema, que viene dada por el operador rotación activa:
$\mathcal{R}_{act}(\alpha, \beta,\gamma)=\mathcal{R}_{pas}^{-1}(\alpha, \beta,\gamma)=\begin{pmatrix} \cos\alpha \cos \beta \cos \gamma - \sin\alpha \sin\gamma & -\cos\alpha \cos \beta \sin \gamma - \sin\alpha\,\cos\gamma & \cos\alpha \sin\beta\\ \sin\alpha \cos \beta \cos \gamma + \cos\alpha \sin\gamma & - \sin\alpha \cos \beta \sin \gamma + \cos\alpha \cos\gamma & \sin\alpha \sin\beta \\ - \sin\beta \cos\gamma & \sin\beta \sin\gamma & \cos \beta \end{pmatrix}$

Rotación espacial con ángulo y eje arbitrarios

Sea la operación de rotación espacial (activa) consistente en el giro antihorario, en un ángulo positivo $0 \leq \phi \leq \pi$ , en torno a la dirección señalada por el vector unitario $\hat{n}$ de coordenadas $\hat{n}=(n_x,n_y,n_z)$ en un sistema cartesiano $OXYZ$ dado.
-La expresión general de la correspondiente matriz de rotación se deriva a partir de la expresión
$\hat{n}=(n_x,n_y,n_z)=n_x \hat{i} + n_y \hat{j} +n_z \hat{k} = \cos(\widehat{\hat{n}\,,\,\hat{i})}\,\hat{i}\, + \,\cos(\widehat{\hat{n}\,,\,\hat{j})}\,\hat{j}\, + \,\cos(\widehat{\hat{n}\,,\,\hat{k})}\,\hat{k}$ ,
o, aplicando la ligadura $|\hat{n}|^2=1=n_x^2+n_y^2+n_z^2$ :
$\hat{n}=(n_x,n_y,n_z)= \cos(\widehat{\hat{n}\,,\,\hat{i})}\,\hat{i}\, + \,\cos(\widehat{\hat{n}\,,\,\hat{j})}\,\hat{j}\, + \Bigl(1-\cos^2(\widehat{\hat{n}\,,\,\hat{i})}-\cos^2(\widehat{\hat{n}\,,\,\hat{j})}\Bigr)^{\frac{1}{2}}$
-el resultado final es:
$\mathcal{R}(\phi, \hat{n}) = \begin{pmatrix} (1-\cos \phi)n_x^2 + \cos \phi & (1-\cos \phi)n_xn_y - \sin \phi \, n_z & (1-\cos \phi)n_xn_z + \sin \phi \, n_y\\ (1- \cos \phi)n_yn_x + \sin \phi \, n_z & (1- \cos \phi)n_y^2 + \cos \phi & (1- \cos \phi)n_yn_z + \sin \phi \, n_x\\ (1- \cos \phi)n_zn_x + \sin \phi \, n_y & (1- \cos \phi)n_zn_y + \sin \phi \, n_x & (1- \cos \phi)n_z^2 + \cos \phi \end{pmatrix}$
cuyos elementos responden a la fórmula:
$\mathcal{R}_{ij}(\phi, \hat{n})=(1- \cos \phi)\, n_in_j + \cos \phi \, \delta_{ij} - \sin \phi \, \epsilon_{ijk} \ n_k$
Propiedades:
$\mathcal{R}(0\,, \hat{n})=I$
$\mathcal{R}(\phi, -\hat{n})= \mathcal{R}(-\phi, \hat{n})$
$\mathcal{R}(\phi, \hat{n})= \mathcal{R}(-\phi, -\hat{n})$
$\mathcal{R}(\pi, \hat{n})= \mathcal{R}(\pi, -\hat{n})$ (¡pero $\mathcal{R}(\phi, \hat{n}) \ne \mathcal{R}(\phi, -\hat{n})$ !) .
$(\mathcal{R}(\phi, \hat{n}))^{-1} = (\mathcal{R}(\phi, \hat{n}))^{T}= \mathcal{R}(-\phi, \hat{n})$
La relación entre los tres parámetros que especifican esta matriz de rotación y una tríada de ángulos de Euler es (cf. [GAL-89], p. 259):
$\cos \phi \, = \, \frac{1}{2}[Tr(\mathcal{R}) \, - \, 1] \quad ; \quad n_k \, = \, \frac{-1}{2\sin \phi} \ \epsilon_{ijk} \ \mathcal{R}_{ij}$ ,
donde $\mathcal{R} \, = \, \mathcal{R}_{act}(\alpha, \beta,\gamma)$ .
Ejemplos (rotaciones activas: se gira el sistema, su vector, en sentido antihorario, un ángulo positivo , en torno a la dirección señalada por el correspondiente vector unitario en un sistema cartesiano dado.
1. Giro en sentido antihorario de un ángulo $\phi > 0$ en torno al eje $OZ$ :
  $\mathcal{R}_{activa}(\phi, \hat{n})=\mathcal{R}_{activa}(\phi, \hat{k})=\begin{pmatrix} \cos\phi & -\sin \phi & 0 \\ \sin\phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{pmatrix}$
2. Giro en sentido antihorario de un ángulo $\phi > 0$ en torno al eje $OY$ :
  $\mathcal{R}_{activa}(\phi, \hat{n})=\mathcal{R}_{activa}(\phi, \hat{j})=\begin{pmatrix} \cos\phi & 0 & \sin \phi\\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{pmatrix}$
3. Giro en sentido antihorario de un ángulo $\phi > 0$ en torno al eje $OX$ :
  $\mathcal{R}_{activa}(\phi, \hat{n})=\mathcal{R}_{activa}(\phi, \hat{i})=\begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\phi & -\sin\phi \\ 0 & \sin\phi & \cos\phi \end{pmatrix}$
  
  Rotaciones elementales (imagen de: https://www.youtube.com/watch?v=8zZk__FwYsk).
Ejemplos (rotaciones pasivas: se giran los ejes; recuérdese que, dado , , representando el lado de la izquierda de la igualdad un giro en sentido horario de los ejes y el lado derecho un giro del sistema el mismo ángulo en valor absoluto pero con sentido antihorario; además, , en este caso los dos lados refiriendo a rotaciones en sentido antihorario):
1. Giro en sentido antihorario de un ángulo $\phi >0$ en torno al eje $OZ$ (este eje no cambia: $OZ'=OZ$ ):
  $\mathcal{R}_{pasiva}(\phi, \hat{n})=\mathcal{R}_{pasiva}(\phi, \hat{k})=\begin{pmatrix} \cos\phi & \sin \phi & 0 \\ -\sin\phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{pmatrix}$
2. Giro en sentido antihorario de un ángulo $\phi >0$ en torno al eje $OY$ (este eje no cambia: $OY'=OY$ ):
  $\mathcal{R}_{pasiva}(\phi, \hat{n})=\mathcal{R}_{pasiva}(\phi, \hat{j})=\begin{pmatrix} \cos\phi & 0 & -\sin \phi\\ 0 & 1 & 0 \\ \sin\phi & 0 & \cos\phi \end{pmatrix}$
3. Giro en sentido antihorario de un ángulo $\phi >0$ en torno al eje $OX$ (este eje no cambia: $OX'=OX$ ):
  $\mathcal{R}_{pasiva}(\phi, \hat{n})=\mathcal{R}_{pasiva}(\phi, \hat{i})=\begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\phi & \sin\phi \\ 0 & -\sin\phi & \cos\phi \end{pmatrix}$

Rotaciones y momento angular

En este apartado va a quedar establecida la acción de los operadores de momento angular como generadores de las rotaciones. Puesto que no se hará uso de la teoría de grupos, el tratamiento será superficial.

1. Rotaciones y momento angular orbital

Dado un sistema físico aislado, cuyo Hamiltoniano será por tanto independiente del parámetro temporal, y asumido que el espacio tridimensional es intrínsecamente isótropo, esto es, en su seno todas las direcciones son equivalentes, la física del sistema debe permanecer invariante bajo rotaciones en ese espacio, o sea, las leyes físicas que atañen al sistema deben permanecer invariantes bajo una rotación en el espacio.
Sea una partícula sin espín, sistema para el que las tres componentes del vector posición integran un C.C.O.C. Se prepara al sistema experimentalmente (medidas de primera especie) en el estado describible, en representación de coordenadas, por el vector $\Psi(\vec{r})$ del Hilbert asociado al sistema en el formalismo mecano-cuántico.
A continuación, se considera una rotación de ángulo $\phi \ge 0$ (sentido antihorario), $0 \le \phi \le \pi$ , alrededor de un eje de dirección dada por el vector unitario $\hat{n}$ , referido a un sistema de ejes cartesianos $OXYZ$ en el espacio. Bajo esta operación (véase [GAL-89], pp. 240ss.):
-un punto de coordenadas antes del giro $\vec{r}$ pasa a tener, en el mismo sistema de referencia (punto de vista activo), la coordenada
$\vec{r'} = \mathcal{R}(\phi, \hat{n}) \ \vec{r} \, \Leftrightarrow \, r_i'\ = \ \mathcal{R}_{ij}(\phi, \hat{n}) \ r_j$ ,
siendo $\mathcal{R}(\phi, \hat{n})$ la correspondiente matriz de rotación, de componentes
$\mathcal{R}_{ij}(\phi, \hat{n}=(1- \cos \phi)\, n_in_j + \cos \phi \, \delta{ij} - \sin \phi \, \epsilon_{ijk}n_k$
-el dispositivo girado preparará al sistema en el estado correspondiente a la nueva función de ondas $\Psi'(\vec{r})$ .
-si la partícula se hallaba en el estado $| \vec{r} >$ (representación de posiciones), probabilidad 100% de ser encontrada bajo medida en la posición $\vec{r}$ , tras la rotación pasará a tener un estado que debe ser proporcional al $| \vec{r'}>= | \mathcal{R}(\phi, \hat{n}) \ \vec{r} \ >$ , transformación de simetría implementable por el operador unitario $U_{\mathcal{R}}$ (teorema de Wigner) :
$| \vec{r} \ > \ \stackrel{\mathcal{R}(\phi, \hat{n})}{\longrightarrow} \ U_{\mathcal{R}}(\phi, \hat{n}) \ | \vec{r} > \propto \ | \mathcal{R}(\phi, \hat{n}) \ \vec{r} >$ ;
por lo tanto, debe ser
$U_{\mathcal{R}} \ | \vec{r} \ > \, = \, \lambda (\mathcal{R} , \vec{r} ) \ | \mathcal{R} \ \vec{r} > \; , \, \lambda \in \mathbb{C} \, , \, | \lambda | =1$
(por isotropía del espacio, debe conservarse para todo par de estados del Hilbert el producto escalar:
$<\Psi_1' \,| \, \Psi_2' > \,= \, < U_{\mathcal{R}} \ \Psi_1 \,| \,U_{\mathcal{R}} \ \Psi_2 > \,= \, <\Psi_1 \,| \, \Psi_2 >$ ).
Con la elección de fases adecuada ([GAL-89], p. 241), se establece que $\lambda$ no depende de $\vec{r}$ , derivándose que
$U_{\mathcal{R}} \ | \vec{r} > \ = \ | \mathcal{R} \ \vec{r} >$ ,
y lo mismo (elección de fases relativas para los autoestados de momento según [GAL-89], p. 129) para los autoestados del operador momento,
$U_{\mathcal{R}} \ | \vec{p} > \ = \ | \mathcal{R} \ \vec{p} >$
A partir de esta última ecuación se establece que la función de onda de una partícula sin grados de libertad internos se transforma bajo rotaciones como un escalar:
$\Psi'(\vec{r}) \, = \, (U_{\mathcal{R}} \ \Psi) (\vec{r}) \, = \,< \vec{r} \,| \,U_{\mathcal{R}} \, |\, \Psi > \, = \, < \mathcal{R}^{-1} \ \vec{r} \, | \, \Psi > \, = \, \Psi(\mathcal{R}^{-1} \ \vec{r} \ )$
$\Phi'(\vec{p}) \, = \,(U_{\mathcal{R}} \ \Phi) (\vec{p}) \, = \,< \vec{p} \,| \,U_{\mathcal{R}} \, |\, \Phi > \, = \, < \mathcal{R}^{-1} \ \vec{p} \, | \, \Phi > \, = \, \Phi(\mathcal{R}^{-1} \ \vec{r} \ )$
-En resumen: a partir de la isotropía asumida del espacio, que conlleva que las probabilidades de transición entre dos estados dados y sus sendos rotados deben conservarse, se deriva (teorema de Wigner) la unitariedad del operador $U_{\mathcal{R}}$ que efectúa la transformación de simetría «rotación en el espacio» de los estados cuánticos, el cual queda explicitado en su acción por este par de ecuaciones (con las elecciones de fases relativas adecuadas entre los estados de la base).

1.1. Rotaciones infinitesimales y momento angular orbital

Considérese ahora la transformación unitaria infinitesimal consistente en la rotación infinitesimal (la operación más próxima al elemento identidad del grupo de rotaciones) de ángulo $\delta$ suficientemente pequeño, esto es, tal que $\cos \delta \approx 1$ y $\sin \delta \approx 0$ , de modo que la matriz de rotación $\mathcal{R}(\delta,\hat{n})$ toma la expresión
$\mathcal{R}(\delta, \hat{n}) \ \approx \ \begin{pmatrix} 1 & -\delta \, n_z & \delta \, n_y\\ \delta \, n_z & 1 & -\delta \, n_x\\ -\delta \, n_y & \delta \, n_x & 1 \end{pmatrix}$
cuyos elementos responden a la fórmula:
$\mathcal{R}_{ij}(\delta, \hat{n}=\delta_{ij} - \delta \, \epsilon_{ijk}n_k$
$\Rightarrow \, \vec{r'} \, = \, \mathcal{R}(\delta, \hat{n}) \ \vec{r} \ \approx \ \begin{pmatrix} 1 & -\delta \, n_z & \delta \, n_y\\ \delta \, n_z & 1 & -\delta \, n_x\\ -\delta \, n_y & \delta \, n_x & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix}$
$= \, \begin{pmatrix} x - \delta n_z y + \delta n_y z \\ \delta n_z x + y - \delta n_x z \\ -\delta n_y x + \delta n_x y +z \end{pmatrix}$
$= \, \begin{pmatrix} x \\ y \\ z \end{pmatrix} \,+ \, \delta \ \begin{pmatrix} -n_z y + n_y z \\ n_z x - n_x z \\ -n_y x + n_x y \end{pmatrix}$
$= \, \begin{pmatrix} x \\ y \\ z \end{pmatrix} \,+ \, \delta \ \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ n_x & n_y & n_z \\ x & y & z \end{vmatrix}$
$= \, \vec{r} \, + \, \delta \ \hat{n} \times \vec{r} \, = \, \vec{r} \, - \, \delta \ \vec{r} \times \hat{n}$
De forma análoga, se obtiene
$\mathcal{R}^{-1}(\delta, \hat{n}) \ \approx \ \begin{pmatrix} 1 & \delta \, n_z & -\delta \, n_y\\ -\delta \, n_z & 1 & \delta \, n_x\\ \delta \, n_y & -\delta \, n_x & 1 \end{pmatrix}$
$\Rightarrow \, \vec{r} \, =\mathcal{R}^{-1}(\delta, \hat{n}) \ \vec{r'} \ \approx \ \begin{pmatrix} x' + \delta n_z y' - \delta n_y z' \\ -\delta n_z x' + y' + \delta n_x z' \\ \delta n_y x' - \delta n_x y' + z' \end{pmatrix}$
$= \, \vec{r'} \, - \, \delta \ \hat{n} \times \vec{r'} \, = \, \vec{r'} \, + \, \delta \ \vec{r'} \times \hat{n}$ ,
y también
$\mathcal{R}^{-1}(\delta, \hat{n}) \ \vec{r} \ \approx \ \, \vec{r} \, - \, \delta \ \hat{n} \times \vec{r} \, = \, \vec{r} \, + \, \delta \ \vec{r} \times \hat{n}$
Por lo tanto, usando las ecuaciones anteriores que explicitan la acción del operador $U_{\mathcal{R}}$ sobre un estado $\Psi$ ,
$\Psi'(\vec{r}) \, = \, (U_{\mathcal{R}} \ \Psi) (\vec{r}) \, = \, \Psi(\mathcal{R}^{-1} \ \vec{r} \ )$ ,
se obtiene que la rotación infinitesimal de ángulo $\delta$ produce
$\Psi'(\vec{r}) \, = \, (U_{\mathcal{R}}(\delta, \hat{n}) \ \Psi) (\vec{r}) \, = \, \Psi(\mathcal{R}^{-1}(\delta, \hat{n}) \ \vec{r} \ ) \, \approx \, \Psi(\vec{r} \, - \, \delta \ \hat{n} \times \vec{r})$ ,
que tras un desarrollo en serie de Taylor cortado en primer orden incluido se convierte en
$\Psi'(\vec{r}) \, = \, (U_{\mathcal{R}}(\delta, \hat{n}) \ \Psi) (\vec{r}) \, \approx \, \Psi(\vec{r}) \, - \, ( \delta \ \hat{n} \times \vec{r}) \cdot \nabla \Psi(\vec{r})$
$= \, \Psi(\vec{r}) \, - \frac{i}{\hbar} \ \delta \ (\hat{n} \times \vec{r}) \cdot \vec{p} \ \Psi(\vec{r})$
-Aplicando la ecuación
$\vec{B} \times \vec{C} \cdot \vec{A} =\vec{B} \cdot \vec{C} \times \vec{A}$ ,
se deriva finalmente:
$\Psi'(\vec{r}) \, = \, (U_{\mathcal{R}}(\delta, \hat{n}) \ \Psi) (\vec{r}) \, \approx \, \Psi(\vec{r}) \, - \frac{i}{\hbar} \ \delta \ \hat{n} \cdot (\vec{r} \times \vec{p}) \ \Psi(\vec{r})$
$\Rightarrow \, \Psi'(\vec{r}) \, = \, (U_{\mathcal{R}}(\delta, \hat{n}) \ \Psi) (\vec{r}) \, \approx \,\Psi(\vec{r}) \, - \frac{i}{\hbar} \ \delta \ \hat{n} \cdot \vec{L} \ \Psi(\vec{r})$ ,
donde $\vec{L}$ representa el momento angular orbital de la partícula, que queda así establecido como el generador de la rotación infinitesimal aplicada:
$U_{\mathcal{R}}(\delta, \hat{n}) \, \approx \, I \, - \, \frac{i}{\hbar} \ \delta \ (\hat{n} \cdot \vec{L})$
Por ejemplo, consideremos el de un giro infinitesimal de ángulo $\delta$ en torno al eje $OZ$ :
$\hat{n}=\hat{k} \Rightarrow \hat{k} \times \vec{r} = x \ \hat{j} - y \ \hat{i}$ ;
$\Psi'(\vec{r}) \, = \, (U_{\mathcal{R}}(\delta, \hat{k}) \ \Psi) (\vec{r}) \, = \, \Psi(\mathcal{R}^{-1}(\delta, \hat{k}) \ \vec{r} \ )$
$\approx \, \Psi(\vec{r} \, - \, \delta \ (x \ \hat{j} - y \ \hat{i})) \, = \, \Psi(x\, + \, \delta \ y \, , \, y\, - \, \delta \ x\,, \,z)$ ,
que tras un desarrollo en serie de Taylor cortado en primer orden incluido se convierte en
$\Psi'(\vec{r}) \, \approx \, \Psi(\vec{r} \, + \, \frac{\partial \Psi}{\partial x} \ (\delta \ y)\, - \, \frac{\partial \Psi}{\partial y} \ (-\delta \ x)$
$= \,\Psi(\vec{r}) \, + \, \delta \ (y \ \frac{\partial \Psi}{\partial x} \, - \, x \ \frac{\partial \Psi}{\partial y}) \, = \,\Psi(\vec{r}) \, + \, \delta \ \frac{i}{\hbar} \ (y \ p_x \, - \, x \ p_y) \ \Psi(\vec{r})$
$= \,\Psi(\vec{r}) \, - \, \frac{i}{\hbar} \ \delta \ (L_z) \ \Psi(\vec{r})= \,\Psi(\vec{r}) \, - \, \ \frac{i}{\hbar} \ \delta\ (\hat{k} \cdot \vec{L}) \ \Psi(\vec{r})$ ,
obteniéndose pues:
$U_{\mathcal{R}}(\delta, \hat{k}) \, \approx \, I \, - \, \frac{i}{\hbar} \ \delta\ (\hat{k} \cdot \vec{L})$ .
-En particular, las tres componentes del momento angular orbital $\vec{L}$ según un sistema de ejes coordenados $OXYZ$ constituyen los sendos generadores de las rotaciones infinitesimales en torno a los correspondientes ejes coordenados.
-Obsérvese que, puesto que las tres componentes de un momento angular no conmutan entre sí, dos rotaciones en torno a diferentes direcciones, en general, no conmutarán entre sí: se trata de un grupo no abeliano. Dos rotaciones sí conmutarán cuando se realicen en torno a la misma dirección.

1.2. Rotaciones finitas y momento angular orbital

Cualquier rotación finita puede considerarse como producida a partir de la aplicación sucesiva de rotaciones infinitesimales, todas alrededor del correspondiente eje de rotación; en particular, puede escribirse
$U_{\mathcal{R}}(\phi + \delta, \hat{n}) \, = \,U_{\mathcal{R}}(\delta, \hat{n}) \ U_{\mathcal{R}}(\phi , \hat{n}) \, = \, (I \, - \, \frac{i}{\hbar} \ \delta \ \hat{n} \cdot \vec{L}) \ U_{\mathcal{R}}(\phi , \hat{n})$
Tomando un desarrollo en serie de Taylor:
$U_{\mathcal{R}}(\phi + \delta, \hat{n}) \, \approx \, U_{\mathcal{R}}(\phi , \hat{n}) \, + \, \delta \ \frac{d \ U_{\mathcal{R}}}{d \ \phi}$
$\Rightarrow \, \delta \ \frac{d \ U_{\mathcal{R}}}{d \ \phi} \, = \, U_{\mathcal{R}}(\phi + \delta, \hat{n}) \, - \, U_{\mathcal{R}}(\phi , \hat{n})$
$= \, (I \, - \, \frac{i}{\hbar} \ \delta \ \hat{n} \cdot \vec{L}) \ U_{\mathcal{R}}(\phi , \hat{n}) \, - \, U_{\mathcal{R}}(\phi , \hat{n})$
$= \, - \, \frac{i}{\hbar} \ \delta \ (\hat{n} \cdot \vec{L}) \ U_{\mathcal{R}}(\phi , \hat{n}) \, \Rightarrow \, \frac{d \ U_{\mathcal{R}}}{d \ \phi} \, = \, - \, \frac{i}{\hbar} \ (\hat{n} \cdot \vec{L}) \ U_{\mathcal{R}}(\phi , \hat{n})$
Se obtiene pues una ecuación diferencial ordinaria lineal de primer orden homogénea, a la que se añade la condición de contorno
$U_{\mathcal{R}}(\phi=0 , \hat{n})\, = \, I$ ,
lo que determina la solución
$U_{\mathcal{R}}(\phi , \hat{n})\, = \, e^{- \frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})}$ ,
que identifica al operador momento angular orbital como el generador de las rotaciones finitas.
La generalización a un sistema de $N$ partículas es directa:
$U_{\mathcal{R}}(\phi , \hat{n})\, = \, e^{- \frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})} \quad , \; \vec{L} \, = \, \sum_i \ \vec{L_i}\,, \,i=1,\ldots,N$ ,
de forma que
$\Psi'( \vec{r}_1, \ldots , \vec{r_N}) \, = \, U_{\mathcal{R}}(\phi, \hat{n}) \ \Psi(\vec{r_1}, \ldots , \vec{r}_N)$
$=\Psi(\mathcal{R}^{-1}\vec{r}_1, \ldots ,\mathcal{R}^{-1}\vec{r}_N)$
$\approx \, e^{- \frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})}\Psi(\vec{r}_1, \ldots , \vec{r}_N)$
Propiedades:
1. Existencia de operador inverso:
  $\forall \; U_{\mathcal{R}}(\phi , \hat{n}) \; \exists \; U_{\mathcal{R}}^{-1}(\phi , \hat{n})$
  tal que
  $U_{\mathcal{R}}(\phi , \hat{n}) \ U_{\mathcal{R}}^{-1}(\phi , \hat{n}) \, = \, U_{\mathcal{R}}^{-1}(\phi , \hat{n}) \ U_{\mathcal{R}}(\phi , \hat{n}) \, = \, I$
2. No conmutatividad:
  $U_{\mathcal{R}}(\phi_1 , \hat{n}_1) \ U_{\mathcal{R}}(\phi_2 , \hat{n}_2) \, \ne \, U_{\mathcal{R}}(\phi_2 , \hat{n}_2) \ U_{\mathcal{R}}(\phi_1 , \hat{n}_1) \quad , \; \phi_1 \ne \phi_2 \; y \; \hat{n}_1 \ne \hat{n}_2$ ,
  una consecuencia directa de que $[\hat{n}_i \cdot \vec{J} \ , \ \hat{n}_j \cdot \vec{J} ] \, \ne 0 \; sii \; i \ne j$
  -Pero dos rotaciones en torno al mismo eje sí conmutan:
  $U_{\mathcal{R}}(\phi_1 , \hat{n}) \ U_{\mathcal{R}}(\phi_2 , \hat{n}) \, = \, U_{\mathcal{R}}(\phi_2 , \hat{n}) \ U_{\mathcal{R}}(\phi_1 , \hat{n}) \, = \, U_{\mathcal{R}}(\phi_1 + \phi_2, \hat{n})$
3. $U_{\mathcal{R}}(\phi_1, \hat{n}_1) \ U_{\mathcal{R}}(\phi_2, \hat{n}_2) \, = \, U_{\mathcal{R}}(\phi_3, \hat{n}_3)$
4. Asociativa:
  $(U_{\mathcal{R}}(\phi_1, \hat{n}_1) \ U_{\mathcal{R}}(\phi_2, \hat{n}_2)) \ U_{\mathcal{R}}(\phi_3, \hat{n}_3) \, = \, U_{\mathcal{R}}(\phi_1, \hat{n}_1) \ (U_{\mathcal{R}}(\phi_2, \hat{n}_2) \ U_{\mathcal{R}}(\phi_3, \hat{n}_3))$
5. $I \ U_{\mathcal{R}}(\phi, \hat{n}) \, = \, U_{\mathcal{R}}(\phi, \hat{n}) \ I \, = \, U_{\mathcal{R}}(\phi, \hat{n})$
6. Relación con los ángulos de Euler:
  $U_{\mathcal{R}}(\alpha, \beta, \gamma)\, = \, e^{- \frac{i}{\hbar} \alpha (\hat{k} \cdot \vec{L})} \ e^{- \frac{i}{\hbar} \beta (\hat{j} \cdot \vec{L})} \ e^{- \frac{i}{\hbar} \gamma (\hat{k} \cdot \vec{L})}$

1.3. Invariancia bajo rotaciones y conservación del momento angular orbital

Bajo la hipótesis de un espacio isótropo, sea un sistema físico sin grados de libertad intrínsecos (sin espín), que supondremos aislado y conservativo (no hay campos externos que le afecten; el Hamiltoniano es independiente del tiempo y representa la energía total del sistema). El sistema se define como invariante bajo rotaciones cuando cada estado del sistema $|\psi>$ y su transformado bajo la transformación de simetría «rotación», $|\psi'> = U_{\mathcal{R}} \ |\psi>$ , evolucionan según la misma ecuación de movimiento, la ecuación de Schrödinger:
$i \hbar \frac{d | \Psi>}{dt}=H|\Psi>$
$i \hbar \frac{d | \Psi'>}{dt}=H|\Psi'>$
(¡mismo operador $H$ en las dos ecuaciones!). Si se cumple esta condición, se implica que:
$i \hbar \frac{d | \Psi'>}{dt} =i \hbar \frac{d U_{\mathcal{R}} | \Psi>}{dt} =i \hbar U_{\mathcal{R}} \frac{d | \Psi>}{dt}= U_{\mathcal{R}} H|\Psi> =H|\Psi'>$ ,
ecuación donde se ha usado que la transformación de simetría $U_{\mathcal{R}}$ es finita continua y no depende del tiempo, como no lo hace $\vec{L}$ (imagen de Schrödinger).
Por lo tanto, $H$ y $U_{\mathcal{R}}$ han de conmutar, y por lo tanto, han de conmutar el operador generador de la simetría y el Hamiltoniano,
$[U_{\mathcal{R}}, H]=0 \Leftrightarrow [\vec{L}, H]=0$ ,
lo que garantiza que el hamiltoniano debe ser invariante bajo la transformación,
$H'=U_{\mathcal{R}}H U^+_{\mathcal{R}} =H$ ,
cumpliéndose así la definición dada de la invariancia bajo rotaciones del sistema en términos de la ES:
$i \hbar \frac{d | \Psi'>}{dt}=H U_{\mathcal{R}} | \Psi>=H|\Psi'>$
El resultado es recíproco: Un sistema físico compuesto por $N$ partículas sin estructura interna (esto, donde los operadores posición $\vec{r}$ y momento $\vec{p}$ de las $N$ partículas integran un C.C.O.C:.) es invariante bajo rotaciones si y sólo si su Hamiltoniano conmuta con el operador momento angular orbital total del sistema.
Como la transformación de simetría $U_{\mathcal{R}}$ es finita continua, con generador $\vec{L}$ independiente del tiempo, se deriva que el momento angular orbital $\vec{L}$ representa una constante del movimiento:
$\left\langle \vec{L} \right\rangle_{\psi(t)} \ne f(t)$ .

1.4. Transformación de estados y observables bajo rotaciones

Bajo la transformación de simetría que constituye el grupo de las rotaciones espaciales finitas, una operación de simetría implementada por el operador unitario
$U_{\mathcal{R}}(\phi , \hat{n})\, = \, e^{- \frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})}$ ,
con el operador momento angular orbital total ${L}$ como su generador, los estados y operadores se transforman según:
$\psi'(\vec{r}) \, = \, (U_{\mathcal{R}} \ \psi) (\vec{r}) \, = \, \psi(\mathcal{R}^{-1} \ \vec{r} \ )$
( $= \, < \vec{r} \ | \ U_{\mathcal{R}} | \psi > \, = \, < \mathcal{R}^{-1} \vec{r} \ | \ \psi >)$ ,
$A' \, = \, U_{\mathcal{R}} \ A \ U^+_{\mathcal{R}} \quad ,\quad A \, = \, U^+_{\mathcal{R}} \ A' \ U_{\mathcal{R}}$ ,
conservándose los elementos de matriz:
$\left\langle \psi' | A' | \varphi' \right\rangle = \left\langle \psi | A | \psi \right\rangle \quad \forall \; | \varphi > \, , \, | \psi > \in \mathcal{H}$ .
Propiedades (¡ya que $U_{\mathcal{R}}$ es unitario!):
-Si $| \psi> = \sum_n \,c_n \, | \phi_n>$ , entonces $| \psi'> = \sum_n \, c_n'| \phi_n'>$ , donde $|c_n|^2=|c_n'|^2$ .
-si $A$ es un observable del sistema, su relación de transformación bajo $U_{\mathcal{R}}$ conlleva que $A'$ es también un observable, y que poseen el mismo espectro, teniéndose:
$A\, |\psi_n>\,=\,a_n\,|\psi_n> \, \Rightarrow A'\, |\psi_n'>\,=\,a_n\,|\psi_n'>$ .
-el subespacio de $\mathcal{H}$ conformado por todos los vectores propios de $A'$ , para un valor propio determinado, es el transformado bajo $U_{\mathcal{R}}$ del subespacio propio de $A$ asociado al mismo valor propio.
-toda relación algebraica entre los observables del sistema se mantiene bajo $U_{\mathcal{R}}$
Ejemplos de transformación de operadores:
1. Operador posición (advertencia: se usa la misma notación que para el vector posición $\vec{r} \in \mathbb{R}^3$ ¡pero ahora se trata de un operador sobre el Hilbert: $\vec{r}\equiv \vec{r}_{op}:\mathcal{H} \rightarrow \mathcal{H}$ !):
  1.1. Rotación finita:
  $\vec{r'} \, = \, U_{\mathcal{R}} \ \vec{r} \ U^+_{\mathcal{R}}$ ;
  $\vec{r'} \, = \, e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})} \, \vec{r} \, e^{ \frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})}$
  $= \, \vec{r} \, + \, [-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L}) \, , \, \vec{r}] \, + \, \frac{1}{2!}\ [ -\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L}) \, \, , \, [-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L}) \, , \, \vec{r} \ ]] \, + \, \ldots$ ,
  donde se ha aplicado la ecuación del cálculo operatorial
  $e^ABe^{-A}=B+[A,B]+\frac{1}{2!} [A,[A,B]]+\ldots$
  -Etapas de cálculo:
  a) $[\hat{n} \cdot \vec{L} \, , \, r_i] \, = \, \sum_j n_j [L_j , r_i] \, = \, \sum_j n_j \ \sum_{kl} \epsilon_{jkl}[r_kp_l , r_i]$
  $= \, \sum_{jkl} n_j \epsilon_{jkl}r_k [p_l , r_i] \, = \, -i \hbar \sum_{jkl}n_j \epsilon_{jkl} r_k \delta_{li}\, = \, -i \hbar \sum_{jk}n_j \epsilon_{jki} r_k$
  $= \, -i \hbar ( \hat{n} \times \vec{r} )_i$
  b) $\Rightarrow \, -i\frac{\phi}{\hbar} [ \hat{n} \cdot \vec{L} \, , \, \vec{r}] \, = \, - \phi \ \hat{n} \times \vec{r} \, = \, \phi \ \vec{r} \times \hat{n}$
  c) $\hat{n} \times \vec{r} \, = \, (n_y z -n_z y ) \hat{i}+ (n_z x -n_x z ) \hat{j}+ (n_x y -n_y x ) \hat{k}$
  d) $\Rightarrow \, [ -\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L}) \, , \, [-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L}) \, , \, \vec{r}]]\,$ $= \, \frac{i}{\hbar} \phi^2 [ \hat{n} \cdot \vec{L} \, , \, \hat{n} \times \vec{r} ]$
  e) $[ \hat{n} \cdot \vec{L} \, , \, \hat{n} \times \vec{r} ]_x \, = \, [ \sum_j n_j L_j \, , \, n_y z - n_z y ] \, = \, n_y [ \hat{n} \cdot \vec{L} \, , z ]\, - \,n_z [ \hat{n} \cdot \vec{L} \, , y ]$
  $= \, (-i \hbar)(n_y( \hat{n} \times \vec{r})_z \, + \, n_z( \hat{n} \times \vec{r})_y )\, = \, -i \hbar (n_y (n_x y - n_y x) - n_z (n_z x - n_x z))$
  $= \, i \hbar [x(n_z^2 +n_y^2) -n_x n_y y - n_x n_z z] \, = \,i \hbar [x(n_y^2 +n_z^2) -n_x n_y y - n_x n_z z]$
  -finalmente:
  $\vec{r'} \, = \ \vec{r} \,- \, \phi \, \hat{n} \times \vec{r} \, + \, \frac{1}{2!} \ \, \frac{i}{\hbar} \phi^2 [ \hat{n} \cdot \vec{L} \, , \, \hat{n} \times \vec{r} ] \, + \, \ldots$
  $\equiv \ \vec{r} \,- \, \phi \, \hat{n} \times \vec{r} \, + \, O_{\ge}(\phi^2)$
  -Para la componente $x$ del operador posición:
  $x' \, = \, x\, - \, \phi \, (\hat{n} \times \vec{r} )_x \, + \, O_{\ge}(\phi^2) \, = \, x\, - \, \phi \, (n_y z -n_z y ) \, + \, O_{\ge}(\phi^2)$ ,
  y expresiones análogas para $y$ y $z$ .
  -Obsérvese que, formalmente, hemos establecido el mismo modo de transformación para el operador posición $\vec{r}_{op}$ bajo la simetría implementada por $U_{\mathcal{R}}$ que para el vector posición $\vec{r} \in \mathbb{R}^3$ bajo la rotación $\mathcal{R}^{-1}$ :
  $\vec{r}' \, = \, \mathcal{R}^{-1}(\phi, \hat{n}) \ \vec{r}$ .
  -Es decir: el operador posición $\vec{r}\equiv \vec{r}_{op}:\mathcal{H} \rightarrow \mathcal{H}$ se transforma bajo una rotación activa $\mathcal{R}(\phi,\hat{n})$ implementada por el operador unitario $U_{\mathcal{R}}=e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})}$ como lo hace el vector posición $\vec{r} \in \mathbb{R}^3$ bajo la correspondiente rotación pasiva dada por la matriz de rotación $\mathcal{R}^{-1}(\phi,\hat{n})$ ; recuérdense las expresiones de las matrices de rotación activa,
  $\mathcal{R}_{ij}(\phi, \hat{n})=(1- \cos \phi)\, n_in_j + \cos \phi \, \delta_{ij} - \sin \phi \, \epsilon_{ijk}n_k$
  y la correspondiente rotación pasiva:
  $\mathcal{R}^{-1}_{ij}(\phi, \hat{n})=(1- \cos \phi)\, n_in_j + \cos \phi \, \delta_{ij} + \sin \phi \, \epsilon_{ijk}n_k =\mathcal{R}_{ij}(-\phi, \hat{n})$
  1.2. Caso particular: rotación infinitesimal:
  $U_{\mathcal{R}}(\delta, \hat{n}) \, \approx \, I \, - \, \frac{i}{\hbar} \ \delta \ (\hat{n} \cdot \vec{L})$
  $\vec{r'} \, = \,(I \, - \, \frac{i}{\hbar} \ \delta \ \hat{n} \cdot \vec{L})\, \vec{r} \,(I \, + \, \frac{i}{\hbar} \ \delta \ \hat{n} \cdot \vec{L})$
  $= \, \vec{r} \, - \, \frac{i}{\hbar} \, \delta \, [\hat{n} \cdot \vec{L} , \vec{r} ] \, + \, O_{\ge}(\phi^2)$
  $\approx \, \vec{r} \, - \, \frac{i}{\hbar} \, \delta \ (i\hbar) \ \vec{r} \times \hat{n}\, = \, \vec{r} \, - \, \delta \ \ \hat{n} \times \vec{r}$
2. Operador momento: con la misma advertencia que antes, y de forma análoga, este operador sobre el Hilbert se transforma según:
  1.1. Rotación finita:
  $\vec{p'} \, = \, U_{\mathcal{R}} \ \vec{p} \ U^+_{\mathcal{R}}$ ;
  $\vec{p'} \, = \, e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})} \, \vec{p} \, e^{ \frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})}$
  $= \, \vec{p} \, + \, [-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L}) \, , \, \vec{p}] \, + \, \frac{1}{2!}\ [ -\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L}) \, \, , \, [-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L}) \, , \, \vec{p}\ ]] \, + \, \ldots$
  $\Rightarrow \vec{p'} \, = \ \vec{p} \,- \, \phi \, \hat{n} \times \vec{p} \, + \, \frac{1}{2!} \ \, \frac{i}{\hbar} \phi^2 [ \hat{n} \cdot \vec{L} \, , \, \hat{n} \times \vec{p} ] \, + \, \ldots$
  $\equiv \ \vec{p} \,- \, \phi \, \hat{n} \times \vec{p} \, + \, O_{\ge}(\phi^2)$
  -Es decir: el operador momento $\vec{p}\equiv \vec{p}_{op}:\mathcal{H} \rightarrow \mathcal{H}$ se transforma bajo una rotación activa $\mathcal{R}(\phi,\hat{n})$ implementada por el operador unitario $U_{\mathcal{R}}=e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{L})}$ como lo haría el vector momento $\vec{p} \in \mathbb{R}^3$ bajo la correspondiente rotación pasiva representada por la matriz de rotación $\mathcal{R}^{-1}(\phi,\hat{n})$ .
  1.2. Caso particular: rotación infinitesimal:
  $U_{\mathcal{R}}(\delta, \hat{n}) \, \approx \, I \, - \, \frac{i}{\hbar} \ \delta \ (\hat{n} \cdot \vec{L})$
  $\vec{p'} \, = \,(I \, - \, \frac{i}{\hbar} \ \delta \ \hat{n} \cdot \vec{L})\, \vec{p} \,(I \, + \, \frac{i}{\hbar} \ \delta \ \hat{n} \cdot \vec{L})$
  $= \, \vec{p} \, - \, \frac{i}{\hbar} \, \delta \, [\hat{n} \cdot \vec{L} , \vec{p} ] \, + \, O_{\ge}(\phi^2)$
  $\approx \, \vec{p} \, - \, \frac{i}{\hbar} \, \delta \ (i\hbar) \ \vec{p} \times \hat{n}\, = \, \vec{p} \, - \, \delta \ \ \hat{n} \times \vec{p}$
3. Operador momento angular: por ejemplo, el operador momento angular $\vec{J}$ se transforma bajo una rotación finita de ángulo $\phi$ en torno al eje OZ según:
  $\vec{J}' \, = \, U_{\mathcal{R}} \ \vec{J} \ U^+_{\mathcal{R}}$ ;
  $\vec{J}' \, = \, e^{-\frac{i}{\hbar} \ \phi \ (\hat{k} \cdot \vec{J})} \, \vec{J} \, e^{ \frac{i}{\hbar} \ \phi \ (\hat{k} \cdot \vec{J})}$
  $\begin{pmatrix} J_x' \\ J_y' \\ J_z' \end{pmatrix} \,= \, \begin{pmatrix} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{pmatrix} \ \begin{pmatrix} J_x \\ J_y \\ J_z \end{pmatrix}$

2. Rotaciones en el espacio de espín

Sea la función de onda general en el espacio de espín
$\chi_S \,= \, \sum_{m_s=-s}^{s} \, c_{m_s} \chi_{s,m_s} \quad , \quad c_{m_s} \, \in \mathbb{C}$
$\chi_S \, \doteq \, \begin{pmatrix} c_{m_s=s} \\ c_{m_s=s-1} \\ \cdots \\ c_{m_s=-s} \end{pmatrix} \quad , \quad \chi^+_S \chi_S \,=\,1 \,=\,\sum_{m_s=-s}^{s} | c_{m_s} |^2$ ,
interpretándose (supuesta cumplida la condición de normalización indicada) cada valor $| c_{m_s} |^2$ como la probabilidad de encontrar a la partícula en el estado de espín $\chi_{s,ms}$ , es decir, con resultado de la medida el valor $\hbar m_s$ para el número cuántico de tercera componente de espín $\vec{S}$ .
El generador de las rotaciones en el espacio de espín en torno a la dirección $\hat{n}$ es el operador $\hat{n} \cdot \vec{S}$ , y los operadores unitarios correspondientes a las rotaciones finitas de ángulo $\phi$ e infinitesimales de ángulo $\delta$ son, respectivamente:
$U_{\mathcal{R}}( \phi, \hat{n})\, \doteq \, U_S( \phi, \hat{n})\, = \, e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{S})}$
$U_{\mathcal{R}}( \delta, \hat{n})\, \doteq \, U_{S}(\delta, \hat{n}) \, \approx \, I \, - \, \frac{i}{\hbar} \ \delta \ (\hat{n} \cdot \vec{S})$
(deducción no trivial; en rigor, la expresión del operador $U_S(\phi, \hat{n})$ debería incorporar un signo $\pm$ global, puesto que el grupo de rotaciones es doblemente conectado; no lo explicitamos, aunque calcularemos que un estado de espín semientero necesitará rotar $4\pi$ para permanecer inalterado; véase [SCH-68], pp. 199-204 para una exposición simple; [GAL-89], pp. 245ss. para una discusión más profunda).
-Por tanto, una función de espín $\chi_S$ se transforma pues bajo rotaciones según
$\chi_S'=U_S( \phi, \hat{n}) \ \chi_S$ .
En particular, en el caso de espín $\frac{1}{2}$ se tiene, bajo una rotación finita:
$\vec{S}=\frac{\hbar}{2} \vec{\sigma}$
$\chi_{S=\frac{1}{2}}'=U_{S=\frac{1}{2}} \ \chi_{S=\frac{1}{2}} \equiv U_{S=\frac{1}{2}} \begin{pmatrix} c_{m_s=+\frac{1}{2}} \\ c_{m_s=-\frac{1}{2}} \end{pmatrix}$
$= e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{S})} \ \chi_{S=\frac{1}{2}}= e^{-i\frac{\phi}{2} \ (\hat{n} \cdot \vec{\sigma})} \ \chi_{S=\frac{1}{2}}$
-El operador de rotación $U_{S=\frac{1}{2}}(\phi, \hat{n})$ admite la expresión:
$U_{\frac{1}{2}}(\phi, \hat{n}) \, = \, \sum_{k=0}^{\infty} \frac{i^{2k}}{(2k)!} (\frac{\phi}{2})^{2k} (\hat{n} \cdot \vec{S})^{2k} - \sum_{k=0}^{\infty} \frac{i^{2k+1}}{(2k+1)!} (\frac{\phi}{2})^{2k+1} (\hat{n} \cdot \vec{S})^{2k+1}$ ,
que, haciendo uso de las propiedades de las matrices de Pauli se convierte en:
$\left. \begin{array}{c} (\vec{\sigma} \cdot \vec{A})(\vec{\sigma} \cdot \vec{B}) = \vec{A} \cdot \vec{B} +i \vec{\sigma}(\vec{A} \times \vec{B}) \\ (\hat{n} \cdot \vec{\sigma})^2 = \hat{n} \cdot \hat{n} +i \vec{\sigma}(\hat{n} \times \hat{n})=I^{(S=\frac{1}{2})}+0 \equiv \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \end{array} \right\}$
$\left. \begin{array}{c} (\hat{n} \cdot \vec{\sigma})^{2k} = I^{(S=\frac{1}{2})} \equiv \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \\ i^{2k}=(-1)^k\ , \, i^{2k+1}=i i^{2k}=i(-1)^k \end{array} \right\}$
$\Rightarrow e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{S})} = \sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k)!} (\frac{\phi}{2})^{2k} - i\sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2k+1)!} (\frac{\phi}{2})^{2k+1} (\hat{n} \cdot \vec{\sigma})$
$\Rightarrow U_{\frac{1}{2}}(\phi, \hat{n}) \, = \, e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{S})} \, = \, (I\cos \frac{\phi}{2} -i\hat{n} \cdot \vec{\sigma} \sin \frac{\phi}{2})$ .
-Por lo tanto, la ecuación de transformación bajo rotaciones finitas de un estado de espín $S=\frac{1}{2}$ tiene la expresión:
$\chi_{S=\frac{1}{2}}'=U_{\frac{1}{2}}(\phi, \hat{n}) \ \chi_{S=\frac{1}{2}} \, = \, e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{S})} \ \chi_{S=\frac{1}{2}} \, = \, (I\cos \frac{\phi}{2} -i \ \hat{n} \cdot \vec{\sigma} \sin \frac{\phi}{2}) \chi_{S=\frac{1}{2}}$
Ejemplos:
1. Rotación finita de ángulo $\phi$ alrededor del eje $OZ$ del estado $S=\frac{1}{2}$ :
  $\chi_{S=\frac{1}{2}}'=U_s \ \chi_{S=\frac{1}{2}}=(I\cos \frac{\phi}{2} -i\hat{k} \cdot \vec{\sigma} \sin \frac{\phi}{2}) \chi_{S=\frac{1}{2}}$
  $=(I\cos \frac{\phi}{2} -i\sigma_z \sin \frac{\phi}{2}) \chi_{S=\frac{1}{2}}$
  $= [ \begin{pmatrix} \cos \frac{\phi}{2} & 0 \\ 0 & \cos \frac{\phi}{2} \end{pmatrix} -i \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \sin \frac{\phi}{2} ] \ \chi_{S=\frac{1}{2}}$
  $= \begin{pmatrix} \cos \frac{\phi}{2} - i\sin \frac{\phi}{2} & 0 \\ 0 & \cos \frac{\phi}{2} +i \sin \frac{\phi}{2}\end{pmatrix} \ \chi_{S=\frac{1}{2}}$
  $= \begin{pmatrix} e^{-i\frac{\phi}{2}} & 0 \\ 0 & e^{i\frac{\phi}{2}}\end{pmatrix} \chi_{S=\frac{1}{2}}$
  $\equiv \begin{pmatrix} e^{-i\frac{\phi}{2}} & 0 \\ 0 & e^{i\frac{\phi}{2}}\end{pmatrix}) \ \begin{pmatrix} c_{m_s=+\frac{1}{2}} \\ c_{m_s=-\frac{1}{2}} \end{pmatrix} =\begin{pmatrix} e^{-i\frac{\phi}{2}} \ c_{m_s=+\frac{1}{2}} \\ e^{i\frac{\phi}{2}} \ c_{m_s=-\frac{1}{2}} \end{pmatrix}$
2. Rotación finita de ángulo $\phi=2\pi$ alrededor del eje $OZ$ del estado $S=\frac{1}{2}$ :
  $\chi_{S=\frac{1}{2}}'=-\chi_{S=\frac{1}{2}}$ .
  Este cambio global resulta indetectable experimentalmente, ya que todas las cantidades medibles (como los elementos de matriz, los valores medios…) dependen bilinealmente del estado (podría observarse de forma local, usando un haz desdoblado y un dispositivo tipo doble rendija, véase [GAL-89]p.262).
3. Rotación finita de ángulo $\phi=2\pi$ alrededor del eje $OZ$ del estado de espín general $\chi_S$ :
  $\chi_{S}'=U_S(\phi=2\pi , \hat{n}=\hat{k}) \ \chi_S = e^{-\frac{i}{\hbar} \ 2\pi \ (\hat{k} \cdot \vec{S})} \ \chi_{S}$
  $= e^{-\frac{2\pi i}{\hbar} \ S_z } \ \sum_{m_s=-s}^{s} \, c_{m_s} \chi_{s,m_s}= e^{-\frac{2\pi i}{\hbar} \ \hbar m_s } \ \sum_{m_s=-s}^{s} \, c_{m_s} \chi_{s,m_s}$
  $= e^{-2\pi i m_s} \ \sum_{m_s=-s}^{s} \, c_{m_s} \chi_{s,m_s} = e^{-2\pi i m_s} \ \chi_{S}$
  $\Rightarrow \chi_{S}'=U_S(\phi=2\pi , \hat{k}) \ \chi_S = (-1)^{2s} \ \chi_S$ ,
  de forma que los estados de espín entero se mantienen inalterados bajo estas rotaciones, mientras que los de espín semi-entero cambian de signo.

3. Rotaciones y momento angular total
3.1. Generador de las rotaciones en sistemas con espín

Dado un sistema físico aislado, cuyo Hamiltoniano será por tanto independiente del parámetro temporal, y asumido que el espacio tridimensional es intrínsecamente isótropo, esto es, en su seno todas las direcciones son equivalentes, la física del sistema debe permanecer invariante bajo rotaciones en ese espacio, o sea, las leyes físicas que atañen al sistema deben permanecer invariantes bajo una rotación en el espacio.
Sea una partícula con espín, sistema para el que las tres componentes del vector posición más la tercera componente del espín integran un C.C.O.C.; dado este C.C.O.C. (representación), $\{\vec{r}, S_z \}$ , para cada ket $| \Psi(t)>\in \mathcal{H}$ la función de onda general en representación de posiciones, $\Psi(\vec{r},\sigma,t)$ , admite desarrollo en serie en términos de las autofunciones de espín:
$\Psi(\vec{r},\sigma,t)\,=\,\sum_{m_s=-s}^{s} \, \psi_{m_s}(\vec{r},t)\, \chi_{s,m_s} \quad ,\; \psi_{m_s}(\vec{r},t)\,=\,< \vec{r} \,\sigma | \Psi(t) >$
-Por tanto, una partícula de espín $S$ es descrita por una función de onda espinor $\Psi(\vec{r},\sigma,t)$ con $2s+1$ componentes $\Psi_{m_s}(\vec{r},t)$ , cada una de ellas asociada a un valor particular de los $2s+1$ valores para el número cuántico de tercera componente $m_s$ ,o sea , equivalentemente, para la variable $\sigma=\hbar m_s$ , la cual, a diferencia de $\vec{r}$ , es una variable discreta.
-En definitiva, el espacio de Hilbert del sistema se realiza para el sistema con espín $S$ como el espacio funcional $L^2(\mathbb{R}^3)\otimes \mathbb{C}^{2s+1}$ .
Pueden usarse diferentes tipos de notaciones para los espinores:
$\Psi(\vec{r},\sigma,t)$
$\doteq \,\sum_{m_s=-s}^{s} \, \psi_{m_s}(\vec{r},t)\, \chi_{s,m_s}$ ,
donde
$\psi_{m_s}(\vec{r},t) =\, < \vec{r},\sigma=\hbar m_s | \Psi(t) >$ .
-En términos matriciales:
$\begin{pmatrix} \psi_{m_s=s}(\vec{r},t) \\ \psi_{m_s=s-1}(\vec{r},t) \\ \cdots \\ \psi_{m_s=-s}(\vec{r},t) \end{pmatrix}$ $=\,\begin{pmatrix} < \vec{r} \,\sigma=\hbar s | \Psi(t) > \\ < \vec{r} \,\sigma=\hbar (s-1) | \Psi(t) > \\ \cdots \\ < \vec{r} \,\sigma=-\hbar s | \Psi(t) > \end{pmatrix}$
El generador de las rotaciones en el espacio de Hilbert asociado a una partícula con espín, por ejemplo su realización funcional $L^2(\mathbb{R}^3)\otimes \mathbb{C}^{2s+1}$ , para una rotación en torno a la dirección $\hat{n}$ , es el operador $\hat{n} \cdot \vec{J}$ , esto es, la proyección del momento angular total $\vec{J}=\vec{L} \otimes I^{(S)}+ I^{(L)}\otimes \vec{S} \doteq \vec{L} + \vec{S}$
sobre esa dirección del espacio, y los operadores unitarios correspondientes a las rotaciones finitas de ángulo $\phi$ e infinitesimales de ángulo $\delta$ son, respectivamente:
$U_{\mathcal{R}}( \phi, \hat{n})=e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{J})}$
$U_{\mathcal{R}}(\delta, \hat{n}) \, \approx \, I \, - \, \frac{i}{\hbar} \ \delta \ (\hat{n} \cdot \vec{J})$
-La deducción de estas expresiones es complicada. En rigor, la expresión del operador $U_{\mathcal{R}}(\phi, \hat{n})$ debería incorporar un signo $\pm$ global; véase [GAL-89], pp. 246. Y es que los operadores $U_{\mathcal{R}}$ forman un grupo isomorfo al grupo de rotaciones sólo si el sistema contiene un número par de partículas de espín semi-entero; si el número es impar, existe sólo un homomorfismo dos a uno entre ambos grupos. En términos de teoría de grupos, las matrices de rotación van a proporcionar una representación proyectiva unitaria del grupo de rotación SO(3); cada una de las dos representaciones (signos $\pm$ ) correspondería a una representación del grupo de cobertura de SO(3), que es SU(2). Todos estos detalles deben estudiarse en el ámbito de la teoría de grupos, no contemplada en estos apuntes.
-Por tanto, un espinor $\Psi(\vec{r},\sigma,t)$ se transforma bajo rotaciones según
$\Psi'(\vec{r},\sigma,t)=U_{\mathcal{R}} \ \Psi(\vec{r},\sigma,t)$ :
-Se prepara al sistema experimentalmente (medidas de primera especie) en el estado describible, en representación de coordenadas, por el espinor $\Psi(\vec{r}, \sigma)$ del Hilbert asociado al sistema en el formalismo mecano-cuántico. A continuación, se considera una rotación de ángulo $\phi \ge 0$ (sentido antihorario), $0 \le \phi \le \pi$ , alrededor de un eje de dirección dada por el vector unitario $\hat{n}$ , referido a un sistema de ejes cartesianos $OXYZ$ en el espacio. Bajo esta operación:
$\Psi'(\vec{r},\sigma,t)\,=\,U_{\mathcal{R}}( \phi, \hat{n}) \ \Psi(\vec{r},\sigma,t)$
$=\, e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{J})} \ \Psi(\vec{r},\sigma,t)\, = \,e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{J})} \ \sum_{m_s=-s}^{s} \, \psi_{m_s}(\vec{r},t)\, \chi_{s,m_s}$
$\equiv \,\begin{pmatrix} \psi'_{m_s=s}(\vec{r},t) \\ \psi'_{m_s=s-1}(\vec{r},t) \\ \cdots \\ \psi_{m_s=-s}(\vec{r},t) \end{pmatrix} \, = \, (\mathcal{D}) \begin{pmatrix} \psi_{m_s=s}(\vec{r},t) \\ \psi_{m_s=s-1}(\vec{r},t) \\ \cdots \\ \psi_{m_s=-s}(\vec{r},t) \end{pmatrix}$ ,
donde $(\mathcal{D})$ representa una matriz de dimensión $(2s+1)(2s+1)$ ,
teniéndose pues elemento a elemento:
$\psi_{m_s}'(\vec{r},t)\,=\, \left( e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \vec{J})} \ \Psi(\vec{r},\sigma,t) \right)_{m_s}(\vec{r},t)$
$\Leftrightarrow \, \psi_{m_s}'(\vec{r},t)\,=\, \sum_{m_s'}\mathcal{D}_{m_s m_s'}(\mathcal{R}) \ \psi_{m_s'} (\mathcal{R}^{-1}\vec{r},t)$
La generalización al sistema de $N$ partículas de espín $S$ es directa (ignoramos el parámetro tiempo por simplicidad de la notación):
$\Psi'(\vec{r}_1,\sigma_1=\hbar m_{s1} ; \ldots ; \vec{r}_N,\sigma_N=\hbar m_{sN}; t)$
$=\,U_{\mathcal{R}}( \phi, \hat{n}) \ \Psi(\vec{r}_1,\sigma_1=\hbar m_{s1} ; \ldots ; \vec{r}_N,\sigma_N=\hbar m_{sN}; t)$
$=\, e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \sum_{k=1}^N \vec{J_k})} \ \Psi(\vec{r}_1,\sigma_1=\hbar m_{s1} ; \ldots ; \vec{r}_N,\sigma_N=\hbar m_{sN}; t)$
$= \,e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \ \sum_{k=1}^N (\vec{L}_k + \vec{S}_k)} \ \sum_{m_{s1}=s_1}^{-s_1} \ldots \sum_{m_{sN}=s_N}^{-s_N} \, \psi_{m_{s1},\ldots,m_{sN}}(\vec{r}_1, \ldots , \vec{r}_N ;t)\, \chi_{s,m_{s1}} \dots \chi_{s,m_{sN}}$
teniéndose pues:
$\psi'_{m_{s1},\ldots,m_{sN}}(\vec{r}_1, \ldots , \vec{r_N} ;t)\,=\, \left( U_{\mathcal{R}}(\hat{n},\phi ) \ \psi \right)_{m_{s1},\ldots,m_{sN}}(\vec{r}_1, \ldots , \vec{r_N} ; t)$
$\, = \, \left( e^{-\frac{i}{\hbar} \ \phi \ (\hat{n} \cdot \sum_{k=1}^N (\vec{L_k} + S_k))} \ \Psi \right)_{m_{s1},\ldots,m_{sN}}(\vec{r}_1, \ldots , \vec{r_N} ; t)$
$\Leftrightarrow \,\psi'_{m_{s1},\ldots,m_{sN}}(\vec{r}_1, \ldots , \vec{r_N} ;t)$
$= \, \sum_{m_{s1}',\ldots,m_{sN}'} \ \mathcal{D}_{ m_{s1} m_{s1}'}^{(1)}(\mathcal{R}) \ \ldots \ \mathcal{D}_{ m_{sN} m_{sN}'}^{(N)}(\mathcal{R})\ \psi_{m_{s1}',\ldots,m_{sN}'} (\mathcal{R}^{-1}\vec{r}_1, \ldots ,\mathcal{R}^{-1}\vec{r}_N;t)$ ,
donde cada operador $\vec{L}_k$ actúa sobre las variables $\vec{r}_k$ , $k=1,\ldots,N$ ; mientras que cada operador $\vec{S}_k$ actúa sobre las variables de espín $m_{sk}$ , $\sigma_k=\hbar m_{sk} \, , \, {sk}=s_k,s_k-1,\ldots,-s_k$ .

3.2. Transformaciones de la base acoplada y expresión matricial de los operadores de rotación

La rotación activa positiva (sentido antihorario) $\mathcal{R} \equiv \mathcal{R}_{act}(\alpha, \beta,\gamma)$ , rotación del sistema, caracterizada por los tres ángulos de Euler $( \alpha, \beta,\gamma )$ , que es equivalente a una rotación de ángulo $\phi$ en torno a la dirección $\hat{n}$ de valores
$\phi= \arccos \{ \frac{1}{2} \ [Tr (\mathcal{R}) -1] \}$ ,
$n_k= -\frac{1}{2\sin \phi} \epsilon_{kij} \mathcal{R}_{ij}$ ,
se corresponde con el operador rotación
$U_{\mathcal{R}}( \alpha, \beta,\gamma )\, = \, e^{\frac{-i \alpha J_z}{\hbar}} \ e^{\frac{-i \beta J_y}{\hbar}} \ e^{\frac{-i \gamma J_z}{\hbar}}$ ,
donde $J_i$ simboliza cada componente del operador momento angular total, el generador de las rotaciones.
Transformación de los estados de la base acoplada, $| JM > \in \mathcal{H}^{(J)}$ bajo el grupo de rotaciones:
$U_{\mathcal{R}}( \alpha, \beta,\gamma ) \ |JM> \, = \,\sum_{M'} \ |JM'><JM' | U_{\mathcal{R}}( \alpha, \beta,\gamma ) |JM>$
$\equiv \,\sum_{M'} \ <JM' | U_{\mathcal{R}}( \alpha, \beta,\gamma ) |JM> \ |JM'>$
$\doteq \,\sum_{M'} \ \mathcal{D}_{M'M}^J ( \alpha, \beta,\gamma ) \ |JM'>$ ,
expresión que define la matriz del operador de rotación $U_{\mathcal{R}}( \alpha, \beta,\gamma )$ en la base acoplada, o matriz de Wigner, de valor:
$\mathcal{D}_{M'M}^J ( \alpha, \beta,\gamma ) \, = \, <JM' | U_{\mathcal{R}}( \alpha, \beta,\gamma ) |JM>$
$=\,<JM' | e^{\frac{-i \alpha J_z}{\hbar}} \ e^{\frac{-i \beta J_y}{\hbar}} \ e^{\frac{-i \gamma J_z}{\hbar}} |JM>$
$=\,e^{-i \alpha M'} \ <JM' | \ e^{\frac{-i \beta J_y}{\hbar}} \ |JM> \ e^{-i \gamma M}$
$\doteq \,e^{-i \alpha M'} \ \mathsf{d}_{M'M}^J ( \beta ) \ e^{-i \gamma M}$ ,
expresión que define la matriz pequeña de Wigner, $\mathsf{d}$ :
$\mathsf{d}_{M'M}^J ( \beta )\,= \, <JM' | \ e^{\frac{-i \beta J_y}{\hbar}} \ | JM>$ .
calculada de forma general por Wigner en 1931 (ésta y variadas fórmulas adicionales pueden encontrarse en el apéndice B de la referencia [GAL-89]).
Caso particular: sea $J=\frac{1}{2}$ :
$e^{\frac{-i \beta J_y}{\hbar}}=e^{-i \frac{\beta }{2}\sigma_y}=I\cos \frac{\beta}{2} -i \sigma_y \sin \frac{\beta}{2}$
$\Rightarrow \, \mathsf{d}^{\frac{1}{2}} ( \beta )\,= \, \begin{pmatrix} \cos \frac{\beta}{2} & -\sin \frac{\beta}{2} \\ \sin \frac{\beta}{2} & \cos \frac{\beta}{2} \end{pmatrix}$
-Por ejemplo:
$\mathsf{d}_{\frac{1}{2} -\frac{1}{2}}^J ( \beta )\,= \, <\frac{1}{2}\frac{1}{2}| \ I \cos \frac{\beta}{2} -i \sigma_y \sin \frac{\beta}{2}\ | \frac{1}{2} -\frac{1}{2}>$
$=1 . \cos \frac{\beta}{2} . 0 \, -i .\sin \frac{\beta}{2} . (-i) = -\sin \frac{\beta}{2}$
$\Rightarrow \, \mathcal{D}^{\frac{1}{2}} ( \alpha ,\beta , \gamma)\,= \, \begin{pmatrix} \cos \frac{\beta}{2} \ e^{ \frac{-i(\alpha + \gamma)}{2}} & -\sin \frac{\beta}{2} \ e^{ \frac{-i(\alpha - \gamma)}{2}} \\ \sin \frac{\beta}{2} \ e^{ \frac{i(\alpha - \gamma)}{2}}& \cos \frac{\beta}{2} \ e^{ \frac{i(\alpha + \gamma)}{2}} \end{pmatrix}$
Transformación de los estados de la base:
$U_{\mathcal{R}}( \alpha, \beta,\gamma ) \ |\frac{1}{2}\frac{1}{2}> \, = \, \cos \frac{\beta}{2} \ e^{ \frac{-i(\alpha + \gamma)}{2}} \ | \frac{1}{2}\frac{1}{2}> \, + \, \sin \frac{\beta}{2} \ e^{ \frac{i(\alpha - \gamma)}{2}} \ | \frac{1}{2} -\frac{1}{2}>$
$U_{\mathcal{R}}( \alpha, \beta,\gamma ) \ |\frac{1}{2} -\frac{1}{2}> \, = \, -\sin \frac{\beta}{2} \ e^{ \frac{-i(\alpha - \gamma)}{2}} \ | \frac{1}{2}\frac{1}{2}> \, + \, \cos \frac{\beta}{2} \ e^{ \frac{i(\alpha + \gamma)}{2}} \ | \frac{1}{2} -\frac{1}{2}>$