La partícula libre 3D

Partícula libre: propagación de una onda plana — Propagación de la función de onda de partículas libres ( 1D); la parte real de la amplitud compleja es azul, la parte imaginaria es verde; no hay una posición definida de la partícula.

Ecuación de Schrödinger para la partícula libre

Sea una partícula libre en el espacio tridimensional, esto es, en el seno de un potencial constante, que elegimos, por simplicidad, nulo, $V(r)=0$ . La correspondiente ecuación de Schrödinger,
$i\hbar \ \frac{\partial}{\partial t}\Psi(\vec{r};t)= H \ \Psi(\vec{r};t)\, = \, [-\frac{\hbar^2}{2m}\nabla^2] \ \Psi(\vec{r};t) \, = \, E \ \Psi(\vec{r};t)$ ,
tiene como soluciones las denominadas ondas planas, que fueron desarrolladas en el caso monodimensional. La generalización a tres dimensiones es directa:
-Considerada una partícula material libre no relativista, de masa $m \ne 0$ , con energía $E$ y momento $\vec{p}$ bien definido, $E=\frac{\vec{p}^2}{2m}$ , se le asocia una onda plana que viaja en la misma dirección, con número de ondas $\vec{k}=\frac{\vec{p}}{\hbar}$ , de expresión
$\Psi(\vec{r};t)\, = \, A \ e^{i[\vec{k}\cdot\vec{r}-\omega(k)t]} \, = \, A \ e^{i[\vec{p}\cdot\vec{r}-E(p)t]/ \hbar}$ ,
donde $A$ es una constante (real o compleja); $\omega(k)=\frac{\hbar k^2}{2m}$ , satisfaciendo el par de ecuaciones diferenciales:
$\hat{\vec{p}} \ \Psi(\vec{r};t) \, = \, -i\hbar \ \nabla\Psi(\vec{r};t)\, = \, \vec{p} \ \Psi(\vec{r};t)$ y
$\hat{E} \ \Psi(\vec{r};t) \, = \, i\hbar \ \frac{\partial}{\partial t}\Psi(\vec{r};t) \, = \, E \ \Psi(\vec{r};t)$ .
La ecuación de Schrödinger se satisface tanto para ondas planas como para paquetes de onda (un paquete no es sino una superposición de las primeras).
Es obvio que una partícula libre constituye un sistema conservativo en el seno de un potencial nulo (constante), de modo que la correspondiente ecuación de Schrödinger independiente del tiempo,
$H \ \psi(\vec{r}) \, = \, [-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})]\psi(\vec{r})\, = \, E \ \psi(\vec{r})$ ,
se reduce en este caso, eligiendo el valor constante del potencial $V(\vec{r})=V_0$ como nulo, a la ecuación de autovectores o valores propios para el operador energía cinética:
$H\psi(\vec{r}) \ = \ -\frac{\hbar^2}{2m}\nabla^2 \ \psi(\vec{r}) \ = \ E\psi(\vec{r})$ .
Las soluciones de esta ecuación vamos a establecer a continuación detalladamente que coinciden con la parte espacial de las ondas planas, las funciones $C \ e^{i \vec{k}\cdot\vec{r} }$ , donde $C$ representa una constante de normalización, autofunciones del Hamiltoniano correspondientes a los autovalores de energía
$E = \frac{\hbar |\vec{k}|^2 }{2m} \ = \ \frac{|\vec{p}|^2 }{2m}$ .
-El Hamiltoniano en este caso, que coincide con el operador energía cinética, tiene pues un espectro continuo, igual a la semirrecta real positiva finita, incluido el cero, $[0\infty )$ , con autovalores infinitamente degenerados, salvo el nulo: la energía depende de $|\vec{k}|$ , y para cada $\vec{k} \ne 0$ son posibles infinitas orientaciones (constituyendo un conjunto no numerable).

Resolución de la ecuación de Schrödinger independiente del tiempo para el sistema conservativo de una partícula libre en coordenadas cartesianas

Sea una partícula libre de masa $m$ , y sea la correspondiente ES independiente del tiempo,
$H \ \psi(\vec{r}) \, = \, [-\frac{\hbar^2}{2m}\nabla^2+V_0 \ ] \ \psi(\vec{r})\, = \, E \ \psi(\vec{r})$ ;
se trata de un Hamiltoniano aditivo en coordenadas cartesianas: no es sino el operador energía cinética (elección $V_0=0$ ):
$H=-\frac{\hbar^2}{2m}\nabla^2=H_x(x) + H_y(y)+ H_z(z)$ ,
donde cada sumando $H_i(r_i)$ tiene la expresión
$H_i(r_i)=-\frac{\hbar^2}{2m} \ \frac{\partial^2}{\partial r_i^2} \quad ; \; i=x,y,z \; ; \; r_i \equiv i$ .
-Separando variables según el procedimiento habitual:
1. Factorización de la función:
$\psi_E(\vec{r}=(x,y,z)) = X(x) \ Y(y) \ Z(z) \equiv \prod_{x,y,z} R_i(r_i)$
2. Sustitución en la ecuación:
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2} \ \} \prod_{x,y,z} R_i(r_i)=E \ \prod_{x,y,z} R_i(r_i)$
3. División por la función:
$\sum_i \{ (-\frac{\hbar^2}{2m}) \frac{1}{R_i(r_i)} \frac{d^2 R_i(r_i)}{d r_i^2}\ \} =E$
4. Igualación de cada sumando de dependencia exclusiva en cada coordenada $r_i$ a una constante con dimensiones de energía, $E_i$ :
$\{ (-\frac{\hbar^2}{2m}) \ \frac{d^2}{d r_i^2} \ \} R_i(r_i)=E_i \ R_i(r_i)$ ,
con la condición
$E=\sum_i E_i=E_x+E_y+E_z$ .
Una vez conseguido convertir el problema tridimensional en la resolución de tres problemas monodimensionales, basta recuperar las correspondientes soluciones del caso monodimensional, las ondas planas $\psi_{k_i}(r_i)=e^{\pm ik_ir_i} \; , \; \vec{p_i}=\hbar \vec{k_i} \; ; \; i=x,y,z \; ; \; r_i \equiv i$ , autofunciones generalizadas de los operadores energía cinética $-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial r_i^2}$ (con autovalor $E_i=\frac{\hbar^2 k_i^2}{2m} \ge 0 \; ; \; i=x,y,z$ ) y momento lineal $p_{r_i}=-i \hbar \frac{\partial}{\partial r_i}$ (autovalor $\pm \hbar k_i$ ), obteniéndose la solución general:
$R_i(r_i)\, = \, Ae^{ik_ir_i} \, + \, Be^{-ik_ir_i} \quad ; \; i=x,y,z \; ; \; r_i \equiv i$ ,
con $A$ y $B$ constantes arbitrarias.
La solución general, por tanto, admite expresión como combinación lineal de funciones del tipo
$\psi_{\vec{k}}(\vec{r}) \,= \, C \ e^{i\ \vec{k} \cdot \vec{r}}\, = \, C \ e^{i\ \vec{p} \cdot \vec{r} / \hbar} \; ; \; \vec{k}=(k_x,k_y,k_z) \; ; \; \vec{p}=(p_x,p_y,p_z)$ ,
donde $C$ es una constante (real o compleja). Estas funciones se denominan ondas planas.

Las ondas planas

Las ondas planas tridimensionales, solución de la ecuación de Schrödinger independiente del tiempo y de expresión general
$\psi_{\vec{k}}(\vec{r}) \,= \, C_k \ e^{i\ \vec{k} \cdot \vec{r}} \; ; \; \vec{k}=(k_x,k_y,k_z)$
$\doteq \psi_{\vec{p}}(\vec{r}) \, = \, C_p \ e^{i\ \vec{p} \cdot \vec{r} / \hbar} \; ; \; \vec{p}=(p_x,p_y,p_z)$ ,
donde $C_k \, , \, C_p$ representan constantes (escalares del cuerpo $\mathbb{C}$ ), son las autofunciones simultáneas de los operadores cuánticos energía cinética y momento lineal, $\{ \hat{T} =-\frac{\hbar^2 \nabla^2}{2m},\hat{\vec{p}}=-i\hbar\nabla \}$ .
Es decir, satisfacen las siguientes ecuaciones de autovalores (supondremos siempre respectivos dominios de definición que garanticen el carácter autoadjunto de los correspondientes operadores):
$\hat{H} \ \psi_{\vec{k}}(\vec{r}) \, = \, \hat{T} \ \psi_{\vec{k}}(\vec{r}) \, = \, (-\frac{\hbar^2}{2m}) \nabla^2 \ \psi_{\vec{k}}(\vec{r}) \, = \, E \psi_{\vec{k}}(\vec{r}) \, = \, (E_x+E_y+E_z) \ \psi_{\vec{k}}(\vec{r})$
$= \, \frac{\hbar^2}{2m} \ \sum_i \ k_i^2 \ \psi_{\vec{k}}(\vec{r}) \, = \, \frac{\hbar |\vec{k}|^2 }{2m} \ \psi_{\vec{k}}(\vec{r}) \, = \, \ \frac{|\vec{p}|^2 }{2m} \ \psi_{\vec{k}}(\vec{r})$
$\vec{\hat{p}} \ \psi_{\vec{k}}(\vec{r}) \, = \, (-i \hbar \nabla ) \ \psi_{\vec{k}}(\vec{r}) \, = \, \vec{p} \ \psi_{\vec{k}}(\vec{r}) \, = \, \hbar \vec{k} \ \psi_{\vec{k}}(\vec{r})$ .
-El espectro del operador energía cinética $\hat{T}$ es continuo e infinitamente degenerado (salvo para el valor nulo de energía), coincidiendo con la semirrecta real positiva, $\sigma(T)=[0,+\infty)$ , mientras que el del operador momento lineal $\hat{\vec{p}}$ es continuo, ocupando toda la recta real, $\sigma(T)=(-\infty,+\infty)$ , y sin degeneración. Todos los valores de $\vec{k}$ son posibles soluciones, y todos los vectores número de ondas de igual módulo proporcionan la misma energía total que, aquí, coincide con la cinética (i.e.: todos los radios $|\vec{k}|$ de una misma esfera, o infinitas orientaciones posibles del vector $\vec{k}$ , proporcionan la misma energía $E=\frac{\hbar^2 k^2}{2m}$ ).
-El número de ondas $\vec{k}$ y la frecuencia cumplen la relación de de Broglie:
$|\vec{k}|=\frac{2\pi}{\lambda}=\frac{ | \vec{p} |}{\hbar}$ y $\omega(k)=2\pi\nu(k)=\frac{E}{\hbar}=\frac{\hbar k^2}{2m}$ .
Normalización de las ondas planas:
Es importante recordar que las soluciones de la ecuación de autovalores obtenidas, las ondas planas, no pertenecen al Hilbert $\mathscr{H}=L^2(\mathbb{R}^3)$ : son «autofunciones generalizadas», asociadas a autovalores (en sentido también generalizado) en la parte continua de los espectros de los operadores. Puesto que estas funciones no son de cuadrado integrable Lebesgue, surge el problema de que es imposible satisfacer el requisito
$\int_{-\infty}^{\infty} \left|\psi_{\vec{k}}(\vec{r}) \right| ^2d\vec{r}=1$ ,
ya que la correspondiente integral resulta divergente.
-Nota: En teoría de espacios de Hilbert, un autovalor $\lambda$ de un operador $\hat{A}$ se dice que lo es en sentido generalizado cuando existe en el espacio una sucesión de vectores, $\{ \psi_n \}_{n=1}^{\infty}$ , todos de norma unidad y satisfaciendo $|| (\hat{A} - \lambda)\psi_n || \xrightarrow{n \rightarrow \infty} 0$ , esto es, $\int_{\mathbb{R}^3} | (\hat{A} - \lambda)\psi_n |^2 d^3\vec{r}=0$ .
-Las ondas planas, pues, representan sistemas que no están ni localizados ni confinados, y para trabajar con ellos se requerirá de la introducción de formas especiales de normalización efectiva:
1. Normalización a la delta de Dirac:
1.1 k-normalización:
$\psi_{\vec{k}}(\vec{r}) \, = \, \frac{1}{(2\pi)^{\frac{3}{2}}}\ e^{i\vec{k}\cdot\vec{r}}$ :
$\int_{\mathbb{R}^3} \psi_{\vec{k}'}^*(\vec{r}) \ \psi_{\vec{k}}(\vec{r}) \ d\vec{r} = \frac{1}{(2\pi)^3} \ \int_{\mathbb{R}^3}e^{i(\vec{k}-\vec{k}') \cdot \vec{r}}\ d\vec{r} =\delta(\vec{k}-\vec{k}')$
1.2 p-normalización:
$\psi_{\vec{p}}(\vec{r}) \, = \, \frac{1}{(2\pi \hbar)^{\frac{3}{2}}}\ e^{i\frac{\vec{p}\cdot\vec{r}}{\hbar}}$ :
$\int_{\mathbb{R}^3} \psi_{\vec{p}'}^*(\vec{r})\ \psi_{\vec{p}}(\vec{r})\ d\vec{r}= \frac{1}{(2\pi \hbar)^{3}} \ \int_{\mathbb{R}^3} e^{i(\vec{p}-\vec{p}') \cdot \vec{r}} \ d\vec{r}=\delta(\vec{p}-\vec{p}')$
-Esta forma equivale a fijar la densidad de probabilidad de encontrar a la partícula en la unidad de volumen como $(2\pi \hbar)^{(-3)}$ , una normalización en sentido relativo, por unidad de volumen y de momento.
1.3 E-normalización:
$\psi_{E_{\pm}}(\vec{r}) \, = \, \frac{1}{(2\pi \hbar)^{\frac{3}{2}}}(\frac{m}{2E})^{\frac{1}{4}} \ e^{\pm i \frac{(+\sqrt{2mE})}{\hbar} \frac{\vec{k}}{|\vec{k} | } \cdot \vec{r}}$ :
$\int_{\mathbb{R}^3} \psi_{E'}^*(\vec{r})\ \psi_{E}(\vec{r})\ d\vec{r}=\delta(E-E')$
2. Normalización por discretización del continuo: se introduce un confinamiento en una región muy extensa, pero de volumen $V$ finito, por ejemplo, una caja cúbica de lado $L$ , arbitrariamente grande pero manteniendo $L^3$ finito, y se imponen condiciones de frontera del tipo periódico:
$\psi(r_i)=\psi(r_i+L) \Rightarrow R_i(r_i)=R_i(r_i+L)$
$\Rightarrow Ae^{ik_ir_i} \, + \, Be^{-ik_ir_i}=Ae^{ik_i(r_i+L)} \, + \, Be^{-ik_i(r_i+L)}$
$\Rightarrow Ae^{ik_ir_i}(1-e^{ik_iL}) \, + \, Be^{-ik_ir_i}(1-e^{-ik_iL}) =0$
$\Rightarrow \left. \begin{array}{l} e^{ik_iL}=1 \\ e^{-ik_iL}=1 \end{array} \right\}$ ,
que conducen a $k_i=\frac{2\pi}{L} n_i\; ; \; n_i=0,\pm 1, \pm 2 \ldots$ , implicándose una discretización del espectro de energía, con puntos espectrales discretos dados por
$E=\frac{\hbar^2}{2m} \frac{4\pi^2}{L^2} \sum_i n_i^2$ .
-Expresiones en L-normalización:
$\psi_{\vec{k}}(\vec{r}) \, = \, \frac{1}{L^{\frac{3}{2}}}\ e^{i\vec{k}\cdot\vec{r}}$ .
$\int_{V} \psi_{\vec{k}'}^*(\vec{r}) \ \psi_{\vec{k}}(\vec{r}) \ d\vec{r} = \frac{1}{L^3} \ \int_{V=L^3}e^{i(\vec{k}-\vec{k}') \cdot \vec{r}}\ d\vec{r} =\delta_{\vec{k},\vec{k}'}$
-Cuanto más grande sea $L$ , más pequeño será el espaciado entre los niveles discretos $E_n$ , pudiendo hacerse casi continuo.
3. Normalización mediante el concepto de probabilidad relativa: se define una función densidad de probabilidad relativa:
$P_{prob.rel.} (\vec{r_1},\vec{r_2};t)=\frac{| \Psi(\vec{r_1};t )|^2}{| \Psi(\vec{r_2};t )|^2 }$ ,
de modo que $P_{prob.rel.} (\vec{r_1},\vec{r_2};t) \ d\vec{r_1} d\vec{r_2}$ represente la probabilidad de encontrar a la partícula en el volumen $d\vec{r_1}$ en torno a $\vec{r_1}$ , relativa a la probabilidad de hacerlo en el volumen $d\vec{r_2}$ en torno a $\vec{r_2}$ ; en el instante $t$ . Para una onda plana, $P_{prob.rel.} (\vec{r_1},\vec{r_2};t)=1 \; , \; \forall t$ , lo que muestra la completa deslocalización de la partícula libre, como ha de ser de acuerdo con el principio de indeterminación, ya que posee un momento $\vec{p}$ completamente determinado, con indeterminación nula.
Las ondas planas constituyen un conjunto completo (en sentido generalizado o impropio) para el Hilbert, de forma que cualquier función de onda admite expresión como superposición de ellas: el desarrollo de Fourier. Un ejemplo lo constituyen los paquetes de ondas.

Resolución de la ecuación de Schrödinger independiente del tiempo para el sistema conservativo de una partícula libre en coordenadas esféricas

Sea una partícula de masa $m$ sin espín, y sea la correspondiente ES independiente del tiempo,
$H \ \psi(\vec{r}) \, = \, [-\frac{\hbar^2}{2m}\nabla^2+V_0 \ ] \ \psi(\vec{r})\, = \, E \ \psi(\vec{r})$ ,
donde el potencial $V_0$ es constante y cuyo valor particular, sin pérdida de generalidad, puede elegirse como nulo. Resuelto este problema anteriormente en coordenadas cartesianas, pasamos ahora a resolverlo en coordenadas esféricas. A este fin, recuperamos los pasos que ya se establecieron en el caso general de un potencial central, repitiendo el procedimiento de separación de variables que transforma la ES inicial en la ecuación radial reducida.
La ecuación de Schrödinger independiente del tiempo es en este caso directamente resoluble introduciendo las coordenadas esféricas para proceder a continuación a la separación de variables:
1. Introduzcamos las coordenadas esféricas, $\vec{r},\theta,\varphi$ :
  $\left. \begin{array}{l} x=r \sin \theta \cos \varphi \,,\; 0 \leq r=|\vec{r}| < \infty \\ y=r \sin \theta \sin \varphi \,,\; 0 \leq \theta \le \pi \\ z=r \cos \theta \,,\; 0 \le \varphi \leq 2\pi \end{array} \right\}$ $\left. \begin{array}{l} r=+\sqrt{x^2+y^2+z^2} \,,\; 0 \leq x < \infty \\ \theta = \arccos \frac{z}{r} \,,\; 0 \leq z < \infty \\ \varphi = \arctan \frac{y}{x} \,,\; 0 \leq y < \infty \end{array} \right\}$
  
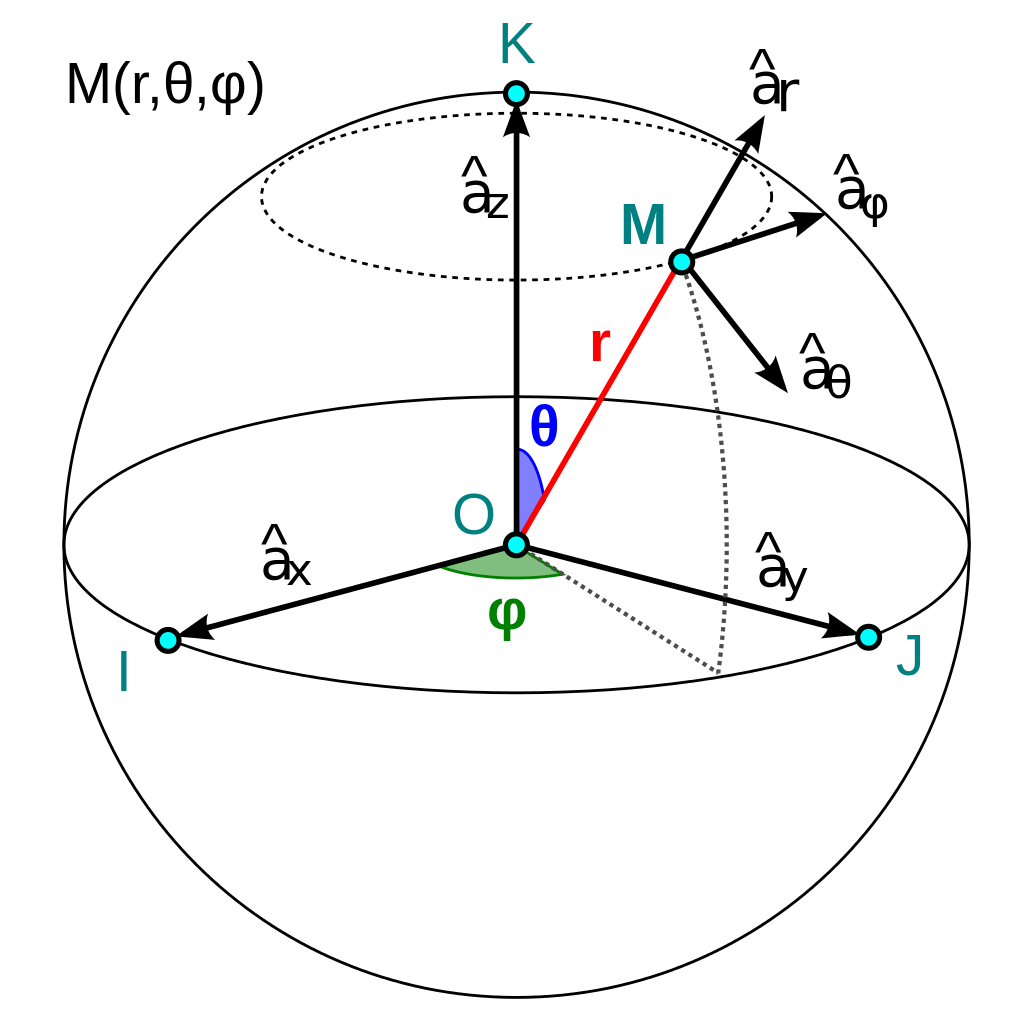
  Coordenadas esféricas de un punto M, imagen de la Wikipedia (derivative work by Josemontero9, from the original
  Coordenadas_eséricas_figura , by Romero Schmidtke).
  
  -En estas coordenadas, un elemento de volumen $dV$ y el operador $\nabla^2$ se expresan, respectivamente:
  $dV \, = \, d^3r \equiv d \vec{r} \, = \, dx \, dy \, dz=r^2 \sin \theta \, dr \, d \theta \, d \varphi$
  $\nabla^2 \, = \, \frac{1}{r^2 \sin \theta} \{ \sin \theta \, \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, + \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin \theta}(\frac{\partial^2}{\partial \varphi^2}) \}$ ,
  de manera que el momento angular orbital y su cuadrado en esféricas resultan ser:
  $L_x\,=\, yp_z-zp_y\,=\,-i\hbar \,(y\frac{\partial}{\partial z} - \,z \frac{\partial}{\partial y}) \, = \, -i\hbar \, (-\sin \varphi \, \frac{\partial}{\partial \theta} \, - \, \cot \theta \, \cos \varphi \, \frac{\partial}{\partial \varphi})$
  $L_y\,=\, zp_x-xp_z\,=\,-i\hbar \,(z\frac{\partial}{\partial x} - x \frac{\partial}{\partial z}) \, = \, -i\hbar \, (\cos \varphi \, \frac{\partial}{\partial \theta} \, - \, \cot \theta \, \sin \varphi \, \frac{\partial}{\partial \varphi})$
  $L_z\,=\, xp_y-yp_x\,=\,-i\hbar \,(x\frac{\partial}{\partial y} - y \frac{\partial}{\partial x}) \, = \, -i\hbar \, \frac{\partial}{\partial \varphi}$
  $\vec{L}^2 \,=\, \vec{L} \cdot \vec{L}\, = \,L_x^2 \,+\, L_y^2 \, +\, L_z^2$ $= \,-\hbar^2 \, [ \,\frac{1}{\sin \theta} \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin^2 \theta}\frac{\partial^2}{\partial \varphi^2} \, ]$ .
2. Ecuación de Schrödinger independiente del tiempo en coordenadas esféricas:
  $H\psi(\vec{r})$
  $= \, \{-\frac{\hbar^2}{2m}[ \ \frac{1}{r^2 \sin \theta} \{ \sin \theta \, \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, + \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin \theta}(\frac{\partial^2}{\partial \varphi^2}) \ ] \, + \, V_0 \ \} \ \psi(\vec{r})$
  $= \, \{-\frac{\hbar^2}{2m}[ \ \frac{1}{r^2} \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2} \ ] \, + \, V_0 \} \psi(\vec{r})$
  $= \, E \ \psi(\vec{r})$
3. Autofunciones: ondas parciales:
  Tanto $\vec{L}$ como $\vec{L}^2$ son operadores puramente angulares, es decir, que no contienen dependencia explícita de la coordenada radial $r=|\vec{r}|$ . Por tanto, para cualquier potencial central (esféricamente simétrico) y, en particular, constante, se satisfacen las conmutaciones:
  $[\vec{L},V(r)]=[\vec{L}^2,V(r)]=0$ .
  Además,
  $[\vec{L}^2,L_i]=0\,, \, i=x,y,z$ ,
  y también ambos operadores $\vec{L}$ y $\vec{L}^2$ conmutan con el operador energía cinética, $T$ , de expresión en esféricas
  $T\, = \, -\frac{\hbar^2}{2m}\nabla^2 \, = \, -\frac{\hbar^2}{2m} [ \ \frac{1}{r^2} \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2} \ ]$ .
  Por todo ello, considerado el operador Hamiltoniano del sistema (conservativo), $H=T+V$ , que representa la energía total del sistema, satisface:
  $[H, \vec{L}]=[H,\vec{L}^2]=0$ ,
  derivándose que el conjunto de operadores $\{ H,\vec{L}^2,L_z \}$ puede ser diagonalizado simultáneamente: integran un C.C.O.C. (en ausencia de grados de libertad adicionales, como pudiera ser el espín) y existe en el espacio una base integrada por autofunciones comunes a los tres operadores, cuya expresión involucrará los armónicos esféricos, las autofunciones comunes de los operadores de momento angular orbital:
  $\vec{L}^2 \,Y_{lm}(\theta, \varphi) \, =\, \hbar^2 \, l(l+1)\, Y_{lm}(\theta, \varphi)$
  $L_z \,Y_{lm}(\theta, \varphi) \, =\, \hbar \, m\, Y_{lm}(\theta, \varphi)$
  $\psi_{Elm}(\vec{r})=R_{El}(r) \ Y_{lm}(\theta,\varphi)$ ,
  donde $R_{El}(r)$ es la denominada función radial, de expresión a determinar por separación de variables.
4. En efecto, por separación de variables:
  Sea la solución de la anterior ES independiente del tiempo poseyendo la forma separada
  $\psi(\vec{r})\, = \, R(r) \ Y(\Omega)$ ;
  entonces, sustituyendo en la ES,
  $H \, \psi(\vec{r}) \, = H\, R(r) \ Y(\Omega)$
  $= \, \{-\frac{\hbar^2}{2m}[ \ \frac{1}{r^2} \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2} \ ] \, + \, V(r) \} \, R(r) \ Y(\Omega)$
  $= \, E \, R(r) \ Y(\Omega)$ ;
  multiplicamos por $-2mr^2/\hbar^2$ y dividimos por $RY$ :
  $\Rightarrow \, [ \ \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, - \, \frac{2mr^2}{\hbar^2} ( V_0 \, - \, E)\, - \, \ \frac{\vec{L}^2}{\hbar^2} \ ] \ R(r) \ Y(\Omega) \, = \, 0$
  $\Rightarrow \, \{ \ \frac{1}{R(r)} \ [ \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, - \, \frac{2mr^2}{\hbar^2} ( V_0 \, - \, E) ] \,R(r) \ \} \, + \, \{ \ - \frac{1}{Y(\Omega)} \ \frac{\vec{L}^2}{\hbar^2} \ Y(\Omega) \} \, = \, 0$
  de donde se derivan las dos ecuaciones (separación):
  1. $-\beta = \, -\frac{1}{Y(\Omega)} \ \vec{L}^2 \ Y(\Omega)$
  $\Rightarrow \, \vec{L}^2 \ Y(\Omega) \, = \, \beta \ \hbar^2 \, Y(\Omega) \$
  $\Rightarrow \, \left\{ \begin{array}{l} Y(\Omega) \ \equiv \ Y_{lm}(\Omega) \\ \beta \, = \, l(l+1) \, , \, l=0,1,2,\ldots \end{array} \right.$
  (¡no confundir la masa con el número cuántico de tercera componente de momento angular orbital!)
  2. $\{ \ \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, - \, \frac{2mr^2}{\hbar^2} [ V_0 \, - \, E] \, \} \, R(r) \, = \, \beta \, R(r)\, = \, l(l+1) \, R(r)$
  $\Rightarrow \, \{ \ \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, - \, \frac{2mr^2}{\hbar^2} V_0 \, - \, l(l+1) \} \, R(r) = -\frac{2mr^2}{\hbar^2} E \, R(r)$
  $\Rightarrow \, \{ \ -\frac{\hbar^2}{2mr^2} \, \frac{\partial}{\partial r}(r^2 \ \frac{\partial}{\partial r}) \, + \, V_0 \,+ \frac{\hbar^2}{2mr^2} \, l(l+1) \} \, R(r) \, = \,E \, R(r)$
  $\Rightarrow \, \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, V_0 \ \} \, R(r) \, = \,E \, R(r)$ ,
  que es la denominada como ecuación radial, y en la que es común incluir en la notación los parámetros $\{ E,l\}$ como subíndices de la función incógnita:
  $\Rightarrow \, \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, V_0 \ \} \, R_{El}(r) \, = \,E \, R_{El}(r)$
Degeneración de la energía:
Como consecuencia de la invariancia rotacional, existe una degeneración energética: ya que para cada valor dado del número cuántico de momento angular orbital $l$ existen $2l + 1$ autofunciones $\psi_{Elm}=R_{El}Y_{lm}$ , correspondientes a los $2l+1$ valores posibles del número cuántico $m$ de tercera componente de momento angular orbital, $m=l,l-1,l-2,\ldots,-l$ , todas ellas satisfaciendo la misma ecuación de ES para un autovalor dado de energía E.
Es decir, fijada una dirección arbitraria en el espacio, debido a su isotropía, el Hamiltoniano correspondiente a un potencial central es invariante bajo rotaciones, de modo que los niveles de energía no pueden depender del número cuántico magnético $m$ (¡no confundir con la masa!).
Ondas parciales:
La expresión de cada función de ondas $\psi(\vec{r})$ como suma de funciones $\psi_{Elm}=R_{El}Y_{lm}$ , autofunciones simultáneas de los operadores $\{ H,\vec{L}^2,L_z \}$ , se denomina «descomposición en ondas parciales» , siendo usual, siguiendo la tradición espectroscópica, referir a los sumandos correspondientes a los valores $l=0,1,2,3,4\ldots$ como sendas ondas o estados s(harp), p(rincipal), d(ifusivo), f(undamental), g (a partir de aquí, orden alfabético)…
Ecuación radial reducida:
Si en la anterior ecuación radial
$\Rightarrow \, \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, V_0 \ \} \, R_{El}(r) \, = \,E \, R_{El}(r)$ ;
se realiza el cambio de función incógnita
$R_{El}(r)=\frac{1}{r} \ u_{El}(r)$ ,
siendo $u(r)$ la función radial reducida, que ha de satisfacer la ecuación radial reducida en onda parcial l:
$\{ -\frac{\hbar^2}{2m} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \, + \, V_0 \ \} \, u_{El}(r) \, = \,E \, u_{El}(r)$
$\equiv \, H_l u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2m} \ \frac{d^2}{d r^2} \,+ \, V_{ef_l}(r) \ \} \ u_{El}(r)\, = \,E \, u_{El}(r)$ ,
donde se ha introducido un potencial efectivo de onda $l$ ,
$V_{ef_l}(r) \,= \, \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \, + \, V_0 \quad , \; l=0,1,2\ldots$ .
El término adicional al potencial $V(r)$ se denomina «barrera centrífuga», constituyendo un potencial repulsivo que se suma al original.
A continuación, se impone la condición de regularidad, de manera que se plantea el siguiente problema de contorno:
$\left. \begin{array}{l} \{ [\ \frac{d^2}{d r^2} \, + \, \frac{l(l+1)}{r^2} \ ] \, + \, \frac{2m}{\hbar^2} (E-V_0) \ \} \, u_{El}(r) \, = \,0 \\ u_{El}(0)=0 \end{array} \right\}$ .
-La condición de integrabilidad no se plantea en este caso, puesto que no se esperan estados ligados.
Resolución por ondas parciales:
1. Onda parcial s (valor $l=0$ ):
  $\left. \begin{array}{l} \{ \frac{d^2}{d r^2} \, + \, \frac{2m}{\hbar^2} (E-V_0) \ \} \, u_{El}(r) \, = \,0 \\ u_{El}(0)=0 \end{array} \right\}$
  -La EDO lineal homogénea $u'' \mp k^2u=0 \, , \, k \in \mathbb{R} \, , \, k>0$ tiene por solución general la combinación lineal de soluciones particulares:
  a) signo (-) : $u(r)=C_1 \ e^{kr} + C_2\ e^{-kr}$
  con $C_1,C_2$ escalares arbitrarios.
  b) signo (+) : $u(r)=C_1 \ e^{+ikr} + C_2\ e^{-ikr}=C'_1 \ cos\ kr + C'_2\ sen \ kr$
  con $C_1,C_2,C'_1,C'_2$ escalares arbitrarios.
  -Es decir:
  $v'' \mp k^2v=0 \, , \, k^2= \frac{2m}{\hbar^2} |E-V_0| \Rightarrow \left\{ \begin{array}{l} (-)\leftrightarrow (E-V_0) < 0 \\ (+)\leftrightarrow (E-V_0) > 0 \\ (k=0) \leftrightarrow E=V_0 \end{array} \right\}$
  $\Rightarrow \left\{ \begin{array}{l} (E-V_0) < 0 \rightarrow k=\frac{+\sqrt{-2m(E-V_0)}}{\hbar} \, , \, \Rightarrow v_{E<V_0}(r)=C_1 \ e^{kr} + C_2\ e^{-kr} \\ (E-V_0) > 0 \rightarrow k=\frac{+\sqrt{2m(E-V_0)}}{\hbar} \Rightarrow v_{E>V_0}(r)=C_1 \ e^{ikr} + C_2\ e^{-ikr} \\ E=V_0 \rightarrow k=0 \Rightarrow v_{V_0}(r)=C_1r +C_2 \end{array} \right.$
  -Casos:
  a) $E=V_0$ : $k=0$ :
  $E=V_0 \Rightarrow u_{V_00}''(r)=0 \Rightarrow u_{V_00}(r)=C_1r +C_2$
  $u_{V_00}(0)=0=C_2 \Rightarrow u_{V_00}(r)=C_1r \Rightarrow R_{V_00}(r)=C_1$
  $\Rightarrow \psi_{E=V_0 0 0}(\vec{r})=C_1 \ Y_{00}(\Omega)\, = \, C$ ,
  esto es, un valor constante.
  -A esta función de onda le corresponde el autovalor $E=V_0$ , no degenerado.
  b) $E<V_0$ : $k=\frac{+\sqrt{-2m(E-V_0)}}{\hbar}$ :
  $E<V_0 \Rightarrow u_{E<V_0 0}(r)=C_1 \ e^{kr} + C_2\ e^{-kr}$
  $u_{E<V_0 0}(0)=0=(C_1 +C_2)e \Rightarrow u_{E<V_0 0}(r)=C_1(e^{kr} - e^{-kr})=2C_1 \ sinh \ kr$
  $\Rightarrow R_{E<V_0 0}(r)=\frac{2C_1}{r} \ sinh \ kr$
  -estas soluciones no son físicamente aceptables ya que divergen para $r \rightarrow \infty$ .
  c) $E> V_0$ : $k=\frac{+\sqrt{2m(E-V_0)}}{\hbar}$ :
  $E>V_0 \Rightarrow u_{E0}(r)=C_1 \ e^{ikr} + C_2\ e^{-ikr} =C'_1 \ cos\ kr + C'_2\ sen \ kr$
  $u_{E> V_0 0}(0)=0=C'_1 \Rightarrow u_{E> V_0 0}(r)=C_2' \ sen \ kr \Rightarrow R_{E> V_0 0}(r)=C_2' \frac{1}{r} sen \ kr$
  $\Rightarrow \psi_{E> V_0 0 0}(\vec{r})=C_2' \frac{1}{r} sen \ kr \ Y_{00}(\Omega)\, = \, C_2' \ k \ j_0(kr) \ Y_{00}(\Omega)$ ,
  donde $c_2'$ es una constante arbitraria y $j_0$ representa la función esférica de Bessel de orden cero, $j_0(x)=\frac{sen x}{x}$ .
2. Ondas parciales $l > 0$ :
  -Casos:
  a) $E=V_0$ : $k=0$ :
  $\left. \begin{array}{l} \{ [\ \frac{d^2}{d r^2} \, + \, \frac{l(l+1)}{r^2} \ ] \ \} \, u_{El}(r) \, = \,0 \\ u_{El}(0)=0 \end{array} \right\}$
  En este caso es conveniente resolver la ecuación radial,
  $\Rightarrow \, \{ [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \ \} \, R_{El}(r)=0$ ,
  $R_{El}(r)=\frac{1}{r} \ u_{El}(r)$ ,
  ecuación que en este caso no proporciona soluciones físicamente aceptables.
  b) $E< V_0$ : $k=\frac{+\sqrt{2m(V_0-E)}}{\hbar}$ :
  $\left. \begin{array}{l} \{ [\ \frac{d^2}{d r^2} \, + \, \frac{l(l+1)}{r^2} \ ] \, + \, \frac{2m}{\hbar^2} (V_0-E) \ \} \, u_{El}(r) \, = \,0 \\ u_{El}(0)=0 \end{array} \right\}$
  -En este caso no se obtienen soluciones físicamente aceptables.
  c) $E> V_0$ : $k=\frac{+\sqrt{2m(E-V_0)}}{\hbar}$ :
  $\left. \begin{array}{l} \{ [\ \frac{d^2}{d r^2} \, + \, \frac{l(l+1)}{r^2} \ ] \, + \, \frac{2m}{\hbar^2} (E-V_0) \ \} \, u_{El}(r) \, = \,0 \\ u_{El}(0)=0 \end{array} \right\}$ .
  En este caso es conveniente resolver la ecuación radial,
  $\Rightarrow \, \{ [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, k^2 \ \} \, R_{El}(r)=0$ ,
  $R_{El}(r)=\frac{1}{r} \ u_{El}(r)$ ,
  ecuación que mediante el cambio de variable
  $\rho=kr \, , \, k=\frac{\sqrt{2m(E-V_0)}}{\hbar}$
  se convierte en la ecuación diferencial esférica de Bessel,
  $[ \ \frac{d^2}{d \rho^2} \, + \, \frac{2}{\rho} \ \frac{d }{d \rho} \,+\, (1 \ - \ \frac{l(l+1)}{\rho^2}) \ ] \, R_{El}(\rho)=0$ ,
  ecuación de soluciones bien conocidas: las funciones esféricas de Bessel (de primera especie) $j_l(\rho=kr)$ , y de segunda especie o funciones esféricas de Neumann, $n_l(\rho=kr) \equiv y_l(\rho=kr)$ . En terminos de ellas, la solución general de la EDO se expresa:
  $R_{El}(\rho)\, = \, C_1 \ j_l(\rho=kr) \, + \, C_2 \ n_l(\rho=kr)$ ,
  donde $C_1, C_2$ son constantes arbitrarias.
Gráficas de las primeras funciones esféricas de Bessel:
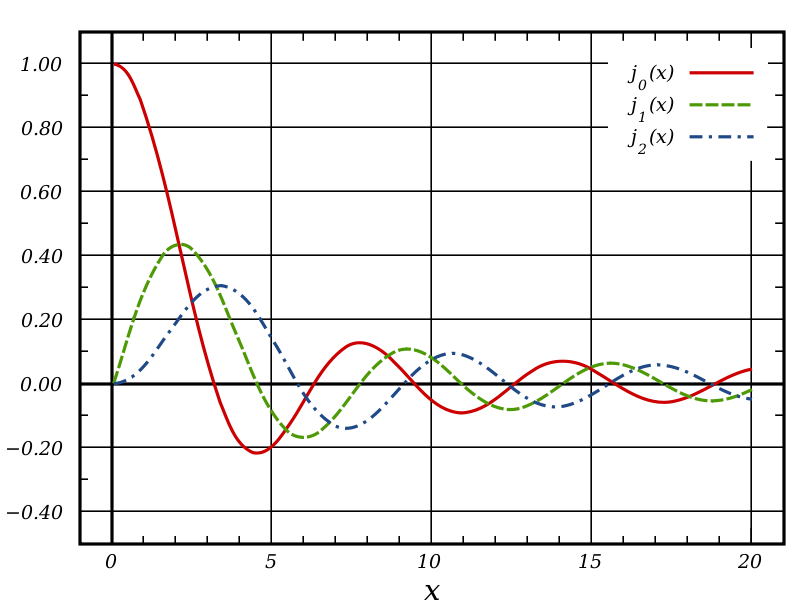
Funciones esféricas de Bessel de primer orden (De Inductiveload – Trabajo propio, made in Inkscape, Dominio público, https://commons.wikimedia.org/w/index.php?curid=3565421).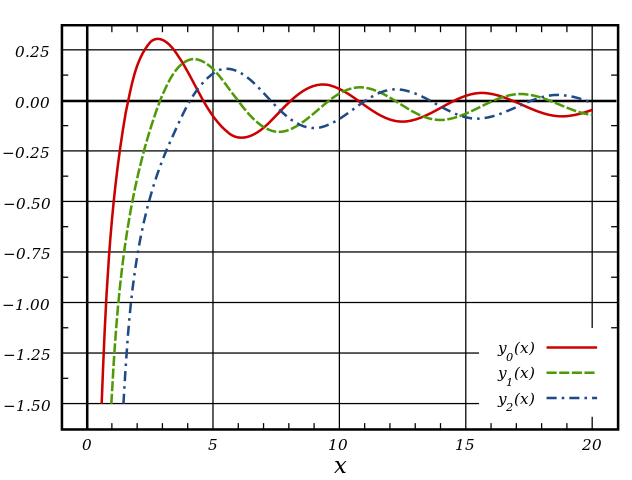

Funciones esféricas de Bessel de segundo orden o funciones de Neumann, lo que en la gráfica se ha notado como $y_l$ y en los apuntes como $n_l$ (De Inductiveload – Trabajo propio, made in Inkscape, Dominio público, https://commons.wikimedia.org/w/index.php?curid=3565427).
En conclusión: planteado el problema de contorno para el tratamiento mecano-cuántico de la partícula libre,
$\left. \begin{array}{l} \{ [\ \frac{d^2}{d r^2} \, + \, \frac{l(l+1)}{r^2} \ ] \, + \, \frac{2m}{\hbar^2} (E-V_0) \ \} \, u_{El}(r) \, = \,0 \\ u_{El}(0)=0 \end{array} \right\}$ ,
se encuentran soluciones en el caso $E > V_0$ que para $l > 0$ adoptan la forma general:
$R_{El}(\rho)\, = \,\frac{u_{El}(\rho)}{\rho}\, = \, C_1 \ j_l(\rho=kr) \, + \, C_2 \ n_l(\rho=kr) \; , \; k=\frac{+\sqrt{2m(E-V_0)}}{\hbar}$
donde $j_l(\rho=kr)$ y $n_l(\rho=kr)$ representan, respectivamente, las funciones esféricas de Bessel de orden primero y segundo:
$j_n(z)\, = \, z^n \ [-\frac{1}{z} \ \frac{d}{dz}]^n \ \frac{\sin z}{z} \, = \,z^n \ \sum_{m=0}^{\infty} \ \frac{(-1)^m }{m! \ (2n+2m+1)!!} \ (\frac{z^2}{2})^m$
$n_n(z)\, = \,y_n(z)\, = \, -z^n \ [-\frac{1}{z} \ \frac{d}{dz}]^n \ \frac{\cos z}{z} \, = \, -\frac{(2n-1)!!}{z^{n+1}} \ [1 \, + \, \sum_{m=1}^{\infty} \ \frac{1 }{m! \ (1-2n)(3-2n)\ldots (2m-1-2n)} \ (\frac{-z^2}{2})^m]$
-La función esférica de Neumann $n_l(\rho)$ posee un polo de orden $l+1$ en el origen, por lo que la función radial reducida no es analítica en el origen:
$n_l(\rho) \ \xrightarrow{\rho \rightarrow 0} \ -\frac{(2l-1)!!}{\rho^{l+1}} \Rightarrow \lim_{\rho \rightarrow 0}u_{El}(\rho)=\lim_{\rho \rightarrow 0} \rho \ n_{l}(\rho)=\lim_{\rho \rightarrow 0} \ -\frac{(2l-1)!!}{\rho^{l}}$ .
-Por el contrario, la solución particular función esférica de Bessel de primer orden sí proporciona una solución analítica en el origen:
$j_l(\rho) \ \xrightarrow{\rho \rightarrow 0} \ \frac{\rho^{l}}{(2l+1)!!} \Rightarrow \lim_{\rho \rightarrow 0}u_{El}(\rho)=\lim_{\rho \rightarrow 0} \rho \ j_{l}(\rho)=\lim_{\rho \rightarrow 0} \ \frac{\rho^{l+1}}{(2l-1)!!}$
-Por tanto, la onda parcial $l \ne 0$ solución de la ES, autofunción simultánea de los operadores $\{ H,\vec{L}^2,L_z \}$ para valores de energía $E > V_0$ y que cumple las condiciones de contorno requeridas toma la expresión final:
$\psi_{Elm}(\vec{r})\, = \, R_{El}(r) \ Y_{lm}(\Omega)\, = \, C \ j_l(kr) \ Y_{lm}(\theta,\varphi)$ ,
$k=\frac{+\sqrt{2m(E-V_0)}}{\hbar}$ ,
autofunciones denominadas «ondas (parciales) esféricas».
Los autovalores correspondientes de energía,
$E\, = \,V_0\,+\,\frac{\hbar^2 k^2}{2m}$ ,
constituyen un espectro continuo de energía, ya que $E$ puede tomar cualquier valor en la semirrecta real positiva $[V_0,+\infty)$ , siendo todos los valores $E > V_0$ degenerados ( $l=0,1,2\ldots$ y , para cada valor de $l$ , el número cuántico magnético o de trecera componente varía según $m=l,l-1,\ldots,-l$ ).
Las ondas parciales esféricas constituyen un conjunto ortonormal completo en el espacio, una base en términos de cuyos vectores puede expresarse cualquier función de onda del espacio.
-La relación entre las funciones de las dos bases viene dada por el desarrollo:
$e^{i \vec{k} \cdot \vec{r}} \,=\, \sum_{l=0}^{\infty}\sum_{m=-l}^{l} \ 4 \pi i^l j_l(kr) \ Y_{lm}^*(\Omega_k) Y_{lm}^*(\Omega_r)\,=\, \sum_{l=0}^{\infty} \ i^l (2l+1) j_l(kr) \ P_l(cos \theta)$ ,
donde $\theta$ es el ángulo entre los vectores $\vec{k}$ y $\vec{r}$ y $P_l$ representa el polinomio de Legendre de grado $l$ .Nota 1: puesto que $[ \vec{L}^2, \vec{p} ] \ne 0$ , son operadores complementarios, no es posible diagonalizarlos simultáneamente. En consecuencia, mientras que las ondas planas no tienen momento angular orbital bien definido, las ondas esféricas carecen de momento lineal bien definido:
$e^{i \vec{k} \cdot \vec{r}} \leftrightarrow C.C.O.C.: \; \{ \hat{H}, \hat{T}, \hat{\vec{p}} \}$
$\psi_{Elm}(\vec{r})\, = \, R_{El}(r) \ Y_{lm}(\Omega)\leftrightarrow C.C.O.C.: \; \{ \hat{H}, \vec{L}^2, L_z \}$ Nota 2: obsérvese que mientras la cardinalidad de la base de ondas esféricas es $\aleph_0$ (número transfinito para la cardinalidad de conjuntos con un número de elementos infinito numerable), la cardinalidad de la base obtenida en la resolución en coordenadas cartesianas es $\aleph_1$ (el menor cardinal mayor que $\aleph_0$ : la cardinalidad de conjuntos con un número de elementos infinito no numerable, como la recta real). Puesto que esta segunda base del mismo Hilbert es base generalizada o impropia, esta diferencia es matemáticamente posible.

Referencias

[ABR-65] Abramowitz, Milton; Stegun, Irene A., eds.; “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables”; Dover; New York, 1965; ISBN 978-0-486-61272-0.

[BAL-98] Ballentine, L.E.; “Quantum Mechanics: A Modern Development”; World Scientific; Singapore, 1998.

[BER-18] Berman, P.R.; “ Introductory Quantum Mechanics: ”; Springer, 2018; https://doi.org/10.1007/978-3-319-68598-4_10.

[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.

[BRA-06] Bransden, B.H. and Joachain, C.J.; «Physics of Atoms & Molecules»; Longman, New York, 1983 (2nd ed.: Pearson; Dorchester, 2000).

[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.

[NEU-91] Neumann, J. von; «Fundamentos matemáticos de la Mecánica Cuántica», CSIC, Raycar, Madrid, 1991.

[RAI-72] Rainville, E.D., «Intermediate Differential Equations», Chelsea Pub. Co.; N.Y., 1972.

[SCH-68] Schiff, L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.

Páginas complementarias

La separación en esféricas y la ecuación diferencial para la parte radial de la función de onda: http://www.sc.ehu.es/sbweb/fisica3/cuantica/separacion/esferica.html
La partícula libre en el blog lamecanicacuantica.blogspot.com (casos monodimensionales): entrada 1 y entrada 2.
Funciones especiales: https://es.mathworks.com/help/matlab/special-functions.html?s_tid=CRUX_lftnav
Funciones esféricas de Bessel:
–http://www.sc.ehu.es/sbweb/fisica3/especial/bessel/bessel.html
-En la Wikipedia: https://es.wikipedia.org/wiki/Funci%C3%B3n_de_Bessel
Funciones de Bessel: http://www.sc.ehu.es/sbweb/fisica3/especial/bessel/bessel.html
Funciones de Bessel en la Wikipedia en inglés:
https://en.wikipedia.org/wiki/Bessel_function#Spherical_Bessel_functions
Funciones de Bessel en la Wikipedia en español: https://es.wikipedia.org/wiki/Funci%C3%B3n_de_Bessel
Polinomios de Legendre:
–http://www.sc.ehu.es/sbweb/fisica3/especial/legendre/legendre.html
-En la Wikipedia: https://es.wikipedia.org/wiki/Polinomios_de_Legendre

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

La partícula libre 3D

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta