Pozos de potencial 3D

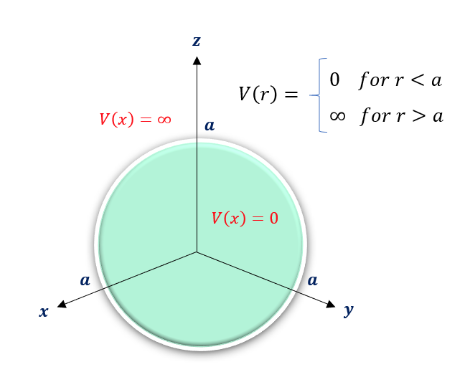
Ecuación de Schrödinger para pozos tridimensionales
Nota previa: antes de abordar estos casos 3D conviene tener bien trabajado los monodimensionales, sobre todo las entradas pozo cuadrado infinito y finito (y, por supuesto, ¡previo a los dos!, el general «Física cuántica no relativista»).

1. Ecuación de Schrödinger tridimensional

Consideremos el caso particular de la ecuación de Schrödinger para el siguiente sistema conservativo: una partícula material (no relativista) de masa $m$ y sin espín, moviéndose en el seno de un potencial real $V(\vec{r})$ (independiente de $\vec{p}$ y de $t$ ); bajo estas condiciones, el Hamiltoniano clásico $H\,=\, \frac{\vec{p}^2}{2m}+V(\vec{r})\;$ es independiente del tiempo y representa la energía total de la partícula, constituyendo una constante del movimiento.
La correspondiente ecuación de Schrödinger tiene la siguiente forma:
$E_{op} \ \Psi(\vec{r};t) = i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=H\Psi(\vec{r};t)=[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})] \Psi(\vec{r};t)$ ,
ecuación en derivadas parciales de segundo orden que, en los casos en que la forma particular del potencial lo permita, admite resolución por el método de separación de variables, de forma que el problema original tridimensional se reduce a inferior dimensión.
-Tras la primera separación de variables, espacial y temporal ( $V \ne V(t)$ ),
$\Psi(\vec{r};t)=\psi(\vec{r})\tau(t)$ ,
se obtiene la ecuación de Schrödinger para los estados estacionarios de energía, a menudo denominada también como ecuación de Schrödinger independiente del tiempo:
$H\psi_E(\vec{r})=[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})]\psi_E(\vec{r})=E\psi_E(\vec{r})$ ,
cuya expresión es la de una ecuación de autovectores o valores propios:
$H\psi_E(\vec{r})=E\psi_E(\vec{r})$ ;
la función $\psi_E(\vec{r})$ se denomina función de onda independiente del tiempo.
Las funciones de onda de expresión separable $\Psi_E(\vec{r};t)=C\,e^{-iEt/\hbar}\ \psi_E(\vec{r})$ se denominan estados estacionarios de energía, y representan soluciones de la ES
$i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=H_{op}\Psi(\vec{r};t)$
que en el caso de un sistema conservativo son autofunciones del operador Hamiltoniano, correspondientes a los valores propios $E$ :
$H\,\Psi_E(\vec{r};t)=E\,\Psi_E(\vec{r};t)$ .
Los estados estacionarios de energía satisfacen también la ecuación:
$i\hbar\frac{\partial}{\partial t}\Psi_E(\vec{r};t)=E\,\Psi_E(\vec{r};t)$ ,
de manera que son autofunciones del operador energía $i\hbar \frac{\partial}{\partial t}$ para los valores propios o autovalores $E$ .
-Nota importante: ¡Los autovalores $E$ son los únicos valores de energía accesibles o permitidos al sistema como resultados de las medidas de la energía, pero las autofunciones de energía $\Psi_E(\vec{r};t)$ NO son los únicos estados accesibles o posibles para el sistema!
En el caso particular de un potencial central, $V(\vec{r})=V(r=|\vec{r}|)$ , situación asociada a la invariancia rotacional, la ecuación es directamente resoluble introduciendo las coordenadas esféricas para proceder a continuación a la separación de variables radial y angulares, obteniéndose la ecuación de Schrödinger independiente del tiempo en coordenadas esféricas:
$H\psi(\vec{r})$
$= \, \{-\frac{\hbar^2}{2m}[ \ \frac{1}{r^2 \sin \theta} \{ \sin \theta \, \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, + \, \frac{\partial}{\partial \theta}(\sin \theta \, \frac{\partial}{\partial \theta}) \, + \, \frac{1}{\sin \theta}(\frac{\partial^2}{\partial \varphi^2}) \ ] \, + \, V(r) \ \} \ \psi(\vec{r})$
$= \, \{-\frac{\hbar^2}{2m}[ \ \frac{1}{r^2} \ \frac{\partial}{\partial r}(r^2 \, \frac{\partial}{\partial r}) \, - \, \frac{\vec{L}^2}{\hbar^2 r^2} \ ] \, + \, V(r) \} \psi(\vec{r})$
$= \, E \ \psi(\vec{r})$
A continuación, se procede a separar las variables radiales de las angulares,
$\psi(\vec{r})\, = \, R(r) \ Y(\Omega)$ ,
de donde se deriva la ES para la función radial,
$\Rightarrow \, \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, V(r) \ \} \, R_{El}(r) \, = \,E \, R_{El}(r)$ .
Un ulterior cambio de función incógnita,
$R_{El}(r)=\frac{1}{r} \ u_{El}(r)$ ,
conduce a la ecuación radial reducida en onda parcial $l$ ,
$\{ -\frac{\hbar^2}{2m} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \, + \, V(r) \ \} \, u_{El}(r) \, = \,E \, u_{El}(r)$
$\equiv \, H_l u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2m} \ \frac{d^2}{d r^2} \,+ \, V_{ef_l}(r) \ \} \ u_{El}(r)\, = \,E \, u_{El}(r)$ ,
donde se ha introducido un potencial efectivo de onda $l$ ,
$V_{ef_l}(r) \,= \, \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \, + \, V(r) \quad , \; l=0,1,2\ldots$ .
El término adicional al potencial $V(r)$ se denomina «barrera centrífuga», constituyendo un potencial repulsivo que se suma al original.
Por lo tanto, para los distintos sistema físicos se plantea resolver el problema de hallar los autoestados del potencial efectivo monodimensional $V_{ef_l}(x)$ , que debe ser definido según:
$V_{ef_l}(x) \,= \, \left\{ \begin{array}{l} \frac{\hbar^2}{2m} \ \frac{l(l+1)}{x^2} \, + \, V(x) \quad x >0 \\ \infty \quad x \le 0 \end{array} \right. \; , \; l=0,1,2\ldots$ ,
con las condiciones de integrabilidad y regularidad (anulación en el origen) para los estados ligados; para los estados de difusión cambiará la normalización y, a menudo, también bastará exigir $u_{El}$ finita en el origen, aunque muchas veces se tendrá su anulación.
En definitiva, se ha reducido el problema de valores propios original a la resolución del conjunto de los sendos problemas reducidos asociados a cada onda parcial $l$ , de expresión:
$\psi_{Elm} \, = \, R_{El}(r) \ Y_{lm}(\Omega)\, = \, \frac{1}{r} \ u_{El}(r) \ Y_{lm}(\Omega)$ .

2. El pozo esférico (central) tridimensional finito

Sea el potencial de pozo cuadrado central (esféricamente simétrico) finito definido según:
$V(r)=\left\{ \begin{array}{l} -V_0 \quad 0 \le r \le a \\ 0 \quad r >a \end{array} \right. ; \quad V_0>0 \, , \, a>0$ ,
esto es, nulo en el exterior de una esfera de radio $a$ y con valor igual a una constante negativa en su interior, al que corresponde el potencial efectivo de onda parcial $l$ :
$V_{ef_l}(r) \,= \, \left\{ \begin{array}{l} \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \, - \, V_0 \quad 0 \le r \le a \\ \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \quad r >a \end{array} \right. \; , \; l=0,1,2\ldots$
un potencial para el que:
$V_+=\lim_{r \rightarrow \infty} V_{efl}(r) =0$ .

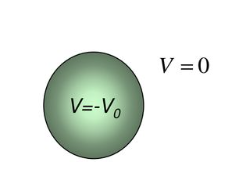
Pozo esférico finito

-El estudio de este pozo va a proporcionar los siguientes resultados: los estados ligados de onda l, de existir serán puntos discretos del intervalo real entre el valor $-V_0$ y el valor $V_+=0$ , $\sigma_p{H} \subset (-V_0,0]$ ; el estado fundamental, de existir, será una onda s, esféricamente simétrico. Los estados de difusión corresponderán a la parte continua del espectro, $\sigma_c(H) \subset [0,\infty)$ (el valor $E=0$ dependiendo del caso concreto podrá ser estado ligado o de difusión).

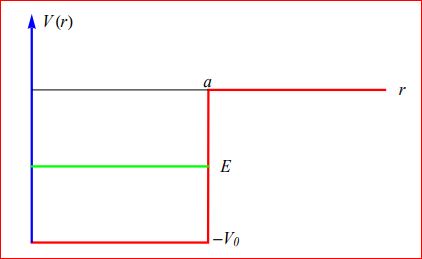
$Pozo cuadrado central o esféricamente simétrico. Si el valor mínimo $latex -V_0$ se desplaza en una cantidad constante , $latex -V_0 + \lambda$ , las autofunciones no cambian, ocurriendo tan sólo un desplazamiento constante, de valor $latex \lambda$ , en los autovalores de energía.$
Pozo cuadrado central o esféricamente simétrico. Si el valor mínimo $-V_0$ se desplaza en una cantidad constante , $-V_0 + \lambda$ , las autofunciones no cambian, ocurriendo tan sólo un desplazamiento constante, de valor $\lambda$ , en los autovalores de energía.

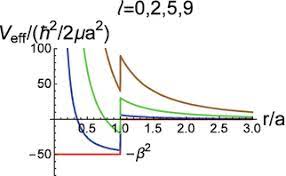
Aspecto del potencial efectivo, en unidades $\frac{\hbar^2}{2ma^2}$ , para algunas ondas parciales (ejemplo general, $\beta^2 \equiv V_0$ y $\mu=m$ ) (imagen en referencia [BER-18], https://doi.org/10.1007/978-3-319-68598-4_10) .
Expresada la función de ondas como
$\psi_{Elm}=R_{El}(r)Y_{lm}(\Omega)=\frac{1}{r}u_{El}(r)Y_{lm}(\Omega)$ ,
las ecuaciones radial y reducida son:
$\left. \begin{array}{l} \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, - \, V_0 \ \} \, R_{El}(r) \, = \,E \, R_{El}(r) \quad 0 \le r \le a \\ \{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \} \, R_{El}(r) \, = \,E \, R_{El}(r)\quad r >a \end{array} \right\}$
$\left. \begin{array}{l} \{ -\frac{\hbar^2}{2m} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \, - \, V_0 \ \} \, u_{El}(r) \, = \,E \, u_{El}(r) \quad 0 \le r \le a \\ \{ -\frac{\hbar^2}{2m} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \ \} \, u_{El}(r) \, = \,E \, u_{El}(r) \quad r >a \end{array} \right\}$
$\equiv \, H_l u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2m} \ \frac{d^2}{d r^2} \,+ \, V_{ef_l}(r) \ \} \ u_{El}(r)\, = \,E \, u_{El}(r)$ ;
las soluciones buscadas han de satisfacer la condición de regularidad,
$u_{El}(0)\, = \, 0 \, , \, \forall l$ ,
con $u_{El}(r) \ \xrightarrow{r\rightarrow 0} \ 0$ más rápido que $r\xrightarrow{r\rightarrow 0} \ 0$ , ya que $R_{El}(r)=u(r)_{El} /r$ debe ser continua (finita) en el origen para todos los valores $l$ ; adicionalmente, los estados ligados (no así los estados de difusión) han de de cumplir también la condición de integrabilidad:
$\int_0^{\infty} \ |u_{El} |^2 \ dr \, = \, 1$ .
Obtención de los estados ligados : intervalo energético :
1. Región $0 \le r \le a$ e intervalo energético $-V_{0} < E < 0$ :
  -Ecuación radial:
  $\{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, - \, V_0 \ \} \, R_{El}(r) \, = \,E \, R_{El}(r)$
  -Se realiza el cambio de variable independiente:
  $\rho=k r \quad , \quad k=\frac{+\sqrt{2m(E+V_0)}}{\hbar}=\frac{+\sqrt{2m(|V_0|-|E|)}}{\hbar}>0 \, , \, \in \mathbb{R}$ ,
  mediante el cual la anterior ecuación se convierte en la ecuación diferencial esférica de Bessel,
  $[ \ \frac{d^2}{d \rho^2} \, + \, \frac{2}{\rho} \ \frac{d }{d \rho} \,+\, (1 \ - \ \frac{l(l+1)}{\rho^2}) \ ] \, R_{El}(\rho)=0$ ,
  ecuación de soluciones bien conocidas: las funciones esféricas de Bessel (de primera especie) $j_l(\rho=kr)$ , y de segunda especie o funciones esféricas de Neumann, $n_l(\rho=kr) \equiv y_l(\rho=kr)$ .
  -En terminos de ellas, la solución general de la EDO se expresa:
  $R_{El}(\rho)\, = \, C_1 \ j_l(\rho=kr) \, + \, C_2 \ n_l(\rho=kr)$ ,
  donde $C_1, C_2$ son constantes arbitrarias.
  -La función esférica de Neumann $n_l(\rho)$ posee un polo de orden $l+1$ en el origen, por lo que la función radial reducida no es analítica en el origen:
  $n_l(\rho) \ \xrightarrow{\rho \rightarrow 0} \ -\frac{(2l-1)!!}{\rho^{l+1}} \Rightarrow \lim_{\rho \rightarrow 0}u_{El}(\rho)=\lim_{\rho \rightarrow 0} \rho \ n_{l}(\rho)=\lim_{\rho \rightarrow 0} \ -\frac{(2l-1)!!}{\rho^{l}}$ .
  -Por el contrario, la solución particular función esférica de Bessel de primer orden sí proporciona una solución analítica en el origen:
  $j_l(\rho) \ \xrightarrow{\rho \rightarrow 0} \ \frac{\rho^{l}}{(2l+1)!!} \Rightarrow \lim_{\rho \rightarrow 0}u_{El}(\rho)=\lim_{\rho \rightarrow 0} \rho \ j_{l}(\rho)=\lim_{\rho \rightarrow 0} \ \frac{\rho^{l+1}}{(2l-1)!!}$
  -Por tanto, la parte radial de la onda parcial $l$ solución de la ES para valores de energía $-V_{0} < E < 0$ y que cumple las condiciones de contorno requeridas, toma la expresión final:
  $R_{El}(r) \, = \, C_1 \ j_l(kr)\, , \, 0 \le r \le a$ ,
  $k=\frac{+\sqrt{2m(E+V_0)}}{\hbar}$ .
2. Región $r >a$ e intervalo energético $-V_{0} < E < 0$ :
  -se realiza el cambio de variable independiente:
  $\rho=i \lambda r \quad , \quad \lambda =\frac{+\sqrt{-2mE}}{\hbar}=\frac{+\sqrt{2m|E|}}{\hbar}>0 \, , \, \lambda \in \mathbb{R}$
  mediante el cual la anterior ecuación se convierte en la ecuación diferencial esférica de Bessel,
  $[ \ \frac{d^2}{d \rho^2} \, + \, \frac{2}{\rho} \ \frac{d }{d \rho} \,+\, (1 \ - \ \frac{l(l+1)}{\rho^2}) \ ] \, R_{El}(\rho)=0$ ,
  ecuación de soluciones bien conocidas: las funciones esféricas de Bessel (de primera especie) $j_l(\rho)$ , y de segunda especie o funciones esféricas de Neumann, $n_l(\rho) \equiv y_l(\rho)$ , o, también, las funciones esféricas de Bessel de tercera clase, o funciones esféricas de Hankel de primera y segunda especie, $h_l^{(1)}(z)= j_l(z) +in_l(z)$ y $h_l^{(2)}(z)= j_l(z) -in_l(z)$ , respectivamente.
  -En terminos de ellas, la solución general de la EDO se expresa:
  $R_{El}(\rho)\, = \, C_1' \ j_l(\rho) \, + \, C_2' \ n_l(\rho)$ ,
  o, alternativamente,
  $R_{El}(\rho)\, = \, A \ h_l^{(1)}(\rho) \, + \, B \ h_l^{(2)}(\rho)$ ,
  donde $C_1', C_2', A, B$ son constantes arbitrarias.
3. El intervalo de valores considerado por ahora no contiene al origen, de forma que por su comportamiento en $r=0$ todos estos tipos de soluciones particulares serían en principio aceptables, pero puesto que las largas distancias corresponden a valores $r >a$ la combinación lineal ha de proporcionar soluciones acotadas a largas distancias. En este límite ( $r\rightarrow \infty \ , \ \rho=i\lambda r \ , \ \lambda > 0$ ) se tienen los siguientes comportamientos asintóticos:
  $\lim_{r \rightarrow \infty } j_l(\rho) = \lim_{r \rightarrow \infty } \frac{1}{\rho}\cos[\rho -\frac{(l+1)\pi}{2}]$
  $= \lim_{r \rightarrow \infty } \frac{-1}{2 \lambda r} [ e^{-\lambda r -i\frac{(l+1)\pi}{2}}-e^{ \lambda r + i\frac{(l+1)\pi}{2}} ] \rightarrow \infty$
  $\lim_{r \rightarrow \infty } n_l(\rho) = \lim_{r \rightarrow \infty } \frac{1}{\rho}\sin[\rho -\frac{(l+1)\pi}{2}] = \lim_{r \rightarrow \infty } \frac{-i}{ \lambda r} \sin [i\lambda r -\frac{(l+1)\pi}{2} ] \rightarrow \infty$
  $\lim_{r \rightarrow \infty } h_l^{(1)}(\rho) = \lim_{r \rightarrow \infty } \frac{1}{\rho}e^{[i\rho -\frac{(l+1)\pi}{2}]} =\lim_{r \rightarrow \infty } \frac{-i}{\lambda r}e^{[-\lambda r -i\frac{(l+1)\pi}{2}]} \rightarrow 0$
  $\lim_{r \rightarrow \infty } h_l^{(2)}(\rho) = \lim_{r \rightarrow \infty } \frac{1}{\rho}e^{-i[\rho -\frac{(l+1)\pi}{2}]} = \lim_{r \rightarrow \infty } \frac{-i}{\lambda r}e^{[\lambda r + i\frac{(l+1)\pi}{2}]} \rightarrow \infty$ ,
  de manera que sólo la función esférica de Hankel de primera especie (también llamada función esférica de Bessel de tercera clase) proporciona el comportamiento asintótico correcto a largas distancias. La función radial queda entonces:
  $\Rightarrow R_{El}(\rho =i \lambda r )\, = \,A \ h_l^{(1)}(\rho )\, = \,A \ (j_l(\rho) +in_l(\rho)) \, , \, r >a$
  $\rho=i \lambda r \quad , \quad \lambda =\frac{+\sqrt{-2mE}}{\hbar}=\frac{+\sqrt{2m|E|}}{\hbar}>0 \, , \, \lambda \in \mathbb{R}$
4. Reuniendo los resultados obtenidos en las dos zonas consideradas, la onda parcial $l$ solución de la ES, autofunción simultánea de los operadores $\{ H,\vec{L}^2,L_z \}$ para valores de energía $-V_{0} < E < 0$ y que cumple las condiciones de contorno requeridas, toma la expresión final:
  $\psi_{Elm}(\vec{r})\, = \, R_{El}(r) \ Y_{lm}(\Omega)$ ,
  donde
  $R_{El}(r)\, = \left. \begin{array}{l} C_1 \ j_l(kr) \quad 0 \le r \le a\\ A \ h_l^{(1)}(i\lambda r) \quad r > a \end{array} \right\}$ ,
  $k=\frac{+\sqrt{2m(E+V_0)}}{\hbar}>0 \, , \, k \in \mathbb{R}$ ,
  $\lambda =\frac{+\sqrt{-2mE}}{\hbar}=\frac{+\sqrt{2m|E|}}{\hbar}>0 \, , \, \lambda \in \mathbb{R}$ ,
  función que ha de ser analítica en el punto de empalme $r=a$ .
  -Estas autofunciones se denominan «ondas l ligadas».
5. El paso siguiente en la resolución es la conexión adecuada entre las dos zonas, para lo que se impone la continuidad de la función radial y su primera derivada en el punto $r=a$ , condición que permitirá obtener los estados ligados, en su caso:
  $\left. \begin{array}{l} C_1 \ j_l(ka)\, = \,A \ h_l^{(1)}(i \lambda a) \\ C_1 \ \frac{d j_l(kr)}{dr}|_{r=a}\, = \, A \ \frac{d h_l^{(1)}(i\lambda r)}{dr}|_{r=a} \end{array} \right\} \Rightarrow \frac{d [\ln{j_l(kr)}]}{dr}|_{r=a}\, = \, \frac{d [\ln{h_l^{(1)}(i\lambda r)}]}{dr}|_{r=a}$ .
  -Empleando las relaciones de recurrencia
  $j_l'(z)=-j_{l+1}(z)+\frac{l}{z}j_l(z)$
  $h_l^{(1)} \ ' (z)=-h_{l+1}^{(1)}(z) + \frac{l}{z} h_l^{(1)}(z)$
  se obtiene:
  $\left. \begin{array}{l} z_1=kr \, , \, \frac{d}{dr}=\frac{d}{dz_1} \frac{dz_1}{dr} =k \frac{d}{dr} \\ z_2=i \lambda r \, , \, \frac{d}{dr}=\frac{d}{dz_2} \frac{dz_2}{dr} =i \lambda \frac{d}{dr} \end{array} \right\} \Rightarrow k \ \frac{ j_l ' (z_1)}{j_l(z_1)}\, = \, i \lambda \ \frac{ h_l^{(1)} \ ' (z_2)}{h_l^{(1)}(z_2)}$
  $\Rightarrow k \ ( \frac{ -j_{l+1}(z_1)}{j_l(z_1)} \, + \, \frac{l}{z_1} )\, = \, i \lambda \ ( - \frac{ h_{l+1}^{(1)} (z_2)}{h_l^{(1)}(z_2)} \, + \, \frac{l}{z_2} )$
  $\Rightarrow k \ \frac{ j_{l+1}(k r)}{j_l(k r)} |_{r=a} \, = \, i \lambda \ \frac{ h_{l+1}^{(1)} (i \lambda r)}{h_l^{(1)}(i \lambda r )} |_{r=a}$ ,
  ecuación que proporciona los autovalores de energía ligados y que, en general y para onda parcial $l$ arbitraria, necesita resolución numérica. Pero las primeras ondas parciales suelen ser las más fáciles, admitiendo en este caso resolución gráfica.
6. Los primeros autovalores de energía, para las primeras ondas parciales, resultan:
  1. 6.1 Onda parcial s (valor $l=0$ ):
    $l=0 \Rightarrow k \ \frac{ j_{1}(k r)}{j_0(k r)} |_{r=a} \, = \, i \lambda \ \frac{ h_{1}^{(1)} (i \lambda r)}{h_0^{(1)}(i \lambda r )} |_{r=a}$
    $\Rightarrow k\frac{kr}{\sin kr} [\frac{\sin kr}{k^2 r^2} - \frac{\cos kr}{kr}] |_{r=a} \, = \, -i \lambda i \frac{i \lambda r}{e^{-\lambda r}}[\frac{1}{i \lambda r} + \frac{i}{- \lambda^2 r^2}]e^{-\lambda r} |_{r=a}$
    $\Rightarrow k^2 r [ \frac{1}{k^2r^2} - \frac{ \cot kr}{kr} ] |_{r=a} \, = \, i \lambda ^2 r [\frac{1}{i \lambda r} - \frac{i}{\lambda^2 r^2} ] |_{r=a}$
    $\Rightarrow k \ \cot \ ka \, = \, -\lambda$ ,
    obteniéndose como ecuación de cuantización de la energía, una ecuación trascendente que ya se analizó en el caso de las soluciones impares para el pozo cuadrado finito monodimensional (donde $\alpha \equiv k$ y $\beta \equiv \lambda$ ) .
    -Parámetros para la resolución gráfica: una posibilidad (existen varias, véase el caso monodimensional) para la resolución gráfica de las anterior ecuación trascendente es dibujar la circunferencia de radio
    $r_o=\frac{a\sqrt{2m|V_o|}}{\hbar}$ , el denominado «parámetro de intensidad o fuerza» del pozo, esto es, la curva
    $\left. \begin{array}{l} \xi = ka \\ \eta = \lambda a \end{array} \right\} \rightarrow \xi^2 \, + \, \eta^2 \, = \, r_o^2$
    (circunferencia $(k^2 a^2 + \lambda^2 a^2)=r_o^2$ ),
    y localizar los puntos de corte con la curva $g(\xi)=-\cot (\xi)$ :
    $\left. \begin{array}{l} \xi \ cotan \xi \, = \, -\eta \\ \xi^2 \, + \, \eta^2 \, = \, r_o^2\end{array} \right\}$ ,
    donde
    $\xi = k a=\frac{a}{\hbar}\sqrt{2m(|V_o|-|E|)}$
    $\eta = \lambda a =\frac{a}{\hbar} \sqrt{-2mE}=\frac{a}{\hbar} \sqrt{2m|E|}$
    y
    $r_o^2=\frac{a^2 2m|V_o|}{\hbar^2}$ ,
    cumpliéndose
    $(k^2 + \lambda^2)\hbar^2 =2mV_o =r_o^2\hbar^2/a^2$ .
    -En la referencia de libre acceso
    https://bingweb.binghamton.edu/~suzuki/QuantumMechanicsII/5-4_Finite_spherical_well.pdf
    se estudia detalladamente este potencial (incluido un estudio detallado del caso especial $E=0$ , que no trataremos aquí), en el caso del deuterón (núcleo del deuterio, $^+H^2$ , compuesto de un neutrón y un protón); ahí puede encontrarse la siguiente figura:
    
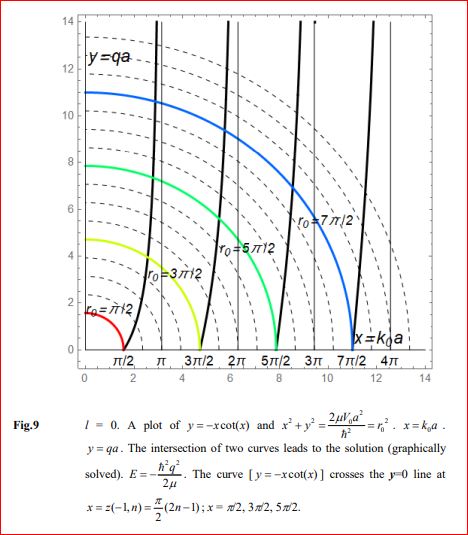
    Estados ligados onda s en el deuterón ( $k_o \equiv k \, , \, q \equiv \lambda$ ).
    
    -Obsérvese que en este caso, el tridimensional, a diferencia de lo que ocurría en el unidimensional, puede no existir un estado ligado en onda s:
    si
    $0 < r_0^2=\frac{2m|V_o|a^2}{\hbar^2} < \frac{\pi^2}{4}$ ,
    entonces no existe ningún punto de corte entre las dos curvas.
    -Por lo mismo, existirá un único estado ligado en onda s cuando
    $\frac{\pi^2}{4} < r_0^2=\frac{2m|V_o|a^2}{\hbar^2} < \frac{9\pi^2}{4}$ ;
    dos estados ligados en onda s cuando
    $\frac{9\pi^2}{4} < r_0^2=\frac{2m|V_o|a^2}{\hbar^2} < \frac{25\pi^2}{4}$ ,
    y así sucesivamente.
  2. 6.2 Onda parcial p (valor $l=1$ ):
    $l=1 \Rightarrow k \ \frac{ j_{2}(k r)}{j_1(k r)} |_{r=a} \, = \, i \lambda \ \frac{ h_{2}^{(1)} (i \lambda r)}{h_1^{(1)}(i \lambda r )} |_{r=a}$
    $\Rightarrow [ \frac{\cot(kr)}{kr} - \frac{ 1}{k^2r^2} ] |_{r=a} \, = \, \frac{1}{\lambda r} + \frac{1}{\lambda^2 r^2} ] |_{r=a}$ ,
    una ecuación trascendente a resolver numérica o gráficamente.
    -Es posible (consúltese la referencia dada) predecir el número de estados ligados en onda p como función del parámetro $r_0=\frac{2m|V_o|a^2}{\hbar^2}$ sin resolver la ecuación trascendente:
    -No existirá un estado ligado en onda p cuando
    $0 < r_0^2=\frac{2m|V_o|a^2}{\hbar^2} < \pi^2$ ,
    -Por lo mismo, existirá un único estado ligado en onda p cuando
    $\pi^2 < r_0^2=z_0=\frac{2m|V_o|a^2}{\hbar^2} < 4\pi^2$ ;
    dos estados ligados en onda p cuando
    $4\pi^2 < r_0^2=\frac{2m|V_o|a^2}{\hbar^2} < 9\pi^2$ ,
    y así sucesivamente.
7. El mínimo valor de $r_0$ a partir del cual aparece un estado ligado $l=1$ , es decir, el valor $r_0 = \pi$ , es mayor que el mínimo valor de $r_0$ a partir del cual se permite un estado ligado $l=0$ , $r_0 = \frac{\pi}{2}$ . Conforme $l$ aumenta, también crece el valor mínimo de $r_0$ que permite un estado ligado $l$ , un resultado esperable por la presencia de la barrera centrífuga en el potencial efectivo; de hecho, para valores del número cuántico $l$ suficientemente grandes, no existirán estados ligados.
8. Si existen estados ligados, el estado fundamental es una onda s.
  -No existen estados ligados en onda s y, por tanto, no existe ningun estado ligado, cuando:
  $\frac{2ma^2|V_0|}{\hbar^2} < \frac{\pi^2}{4}$
9. Otros resultados (véase referencia [GAL-78]pp. 291-293):
  -El número de estados ligados en onda s viene dado por $N_s=Ent \ [\frac{1}{2} + \frac{a |V_0|^{\frac{1}{2}}a}{\pi}]$ ,
  donde $Ent \ [x]$ significa el mayor entero menor que x.
  -Para onda s no hay estados ligados de energía nula, $E=0$ .
  -Existe un estado ligado de energía nula $l > 0$ sólo si $j_{l-1}(|V_0|^{\frac{1}{2}}a)=0$ , autoestado que, aunque es de cuadrado integrable, no presenta el decaimiento exponencial típico de los restantes estados ligados (de energía negativa).
En resumen, en la resolución se han presentado dos casos:
a) $\frac{2ma^2|V_0|}{\hbar^2} < \frac{\pi^2}{4}$ :
–No existen estados ligados, sólo estados de difusión, correspondientes a valores $E \ge 0$ , integrando la parte continua del espectro, $\sigma_c(H) = [0,\infty)$ , con autofunciones que presentan conducta oscilatoria a largas distancias y satisfacen la condición de regularidad pero no así la condición de integrabilidad.
b) $\frac{2ma^2|V_0|}{\hbar^2} \ge \frac{\pi^2}{4}$ :
-Se presentan tanto estados de difusión, para $E \ge 0$ , como estados ligados en algunas ondas l, teniéndose para la parte discreta del espectro que $\sigma_p(H) \subset (-|V_{0}| ,0]$ , con autofunciones que satisfacen tanto la condición de regularidad como la de integrabilidad.
El valor $E=0$ puede ser, dependiendo del caso, o bien un estado ligado, o bien un estado de difusión.
A diferencia de lo que sucede en los casos monodimensional y bidimensional, donde hay siempre al menos un estado ligado, en tres dimensiones un pozo, por ejemplo si es demasiado estrecho o poco profundo, o ambas cosas, puede carecer de estados ligados. Además, los estados ligados en el caso tridimensional sí pueden presentar degeneración: aunque estados de energía correspondientes a distintas ondas parciales (distintos valores de $l$ ) no suelen estar degenerados, la degeneración en el número cuántico de tercera componente está presente: cada nivel de energía de onda parcial $E_{l}$ es $(2l+1)$ veces degenerado (algo común a todos los potenciales centrales).

2. El pozo esférico (central) tridimensional infinito

Sea el potencial de pozo cuadrado central (esféricamente simétrico) finito definido según:
$V(r)=\left\{ \begin{array}{l} 0 \quad 0 \le r \le a \\ \infty \quad r >a \end{array} \right. \; , \, a>0$ ,
esto es, nulo sobre y en el interior de una esfera de radio $a$ y con valor repulsivo infinito en su exterior; el potencial efectivo de onda parcial $l$ toma la expresión:
$V_{ef_l}(r) \,= \, \left\{ \begin{array}{l} \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \quad 0 \le r \le a \\ \infty \quad r >a \end{array} \right. \; , \; l=0,1,2\ldots$ ,
un potencial para el que:
$V_+ =\lim_{r \rightarrow \infty} V_{ef_l}(r) \,= \, \infty \, , \, \forall l$ .

-Para este pozo, las energías de los estados ligados en onda l, en número infinito, estarán comprendidas en el intervalo de energia $(0,+\infty)$ (comparando con el caso finito anterior, correspondería a un fondo del pozo en $V_0=0$ y una profundidad infinita).
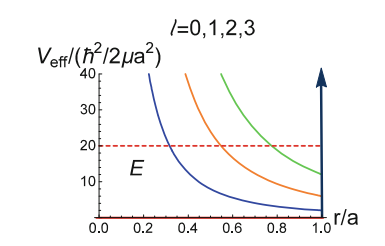
$Aspecto del potencial efectivo en un pozo central infinito, en unidades $latex \frac{\hbar^2}{2ma^2}$ , para algunas ondas parciales$
Aspecto del potencial efectivo, en unidades $\frac{\hbar^2}{2ma^2}$ , para algunas ondas parciales ( $\mu=m$ ) (imagen en referencia [BER-18], https://doi.org/10.1007/978-3-319-68598-4_10) .
Es evidente que en la zona exterior de la esfera ha de imponerse la condición de contorno
$R_{El}=0 \quad \forall r > a$ ;
mientras que la ecuación para la función radial en la zona $0 \le r \le a$ toma la forma
$-\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \ R_{El}(r) \, = \,E \ R_{El}(r) \quad 0 \le r \le a$ .
-La conexión de ambas zonas, mediante la condición adicional de anulación de la función radial en $r=a$ , hará emerger la cuantización del espectro del Hamiltoniano.
Resolución: estados ligados :
1. Onda s:
  -En este caso, la ecuación radial reducida es
  $-\frac{\hbar^2}{2m} \ \frac{d^2}{d r^2} \ u_{E0}(r) \, = \,E \, u_{E0}(r)$
  $\Rightarrow \frac{d^2}{d r^2} \ u_{E0}(r) \, + \, \frac{2m}{\hbar^2} \ E \, u_{E0}(r) \, = \, 0 \; , \; 0 \le r \le a$ .
  -Recordando que la EDO lineal homogénea $u'' + k^2u=0 \, , \, k \in \mathbb{R} \, , \, k>0$ tiene por solución general la combinación lineal de soluciones particulares:
  $u(r)=C_1 \ e^{+ikr} + C_2\ e^{-ikr}=C_1' \ cos\ kr + C_2'\ sen \ kr$
  con $C_1,C_2,C_1',C_2'$ escalares arbitrarios,
  es directo obtener la solución general para valores $E>0$ :
  $u_{E0}(r) \, = \,C'_1 \ cos\ kr + C'_2\ sen \ kr$
  $k=\frac{\sqrt{2mE}}{\hbar} \; , \; k > 0 \, , \, k \in \mathbb{R}$ .
  -Puesto que la solución ha de anularse en el origen, condición de regularidad, finalmente se obtiene la autofunción reducida en onda s de expresión:
  $u_{E0}(r) \, = \, C_2' \ \sin \ kr$ ,
  $k=\frac{+\sqrt{2mE}}{\hbar}>0 \, , \, k \in \mathbb{R}$ .
  -La condición de anulación en $r=a$ proporciona la ecuación de cuantización de la energía que permite obtener los correspondientes autovalores:
  $u_{E0}(r=a) = 0= C_2' \ \sin \ ka \Rightarrow k \doteq k_{n0} \, = \, \frac{n\pi}{a} \; , \; n=1,2,3\ldots$ .
  -Por tanto, las ondas parciales s solución de la ES que cumplen todas las condiciones de contorno requeridas toman la expresión final:
  $\Rightarrow \psi_{E_{n0}00}(\vec{r})\, = \, R_{E_{n0}0}(r) \ Y_{00}(\Omega) \quad , \quad n=1,2\ldots$ ,
  donde
  $R_{E_{n0}0}(r)\, = \left. \begin{array}{l} C_2' \ \frac{sen \ k_{n0}r}{r} = C_2' \ k_{n0} \ j_0(k_{n0}r) \quad 0 \le r \le a\\ 0 \quad r \ge a \end{array} \right\}$ ,
  cuyo correspondiente autovalor es:
  $E_{n0}=\frac{\hbar^2k_{n0}^2}{2m} \, = \,\frac{\hbar^2 n^2 \pi^2}{2ma^2}$ ,
  o, de forma equivalente,
  $E_{n0}=\frac{\hbar^2x_{n0}^2}{2ma^2}$ ,
  donde $x_{n0}$ representa el n-ésimo cero de la función esférica de Bessel de primera especie $j_0(x)$ .
  -La constante de normalización $C_2'$ toma el valor:
  $\int_0^{\infty} \ |R_{E_{n0}0}|^2 \ r^2dr \,=\, \int_0^a \ |C_2' \ sen \ k_{n0}r (r)|^2 \ dr\,=\,1 \Rightarrow C_2'=\sqrt{\frac{2}{a}}$ .
2. Ondas $l >0$ :
  -En este caso partimos de la ecuación radial:
  $-\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \ R_{El}(r) \, = \,E \ R_{El}(r) \quad 0 \le r \le a$
  $[ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \, + \, \frac{2m}{\hbar^2} \ E\ ] \ R_{El}(r) \, = \,0 \ \quad 0 \le r \le a$
  -Se realiza el cambio de variable independiente ( $E>0$ ):
  $\rho=k r \quad , \quad k=\frac{+\sqrt{2mE}}{\hbar}>0 \, , \, \in \mathbb{R}$ ,
  mediante el cual la anterior ecuación se convierte en la ecuación diferencial esférica de Bessel,
  $[ \ \frac{d^2}{d \rho^2} \, + \, \frac{2}{\rho} \ \frac{d }{d \rho} \,+\, (1 \ - \ \frac{l(l+1)}{\rho^2}) \ ] \, R_{El}(\rho)=0$ ,
  ecuación de soluciones bien conocidas: las funciones esféricas de Bessel (de primera especie) $j_l(\rho=kr)$ , y de segunda especie o funciones esféricas de Neumann, $n_l(\rho=kr) \equiv y_l(\rho=kr)$ .
  -En terminos de ellas, la solución general de la EDO se expresa:
  $R_{El}(\rho)\, = \, C_1 \ j_l(\rho=kr) \, + \, C_2 \ n_l(\rho=kr)$ ,
  donde $C_1, C_2$ son constantes arbitrarias.
  -Imponiendo la condición de regularidad en el origen, se descarta la solución particular $n_l(r) \xrightarrow{r \rightarrow 0} r^{-l-1}$ , de donde se concluye
  $R_{El}(r)\, = \left. \begin{array}{l} C_1 \ j_l(kr) \quad 0 \le r \le a\\ 0 \quad r > a \end{array} \right\}$ .
  -Para determinar los autovalores se impone la condición de frontera de anulación de la función de onda en $r=a$ , de donde se deriva la ecuación de cuantización de la energía, cuyas raíces los proporcionan:
  $R_{El}(a)=0 \Rightarrow j_l(ka)=0$ ,
  una ecuación a resolver numéricamente, y cuyas soluciones se expresan por tanto en términos de los ceros $x_{nl} \, , \, n=1,2\ldots$ de la función esférica de Bessel de primera especie $j_l(x)$ :
  $R_{El}(r=a) = 0 \Rightarrow ka=x_{nl}\; , \; n=1,2,3\ldots$
  $\Rightarrow k \doteq k_{nl} \, = \, \frac{x_{nl}}{a} \; , \; E_{nl}=\frac{\hbar^2}{2ma^2} \ x_{nl}^2 \; , \, n=1,2,3\ldots$ ,
  donde $x_{nl}$ representa el n-ésimo cero de la función esférica de Bessel de primera especie $j_l(x)$ .
  Nota: cf. [ABR]cap.9, p. 440: Los ceros de las funciones esféricas de Bessel $j_n(x)$ e $y_n(x)$ coinciden con los de las funciones de Bessel de primera especie $J_{n+\frac{1}{2}}(x)$ y de segunda especie $Y_{n+\frac{1}{2}}(x)$ , respectivamente.
  -Por tanto, la onda parcial $l$ solución de la ES, autofunción simultánea de los operadores $\{ H,\vec{L}^2,L_z \}$ para valores de energía ligados $E \equiv E_{nl} > 0$ y que cumple las condiciones de contorno requeridas, toma la expresión final:
  $\psi_{E_{nl}lm}(\vec{r})\, = \, R_{E_{nl}l}(r) \ Y_{lm}(\Omega)$ ,
  donde
  $R_{E_{nl}l}(r)\, = \left. \begin{array}{l} C_{E_{nl} l} \ j_l(k_{nl}r)= C_{E_{nl} l} \ j_l(\frac{x_{nl}}{a}r) \quad 0 \le r \le a\\ 0 \quad r \ge a \end{array} \right\}$ ,
  cuyo correspondiente autovalor es:
  $E_{nl}=\frac{\hbar^2x_{nl}^2}{2ma^2}$ ,
  donde $C_{E_{nl}l}$ es la adecuada constante de normalización y $x_{nl}$ representa el n-ésimo cero de la función esférica de Bessel de primera especie $j_l(x)$ .
  -Estas autofunciones se denominan «ondas l ligadas».
Las siguientes figuras y tabla muestran las primeras funciones esféricas de Bessel y sus ceros:

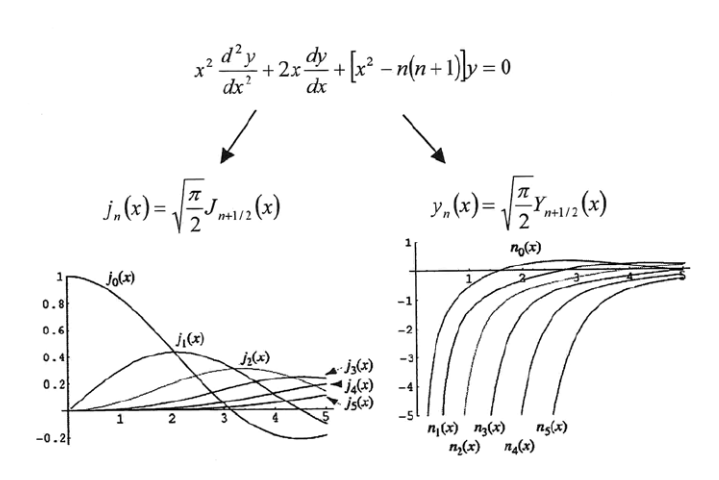
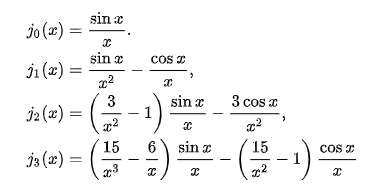
Primeras funciones esféricas de Bessel.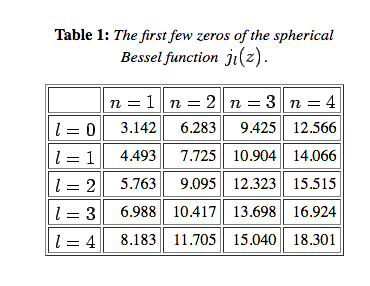

Expresiones, gráficas y ceros de las primeras funciones esféricas de Bessel (https://farside.ph.utexas.edu/teaching/qmech/Quantum/node81.html).
El pozo infinito posee pues infinitos estados ligados; además, todos ellos, salvo el estado fundamental, que es la onda s, son degenerados: la energía no depende del número cuántico magnético $m$ , que posee $2l+1$ valores para cada onda $l$ . Su ordenación energética se indica en las siguientes figuras:
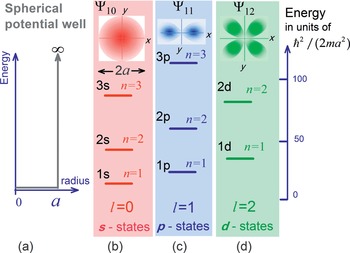
Primeras ondas parciales en un pozo esférico infinito (Fuente: S. V. Gaponenko&H.V. Demir, Applied Nanophotonics, Cambridge).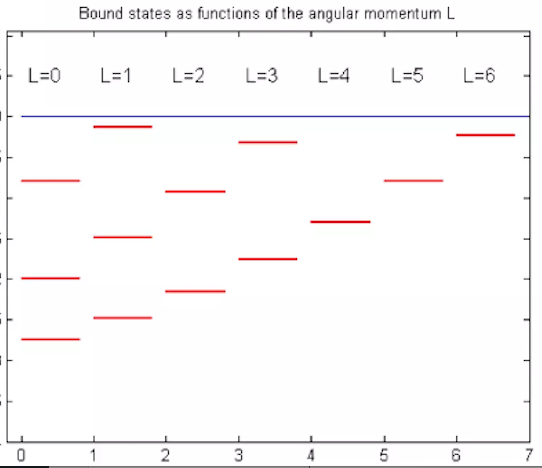

Ordenación de los primeros estados ligados de un pozo infinito 3D (imagen: Bound states in 1d, 2d and 3d quantum wells, by A. Aslam & M. Vasu).
Una calculadora de los valores de los estados ligados del pozo esférico infinito la proporciona en línea el proyecto Wolfram:
Captura de pantalle de la calculadora de niveles de energía del pozo esférico infinito: Demostraciones Wolfram (S. M. Blinder,»Particle in an Infinite Spherical Well»).
La siguiente figura muestra la ordenación de los primeros nives de energía de un pozo esférico infinito tridimensional, en comparación con el caso de un potencial parabólico (HO, oscilador armónico):
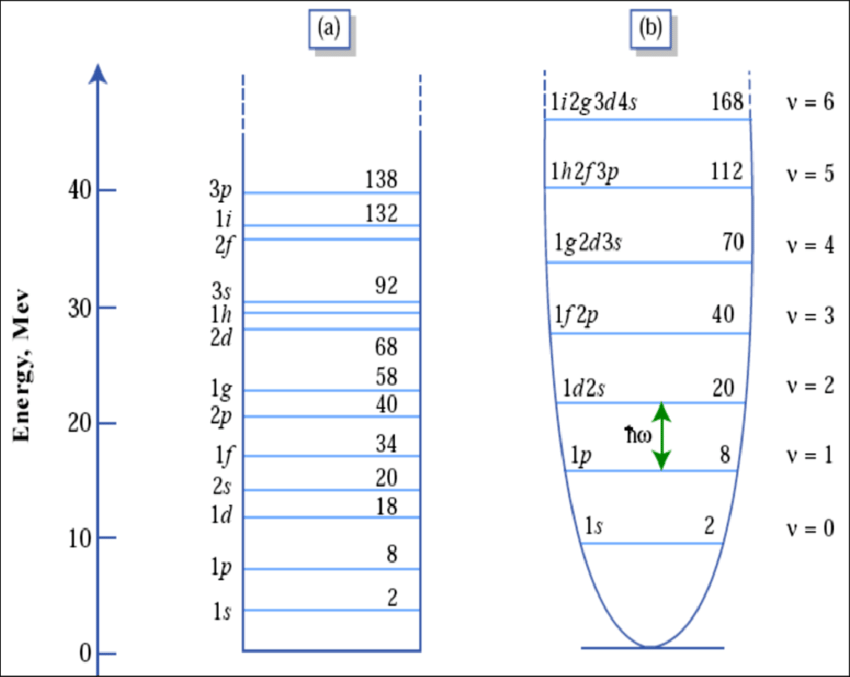
Primeros niveles de energía ligados en un ejemplo de pozo esférico infinito simétrico y en un pozo parabólico (Fuente: K. Abdullah, Fundamental in Nuclear Physics).

3. El pozo prismático infinito tridimensional: la caja impenetrable

Sea una partícula de masa $m$ , sin espín, en interior de una caja prismática rectangular de lados $L_i \, , \, i=x,y,z$ y paredes impenetrables, de tal forma que la partícula está sometida al siguiente potencial:
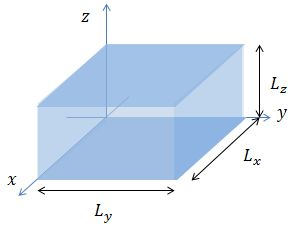
$V(\vec{r}) \,= \, \left\{ \begin{array}{l} 0 \quad 0 \le r_i \le L_i \\ \infty \quad r_i < 0 \, , \, r_i > L_i \end{array} \right.$
La anterior ES independiente del tiempo contiene en este caso un potencial $V(\vec{r})$ que en el interior de la caja y sobre sus caras admite expresión aditiva en coordenadas cartesianas de la forma:
$V(\vec{r})=V_x(x) + V_y(y)+ V_z(z)=0+0+0$ ,
de modo que el operador Hamiltoniano resulta ser
$H=-\frac{\hbar^2}{2m}\nabla^2+0=H_x(x) + H_y(y)+ H_z(z)$ ,
donde cada sumando $H_i(r_i)$ tiene la expresión
$H_i(r_i)=-\frac{\hbar^2}{2m} \ \frac{\partial^2}{\partial r_i^2} \quad ; \; i=x,y,z \; ; \; r_i \equiv i$ ,
y la ecuación de Schrödinger independiente del tiempo en coordenadas cartesianas toma la forma en la región $0 \le r_i \le L_i$ :
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2} \} \psi_E(\vec{r})=E \ \psi_E(\vec{r})$ ,
ecuación a la que se añade la condición de frontera de anulación de la función de onda sobre las paredes de la caja.
Esta expresión del Hamiltoniano permite la búsqueda de soluciones por el método de separación de variables, esto es, sustituir la solución expresándola según
$\psi_E(\vec{r}=(x,y,z)) = X(x) \ Y(y) \ Z(z) \equiv \prod_{x,y,z} R_i(r_i)\; , \; i=x,y,z$ ,
junto con las condiciones de frontera
$R_i(r_i)=0 \quad \forall r_i \le 0 \, , \, \forall r_i \ge L_i \; , \; i=x,y,z$
y a continuación realizar el procedimiento habitual:
1. Sustitución en la ecuación:
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2} \ \} \prod_{x,y,z} R_i(r_i)=E \ \prod_{x,y,z} R_i(r_i)$
2. División por la función:
$\sum_i \{ (-\frac{\hbar^2}{2m}) \frac{1}{R_i(r_i)} \frac{d^2 R_i(r_i)}{d r_i^2} \ \} =E$
3. Igualación de cada sumando de dependencia exclusiva en cada coordenada $r_i$ a una constante con dimensiones de energía, $E_i$ :
$\{ (-\frac{\hbar^2}{2m}) \ \frac{d^2}{d r_i^2} \ \} R_i(r_i)=E_i \ R_i(r_i)$ ,
con la condición
$E=\sum_i E_i=E_x+E_y+E_z$ .
Por tanto, se ha conseguido convertir el problema tridimensional en la resolución de tres problemas monodimensionales.
4. Resolución monodimensional:
$0 \le r_i \le L_i \rightarrow -\frac{\hbar^2}{2m} \ \frac{d^2 R_i(r_i)}{d r_i^2}\,=\,E_i \ R_i(r_i)$
$\Rightarrow \frac{d^2 R_i(r_i)}{d r_i^2} \,+\, \frac{2m}{\hbar^2} E_i \ R_i(r_i) \, = \, 0$
-La EDO lineal homogénea $u'' \mp k^2u=0 \, , \, k \in \mathbb{R} \, , \, k>0$ tiene por solución general la combinación lineal de soluciones particulares:
a) signo (-) : $u(r)=C_1 \ e^{kr} + C_2\ e^{-kr}$
con $C_1,C_2$ escalares arbitrarios.
b) signo (+) : $u(r)=C_1 \ e^{+ikr} + C_2\ e^{-ikr}=C'_1 \ cos\ kr + C'_2\ sen \ kr$
con $C_1,C_2,C'_1,C'_2$ escalares arbitrarios.
-Buscamos soluciones que se anulen sobre las paredes de la caja, por tanto, ha de ser cada constante de separación $E_i$ positiva, para que las soluciones se correspondan con las funciones oscilatorias, siendo directo obtener la solución general para valores $E>0$ :
$R_{i,E_i}(r_i)=C_1 \ cos\ k_ir_i + C_2\ sen \ k_ir_i$ ,
donde $C_1,C_2$ son escalares arbitrarios y
$k_i=\frac{+\sqrt{2mE_i}}{\hbar}>0 \, , \, E_i > 0\, , \, k_i > 0 \, , \, k_i \in \mathbb{R}\, , \, i=x,y,z$
-Puesto que la solución ha de anularse en el origen y en $L_i$ , las soluciones particulares adecuadas, las que satisfacen las condiciones de frontera impuestas, son las que presentan dependencia sinusoidal:
$R_{i,E_i}(0)=0=C_1 \Rightarrow R_{i,E_i}(r_i) \, = \, C_2 \ sen \ k_ir_i$ ,
$R_{i,E_i}(L_i)=0=C_1 \ sen \ k_iL_i \Rightarrow k_iL_i = n_i \pi \, , \, n_i=1,2,3\ldots (k_i \ne 0)$
-Finalmente, pues, la solución queda:
$R_{i,E_i}(r_i)\, =\, C_2 \ sen \ k_ir_i \, =\, C_2 \ sen \ (\frac{n_i \pi}{L_i}r_i)$
$E_i \, = \, \frac{\hbar^2}{2m} \ \frac{\pi^2}{L_i^2} \ n_i^2 \, , \, n_i=1,2,3\ldots$ ,
soluciones que, una vez normalizadas,
$\int_{-\infty}^{+\infty} \ |N|^2 | R_{i,E_i}(r_i) |^2 dr_i\, =\, 1$
$|N|^2 \int_{-\infty}^{+\infty} \ |sen (\frac{n_i \pi}{L_i}r_i) |^2 dr_i\, =\,|N|^2 [\frac{r_i}{2} -(\sin (\frac{2n_i \pi}{L_i}r_i) )\frac{L_i}{4n_i\pi}]|_0^{L_i}\,=\, |N|^2 \ \frac{L_i}{2}$
$|N|=(\frac{2}{L_i})^{\frac{1}{2}}$ ,
toman la forma normalizada:
$R_{i,E_i}(r_i)\, =\, (\frac{2}{L_i})^{\frac{1}{2}} \ sen \ (\frac{n_i \pi}{L_i}r_i)$ ,
que representa una onda estacionaria, con nodos sobre la superficie de la caja.
Reuniendo las tres dimensiones, las autofunciones y autovalores resultan:
$\psi_{E(n_x,n_y,n_z)}(\vec{r}) \equiv \psi_{n_x,n_y,n_z}(x,y,z) \, = \, (\frac{8}{L_xL_yL_z})^{\frac{1}{2}} \ sen \ (\frac{n_x \pi}{L_x}x) \ sen \ (\frac{n_y \pi}{L_y}y) \ sen \ (\frac{n_z \pi}{L_z}z)$
$E(n_x,n_y,n_z) \, =\, \frac{\hbar^2\pi^2}{2m} \ [(\frac{n_x}{L_x})^2 + (\frac{n_y}{L_y})^2 + (\frac{n_z}{L_z})^2 ]$
$n_x,n_y,n_z=1,2,3\ldots$ .

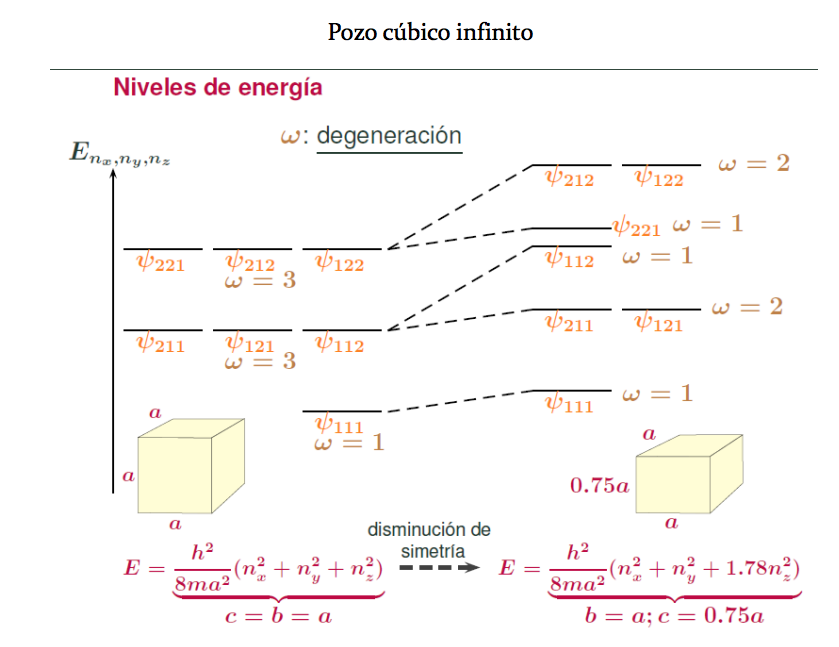
4. El pozo cúbico infinito tridimensional: la caja cúbica impenetrable

En particular, para una caja cúbica, $L_x=L_y=L_z\equiv L$ , se obtiene:
$\Rightarrow \psi_{E(n_x,n_y,n_z)}(\vec{r}) \equiv \psi_{n_x,n_y,n_z}(x,y,z) \, = \, (\frac{8}{L^3})^{\frac{1}{2}} \ sen (\frac{n_x \pi}{L}x) \ sen (\frac{n_y \pi}{L}y) \ sen (\frac{n_z \pi}{L}z)$
$E(n_x,n_y,n_z) \equiv E_n\, =\, \frac{\hbar^2\pi^2}{2mL^2} \ n^2$
$n_x,n_y,n_z=1,2,3\ldots \quad , \quad n^2=n_x^2 + n_y^2 + n_z^2 =3,6,9\ldots$ .
-El estado fundamental, pues, es el estado $\psi_{E(1,1,1)}$ de energía
$E_{GS}=E_{1,1,1}\, = \, 3 \ \frac{\hbar^2\pi^2}{2mL^2}$ ,
un estado no degenerado; el primer estado excitado es de energía
$E_{exc.1}\, = \,6 \ \frac{\hbar^2\pi^2}{2mL^2}=2E_{GS}$ ,
con degeneración 3, correspondiente a los tres conjuntos de valores de los tres números cuánticos $n_i$ que comparten autovalor:
$n_x=2,n_y=n_z=1;n_x=1,n_y=2,n_z=1;n_x=1,n_y=n_y=1,n_z=2$
-La siguiente figura ilustra la sucesión de niveles:

Niveles de energía en una caja cúbica y su degeneración.

Niveles de energía en el pozo cúbico infinito y su variación al perderse la simetría ( Fuente: Modelos tridimensionales para pozos).

En la siguiente figura se muestran las primeras funciones de onda:
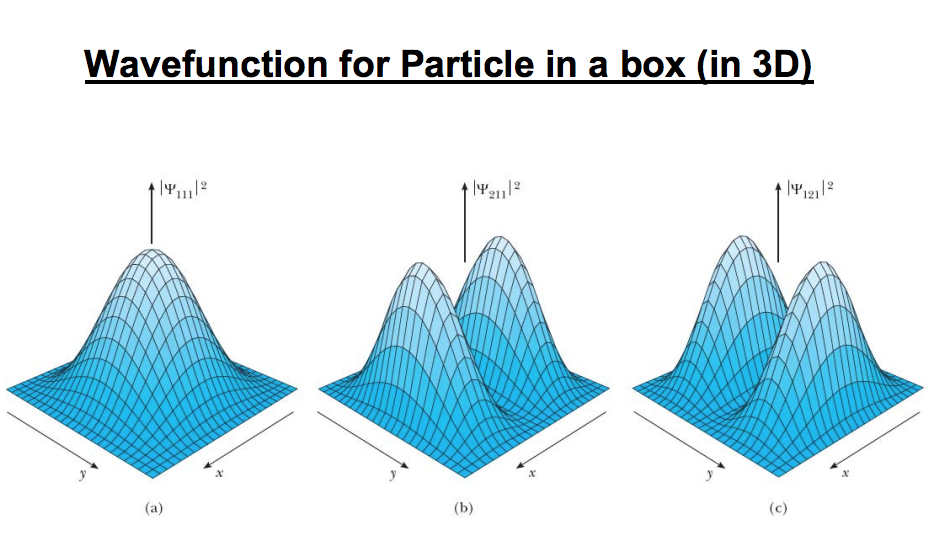
Funciones de onda en una caja cúbica tridimensional (imagen: https://web.iitd.ac.in/~pramitc/Lecture%20review%207_Particle%20in%20a%20box%20%283D&2D%29.pdf).

Referencias

[ABR-65] Abramowitz, Milton; Stegun, Irene A., eds.; “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables”; Dover; New York, 1965; ISBN 978-0-486-61272-0.

[BAL-98] Ballentine, L.E.; “Quantum Mechanics: A Modern Development”; World Scientific; Singapore, 1998.

[BER-18] Berman, P.R.; “ Introductory Quantum Mechanics: ”; Springer, 2018; https://doi.org/10.1007/978-3-319-68598-4_10.

[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.

[BRA-06] Bransden, B.H. and Joachain, C.J.; «Physics of Atoms & Molecules»; Longman, New York, 1983 (2nd ed.: Pearson; Dorchester, 2000).

[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.

[NEU-91] Neumann, J. von; «Fundamentos matemáticos de la Mecánica Cuántica», CSIC, Raycar, Madrid, 1991.

[RAI-72] Rainville, E.D., «Intermediate Differential Equations», Chelsea Pub. Co.; N.Y., 1972.

[SCH-68] Schiff, L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.

Páginas complementarias

La función de onda radial en el blog lamecanicacuantica.blogspot.com
Wolfram: https://demonstrations.wolfram.com/ParticlesIn1DAnd3DBoxes/
Particle in 2D y 3D boxes: https://web.iitd.ac.in/~pramitc/Lecture%20review%207_Particle%20in%20a%20box%20%283D&2D%29.pdf
La caja de potencial: http://www.sc.ehu.es/sbweb/fisica3/cuantica/separacion/separacion.html
Partícula en una caja tridimensional: https://web.iitd.ac.in/~pramitc/Lecture.pdf
Estados ligados en un pozo de potencial esféricamente simétrico: https://quantummechanics.ucsd.edu/ph130a/130_notes/node227.html
Finite spherical square well potential: deuteron, with the use of Mathematica, by Masatsugu Sei Suzuki and Itsuko S. Suzukhttps; Department of Physics, SUNY at Binghamton: https://bingweb.binghamton.edu/~suzuki/QuantumMechanicsII/5-4_Finite_spherical_well.pdf
Página interactiva para, a partir de las funciones esféricas de Bessel y de Hankel, encontrar las soluciones a la ecuación de Schrödinger en el pozo cuadrado 3D (un átomo): https://support.ptc.com/help/mathcad/r9.0/es/index.html#page/PTC_Mathcad_Help/example_bessel_functions.html
Modelos para pozos tridimensionales
Funciones especiales: https://es.mathworks.com/help/matlab/special-functions.html?s_tid=CRUX_lftnav
Funciones de Bessel: http://www.sc.ehu.es/sbweb/fisica3/especial/bessel/bessel.html
NIST Digital Library of Mathematical Functions
Funciones de Bessel en la Wikipedia en inglés:
https://en.wikipedia.org/wiki/Bessel_function#Spherical_Bessel_functions
Funciones de Bessel en la Wikipedia en español: https://es.wikipedia.org/wiki/Funci%C3%B3n_de_Bessel
Modelos para pozos tridimensionales: http://www.fisica.unlp.edu.ar/materias/expcuani/2019-centros-f/centros%20F%20pozos%20de%20potencial%20-%20Leo.pdf
Wolfram:
-Particle in an Infinite Circular Well: https://demonstrations.wolfram.com/ParticleInAnInfiniteCircularWell/
-Particle in an Infinite Spherical Well: https://demonstrations.wolfram.com/ParticleInAnInfiniteSphericalWell/

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

Pozos de potencial 3D

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta