El oscilador armónico 3D

Potencial del oscilador armonico vs. el potencial de Morse — El potencial HO es un buen modelo para explicar la energía de vibración de un enlace molecular (en la figura, representada como un pot. de Morse) en las proximidades de la distancia de equilibrio (imagen y ampliación en : https://www.uco.es/organiza/departamentos/quimica-fisica/quimica-fisica/QuiFis/L4_QF_10_11.pdf).

Ecuación de Schrödinger independiente del tiempo para el potencial del oscilador armónico en tres dimensiones

Sea una partícula de masa $m$ en el seno de un potencial de oscilador armónico tridimensional, de expresión:
$V_{HO} \equiv V(\vec{r}) \, = \, \frac{1}{2} (k_xx^2 + k_yy^2 + k_zz^2)\, + \, V_0$ ,
donde
$k_i= m\omega_i^2 \leftrightarrow \omega_i=+\sqrt{\frac{k_i}{m}} \leftrightarrow \alpha_i=+\sqrt{\frac{m\omega_i}{\hbar}} \; , \; i=x,y,z$
son distintas formas de elegir la constante característica y el potencial $V_0$ es una constante que puede tomarse como cero sin pérdida de generalidad.
-En el caso isótropo, $k_x=k_y=k_z=k$ , el potencial del oscilador armónico se convierte en un potencial central:
$V_{HOc} \equiv V(r=|\vec{r}|)\, = \, \frac{1}{2} k (x^2 + y^2 + z^2)\, + \, V_0 \, = \, \frac{1}{2} k r^2 \, + \, V_0$ ,
donde
$k= m\omega^2 \leftrightarrow \omega=+\sqrt{\frac{k}{m}} \leftrightarrow \alpha=+\sqrt{\frac{m\omega}{\hbar}}$ .
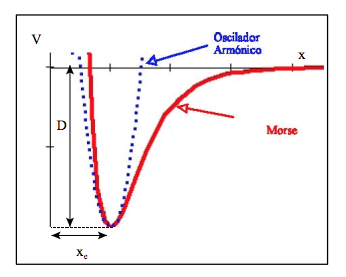
-Como ya se indicó en el estudio del caso unidimensional, el potencial de oscilador armónico (HO) es un buen modelo para estudiar potenciales continuos en la vecindad de sus puntos de equilibrio. Por ejemplo, el potencial HO tridimensional se emplea en el estudio de la vibración de los enlaces: la energía de una molécula diatómica debe poseer un mínimo, que determina el punto de equilibrio, a una distancia determinada entre los dos átomos, para que la molécula sea estable. Si la distancia interatómica $r$ no está próxima al valor crítico $r_{min}$ que proporciona el mínimo de energía, $V_{min}$ , la molécula no se forma, o se disocia, ya que el potencial se hace repulsivo. La figura en portada ilustra como el potencial HO es una buena aproximación en el mínimo para el potencial empírico de Morse, un potencial usado con frecuencia para representar de forma aproximada la forma del potencial molecular diatómico en términos de la distancia interatómica y cuya forma matemática es la siguiente:
$V(r)\, = \, V_{min} \ [1\, - \, e^{-a(r-r_{min})}]^2$ ,
donde $a$ es un parámetro característico de cada enlace.
-Por tanto, la energía potencial de las vibraciones moleculares puede aproximarse mediante la función parabólica de un oscilador armónico isótropo sólo en el entorno de la distancia internuclear de equilibrio, es decir, para los primeros niveles de energía. El potencial del oscilador armónico es un potencial confinador, con infinitos estados de energía accesibles para el sistema, incapaz en consecuencia de explicar la disociación molecular para grandes vibraciones, esto es, la ruptura del enlace. Un potencial como el de Morse, con un número finito de estados ligados, sí es capaz de dar cuenta del fenómeno; obsérvese la siguiente figura: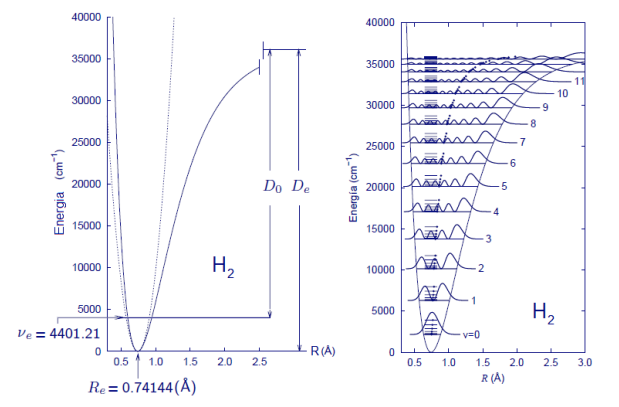

Niveles de energía vibracional de la molécula diatómica H_2, mostrando la la energía de disociación (fuente: tesis doctoral, cap. 3).

Resolución 1: El potencial del oscilador 3D como un potencial aditivo en coordenadas cartesianas

Sea la expresión del potencial HO general (no necesariamente isótropo) $V(\vec{r})$ en coordenadas cartesianas, una expresión aditiva:
$V(\vec{r})=V_x(x) + V_y(y)+ V_z(z)=\, = \, \frac{1}{2} (k_x x^2 +k_yy^2 +k_zz^2)$ ,
de modo que el operador Hamiltoniano resulta ser
$H=-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})=H_x(x) + H_y(y)+ H_z(z)$ ,
donde cada sumando $H_i(r_i)$ tiene la expresión
$H_i(r_i)=-\frac{\hbar^2}{2m} \ \frac{\partial^2}{\partial r_i^2} \ + \ V_i(r_i) \quad ; \; i=x,y,z \; ; \; r_i \equiv i$ ,
y la ecuación de Schrödinger independiente del tiempo es:
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2}\, + \, \sum_i V_i(r_i) \} \psi_E(\vec{r})=E \ \psi_E(\vec{r})$
-Esta expresión del Hamiltoniano permite la búsqueda de soluciones por el método de separación de variables, esto es, sustituir la solución expresándola según
$\psi_E(\vec{r}=(x,y,z)) = X(x) \ Y(y) \ Z(z) \equiv \prod_{x,y,z} R_i(r_i)$
y realizar el procedimiento habitual:
1. Sustitución en la ecuación:
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2}\, + \, \sum_i V_i(r_i) \} \prod_{x,y,z} R_i(r_i)=E \ \prod_{x,y,z} R_i(r_i)$
2. División por la función:
$\sum_i \{ (-\frac{\hbar^2}{2m}) \frac{1}{R_i(r_i)} \frac{d^2 R_i(r_i)}{d r_i^2}\, + \, V_i(r_i) \} =E$
3. Igualación de cada sumando de dependencia exclusiva en cada coordenada $r_i$ a una constante con dimensiones de energía, $E_i$ :
$\{ (-\frac{\hbar^2}{2m}) \ \frac{d^2}{d r_i^2}\, + \, V_i(r_i) \} R_i(r_i)=E_i \ R_i(r_i)$ ,
con la condición
$E=\sum_i E_i=E_x+E_y+E_z$ .
Por tanto, se ha conseguido convertir el problema tridimensional en la resolución de tres problemas monodimensionales.
Resolución:
$H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2}\, + \, \sum_i \frac{1}{2} k_i r_i^2 \} \psi_E(\vec{r})=E \ \psi_E(\vec{r})$
$\psi_E(\vec{r}=(x,y,z)) = X(x) \ Y(y) \ Z(z) \equiv \prod_{x,y,z} R_i(r_i)$
$\Rightarrow H\psi_E(\vec{r}=(x,y,z)) = \{ -\frac{\hbar^2}{2m} \ \sum_i \frac{\partial^2}{\partial r_i^2}\, + \,\frac{1}{2} k_i r_i^2 \} \prod_{x,y,z} R_i(r_i)=E \ \prod_{x,y,z} R_i(r_i)$
$\Rightarrow \sum_i \{ (-\frac{\hbar^2}{2m}) \frac{1}{R_i(r_i)} \frac{d^2 R_i(r_i)}{d r_i^2}\, + \,\frac{1}{2} k_i r_i^2 \} =E$
$\Rightarrow\{ (-\frac{\hbar^2}{2m}) \ \frac{d^2}{d r_i^2}\, + \,\frac{1}{2} k_i r_i^2 \} R_i(r_i)=E_i \ R_i(r_i)$ ,
con la condición
$E=\sum_i E_i=E_x+E_y+E_z$ .
La anterior EDO es la de un oscilador armónico unidimensional, ya resuelta, de modo que basta recuperar los resultados del caso monodimensional, para el que las autofunciones y autovalores son:
$\psi_n(x)=C_n\ e^{-\alpha^2x^2/2}\ H_n(\alpha x)\;,\;n=0,1,2\ldots$
$=C_n\ e^{-\alpha^2x^2/2} \left \{ \begin{matrix} (-1)^{\frac{n}{2}}\frac{n!}{(\frac{n}{2})!}\ M(-\frac{n}{2},\frac{1}{2};\alpha^2x^2)\;,\;n=0,2,4\ldots \\ (-1)^{\frac{n-1}{2}}\frac{n!}{(\frac{n-1}{2})!}\ 2\alpha x\ M(-\frac{n-1}{2},\frac{3}{2};\alpha^2x^2)\;,\;n=1,3,5\ldots \end{matrix}\right.$
-Normalización:
$\int_{-\infty}^{+\infty}|\psi_n(x)|^2dx=1$
$=|C_n|^2\ \int_{-\infty}^{+\infty}e^{-\alpha^2x^2}\ H_n^2(\alpha x)dx$
$=|C_n|^2\frac{1}{\alpha} \int_{-\infty}^{+\infty}e^{-z^2}\ H_n^2(z)dz=|C_n|^2\ \frac{\sqrt{\pi}}{\alpha}2^nn!$
$\Rightarrow |C_n|=\frac{\sqrt{\alpha}}{\pi^{\frac{1}{4}}\sqrt{2^nn!}}$
$\Rightarrow \psi_n(x)=(\frac{\alpha}{\sqrt{\pi}2^nn!})^{\frac{1}{2}}e^{-\alpha^2x^2/2}\ H_n(\alpha x)\;,\;n=0,1,2\ldots$
$=(\frac{\alpha}{\sqrt{\pi}2^nn!})^{\frac{1}{2}}\ e^{-\alpha^2x^2/2} \left \{ \begin{matrix} (-1)^{\frac{n}{2}}\frac{n!}{(\frac{n}{2})!}\ M(-\frac{n}{2},\frac{1}{2};\alpha^2x^2)\;,\;n=0,2,4\ldots \\ (-1)^{\frac{n-1}{2}}\frac{n!}{(\frac{n-1}{2})!}\ 2\alpha x\ M(-\frac{n-1}{2},\frac{3}{2};\alpha^2x^2)\;,\;n=1,3,5\ldots \end{matrix}\right.$
donde
$\alpha=(\frac{mk}{\hbar^2})^{\frac{1}{4}}=(\frac{m\omega}{\hbar})^{\frac{1}{2}}$ ( $[\alpha]=L^{-1}$ ).
-Estas autofunciones constituyen un sistema ortonormal:
$\int_{-\infty}^{+\infty}\psi_n^*(x)\psi_m(x)dx=\delta_{n,m}$
-Cada autofunción $\psi_n(x)$ corresponde al autovalor de energía:
$E_n=(n+\frac{1}{2})\hbar \omega=(n+\frac{1}{2})h \nu \;,\;n=0,1,2\ldots$
donde
$\nu=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}$
-En las fórmulas anteriores, $H_n(\alpha x)$ y $M(a,b;\alpha^2x^2)$ representan, respectivamente, el polinomio de Hermite de grado $n$ y la función hipergeométrica confluente.
Reuniendo los resultados monodimensionales, las autofunciones en términos de los polinomios de Hermite y autovalores del caso 3D resultan ser:
-Autofunciones:
$\psi_{n_xn_yn_z}(x,y,z)\, = \, N_{n_x}N_{n_x}N_{n_z} \ e^{-\frac{1}{2}(\alpha_x^2x^2+\alpha_y^2y^2+\alpha_z^2z^2)}\ H_n(\alpha_x x) H_n(\alpha_y y)H_n(\alpha_z z)$ ,
donde
$n_i=0,1,2\ldots \quad , \quad \alpha_i\, = \, (\frac{mk_i}{\hbar^2})^{\frac{1}{4}}$
y las constantes de normalización valen
$N_{n_i} \, = \, (\frac{\alpha_i}{2^{n_i \pi n_i!}})^{\frac{1}{2}}$
-Autovalores:
$E_{n_xn_yn_z}\, = \, \sum_{i=x,y,z} \ E_{n_i} \, = \, \sum_{i=x,y,z} \ (n_i + \frac{1}{2}) \ \hbar \omega_i$ ,
$\omega_i = \frac{k_i}{m}$ ,
ya que la constante de oscilador es distinta en cada eje coordenado, en general.
-Estado fundamental:
$E_{GS}=\, \frac{1}{2}\sum_{i=x,y,z} \ \hbar \omega_i$
Caso particular: oscilador armónico isótropo.
-En este caso, $k_x=k_y=k_z=k$ , $V(\vec{r})=V(r)=\frac{1}{2} k r^2$ , esto es, se trata de un potencial central, para el que las anteriores expresiones se convierten en:
-Autofunciones:
$\psi_{n_xn_yn_z}(x,y,z)\, = \, C \ e^{-\frac{1}{2}\alpha^2r^2}\ H_{n_x}(\alpha x) H_{n_y}(\alpha y)H_{n_z}(\alpha z)$ ,
donde
$n_i=0,1,2\ldots$ , $\alpha\, = \, (\frac{mk}{\hbar^2})^{\frac{1}{4}}=(\frac{m^2\omega^2}{\hbar^2})^{\frac{1}{4}}=(\frac{m\omega}{\hbar})^{\frac{1}{2}}$
y la constante de normalización vale
$C \, = \, (\frac{m\omega}{\hbar \pi})^{\frac{3}{4}}\frac{1}{(2^N \ n_x! n_y! n_z!)^{\frac{1}{2}}}$ ;
la paridad de cada estado la determina el polinomio de Hermite:
$P (\psi_{n_xn_yn_z})=(-1)^{n_x+n_y+n_z}=(-1)^{N}$ ,
denominándose $N$ como el número cuántico del oscilador armónico.
-Autovalores:
$E_{n_xn_yn_z} \equiv E_{N=n_x+n_y+n_z}\, = \, (N + \frac{3}{2}) \ \hbar \omega$ ,
$N=n_x+n_y+n_z=0,1,2,3\dots$ ,
$\omega = \frac{k}{m}$ .
-El estado fundamental resulta ser pues:
$E_{GS}=E_0=E_{N=0}=\frac{3}{2} \ \hbar \omega$ ,
sin degeneración.
-Los estados excitados ( $N=1,2\ldots$ ) sí presentan degeneración, la cual viene dada por
$D(N)=\frac{1}{2} (N+1)(N+2)$
(si hay espín, la degeneración es el doble de la fórmula).
-En efecto:
a) Es evidente que todo conjunto de tres números nulos o enteros positivos $(n_x,n_y,n_z)$ cuya suma genere el mismo resultado $N=n_x+n_y+n_z$ corresponderán a sendos estados distintos degenerados en energía, salvo en el caso de que los tres sean nulos (estado fundamental).
b) La cuestión a resolver entonces es: dado un valor $N \ne 0$ , ¿cuántas tríadas diferentes de valores $(n_x,n_y,n_z)$ lo generan como resultado de su suma? El cálculo puede hacerse:
-se considera $n_x$ fijo; debe estar entre $n_x=0$ y $n_x=N$ , es decir, $N-n_x=n_y+n_z$ , por lo que:
$\Rightarrow (n_y, n_z) = (0,N-n_x), (1,N-n_x-1), \ldots, (N-n_x,0)$ ,
esto es, una vez fijados $n_x$ y $N$ , hay $N-n_x+1$ posibilidades distintas de sumar $n_y + n_z$ para obtener $N-n_x$ .
c) Como, una vez fijado $N$ , hay $N+1$ valores posibles para $n_x$ , que son los $n_x=0,1,2,\ldots,N$ , se tiene:
$D(N)=\sum_{n_x=0}^{N} (N-n_x+1)=(N+1)\sum_{n_x=0}^{N} 1 \ - \ \sum_{n_x=0}^{N} n_x$
$=(N+1)^2 \ - \ \frac{1}{2} N(N+1)=(N+1)(N+1-\frac{N}{2})$
$= (N+1)(\frac{2N+2-N}{2})=(N+1)(\frac{N+2}{2})=\frac{1}{2} (N+1)(N+2)$
(la suma de una serie aritmética es igual al número de términos*(primer término + último término)/2 ).
-Ejemplos:
N=1: el estado $N=1$ , con una energía $E_{1}=E_{N=1}=\frac{5}{2} \ \hbar \omega$ , presenta degeneración 3, ya que los tres tripletes $(n_x,n_y,n_z)$ con valores $(1,0,0), (0,1,0), (0,0,1)$ conducen al mismo autovalor.
N=2: el estado $N=2$ , con una energía $E_{2}=E_{N=2}=\frac{7}{2} \ \hbar \omega$ , presenta degeneración 6, ya que los seis tripletes $(n_x,n_y,n_z)$ con valores $(2,0,0), (0,2,0), (0,0,2),(0,1,1), (1,0,1), (1,1,0)$ conducen al mismo autovalor.
-La figura siguiente muestra los primeros estados de energía de un oscilador armónico isótropo tridimensional:

Primeros niveles de energía en el oscilador armónico tridimensional y su degeneración (imagen: https://web1.eng.famu.fsu.edu/~dommelen/quantum/style_a/harm.html).
Las siguientes figuras muestran algunas de las densidades de probabilidad, $|\psi_{n_xn_yn_z}(x,y,z)|^2$ ; donde hay más oscuridad, mayor es la probabilidad de localizar a la partícula:
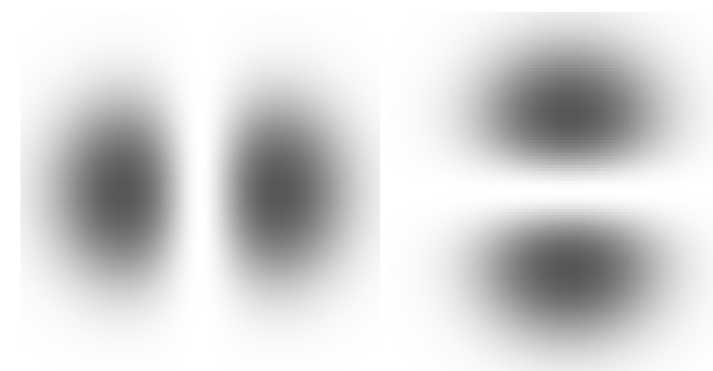
$Densidades de probabilidad para las funciones de onda $latex \psi_{100}$ y $latex \psi_{100}$ (imagen: https://web1.eng.famu.fsu.edu/~dommelen/quantum/style_a/harm.html).$
Densidades de probabilidad para las funciones de onda $\psi_{100}$ y $\psi_{010}$ vistas a lo largo del eje OZ (imagen: https://web1.eng.famu.fsu.edu/~dommelen/quantum/style_a/harm.html).

$Densidad de probabilidad para la función de onda $latex \psi_{213}$ (imagen: https://web1.eng.famu.fsu.edu/~dommelen/quantum/style_a/harm.html).$
Densidad de probabilidad para la función de onda $\psi_{213}$ vista a lo largo del eje OZ (imagen: https://web1.eng.famu.fsu.edu/~dommelen/quantum/style_a/harm.html).
Hay que tener siempre presente que, mientras que los autovalores del Hamiltoniano representan los únicos valores de energía posibles como resultado de la medida del observable energía del correspondiente sistema cuántico (sistema conservativo), los estados accesibles no son sólo las correspondientes autofunciones: una combinación lineal de funciones de la base ortonormal que integran las autofunciones de energía representa un estado posible para el sistema (principio de superposición). Por ejemplo, en el caso del oscilador isótropo, la combinación lineal
$\Psi(\vec{r})=\sum_{n_x=0}^{\infty}\sum_{n_y=0}^{\infty}\sum_{n_z=0}^{\infty} C_{n_xn_yn_z} \ \psi_{n_xn_yn_z}(\vec{r}) \quad , \; C_{n_xn_yn_z}=< \psi_{n_xn_yn_z} | \Psi>$
representa un posible estado del sistema, sobre el que la medida de la energía dará una colección de resultados coincidente con una distribución estadística: un subconjunto de los autovalores de energía con sus sendas probabilidades asociadas, distribución que deberá estar convenientemente normalizada a la unidad si la función de onda lo está.
-La figura siguiente muestra un ejemplo de la densidad de probabilidad correspondiente a una de estas posibles funciones: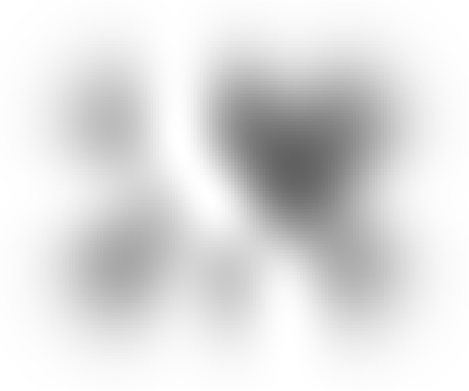

Densidad de probabilidad de un estado del HO isótropo que no es una autofunción (fuente: figura 4.6 en: https://web1.eng.famu.fsu.edu/~dommelen/quantum/style_a/harm.html#fig:harm213).

Resolución 2: El potencial del oscilador isótropo 3D como un potencial central

El oscilador armónico isótropo es un potencial central, de expresión general:
$V_{HOc} \equiv V(r=|\vec{r}|)\, = \, \frac{1}{2} k (x^2 + y^2 + z^2)\, + \, V_0 \, = \, \frac{1}{2} k r^2 \, + \, V_0$ ,
donde
$k= m\omega^2 \leftrightarrow \omega=+\sqrt{\frac{k}{m}} \leftrightarrow \alpha=+\sqrt{\frac{m\omega}{\hbar}}$
y elegimos $V_0=0$ , una elección arbitraria del origen de energías que conduce a que todos los estados ligados, en número infinito numerable, pertenezcan a autovalores positivos de energía, extendiéndose sobre la recta real positiva, $\sigma (H)=\sigma_p(H) \subset \{ \mathbb{R}^+ - 0\}$ .
Como consecuencia de la simetría esférica del potencial es posible diagonalizar simultáneamente el conjunto de operadores $\{ H,\vec{L}^2,L_z \}$ ; recuperando los resultados generales de la resolución en coordenadas esféricas y separación de variables en el caso de un potencial central (véase apartado 4 de la entrada de potenciales separables), se tiene que las autofunciones toman la expresión general
$\psi_{Elm}=R_{El}(r)Y_{lm}(\Omega)=\frac{1}{r}u_{El}(r)Y_{lm}(\Omega)$ ,
donde las funciones $Y_{lm}(\Omega)$ representan los armónicos esféricos y las ecuaciones diferenciales respectivas que han de satisfacer las funciones radial $R_{nl}$ y radial reducida $u_{nl}=r \ R_{nl}$ son:
$\{ -\frac{\hbar^2}{2m} \, [ \ \frac{d^2}{d r^2} \, + \, \frac{2}{r} \ \frac{d }{d r} \, - \frac{l(l+1)}{r^2} \ ] \, + \, \frac{1}{2} k r^2 \ \} \, R_{El}(r) \, = \,E \, R_{El}(r)$
$-\frac{\hbar^2}{2m} [\ \frac{d^2}{d r^2} \, - \, \frac{l(l+1)}{r^2} \ ] \, + \,\frac{1}{2} k r^2 \ \} \, u_{El}(r) \, = \,E \, u_{El}(r)$
$\equiv \, H_l u_{El}(r) \, = \, \{ -\frac{\hbar^2}{2m} \ \frac{d^2}{d r^2} \,+ \, V_{ef_l}(r) \ \} \ u_{El}(r)\, = \,E \, u_{El}(r)$ ;
-En este caso el potencial efectivo de onda parcial $l$ tiene la expresión:
$V_{ef_l}(r) \,= \, \frac{\hbar^2}{2m} \ \frac{l(l+1)}{r^2} \, + \frac{1}{2} m \omega^2 r^2\; , \; l=0,1,2\ldots$ ,
un potencial para el que
$V_{+}=\lim_{r \rightarrow \infty} V_{efl}(r) =+ \infty$ ;
se trata de un potencial confinador, con un espectro puramente discreto constituido por infinitos estados ligados de energía positiva.
–Las soluciones buscadas, las físicamente aceptables, han de satisfacer la condición de regularidad,
$u_{El}(0)\, = \, 0 \, , \, \forall l$ ,
con $u_{El}(r) \ \xrightarrow{r\rightarrow 0} \ 0$ más rápido que $r^l \xrightarrow{r\rightarrow 0} \ 0$ ( $u_{El}(r) \ \xrightarrow{r\rightarrow 0} \sim r^{l+1}$ ) , ya que $R_{El}(r)=u(r)_{El} /r$ debe ser continua (finita) en el origen para todos los valores $l$ ; adicionalmente, los estados ligados han de de cumplir también la condición de integrabilidad, que añadiendo la normalización a la unidad se expresa imponiendo:
$\int_0^{\infty} \ |u_{El} |^2 \ dr \, = \, 1$ .
Realizando en la anterior EDO radial reducida el cambio de variable independiente
$\rho = \alpha \ r \quad, \quad \alpha\, = \, ( \frac{m \ k}{\hbar^2})^{\frac{1}{4}} \, = \, ( \frac{m\omega}{\hbar} )^{\frac{1}{2}}$ ,
e introduciendo el cambio de parámetro energético,
$\lambda \, = \, \frac{2E}{\hbar \omega}$ ,
se obtiene la nueva ecuación
$[\ \frac{d^2}{d \rho^2} \, - \, \frac{l(l+1)}{\rho^2} \, - \, \rho^2 \, + \,\lambda \ \} \, u_{El}(\rho) \, = \, 0$ ,
que nos proporciona los siguientes comportamientos asintóticos:
1. Si $\rho \rightarrow +\infty$ ,
$[\ \frac{d^2}{d \rho^2} \, - \, \rho^2 \ \} \, u_{El}(\rho) \, = \, 0$ ,
por lo que a largas distancias se tendrá (como directamente puede comprobarse también de la solución obtenida en coordenadas cartesianas):
$u_{El}(\rho) \, \xrightarrow{\rho \rightarrow \infty} \, \rho^{a} \ e^{\pm \frac{\rho^2}{2}}$ ,
siendo $a$ un valor finito, de modo que, para conseguir el comportamiento correcto a largas distancias, la acotación, se ha de seleccionar
$u_{El}(\rho) \, \xrightarrow{\rho \rightarrow \infty} \, \rho^{a} \ e^{- \frac{\rho^2}{2}}$ .
2. Por otra parte, en el límite de las pequeñas distancias, si calculamos la ecuación indicial de la anterior EDO en el origen, $c^2 + (p_o-1)c + q_0=0$ , obtenemos:
$\left. \begin{array}{l} u_{El}''(\rho) \, + \, [\ \, - \, \frac{l(l+1)}{\rho^2} \, - \, \rho^2 \, + \,\lambda \ \} \, u_{El}(\rho) \, = \, 0 \\ \equiv u_{El}''(\rho) \, + \, p(\rho) \ u_{El}'(\rho)\, + \, q(\rho) \ u_{El}(\rho)\, = \, 0 \end{array} \right\}$ $\left. \begin{array}{l} p(\rho) = 0 \quad \text{anali'tica en} \quad \rho=0 \\ q(\rho) =-\frac{l(l+1)}{\rho^2} - \rho^2 + \lambda \quad \text{polo doble en} \quad \rho=0 \end{array} \right\}$
$\Rightarrow \left\{ \begin{array}{l} p_0 \, = \, \lim_{\rho \rightarrow 0} \ \rho \ p(\rho) \, = \, 0 \\ q_0 =\lim_{\rho \rightarrow 0} \ \rho^2 \ q(\rho)\ = \ -l(l+1) \end{array} \right\} \Rightarrow c^2 - c -l(l+1)=0$
$\Rightarrow \left\{ \begin{array}{l} c=l+1 \rightarrow u_{El}(\rho)= \sum_k a_k\ \rho^{k+l+1} \quad \text{anali'tica en} \quad \rho=0\\ c=-l \rightarrow u_{El}(\rho)= \sum_k a_k\ \rho^{k-l} \quad \text{no anali'tica en} \quad \rho=0 \end{array} \right\}$ , lo que ahora lleva a seleccionar la solución regular en el origen, asociada a la raíz indicial $l+1$ y de comportamiento asintótico a pequeñas distancias dado por:
$u_{El}(\rho) \, \xrightarrow{\rho \rightarrow 0} \, \rho^{l+1}$ .
Reuniendo resultados, los comportamientos asintóticos seleccionados sugieren el cambio de función incógnita en la EDO
$u_{El}(\rho) \, = \, \rho^{l+1} \ e^{- \frac{\rho^2}{2}} \ v_{El}(\rho)$ ,
tras el cual se obtiene la nueva EDO
$\{ \frac{d^2}{d \rho^2} \, + \, 2 \ ( \frac{l+1}{\rho} - \rho ) \ \frac{d}{d \rho} \, + \, [ \ \lambda \ - \ 2 (l+\frac{3}{2} \ ) \ ] \ \} \ v_{El}(\rho) \, = \, 0$ ,
que tras el cambio de variable independiente
$\xi \ = \ \rho^2$
se convierte finalmente en la EDO hipergeométrica confluente:
$\{ \xi \ \frac{d^2}{d \xi^2} \, + \, [ \ (l+\frac{3}{2} \ ) \ - \ \xi \ ] \ \frac{d}{d \xi} \, - \, [ \ \frac{1}{2} (l+\frac{3}{2} \ ) \ - \ \frac{\lambda}{4}] \ \} \ v_{El}(\xi) \, = \, 0$ ,
siendo la solución regular en el origen la siguiente:
$v(\xi) \, = \, C \ M(\frac{1}{2} (l+\frac{3}{2} ) - \frac{\lambda}{4},(l+\frac{3}{2}); \xi)$ ,
donde $C$ es una constante arbitraria y $M(a,b;z)$ representa la función hipergeométrica confluente o función de Kummer, de expresión:
$M(a,c;z)\, = \, 1 \, + \, \sum_{k=1}^{\infty} \ \frac{(a)_k z^k}{k! (c)_k} \quad |z| < \infty \quad, \quad c \ne 0 \,, \, c$ distinto de entero negativo.
-Nota: el factorial generalizado $(\beta)_n$ se define según:
$(\beta)_n=\beta \cdot (\beta + 1) \cdot (\beta + 2) \dots (\beta + n - 2) \cdot (\beta + n - 1)$ , siendo $n$ entero positivo; $(\beta)_0=1$ .
Nota: La ecuación hipergeométrica confluente, o ecuación de Kummer-Laplace, de expresión general (véase [ABR] cap. 13, p. 504ss.):
$z\frac{d^2 \omega}{d z} + (c-z)\frac{d \omega}{d z} - a\omega=0$ ,
es una ecuación que posee dos singularidades, una regular en el origen y otra irregular en el infinito, obtenida a partir de la EDO fuchsiana general con sólo tres singularidades regulares en los puntos complejos $z=0$ , $z=b$ y $z=\infty$ , de expresión
$z(1-\frac{z}{b}) \ y'' +[(c-z) -\frac{(a+1)}{b}z ] \ y' -a \ y=0$ ,
mediante la confluencia de singularidades $b \rightarrow \infty$ .
-La resolución por series en torno al origen de la ecuación hipergeométrica confluente permite obtener su solución general, de expresión
$\omega(z)\, = \, C_1 \ M(a,c;z) \, + \, C_2 \ z^{1-c} \ M(1+a-c,2-c;z) \quad , \quad 0 < |z| < \infty$ ,
donde $C_1, C_2$ son constante arbitrarias; $M(a,c;z) \equiv _1F_1(a,c:z)$ es la función hipergeométrica confluente; las dos soluciones particulares son válidas, respectivamente, para:
a) solución $C_1 \ M(a,c;z)$ : validez en $|z| < \infty$ si y sólo si $c \ne 0 \,, \, c$ distinto de entero negativo;
b) solución $C_2 \ z^{1-c} \ M(1+a-c,2-c;z)$ : validez en $0 <|z| < \infty$ si y sólo si $c \ne 2 \,,\, c$ distinto de entero positivo.
-La función hipergeométrica confluente o función de Kummer se expresa:
$M(a,c;z)\, = \, 1 \, + \, \sum_{k=1}^{\infty} \ \frac{(a)_k z^k}{k! (c)_k} \quad |z| < \infty \quad, \quad c \ne 0 \,, \, c$ distinto de entero negativo.
–Estas funciones poseen numerosas aplicaciones en Física.

Autofunciones de energía y su degeneración

Las autofunciones de energía de los estados ligados del HO, además de satisfacer la condición de regularidad, deben ser normalizables en sentido estándar, esto es, pertenecer al Hilbert (espacio de las funciones de cuadrado integrable Lebesgue en la especificación funcional usual). Puesto que el comportamiento asintótico a largas distancias de la función hipergeométrica confluente es
$M(a,c;x) \, \xrightarrow{x \rightarrow \infty} \, x^{a-c} \ e^x$
$\Rightarrow M(\frac{1}{2} (l+\frac{3}{2} ) - \frac{\lambda}{4},(l+\frac{3}{2}); \xi)\, \xrightarrow{\xi \rightarrow \infty} \, \xi^{-\frac{1}{2}(l+\frac{3}{2} + \frac{\lambda}{2}) } \ e^{\xi}$ ,
se tiene que, para evitar la divergencia, hay que cortar la serie, convertirla en un polinomio finito: sólo cuando conste de un número finito de términos la integrabilidad requerida de la solución se satisfará. Surge por tanto del formalismo matemático la condición de cuantización: sólo para algunos valores de la energía, parámetro $E$ , habrá estado ligado: cuando se satisfaga:
$\frac{1}{2} (l+\frac{3}{2} ) - \frac{\lambda}{4}\, = \, -n_r \quad , \quad n_r=0,1,2\ldots$ ,
siendo $n_r$ denominado como «el número cuántico radial«.
La condición de cuantización de la energía permite obtener los correspondientes autovalores o niveles de energía ligados del oscilador armónico isótropo tridimensional:
$\frac{\lambda}{4}\, = \,\frac{1}{2} (l+\frac{3}{2} )+n_r \Rightarrow \lambda \, = \,2 \ (2n_r+l+\frac{3}{2})$
$\Rightarrow \lambda \, = \,2 \ (N+\frac{3}{2}) \quad , \quad N=(2n_r+l)=0,1,2\ldots$
$\Rightarrow E\equiv E_{n_rl}=(2n_r+l+\frac{3}{2}) \ \hbar \omega=(N+\frac{3}{2}) \ \hbar \omega \quad , \quad n_r,N=0,1,2\ldots$
$\Rightarrow E\equiv E_{nl}=(2n+l-\frac{1}{2}) \ \hbar \omega \quad , \quad n=n_r+1=\frac{N-l+2}{2} =1,2\ldots$
-El estado fundamental o estado más bajo en energía es:
$n_r=l=N=0 \Rightarrow E_{GS} \equiv E_{0}= \frac{3}{2} \ \hbar \omega$
-La expresión que nos indica la energía de los estados ligados excitados relativa al estado fundamental:
$E_{n_rl}-E_{0}=(2n_r+l) \ \hbar \omega = N \ \hbar \omega$
( $E_{nl}-E_{0}=(2n+l-2) \ \hbar \omega = N \ \hbar \omega$ )
Degeneración energética: es evidente que todas las parejas de valores $(n_r,l)$ que proporcionan el mismo autovalor de energía identifican estados ligados con la misma energía, $E \equiv E_N=(N+\frac{3}{2})\hbar \omega$ .
-La energía además no depende del número cuántico de tercera componente de momento angular orbital, o número cuántico magnético $m$ , que para cada valor de $l$ puede tomar los $(2l+1)$ valores $m=l,l-1,\ldots,-l$ , de modo que:
$D(N)=\sum_{n_r , l} \ (2l+1)$
-Puesto que a cada valor $n_r$ le corresponde, dado un $N$ , un valor fijo $l=N-2n_r$ , y viceversa, esto es, a cada valor $l$ le corresponde, dado un $N$ , un valor fijo $n_r=\frac{N-l}{2}$ , se tiene entonces que la degeneración de cada nivel $E_N$ es, teniendo en cuenta que $l \le N$ :
$N par \Rightarrow \begin{vmatrix} l=0 \\ n_r=\frac{N}{2} \end{vmatrix}$ $\begin{vmatrix} l=2 \\ n_r=\frac{N}{2}-1 \end{vmatrix}$ $\begin{vmatrix} l=4 \\ n_r=\frac{N}{2}-2 \end{vmatrix}$ $\begin{vmatrix} \cdots \\ n_r=\cdots \end{vmatrix}$ $\begin{vmatrix} N-2 \\ 1 \end{vmatrix}$ $\begin{vmatrix} N \\ 0 \end{vmatrix}$
$N impar \Rightarrow \begin{vmatrix} l=1 \\ n_r=\frac{N}{2}-\frac{1}{2} \end{vmatrix}$ $\begin{vmatrix} l=3 \\ n_r=\frac{N}{2}-\frac{3}{2}\end{vmatrix}$ $\begin{vmatrix} l=5 \\ n_r=\frac{N}{2}-\frac{5}{2}\end{vmatrix}$ $\begin{vmatrix} \cdots \\ n_r=\cdots \end{vmatrix}$ $\begin{vmatrix} N-2 \\ 1 \end{vmatrix}$ $\begin{vmatrix} N \\ 0 \end{vmatrix}$ ,
de donde se implica finalmente:
$D(N)=\sum_{n_r , l} \ (2l+1)= \left. \begin{array}{l} \frac{1}{2} (1+2N+1)(\frac{N+2}{2}) \quad \text{si N par} \\ \frac{1}{2} (3+2N+1)(\frac{N+1}{2}) \quad \text{si N impar}\end{array} \right\}$
$\Rightarrow D(N)=\frac{1}{2}(N+2)(N+1)$ ,
ya que, para cada $N$ fijo, el número de valores posibles de $l$ es $[\frac{N}{2}]+1$ , donde $[x]$ significa «parte entera de x», esto es, el mayor entero menor o igual que x,
$[\frac{N}{2}] +1= \left. \begin{array}{l} \frac{N+2}{2} \quad \text{si N par} \\ \frac{N+1}{2} \quad \text{si N impar}\end{array} \right\}$ .
(Nota: suma de la serie aritmética=número de términos*(primer término + último término)/2 ).
–Al incorporar el espín, esta degeneración se doblará.
Cada valor de $N$ determina lo que se denomina una «capa de estados del oscilador«. La siguiente tabla proporciona las primeras de ellas:
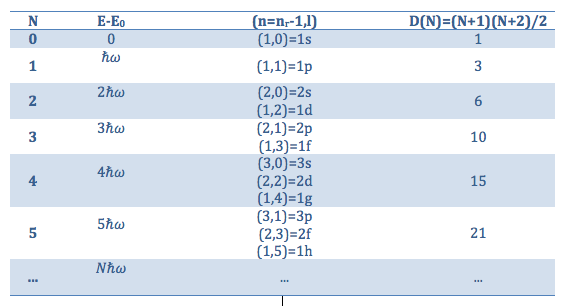
Primeras capas de estados ligados del oscilador armónico isótropo tridimensional (atención: ¡con la notación de estos apuntes, debe ser $n=n_r + 1$ )!
Relaciones, valores y significado de los distintos números cuánticos manejados:
$\left\{ \begin{array}{l} n_r \, = \, \frac{1}{2}(N-l) \quad , \quad n_r=0,1,2\ldots \quad , \quad n_r \le \frac{N}{2} \\ n = n_r-1= \frac{1}{2}(N-l+2) \quad , \quad n=1,2\ldots \quad , \quad n \le (\frac{N}{2}+1) \\ N \, = \, 2n_r + l \quad , \quad N=0,1,2\ldots \quad , \quad N \ge 2n_r \\ l \, = \, N-2n_r \quad , \quad l=0,1,2\ldots \quad , \quad l \le N \end{array} \right\}$
-Nota: obsérvese que, a diferencia de lo que ocurre en el caso atómico, no hay restricción alguna sobre el valor del número cuántico de momento angular orbital $l$ respecto al número cuántico radial: puede ser $l > n_r$ .
-El número cuántico radial $n_r$ se corresponde con el número de nodos o ceros de la función radial reducida $u_{n_rl}(r)$ en $(0,\infty)$ , a los que se añade el nodo en el origen.
-La función radial $R_{n_rl}(r)$ posee $n_r$ nodos, excluidos los dos adicionales en el origen y en el punto del infinito.
Autofunciones normalizadas de energía: Una vez normalizadas, las autofunciones de energía del oscilador armónico isótropo tridimensional tienen la expresión general:
$\psi_{nlm}(\vec{r}) \, = \, N_{nl} \ R_{nl}(r) \ Y_{lm}(\Omega) \, = \, N_{nl} \ \frac{1}{r} \ u_{nl}(r) \ Y_{lm}(\Omega)$
$= \, N_{nl} \ r^l \ e^{-\frac{\alpha^2 r^2}{2}} \ M(-n+1,l+\frac{3}{2};\alpha^2 r^2) \ Y_{lm}(\theta,\varphi)$ ,
donde
$n=n_r+1 \quad , \quad n=1,2,3\ldots$
$\alpha=+\sqrt{\frac{m\omega}{\hbar}} \quad , \quad [\alpha]=L^{-1}$ (dimensiones de 1/longitud)
y $N_{nl}$ es la correspondiente constante de normalización, de expresión
$N_{nl}\, = \, [ \frac{2 \ \alpha^{2l + \frac{3}{2}} \ \Gamma( l+\frac{3}{2} +n-1)}{(n-1)!) \ \Gamma^2 (l+\frac{3}{2})} ]^{\frac{1}{2}}$
salvo fase.
-La expresión también puede darse en términos de los polinomios generalizados de Laguerre, haciendo uso de la relación
$M(-m,k+1;\rho)\, = \, \frac{m!}{(k+1)_m} \ L_{m}^{k}(\rho)$
$\Rightarrow M(-n+1,l+\frac{3}{2};\alpha^2 r^2) \, = \, L_{n-1}^{l+\frac{1}{2}}(\alpha^2 r^2)\ \frac{(n-1)!}{(l+\frac{3}{2})_{n-1}}$ ,
obteniéndose:
$\psi_{nlm}(\vec{r}) \, = \, N_{nl} \ r^l \ e^{-\frac{\alpha^2 r^2}{2}} \ \frac{(n-1)!}{(l+\frac{3}{2})_{n-1}} \ L_{n-1}^{l+\frac{1}{2}}(\alpha^2 r^2)\ Y_{lm}(\theta,\varphi)$ .
-Nota: el símbolo $(a)_n$ representa la función factorial generalizada, $(a)_n=a(a+1)(a+2) \ldots (a+n-1)$
(por ejemplo: $n!\equiv (1)_n$ ).
Paridad: La paridad de las autofunciones del HO isótropo tridimensional la marcan los armónicos esféricos, es decir, la proporciona el factor $(-1)^l$ . De modo que la paridad de cada estado de energía $E_N$ es $(-1)^N$ , ya que, en cada capa de oscilador, todos los estados poseen valores de $l$ pares cuando $N$ es par , e impares cuando $N$ es impar.
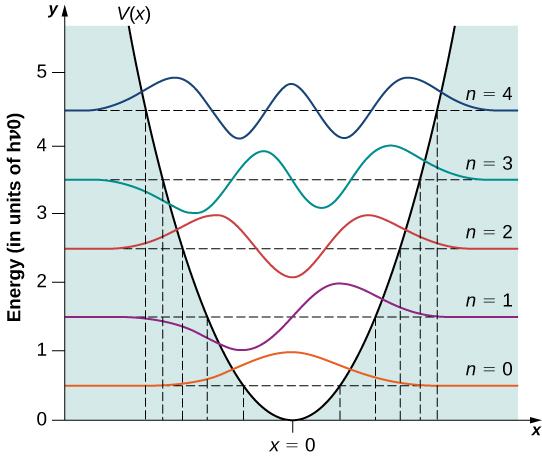
Las primeras cinco autofunciones de energía del oscilador armónico.
La siguiente figura muestra la ordenación de los primeros nives de energía de un pozo esférico infinito tridimensional, en comparación con el presente caso de un potencial parabólico:
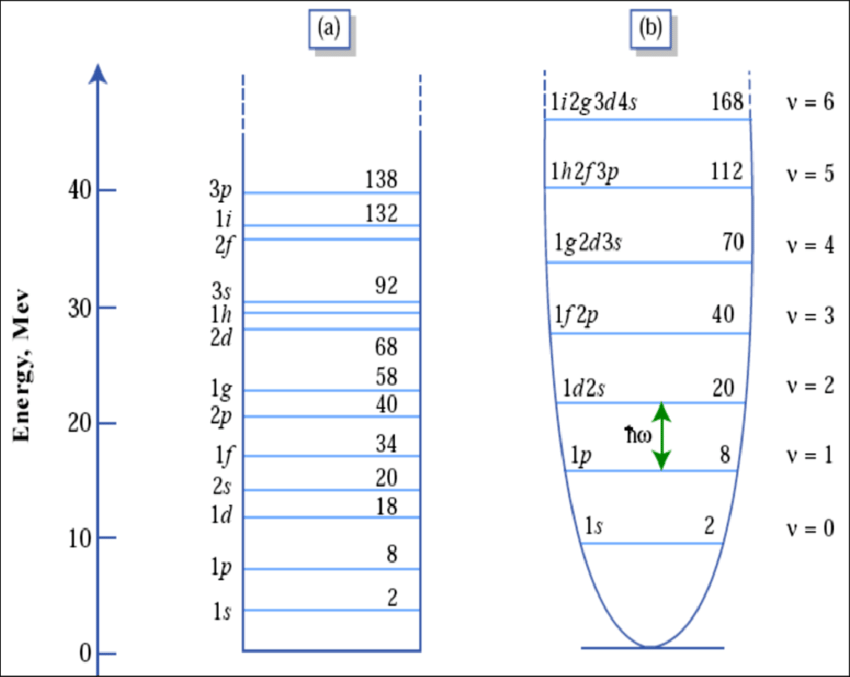
Primeros niveles de energía ligados en un ejemplo de pozo esférico infinito simétrico y en un pozo parabólico (Fuente: K. Abdullah, Fundamental in Nuclear Physics).

Referencias

[ABR-65] Abramowitz, Milton; Stegun, Irene A., eds.; “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables”; Dover; New York, 1965; ISBN 978-0-486-61272-0.

[BAL-98] Ballentine, L.E.; “Quantum Mechanics: A Modern Development”; World Scientific; Singapore, 1998.

[BER-18] Berman, P.R.; “ Introductory Quantum Mechanics: ”; Springer, 2018; https://doi.org/10.1007/978-3-319-68598-4_10.

[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.

[BRA-06] Bransden, B.H. and Joachain, C.J.; «Physics of Atoms & Molecules»; Longman, New York, 1983 (2nd ed.: Pearson; Dorchester, 2000).

[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.

[NEU-91] Neumann, J. von; «Fundamentos matemáticos de la Mecánica Cuántica», CSIC, Raycar, Madrid, 1991.

[RAI-72] Rainville, E.D., «Intermediate Differential Equations», Chelsea Pub. Co.; N.Y., 1972.

[SCH-68] Schiff, L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.

Páginas complementarias

La función de onda radial en el blog lamecanicacuantica.blogspot.com
El oscilador armónico en tres dimensiones: http://www.sc.ehu.es/sbweb/fisica3/cuantica/armonico/armonico_3.html
The isotropic 3D harmonic oscillator: http://quantum.phys.unm.edu/521-07/isotropic3DharmonicOscillator.pdf
The harmonic oscillator: https://web1.eng.famu.fsu.edu/~dommelen/quantum/style_a/harm.html
El oscilador armónico tridimensional clásico: http://tesla.us.es/wiki/index.php/Oscilador_arm%C3%B3nico_tridimensional
NIST Digital Library of Mathematical Functions
La función hipergeométrica confluente:
-en Wolfram mathworld: https://mathworld.wolfram.com/ConfluentHypergeometricFunctionoftheFirstKind.html
-en la Wikipedia: https://en.wikipedia.org/wiki/Confluent_hypergeometric_function
Las funciones asociadas de Laguerre:
-en Wolfram mathworld: https://mathworld.wolfram.com/AssociatedLaguerrePolynomial.html
-en la Wikipedia: https://en.wikipedia.org/wiki/Laguerre_polynomials#Generalized_Laguerre_polynomials
Oscilador armónico y absorción de radiación, archivo del Dpto. de Química-Física de la Univ. de Sevilla: https://www.uco.es/organiza/departamentos/quimica-fisica/quimica-fisica/QuiFis/L4_QF_10_11.pdf
Harmonic oscillator demostrations en Wolfram: https://demonstrations.wolfram.com/search.html?query=harmonic+oscillator
Java applet para el HO: https://www.compadre.org/quantum/items/detail.cfm?ID=1490

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

El oscilador armónico 3D

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta