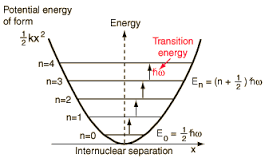
El potencial del oscilador armónico
- Sea una partícula de masa
en movimiento unidimensional, sometida a una fuerza atractiva dirigida hacia un centro fijo
y proporcional a la distancia a dicho centro,
(ley de Hooke), donde
representa una constante
y se ha elegido el origen como centro de fuerzas. Se genera un movimiento oscilatorio o vibratorio alrededor de la posición de equilibrio, teniendo el correspondiente potencial la expresión:
donde se suele elegir(elección arbitraria del origen de energías).
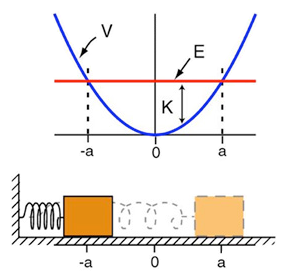
Potencial del oscilador armónico: a y -a serían los puntos de retroceso clásicos para la E dada ( imagen del blog http://la-mecanica-cuantica.blogspot.com.es/). - El potencial del oscilador armónico constituye una excelente aproximación para la mayoría de los potenciales continuos en la proximidad de un punto de equilibrio.
-En efecto: sea un potencial arbitrario, continuo, que desarrollado en serie de Taylor alrededor de un punto cualquiera
, donde suponemos posee un mínimo, se expresa
con, de forma que
.
-Es decir, el oscilador armónico lineal es una buena aproximación para los problemas físicos en que se tienen pequeñas oscilaciones alrededor de un punto de equilibrio estable, algo muy frecuente. Por ejemplo, éste es el caso de los movimientos vibracionales de los átomos y núcleos en las moléculas, como se muestra en la siguiente figura: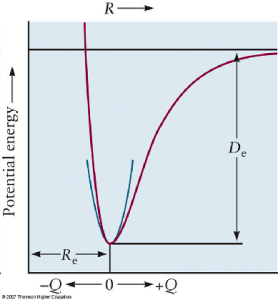
Potential energy curve of a chemical bond as a function of R, the separation between the two nuclei in the bond. The small blue curve is an approximate harmonic oscillator curve fit to the true potential energy curve at low energies (imagen de http://chemwiki.ucdavis.edu/Wikitexts/New_York_University/CHEMUA_127%3A_Advanced_General_Chemistry_I ). - El pozo del oscilador armónico es uno de los escasos potenciales que admite resolución analítica completa. Además, cumple la condición
, de modo que el espectro del correspondiente Hamiltoniano es por completo discreto, poseyendo un número infinito de estados ligados: se trata de un potencial confinador, para el que usualmente se elige
, de forma que todos los autovalores se fijan positivos.
- Resolución del problema de autovalores de energía o ecuación de Schrödinger independiente del tiempo:
con la condiciones de contorno:
continuas
.
Nota: una buena referencia para la resolución de este tipo de EDO y las funciones especiales que aparecen es: E. D. Rainville, Intermediate Differential Equations, Chelsea Pub. Co.; N.Y., 1972.- Resolución vía los polinomios de Hermite:
-
- Realizamos los cambios
donde la nueva variable independientees adimensional; en términos de ella la EDO se expresa:
expresión que recibe el nombre de «ecuación de Schrödinger reducida«. - La ecuación de Schrödinger reducida carece de singularidades en el plano finito, poseyendo una única singularidad irregular en el punto
(considerada como EDO general con
).
-Respecto al comportamiento asintótico: a largas distancias,, y para todo valor finito
, se tiene que
es despreciable frente a
, de forma que en el
la anterior EDO se convierte en la
.
-Esta última ecuación puede comprobarse por sustitución que, parasuficientemente grande, posee soluciones particulares de la forma
,
siendouna constante finita, ya que:
,
por lo que, paramuy grande,
.
-Todo lo anterior sugiere hacer en la ecuación reducida de Schrödinger el cambio
,
ya quedebe conservarse acotado. Procediendo al cambio de función incógnita indicado, se obtiene finalmente una EDO de Hermite:
,
que posee también una única singularidad irregular en.
- La EDO de Hermite puede resolverse realizando un desarrollo en serie de potencias en torno al origen:
-Separando coeficientes pares e impares:
Pares:
donde
Impares:
donde
-Nota: el factorial generalizadose define según:
, siendo
entero positivo;
.
- La solución general de la EDO de Hermite anterior se expresa pues:
dondey
representan constantes arbitrarias.
-Las soluciones particularese
, así como su combinación lineal, son soluciones válidas de la EDO
, donde se tiene convergencia de las series.
-Comportamiento a largas distancias:
a) Serie de potencias pares: solución:
,
que es la misma razón que presentan los coeficientes del desarrollo de la función,
por lo que se implica el comportamiento a largas distancias:
,
siendouna constante finita.
b) Serie de potencias impares: solución:
,
así que, como en el caso anterior de las soluciones pares, se presentará en general una divergencia a largas distancias. - Acotación a largas distancias (
): a continuación se deben imponer las condiciones de contorno sobre las anteriores soluciones, a fin de extraer las soluciones físicamente aceptables del problema.
-Para que las solucionesy
permanezcan acotadas a largas distancias, puede demostrarse que es condición necesaria y suficiente que las correspondientes series se corten, conteniendo sólo un número finito de términos. En otras palabras, las soluciones físicamente aceptables se corresponden con las formas anteriores cuando las series infinitas se convierten en sendos polinomios finitos:
- Polinomios pares:
-Para que se corte la serie se ha de tener:
,
expresión de un polinomio finito de grado.
-Multiplicando por la constante global adecuada (elección) esta solución particular admite expresión en términos de los polinomios de Hermite de grado par
:
- Polinomios impares:
-Para que se corte la serie se ha de tener:
,
expresión de un polinomio finito de grado.
-Multiplicando por la constante global adecuada (elección) esta solución particular admite expresión en términos de los polinomios de Hermite de grado impar
:
- Polinomios pares:
- Realizamos los cambios
- Las condiciones que cortan las series generan la cuantización de la energía:
- Propiedades de los polinomios de Hermite:
- Definición:
donderepresenta la parte entera de
, o mayor entero menor o igual que
.
- Primeros polinomios:
- Fórmula de Rodrigues:
- Función generatriz:
- Ortogonalidad:
- Relaciones de recurrencia:
- Otras propiedades:
- Definición:
-
- Resolución vía la función hipergeométrica confluente:
- Partimos de la EDO de Hermite
y realizamos el cambio:
,
expresión de la EDO hipergeométrica confluente, denominada así por obtenerse a partir de una EDO de Fuchs general:
-EDO general de Fuchs:,
que posee sendas singularidades regulares en los puntos finitosy en el punto del infinito,
(
), una ecuación que se convierte en la hipergeométrica usual para
.
-A partir de la general de Fuchs, se obtiene la EDO hipergeométrica confluente cuando se produce la confluencia de singularidades, llegándose a la ecuación:
,
o EDO hipergeométrica confluente, la cual presenta dos singularidades, una regular eny otra irregular en
.
- La solución general de la hipergeométrica confluente se expresa como la combinación lineal con constantes arbitrarias de las dos soluciones particulares:
y donderepresenta la función hipergeométrica confluente, o función de Kummer:
- Propiedades de la función hipergeométrica confluente:
-Comportamiento asintótico:
donde
yrepresenta la función gamma, de expresión
o, más generalmente,
-Algunas propiedades de la función gamma:
- Por tanto, la solución general de la ecuación de Schrödinger independiente del tiempo para el potencial del oscilador armónico puede también expresarse como:
-Comportamiento asintótico: salvo en los casos
1:
2:
la funciónpresentará un comportamiento asintótico según
que la hace físicamente inaceptable, de forma que debe imponerse
condiciones que proporcionan la cuantización de la energía:
- Es obvio que esta forma de expresar las soluciones coincide con la anterior:
- Notas:
-Otra solución particular de la ecuación hipergeométrica confluente
la proporciona la función hipergeométrica confluente de 2ª clase o función de Kummer de 2ª clase:
donde
-La función de Hermite de grado, o solución particular
de la EDO de Hermite
se expresa como
y cuandoes un entero, la función de Hermite se reduce al correspondiente polinomio de Hermite
.
- Partimos de la EDO de Hermite
- Se obtiene pues un espectro de energías mecánico-cuántico constituido por una secuencia infinita de niveles discretos, asociados a sendos estados ligados de la partícula:
-Los niveles están igualmente espaciados,, y no presentan degeneración; se satisface el teorema de oscilación y las autofunciones presentan paridad definida, como corresponde ya que el potencial unidimensional se ha tomado simétrico respecto al origen,
:
es una función par cuandoes par, e impar cuando
es impar.
- El nivel más bajo en energía o estado fundamental posee una energía
valor denominado energía del punto cero y de existencia trabada con el principio de indeterminación (la partícula no puede estar «en reposo» en el origen de energías o estado fundamental). - Obsérvese que, aparte de la energía del punto cero (que no afecta al cáculo de diferencias de energías entre niveles), los resultados para las energías del oscilador aquí encontrados son coherentes con el postulado de cuantización de Planck,
.
- Resumiendo, las autofunciones y autovalores son:
-Normalización:
donde
(
).
-Estas autofunciones constituyen un sistema ortonormal:
-Cada autofuncióncorresponde al autovalor de energía:
donde
-Las siguientes figuras ilustran la forma de las primeras autofunciones y sus correspondientes densidades de probabilidad: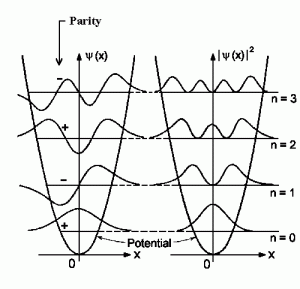
Imagen de http://www.pci.tu-bs.de/aggericke/PC3e_osv/Kap_III/Molekuelschwingungen.htm. 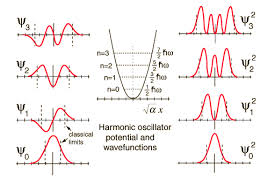
Imagen de http://physics.stackexchange.com. 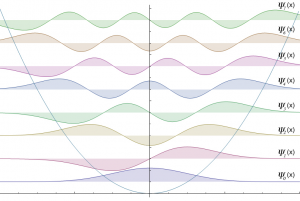
Wavefunction representations for the first eight bound eigenstates, n = 0 to 7. The horizontal axis shows the position x. Note: The graphs are not normalized (imagen y texto de la Wikipedia). 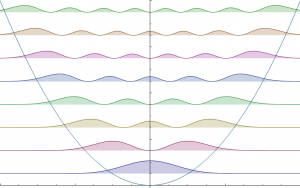
Densidades de probabilidad correspondientes a las 8 funciones de onda de la anterior figura (imagen de la Wikipedia).
- Resolución vía los polinomios de Hermite:
- Valores medios:
- Elementos no diagonales de
y
:
- Oscilador armónico y principio de indeterminación:
-La igualdad se tiene para el estado fundamental,:
es una gaussiana.
- Comparación con el caso clásico:
- Mientras que en el caso clásico la energía de la partícula puede tomar cualquier valor en un continuo que incluye el origen, en el oscilador mecano-cuántico aparece una cuantización o discretización de la energía, con una energía del punto cero o valor más bajo no nulo:
- Respecto a la posición de la partícula:
- Las siguientes figuras ilustran una comparación entre la predicción mecáno-cuántica para los resultados de las medidas del observable posición y el valor clásico:
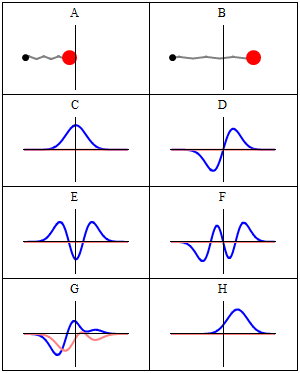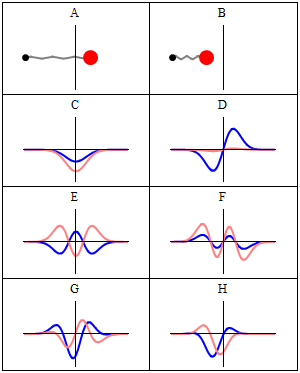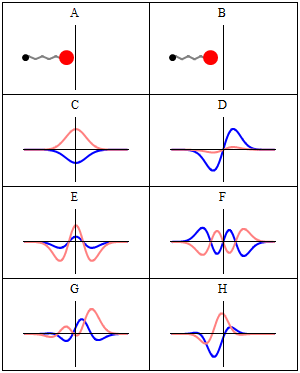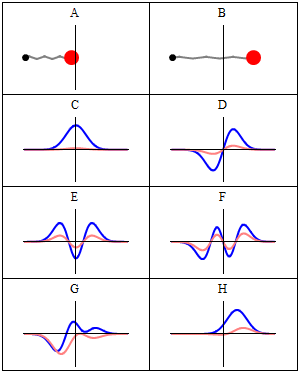
A harmonic oscillator in classical mechanics (A-B) and quantum mechanics (C-H). In (A-B), a ball, attached to a spring (gray line), oscillates back and forth. In (C-H), wavefunction solutions to the Time-Dependent Schrödinger Equation are shown for the same potential. The horizontal axis is position, the vertical axis is the real part (blue) or imaginary part (red) of the wavefunction. (C,D,E,F) are stationary states (energy eigenstates), which come from solutions to the Time-Independent Schrodinger Equation. (G-H) are non-stationary states, solutions to the Time-Dependent but not Time-Independent Schrödinger Equation. (G) is a randomly-generated superposition of the four states (C-F). H is a «coherent state» («Glauber state«) which somewhat resembles the classical state B (imagen y texto de la Wikipedia). –NOTA: recuérdese que, si bien es cierto que los autovalores de energía son los únicos valores de energía permitidos al sistema (¡esto es, los únicos valores que pueden obtenerse al medir la energía!), las autofunciones de energía constituyen sólo una base: cualquier combinación lineal de ellas, que no constituye en general una autofunción, representa no obstante un estado posible para el sistema.
- Densidad de probabilidad clásica:
-La densidad de probabilidad clásica de encontrar a la partícula en la posición, función
, tiene la expresión:
-El movimiento clásico tiene lugar entre los límites marcados por los dos puntos de retroceso, o puntos en los que
, es decir
-La funcióncrece al acercarse a los puntos de retroceso,
.
- Mecano-cuánticamente es posible encontrar a la partícula fuera de la zona entre los dos puntos de retroceso o zona clásicamente prohibida.
-A diferencia del caso clásico, el resultado cuántico proporciona en general mayor probabilidad de encontrar a la partícula en otros puntos distintos a los de retroceso. Por ejemplo, en el estado fundamental es en el origen donde es más probable encontrar a la partícula.
-Hay probabilidad no nula de encontrar a la partícula más allá de los puntos de retroceso, fuera del intervalo, esto es, en la zona clásicamente prohibida.
-Dentro del intervalola densidad de probabilidad
presenta oscilaciones.
- Las siguientes figuras permiten comparar las predicciones cuántica y clásica para la densidad de probabilidad de posición:
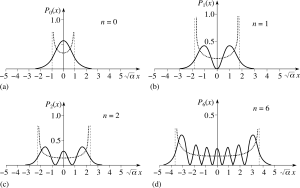
The probability density functions for the harmonic oscillator. Four cases are shown for particles in energy levels given by the quantum number n = 0, 1, 2, and 6. The dotted curves show the corresponding classical calculation of the probability density, with the dashed lines the classical limits of the oscillation (imagen y texto de http://www.met.reading.ac.uk/pplato2/h-flap/phys11_2.html). 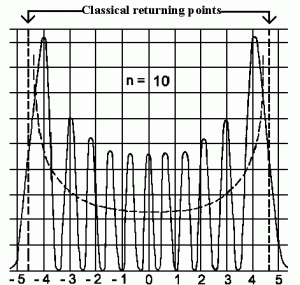
The detection probability for the vibrational state n=10. The dashed line gives us the classical detection probability (texto e imagen de http://www.pci.tu-bs.de/aggericke/PC3e_osv/Kap_III/Molekuelschwingungen.htm). 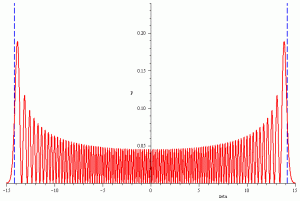
Graph of the probability distribution of the 100th state of the quantum harmonic oscillator (generated using the power series method; texto e imagen de http://comp-physics.blogspot.com.es/2013/01/maple-qho.html). -El desarrollo de
para
muy grande conduce al resultado (cf. [GAL-89], vol. 1, pág. 187):
,
del que, sustituyendo el coseno cuadrado por su valor medio,, se deriva la densidad clásica.
-Las anteriores gráficas muestran pues como, en una ilustración del principio de correspondencia, las predicciones cuánticas convergen a las clásicas en el límite, algo que la siguiente app permite visualizar:
Quantum/Classical Correspondence for the Harmonic Oscillator from the Wolfram Demonstrations Project by Niels Walet
- Las siguientes figuras ilustran una comparación entre la predicción mecáno-cuántica para los resultados de las medidas del observable posición y el valor clásico:
- Mientras que en el caso clásico la energía de la partícula puede tomar cualquier valor en un continuo que incluye el origen, en el oscilador mecano-cuántico aparece una cuantización o discretización de la energía, con una energía del punto cero o valor más bajo no nulo:
- En el problema estudiado, Hamiltoniano del pozo de oscilador armónico, resulta por tanto:
: infinitos estados ligados, sin degeneración; se satisface el teorema de oscilación.
Referencias
[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.
[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.
[RAI-72] Rainville, E.D., «Intermediate Differential Equations», Chelsea Pub. Co.; N.Y., 1972.
[SCH-68] Schiff,L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.
Páginas complementarias
http://www.met.reading.ac.uk/pplato2/h-flap/phys11_2.html
http://www.uco.es/hbarra/index.php/fc/apuntesfc/185-fc0606
http://www.uco.es/hbarra/index.php/fc/apuntesfc/187-fc0608
http://la-mecanica-cuantica.blogspot.com.es/2009/08/oscilador-armonico-simple-solucion.html
APPS
http://www.sc.ehu.es/sbweb/fisica/cuantica/armonico/armonico.html
http://www.st-andrews.ac.uk/physics/quvis/embed_item_3.php?anim_id=4&file_sys=index_phys
http://www.uco.es/hbarra/index.php/fc/appletsfc/160-oscilador
http://www.uco.es/hbarra/index.php/fc/appletsfc/161-schrodingeroscilador
http://www.st-andrews.ac.uk/physics/quvis/embed_item_3.php?anim_id=22&file_sys=index_phys
http://www.uco.es/hbarra/index.php/fc/appletsfc/162-osciladorlimiteclasico
a su vez todo está dotado de una lógica matemática, que quizás permita explicar que se pueda matematizar esto, y medirlo armónicamente o lleno de ira desequilibrado…
Saludos.
Existe una probable forma diferente de acercarse al oscilador armónico desde un planteamiento diferente:
https://opensea.io/collection/el-holograma-de-xose-ionaton
Al trasladar el «lugar» de medición del ángulo al otro extremo de la hipotenusa del triángulo rectángulo isósceles (TRI), ocurre que se pueden plantear y postular o axiomatizar y teorematizar y conjeturar varios conceptos «novedosos»:
A)Al interior de un TRI se pueden inscribir la totalidad de triángulos rectángulos (TR) posibles, representados como sus «TR semejantes», siempre acompañados de un trisngulo escaleno que «completa» al TRI, presentando el modelo «Invarianciade Escala» u «holofractalidad».
B)Cada punto de intersección de la hipotenusa con el «cateto base» es una o marca una cirtadurade Dedekind, llenando la «recta numérica», pues como se ve en los diagramas de los NFT en Opensea, cada hipotenusa interseca al arco 1/8 o 1/4 de π (dependiendo si es en grados o radianes) demostrando que «existen infinitas hipotenusas de TR» que intersecan el arco inscrito en el TRI.
C) El TR con hipotenusa = √5 es el que marca la mitad de «larecta numerica de longitud L o «1», de ∅ a 1, suendo el estado de menor energía, solo «menor» que el estado de hipotenusa de medida= √2, requiriendo «infinita energía» para llenar la recta L=0,1 de «numeros» representados por las Hipotenusas que son «Raices cuadradas», excepto en las «Ternas pitagoricas». Presentando también un nuevo acercamiento a los números imaginarios y a los números modulares (mod) y, sobre todo: a los números primos, al asociar, además, el que: Cada intersección de la hipotenusa con el arco segmento permitextrazar unatangenteque «rrecorre completamente el segmento S=(√2)-1 y al cateto vertical= L o 1/2 L, dependiendo si se toma L como el radio o el perímetro del círculo de dinde se obtiene el arco segmento al interior del TRI.
D)Es posible que, al desdoblarse del estado 2Dimensional (2D) al 3Dimensional (3D o Cubo) las «transfirmaciones de √2 → L y √5 → √3 representen lo que se indica en la conjetura de Maldacena, dinde un espacio 2D sin gravedad es equivalente a un espacio 3D con gravedad.
E)Es posible que las «12 divisiones» o líneas divisorias al interior del TRI representen las Cuerdas o Supercuerdas, 11 rectas y el arco de circunferencia, con 5 «Campos energéticos o bosónicos» (QFT) al interior del TR Inscrito en el TRI y 22 subcampos matéricos o fermiónicos (QFT) al interior del Triángulo Escaleno.
F)El espacio hiperbólico y esférico «son contínuos» y serían una proyección del espacio plano euclidiano.
G)El espín deforma espiral e hiperbólicamente al «cubo elemental» conformado por 4 tetraedros irregulares de 3 caras TRI y una cara Triángulo isóceles equilátero, habiendo 8 de estos cubos y 32 de dichos tetraedros.
H)Las 2 áreas triangulares «afuera» del arco segmento 1/8 o 1/4 de π corresponderían a la llamada materia oscura uno y energía oscura otro.
I)Se soluciona la incompletud (irracionalidad) y la tautología autorreferencia de los teoremas de Gödel con el Axioma: 1=∅=∞ y n=1/∞, textualmente:
Lo Uno es Absoluto e Infinito y cada nunero «n» es un infinitavo.
J)Es posible obtener muchas de las constantes matematicas y físicas de lasrelaciones matematicas entre las más de 100 longitudes de los másde 109 segnentos de rectas y «3 segmentos de curva» que se encuentran en la figura diagrama del link, llamado:
El Holograma de Xosé IónAtón.© US Copyright Office, Feb. 2022.
José Antonio Palos C. DR 2023.
Mi saludo cordial. Con respecto al valor de la Energía MÍNIMA que se le asigna a un Oscilador Cuántico Elemental deducido de la Ecuación de Onda de Schrodinger, que’ valor de Energía para este Oscilador se obtendría en el hipotético caso de que la UNIDAD DE MEDIDA de la Constante de Planck NO fuese la de un Cuanto de Acción (Joule x SEGUNDO) sino un Cuanto de ENERGÍA (Joule)?