Barrera finita en el interior de un pozo infinito
(doble pozo dentro de uno infinito)
- Función potencial
:
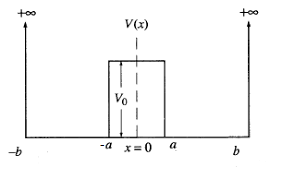
,
dondees un número real positivo, con dimensiones de energía.
-Se trata de una función con discontinuidades de segunda especie en los puntos, puntos en los que se sitúan sendas barreras impenetrables de potencial; por lo tanto, en ellos se debe imponer la condición de frontera de anulación de la función de onda
: se produce el confinamiento o ligadura de la partícula en el interior del intervalo
de la recta real, de longitud
; la derivada primera de la función de onda presentará discontinuidades en ambos extremos. Por otra parte, el potencial presenta discontinuidades de primera especie en los puntos
, puntos en los que habrá que proceder al empalme o conexión de las respectivas soluciones en las zonas I y II que garantice la continuidad de la función de onda y su primera derivada.
- Problema de autovalores de energía:
,
y buscamos solucionesque sean funciones continuas y con derivada primera
también continua allí donde
es finito: en el intervalo
; las funciones
tendrán sendos nodos en los puntos extremos
:
(donde
presentará una discontinuidad de primera especie).
- La solución general de una EDO
,
donde,
, tiene la expresión:
-Signo (-) :
conescalares arbitrarios.
-Signo (+) :
conescalares arbitrarios.
- En las dos regiones espaciales consideradas, I:
y II:
, las respectivas formas de la EDO planteada son:
Zona II ::
Zona I ::
- Puesto que el potencial es simétrico en torno al origen, sabemos de antemano que los autoestados van a tener paridad definida; por ello, iremos incorporando la paridad de partida, limitándonos además a resolver en la parte positiva del eje real.
:
- Forma A de resolución:
- -Zona
:
:
cony
escalares arbitrarios.
-Zona:
:
cony
escalares arbitrarios.
-Zona:
.
- Soluciones pares
para
:
- Por ser la función par, ha de tenerse
.
- La función de onda par tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda:
- Por tanto, se obtiene la condición de cuantización de la energía o ecuación cuyas raíces proporcionan los autovalores correspondientes a las autofunciones pares:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía
, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones pares.
- La gráfica para la resolución gráfica se esboza tras la solución impar.
- Expresión de las autofunciones pares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores pares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
- Por ser la función par, ha de tenerse
- Soluciones impares
para
:
- Por ser la función impar, ha de tenerse
.
- La función de onda impar tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda:
- Por tanto, se obtiene la condición de cuantización o ecuación cuyas raíces proporcionan los autovalores correspondientes a las autofunciones impares:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones impares.
- Resolución gráfica: gráfica conjunta con las autofunciones pares más adelante.
- Expresión de las autofunciones impares
:
donde
;
;
son los distintos autovalores impares, obtenidos a partir de la resolución de la ecuación de autovalores impares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
-Nota: equivalentemente, se puede expresar:
- Por ser la función impar, ha de tenerse
- -Zona
- Forma B de resolución:
- En esta segunda forma de resolución, lo que se hace es usar en la zona I para la expresión de la función de onda
una expresión trigonométrica para el seno de la diferencia entre dos ángulos:
- -Zona
:
:
,
cony
escalares arbitrarios.
-Zona:
:
cony
escalares arbitrarios.
-Zona:
.
- Como ha de tenerse anulación de la función de onda en
, se deriva:
;
elegimosy tomando
conseguimos incorporar de partida en la función de onda la condición de contorno.
- Soluciones pares
para
:
- Por ser la función par, ha de tenerse
.
- La función de onda par tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
: ya incorporada.
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda, se llega a la misma condición de cuantización para los autovalores de energía correspondientes a las autofunciones pares que se obtuvo antes por el camino A:
.
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones pares.
- Expresión de las autofunciones pares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores pares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
- Por ser la función par, ha de tenerse
- Soluciones impares
para
:
- Por ser la función impar, ha de tenerse
.
- La función de onda impar tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
: ya incorporada.
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda, se llega a la misma condición de cuantización para los autovalores de energía correspondientes a las autofunciones impares que se obtuvo antes por el camino A:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones impares.
- Expresión de las autofunciones impares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores impares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
-Nota: equivalentemente, se puede expresar:
- Por ser la función impar, ha de tenerse
- En esta segunda forma de resolución, lo que se hace es usar en la zona I para la expresión de la función de onda
- Esbozo de los resultados a que llevaría una resolución gráfica:
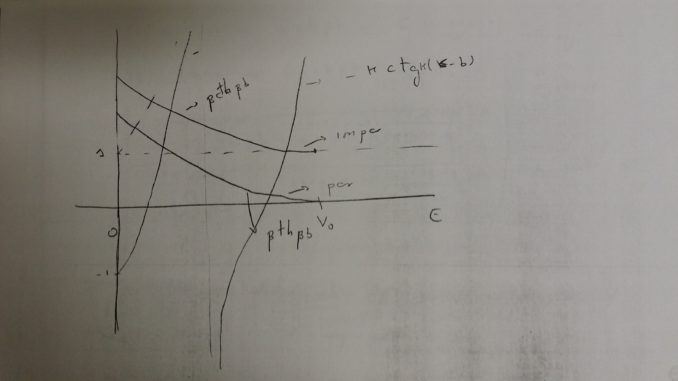
- Forma A de resolución:
:
-
- Forma A de resolución:
- -Zona
:
:
cony
escalares arbitrarios.
-Zona:
:
cony
escalares arbitrarios.
-Zona:
.
- Soluciones pares
para
:
- Por ser la función par, ha de tenerse
.
- La función de onda par tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda:
- Por tanto, se obtiene la condición de cuantización de la energía o ecuación cuyas raíces proporcionan los autovalores correspondientes a las autofunciones pares:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía
, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones pares.
- La gráfica para la resolución gráfica se esboza tras la solución impar.
- Expresión de las autofunciones pares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores pares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
- Por ser la función par, ha de tenerse
- Soluciones impares
para
:
- Por ser la función impar, ha de tenerse
.
- La función de onda impar tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda:
- Por tanto, se obtiene la condición de cuantización o ecuación cuyas raíces proporcionan los autovalores correspondientes a las autofunciones impares:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones impares.
- Resolución gráfica: gráfica conjunta con las autofunciones pares más adelante.
- Expresión de las autofunciones impares
:
donde
;
;
son los distintos autovalores impares, obtenidos a partir de la resolución de la ecuación de autovalores impares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
-Nota: equivalentemente, se puede expresar:
- Por ser la función impar, ha de tenerse
- -Zona
- Forma B de resolución:
- En esta segunda forma de resolución, lo que se hace es usar en la zona I para la expresión de la función de onda
una expresión trigonométrica para el seno de la diferencia entre dos ángulos:
- -Zona
:
:
,
cony
escalares arbitrarios.
-Zona:
:
cony
escalares arbitrarios.
-Zona:
.
- Como ha de tenerse anulación de la función de onda en
, se deriva:
;
elegimosy tomando
conseguimos incorporar de partida en la función de onda la condición de contorno.
- Soluciones pares
para
:
- Por ser la función par, ha de tenerse
.
- La función de onda par tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
: ya incorporada.
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda, se llega a la misma condición de cuantización para los autovalores de energía correspondientes a las autofunciones pares que se obtuvo antes por el camino A:
.
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones pares.
- Expresión de las autofunciones pares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores pares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
- Por ser la función par, ha de tenerse
- Soluciones impares
para
:
- Por ser la función impar, ha de tenerse
.
- La función de onda impar tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
: ya incorporada.
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda, se llega a la misma condición de cuantización para los autovalores de energía correspondientes a las autofunciones impares que se obtuvo antes por el camino A:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones impares.
- Expresión de las autofunciones impares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores impares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
-Nota: equivalentemente, se puede expresar:
- Por ser la función impar, ha de tenerse
- En esta segunda forma de resolución, lo que se hace es usar en la zona I para la expresión de la función de onda
- Forma A de resolución:
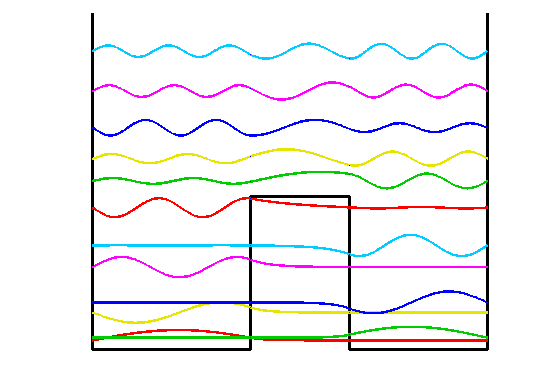
- Las siguiente imágenes nos muestran los correspondiente estados ligados, que satisfacen el teorema de Sturm:
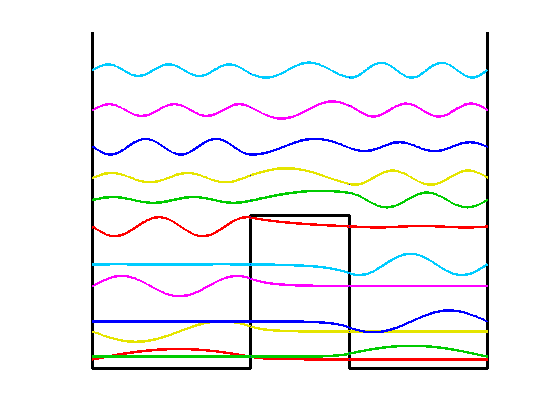
Imagen desde: https://www.mathworks.com/examples/matlab/community/22668-double-well-schr-ouml-dinger-eigenstates; también en: http://www.chebfun.org/examples/ode-eig/DoubleWell.html - Nota: los resultados para
se podían haber deducido sin más a partir de los correspondientes a
: hubiera bastado para ello sustituir el parámetro
del cálculo
por
(es decir:
. Por ejemplo, si partimos de la ecuación de los autovalores pares en el tramo de energías
,
,
y realizamos la sustitución indicada, se deriva:
.
- Caso límite: En el límite
, se obtienen los resultados del pozo cuadrado infinito, como es fácil comprobar. En efecto, por ejemplo, el límite
proporciona:
(autovalores de los autoestados pares del pozo infinito).
- En el problema estudiado, Hamiltoniano del pozo cuadrado infinito con barrera interior, resulta por tanto:
: infinitos estados ligados, sin degeneración; se satisface el teorema de oscilación.
- La siguiente figura es una captura de pantalla de los resultados de una búsqueda por imágenes en Google con la entrada «quantum double well»: permite hacerse una idea de la variedad de potenciales que se pueden plantear… Y todos se resuelven similarmente.

-
Referencias
[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.
[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.
[SCH-68] Schiff,L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.
Páginas complementarias
http://en.wikipedia.org/wiki/Particle_in_a_box
http://www.uco.es/hbarra/index.php/fc/apuntesfc/334-fc0303
http://eltamiz.com/2008/05/15/cuantica-sin-formulas-el-pozo-de-potencial-infinito/
https://pdfs.semanticscholar.org/bdfe/1f288ec26c0284505a6a61c95aa6ba32b333.pdf
http://www.hep.manchester.ac.uk/u/forshaw/BoseFermi/Double%20Well.html
https://arxiv.org/pdf/1209.2521.pdf
APPS
- http://www.sc.ehu.es/sbweb/fisica/cuantica/pozo/caja.htm
- http://www.uco.es/hbarra/index.php/fc/appletsfc/70-pozo-infinito
- http://www.uco.es/hbarra/index.php/fc/appletsfc/71-paquete-pozo-infinito
- http://www.st-andrews.ac.uk/physics/quvis/embed_item_3.php?anim_id=24&file_sys=index_phys
-
Wave Packets for Particle in a Box from the Wolfram Demonstrations Project by Andrés Santos.
- Probability Density in an Infinite Square Well from the Wolfram Demonstrations Project by Carlos Anton Solanas.
- Quantum Particles in an Infinite Square Potential Well from the Wolfram Demonstrations Project by Jeff Bryant.
- Exact Solution for Rectangular Double-Well Potential from the Wolfram Demonstrations Project, por S.M. Blinder: http://demonstrations.wolfram.com/ExactSolutionForRectangularDoubleWellPotential/
- El doble pozo en MATLAB: https://www.mathworks.com/examples/matlab/community/22668-double-well-schr-ouml-dinger-eigenstates; también en: http://www.chebfun.org/examples/ode-eig/DoubleWell.html.
- Otros tipos de pozos en MATLAB: https://www.mathworks.com/examples/matlab/community/22670-eigenstates-of-the-schroedinger-equation .
- El paquete de ondas gaussiano en un potencial con dos mínimos:
https://www.youtube.com/watch?v=SKatmNFzmis (created by Biswaroop Mukherjee under the guidance of Dr. Antonio Nassar as a part of a Studies in Scientific Research project in Harvard-Westlake School, North Hollywood, CA.):
This plot shows the progression of the probability density of the single-dimensional wavepacket in time. This is a Quantum Tunneling simulation in Mathematica that solves the time-dependent schroedinger equation. Here, a gaussian wavepacket is placed in a potential system that has two stable states (bistable). This simulation was created as a quantum extension of the classic stochastic resonance phenomenon, where a particle oscillates between the two stable states. Here, however, the probability density function (pdf) of the particle’s position is not a delta function (and thus could have a finite density in both wells simultaneously). However, in this case, the pdf seems to pass through a half-period of oscillation between two wells, and it is possible that a longer simulation will reveal the clear oscillation. However, this is still not a recreation of stochastic resonance – which needs a periodic and a random fluctuation of the potential.
Dejar una contestacion