Potenciales con deltas

Nota previa: La distribución delta de Dirac

En el enlace Funcionales y distribuciones se encuentra una introducción a las funciones generalizadas y distribuciones, incluyendo una lista de propiedades básicas de la delta de Dirac.

Potenciales tipo delta

Se denominan potenciales tipo delta aquellos que contienen una distribución delta de Dirac en su expresión, o sea, un potencial cuya expresión contiene al menos un término de la forma
$l \cdot V_o\ \delta(x-x_o)\;,\;l>0$ ,
donde la constante real $V_o$ tiene dimensiones de energía y puede ser negativa (pozo) o positiva; el parámetro real positivo $l$ tendrá por tanto dimensiones de longitud.
-La constante $\lambda=l \cdot V_o$ ha de tener dimensiones de energía por longitud, ya que ha de ser
$\int V(x)dx = \int \lambda \delta (x) dx=\lambda$ .
-Si $V_o<0$ , se tratará de un pozo con una delta atractiva situada en $x=x_o$ : habrá que estudiar la existencia de posibles estados ligados en el rango de energías $E<0$ , y los estados de difusión que aparecerán para $E>0$ :

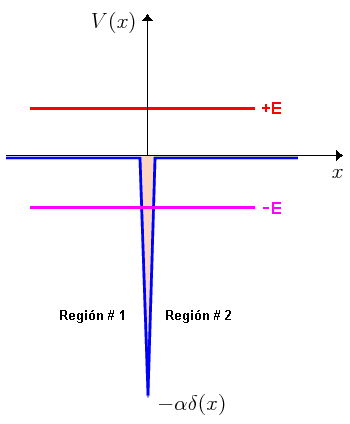
$\alpha=-V_o \cdot l$ del presente texto; en la figura, a diferencia de en este texto, el símbolo «E» se considera con valores siempre positivos (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html).

-Si $V_o>0$ , se tratará de un potencial con una delta repulsiva situada en $x=x_o$ , sin estados ligados y para el que sólo habrá que estudiar las soluciones, estados de difusión, en el rango de energías $E>0$ :

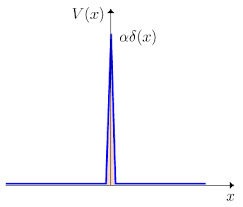
$\alpha=-V_o \cdot l$ del presente texto (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html).

Ejemplo 1: Potencial pozo con delta en el origen

Sea el potencial de expresión
$V(x)=l \cdot V_o\ \delta(x)\;,\;V_o<0\;,\;l>0\; , \, \lambda=l \cdot V_o<0$

$\alpha=-V_o \cdot l$ del presente texto; en la figura, a diferencia de en este texto, E se considera siempre positivo (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html).
Problema de autovalores de energía:
$\frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}[E-V(x)]\psi(x)=0$ ,
ecuación que conviene reescribir como
$\frac{d^2\psi}{dx^2}+[\epsilon-v(x)]\psi(x)=0$ ,
donde se ha introducido
$\epsilon =\frac{2m}{\hbar^2}E \quad , \quad v(x)=\frac{2m}{\hbar^2}V(x)$ .
-A esta EDO (ecuación diferencial ordinaria) habrán de añadirse las condiciones de contorno adecuadas que permitan obtener las soluciones físicamente aceptables del problema planteado.
Buscamos soluciones $\psi(x)$ que cumplan las condiciones:
-función $\psi(x)$ continua $\forall x \in \mathbb{R}$ .
-su derivada primera $\psi'(x)$ continua $\forall x\ne 0$ y con una discontinuidad de primera especie en el punto $x=0$ , en donde habrá de poseer un salto cuyo valor hemos de determinar:
-En $x=0$ :
$0=\lim_{\eta \rightarrow 0}\int_{-\eta}^{+\eta}[\frac{d^2\psi}{dx^2}+(\epsilon-v(x))\psi]dx$
$=\lim_{\eta \rightarrow 0}[\psi'(+\eta)-\psi'(-\eta)+\epsilon \int_{-\eta}^{+\eta}\psi(x) dx -\lambda_1 \int_{-\eta}^{+\eta}\delta(x)\psi(x) dx]$
$=\lim_{\eta \rightarrow 0}[\psi'(+\eta)-\psi'(-\eta)+\epsilon \int_{-\eta}^{+\eta}\psi dx -\lambda_1 \psi(0)]$
$\Rightarrow \lim_{\eta \rightarrow 0}[\psi'(+\eta)-\psi'(-\eta)]$
$=\lambda_1 \psi(0)-\epsilon \lim_{\eta \rightarrow 0}\int_{-\eta}^{+\eta}\psi dx$
$\approx \lambda_1 \psi(0) -\lim_{\eta \rightarrow 0}\epsilon \ 2\eta \ \psi(0)= \lambda_1 \psi(0)$
por continuidad de $\psi$ en $x=0$ y donde $\lambda_1=\frac{2mV_ol}{\hbar^2} < 0$ .
-Por tanto, las condiciones de contorno a imponer $x=0$ son:
1: $\psi$ continua en $x=0$
2: $\psi'(0^+)-\psi'(0^-)\approx \lambda_1 \psi(0)=\frac{2mV_ol}{\hbar^2} \psi(0)$ ,
donde:
$\psi'(0^{\pm})=\lim_{\eta \rightarrow 0}\psi'(0\pm \eta) .$
Dividimos el eje $OX$ en las dos zonas delimitadas por el punto donde se sitúa la delta, en el ejemplo el origen:
Zona I : $x<0$
Zona II : $x>0$
-La forma concreta de la EDO planteada para todos los puntos donde el potencial es nulo, esto es, $x\ne 0$ , es:
$\quad \frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}E\psi(x)=0$
La solución general de una EDO
$\frac{d^2\psi}{dx^2} \mp k^2\psi=0$ ,
donde $k>0$ , $k \in \mathbb{R}$ , tiene la expresión:
-Signo (-) : $\psi(x)=C_1 e^{kx} + C_2 e^{-kx}$
con $C_1,C_2$ escalares arbitrarios.
-Signo (+) : $\psi(x)=C_1 e^{+ikx} + C_2 e^{-ikx}=C'_1 cos kx + C'_2 sen kx$
con $C_1,C_2,C'_1,C'_2$ escalares arbitrarios.
-Por tanto, identificando $k=\frac{+\sqrt{2m|E|}}{\hbar} > 0$ , será el signo de $E$ el que marque el tipo de solución:
Se presentan pues los casos:
1. :
  1. Solución de la EDO:
    Zona I : $x<0$ : $\psi(x)=F e^{kx} + G e^{-kx}$
    Zona II: $x>0$ : $\psi(x)=A e^{kx} + B e^{-kx}$
    donde $k=\frac{+\sqrt{2m|E|}}{\hbar}=\frac{+\sqrt{-2mE}}{\hbar} > 0$ .
  2. Imposición condiciones de contorno:
    -Acotación $x \rightarrow -\infty \Rightarrow G=0$
    -Acotación $x \rightarrow +\infty \Rightarrow A=0$
    -Continuidad de $\psi$ en $x=0$ : $F=B$
    -Salto de $\psi'$ en $x=0$ : $\psi'(0^+)-\psi'(0^-)=\lambda_1 \psi(0)$ :
    $-kB-kF =\lambda_1 B$
    $\Rightarrow -2Bk=\lambda_1 B \ \Rightarrow -2k=\lambda_1$ ,
    donde $\lambda_1 =\frac{2m\lambda}{\hbar^2}=\frac{2mV_ol}{\hbar^2}<0$ .
  3. Se obtiene así la condición de cuantización que proporciona los valores de energía $E$ para los cuales existe solución físicamente aceptable:
    $k=-\frac{\lambda_1}{2} \Rightarrow E=-\frac{\hbar^2 k^2}{2m}=-\frac{\hbar^2\lambda_1^2}{8m}=-\frac{m\ V_o^2 l^2}{2\hbar^2}$
    -Se obtiene pues un solo autovalor, con una sola autofunción asociada, de expresión:
    $\psi(x)= \left\{ \begin{matrix} B e^{kx} \quad \mbox{si } x < 0 \\ Be^{-kx} \quad \mbox{si } x > 0 \end{matrix}\right.=Be^{-k|x|}\; \forall \,x$
    que se representa en la siguiente figura: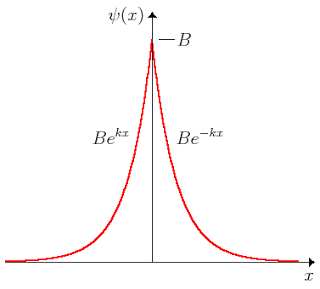
    
    Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html.
    
    -La constante $B$ queda fijada por normalización:
    $\int_{-\infty}^{+\infty} |\psi(x)|^2dx=1 \Rightarrow B=\sqrt{k}=\frac{\sqrt{m|V_o|l}}{\hbar}$
    de manera que la autofunción normalizada es:
    $\psi(x)=\frac{\sqrt{m|V_o|l}}{\hbar}e^{-\frac{m|V_o|l }{\hbar^2}|x|}\;,\;\forall x \in \mathbb{R}$
2. :
  1. Solución de la EDO:
    Zona I : $x<0$ : $\psi(x)=A e^{ikx} + B e^{-ikx}$
    Zona II : $x>0$ : $\psi(x)=F e^{ikx} + G e^{-ikx}$
    donde en este caso $k=\frac{+\sqrt{2m|E|}}{\hbar}=\frac{+\sqrt{2mE}}{\hbar} > 0$ :
    
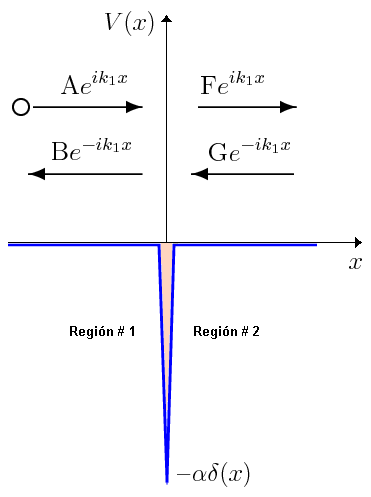
    $\alpha=-\lambda=-V_o \cdot l$ de este texto y también $k_1=k$ (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html).
  2. En este caso las soluciones representan estados de difusión, de forma que como soluciones particulares linealmente independientes podemos elegir las asociadas a un sentido de incidencia dado: solución $\psi_{izqa}$ correspondiente a incidencia desde la izquierda (se fijará $G=0$ ), y solución $\psi_{dcha}$ correspondiente a incidencia desde la derecha (se fijará $A=0$ ).
  3. Imposición condiciones de contorno para $\psi_{izqa}(x)$ :
    -Continuidad de $\psi$ en $x=0$ :
    $\rightarrow$ ecuación 1: $\lim_{x \rightarrow 0^-}\psi(x)=\lim_{x \rightarrow 0^+}\psi(x)$
    $\Rightarrow A+ B=F$
    -Salto de $\psi'$ en $x=0$ :
    $\rightarrow$ ecuación 2: $\psi'(0^+)-\psi'(0^-)=\lambda_1 \psi(0) =\frac{2m}{\hbar^2}\lambda \psi(0)$ :
    $\Rightarrow ik(F-A+B)=\frac{2m}{\hbar^2} \lambda (A+B)=\lambda_1 (A+B)$
  4. Resolución para $\psi_{izqa}(x)$ : tenemos dos ecuaciones y tres incógnitas:
    $B=\frac{\lambda_1}{2ik - \lambda_1}A$
    $F=\frac{2ik}{2ik - \lambda_1}A$ .
  5. Obtenida la solución, pueden calcularse los correspondientes coeficientes de reflexión y transmisión:
    -Se define el coeficiente de transmisión $T$ como el cociente entre los módulos de los vectores densidad de corriente transmitida e incidente:
    $T=\frac{|\vec{j}_{trans}(x;t)|}{|\vec{j}_{inci}(x;t)|}=\frac{|\vec{v}| \cdot |F|^2}{|\vec{v}| \cdot |A|^2}$
    -Se define el coeficiente de reflexión R como el cociente entre los módulos de los vectores densidad de corriente reflejada e incidente:
    $R=\frac{|\vec{j}_{refl}(x;t)|}{|\vec{j}_{inci}(x;t)|}=\frac{|\vec{v}| \cdot |B|^2}{|\vec{v}| \cdot |A|^2}$
    -Ambos son independientes de la normalización aplicada y satisfacen $R+T=1$ .
  6. En este caso:
    $R=\frac{|B|^2}{|A|^2}=|\frac{\lambda_1}{2ik - \lambda_1}|^2 =\frac{1}{1+\frac{4k^2 }{\lambda_1^2}}= \frac{1}{1+\frac{2\hbar^2 E}{mV_o^2l^2}}$
    $T=\frac{|F|^2}{|A|^2}=1-R=\frac{4k^2}{4k^2+\lambda_1^2}=\frac{1}{1+\frac{mV_o^2l^2}{2\hbar^2 E}}$
    -La siguiente figura ilustra la forma de estos coeficientes: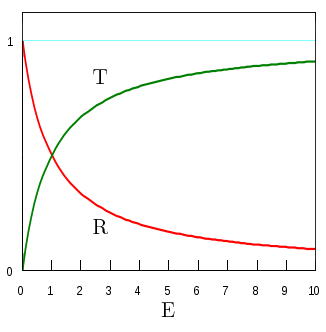
    
    Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html.
  7. Los estados de difusión pertenecen a energías del continuo en el espectro del Hamiltoniano, que presenta doble degeneración: $\forall E>0$ aparecen dos estados de difusión linealmente independientes (por ejemplo, $\psi_{izqa}$ y $\psi_{dcha}$ ).
Nota: para el potencial con delta de expresión
$V(x)=l \cdot V_o\ \delta(x)\;,\;V_o>0\;,\;l>0$ es fácil comprobar que:
-si $E<0$ el potencial carece de autofunciones: el problema de autovalores de la energía no tiene solución alguna físicamente aceptable.
-si $E>0$ la resolución es idéntica a la hecha en el caso $\lambda <0$ : son válidas las mismas expresiones para los coeficientes de reflexión y transmisión (tan sólo cambia el signo del parámetro $V_o$ , lo que, puesto que aparece siempre al cuadrado en las fórmulas de los coeficientes $R$ y $T$ , no los altera).

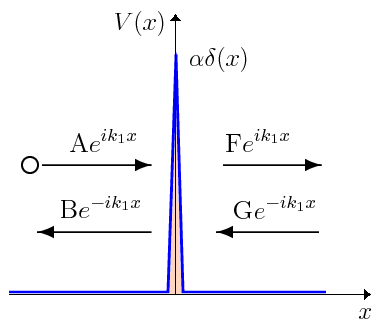
$\alpha=-\lambda=-V_o \cdot l$ del texto (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html).

Ejemplo 2: Potencial pozo con doble delta

El potencial pozo simétrico de doble delta tiene la expresión:
$V(x)=\lambda [\delta(x+a)+\delta(x-a)]\quad , \;a > 0\;,\;\lambda=\mbox{constante}\;,\;\lambda<0$ .

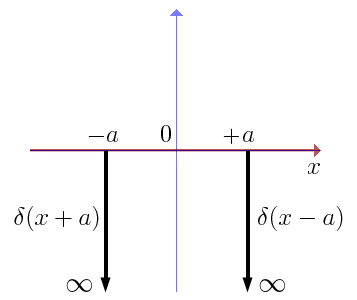
Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html.

-La constante $\lambda$ ha de tener dimensiones de energía por longitud, ya que ha de ser
$\int V(x)dx = \int \lambda \delta (x) dx=\lambda$ .
Problema de autovalores de energía:
$\frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}[E-V(x)]\psi(x)=0$ ,
ecuación que conviene reescribir como
$\frac{d^2\psi}{dx^2}+[\epsilon-v(x)]\psi(x)=0$ ,
donde se ha introducido
$\epsilon =\frac{2m}{\hbar^2}E \; , \; v(x)=\frac{2m}{\hbar^2}V(x)$ .
-A esta EDO (ecuación diferencial ordinaria) habrán de añadirse las condiciones de contorno adecuadas que permitan obtener las soluciones físicamente aceptables del problema planteado.
Buscamos soluciones $\psi(x)$ que cumplan las condiciones:
-función $\psi(x)$ continua $\forall x \in \mathbb{R}$ .
-su derivada primera $\psi'(x)$ continua $\forall x\ne \pm a \in \mathbb{R}$ y con discontinuidades de primera especie en los puntos $x=\pm a$ , en los cuales habrá de poseer un salto de valor:
-En $x=+a$ :
$0=\lim_{\eta \rightarrow 0}\int_{a-\eta}^{a+\eta}[\frac{d^2\psi}{dx^2}+(\epsilon-v(x))\psi]dx$
$=\lim_{\eta \rightarrow 0}[\psi'(a+\eta)-\psi'(a-\eta)+\epsilon \int_{a-\eta}^{a+\eta}\psi dx$
$-\lambda' \int_{a-\eta}^{a+\eta}\delta(x+a)\psi(x) dx -\lambda' \int_{a-\eta}^{a+\eta}\delta(x-a)\psi(x) dx]$
$=\lim_{\eta \rightarrow 0}[\psi'(a+\eta)-\psi'(a-\eta)+\epsilon \int_{a-\eta}^{a+\eta}\psi dx -\lambda' \psi(a)]$
$\Rightarrow \lim_{\eta \rightarrow 0}[\psi'(a+\eta)-\psi'(a-\eta)]$
$=\lambda' \psi(a)-\epsilon \lim_{\eta \rightarrow 0}\int_{a-\eta}^{a+\eta}\psi dx$
$\approx \lambda' \psi(a) -\lim_{\eta \rightarrow 0}\epsilon \ 2\eta \ \psi(a)= \lambda' \psi(a)$
por continuidad de $\psi$ en $x=a$ y donde $\lambda'=\frac{2m}{\hbar^2}\lambda$ ;
$-\lambda' \int_{a-\eta}^{a+\eta}\delta(x+a)\psi(x) dx=0$
ya que $-a \notin (a-\eta,a+\eta)$ .
-En $x=-a$ , análogamente:
$\lim_{\eta \rightarrow 0}[\psi'(-a+\eta)-\psi'(-a-\eta)]$
$=\lambda' \psi(-a)-\epsilon \lim_{\eta \rightarrow 0}\int_{-a-\eta}^{-a+\eta}\psi dx$
$\approx \lambda' \psi(-a) -\lim_{\eta \rightarrow 0}\epsilon \ 2 \eta \ \psi(-a)=\ \lambda' \psi(-a)$
-Por tanto, las condiciones de contorno a imponer en los puntos $x=\pm a$ son:
1: $\psi$ continua en $x=\pm a$
2: $\lim_{\eta \rightarrow 0}[\psi'(\pm a+\eta)-\psi'(\pm a-\eta)]\approx \lambda' \psi(\pm a)=\frac{2m}{\hbar^2}\lambda \psi(\pm a)$
Dividimos el eje $OX$ en tres zonas delimitadas por los puntos $x=\pm a$ donde se sitúan las deltas:
Zona III : $x<-a$
Zona I’ : $-a<x<+a$
Zona II : $x>+a$
-La forma concreta de la EDO planteada para todos los puntos donde el potencial es nulo, esto es, $x\ne \pm a$ , es:
$\quad \frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}E\psi(x)=0$
La solución general de una EDO
$\frac{d^2\psi}{dx^2} \mp k^2\psi=0$ ,
donde $k>0$ , $k \in \mathbb{R}$ , tiene la expresión:
-Signo (-) : $\psi(x)=C_1 e^{kx} + C_2 e^{-kx}$
con $C_1,C_2$ escalares arbitrarios.
-Signo (+) : $\psi(x)=C_1 e^{+ikx} + C_2 e^{-ikx}=C'_1 cos kx + C'_2 sen kx$
con $C_1,C_2,C'_1,C'_2$ escalares arbitrarios.
-Por tanto, identificando $k=\frac{+\sqrt{2m|E|}}{\hbar} > 0$ , será el signo de $E$ el que marque el tipo de solución:

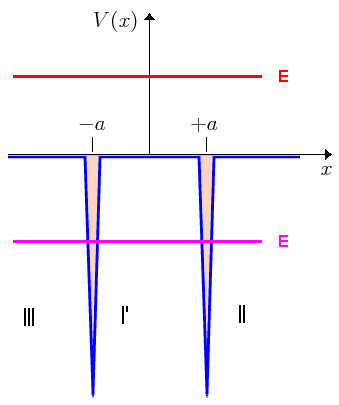
Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html.
Se presentan pues los casos:
1. :
  1. Solución de la EDO:
    Zona III : $x<-a$ : $\psi(x)=F e^{kx} + G e^{-kx}$
    Zona I’ : $-a<x<+a$ : $\psi(x)=A' e^{kx} + B' e^{-kx}$
    Zona II : $x>+a$ : $\psi(x)=C e^{kx} + D e^{-kx}$
    donde en este caso $k=\frac{+\sqrt{2m|E|}}{\hbar}=\frac{+\sqrt{-2mE}}{\hbar} > 0$ .
  2. Imposición primeras condiciones de contorno y requisito de paridad:
    -Acotación $x \rightarrow -\infty \Rightarrow G=0$
    -Acotación $x \rightarrow +\infty \Rightarrow C=0$
    -Paridad de las autofunciones: las soluciones tienden a cero a largas distancias, $|x| \rightarrow \infty$ , esto es, representan estados ligados de un potencial monodimensional: por tanto, son no degeneradas y poseen paridad definida. Incorporamos esta característica de forma que podemos limitarnos a trabajar obteniendo la forma de las correspondientes soluciones pares e impares en la semirrecta real positiva, $x> 0$ :
    Zona I : $0< x < +a$ : $\psi(x)=A' e^{kx} + B' e^{-kx}=A cosh (kx) + B senh (kx)$
    Zona II : $x> +a$ :
    $\psi(x)=D e^{-kx}$
  3. Autofunciones ligadas pares :
    1. Imposición restantes condiciones de contorno:
      -Por ser una función par: $\psi'_+(0)=0 \Rightarrow B=0$
      -Continuidad de $\psi_+$ en $x=a$ :
      $A cosh(ka)=D e^{-ka}$
      $\Rightarrow D=A e^{ka}cosh(ka)$
      -Salto de $\psi_+'$ en $x=a$ : $\psi_+'(a^+)-\psi_+'(a^-)=\frac{2m}{\hbar^2}\lambda \psi_+(a)$ :
      $-kDe^{-ka}-kA senh(ka)= \frac{2m}{\hbar^2}\lambda D e^{-ka}$
      $\Rightarrow kA senh(ka)=-kDe^{-ka}-\frac{2m}{\hbar^2}\lambda D e^{-ka}$
    2. Dividiendo las dos ecuaciones anteriores se obtiene la condición de cuantización para las autofunciones pares o ecuación que proporciona los valores de energía $E$ para los cuales existe solución par:
      $tanh(ka)=-\frac{2m\lambda}{\hbar^2 k}-1 \Rightarrow e^{-2ka}=-(\frac{\hbar^2 k}{m\lambda}+1)$
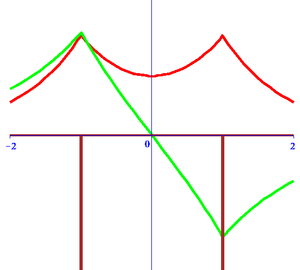
      -Se trata de una ecuación trascendente que puede resolverse representando gráficamente las dos curvas $f_1(k)= e^{-2ka}$ y $f_2(k)=-(\frac{\hbar^2 k}{m\lambda}+1):$
      
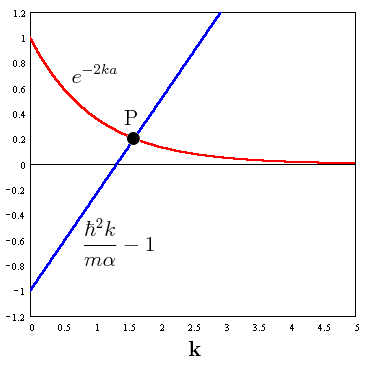
      $\alpha=-\lambda$ del texto (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html).
      
      -Obsérvese que el valor de energía
      $E_+=-\frac{\hbar^2 k_+^2}{2m}< 0$ ,
      o único autovalor para el que existe solución par físicamente aceptable para el problema de autovalores planteado, correspondiente al punto de corte de las dos curvas en la anterior gráfica, cumple:
      $0 < k_+=\frac{+\sqrt{-2mE_+}}{\hbar} > \frac{m |\lambda|}{\hbar^2}$
      -Existe pues un solo estado ligado par, de expresión:
      $\psi_+(x) \left\{ \begin{matrix} A e^{ka}cosh(ka) e^{kx}=A cosh(ka) e^{k(x+a)} \quad \mbox{si } x < -a \\ A cosh(kx) \quad \mbox{si } -a < x < +a \\ A e^{ka}cosh(ka) e^{-kx}=A cosh(ka) e^{-k(x-a)} \quad \mbox{si } x> +a \end{matrix}\right.$
      -Equivalentemente:
      $\psi_+(x) \left\{ \begin{matrix} A cosh(kx) \quad \mbox{si } 0 < |x| < +a \\ A e^{ka}cosh(ka) e^{-k|x|}=A cosh(ka) e^{-k(|x|-a)} \quad \mbox{si } |x| > +a \end{matrix}\right.$
      -La constante $A$ queda fijada por normalización:
      $\int_{-\infty}^{+\infty} |\psi_+(x)|^2dx=1 \Rightarrow A=[a+\frac{cosh^2ka}{k}+\frac{senh(2ka)}{2k}]^{-\frac{1}{2}}$
      -En la siguiente figura se representa la forma general de esta autofunción par: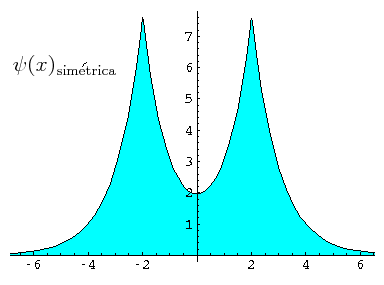
      
      $\alpha=-\lambda$ del texto (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html).
  4. Autofunciones ligadas impares :
    1. Imposición restantes condiciones de contorno:
      -Por ser una función impar: $\psi_-(0)=0 \Rightarrow A=0$
      -Continuidad de $\psi_-$ en $x=a$ :
      $B senh(ka)=D e^{-ka}$
      $\Rightarrow D=B e^{ka}senh(ka)$
      -Salto de $\psi_-'$ en $x=a$ : $\psi_-'(a^+)-\psi_-'(a^-)=\frac{2m}{\hbar^2}\lambda \psi_-(a)$ :
      $-kDe^{-ka}-kB cosh(ka)= \frac{2m}{\hbar^2}\lambda D e^{-ka}$
      $\Rightarrow kB cosh(ka)=-kDe^{-ka}-\frac{2m}{\hbar^2}\lambda D e^{-ka}$
    2. Dividiendo las dos ecuaciones anteriores se obtiene la condición de cuantización para las autofunciones impares o ecuación que proporciona los valores de energía $E$ para los cuales existe solución impar:
      $cotanh(ka)=-\frac{2m\lambda}{\hbar^2 k}-1 \Rightarrow e^{-2ka}=(\frac{\hbar^2 k}{m\lambda}+1)$
      -Se trata de una ecuación trascendente que puede resolverse representando gráficamente las dos curvas $f_1(k)= e^{-2ka}$ y $f_2(k)=(\frac{\hbar^2 k}{m\lambda}+1)$ :
      
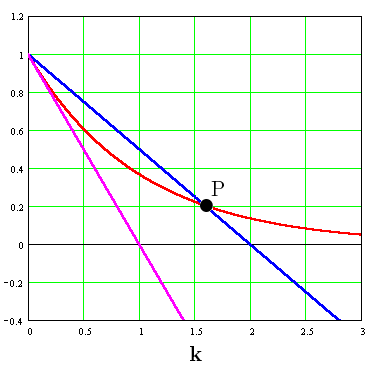
      -Las líneas rosa y azul corresponden a la representación de la función $f_2(k)$ para dos valores distintos de la pendiente (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html).
      
      -Obsérvese que el valor de energía
      $E_-=-\frac{\hbar^2 k_-^2}{2m}< 0$ ,
      o único autovalor para el que, en su caso (cuando el valor de la pendiente $\frac{\hbar^2}{m\lambda}$ lo permita), existe solución impar físicamente aceptable para el problema de autovalores planteado, correspondiente al punto de corte de las dos curvas en la anterior gráfica, cumple:
      $0 < k_-=\frac{+\sqrt{-2mE_-}}{\hbar} < \frac{m |\lambda|}{\hbar^2}$
      -Por tanto, puede existir un solo estado ligado impar (¡o no!), de expresión:
      $\psi_-(x) \left\{ \begin{matrix} -B e^{ka}senh(ka) e^{kx}=-B senh(ka) e^{k(x+a)} \quad \mbox{si } x < -a \\ B senh(kx) \quad \mbox{si } -a < x < +a \\ B e^{ka}senh(ka) e^{-kx}=B senh(ka) e^{-k(x-a)} \quad \mbox{si } x > +a \end{matrix}\right.$
      -Equivalentemente:
      $\psi_-(x) \left\{ \begin{matrix} B senh(kx) \quad \mbox{si } 0 < |x| < +a \\ B e^{ka}senh(ka) \frac{x}{|x|}e^{-k|x|}=B cosh(ka) \frac{x}{|x|}e^{-k(|x|-a)} \quad \mbox{si } |x| > +a \end{matrix}\right.$
      -La constante $B$ queda fijada por normalización:
      $\int_{-\infty}^{+\infty} |\psi_-(x)|^2dx=1 \Rightarrow B=[\cdots]^{-\frac{1}{2}}$
      -En la siguiente figura se representa la forma general de esta función impar: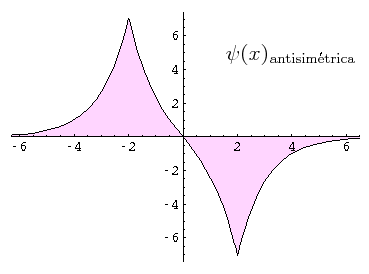
      
      Autofunción impar (imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-Dirac.html).
2. :
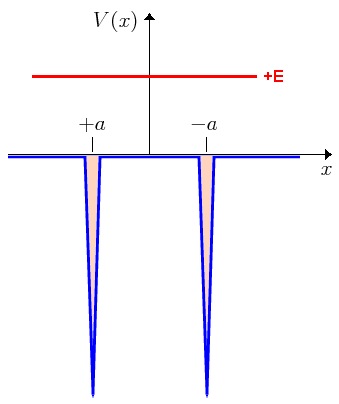
  Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html.
  1. Solución de la EDO:
    Zona III : $x<-a$ : $\psi(x)=F e^{ikx} + G e^{-ikx}$
    Zona I’ : $-a<x<+a$ : $\psi(x)=A e^{ikx} + B e^{-ikx}$
    Zona II : $x>+a$ : $\psi(x)=C e^{ikx} + D e^{-ikx}$
    donde en este caso $k=\frac{+\sqrt{2m|E|}}{\hbar} = \frac{+\sqrt{2mE}}{\hbar} > 0$ .
  2. En este caso las soluciones representan estados de difusión, de forma que como soluciones particulares linealmente independientes podemos elegir las asociadas a un sentido de incidencia dado: solución $\psi_{izqa}$ correspondiente a incidencia desde la izquierda (se fijará $D=0$ ), y solución $\psi_{dcha}$ correspondiente a incidencia desde la derecha (se fijará $F=0$ ).
  3. Imposición condiciones de contorno para $\psi_{izqa}(x)$ :
    -Por simplificación, fijamos $F=1$ (una vez resuelto el problema, bastará renormalizar la solución).
    -a) Continuidad de $\psi$ en $x=-a$ :
    $\rightarrow$ ecuación 1: $\lim_{x \rightarrow -a^-}\psi(x)=\lim_{x \rightarrow -a^+}\psi(x)$
    $\Rightarrow e^{-ika} + G e^{ika}=A e^{-ika} + B e^{ika}$
    -b) Salto de $\psi'$ en $x=-a$ :
    $\rightarrow$ ecuación 2: $\psi'(-a^-)-\psi'(-a^+)=-\frac{2m}{\hbar^2}\lambda \psi(-a)$ :
    $\Rightarrow ik (e^{-ika} - G e^{ika}-A e^{-ika}+B e^{ika})$
    $=-\frac{2m}{\hbar^2}\lambda (e^{-ika}+G e^{ika})$
    -c) Continuidad de $\psi$ en $x=+a$ :
    $\rightarrow$ ecuación 3: $\lim_{x \rightarrow +a^-}\psi(x)=\lim_{x \rightarrow +a^+}\psi(x)$
    $\Rightarrow A e^{ika} + B e^{-ika}=C e^{ika}$
    -d) Salto de $\psi'$ en $x=+a$ :
    $\rightarrow$ ecuación 4: $\psi'(+a^-)-\psi'(+a^+)=-\frac{2m}{\hbar^2}\lambda \psi(+a)$ :
    $\Rightarrow ik(A e^{ika}-B e^{-ika}-C e^{ika})$
    $= -\frac{2m}{\hbar^2}\lambda C e^{ika}$
  4. Resolución para $\psi_{izqa}(x)$ :
    –Paso 1: (ik x ecuación 3) + (ecuación 4):
    $\Rightarrow A=C (1-\frac{2m}{\hbar^2}\frac{\lambda}{2ik})=C (1+i\frac{\alpha}{k})$
    donde $\alpha=\frac{m\lambda}{\hbar^2}$ .
    –Paso 2: (ik x ecuación 3) – (ecuación 4):
    $\Rightarrow B=C (-i\frac{\alpha}{k}) e^{2ika}$
    –Paso 3: sustitución de las anteriores expresiones para $A$ y $B$ en la ecuación 1 y división por $ik$ :
    $\rightarrow$ ecuación 1′: $C (1+i\frac{\alpha}{k}) e^{-ika} + C (-i\frac{\alpha}{k}) e^{3ika}= -e^{-ika}+G e^{ika}$
    –Paso 4: sustitución de las anteriores expresiones para $A$ y $B$ en la ecuación 2 y división por $ik$ :
    $\rightarrow$ ecuación 2′: $C (1+i\frac{\alpha}{k}) e^{-ika} + C (i\frac{\alpha}{k}) e^{3ika} -e^{-ika}+G e^{ika}$
    $=(\frac{2\alpha}{ik}) (e^{-ika}+G e^{ika})$
    –Paso 5: (1+2i alfa/k)(ecuación 1′) + (ecuación 2′):
    $\Rightarrow C [(1+i\frac{\alpha}{k})^2e^{-2ika}+\frac{\alpha^2}{k^2}e^{2ika}]=e^{-2ika}$
    –Paso 6: la sustitución de la anterior expresión para $C$ en la ecuación 1′ permite obtener $B$ .
  5. Obtenida la solución, pueden calcularse los correspondientes coeficientes de reflexión y transmisión:
    -Se define el coeficiente de transmisión $T$ como el cociente entre los módulos de los vectores densidad de corriente transmitida e incidente:
    $T=\frac{|\vec{j}_{trans}(x;t)|}{|\vec{j}_{inci}(x;t)|}=\frac{|\vec{v}| \cdot |C|^2}{|\vec{v}| \cdot |F|^2}$
    -Se define el coeficiente de reflexión R como el cociente entre los módulos de los vectores densidad de corriente reflejada e incidente:
    $R=\frac{|\vec{j}_{refl}(x;t)|}{|\vec{j}_{inci}(x;t)|}=\frac{|\vec{v}| \cdot |G|^2}{|\vec{v}| \cdot |F|^2}$
    -Ambos son independientes de la normalización aplicada y satisfacen $R+T=1$ .
    -En este caso (la normalización impuesta ha fijado $F=1$ ) :
    $T=|C|^2=[1+4\frac{\alpha^2}{k^2}[cos(2ka)+\frac{\alpha}{k}sen(2ka)]^2]^{-1}$
    $R=|G|^2=1-T$
    donde $\alpha=\frac{m\lambda}{\hbar^2}$ .
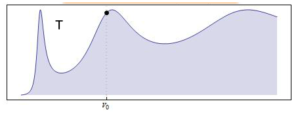
  6. La figura siguiente nos muestra el aspecto típico del factor de transmisión $T$ en estos problemas:
  7. Los estados de difusión pertenecen a energías del continuo en el espectro del Hamiltoniano, que presenta doble degeneración: $\forall E>0$ aparecen dos estados de difusión linealmente independientes (por ejemplo, $\psi_{izqa}$ y $\psi_{dcha}$ ).
Nota: para el potencial con doble delta de expresión
$V(x)=\lambda [\delta(x+a)+\delta(x-a)]\quad , \;a > 0\;,\;\lambda=\mbox{constante}\;,\;\lambda>0$
es fácil comprobar que:
-si $E<0$ el potencial carece de autofunciones: el problema de autovalores de la energía no tiene solución alguna físicamente aceptable.
-si $E>0$ la resolución es idéntica a la hecha en el caso $\lambda <0$ : son válidas las mismas expresiones para los coeficientes de reflexión y transmisión (tan sólo cambia el signo del parámetro $\alpha$ ).
En el problema resuelto, se ha supuesto un doble pozo de potencial delta donde ambas deltas llevan el mismo coeficiente $\lambda$ , esto es, tienen la misma intensidad. La resolución del doble pozo de potencial con deltas de intensidades diferentes requiere pequeñas modificaciones del ejemplo desarrollado.
El interés físico del pozo de potencial de doble delta es la representación (idealizada) de átomos individuales como cargas puntuales, permitiendo modelar y tratar mecano-cuánticamente una molécula diatómica.