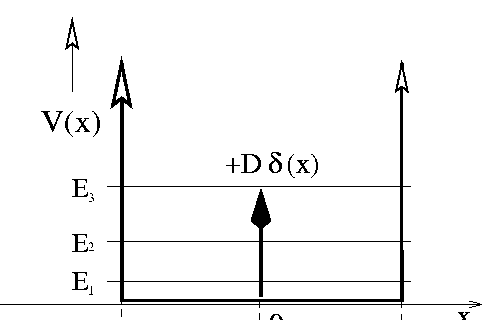
Pozo infinito con barrera delta

El pozo cuadrado infinito con barrera delta

Función potencial $V(x)$ :
$V(x) = \left \{ \begin{matrix} \lambda \ \delta(x-\frac{L}{2}) & \mbox{si } 0 < x < L \; , \;\lambda=l\cdot V_o > 0 \, , \; zonas \; \; I \, \mbox{y} \, II \\ +\infty & \mbox{si } x \le 0\; ,\; x \ge L \; , \; zona \; \; III \; \end{matrix}\right.$
-Se trata de una función con discontinuidades de segunda especie en los puntos $x=0$ y $x=L$ , puntos en los que se sitúan sendas barreras impenetrables de potencial; por lo tanto, en ellos se debe imponer la condición de frontera de anulación de la función de onda $\psi(x)$ : se produce el confinamiento o ligadura de la partícula en el interior del intervalo $(0,L)$ de la recta real.
-Además, la presencia de la delta en $x=\frac{L}{2}$ provoca que, mientras la función de onda es continua en ese punto, la derivada primera presenta un salto finito o discontinuidad de primera especie.
Problema de autovalores de energía:
$\frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}[E-V(x)]\psi(x)=0$ ,
y buscamos soluciones $\psi(x)$ que sean funciones continuas y con derivada primera $\psi'(x)$ también continua allí donde $V(x)$ es finito: en los intervalos $(0,\frac{L}{2})$ y $(\frac{L}{2},L)$ .
-Las funciones $\psi(x)$ tendrán sendos nodos en los puntos extremos $x=0$ y $x=L$ : $\psi(0)=\psi(L)=0$ ,
en los que $\psi'(x)$ presentará una discontinuidad de primera especie, al igual que en $x=\frac{L}{2}$ .
La solución general de una EDO
$\frac{d^2\psi}{dx^2} \mp k^2\psi=0$ ,
donde $k>0$ , $k \in \mathbb{R}$ , tiene la expresión:
-Signo (-) : $\psi(x)=C_1 \ e^{kx} + C_2\ e^{-kx}$
con $C_1,C_2$ escalares arbitrarios.
-Signo (+) : $\psi(x)=C_1 \ e^{+ikx} + C_2\ e^{-ikx}=C'_1 \ cos\ kx + C'_2\ sen \ kx$
con $C_1,C_2,C'_1,C'_2$ escalares arbitrarios.
Dividimos la región espacial $0<x<L$ en las dos subzonas izquierda I y derecha II:
Zona I: $0<x< \frac{L}{2}$
Zona II: $\frac{L}{2} <x < L$
-En ambas zonas I y II la forma concreta de la EDO planteada es:
$\quad \frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}[E]\psi(x)=0$ .
Cuantización de la energía:
1. :
  1. -Zona I: $0<x< \frac{L}{2}$ :
    $\psi_{I}(x)=A \ e^{kx} + B\ e^{-kx}$ ,
    -Zona II: $\frac{L}{2} <x < L$ :
    $\psi_{II}(x)=C \ e^{kx} + D\ e^{-kx}$ ,
    con $k=\frac{+\sqrt{2m(-E)}}{\hbar}>0$ y $A,B,C,D$ escalares arbitrarios.
    -Zona III: $x\le 0$ y $x \ge L$ : $\psi_{III}(x)=0 \, , \; \forall x$ .
  2. Imponiendo las condiciones para que la solución sea físicamente aceptable:
    -Anulación $x=0 \Rightarrow 0=A+B$
    -Anulación $x=L \Rightarrow 0=C \ e^{+kL} + D\ e^{-kL}$
    -Continuidad en $\frac{L}{2}$ : $A\ e^{+k\frac{L}{2}} + B\ e^{-k\frac{L}{2}} = C\ e^{+k\frac{L}{2}} + D\ e^{-k\frac{L}{2}}$
    -Salto de la derivada primera $\psi'$ en $x=\frac{L}{2}$ :
    $\psi'(\frac{L}{2}^+)-\psi'(\frac{L}{2}^-)=\lambda_1 \psi(\frac{L}{2}) =\frac{2m}{\hbar^2}\lambda \psi(\frac{L}{2})$
  3. Puesto que el anterior conjunto de condiciones conduce a la solución trivial, la conclusión es que no existen soluciones físicamente aceptables del problema de autovalores de energía para valores del parámetro de separación $E<0$ .
2. :
  1. Expresión de la función de onda:
    -Zona I : $\psi_I(x)=A' \ e^{+ikx} + B'\ e^{-ikx}=A \ cos\ kx + B\ sen \ kx$
    -Zona II : $\psi_{II}(x)=C' \ e^{+ikx} + D'\ e^{-ikx}=C \ cos\ kx + D\ sen \ kx$ ,
    que por conveniencia práctica elegimos sustituir por la forma equivalente
    $\psi_{II}(x)=F\ sen \ k(x-c)$ ,
    con $k=\frac{+\sqrt{2m(E)}}{\hbar}>0$
    y $A,B,A',B',C,D,C',D',F$ y $c$ representando escalares arbitrarios.
  2. Imponiendo las condiciones de contorno en $x=0$ y $x=L$ :
    -Anulación en $x=0$ :
    $\Rightarrow A\cdot 1 + B \cdot 0=0 \Rightarrow A=0 \Rightarrow \psi_I(x)=B\ sen \ kx$
    -Anulación $x=L$ :
    $\psi_{II}(L)=0=F \ sen\ k(L-c)$ $=F(sen\ kL\ cos \ kc - cos\ kL\ sen\ kc)$
    $\Rightarrow \frac{sen\ kL}{cos\ kL}=\frac{sen\ k c}{cos\ k c}$ ;
    elegimos $c=L$ y tomando la forma general para la función de onda en la región II como
    $\psi_{II}(x)=F\ sen \ k(x-L)$
    conseguimos incorporar de partida en la función de onda la condición de contorno $\psi(L)=0$ .
  3. Imposición de las condiciones de contorno en $x=\frac{L}{2}$ :
    -Continuidad de la función de onda en $x=\frac{L}{2}$ :
    $B\ sen\ k\frac{L}{2}=F\ sen\ k(\frac{L}{2}-L)=F\ sen\ (k(-\frac{L}{2}))=-F\ sen\ (k\frac{L}{2})$ ,
    de donde se implica una disyuntiva:
    O bien $B=-F$ ,
    o bien (¡de forma alternativa!) $sen\ (k\frac{L}{2})=0$ .
    -Discontinuidad de la primera derivada de la función de onda en $x=\frac{L}{2}$ :
    $\psi'(\frac{L}{2}^+)-\psi'(\frac{L}{2}^-)=\frac{2m\lambda}{\hbar^2} \psi(\frac{L}{2})$
    $\Rightarrow \psi'_{II}(\frac{L}{2}) - \psi'_{I}(\frac{L}{2})$ $=\frac{2m\lambda}{\hbar^2} \psi (\frac{L}{2})$
    $\Rightarrow Fk\ cos\ (k(\frac{L}{2}-L))-Bk\ cos\ k(\frac{L}{2})=\frac{2m}{\hbar^2}\lambda B\ sen\ k(\frac{L}{2})$
    $\Rightarrow k(F-B)\ cos\ k(\frac{L}{2})=\frac{2m}{\hbar^2}\lambda B\ sen\ k(\frac{L}{2})$
  4. Se obtienen pues dos tipos de soluciones:
    1. Autovalores de energía obtenibles de forma analítica: corresponden al caso en que $B=F$ .
      -En efecto, en este caso se deriva que
      $B=F \Rightarrow sen\ (k\frac{L}{2})=0 \Rightarrow k_n\frac{L}{2}= n \pi \, , n=1,2\ldots$ ,
      de manera que se obtienen los autovalores discretos
      $E_{n}=\frac{\hbar^2 k_n^2}{2m}=\frac{\hbar^2 \pi^2 (2n)^2}{2mL^2}=\frac{\hbar^2 \pi^2 2n^2}{mL^2}$ ,
      que coinciden con los autovalores del pozo infinito sin delta correspondientes a los estados excitados con número cuántico par (primer estado excitado, tercer estado excitado, etc.). Algo que es lógico y esperable, ya que estos estados se anulan en $x=\frac{L}{2}$ , por lo que «no sienten» la delta.
      -Representaremos estos estados como $\psi_n$ , y sus correspondientes estados como $E_n$ , con $n=1$ (primer estado excitado), $n=2$ (tercer estado excitado), etc.
    2. Autovalores de energía obtenibles de forma gráfica o numérica: corresponden al caso en que $B=-F$ .
      -En este caso se obtiene la ecuación de autovalores o condición de cuantización:
      $B=-F \Rightarrow -Bk\ cos\ (k(\frac{L}{2}-L))-Bk\ cos\ k(\frac{L}{2})=\frac{2m}{\hbar^2}\lambda B\ sen\ k(\frac{L}{2})$
      $\Rightarrow -2Bk\ cos\ k(\frac{L}{2})=\frac{2m}{\hbar^2}\lambda B\ sen\ k(\frac{L}{2})$
      $\Rightarrow tan\ k(\frac{L}{2})=-\frac{\hbar^2k}{m\lambda}$
      -Esta ecuación admite resolución gráfica; puede consultarse en el siguiente enlace (en el artículo se traslada el potencial para hacerlo simétrico, colocando la delta en el origen, lo que por supuesto no afecta a la forma de las soluciones, sólo las desplaza también; además, la anchura del pozo se toma como $2a$ , de forma que nuestra $L$ se reemplaza por $L=2a$ ):
      –Griffiths, Introduction to quantum mechanics y solucionario 1 y solucionario 2.
      (enlace caído anterior: https://www.fisica.net/mecanica-quantica/Griffiths%20-%20Introduction%20to%20quantum%20mechanics.pdf).
      -Representaremos estos estados como $\psi_{n'}$ , y sus correspondientes estados como $E_{n'}$ , con $n'=1$ (estado fundamental, la raíz más pequeña de la condición de cuantización anterior), $n'=2$ (segundo estado excitado), etc.
  5. Como se muestra en este enlace:
    http://www.sc.ehu.es/sbweb/fisica3/cuantica/pozo/delta_1.html ,
    los primeros estados excitados tienen la forma (notación y figura de la anterior web, la delta ha pasado al origen):
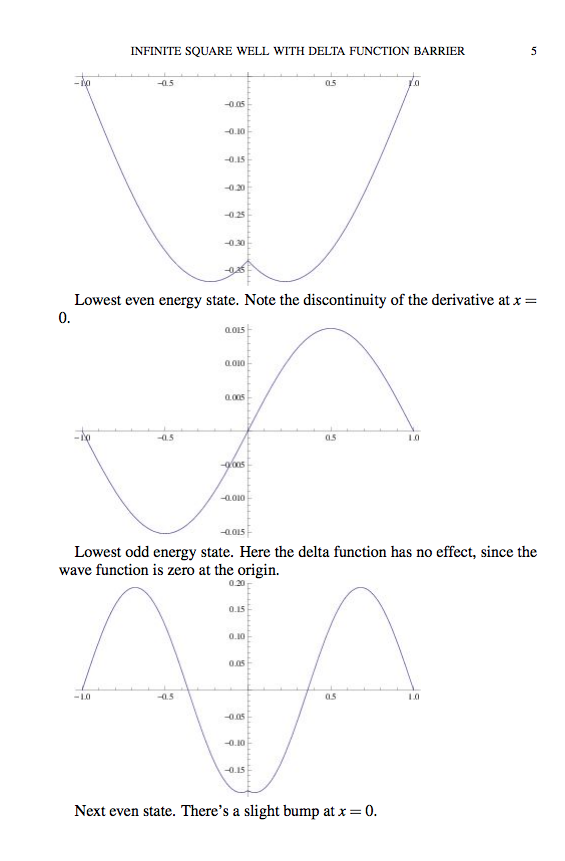
  6. Aparece pues el fenómeno de cuantización de la energía, ya que sólo hay solución físicamente aceptable del problema de autovalores para algunos valores discretos de energía. Las autofunciones correspondientes a estos estados ligados tienen la forma:
    -Autofunciones que no se anulan en $x=\frac{L}{2}$ , correspondientes al estado fundamental (autovalor más pequeño) y a los estados excitados segundo, cuarto, etc.:
    $\psi_{n'}(x) = \left \{ \begin{matrix} B_{n'}\ sen\ k_{n'} x & \mbox{si } 0 < x < \frac{L}{2} \; , \; zona \; \; I \\ -B_{n'}\ sen\ k_{n'} (x-L) & \mbox{si } \frac{L}{2} < x < L \; , \; zona \; \; II \\ 0 & \mbox{si } x \le 0\; ,\; x \ge L \; \; zona \; \; III \; \end{matrix}\right.$ ,
    donde los valores $k_{n'}=\frac{+\sqrt{2m(E_{n'})}}{\hbar}$ vienen dados a partir de los autovalores $E_{n'}$ o raíces de la condición de cuantización
    $tan\ k_{n'}(\frac{L}{2})=-\frac{\hbar^2k_{n'}}{m\lambda}$
    y la constante $B_{n'}$ se ha de determinar por normalización de la función de onda $\psi_{n'}(x)$ .
    -Autofunciones que se anulan en $x=\frac{L}{2}$ , correspondientes a los estados excitados primero, $n=1$ ; tercero, $n=2$ , etc., cuyas energías correspondientes son $E_n=\frac{\hbar^2 k_n^2}{2m}=\frac{\hbar^2 \pi^2 2n^2}{mL^2}$ , $k_n=\frac{+\sqrt{2m(E_n)}}{\hbar}=\frac{2\pi n}{L}$ :
    $\psi_n(x) = \left \{ \begin{matrix} B_n\ sen\ k_n x & \mbox{si } 0 < x < \frac{L}{2} \; , \; zona \; \; I \\ B_n\ sen\ k_n (x-L) & \mbox{si } \frac{L}{2} < x < L \; , \; zona \; \; II \\ 0 & \mbox{si } x \le 0\; ,\; x \ge L \; \; zona \; \; III \; \end{matrix}\right.$ ,
    donde la constante $B_n$ se ha de determinar por normalización de la función de onda $\psi_n(x)$ .
En el problema estudiado, Hamiltoniano del pozo cuadrado infinito con barrera delta, o caja de paredes impenetrables con delta de Dirac en su mitad, resulta por tanto:
$\sigma(H)=\sigma_p(H)\subset(0\, ,+\infty)$ : infinitos estados ligados, sin degeneración; se satisface el teorema de oscilación.