Suma de momentos angulares

Suma de operadores de momento angular: coeficientes de Clebsch-Gordan

Sean $\vec{J}_1$ y $\vec{J}_2$ sendos operadores de momento angular en dos subsistemas cinemáticamente independientes, $[\vec{J}_1, \vec{J}_2]=0$ , actuando en los sendos espacios $\mathcal{H}^{(J_i)} \, , \, i=1,2$ , de correspondientes dimensiones finitas $(2J_i +1)\, , \, i=1,2$ .
-Puede comprobarse que el operador suma de los dos dados,
$\vec{J} \, = \, \vec{J_1} \, + \, \vec{J_2} \, \doteq \, \vec{J_1}\otimes I_2 \, + I_1 \otimes \vec{J_2}$ ,
que actúa en el espacio $\mathcal{H}^{(J_1;J_2)} \doteq \mathcal{H}^{(J_1)} \otimes \mathcal{H}^{(J_2)}$ , asociado a la unión de los subsistemas, y que está engendrado por la unión de las dos bases ortonormales comunes a $\vec{J}_1^2$ y $J_{z1}$ , de un lado, y a $\vec{J}_2^2$ y $J_{z2}$ , de otro, cuya dimensión es $(2J_1+1)(2J_2+1)$ , es también un operador de momento angular, esto es, satisface las reglas de conmutación definitorias, esto es:
$[J_i\,,\,J_j]=i\hbar \, \epsilon_{ijk}\,J_k\,;\, i,j,k=1,2,3$ ,
o, en notación compacta equivalente:
$\vec{J} \times \vec{J}\,=\,i\hbar \,\vec{J}$ .
-En espacios bipartitos, el operador $\vec{J}$ se suele denominar operador de momento angular total.
Una forma posible de expresar los estados y valores propios del operador momento angular total es a través de los coeficientes de Clebsh-Gordan. Para obtenerlos, partimos del hecho de que los cuatro operadores $\vec{J}_1^2, \vec{J}_{z1} , \vec{J}_2^2, \vec{J}_{z2}$ conmutan entre sí, por lo que pueden formar parte conjunta de un C.C.O.C., en unión con los, en su caso, observables que se requieran, y que se simbolizarán en principio por unas variables $\alpha_i$ .
-Sea
$|J_1\, M_1\,J_2\, M_2\,\alpha_1 \alpha_2 > \, \equiv \, |J_1\, M_1 \, \alpha_1>\, \otimes \, |J_2\, M_2\,\alpha_2 >$
un vector de la base ortonormal asociada al C.C.O.C. elegido en el Hilbert $\mathcal{H}^{(J_1;\alpha_1)} \otimes \mathcal{H}^{(J_2;\alpha_2)}$ , el cual satisfará el conjunto de ecuaciones:
$\left. \begin{array}{l} \vec{J_i}^2 \,|J_1\, M_1\,J_2\, M_2\,\alpha_1 \alpha_2 > \, \,=\,\hbar^2J_i(J_i+1) \,|J_1\, M_1\,J_2\, M_2\,\alpha_1 \alpha_2 > \\ J_{zi} \, | J_1\, M_1\,J_2\, M_2 \, \alpha_1 \alpha_2 > \, = \, \hbar M_i \,|J_1\, M_1\,J_2\, M_2\,\alpha_1 \alpha_2 > \end{array} \right\} \,, \, i=1,2$ .
Puesto que los observables adicionales, asociados con los números cuánticos $\alpha_i$ presentes en los estados cuánticos, no van a jugar ningún papel en el siguiente desarrollo, los suprimiremos a partir de aquí en la notación, es decir, consideraremos los espacios $\mathcal{H}^{(J_1)}$ , $\mathcal{H}^{(J_2)}$ , de dimensiones $(2J_1+1)$ y $(2J_2+1)$ ; trabajaremos en el Hilbert $\mathcal{H}^{(J_1;J_2)}$ , con dimensión igual a $(2J_1+1)(2J_2+1)$ . El que uno, o los dos, subespacios $\mathcal{H}^{(J_i)}$ fueran impropios, no modificaría el desarrollo teórico: simplemente los adicionales $\alpha_i$ que se deberían añadir se están tomando en lo que sigue como fijos.
Así pues, para unos valores dados de los números cuánticos $J_1$ y $J_2$ , el conjunto de vectores
$\{| J_1\, M_1 \, J_2\, M_2 > \equiv | J_1\, M_1 > \otimes | J_2\, M_2 >\}_{M_i=-J_i,-J_i+1,\ldots,J_i \; , \; i=1,2}$ ,
autovectores simultáneos de los cuatro operadores $\vec{J_i}^2$ y $J_{zi}$ , $i=1,2$ , generan un subespacio de Hilbert $\mathcal{H}^{(J_1;J_2)}$ , de dimensión $(2J_1+1)(2J_2+1)$ .
Dado que tanto $\vec{J}=\vec{J_1} + \vec{J_2}$ como $J_z=J_{z1} + J_{z2}$ conmutan con $\vec{J_i}^2$ , $i=1,2$ , es posible localizar un conjunto de vectores normalizados $| J_1\, J_2 \, J\, M >$ que satisfacen el conjunto de ecuaciones:
$\left. \begin{array}{l} \vec{J_i}^2 \,|J_1\, J_2\,J\, M > \,=\,\hbar^2J_i(J_i+1) \,|J_1\, J_2\,J\, M > \,, i=1,2\\ \vec{J}^2 \,|J_1\, J_2\,J\, M > \, = \,\hbar^2J(J+1) \,|J_1\, J_2\,J\, M > \\ J_{z} \, | J_1\, J_2\,J\, M > \, = \, \hbar M \,|J_1\, J_2\,J\, M > \end{array} \right\}$ .
Es decir, un conjunto C.C.O.C. alternativo es uno que integre los operadores $\{ \vec{J_1}^2 , \vec{J_2}^2,\vec{J}^2,J_z \}$ , junto con, en su caso, otros observables que conmuten entre sí y con todos ellos (los que antes indicábamos con los parámetros $\alpha$ ), cuyos autovectores simultáneos, integrantes de una base ortonormal del Hilbert $\mathcal{H}^{(J_1;J_2)}$ , son los estados $| J_1\, J_2 \, J\, M \, (\alpha)>$ antes indicados.
El problema que se plantea, la suma de momentos angulares, consiste en, dados unos operadores de momento angular $\vec{J}_1$ y $\vec{J}_2$ , y dada su suma $\vec{J} \, = \, \vec{J_1} \, + \, \vec{J_2}$ , determinar :
1. Los valores posibles de los números cuánticos de momento angular total, $J$ , y de tercera componente de momento angular total $M$ , así como la posible degeneración involucrada.
2. Las relaciones entre los vectores que especifican cada representación, esto es, la expresión de los estados $| J_1\, J_2 \, J\, M >$ en términos de los $|J_1\, M_1\,J_2\, M_2 >$ , y viceversa.
-En definitiva, se trata de especificar la correspondiente transformación unitaria que proporciona la rotación de ejes deseada en el espacio $\mathcal{H}^{(J_1;J_2)}$ .
En el formalismo clásico, la solución al problema es que el momento angular total clásico toma cualquier valor entre $|J_1\,-\,J_2|$ y $(J_1 \,+\, J_2)$ , mientras que el valor de la tercera componente $M$ llena el intervalo continuo $[-J\,,\,J]$ . En el formalismo cuántico, las reglas de conmutación $[J_n\,,\,J_m]\,=\,i \hbar \,\epsilon_{nml} \ J_l$ características (definitorias) de todo operador de momento angular conllevan la discretización de los valores permitidos.

Coeficientes de Clebsch-Gordan

Sean las dos bases ortonormales en el subespacio de Hilbert $\mathcal{H}^{(J_1;J_2)}$ , para valores de $J_1$ y $J_2$ fijos:
$\{| J_1\, M_1 \, J_2\, M_2 > \equiv | J_1\, M_1 > \otimes | J_2\, M_2 >\}_{M_i=-J_i,-J_i+1,\ldots,J_i \; , \; i=1,2}$
y
$\{| J_1\, J_2 \, J\, M >_{J \,;\,M=-J,-J+1,\ldots,J}$ , para todos los $J$ posibles (por determinar).
Todo vector del subespacio admite expresión en términos de las dos bases, es decir,
$\forall |\psi> \in \mathcal{H}^{(J_1;J_2)}$ se tiene que:
$\begin{array}{c}|\psi> \,=\, \sum_{M_1,M_2}\, C^{(a)}(J_1\,M_1\,,\,J_2\,M_2)\, | J_1\, M_1 \, J_2\, M_2 > \\ =\, \sum_{J,M}\, C^{(b)}(J_1\,J_2\,,\,J\,M)\, | J_1\, J_2 \, J\, M > \end{array}$ .
-En particular, la transformación unitaria entre las dos bases admite expresión como:
$| J_1\, J_2 \, J\, M >\,=\, \sum_{M_1,M_2}\, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\, | J_1\, M_1 \, J_2\, M_2 >$ ,
expresión que define en una notación frecuente (no es la única en los textos) los coeficientes de acoplamiento angular denominados como «de Clebsch-Gordan«,
$C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J\, M >$ ,
coeficientes que conviene indicar nunca dependerán, en su caso, de los números cuánticos adicionales $\alpha$ que, por ello mismo, se vienen omitiendo en la notación.
Determinación de los valores posibles para los números cuánticos y :
1. Para cada $J$ determinado, se tiene que $M$ toma los valores $M\in {-J, -J+1,\ldots,J}$ .
2. Puesto que $J_z=J_{z1}+J_{z2}$ , se ha de cumplir:
  $J_z\,| J_1\, M_1 \, J_2\, M_2 > \,=\,(J_{z1}+J_{z2})\,| J_1\, M_1 \, J_2\, M_2 > \,=\,\hbar\,(M_1+M_2)\,| J_1\, M_1 \, J_2\, M_2 >$
  $\Rightarrow \, J_z\,| J_1\, J_2 \, J\, M >\,=\,\hbar \,M\,| J_1\, J_2 \, J\, M >$
  $=\,(\hbar \,M)\, \sum_{M_1,M_2}\, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,| J_1\, M_1 \, J_2\, M_2 >$ $=\,(J_{z1}+J_{z2})\, \sum_{M_1,M_2}\, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,| J_1\, M_1 \, J_2\, M_2 >$
  $=\,\sum_{M_1,M_2}\, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,\hbar \,(M_1+M_2)\,| J_1\, M_1 \, J_2\, M_2 >$
  $\Rightarrow \,\hbar \,M\,C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,\hbar\,(M_1+M_2) \, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)$
  $\Rightarrow ((M_1+M_2) \ne M \, \Rightarrow \, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,0)$ ,
  lo que permite simplificar la notación:
  $C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\, \equiv \,C(J_1\,J_2\,J\,|\,M_1\,M-M_1\,M)$
  $\equiv \,C(J_1\,J_2\,J\,|\,M_1\,M-M_1)$ .
3. A partir de los rangos de valores
  $J_i \ge 0$ , $M_i \in \{-J_i, -J_i+1,\ldots,J_i\}$ , $i=1,2$ , $M \in \{-J, -J+1,\ldots,J\}$ ,
  la condición $M=M_1+M_2$ conduce a que el valor máximo de $M$ sea $M_{max}=J_1+J_2$ , de manera que $J$ no podrá tomar valores superiores a $J_{max}=J_1+J_2$ .
  -Obsérvese que el hecho de que el valor mínimo de $M$ sea $M_{min}=-J_1-J_2$ no implica que el valor mínimo de $J$ sea $-J_1-J_2$ , ya que al ser ambos $J_i$ no-negativos, se implicaría $J_{min}< 0$ .
4. Dados los valores máximos de $J$ y $M$ , sólo un término contribuye al desarrollo:
  $| J_1\, J_2 \, J=J_1+J_2\, M=M_1+M_2>$
  $=\, C(J_1\,J_2\,J=J_1+J_2\,|\,M_1\,M_2\,M=M_1+M_2)\, | J_1\, M_1=J_1 \, J_2\, M_2=J_2 >$ ,
  de donde, dada la normalización del estado, se infiere
  $|C(J_1\,J_2\,J=J_1+J_2\,|\,M_1\,M_2\,M=M_1+M_2)|^2\,=\, 1\, \Rightarrow C=\exp{i\beta}\,,\,\beta \in \mathbb{R}$ .
5. Sea ahora el estado con valor máximo de $J$ y valor $M=M_{max}-1=J_1+J_2-1$ :
  $| J_1\, J_2 \, J=J_1+J_2\, M=M_1+M_2-1>$
  $=\, C(J_1\,J_2\,J=J_1+J_2\,|\,M_1=J_1\,M_2=J_2-1\,M=M_1+M_2-1)$
  $| J_1\, M_1=J_1 \, J_2\, M_2=J_2-1 >$
  $+\, C(J_1\,J_2\,J=J_1+J_2\,|\,M_1=J_1-1\,M_2=J_2\,M=M_1+M_2-1)$
  $| J_1\, M_1=J_1-1 \, J_2\, M_2=J_2 >$ ,
  existente siempre que ninguno de los dos momentos angulares que se suman sea nulo.
  -Esta ecuación es válida para dos valores de $J$ , que son $J=J_1+J_2$ y $J=J_1+J_2-1$ ( $J$ no puede ser menor ya que ha de ser mayor o igual que el número cuántico de tercera componente $M=M_1+M_2-1$ ).
  -Por tanto, hemos obtenido dos ecuaciones linealmente independientes.
6. Sea ahora el estado con valor máximo de $J$ y valor $M=M_{max}-2=J_1+J_2-2$ :
  $| J_1\, J_2 \, J=J_1+J_2\, M=M_1+M_2-2>$
  $=\, C(J_1\,J_2\,J=J_1+J_2\,|\,M_1=J_1\,M_2=J_2-2\,M=M_1+M_2-2)$
  $| J_1\, M_1=J_1 \, J_2\, M_2=J_2-2 >$
  $+\, C(J_1\,J_2\,J=J_1+J_2\,|\,M_1=J_1-2\,M_2=J_2\,M=M_1+M_2-2)$
  $| J_1\, M_1=J_1-2 \, J_2\, M_2=J_2 >$
  $+\, C(J_1\,J_2\,J=J_1+J_2\,|\,M_1=J_1-1\,M_2=J_2-1\,M=M_1+M_2-2)$
  $| J_1\, M_1=J_1-1 \, J_2\, M_2=J_2-1 >$ ,
  existente siempre que ninguno de los dos momentos angulares que se suman sea cero o la unidad.
  -Esta ecuación es válida para tres valores de $J$ , que son $J=J_1+J_2$ , $J=J_1+J_2-1$ y $J=J_1+J_2-2$ ( $J$ no puede ser menor ya que ha de ser mayor o igual que el número cuántico de tercera componente $M=M_1+M_2-2$ ).
  -en este caso, pues, hemos obtenido tres ecuaciones linealmente independientes
7. El proceso se continúa, obteniendo una serie de sistemas de una, dos, tres… ecuaciones para la secuencia de estados $| J_1\, J_2 \, J=J_1+J_2\, M>$ con $M=M_{max}, M_{max}-1, M_{max}-2,\ldots$ . La pregunta pendiente es: ¿cuál es el valor mínimo de $J$ ? (valor que ha de ser siempre no-negativo).
  -Obsérvese que, puesto que $M$ varía en unidades, en esta secuencia anterior $J$ también resulta obligado a descender en saltos de valor unidad. Si se continúa el procedimiento anterior, llegando al valor mínimo de $M$ , esto es, $M_{min}=-J_1-J_2$ , se configura que dicho valor mínimo de $J$ resultaría ser $|J_1-J_2|$ .
  -Este resultado se puede confirmar:
  $dim(\mathcal{H}^{(J_1,J_2)})\,=\,(2J_1+1)(2J_2+1)\,=\,\sum_{M_1=-J_1}^{J_1} \,\sum_{M_2=-J_2}^{J_2}\,1$
  $=\,\sum_{J=J_{min}}^{J=J_{max}=J_1+J_2} \,\sum_{M=-J}^{J}\,1\, =\,\sum_{J=J_{min}}^{J=J_{max}=J_1+J_2} \,(2J+1)$
  $=\,\sum_{J=J_{min}}^{J=J_{max}=J_1+J_2} \,1\,+\, 2\sum_{J=J_{min}}^{J=J_{max}=J_1+J_2} \,J$
  $=\,(J_{max}-J_{min}\,+1)\,+\,2\,\frac{J_{min}+J_1+J_2}{2}\,(J_1+J_2-J_{min}+1)$
  $\Rightarrow J_{min}^2=(J_1-J_2)^2 \Rightarrow J_{min}=\pm (J_1-J_2) \Rightarrow J_{min}=|J_1-J_2|$
  (ya que $J_{min} \ge 0$ ).
En resumen: Dados dos momentos angulares $\vec{J_1}$ y $\vec{J_2}$ , los únicos valores posibles para los números cuánticos del momento angular suma $\vec{J_1}+ \vec{J_2}$ y su tercera componente $J_z=J_{z1}+J_{z2}$ son:
$J=J_1+J_2\,,\,J_1+J_2-1\,,\ldots \,,|J_1-J_2|$ ;
dado $J$ , $M=J\,,\,J-1\,,\ldots \,,-J$ .
Determinación de los coeficientes: convenio de Condon-Shortley ampliado:
1. Según ha quedado establecido:
  $C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,0$ si $J \notin \{ |J_1-J_2|\,,\, |J_1-J_2|+1\,,\ldots \,, \, J_1+J_2 \}$
  $C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,0$ si $M \ne M_1+M_2$
  $|\,C(J_1\,J_2\,J=J_1+J_2 \,|\,M_1=J_1\,M_2=J_2\,M=J_1+J_2)\,| \,=\,1$
2. Para calcular los restantes coeficientes, se hacen actuar los operadores escalón, $J_{\pm}$ :
  $J_{\pm}= J_{\pm 1} + J_{\pm 2} = (J_{x1} + J_{x1})\,\pm\,i\, (J_{y1} +J_{y2})$ ,
  lo que se realiza, a efectos de determinar unívocamente los valores, estableciendo un convenio que fije las fases relativas entre estados, en particular el convenio de Condon-Shortley antes ya establecido, que conlleva que todos los elementos de las matrices correspondientes a los operadores escalón sean no-negativos.
  Por tanto, ampliando ahora este convenio, se establecen tres proposiciones:
  -Proposición 1 (P1): se fija la fase relativa entre los estados:
  $J_{\pm i} \, |J_i\, M_i>$ y $|J_i\, M_i \pm 1 >$ , $i=1,2$ ,
  $J_{\pm} \, |J\, M>$ y $|J\, M \pm 1 >$
  como nula (cf. [GAL-89]p.249; en los seis casos), lo que equivale a fijar todos los elementos de las matrices correspondientes a los seis operadores escalón ( $J_{\pm 1}$ , $J_{\pm 2}$ y $J_{\pm}$ ) como reales no-negativos:
  P1:
  P1.1: $\left\langle J_1\, M_1\, J_2\, M_2 | \, J_{\pm i} | \, J_1\, \, M_1' \, J_2\, \, M_2'\right\rangle \,=\, \delta_{M_i,M_i' \pm 1} \, \hbar \sqrt{J_i(J_i+1)-M_i M_i'} \, \ge \,0$ , $i=1,2$
  P1.2: $\left\langle J_1\, J_2\, J\, M | \, J_{\pm} | \, J_1\, \, J_2 \, J\, \, M'\right\rangle \,=\, \delta_{M,M' \pm 1} \, \hbar \sqrt{J(J+1)-M M'} \, \ge \,0$
  -Proposición 2 (P2): se toma la componente del estado $| J_1 \, J_2 \, J\, M=J>$ según el estado $| J_1\, M_1=J_1\, J_2\, M_2=J-J_1>$ como real no-negativa:
  P2: $\forall J\,:\,C(J_1\,J_2\,J|\,M_1=J_1\,M_2=J-J_1\,M=J)\, \ge \,0$
3. Aplicado el convenio, se implica que todos los coeficientes de Clebsh-Gordan resultan reales y, en particular, el valor $C(J_1\,J_2\,J=J_{max}=J_1+J_2|\,M_1=J_1\,M_2=J_2\,M=M_{max}=M_1+M_2)\,=1$ .
Determinación de los coeficientes: esbozo de un procedimiento (cf. [GAL-89], pp. 265ss.):
1. Se parte del estado
  $| J_1\, J_2 \, J\, M >\,=\,| J\, M >\,=\, \sum_{M_1,M_2}\, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\, | J_1\, M_1 \, J_2\, M_2 >$ ,
  y se aplican los operadores escalón:
  $J_{\pm} \,| J\, M >\,=\, \hbar [(J \mp M)\,(J \pm M + 1)]^{\frac{1}{2}}\,| J\, M \pm 1 >$ ;
  $=\, \hbar \, [(J \mp M)\,(J \pm M + 1)]^{\frac{1}{2}}\,\sum_{M_1,M_2} C(J_1\,J_2\,J|\,M_1\,M_2\,M \pm 1)\, | J_1\,M_1\,J_2\,M_2\,>$
  $=\, \hbar \,\sum_{M_1,M_2} C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\, \lbrace [(J_1 \mp M_1)(J_1 \pm M_1 + 1)]^{\frac{1}{2}}\,| J_1\, M_1 \pm 1\, J_2\, M_2 >$
  $+\, [(J_2 \mp M_2)(J_2 \pm M_2 + 1)]^{\frac{1}{2}}\,| J_1\, M_1\, J_2\, M_2 \pm 1 > \rbrace \,$ ;
  a continuación, se multiplica a la izquierda por el bra $<J_1 \bar{M_1} J_2 \bar{M_2}|$ , donde $\bar{M_i}$ representa un valor fijo de la correspondiente variable, obteniéndose:
  $[(J \mp M)\,(J \pm M + 1)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\, \bar{M_1}\,\bar{M_2}\,M \pm 1) \, \delta_{M_1, \bar{M_1}}\, \delta_{M_2, \bar{M_2}}$
  $=\,\delta_{M_1 \pm 1, \bar{M_1}}\, \delta_{M_2,\bar{M_2}} \,C(J_1\,J_2\,J\,|\,\bar{M_1} \mp 1\,\bar{M_2}\,M )\,[(J_1 \mp \bar{M_1} +1)(J_1 \pm \bar{M_1})]^{\frac{1}{2}}$ $+\,\delta_{M_1, \bar{M_1}}\, \delta_{M_2 \pm 1, \bar{M_2}} \,C(J_1\,J_2\,J\,|\,\bar{M_1} \,\bar{M_2} \mp 1\,M)\,[(J_2 \mp \bar{M_2} +1)(J_2 \pm \bar{M_2})]^{\frac{1}{2}}$ ,
  esto es:
  $[(J \mp M)\,(J \pm M + 1)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\, M_1\,M_2\,M \pm 1)$
  $=\, [(J_1 \mp M_1 +1)(J_1 \pm M_1)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\,M_1 \mp 1\,M_2\,M)$
  $+\, [(J_2 \mp M_2 +1)(J_2 \pm M_2)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\,M_1\,M_2 \mp 1\,M)$ .
  -Estas dos ecuaciones, junto con las condiciones de ortonormalización de los estados, constituyen la «llave maestra» para la obtención de los valores de los distintos coeficientes de Clebsch-Gordan.
2. Comenzamos imponiendo en la primera ecuación anterior, la correspondiente al operador escalón up, $J_+$ , el valor $M=J$ :
  $0\,=\, [(J_1 - M_1 +1)(J_1 + M_1)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\,M_1 - 1\,M_2\,J)$
  $+\, [(J_2 - M_2 +1)(J_2 + M_2)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\,M_1\,M_2 - 1\,J)$ ,
  donde es obvio que
  $C(J_1\,J_2\,J\,|\,M_1 - 1\,M_2\,J)\, \equiv C(J_1\,J_2\,J\,|\,M_1 - 1\,J-M_1+1\,J)$ y
  $C(J_1\,J_2\,J\,|\,M_1\,M_2 - 1\,J)\, \equiv C(J_1\,J_2\,J\,|\,M_1\,J-M_1\,J)$ ,
  ya que $M_1 + M_2 -1=J \, \Rightarrow \, M_2=J-M_1 + 1$ .
3. A continuación, partiendo del valor $M_{1max}=J_1$ , esta ecuación permite obtener todos los coeficientes $C(J_1\,J_2\,J\,|\,M_1\,J-M_1\,J)$ en términos del $C(J_1\,J_2\,J\,|\,J_1\,J-J_1\,J)$ :
  -Si $M_{1}=J_1$ :
  $\sqrt{2J_1}\,C(J_1\,J_2\,J\,|\,J_1 - 1\,J-J_1+1\,J)$
  $=\, -\sqrt{(J_2 - J +J_1)(J_2 + J - J_1+1)} \, C(J_1\,J_2\,J\,|\,J_1\,J-J_1\,J)$
  -Si $M_{1}=J_1-1$ :
  $\sqrt{2(2J_1-1)}\,C(J_1\,J_2\,J\,|\,J_1 - 2\,J-J_1+2\,J)$
  $=\, -\sqrt{(J_2 - J +J_1+1)(J_2 + J - J_1)} \, C(J_1\,J_2\,J\,|\,J_1-1\,J-J_1+1\,J)$
  $=\, -\sqrt{(J_2 - J +J_1+1)(J_2 + J - J_1)}\,\frac{-\sqrt{(J_2 - J +J_1)(J_2 + J - J_1+1)}}{\sqrt{2J_1}}$
  $C(J_1\,J_2\,J\,|\,J_1\,J-J_1\,J)$
4. Puesto que todos los coeficientes de Clebsch-Gordan involucrados en las anteriores ecuaciones son reales, fijado $C(J_1\,J_2\,J\,|\,J_1\,J-J_1\,J)\, \ge \,0$ , se garantiza el carácter también real de todos los coeficientes $C(J_1\,J_2\,J\,|\,M_1\,J-M_1\,J)$ . A partir de estos, usando la segunda ecuación de la «llave maestra», la correspondiente al operador escalón down $J_-$ :
  $[(J + M)\,(J - M + 1)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\, M_1\,M_2\,M - 1)$
  $=\, [(J_1 + M_1 +1)(J_1 - M_1)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\,M_1 + 1\,M_2\,M)$
  $+\, [(J_2 + M_2 +1)(J_2 - M_2)]^{\frac{1}{2}}\,C(J_1\,J_2\,J\,|\,M_1\,M_2 + 1\,M)$ ,
  ecuación que permite calcular los restantes coeficientes, que serán también todos reales, ya que todos los coeficientes en la ecuación lo son.
-Nota: en la referencia [GAL-89], p. 400, se encuentra la expresión de una fórmula general para el cálculo de los coeficientes de C.-G.; en cualquier caso, resulta mucho más práctico en su empleo obtenerlos a partir de las numerosas tablas de sus valores disponibles.
Propiedades: Los coeficientes de Clebsch-Gordan, que son las componentes de la transformación unitaria en el espacio de Hilbert , para valores de y fijos, entre las dos representaciones
,
y
, para todos los posibles,
definidos a partir de la ecuación

(expresión general de una transformación unitaria U, definida según entre sendas bases y , de elementos ),
poseen las siguientes propiedades (resumen):
1. Algunos valores particulares especiales:
  1.1. $C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,0$ si $J \notin \{ |J_1-J_2|\,,\, |J_1-J_2|+1\,,\ldots \,, \, J_1+J_2 \}$
  1.2. $C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,0$ si $M \ne M_1+M_2$
  1.3. $C(J_1\,J_2\,J\,|\,0\,0\,0)\,=\,0$ si $J_1+J_2+J_3$ es impar.
  1.4. $|\,C(J_1\,J_2\,J=J_1+J_2 \,|\,M_1=J_1\,M_2=J_2\,M=J_1+J_2)\,| \,=\,1$
  1.5. $\,C(J_1\,0\,J_3 \,|\,M_1\,0\,M_3)\, \,=\,\delta_{J_1,J_3}\,\delta_{M_1,M_3}$
  1.6. $\,C(J\,J\,0 \,|\,M\,-M\,0)\, \,=\,(-1)^(J-M)\, \frac{1}{\sqrt{2J+1}}$
2. Adoptado el convenio de Condon-Shortley, todos los coeficientes son reales:
  $C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\, < J_1\, M_1 \, J_2\, M_2 \, | \,| J_1\, J_2 \, J\, M >$
  $=\, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J\, M >^*\,=\,< J_1\, J_2 \, J\, M \, | \, J_1\, M_1 \, J_2 \, M_2 >$ $=\,C^*(J_1\,J_2\,J\,|\,M_1\,M_2\,M)$
3. Relaciones de unitariedad:
  3.1. $\sum_{J,M} < J_1\, M_1 \, J_2\, M_2 \, | \,| J_1\, J_2 \, J\, M > \, < J_1\, J_2 \, J\, M \, | \, J_1\, M_1 \, J_2 \, M_2 > \,= \,I$
  $\equiv \sum_{J,M} C^2(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,1$
  3.2. $\sum{M_1,M_2} < J_1\, J_2 \, J\, M \, | \,| J_1\, M_1 \, J_2\, M_2 > \, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J \, M > \,= \,I$
  $\equiv \sum_{M_1,M_2} C^2(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,1$
4. Relación inversa:
  $| J_1\, M_1 \, J_2\, M_2 >\,=\, \sum_{J,M}\, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\, | \,J_1\, J_2 \, J\, M >$
5. Relación de ortogonalidad: la matriz de transformación, por ser unitaria y real, es también ortogonal:
  $U_{ij}= < b_i | a_j > \, \equiv \, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J\, M > \,=\, C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)$
  $\; =\,C^*(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,=\,< J_1\, J_2 \, J\, M \, | \, J_1\, M_1 \, J_2 \, M_2 >$
  5.1. $\sum_i U_{ki}U_{ji}\,=\, \sum_{J,M} \, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J\, M > \, < J_1\, M_1' \, J_2\, M_2' \, | \, J_1\, J_2 \, J\, M >$
  $=\, \sum_{J,M} \, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J\, M > \, < J_1\, J_2 \, J\, M \, | \, J_1\, M_1' \, J_2\, M_2' >$
  $\; = \, \delta_{M_1,M_1'} \, \delta_{M_2,M_2'}$ ,
  esto es:
  $\sum_{J,M} \,C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,C(J_1\,J_2\,J\,|\,M_1'\,M_2'\,M)\,=\, \delta_{M_1,M_1'} \, \delta_{M_2,M_2'}$ .
  5.2. $\sum_i U_{ik}U_{ij} \,=\, \sum_{M_1,M_2} \, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J\, M > \, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J'\, M' >$
  $=\, \sum_{M_1,M_2} \, < J_1\, J_2 \, J\, M \, | \, J_1\, M_1 \, J_2\, M_2 > \, < J_1\, M_1 \, J_2\, M_2 \, | \, J_1\, J_2 \, J'\, M' >$
  $\; = \, \delta_{J,J'} \, \delta_{M,M'}$ ,
  esto es:
  $\sum_{M_1,M_2} \,C(J_1\,J_2\,J\,|\,M_1\,M_2\,M)\,C(J_1\,J_2\,J'\,|\,M_1\,M_2\,M')\,=\, \delta_{J,J'} \, \delta_{M,M'}$ .
  Notas:
  -una matriz $R$ es ortogonal $\Leftrightarrow \sum_i R_{ki}R_{ji}=\sum_i R_{ik}R_{ij}=\delta_{kj} \Leftrightarrow RR^T=R^TR=I \Leftrightarrow R^T=R^{-1}$
  (toda matriz real ortogonal es real unitaria, y viceversa).
  -U es unitaria $\Leftrightarrow U^{-1}=U^+ \;; \; U^{+}=(U^T)^* \, \rightarrow \, U \; real \, \Rightarrow U^T=U^{-1} \, \equiv \, U \; ortogonal$
  (utilizando en ambas deducciones la identidad de Parseval y el hecho de que todos los coeficientes de C.-G. son reales).
6. Propiedades de simetría:
  6.1. $C(J_1\,J_2\,J_3\,|\,M_1\,M_2\,M_3)\,=\, (-1)^(J_1+J_2-J_3) \, C(J_1\,J_2\,J_3\,|\,M_2\,M_1\,M_3)$
  6.2. $C(J_1\,J_2\,J_3\,|\,M_1\,M_2\,M_3)\,=\, (-1)^(J_1+J_2-J_3) \, C(J_1\,J_2\,J_3\,|\,-M_1\,-M_2\,-M_3)$
  6.3 $C(J_1\,J_2\,J_3\,|\,M_1\,M_2\,M_3)\,=\, (-1)^(J_1-M_1) \, \sqrt{\frac{2J_3+1}{2J_2+1}} \, C(J_1\,J_3\,J_2\,|\,M_1\,-M_3\,-M_2)$
  6.4. $C(J_1\,J_2\,J_3\,|\,M_1\,M_2\,M_3)\,=\, (-1)^(J_2+M_2) \, \sqrt{\frac{2J_3+1}{2J_1+1}} \, C(J_3\,J_2\,J_1\,|\,-M_3\,M_2\,-M_1)$
  6.5. $C(J_1\,J_2\,J_3\,|\,M_1\,M_2\,M_3)\,=\, (-1)^(J_1-M_1) \, \sqrt{\frac{2J_3+1}{2J_2+1}} \, C(J_3\,J_1\,J_2\,|\,M_3\,-M_1\,M_2)$
  6.6. $C(J_1\,J_2\,J_3\,|\,M_1\,M_2\,M_3)\,=\, (-1)^(J_2+M_2) \, \sqrt{\frac{2J_3+1}{2J_1+1}} \, C(J_2\,J_3\,J_1\,|\,-M_2\,M_3\,-M_1)$
  (donde las tres últimas expresiones se derivan de las tres primeras).
Tablas de coeficientes de Clebsch-Gordan: pueden encontrarse numerosas tablas en internet, por ejemplo, en las páginas:
–Wikipedia: Anexo
–https://www.uco.es/hbarra/index.php/utilidades/83-cg: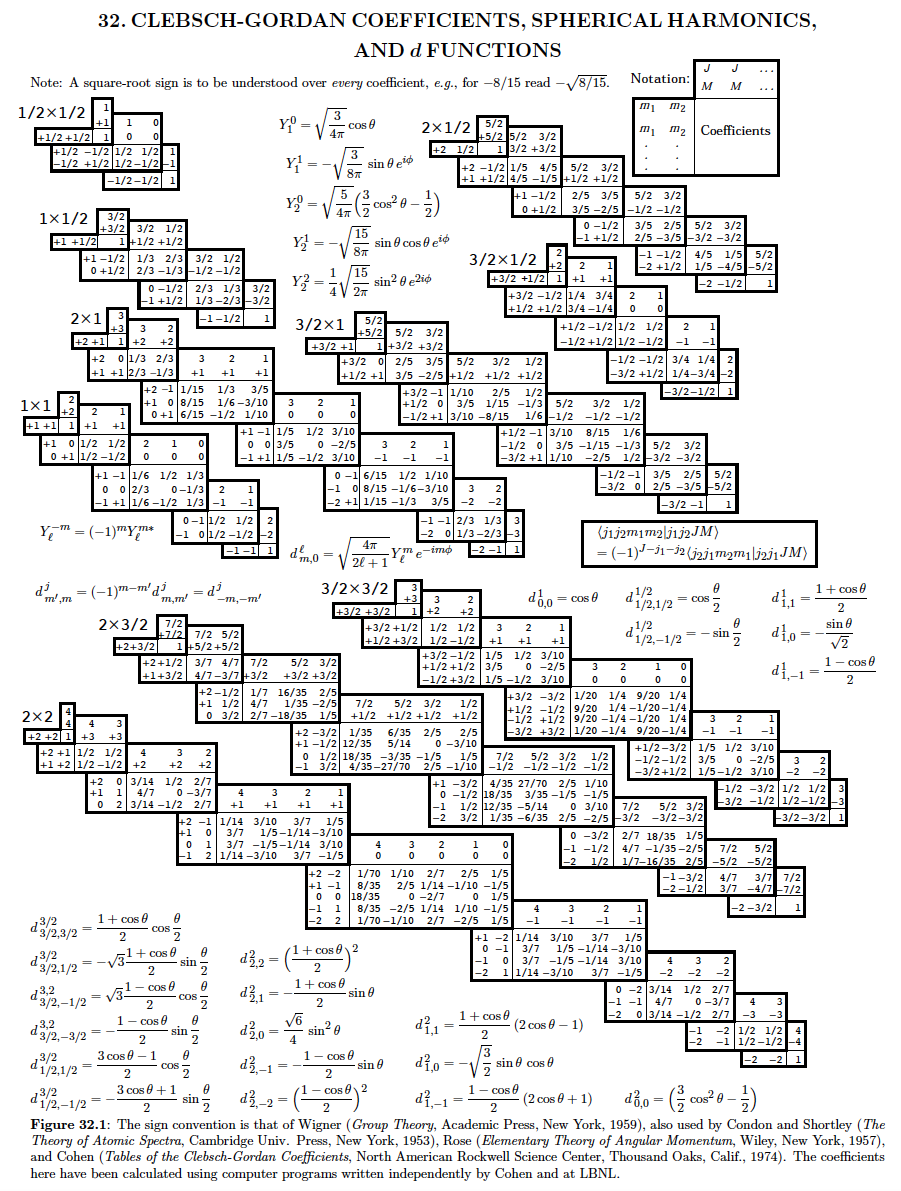

Tabla de coeficientes de Clebsch-Gordan (fuente: ver pie figura, procedente de https://www.uco.es/hbarra/index.php/utilidades/83-cg).

Momento angular total

Considérese una partícula con espín $\vec{S}$ y momento angular orbital $\vec{L}$ . La suma de ambos, esto es, $\vec{J}=\vec{L}+\vec{S}$ , define un operador que, puesto que los sumandos, operadores $\vec{L} , \vec{S}$ , actúan en sendos espacios independientes, conmutan entre sí, luego el operador suma, denominado como momento angular total de la partícula y que actúa en el espacio $\mathcal{H}^{(J)}=\mathcal{H}^{(L;S)}$ , queda definido como un operador de momento angular, ya que sus componentes satisfacen las relaciones de conmutación definitorias:
$\vec{J} \equiv (J_1,J_2,J_3) \;;\; [J_i\,,\,J_j]=i\hbar \, \epsilon_{ijk}\,J_k\,;\, i,j,k=1,2,3$
Dado un sistema de $N$ partículas, el operador momento angular total del sistema se define como la suma para todas las partículas de los operadores momentos angulares totales individuales:
$\vec{J}=\sum_{i=1}^N \,\vec{J_i}=\sum_{i=1}^N \,\vec{L_i}\,+\, \sum_{i=1}^N \,\vec{S_i} \,=\, \vec{L}\,+\, \vec{S}\quad, \; i=1,\ldots,N$ ,
donde aparecen y quedan definidos los operadores momento angular orbital total $\vec{L}$ y momento angular de espín o espín total $\vec{S}$ del sistema , satisfaciéndose las relaciones de conmutación en su actuación sobre $\mathcal{H}^{(J))} \equiv \mathcal{H}^{(L;S)}$ :
$[\vec{L_i},\vec{L_j}]=\delta_{i,j}\,,\; i,j=1,\ldots,N$
$[\vec{S_i},\vec{S_j}]=\delta_{i,j}\,,\; i,j=1,\ldots,N$
$[\vec{J_i},\vec{J_j}]=\delta_{i,j}\,,\; i,j=1,\ldots,N$
$\vec{J} \equiv (J_1,J_2,J_3) \;;\; [J_i\,,\,J_j]=i\hbar \, \epsilon_{ijk}\,J_k\,;\, i,j,k=1,2,3$
$\vec{L} \equiv (L_1,L_2,L_3) \;;\; [L_i\,,\,L_j]=i\hbar \, \epsilon_{ijk}\,L_k\,;\, i,j,k=1,2,3$
$\vec{S} \equiv (S_1,S_2,S_3) \;;\; [S_i\,,\,S_j]=i\hbar \, \epsilon_{ijk}\,S_k\,;\, i,j,k=1,2,3$
-Nota: ¡es muy importante no confundir en las fórmulas índices de partícula con índices de componentes!
El espacio de Hilbert $\mathcal{H}^{(J)}$ tiene dimensión $2J+1$ , y es usual considerar en él la base de componentes
$\{ |J M_J> \}_{M_J=J,J-1,\ldots,-J}$ ,
de forma que cualquier estado del Hilbert admite desarrollo
$|\Psi> \, = \, \sum_{M_J=J}^{-J}\, a_{M_J} \, |\, J M_J >$ .
-Obsérvese que la dimensión del espacio $\mathcal{H}^{(J)}$ es $2J+1$ , de forma que, cuando $\mathcal{H}^{(J)} \equiv \mathcal{H}^{(L;S)}$ , de modo que $\vec{J}=\vec{L}+\vec{S}$ , la dimensión es $2J+1=(2L+1)(2S+1)$ . Por ejemplo, si $L=0$ y $S=\frac{1}{2}$ , entonces la dimensión es 2; si $L=1$ y $S=\frac{1}{2}$ , entonces la dimensión es 6, etc.

Adición de los momentos angular orbital y de espín monoparticulares

Considérese una partícula con espín $\vec{s}$ y momento angular orbital $\vec{l}$ , siendo su momento angular total la suma $\vec{j}=\vec{l}+\vec{s}$ de ambos.
En el espacio de Hilbert $\mathcal{H}^{(l)}$ las autofunciones simultáneas de los operadores $\vec{l}^2$ y $l_z$ son (en representación de coordenadas y coordenadas esféricas) los armónicos esféricos $Y_{lm_l}(\Omega)$ , siendo $l$ el número cuántico de momento angular orbital. El conjunto integrado por todos ellos, para todos los correspondientes valores del número cuántico de tercera componente $m_l=l,l-1,\ldots,-l$ , constituye una base ortonormal en el espacio para cada $l$ determinado; análogamente, en el espacio de espín $\mathcal{H}^{(s)}$ las autofunciones simultáneas de los operadores $\vec{s}^2$ y $s_z$ son las funciones de espín $\chi_{s,m_s}\,,\,m_s=s,s-1,\ldots,-s$ , base en $\mathcal{H}^{(s)}$ .
Las autofunciones simultáneas de los cuatro operadores $\vec{l}^2,l_z,\vec{s}^2,s_z$ , funciones del espacio $\mathcal{H}^{(j)}=\mathcal{H}^{(l;s)}$ , se podrán expresar como producto directo de las funciones orbitales y de espín, ya que los correspondientes pares de operadores actúan separadamente sobre los sendos espacios orbital y de espín (caso particular):
$\{| l\, m_l \, s\, m_s > \equiv | l\, m_l > \otimes | s\, m_s >\}_{m_l=-l,-l+1,\ldots,l\;,\,m_s=-s,-s+1,\ldots,s}$ ,
siendo también frecuentes las notaciones equivalentes en representación de posiciones:
$| l\, m_l \, s\, m_s > \, \equiv \,| l\, m_l > \otimes | s\, m_s >$
$\rightarrow \, \, < \hat{r} \,| \, l\, m_l> | \, s\, m_s > \equiv \, \psi_{l m_l s m_s} \, \doteq \, Y_{l m_l} \cdot \chi_{s m_s}$ ,
$Y_{lm}(\theta, \varphi) \, =\, < \hat{r} (\theta , \varphi) \, | \, lm>$
$=\, \int Y_{lm}(\theta ', \varphi ') \,\delta(\vec{r}-\vec{r}' )\, d \vec{r}' \,= \, \int Y_{lm}(\theta', \varphi ') \,\delta(\Omega-\Omega ' )\, d \Omega'$ ,
denominándose su conjunto completo como la base no acoplada.
-El espinor correspondiente sería en este caso:
$\Psi_{l s m_l m_s}(\hat{r},\sigma,t)$
$\doteq \,\sum_{m_s'=-s}^{s} \, \psi_{m_s'}(\hat{r},t)\, \chi_{s,m_s'}\, \delta_{m_s',m_s}$
$\doteq \, \psi_{m_s}(\hat{r},t)\, \chi_{s,m_s}\, = Y_{l m_l} \cdot \chi_{s m_s}$
$\doteq \, \begin{pmatrix} 0 \\ \cdots \\ 0 \\ \psi_{m_s=s}(\hat{r},t)\equiv \, < \,\hat{r}, \,l \ m_l \ ; \ \sigma=\hbar m_s \, | \,\Psi(t) > \,= Y_{l m_l}(\Omega (t)) \\ 0 \\ \cdots \\ 0 \end{pmatrix}$
Los números cuánticos de momento angular total $\vec{j} = \vec{l} + \vec{s}$ , $j$ y $m_j$ toman los valores:
$\left. \begin{array}{l} j=s \quad si \quad l=0 \\ j=l \quad si \quad s=0 \\ j=l+s, l+s-1,\ldots,|l-s| \quad si \; ambos \quad l,s>0 \\ dado \quad j\;, \quad m_j=j,j-1\ldots,-j \end{array} \right\}$
Una base alternativa es la denominada como base acoplada, integrada por autofunciones simultáneas de los cuatro operadores $\vec{l}^2,\vec{s}^2,\vec{j}^2, j_z$ :
$\{ | l\, s \, j\, m_j > \}_{j \,;\,m_j=-j,-j+1,\ldots,j}$ , para cada valor posible de $j$ fijados el par $l,s$ ,
usándose también las notaciones alternativas en representación de posiciones:
$| l\, s \, j\, m_j > \, \rightarrow \, <\hat{r} \, | \,l\, s \, j\, m_j > \, \equiv \, \psi_{l s j m_j} \, \doteq \, \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi;\sigma)$
-En la base acoplada no todos los operadores del C.C.O.C. actúan separadamente sobre los espacios orbital y de espín, de modo que el espinor no factorizará como antes. Esta base se suele utilizar cuando, a causa de una interacción física entre dos momentos angulares, estos ya no son constantes del movimiento independientes, de modo que sus valores individuales ya no siguen leyes de conservación, pero su suma, el momento angular total, sí se conserva.
-Las funciones $\mathcal{Y}_{l s}^{j m_j}$ se denominan armónicos esféricos vectoriales.
Las ecuaciones del cambio de base vienen dadas por los adecuados coeficientes de Clebsch-Gordan:
$| l\, s \, j\, m_j >\,=\, \sum_{m_l,m_s}\, C(l\,s\,j\,|\,m_l\,m_s\,m_j)\, | l\, m_l \, s\, m_s >$ ,
$| l\, m_l \, s\, m_s >\,=\, \sum_{j,m_j}\, C(l\,s\,j\,|\,m_l\,m_s\,m_j)\, | \,l\, s \, j\, m_j >$ ;
teniéndose pues
$| l\, s \, j\, m_j > \, \rightarrow \, \psi_{l s j m_j} \, \doteq \, \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi;\sigma )$
$=\, \sum_{m_l,m_s}\, C(l\,s\,j\,|\,m_l\,m_s\,m_j)\, Y_{l m_l} \cdot \chi_{s m_s}$
Expresión del espinor:
$\Psi_{l s j m_j}(\hat{r},\sigma,t) \, \doteq \, \mathcal{Y}_{l s}^{j m_j}(\theta,\varphi;\sigma) \, \doteq \,\sum_{m_s=-s}^{s} \, [ \ \sum_{m_l=-l}^{l} \, C(l\,s\,j\,|\,m_l\,m_s\,m_j)\, Y_{l m_l}(\Omega) \ ] \ \chi_{s,m_s}$ ,
una matriz de $2s+1$ elementos:
$\Psi_{l s j m_j}(\hat{r},\sigma,t) \doteq \, \begin{pmatrix} \sum_{m_l=-l}^{l} \, C(l\,s\,j\,|\,m_l=m_j - s\,m_s=s\,m_j)\, Y_{l m_l=m_j-s}(\Omega (t)) \\ \sum_{m_l=-l}^{l} \, C(l\,s\,j\,|\,m_l=m_j - s+1\,m_s=s-1\,m_j)\, Y_{l m_l=m_j-s+1}(\Omega (t))\\ \cdots \\ \sum_{m_l=-l}^{l} \, C(l\,s\,j\,|\,m_l=m_j + s\,m_s=-s \,m_j)\, Y_{l m_l=m_j+s}(\Omega (t))\end{pmatrix}$

Ejemplo: el caso de espín $\frac{1}{2}$

En el caso de una partícula de espín , sustituyendo los valores de los coeficientes de C.-G., las anteriores expresiones se convierten en:
,
,
de modo que a partir de la tabla de coeficientes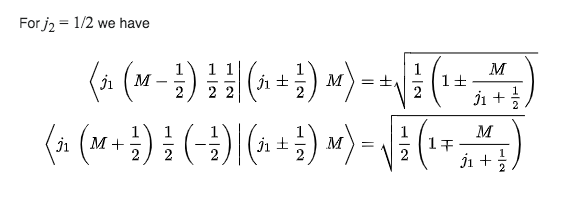

Coeficientes de Clebsch-Gordon para $j_2=1/2$ (fuente: Wikipedia).

se obtiene:
1. Caso $l=0$ :
  1.A: $Y_{00} \cdot \chi_{\frac{1}{2} m_s}=\mathcal{Y}_{0 \ \frac{1}{2}}^{\frac{1}{2} \ \frac{1}{2}} \ \delta_{m_s,\frac{1}{2}} \, + \, \mathcal{Y}_{0 \ \frac{1}{2}}^{\frac{1}{2} \ -\frac{1}{2}} \ \delta_{m_s,-\frac{1}{2}}$
  1.B: $\mathcal{Y}_{0 \ \frac{1}{2}}^{\frac{1}{2} \ m_j} \, =\,Y_{00} \ \chi_{ \frac{1}{2} \ m_s } \ \delta_{m_s, +\frac{1}{2} } \,+ \,Y_{00} \ \chi_{ \frac{1}{2} \ m_s }\ \delta_{m_s, -\frac{1}{2} }$
2. Caso $l \ne 0$ :
  2.A: $Y_{l \ m_l} \cdot \chi_{\frac{1}{2} m_s} \,=\, \sum_{j=l \pm \frac{1}{2}, m_j=m_l+m_s}\,C(l\,\frac{1}{2}\,l \pm \frac{1}{2}\,|\,m_l\,m_s\,m_j) \mathcal{Y}_{l \ \frac{1}{2}}^{l \pm \frac{1}{2} \ m_j}$
  $=\,C(l\,\frac{1}{2}\,l + \frac{1}{2}\,|\,m_l\,m_s\,m_j) \mathcal{Y}_{l \ \frac{1}{2}}^{l + \frac{1}{2} \ m_j}\,\delta_{m_j,m_l+m_s} +\,C(l\,\frac{1}{2}\,l - \frac{1}{2}\,|\,m_l\,m_s\,m_j) \mathcal{Y}_{l \ \frac{1}{2}}^{l - \frac{1}{2} \ m_j}\,\delta_{m_j,m_l+m_s}$ $=\, [ \, \sqrt{ \frac{l+m_j+\frac{1}{2}}{2l+1}} \, \mathcal{Y}_{l \ \frac{1}{2}}^{l + \frac{1}{2} \ m_l + \frac{1}{2}} \, + \, \sqrt{ \frac{l-m_j+\frac{1}{2}}{2l+1}} \, \mathcal{Y}_{l \ \frac{1}{2}}^{l - \frac{1}{2} \ m_l + \frac{1}{2}} \,] \delta_{m_s, +\frac{1}{2}}$
  $+\,[ \, \sqrt{ \frac{l-m_j+\frac{1}{2}}{2l+1}} \, \mathcal{Y}_{l \ \frac{1}{2}}^{l + \frac{1}{2} \ m_l - \frac{1}{2}} \, +\, \sqrt{ \frac{l+m_j+\frac{1}{2}}{2l+1}} \, \mathcal{Y}_{l \ \frac{1}{2}}^{l - \frac{1}{2} \ m_l - \frac{1}{2}} \,] \delta_{m_s, -\frac{1}{2}}$
  2.B: $\mathcal{Y}_{l \ \frac{1}{2}}^{j \ m_j} \, =\,\sum_{m_l, m_s= \pm \frac{1}{2}} \, C(l\,\frac{1}{2}\,j\,|\,m_l\,m_s\,m_j)\, Y_{l \ m_l} \cdot \chi_{\frac{1}{2} \ m_s}$
  $=\,C(l\,\frac{1}{2}\,j\,|\,m_j - \frac{1}{2} \,\frac{1}{2} \, m_j)\,Y_{l \ m_j-\frac{1}{2}} \cdot \chi_{\frac{1}{2} \ \frac{1}{2}}$
  $+ \, C(l\,\frac{1}{2}\,j\,|\,m_j + \frac{1}{2} \,-\frac{1}{2} \, m_j)\,Y_{l \ m_j+\frac{1}{2}} \cdot \chi_{\frac{1}{2} \ -\frac{1}{2}}$
  $\Rightarrow \,\mathcal{Y}_{l \ \frac{1}{2}}^{l \pm \frac{1}{2} \ m_j} \, =\,\sqrt{ \frac{l \pm m_j+\frac{1}{2}}{2l+1}} \,Y_{l \ m_j-\frac{1}{2}} \cdot \chi_{\frac{1}{2} \ \frac{1}{2}} \, + \,\sqrt{ \frac{l \mp m_j+\frac{1}{2}}{2l+1}} \,Y_{l \ m_j+\frac{1}{2}} \cdot \chi_{\frac{1}{2} \ -\frac{1}{2}}$ ,
  esto es, el espinor:
  $\mathcal{Y}_{l \ \frac{1}{2}}^{l \pm \frac{1}{2} \ m_j}\,\doteq \, \begin{pmatrix} \pm \sqrt{ \frac{l \pm m_j+\frac{1}{2}}{2l+1}} \,Y_{l \ m_j-\frac{1}{2}} \\ \sqrt{\frac{l \mp m_j+\frac{1}{2}}{2l+1}} \,Y_{l \ m_j+\frac{1}{2}} \end{pmatrix}$

Adición de dos espines $\frac{1}{2}$

Sean dos partículas de espín $\frac{1}{2}$ ; el espín total $\vec{S}=\vec{s}_1 + \vec{s}_2$ del sistema compuesto nos va a permitir usar la base acoplada en el espacio de espín suma $\mathcal{H}^{(s_1;s_2)}$ , de dimensión 4.
Todo vector del subespacio admite expresión en términos de las dos bases antes consideradas, es decir,
$\forall \chi \in \mathcal{H}^{(s_1;s_2)}$ se tiene que:
$\begin{array}{c} | \chi > \,=\, \sum_{m_1,m_2}\, C^{(a)}(s_1\,m_1\,,\,s_2\,m_2)\, | s_1\, m_1 \, s_2\, m_2 > \\ =\, \sum_{S,M}\, C^{(b)}(s_1\,s_2\,,\,S\,M)\, | s_1\, s_2 \, S\, M > \end{array}$ .
-En particular, la transformación unitaria entre las dos bases admite expresión como:
$| s_1\, s_2 \, S\, M >\,=\, \sum_{m_1,m_2}\, C(s_1\,s_2\,S\,|\,m_1\,m_2\,M)\, | s_1\, m_1 \, s_2\, m_2 >$ .
Incorporando la notación usual para el caso de espín $\frac{1}{2}$ :
-Base no acoplada (representación $\vec{s}_1^2, \vec{s}_{z1} , \vec{s}_2^2, \vec{s}_{z2}$ ):
$\{ \alpha(1) \ \alpha(2) \; , \; \alpha(1) \ \beta(2) \; , \; \beta(1) \ \alpha(2) \; , \; \beta(1) \ \beta(2) \}$
-Base acoplada: (representación $\vec{s}_1^2,\vec{s}_2^2,\vec{S}^2, \vec{S}_{z}$ ); funciones $\chi_{SM} \in \mathcal{H}^{(s_1;s_2)}$ ; valores $S=1,0$ :
$\{ \chi_{00} \; , \; \chi_{1+1} \; , \; \chi_{10} \; , \;\chi_{1-1} \}$
-Transformación unitaria:
$\chi_{SM}(1,2) \, = \, \sum_{m_1 m_2} C(\frac{1}{2} \frac{1}{2} S | m_1 m_2 M=m_1+m_2) \chi_{\frac{1}{2}m_1}^{(1)}(1) \ \chi_{\frac{1}{2} m_2}^{(2)}(2)$ ,
obteniéndose las expresiones:
$\chi_{00}(1,2) \, = \, \frac{1}{\sqrt{2}} \ [\alpha(1) \ \beta(2) \; - \; \beta(1) \ \alpha(2)]$
$\chi_{1+1} (1,2)\, = \,\alpha(1) \ \alpha(2)$
$\chi_{10} (1,2)\, = \, \frac{1}{\sqrt{2}} \ [\alpha(1) \ \beta(2) \; + \; \beta(1) \ \alpha(2)]$
$\chi_{1-1} (1,2)\, = \,\beta(1) \ \beta(2)$ .
La función $\chi_{00}$ , antisimétrica bajo el intercambio de las dos partículas, se denomina singlete de espín, mientras que las tres funciones con $S=1$ , simétricas, integran el denominado triplete de espín.