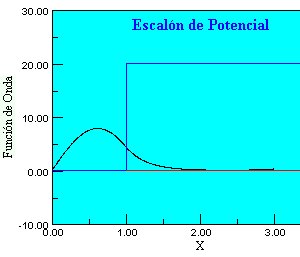
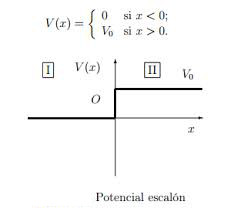
El potencial escalón
- Función potencial
:
donde se ha elegido el potencial de forma que el punto de retroceso clásico para una partícula (cuando) se sitúe en el origen.
Se trata pues de una función continua a trozos, con una discontinuidad de primera especie en el origen. - Problema de autovalores de energía:
,
y buscamos solucionesque sean funciones ella y su derivada primera
continuas
(siempre que
sea finito
).
- Dependiendo de la región espacial considerada, la forma concreta de la EDO planteada es:
Zona I:
Zona II: - La solución general de una EDO
,
donde,
, tiene la expresión:
-Signo (-) :
conescalares arbitrarios.
-Signo (+) :
conescalares arbitrarios.
- Se presentan pues los casos:
:
- Zona I:
:
con
yescalares arbitrarios.
- Zona II:
:
con
yescalares arbitrarios.
- Imponiendo las condiciones:
-Acotación
-Acotación
-Continuidad deen
:
-Continuidad deen
:
Puesto que este conjunto de condiciones es imposible de satisfacer, la conclusión es que no existen efectivamente soluciones físicamente aceptables del problema de autovalores de energía para valores del parámetro de separación.
- Zona I:
:
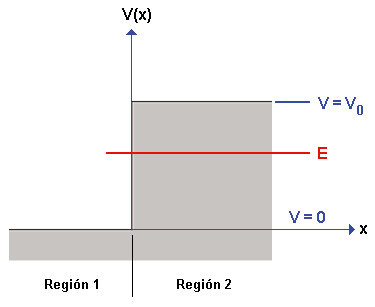
Imagen del blog la-mecanica-cuantica-blogspot.com. - Zona I:
:
; con
yescalares arbitrarios.
- Zona II:
:
; con
yescalares arbitrarios.
- Imponiendo las condiciones:
-Acotación
-Continuidad deen
:
-Continuidad deen
:
- Resolviendo:
con la constantea fijar a partir de la preceptiva normalización.
-Equivalentemente, la solución puede expresarse en términos de la constante(a determinar por normalización):
- La autofunción anterior puede expresarse:
, con
La forma general de este tipo de autofunciones de energía se representa en la siguiente figura: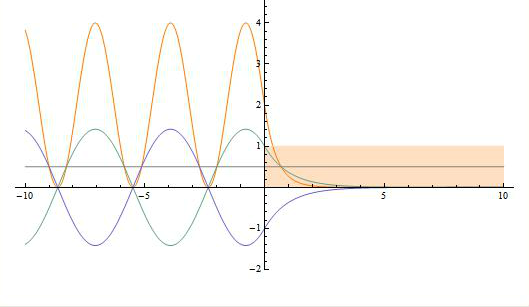
Stationary wave function of an incident free particle over a potential step. Shown are the absolute square (orange), the real part (green), the imaginary part (dark blue) of the wave function, and the energy (gray) of the incident particle. The height of the potential energy step () is shown in light orange. Imagen y texto: http://demonstrations.wolfram.com/ScatteringOverPotentialStep/ (Wolfram Demostrations Project). - La densidad de probabilidad (por unidad de volumen) viene dada:
-La representación general adopta pues la forma:
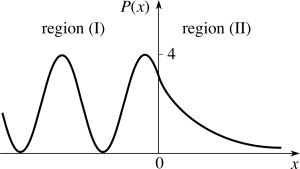
-En la región I () presenta un carácter oscilatorio, consecuencia de la interferencia entre dos ondas que producen una onda estacionaria.
-Proporciona una probabilidad no nula de encontrar a la partícula a la derecha del origen (en general, del punto donde se produzca el salto del potencial). Este hecho no se produce en Física Clásica, donde la regiónresulta estrictamente prohibida o inaccesible a la partícula con
, pues tendría en ella una energía cinética negativa. En cambio, en Física Cuántica hay probabilidad no nula de penetrar el salto o barrera en
(¡sin que ello signifique asumir que el resultado de la medida de la energía cinética pueda ser un número negativo!: recordemos que el espectro del operador energía cinética
se sitúa sobre la semirrecta real positiva).
-El parámetrose define como la profundidad de penetración en el escalón, y caracteriza este efecto; se satisface
.
-Y es que, para detectar experimentalmente, esto es, observar a la partícula en la región, habría que localizarla dentro de una distancia del orden de
, a fin de que
sea apreciable. Pero entonces, el momento debe presentar una indeterminación
, que conlleva a su vez una indeterminación en la energía
, de manera que ya no tendrá sentido afirmar que el resultado de una medida de la energía total de la partícula puede ser menor que
.
-En definitiva, la penetración de la función de onda en la región II, clásicamente prohibida, es una manifestación más de la naturaleza cuántica del fenómeno. - Recordemos la definición del vector densidad de corriente de probabilidad:
.
- En la región I,
, la solución representa una superposición de dos ondas planas viajeras,
,
asociadas interpretativamente a movimientos con sendos sentidos positivo y negativo a lo largo del eje; el correspondiente vector densidad de corriente de probabilidad total es nulo, en coherencia con el hecho de que la transmisión es nula:
, donde
.
-En la región II,, es trivial obtener también
.
-Suele enunciarse una interpretación (o relato verbal asociado a una visualización con localización en el espacio-tiempo: una imagen mental confortable para la mente humana) en la que en esta regiónse considera el sumando
como una onda viajera incidente desde la izquierda (
) hacia el salto del potencial en
, mientras que el sumando
se asocia con una onda viajera reflejada, de amplitudes respectivas
y
; la solución del problema de autovalores de la energía
obtenida no es sino una combinación lineal o superposición de ambas. La función en la zona II, por su parte, correspondería a lo que se suele denominar una onda evanescente.
- Coeficientes de reflexión
y transmisión
:
-Se define el coeficiente de reflexióncomo el cociente entre los módulos de los vectores densidad de corriente reflejada (la correspondiente a la onda plana «reflejada», zona I, sumando
) e «incidente» (la correspondiente a la onda plana incidente, zona I, sumando
) :
-Se define el coeficiente de transmisióncomo el cociente entre los módulos de los vectores densidad de corriente transmitida (la correspondiente a la onda en la zona II,
) e incidente:
(ambos independientes de la normalización aplicada).
-Se relacionan según:.
- En el caso presente,
, los coeficientes valen:
: se produce reflexión total, y las predicciones clásica y cuántica coinciden en cuanto al coeficiente de reflexión: toda partícula con energía
será reflejada con probabilidad 1, o sea, certeza.
- Respecto al coeficiente de transmisión
, en el caso presente
, luego
: ausencia total de transmisión, en coherencia con una reflexión total cuando
.
- Resolución e interpretación en términos de paquetes de onda: Para tiempos en que la partícula está lejos de la zona en que se produce el salto de potencial, se considera un paquete de ondas incidente desde la izquierda (
), que generará en el futuro el paquete de ondas reflejado y la onda evanescente, produciéndose una superposición o interferencia entre funciones. Las siguientes simulaciones ilustran esta situación:
–http://www.uco.es/hbarra/index.php/fc/appletsfc/65-schrodinger-escalon
-Vídeos en YouTube:
a) https://youtu.be/r8kvB1UBSX0 (por «nicolò gregori»):b) https://youtu.be/9P00eol9eko (S. Brandt and H.D. Dahmen, The Picture Book of Quantum Mechanics, Springer 2012):
c)https://youtu.be/9P00eol9eko (S. Brandt and H.D. Dahmen, The Picture Book of Quantum Mechanics, Springer 2012):
-Nota filosófica: ¿Qué es el tiempo? Nadie lo sabe. ¿Es suprimible en física, reducible a un mero constructo intelectual del ser humano, esclavo de sus percepciones empíricas macroscópicas, tan limitadas? Algunos lo postulan. ¿Y qué pasa con la flecha termodinámica?…
-El tiempo en cuántica: NO es un observable (¡no se define un operador autoadjunto «tiempo»!), es un simple parámetro. - En resumen: hemos encontrado una sola solución físicamente aceptable
en el rango
, de forma que todos estos puntos
reales pertenecen a la parte continua del espectro
y no presentan degeneración (en este rango de energías el problema de autovalores sólo tiene solución físicamente aceptable para incidencia desde la izquierda).
- Límite
: Si colocamos un escalón de altura infinita, habremos de imponer la condición de contorno
,
y en efecto se tiene, de forma que la función de onda se anula en toda la región II.
-En este caso la autofunción que se obtiene es:
cuya correspondiente primera derivadapresenta en el origen una discontinuidad de primera especie, con salto:
- Zona I:
:
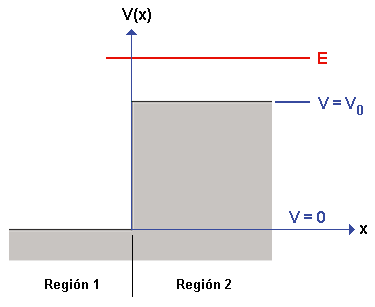
Imagen del blog la-mecanica-cuantica-blogspot.com. - Zona I:
:
; con
yescalares arbitrarios.
- Zona II:
:
; con
yescalares arbitrarios.
-Es decir, en este caso la forma de las soluciones es oscilatoria en las dos regiones. - Imponiendo las condiciones de frontera:
-Continuidad deen
:
-Continuidad deen
:
- Al par de ecuaciones anteriores se añade la condición de normalización, de forma que de las cuatro constantes que aparecen, sólo una permanece arbitraria: hay infinitas soluciones presentes (¡máximo dos linealmente independientes!). Este hecho se corresponde con que en efecto pueden considerarse infinitas situaciones, entre ellas vamos a seleccionar las que son compatibles con un relato «pseudoclásico» según el cual:
a) Una partícula se acerca al escalón procedente de la izquierda, esto es, viaja desde.
b) Una partícula se acerca al escalón procedente de la derecha, esto es, viaja desde.
c) Cualquier combinación lineal de las dos situaciones anteriores.
-Todos estos puntosreales pertenecen a la parte continua del espectro
y presentan degeneración doble (la máxima degeneración posible: sólo pueden existir dos soluciones particulares linealmente independientes, puesto que la ecuación diferencial es de segundo orden).
- Estudiemos las dos situaciones a) y b) anteriores:
- Incidencia desde la izquierda (
):
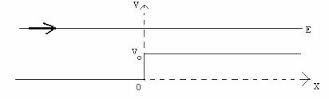
- Para una partícula que incide desde
, debe tenerse
, esto es,
por lo que las ecuaciones resultantes de imponer las condiciones de contorno se convierten en:
-Continuidad deen
:
-Continuidad deen
:
-Las correspondientes autofunción y densidad de probabilidad se ilustran en las siguientes figuras: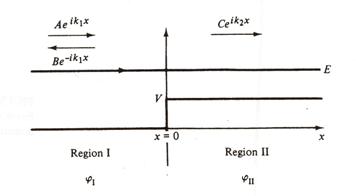
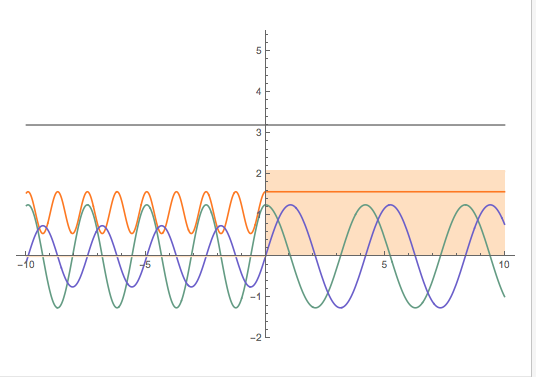
Stationary wave function of an incident free particle over a potential step. Shown are the absolute square (orange), the real part (green), the imaginary part (dark blue) of the wave function, and the energy (gray) of the incident particle. The height of the potential energy step (Subscript[V, 0]) is shown in light orange. -Imagen de: Wolfram demostration Project (http://demonstrations.wolfram.com/ScatteringOverPotentialStep/).
- Cálculos:
(puesto que, las ondas incidente y reflejada están en fase)
,
con.
-Se cumple la ecuación de conservación del flujo:
,
que no es sino la ecuación de conservación del flujo, que establece que el flujo transmitido es igual al flujo incidente menos el flujo reflejado. - Vídeos ilustrativos para un paquete de ondas en esta situación, en la que la partícula se encuentra un escalón ascendente:
–https://youtu.be/0GxFgF1lKHY (S. Brandt and H.D. Dahmen, The Picture Book of Quantum Mechanics, Springer 2012):
–https://youtu.be/cK-L-_zCBAQ (S. Brandt and H.D. Dahmen, The Picture Book of Quantum Mechanics, Springer 2012):
- Coeficientes de reflexión
y transmisión
:
cony satisfaciéndose siempre
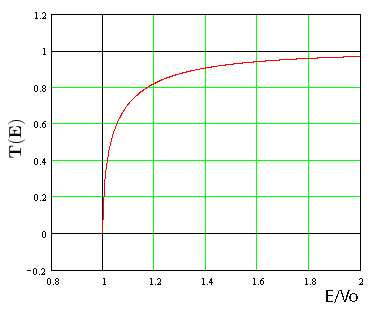
-Estos coeficientes se representan en la siguiente figura: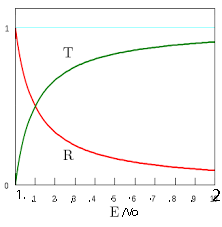
Imagen (modificada) del blog la-mecanica-cuantica-blogspot.com. - Análisis: Para cada
la función de onda describiendo el movimiento de la partícula es parcialmente reflejada y transmitida por el potencial escalón; la densidad de corriente o flujo de probabilidad por tanto se divide en dos componentes, reflejada y transmitida, conservándose siempre el flujo de probabilidad total (
).
-En cada suceso individual la partícula será siempre o reflejada o transmitida, con probabilidades respectivasy
, proporcionadas experimentalmente por la observación de un gran número de sucesos individuales idénticos.
-En la siguiente figura se ilustra la interpretación, tomándose:
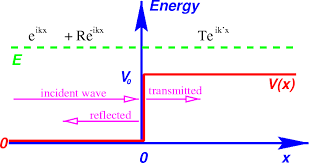
Imagen de: https://quantummechanics.ucsd.edu/ph130a/130_notes/node149.html. - Nota: analogía ondulatoria en Óptica Física: consideradas las dos regiones I (
) y II (
) como dos medios con sendos y diferentes índices de refracción
y
, dada una onda que incide perpendicularmente sobre la interfase que los separa se satisface en Óptica la ecuación
donderepresentan las longitudes de onda en cada medio. Introduciendo la relación de de Broglie
se obtiene
derivándose en efecto el coeficiente de reflexión óptico clásico correcto:
- Para una partícula que incide desde
- Incidencia desde la derecha (
):
- Para una partícula que incide desde
debe tenerse
, esto es,
por lo que las ecuaciones resultantes de imponer las condiciones de contorno se convierten en:
-Continuidad deen
:
-Continuidad deen
:
- Cálculos:
(obsérvese que, a diferencia del caso de incidencia desde la izquierda, ahora las ondas incidente y reflejada están en contrafase pues).
,
con.
–Conservación del flujo:
,
que no es de nuevo sino la ecuación de conservación del flujo. - Vídeo ilustrativo para un paquete de ondas en esta situación de incidencia desde la derecha, en la que la partícula se encuentra un escalón descendente: https://youtu.be/ez0NgSDMy8k (S. Brandt and H.D. Dahmen, The Picture Book of Quantum Mechanics, Springer 2012):
- Coeficientes de reflexión
y transmisión
:
cony satisfaciéndose siempre
-Los resultados para estos coeficientes pues no cambian respecto al caso de incidencia desde la izquierda:(y
) . Lo que origina el fenómeno no es un incremento o decremento de la magnitud del potencial en el origen, específicamente, sino un cambio brusco o salto de potencial (análogamente a como en Óptica es el hecho de un cambio en el indice de refracción lo importante, y no si el orden de magnitud del índice de refracción aumenta o disminuye).
- Para una partícula que incide desde
- Incidencia desde la izquierda (
- Principio de reciprocidad: en la resolución de un problema como el aquí planteado, es indiferente el sentido de incidencia de la partícula que se escoja, de entre los dos posibles.
- Interpretación en términos de paquetes de onda: Para tiempos remotos, se considera un paquete de ondas incidente, que generará en el futuro sendos paquetes de onda reflejado y transmitido. Las distintas simulaciones en esta entrada ilustran esta situación.
-Es interesante señalar que los tiempos de retardo en las correspondientes reflexión y transmisión de los paquetes resultan iguales y de orden menor que el tiempo característico en que el centro del paquete en cuestión recorre su propia extensión, lo que conlleva que su medida sea muy difícil en la práctica. - En definitiva, para
se tendrá reflexión parcial apreciable de la onda incidente siempre que el potencial presente un cambio brusco de valor, o salto de primera especie, en una distancia del orden de la longitud de onda de de Broglie asociada a la partícula incidente (algo demostrable vía la preceptiva resolución del correspondiente problema de autovalores). Por el contrario, si el potencial se mantiene aproximadamente constante en distancias del orden de esa longitud de onda de de Broglie, la reflexión será despreciable.
- Zona I:
- Caso
:
- Zona I:
:
conescalares arbitrarios.
- Zona II:
:
con
yescalares arbitrarios.
- Imponiendo las condiciones:
-Acotación
-Acotación
-Continuidad deen
:
-Continuidad deen
:
Puesto que este conjunto de condiciones es imposible de satisfacer, salvo para la solución trivial, la conclusión es que no existen soluciones físicamente aceptables del problema de autovalores de energía para el valor del parámetro de separación
, es decir,
.
- Zona I:
- Caso
:
- Zona I:
:
con
yescalares arbitrarios.
- Zona II:
:
conescalares arbitrarios.
- Imponiendo las condiciones de frontera:
-Acotación
-Continuidad deen
:
-Continuidad deen
:
- Al par de ecuaciones anteriores se añade la condición de normalización, de forma que la única constante arbitraria que aparece,
, queda fijada. Por tanto, existe una única solución al problema de autovalores planteado: el punto
pertenece al espectro del Hamiltoniano,
, y no presenta degeneración.
- Zona I:
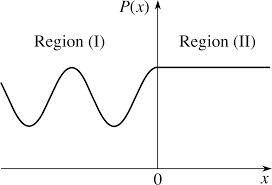
- Todos los resultados anteriormente obtenidos son válidos para un potencial general como el representado a la derecha en la siguiente figura:
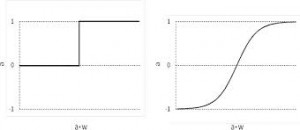
siempre que el orden de la distancia en que se produce el salto sea comparable a la longitud de onda de de Broglie de la partícula involucrada en el proceso. - En el límite clásico,
, y cualquier potencial satisfará la condición
en un intervalo de longitud tendiendo a cero, de manera que se recupera el resultado clásico: Reflexión total
(transmisión nula,
) para
y reflexión nula,
(transmisión total,
) siempre que
.
- Reuniendo resultados, la figura siguiente ilustra los resultados obtenidos para los coeficiente de reflexión y transmisión en todo el rango de autovalores:
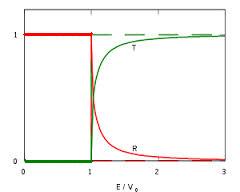
Imagen de la Wikipedia. -Obsérvese que en efecto se satisface:
.
- La siguiente simulación, en un vídeo de YouTube, ilustra como, conforme la energía
se crece, acercándose a la altura de la barrera, los estados estacionarios solución del caso
tienden hacia los del caso
:
-https://youtu.be/1TCHnpWoSzw ( S. Brandt and H.D. Dahmen, The Picture Book of Quantum Mechanics, Springer 2012:
- En el problema estudiado, Hamiltoniano del potencial escalón, resulta por tanto que
, donde
es simplemente degenerado y
es doblemente degenerado.
- Otro vídeo de YouTube, recogiendo varios casos:
–https://youtu.be/XQPtmSRi7OI (por Carla Mariela):
Referencias
[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.
[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.
[SCH-68] Schiff,L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.
Páginas complementarias
http://www.uco.es/hbarra/index.php/fc/apuntesfc/329-fc0301
www.lfp.uba.ar/es/notas%20de%20cursos/notasmecanicacuantica/09Ejemplos.pdf
http://la-mecanica-cuantica.blogspot.com.es/2010/07/transmision-y-reflexion-de-particulas-i.html
http://www.met.reading.ac.uk/pplato2/h-flap/phys11_1.html
APPS
- http://www.sc.ehu.es/sbweb/fisica/cuantica/escalon1/escalon1.htm
- http://www.sc.ehu.es/sbweb/fisica/cuantica/escalon2/escalon2.htm
- http://www.uco.es/hbarra/index.php/fc/appletsfc/64-escalon
- http://www.uco.es/hbarra/index.php/fc/appletsfc/65-schrodinger-escalon
-
Scattering over Potential Step from the Wolfram Demonstrations Project by Mahn-Soo Choi
Muy buen articulo! Muchisimas gracias!!!
como se obtiene la normalizacion de la función para el caso E<V0