La ecuación de Schrödinger y la conservación de la probabilidad

La ecuación de Schrödinger

En entradas anteriores, hemos expuesto:
1. Considerada una partícula material, de masa $m \ne 0$ , moviéndose a lo largo del eje $OX$ en sentido positivo (caso no relativista y monodimensional), con energía $E$ y momento $\vec{p}=p_x\hat{i}\;,\, p_x>0\,,$ bien definido, se le asocia una onda plana que viaja en la misma dirección, con número de ondas $k=\frac{2\pi}{\lambda}$ fijo, de expresión $\psi(x;t)=Ae^{i[kx-\omega(k)t]}$ , donde $A$ es una constante (real o compleja); el número de ondas $k$ y la frecuencia vienen dados por la relación de de Broglie, $k=\frac{2\pi}{\lambda}=\frac{p_x}{\hbar}$ y $\omega=2\pi\nu=\frac{E}{\hbar}$ .
2. Para una partícula material libre no relativista, $E=\frac{p_x^2}{2m}$ , por lo que $\omega(k)=\frac{E(p_x)}{\hbar}=\frac{E(k)}{\hbar}=\frac{ \hbar k^2}{2m}$ , resultando pues $v_f=\frac{\hbar k}{2m}$ y $v_g=\frac{\hbar k}{m}$ .
3. La onda plana puede escribirse pues como $\psi(x;t)=Ae^{i[p_xx-E(p_x)t]/ \hbar}$ , que satisface el par de ecuaciones diferenciales $-i\hbar\frac{\partial }{\partial x}\psi(x;t)=p_x\psi(x;t)$ y $i\hbar\frac{\partial }{\partial t}\psi(x;t)=E\psi(x;t)$ .
4. La generalización al caso tridimensional, para una partícula no relativista de masa $m$ , es la onda plana $\psi(\vec{r};t)=Ae^{i[\vec{k}\cdot\vec{r}-\omega(k)t]}=Ae^{i[\vec{p}\cdot\vec{r}-E(p)t]/ \hbar}$ , donde $\vec{p}=\hbar\vec{k}$ , $\omega(k)=\frac{\hbar k^2}{2m}$ , satisfaciendo el par de ecuaciones diferenciales $-i\hbar\nabla\psi(\vec{r};t)=\vec{p}\psi(\vec{r};t)$ y $i\hbar\frac{\partial}{\partial t}\psi(\vec{r};t)=E\psi(\vec{r};t)$ .
5. El examen de las ecuaciones anteriores muestra que, para una partícula material libre, de masa $m$ , la energía y el momento pueden representarse por sendos operadores diferenciales $E_{op}=i\hbar\frac{\partial}{\partial t}$ y $\vec{p}_{op}= -i\hbar\nabla$ , actuando sobre la función de onda $\psi(\vec{r};t)$ . Esta representación constituye un postulado de la Mecánica Cuántica, que se establece para toda partícula, libre o bajo la acción de un potencial $V$ (bajo condiciones a detallar más adelante).
La ecuación general que satisfacen las funciones de onda se establece como postulado, pero es conveniente reflexionar que es muy conveniente que sea como es, es decir, que:
1. Tenga la forma de una ecuación en derivadas parciales.
2. Sea lineal y homogénea, a fin de satisfacer el principio de superposición.
3. Sea de primer orden en $t$ : a fin de que baste con especificar $\Psi$ en cierto $t$ para obtener una solución única (una ecuación de orden superior requeriría condiciones adicionales).
4. En el límite macroscópico permita recuperar los resultados clásicos (principio de correspondencia, que rige cuando $\lambda_B \rightarrow 0$ : en el límite de muy pequeñas longitudes de onda de de Broglie, se establece la Mecánica Clásica como la aproximación correcta de la Mecánica Ondulatoria).
Para la partícula material libre, caso monodimensional, la ecuación de Schrödinger se obtiene como traslación directa de la relación $E(p_x)=\frac{p_x^2}{2m}$ , sustituyendo energía y momento por sus correspondientes operadores representativos en el formalismo:
$i\hbar\frac{\partial \Psi(x;t)}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2 \Psi(x;t)}{\partial x^2}$
Y lo mismo para el caso tridimensional:
ES para la partícula material libre (no relativista):
$i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2 \Psi(\vec{r};t)$ .
Es evidente que la ecuación de Schrödinger anterior se satisface tanto para ondas planas como para paquetes de onda (un paquete no es sino una superposición de las primeras).
Una vez postulada, la aceptación o rechazo se debe inferir a partir del éxito predictivo que proporcione.
La ecuación se postula también como válida en el caso de una partícula material moviéndose en el seno de un potencial real $V(\vec{r};t)$ (independiente de $\vec{p}$ ), del cual se derivan fuerzas actuantes según $\vec{F}(\vec{r};t)=-\nabla V(\vec{r};t)$ y en el que el Hamiltoniano clásico $H=\frac{\vec{p}^2}{2m}+V(\vec{r};t)$ representa la energía total de la partícula.
Nota: obsérvese que lo que se suele denominar como «sistema conservativo» es aún más restrictivo: añade además de lo anterior la condición de que el Hamiltoniano no dependa del tiempo.
Para escribir entonces la correspondiente ecuación de Schrödinger (ES), basta postular como operador Hamiltoniano el operador autoadjunto $H_{op}=H_{clasico}(\vec{r}_{op};\vec{p}_{op}=-i\hbar \nabla;t)=-\frac{\hbar^2\nabla^2}{2m}+V_{op}(\vec{r};t)$ , escribiendo la ES como:
ES para la partícula material en el seno de un potencial real $V(\vec{r};t)$ (no relativista):
$i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=H_{op}\Psi(\vec{r};t)=[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r};t)] \Psi(\vec{r};t)$ ,
donde se sobreentiende que se involucran los operadores correspondientes, aunque no se note expresamente (es decir, por ejemplo, que $V(\vec{r};t)\Psi(\vec{r};t) \equiv V_{op}(\vec{r};t)\Psi(\vec{r};t)$ ).
Obsérvese que se trata de una ecuación conforme a lo requerido:
ES: una ecuación en derivadas parciales; lineal; de primer orden en el tiempo $t$ ; de segundo orden en las coordenadas espaciales.
-Y, además, es determinista: proporciona la evolución temporal de la función $\Psi(\vec{r};t)$ a partir de una condición inicial $\Psi(\vec{r};t=t_0)$ .
La forma de la ES garantiza también que:
1. De la continuidad de la función potencial $V(\vec{r};t)$ respecto a las tres coordenadas espaciales $x\,,\,y\,,\,z$ se infiere la continuidad de las funciones $\Psi(\vec{r};t)\,,\, \frac{\partial \Psi(\vec{r};t)}{\partial t}\,,\;\nabla \Psi(\vec{r};t)$ y $\nabla^2 \Psi(\vec{r};t)$ respecto a esas mismas coordenadas.
2. Si la función potencial $V(\vec{r};t)$ respecto a las coordenadas espaciales $(x,y,z)$ presentara discontinuidades de primera especie (i.e.: presentara continuidad sólo a trozos), entonces $\Psi(\vec{r};t)\,,\, \frac{\partial \Psi(\vec{r};t)}{\partial t}\,,\;\nabla \Psi(\vec{r};t)$ serían continuas pero $\nabla^2 \Psi(\vec{r};t)$ sería sólo continua a trozos (respecto a las tres coordenadas espaciales).
3. Si la función potencial $V(\vec{r};t)$ respecto a las tres coordenadas espaciales $x\,,\,y\,,\,z$ presentara discontinuidades de segunda especie (por ejemplo: casos con pozos infinitos), entonces $\Psi(\vec{r};t)\,,\, \frac{\partial \Psi(\vec{r};t)}{\partial t}$ serían continuas; $\nabla \Psi(\vec{r};t)$ sería continua a trozos y $\nabla^2 \Psi(\vec{r};t)$ presentaría también discontinuidades de segunda especie (respecto a $x,y,z$ ). En estos casos se deberán incorporar condiciones de contorno que anulen la función de onda allí donde el potencial tome valores infinitos.
4. Si la función potencial $V(\vec{r};t)$ es una función continua del tiempo, también lo serán $\Psi(\vec{r};t)\,,\, \frac{\partial \Psi(\vec{r};t)}{\partial t}$ (respecto a $t$ ) .
5. Si la función potencial $V(\vec{r};t)$ presentara discontinuidades de primera especie en su variación temporal, $\Psi(\vec{r};t)$ será una función continua, pero $\frac{\partial \Psi(\vec{r};t)}{\partial t}$ también será sólo continua a trozos (consideradas como funciones de $t$ ).
La ES, base de la Mecánica Cuántica no relativista, fue propuesta por Schrödinger en 1926, acompañándola de su aplicación con éxito rotundo a la resolución de problemas como el átomo de Hidrógeno, el oscilador armónico y otros; también mostró técnicas perturbativas de resolución aproximada para la ecuación, indicadas para problemas cuya resolución analítica se hacía demasiado complicada o imposible.
La ES surge de la ecuación clásica de Hamilton-Jacobi en el límite $h \rightarrow 0$ (véase [GAL-89], I, pp. 152ss.), un resultado de acuerdo de nuevo con el principio de correspondencia y que establece su límite clásico.

Probabilidad y su conservación

Born, 1926: Postulado: El cuadrado del valor absoluto de la función de onda, $| \psi(\vec{r},t)|^2$ , representa la densidad de probabilidad de que el resultado de un experimento de determinación de la posición de la partícula sea: «posición $\vec{r}$ en el instante $t$ «. Esto es, $| \psi(\vec{r},t)|^2$ como densidad de probabilidad de posición por unidad de volumen.
Nota: éste es un enunciado moderno; Born, en su escrito original de 1926, enunciaba su interpretación en los términos clásicos de un electrón que posee posición y momento bien definidos en todo momento, algo erróneo en Mecánica Cuántica moderna.
Consecuentemente, la probabilidad de encontrar a la partícula en un elemento de volumen $d\vec{r}$ en el instante $t$ viene dada por $| \psi(\vec{r},t)|^2d\vec{r}$ ; la de encontrarla en una región $V$ del espacio en $t$ es $\int_V|\psi(\vec{r},t)|^2d\vec{r}$ , supuesta la normalización $\int_{\mathbb{R}^3}\left|\psi(\vec{r};t)\right|^2d\vec{r}=1$ (la probabilidad de encontrarla en algún punto de todo el espacio ha de ser la unidad).
Esta probabilidad no es la probabilidad clásica de encontrar a una partícula que está antes de la medida en alguna parte localizada pero desconocida del espacio, sino la probabilidad de que, por la interacción con el aparato de medida, la conjunción sistema-aparato dé lugar o provoque un resultado de valor medido para la posición (actualización de valor del observable posición que provoca un cambio en la distribución de probabilidad correspondiente a otro(s) observables, complementario(s) al medido).
Es obvio que dos funciones de onda $\psi_1(\vec{r};t)$ y $\psi_2(\vec{r};t)=e^{ai}\psi_1(\vec{r};t)$ , con $a \in \mathbb{R}$ , esto es, dos funciones de onda que difieran entre sí sólo en un factor de fase, proporcionan la misma densidad de probabilidad: son equivalentes. Ahora bien, a la hora de producir interferencias, las fases relativas entre funciones de onda sí son importantes y han de tenerse en cuenta.
Interpretación estadística: imaginemos un gran número $n$ de sistemas idénticos e idénticamente preparados, en las mismas condiciones, compuestos cada uno por una partícula de masa $m$ ; sea $\psi(\vec{r};t)$ la función de onda asociada, la misma para todos ellos. Si realizamos un experimento de determinación de la posición en cada una de estas copias idénticas del mismo sistema, en un mismo elemento de volumen $d\vec{r}$ y en el mismo instante $t$ , se tendrá que $\lim_{n\rightarrow \infty} \frac{n(\vec{r};t)}{n}=|\psi(\vec{r};t)|^2d\vec{r}$ , siendo $n(\vec{r};t)$ el número de copias en que el resultado del experimento ha sido la detección positiva de la partícula en $d\vec{r}$ .
Es decir, la colección de valores obtenidos en la medida del observable posición, o sea, las frecuencias de repetición de cada resultado posible, en el límite de muchos sistemas, $\lim{n \rightarrow \infty}$ , generan una distribución de probabilidad de la magnitud física posición. Si procedemos igual para todos los observables de un C.C.O.C del sistema, tendremos caracterizado operacionalmente al sistema de la forma máxima posible, en términos predictivos.
Respecto a la medida simultánea a la posición (por ejemplo) de otros observables sobre el sistema, se dan dos situaciones: 1) Los observables compatibles no tendrán limitación fundamental a la precisión con que pudieran ser medidos; 2) Los observables complementarios sólo podrían ser determinados con una precisión que cumpla la correspondiente relación de indeterminación que liga el producto de las desviaciones típicas de los dos operadores a medir simultáneamente (posición y este segundo complementario).
La condición de normalización para la anterior función de onda, la onda plana, se encuentra con el problema de que es imposible satisfacer el requisito
$\int_{\mathbb{R}^3}\left|\psi(\vec{r};t)\right|^2d\vec{r}=1$ ( $\int_{-\infty}^{\infty}\left|\psi(x;t)\right|^2dx=1$ en el caso monodimensional),
ya que las correspondientes integrales resultan ser divergentes. Ante este resultado, y dado que $\left|\psi(\vec{r};t)\right|^2=|A|^2$ , esto es, constante, hay igual probabilidad de encontrar a la partícula en cualquier punto del espacio, se interpreta la onda plana como correspondiente al estado de preparación de la partícula en que ésta tiene un momento perfectamente definido y está completamente deslocalizada, de acuerdo con el Principio de indeterminación.
Si nos restringimos al caso en que suponemos la partícula confinada en una región muy extensa, pero de volumen $V$ finito, la condición de normalización de la densidad de probabilidad adquiere la expresión $\int_{V}\left|\psi(\vec{r};t)\right|^2d\vec{r}=1$ (una partícula a la que se le asocie esta función de onda tendrá necesariamente también una indeterminación en su momento que permita satisfacer el correspondiente principio de indeterminación posición-momento).
En general, para tratar funciones que no sean normalizables hay distintas posibilidades: confinar el sistema en una región del espacio; introducir la delta de Dirac; etc.
-Por ejemplo, para la onda plana, que no es una función de cuadrado integrable, puede también recurrirse a una normalización en sentido relativo (cf. [GAL-89], pp. 81-82), de forma que la probabilidad de encontrar a la partícula en la unidad de volumen sea $(2\pi \hbar)^{-3}$ . Es decir, tomar $\psi(\vec{r};t)=\frac{1}{ (2\pi \hbar)^{\frac{3}{2}}}e^{i\vec{p}\cdot \vec{r}/\hbar}$ ; las dimensiones para el paquete son de $L^{-\frac{3}{2}}$ , donde $L$ simboliza longitud.

Funciones en el espacio $L^2(\mathbb{R}^3)$

Consideremos el espacio de Hilbert $\mathscr{H}=L^2(\mathbb{R}^3)$ de las funciones complejas de cuadrado Lebesgue-integrable, integrado por funciones que obviamente podrán ser siempre ser normalizadas dividiéndolas por su norma $||\Psi ||$ .
Obsérvese que las ondas planas son idealizaciones con $\Delta p \rightarrow 0$ , momento perfectamente definido, que no pertenecen al Hilbert $\mathscr{H}=L^2(\mathbb{R}^3)$ establecido. Su inclusión no obstante en el formalismo, preconizada ya por Dirac en 1930, es general, aunque no representan estados físicamente realizables. Los estados realizables, en general correspondientes a la preparación del sistema en un estado puro, autofunción simultánea de un C.C.O.C., vendrán representados por kets ortogonales pertenecientes al Hilbert $\mathscr{H}$ del sistema.
Dentro de este Hilbert, nos restringiremos también (en principio) a funciones de onda $\Psi$ en el subespacio de Hilbert de Sóbolev, $\mathscr{S} \lhd \mathscr{H}$ , integrado por aquellas funciones de $\mathscr{H}$ que cumplan que también $\nabla \psi(\vec{r};t)$ y $\nabla^2 \psi(\vec{r};t)$ pertenezcan al Hilbert.
Puede demostrarse que se satisfacen los siguientes teoremas:
1. Teorema 1: Dada $f\in \mathscr{H}=L^2(\mathbb{R}^3)$ con derivadas primeras y segundas también en $\mathscr{H}$ , se implica que $f$ es continua y satisface $\lim_{|\vec{r}|\rightarrow \infty}f(\vec{r})=0$ .
  -Nota: Más generalmente (cf. R.D. Richtmyer; Principles of Advanced Mathematical Physics, Springer-Verlag, 1997, p. 97), se tiene:
  Dada $f\in \mathscr{H}=L^2(\mathbb{R}^n)$ con todas sus derivadas hasta orden $k$ , donde $k$ es el entero menor que satisface $k > \frac{n}{2}$ , también en $\mathscr{H}$ , se implica que $f$ es continua y satisface $\lim_{|\vec{r}|\rightarrow \infty}f(\vec{r})=0$ .
2. Teorema 2 (implicado a partir del anterior teorema 1): Dada , se cumple:
  1. $\int_{\mathbb{R}^3}\nabla \cdot [\Psi^*(\nabla \Psi)]d\vec{r}=\oint_{S\rightarrow \infty}\Psi^*(\nabla \Psi)\cdot d\vec{S}=0$ ,
  2. $\int_{\mathbb{R}^3}\nabla \cdot [(\nabla \Psi^*)\Psi]d\vec{r}=\oint_{S\rightarrow \infty}(\nabla \Psi^*)\Psi\cdot d\vec{S}=0$ ,
  donde $d\vec{S}$ representa el vector de área $dS$ , normal a la superficie y sentido hacia fuera.
  –Nota: obsérvese el carácter complejo y vectorial de las cantidades del tipo $\Psi^*(\nabla \Psi)$ , de forma que se tiene:
  $\nabla \cdot [\Psi^*(\nabla \Psi)]=\sum_{i=x,y,z} \frac{\partial}{\partial r_i}[\Psi^* \frac{\partial \Psi}{\partial r_i}]$ ;
  $\oint_{S}\Psi^*(\nabla \Psi)\cdot d\vec{S}=\oint_{S} Re\{\Psi^*(\nabla \Psi)\}\cdot d\vec{S} + i\oint_{S} Im\{\Psi^*(\nabla \Psi)\}\cdot d\vec{S}$ .
Teorema de la divergencia o de Gauss: Dado un campo vectorial $\vec{F}:V \subset {\mathbb{R}^3} \rightarrow {\mathbb{R}^3}$ , tal que todas sus derivadas parciales de primer orden son funciones continuas, y siendo la región $V$ de borde $S$ , orientado con la normal unitaria exterior $\hat{n}$ , se satisface:
$\int_{V} \nabla \cdot \vec{F} dV = \oint_{S}\vec{F} \cdot \hat{n}\,dS$ .

Conservación de la probabilidad y ecuación de continuidad

Vector densidad de corriente y ecuación de continuidad:
1. Partimos de la expresión de la derivada temporal para la probabilidad de encontrar a la partícula en un volumen finito dado $V \subset \mathbb{R}^3$ , y consideraremos funciones de onda $\Psi$ en el subespacio de Hilbert de Sóbolev, $\mathscr{S} \lhd \mathscr{H}$ :
  $\frac{\partial}{\partial t}\int_{V}\left|\Psi(\vec{r};t)\right|^2d\vec{r}$
  $=\int_{V}[\Psi^*(\vec{r};t)\frac{\partial \Psi(\vec{r};t)}{\partial t}+\frac{\partial \Psi^*(\vec{r};t)}{\partial t}\Psi(\vec{r};t)]d\vec{r}$ .
2. Las funciones $\Psi$ y $\Psi^*$ satisfacen las sendas ecuaciones de Schrödinger:
  $i\hbar\frac{\partial \Psi(\vec{r};t)}{\partial t}=H_{op}\Psi(\vec{r};t)=[-\frac{\hbar^2}{2m}\nabla^2+V_{op}(\vec{r};t)] \Psi(\vec{r};t)$ ,
  $-i\hbar\frac{\partial \Psi^*(\vec{r};t)}{\partial t}=[H_{op}\Psi(\vec{r};t)]^*=[-\frac{\hbar^2}{2m}\nabla^2+V_{op}(\vec{r};t)] \Psi^*(\vec{r};t)$ ,
  donde se considera un operador potencial $V_{op}(\vec{r;t})$ real, definido según:
  $V_{op}\Psi(\vec{r};t)=V(\vec{r};t) \Psi(\vec{r};t)$ .
3. Sustituyendo las dos expresiones anteriores de la ES para las derivadas temporales de $\Psi$ y $\Psi^*$ se deriva:
  $\frac{\partial}{\partial t} \int_{V}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=\frac{1}{i\hbar}\int_{V}\{\Psi^*(\vec{r};t)[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r};t)]\Psi(\vec{r};t)$
  $+\Psi(\vec{r};t)[\frac{\hbar^2}{2m}\nabla^2-V(\vec{r};t)]\Psi^*(\vec{r};t)\}d\vec{r}$
  $=\frac{i\hbar}{2m}\int_{V}\{\Psi^*( \nabla^2 \Psi)-(\nabla^2\Psi^*) \Psi \}d\vec{r}$
4. A continuación, se introduce el vector densidad de corriente de probabilidad, $\vec{j}(\vec{r};t)$ , definido según
  $\vec{j}(\vec{r};t)= -\frac{i\hbar}{2m}[ \Psi^*( \nabla \Psi)-(\nabla\Psi^*) \Psi ] =Re\{ -\frac{i\hbar}{m}\Psi^*( \nabla \Psi) \}$
  (se ha hecho uso de $Re\{ia^*b\}=\frac{i}{2}(a^*b-b^*a)$ ).
  -La divergencia de este vector resulta ser:
  $\nabla \cdot \vec{j}(\vec{r};t)= -\frac{i\hbar}{2m}[ \Psi^*( \nabla^2 \Psi)-(\nabla^2\Psi^*) \Psi ]$ .
  (se ha hecho uso de $\nabla \cdot (a\vec{b})= a\nabla \cdot \vec{b}+ (\nabla a)\cdot \vec{b}$ ).
5. Así pues, la integral inicial queda:
  $\frac{\partial}{\partial t} \int_{V}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=-\int_{V} \nabla \cdot \vec{j}(\vec{r};t)d\vec{r}$ ,
  de donde se deduce la ecuación
  $\frac{\partial \left|\Psi(\vec{r};t)\right|^2}{\partial t}+\nabla \cdot \vec{j}(\vec{r};t)=0$ ,
  denominada ecuación de continuidad, que debe satisfacer toda función de onda solución de la ES para un potencial $V(\vec{r};t)$ real.
6. Aplicando el teorema de la divergencia a la anterior integral de volumen, se deriva la igualdad:
  $\frac{\partial}{\partial t} \int_{V}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=-\int_{V} \nabla \cdot \vec{j}(\vec{r};t)d\vec{r}$
  $=-\oint_{S}\vec{j}(\vec{r};t) \cdot d\vec{S}=-\oint_{S}\vec{j}(\vec{r};t) \cdot \hat{n}\,dS$
  donde la integral sobre el volumen $V$ se ha convertido en una integral sobre la superficie cerrada $S$ que lo delimita; en la fórmula, $\hat{n}$ representa un vector unitario normal a la superficie elemental $dS$ y sentido hacia fuera ( $\vec{j} \cdot \hat{n}>0$ ) .
7. Podría trazarse una analogía entre la ecuación de continuidad obtenida para la densidad de probabilidad y la correspondiente a un fluido:
  1. Sea un fluido de densidad $\rho(\vec{r};t)$ para el que la variación de masa de la cantidad del mismo contenida en un volumen finito dado $V$ , delimitado por una superficie $S$ , entre dos instantes muy próximos, viene dada en ausencia de fuentes y sumideros por
    $\int_{V}[\rho(\vec{r};t+dt)-\rho(\vec{r};t) ]d\vec{r}\approx [\int_{v}\frac{\partial \rho(\vec{r};t)}{\partial t}d\vec{r}\,]dt$ ,
    variación debida la diferencia entre, de un lado, la cantidad de fluido que sale desde el volumen $V$ a través de la superficie cerrada $S$ que lo delimita y, de otro, la que penetra.
  2. Es decir, la variación se debe a la existencia de un vector densidad de corriente de fluido, $\vec{j}(\vec{r};t)$ , cuyo flujo a través de la superficie cerrada $S$ proporciona la cantidad neta de fluido que atraviesa $S$ , por unidad de tiempo, teniéndose
    $\int_{v}\frac{\partial \rho(\vec{r};t)}{\partial t}d\vec{r}=-\oint_{S}\vec{j}(\vec{r};t) \cdot d\vec{S}=-\oint_{S}\vec{j}(\vec{r};t) \cdot \hat{n}\,dS$ ,
    donde se ha supuesto disminución de la cantidad de fluido, $\frac{\partial \rho}{\partial t}<0$ , y donde $\hat{n}$ representa un vector unitario normal a la superficie $S$ y sentido hacia fuera ( $\vec{j} \cdot \hat{n}>0$ ) .
  3. Aplicando a continuación el teorema de la divergencia, se obtiene:
    $\int_{v}\frac{\partial \rho(\vec{r};t)}{\partial t}d\vec{r}=-\int_{v}\nabla \cdot \vec{j}(\vec{r};t)d\vec{r}\,]dt$ ,
    de donde se deriva finalmente la ecuación de continuidad para el fluido:
    $\frac{\partial \rho(\vec{r};t)}{\partial t}+\nabla \cdot \vec{j}(\vec{r};t)=0$ ,
    la cual expresa la conservación de la cantidad del fluido.
    Nota: otra ecuación de continuidad análoga aparece también en Electrodinámica, expresando en este caso la conservación de la carga.
8. Así pues, hecha la interpretación de $\left|\Psi(\vec{r};t)\right|^2$ como una densidad de probabilidad, por unidad de volumen, esta función satisface una ecuación de continuidad,
  $\frac{\partial \left|\Psi(\vec{r};t)\right|^2}{\partial t}+\nabla \cdot \vec{j}(\vec{r};t)=0$ ,
  viniendo expresado el correspondiente vector de densidad de corriente de probabilidad como
  $\vec{j}(\vec{r};t)= -\frac{i\hbar}{2m}[ \Psi^*( \nabla \Psi)-(\nabla\Psi^*) \Psi ] =Re\{ -\frac{i\hbar}{m}\Psi^*( \nabla \Psi) \}$ .
9. Obsérvese que:
  -Nota 1:
  1) Para funciones de onda $\Psi(\vec{r};t)$ reales, la densidad de corriente se anula;
  2) La continuidad de $\Psi$ y $\nabla \Psi$ establece la continuidad de $\left|\Psi(\vec{r};t)\right|^2$ y de $\vec{j}$ .
  -Nota 2 (cf. [SCH-68], p. 27): No es correcto interpretar $\vec{j}(\vec{r};t)$ como un flujo medio en la posición $\vec{r}$ en el instante $t$ , ya que $\vec{j}$ no es susceptible de medida directa en el sentido en que $\left|\Psi(\vec{r};t)\right|^2$ sí lo es. Y ello porque una medida del flujo medio local implicaría medidas simultáneas de posición y momento con precisión más allá de la permitida por el Principio de indeterminación. No obstante, resulta útil interpretar $\vec{j}$ como un vector flujo, especialmente en los problemas en que su dependencia con $\vec{r}$ o no existe o es muy débil, de manera que una determinación precisa de la velocidad puede hacerse.
Conservación de la probabilidad:
1. Las ecuaciones anteriores se han obtenido para cualquier función de onda solución de una ES para un potencial real $V(\vec{r};t)$ , involucrando una región del espacio con volumen finito $V$ . Supongamos ahora que extendemos la región hasta todo el espacio $\mathbb{R}^3$ , de forma que $dS \rightarrow \infty$ . Suponiendo que $\Psi \in \mathscr{S}$ , se satisface
  $\lim_{| \vec{r}| \rightarrow \infty} \Psi \rightarrow 0$ ,
  por lo que se cumple el teorema 2 indicado anteriormente, de forma que la integral de superficie en la expresión para la derivada temporal de la densidad de probabilidad,
  $\frac{\partial}{\partial t} \int_{V}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=-\oint_{S}\vec{j}(\vec{r};t) \cdot d\vec{S}=-\oint_{S}\vec{j}(\vec{r};t) \cdot \hat{n}\,dS$ ,
  se anula y, por tanto, se satisface la ley de conservación de la probabilidad requerida:
  $\frac{\partial}{\partial t}\int_{\mathbb{R}^3}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=0$ .
2. Consecuentemente, si la función de onda está normalizada en un instante inicial $t_o$ ,
  $\int_{\mathbb{R}^3}\left|\Psi(\vec{r};t_o)\right|^2d\vec{r}=1$ ,
  permanece ya normalizada en su evolución temporal:
  $\int_{\mathbb{R}^3}\left|\Psi(\vec{r};t)\right|^2d\vec{r}=1\;\; \forall t$ .

Nota matemática (repetición)

Puede demostrarse que se satisfacen los siguientes teoremas:
1. Teorema 1: Dada $f\in \mathscr{H}=L^2(\mathbb{R}^3)$ con derivadas primeras y segundas también en $\mathscr{H}$ , se implica que $f$ es continua y satisface $\lim_{|\vec{r}|\rightarrow \infty}f(\vec{r})=0$ .
  Nota: Más generalmente (cf. R.D. Richtmyer; Principles of Advanced Mathematical Physics, Springer-Verlag, 1997, p. 97), se tiene:
  Dada $f\in \mathscr{H}=L^2(\mathbb{R}^n)$ con todas sus derivadas hasta orden $k$ , donde $k$ es el entero menor que satisface $k > \frac{n}{2}$ , también en $\mathscr{H}$ , se implica que $f$ es continua y satisface $\lim_{|\vec{r}|\rightarrow \infty}f(\vec{r})=0$ .
2. Teorema 2 (implicado a partir del anterior teorema 1): Dada , se cumple:
  1. $\int_{\mathbb{R}^3}\nabla \cdot [\Psi^*(\nabla \Psi)]d\vec{r}=\oint_{S\rightarrow \infty}\Psi^*(\nabla \Psi)\cdot d\vec{S}=0$ ,
  2. $\int_{\mathbb{R}^3}\nabla \cdot [(\nabla \Psi^*)\Psi]d\vec{r}=\oint_{S\rightarrow \infty}(\nabla \Psi^*)\Psi\cdot d\vec{S}=0$ ,
  donde $d\vec{S}$ representa el vector de área $dS$ , normal a la superficie y sentido hacia fuera.
  Nota: obsérvese el carácter complejo y vectorial de las cantidades del tipo $\Psi^*(\nabla \Psi)$ , de forma que se tiene:
  $\nabla \cdot [\Psi^*(\nabla \Psi)]=\sum_{i=x,y,z} \frac{\partial}{\partial r_i}[\Psi^* \frac{\partial \Psi^*}{\partial r_i}]$ ;
  $\oint_{S}\Psi^*(\nabla \Psi)\cdot d\vec{S}=\oint_{S} Re\{\Psi^*(\nabla \Psi)\}\cdot d\vec{S} + i\oint_{S} Im\{\Psi^*(\nabla \Psi)\}\cdot d\vec{S}$ .
3. Teorema de la divergencia o de Gauss: Dado un campo vectorial $\vec{F}:V \subset {\mathbb{R}^3} \rightarrow {\mathbb{R}^3}$ , tal que todas sus derivadas parciales de primer orden son funciones continuas, y siendo la región $V$ de borde $S$ , orientado con la normal unitaria exterior $\hat{n}$ , se satisface:
  $\int_{V} \nabla \cdot \vec{F} dV = \oint_{S}\vec{F} \cdot \hat{n}\,dS$ .

Referencias

[BOH-89] Bohm, D.; Quantum Theory; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; Quantum Mechanics; 2nd ed., Pearson; Dorchester, 2000.

[GAL-89] Galindo, A. y Pascual, P.; Mecánica Cuántica, Eudema, 1989.

[SCH-68] Schiff,L.I.; Quantum Mechanics; 3º ed., McGraw; 1968.

Páginas complementarias

http://la-mecanica-cuantica.blogspot.com.es/2009/08/la-ecuacion-de-schrodinger.html

APPS

http://www.uco.es/hbarra/index.php/fc/appletsfc

Quantized Solutions of the 1D Schrödinger Equation for a Harmonic Oscillator from the Wolfram Demonstrations Project by Jamie Williams

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

La ecuación de Schrödinger y la conservación de la probabilidad

Sé el primero en comentar

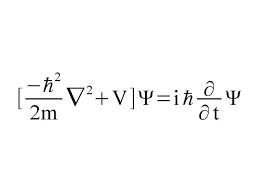
Dejar una contestacion Cancelar la respuesta