La onda y su ecuación de onda
- El punto de partida de la denominada Mecánica Ondulatoria, desarrollada por Schrödinger, es la onda de materia de de Broglie y la consideración del átomo como un sistema de vibraciones continuas.
- Si hay una onda «asociada» a cada partícula material, parece que debiera haber una ecuación de ondas que rija su evolución. Schrödinger la estableció en una serie de trabajos que publicó en 1926, sus famosas «cuatro comunicaciones«, pero no va a ser él mismo el que sea capaz de interpretar correctamente la función solución de su famosa ecuación.
- Su experiencia previa en el cálculo variacional y con problemas de autovalores en ecuaciones con condiciones de contorno le permitieron desarrollar un formalismo matemático continuo, en términos de ecuaciones diferenciales, en el que los valores de energía permitidos surgen como autovalores de un operador, sin apelar a la discontinuidad de los saltos cuánticos del formalismo matricial rival que poco antes, en 1925, habían desarrollado Heisenberg, Jordan y Born (véase también «Los Modelos Matemáticos de la Mecánica Cuántica, por F. Bombal, y la referencia [GAL-89], pp. 50-55).
- En sus comunicaciones, obtuvo primero la hoy denominada «ecuación de Schrödinger independiente del tiempo para un estado estacionario de energía«, a partir de la ecuación de Hamilton-Jacobi para un sistema cuyo Hamiltoniano sea constante del movimiento y coincida con la energía; finalmente, derivaba la desde entonces famosa «ecuación de Schrödinger» general, dependiente del tiempo, que es una ecuación de ondas:
- De partida, en vez de imponer condiciones de cuantización, introduce una función desconocida
, relacionada con la función característica del sistema, consiguiendo expresar la ecuación de Hamilton como una forma cuadrática
en
y sus derivadas primeras,
. A continuación, aplica una condición variacional de «búsqueda de una
real, unívoca, finita, continua, con derivadas primeras continuas, que haga extremal la integral de
extendida a todo el espacio de configuración». Obtiene así la correspondiente ecuación de Euler del problema variacional planteado, que es la denominada «ecuación de Schrödinger independiente del tiempo para un estado estacionario de energía»:
.
- Resuelta la ecuación, con ayuda de Weyl, Schrödinger obtuvo el espectro del átomo de hidrógeno, partes discreta y continua, para lo que añadió la condición
a largas distancias.
- Posteriormente, reinicia el trabajo partiendo de una ecuación de ondas típica
, con una función
sinusoidal para la que se ha establecido la velocidad de propagación mediante las relaciones de de Broglie. Resuelta la ecuación, de la multiplicidad de soluciones obtenidas escogía las correspondientes a los procesos estacionarios, imponiendo las apropiadas condiciones de contorno: exigiendo a la función
ser unívoca, finita y continua en todo el espacio de configuración.
- Mediante la aplicación al oscilador armónico lineal y algunos sistemas atómicos simples, fue capaz de reproducir los mismos resultados que se habían alcanzado con la Mecánica Matricial de Born, Heisenberg y Jordan.
- Como ecuación general establecía la ecuación de Schrödinger dependiente del tiempo, verdadera ecuación de ondas, pues contiene
y la
es ya compleja:
.
- De partida, en vez de imponer condiciones de cuantización, introduce una función desconocida
- En 1927 la Mecánica Ondulatoria («M.O.» en lo siguiente) de Schrödinger se ha consolidado ya como un método válido y matemáticamente simple para el tratamiento de los fenómenos atómicos. De hecho, dadas la elegancia y simplicidad del tratamiento de la M.O. para problemas como el átomo de hidrógeno, frente al complicado tratamiento algebraico que requería la Mecánica Matricial, fue la adoptada rápidamente por la mayoría de los físicos; la opinión favorable a ella se incrementó cuando el abordaje de sistemas más complejos evidenció aún más las limitaciones prácticas de los métodos matriciales. De hecho, la conveniencia del método de Schrödinger era tan manifiesta que hasta Heisenberg y Born lo adoptaron ya en 1926 para sus trabajos sobre el átomo de Helio y las colisiones atómicas, respectivamente.
- Sin embargo, la M.O. carecía de una interpretación aceptada por todos. Schrödinger la concibió inicialmente como la teoría que permitiría restaurar en Física Atómica el principio de continuidad del cambio, abandonado desde los trabajos de Planck de 1900:
-Asociando las partículas con ondas materiales, totalmente análogas a las electromagnéticas o sonoras, pensaba poder resolver todos los problemas pendientes: la Mecánica Cuántica como una auténtica física de ondas:
 «El proceso mecánico real sólo puede representarse apropiadamente como un proceso ondulatorio y no por el movimiento de puntos materiales en el espacio«.
«El proceso mecánico real sólo puede representarse apropiadamente como un proceso ondulatorio y no por el movimiento de puntos materiales en el espacio«.
 Schrödinger, en carta a Max Planck, mayo 1926, cit. en [JAM-74], p. 29):
Schrödinger, en carta a Max Planck, mayo 1926, cit. en [JAM-74], p. 29):
 “The concept ‘energy’ is something that we have derived from macros-copic experience and really only from macroscopic experience. I do not believe that it can be taken over into micromechanics just like that, so that one may speak of the energy of a single partial oscillation. The energetic property of the individual partial oscillation is its frequency”.
“The concept ‘energy’ is something that we have derived from macros-copic experience and really only from macroscopic experience. I do not believe that it can be taken over into micromechanics just like that, so that one may speak of the energy of a single partial oscillation. The energetic property of the individual partial oscillation is its frequency”.
-Su interpretación hacía desaparecer los «saltos cuánticos», negando su existencia, pues cuando un átomo realizaba una transición entre dos estados estacionarios, la radiación no era producto de una variación brusca de la energía con la subsiguiente emisión de un cuanto de luz, sino el resultado de la excitación simultánea de dos vibraciones materiales estacionarias cuyas interferencias daban lugar a la emisión de ondas electromagnéticas. Así se expresaba Schrödinger al respecto en su primera comunicación:
 “Se puede, por tanto, intentar asociar la función
“Se puede, por tanto, intentar asociar la función con un proceso vibratorio en el átomo, proceso posiblemente más real que las órbitas electrónicas, cuya existencia está siendo muy cuestionada actualmente.(…) El misterioso requisito de los números enteros no entra ya en las reglas de cuantización, sino que ha retrocedido, por así decir, un paso atrás, al demostrar que es el resultado de la finitud y univocidad de una cierta función espacial.(…) No hace falta decir cuánto más agradable sería concebir una transición cuántica como un intercambio de energía de un modo de vibración a otro, que considerarla como un salto de electrones”.
-Tengamos presente que el concepto de «salto cuántico» del electrón entre órbitas era aborrecido entre los físicos más tradicionalistas, enemigos de la ruptura con el continuismo clásico y con la para ellos también imprescindible visualización de los fenómenos en el espacio-tiempo. Y es que conviene recordar las palabras de Max Born, quien va a ser el “padre” de la interpretación probabilística de la función de onda de Schrödinger:
 Max Born; “Das Adibatenprinzip in Quantenmechanik”, Zeitschrift für Physik 40 (1926) 167-192:
Max Born; “Das Adibatenprinzip in Quantenmechanik”, Zeitschrift für Physik 40 (1926) 167-192:
 “The individual process, the ‘quantum jump’, is therefore not causally determined in contrast to the a-priori probability of its occurrence; this probability is ascertainable by the integration of Schrödinger’s differential equation which is completely analogous to the corresponding equation in classical mechanics, putting into relation two stationary time-intervals separated by a finite temporal interval. The jump thus passes over a considerable abyss (“der Sprung geht also über einen beträchtlichen Abgrund”); whatever occurs during the transition can hardly be described within the conceptual framework of Bohr’s theory, nay, probably in no language which lends itself to visualizability”.
“The individual process, the ‘quantum jump’, is therefore not causally determined in contrast to the a-priori probability of its occurrence; this probability is ascertainable by the integration of Schrödinger’s differential equation which is completely analogous to the corresponding equation in classical mechanics, putting into relation two stationary time-intervals separated by a finite temporal interval. The jump thus passes over a considerable abyss (“der Sprung geht also über einen beträchtlichen Abgrund”); whatever occurs during the transition can hardly be described within the conceptual framework of Bohr’s theory, nay, probably in no language which lends itself to visualizability”. - El desarrollo posterior de la nueva Teoría Cuántica conservará la preferencia por el formalismo matemático ondulatorio, pero desechará tajantemente la interpretación ontológica en términos de ondas con las que Schrödinger pretendió restaurar la continuidad en la Física. La nueva teoría acabó consolidándose en el sentido interpretativo (¿neopositivista?: instrumentalista) que había acompañado desde el principio a la Mecánica Matricial, de la mano del equipo de físicos liderado por N. Bohr. Y la interpretación ortodoxa logró una aceptación (casi) unánime; por ejemplo, así se expresaba respecto al fracaso del proyecto de Schrödinger el propio L. de Broglie, su inspirador:
 L. de Broglie; «La física nueva y los cuantos», Losada, Buenos Aires, 1941; cit. en [ICA-91], p. 110:
L. de Broglie; «La física nueva y los cuantos», Losada, Buenos Aires, 1941; cit. en [ICA-91], p. 110:
 “Es difícil dar a la onda
“Es difícil dar a la onda de la Mecánica Ondulatoria la misma significación física que podían poseer las ondas consideradas por la Física Clásica. En efecto, en Física Clásica las magnitudes que se propagan por ondas, están referidas a las vibraciones de un medio, cuya existencia es real o supuesta; deben, por consiguiente, representando un fenómeno real, expresarse por una función real. Si a veces se juzga útil, como sucede en los cálculos de la óptica, reemplazar estas funciones reales por cantidades complejas, de las cuales son sus partes reales, ello no es más que un artificio de cálculo, del que se podría siempre prescindir. Por el contrario, en Mecánica Ondulatoria, debido a la presencia de coeficientes imaginarios en la misma ecuación de propagación, el carácter complejo de la función de onda
se manifiesta como esencial y se opone a toda tentativa que se realice para considerar la onda de la Mecánica Ondulatoria como una realidad física que corresponda a las vibraciones de algún medio”.
La «función de onda» : un campo de probabilidad
- Asumimos como un axioma o postulado fundamental del formalismo matemático cuántico la ecuación de Schrödinger,
,
válida para una partícula material no relativista, de masa invariante, sin espín, libre o bajo la acción de un potencial real
, independiente de
, cuyo Hamiltoniano clásico es de la forma
y representa la energía total del sistema. - Sus soluciones son funciones complejas, de forma que:
.
- Schrödinger interpretó primero que
representaría la densidad de carga electrónica en el átomo, pero el formalismo postularía de forma definitiva una interpretación probabilística, establecida prontamente por Born en 1926, en su estudio sobre las colisiones atómicas, realizado con el formalismo de la ecuación de Schrödinger.
- Born, 1926: Postulado: El cuadrado del valor absoluto de la función de onda,
, supuesta normalizada de forma que
, representa la densidad de probabilidad de que el resultado de un experimento de determinación de la posición de la partícula sea: «posición
en el instante
«. Esto es:
se interpreta como una densidad de probabilidad de posición (probabilidad por unidad de volumen).
-Nota: éste es un enunciado moderno; Born, en su escrito original de 1926, enunció su interpretación en los términos clásicos de un electrón que posee posición y momento bien definidos en todo momento, algo inconsistente en M.C. moderna. - Consecuentemente, la probabilidad de encontrar a la partícula en un elemento de volumen
en el instante
viene dada por
; la de encontrarla en una región
del espacio en el instante
es
(supuesta la normalización indicada).
- Obsérvese que, en términos matemáticos, imponer la condición de normalización
(interpretada en el sentido de que la probabilidad de encontrar la partícula en algún punto de todo el espacio ha de ser la unidad), es imponer que la función
sea
, es decir, de cuadrado integrable Lebesgue.
- La densidad de probabilidad
no especifica por completo el vector de estado cuántico
. La fase juega un papel importante en fenómenos cruciales, por ejemplo aquellos en que se producen interferencias.
- Dimensiones de
: según la anterior condición de normalización, las dimensiones de la función de onda, en el caso de un sistema compuesto por una sola partícula, deben ser
, donde
simboliza longitud. En general, la función de onda (parte espacial, sin considerar espines) para un sistema de
partículas, caso
dimensional, tiene dimensiones
.
- Importante: Esta probabilidad NO es la probabilidad clásica de encontrar a una partícula que está antes de la medida en alguna parte del espacio, sino la probabilidad de que, por la interacción con el aparato de medida, la conjunción sistema-aparato dé lugar o provoque un resultado de valor medido para la posición (actualización de valor del observable posición que provoca un cambio en la distribución de probabilidad correspondiente a los observables complementarios al medido) (cf. principio de indeterminación).

Stodolna, A. S., et al. «Viewpoint: A New Look at the Hydrogen Wave Function.» Phys. Rev. Lett 110 (2013): 213001. - Frases célebres:
 P. Jordan; Quantenphysikalische Bemerkungen zur Biologie und Psychologie, Erkenntnis 4, 1934, pp. 215-252:
P. Jordan; Quantenphysikalische Bemerkungen zur Biologie und Psychologie, Erkenntnis 4, 1934, pp. 215-252:
 “(In a measurement of position, for example, as performed with the gamma-ray microscope), the electron is forced to a decision. We compel it to assume a definite position; previously it was, in general, neither here nor there; it had not yet made its decision for a definite position. (…)We ourselves produce the results of measurement [Wir selber rufen die Tatbestände hervor]”.
“(In a measurement of position, for example, as performed with the gamma-ray microscope), the electron is forced to a decision. We compel it to assume a definite position; previously it was, in general, neither here nor there; it had not yet made its decision for a definite position. (…)We ourselves produce the results of measurement [Wir selber rufen die Tatbestände hervor]”.
 N. Bohr; «Atomic Theory and the description of nature», Cambridge Univ., Cambridge, 1934:
N. Bohr; «Atomic Theory and the description of nature», Cambridge Univ., Cambridge, 1934:
 “(A subsequent measurement deprives to a certain degree the information obtained through a previous measurement of its predictive significance… these facts…) not only set a limit to the extent of the information obtained by measurement, but they also set a limit to the meaning which we may attribute to such information. We meet here in a new light the old truth that in our description of nature the purpose is not to disclose the real essence of the phenomena but only to track down, so far as it is possible, relations between the manifold aspects of our experience”.
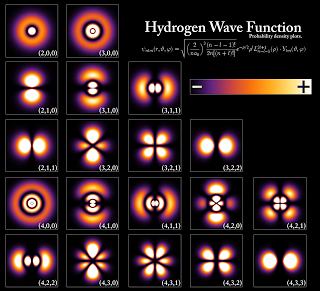
“(A subsequent measurement deprives to a certain degree the information obtained through a previous measurement of its predictive significance… these facts…) not only set a limit to the extent of the information obtained by measurement, but they also set a limit to the meaning which we may attribute to such information. We meet here in a new light the old truth that in our description of nature the purpose is not to disclose the real essence of the phenomena but only to track down, so far as it is possible, relations between the manifold aspects of our experience”. - Densidades radiales y angulares de probabilidad de posición en el átomo de Hidrógeno: las siguientes imágenes muestran, respectivamente, las densidades de probabilidad radial y angular (armónicos esféricos) en los primeros estados propios de energía del átomo de Hidrógeno:
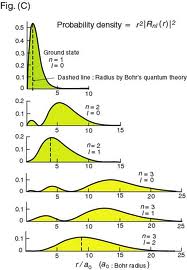
Densidad radial de probabilidad de posición en algunos de los estados del átomo de hidrógeno (imagen de cuentoscuanticos.com). 
Densidad angular de probabilidad de posición en algunos de los estados del átomo de Hidrógeno (imagen de: cuentoscuanticos.com). - Las funciones de onda del átomo de Hidrógeno:

Hydrogen Density Plots: wavefunctions of the electron in a hydrogen atom at different energy levels. The brighter areas represent a higher probability of finding the electron. Imagen y texto: PoorLeno, Public domain, via Wikimedia Commons, URL: https://commons.wikimedia.org/wiki/File:Hydrogen_Density_Plots.png -Imágenes adicionales y ecuaciones para diferentes orbitales del átomo de Hidrógeno pueden obtenerse en hyperphysics; también puede consultarse: imaging the Hydrogen’s orbitals.
- Las «imágenes» de la física precuántica y cuántica para un átomo de Hidrógeno en el estado fundamental, por tanto, son radicalmente diferentes:
-En la imagen pre-cuántica (modelo de Bohr), el electrón está en órbita alrededor del núcleo atómico:
Imagen: http://molaire1.perso.sfr.fr/e_quantic2.html -La imagen cuántica sustituye la órbita por un «orbital» o «nube» de probabilidad:
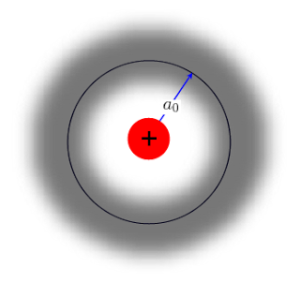
Imagen de la nube de probabilidad correspondiente al estado fundamental del átomo de hidrógeno (imagen procedente del blog la-mecanica-cuantica.blogspot.com.es/).
- Es obvio que dos funciones de onda
y
, con
, esto es, dos funciones de onda que difieran entre sí sólo en un factor de fase, proporcionan la misma densidad de probabilidad: son equivalentes. Ahora bien, a la hora de producir interferencias, las fases relativas entre funciones de onda sí son importantes y han de tenerse en cuenta.
-Por ejemplo: dadas dos funciones de onday
, con
y
reales, su combinación lineal con coeficientes escalares arbitrarios
, complejos, representa otra función de onda
, por aplicación del principio de superposición, que rige debido a la linealidad del espacio matemático de Hilbert, el marco teórico definitivo que se adoptaría a partir de la formulación rigurosa que desarrolló J. von Neumann, cf. Mathematische Grundlagen der Quantenmechanik, Springer, Berlín, 1932. La función de onda superpuesta
proporciona la densidad de probabilidad:
.
-El tercer sumando en la anterior expresión, que es el que provoca que las distribuciones de probabilidad asociadas a las funciones que se suman no sea la suma directa de las distribuciones de probabilidad asociadas a las dos funciones superpuestas,y
, es el que justifica los fenómenos observados de interferencia (por ejemplo, en el experimento de la doble rendija).
- La función de onda
, también denominada «amplitud de probabilidad», no tiene en sí misma significado físico directo: no es en sí misma algo determinable experimentalmente, pues carece de la realidad física por ejemplo de una onda elástica o una onda de sonido: no es un observable, es una onda abstracta (la función suele ser compleja, de hecho), una función matemática cuya interpretación es estadística, y que se postula proporciona toda la información que puede obtenerse experimentalmente sobre el sistema a que se asocia.
- Interpretación estadística: imaginemos un gran número
de sistemas idénticos e idénticamente preparados, en las mismas condiciones, compuestos cada uno por una partícula de masa
; sea
la función normalizada asociada, la misma para todos ellos. Si realizamos un experimento de determinación de la posición en cada una de estas copias idénticas del mismo sistema, en un mismo elemento de volumen
y en el mismo instante
, se tendrá que
, siendo
el número de copias en que el resultado del experimento ha sido la detección positiva de la partícula en
.
- Es decir, la colección de valores obtenidos en la medida del observable posición, o sea, las frecuencias de repetición de cada resultado posible, cuando se han llevado a cabo medidas sobre muchos sistemas,
, generan una distribución de probabilidad de la magnitud física posición. Si pudiéramos proceder igual para todos los observables del sistema, tendríamos caracterizado operacionalmente al sistema de la forma máxima posible, en términos predictivos.
–Pero, respecto a la medida simultánea a la posición (el observable que nos ocupa en este ejemplo, puede decirse lo mismo de cualquier otro) de otros observables sobre el mismo sistema, hay que tener en cuenta que se van a presentar dos situaciones:- Dos observables «compatibles» (no ligados por una relación de indeterminación) no tendrán limitación fundamental a la precisión con que pueden ser medidos en un mismo experimento;
- Dos observables «complementarios» o «conjugados» (ligados entre sí por una relación de indeterminación) sólo podrán ser determinados simultáneamente con una precisión que cumpla la correspondiente relación de indeterminación que liga el producto de sus desviaciones típicas.
- Por lo tanto, mientras que clásicamente es posible, en principio, preparar al sistema sin limitaciones en cuanto a la determinación completa con precisión ilimitada -salvo limitaciones de orden experimental práctico- de cualquier conjunto de observables como, por ejemplo, posición y momento, ello no va a ser posible en mecánica cuántica. En efecto, en mecánica cuántica va a haber observables incompatibles o complementarios, como dichos posición y momento, que por el principio de indeterminación no van a ser simultáneamente medibles con precisión ilimitada. Se trata de una restricción de orden fundamental, de principio, y no por limitaciones operativas prácticas como es el caso en física clásica.
- Asimismo, el resultado de una medida en física cuántica no es concebible como la revelación de un valor poseído por la correspondiente magnitud en el sistema antes de la medida, ni es legítimo inferir que ése es el valor de la magnitud en el sistema tras la medida. La conjunción aparato-sistema que constituye el acto o experimento de cada medida establece unas correlaciones que alteran ineludiblemente las distribuciones de probabilidad correspondientes a los observables complementarios a los medidos en cada experimento.
- La Teoría Cuántica es, por tanto, una teoría estadística: dos sistemas que son copias idénticas, en composición y preparación, comparten la misma función de onda asociada, y por ello poseen las mismas distribuciones de probabilidad para los resultados de las mismas medidas (es decir, de los mismos experimentos de determinación), sobre el sistema, de un conjunto de observables del mismo.
-Si se miden simultáneamente sobre cualquiera de los sistemas de la colectividad estadística varios observables compatibles entre sí, para los cuales la correspondiente función de onda compartida por todos los sistemas constituye una autofunción común, entonces los resultados de las medidas de cada observable serán los mismos para todos los sistemas individuales, y habrá certeza sobre esos resultados, para cada observable y sobre cada sistema individual.
-Pero la medida de otros observables que sean incompatibles con los anteriores, para los que esa función de onda que representa el estado cuántico del sistema no puede ser una autofunción, proporcionará en general un resultado diferente sobre cada copia individual del conjunto estadístico, aunque se trate del mismo tipo de experimento o medida.
-
- Nota: la anterior interpretación estadística debe entenderse:
- En la interpretación ortodoxa, la función de onda describe o se asocia con un sistema individual, recibiendo una interpretación estadística en términos de la colección de resultados obtenidos sobre una colección de sistemas idénticos e idénticamente preparados.
- En algunas interpretaciones estadísticas plausibles («interpretación estadística» refiere ahora a la propia teoría cuántica) la función de onda no se toma como describiendo el sistema individual, sino que se asocia a un «ensemble» o colección de sistemas idénticos e idénticamente preparados.
-En cualquier caso, los sistemas individuales, bajo toda interpretación plausible (esto es, no contradicha experimentalmente), se asumen con comportamiento no clásico: el adjetivo «estadístico» tiene un sentido fundamental, por completo diferente al que posee en la descripción estadística clásica de, por ejemplo, la Mecánica Estadística de Maxwell-Boltzmann (quedan descartadas las variables ocultas»).
- En definitiva: la teoría cuántica no es una física de ondas, sino de campos (¿la vieja dualidad onda-corpúsculo transmutada en una dualidad campo-partícula?).
- La materia y la radiación están cuantizadas.
- El azar rige la Naturaleza, desterrando la causalidad en los eventos individuales.
- La ecuación de Schrödinger, la ecuación de campo no relativista, rige la evolución temporal del campo
, estableciendo el principio de causalidad para el comportamiento estadístico (en ausencia de interacciones sobre el sistema).
- La cuantización de un campo de materia puede afirmarse como el mecanismo matemático que aflora las «partículas», que pueden concebirse de esta manera como las excitaciones elementales del campo, de forma similar a como el fotón es el cuanto de excitación del campo electromagnético cuantizado.
- En cita de S. Weinberg, recogida por A. Hobson:
 «Material particles could be understood as the quanta of various fields, in just the same way the photon is the quantum of the electromagnetic field. There was supposed to be one field for each type of elementary particle. Thus, the inhabitants of the universe were conceived to be a set of fields -an electron field, a proton field, an electromagnetic field- and particles were reduced to mere epiphenomena. In its essentials, this point the view has survived to the present day, and forms the central dogma of quantum field theory: the essential reality is a set of fields subject to the rules of special relativity and quantum mechanics; and all else is derived as a consequence of the quantum dynamics of these fields«.
«Material particles could be understood as the quanta of various fields, in just the same way the photon is the quantum of the electromagnetic field. There was supposed to be one field for each type of elementary particle. Thus, the inhabitants of the universe were conceived to be a set of fields -an electron field, a proton field, an electromagnetic field- and particles were reduced to mere epiphenomena. In its essentials, this point the view has survived to the present day, and forms the central dogma of quantum field theory: the essential reality is a set of fields subject to the rules of special relativity and quantum mechanics; and all else is derived as a consequence of the quantum dynamics of these fields«. - Sin embargo, para un proponente de la teoría de cuerdas, la ontología de la realidad se compondría de «cuerdas» vibrantes en un espacio multidimensional, y las partículas serían los estados vibratorios de esos filamentos… En Ciencia, nada puede considerarse definitivo.
- Nota: la anterior interpretación estadística debe entenderse:
Mecánica Cuántica en el espacio de Hilbert
- Cronología abreviada del desarrollo del formalismo cuántico:
- 1925: Mecánica de Matrices: Born, Heisenberg, Jordan.
- 1926: Mecánica Ondulatoria: Schrödinger.
- 1926: Shrödinger establece una primera equivalencia entre ambas mecánicas.
- 1926: Born enuncia una primera interpretación probabilística de
.
- 1927: Dirac establece mediante una teoría de transformaciones canónicas, por matrices discretas o continuas, la unificación de los formalismos de la Mecánica de matrices y la Mecánica Ondulatoria: «Las funciones propias de la ecuación de Schrödinger son precisamente los elementos de la matriz de transformación, o las funciones de transformación, que permiten transformar el esquema de la representación matricial a un esquema en que el Hamiltoniano es una matriz diagonal» (Dirac, P.A.M.; «The Physical Interpretation of the Quantum Dynamics«, Proceedings of the Royal Society (London) A113(1927)621-641.
- La equivalencia matemática entre los distintos formalismos queda plenamente demostrada en 1932, cuando von Neumann presente la M.C. formalizada como un cálculo de operadores autoadjuntos en un espacio de Hilbert
, en su libro «Fundamentos matemáticos de la Mecánica Cuántica«. Desde ese momento, los espacios de funciones que intervenían en los distintos formalismos publicados quedaron establecidos definitivamente como equivalentes, dos espacios isomorfos e isométricos (véase de nuevo «Los Modelos Matemáticos de la Mecánica Cuántica, por F. Bombal):
-Mecánica Matricial: representación espaciode las secuencias de números complejos tales que
converge.
-Mecánica Ondulatoria: representación espaciode las funciones complejas de cuadrado Lebesgue-integrable.
-Isomorfismo: resolver el problema de autovalores de un operador enes equivalente a diagonalizar la correspondiente matriz en
.
- Algunos postulados (se sigue la notación de la referencia [GAL-89]; para un resumen de la teoría de espacios de Hilbert que se va a utilizar, puede verse la entrada «Las matemáticas de la cuántica» y todos sus enlaces):
- Postulado 1: A cada sistema físico que se pretenda describir en el marco de la MC, se le hace corresponder un espacio de Hilbert
complejo y separable. Cada «estado puro» del sistema en un instante
, en el que el sistema ha sido preparado de forma que el conocimiento predictivo sobre el mismo es máximo, se representa por un rayo unidad
, o conjunto de vectores de norma unidad, integrado por diferentes vectores de estado o kets
que difieren entre sí únicamente en factores de fase (escalares de norma unidad).
- «Estado puro» y «estado mezcla»; modalidades de medidas:
- En Mecánica cuántica se distingue entre dos tipos de operaciones de «medida» (cf. [GAL-89], pp. 62-65): de primera especie, o «preparaciones«, y de segunda especie. Con las primeras se pretende «preparar» un sistema físico en un determinado estado, en el que se tiene certeza de lo que se va a obtener al medir determinados observables; con las segundas se pretende realizar una medida concreta de algunas propiedades («observables»), es decir, obtener un resultado para esas propiedades.
- Postulado 1: A cada sistema físico que se pretenda describir en el marco de la MC, se le hace corresponder un espacio de Hilbert
- Cuando la preparación es maximal, esto es, preparamos un sistema cuántico controlando el número máximo de observables compatibles independientes, se produce un estado para el sistema en que se dispone de la mayor información cuántica posible, denominándose estado puro. En caso contrario, cuando la preparación no es maximal, se denomina estado mezcla.
- Los estados puros se representan o asocian a vectores del espacio de Hilbert asociado al sistema físico: los vectores de estado normalizados
o «kets».
- Los estados mezcla se asocian o representan por un operador densidad,
, donde
representa la probabilidad de que el sistema se halle en el estado puro
. En este caso, los distintos estados
son vectores del Hilbert normalizados (¡no necesariamente ortogonales entre sí!).
-Por ejemplo: éste es el caso cuando se prepara un haz de electrones mediante un selector de velocidades, de forma que el momento lineal está bien definido (en «cierto sentido límite», Galindo&Pascual dixit), pero no se dispone de información máxima respecto a la componente de espín según una dirección dada, de forma que hay 50% de posibilidad para las dos orientaciones posibles. - El que la preparación del sistema en un estado puro sea maximal refiere al hecho de que se ha controlado el mayor número posible de observables compatibles: en el sentido de que la medida del correspondiente número máximo de magnitudes físicas compatibles independientes, sobre una colección de sistemas idénticos en ese mismo estado (puro) en ese instante
, dará con certeza un resultado para cada uno; las medidas para los restantes observables sí presentarán dispersión.
-Nota: la recíproca no es cierta: no siempre los vectores de norma unidad del Hilbert representan un estado puro del sistema, ya que pueden existir reglas de superselección que restrinjan (véase [GAL-89]). Y es que, dado un vector del Hilbert combinación lineal arbitrario de otros, representativos éstos de estados puros del sistema, no siempre está asegurada la existencia de un C.C.O.C. que posibilite la preparación del sistema en un estado puro asociado a esa combinación lineal. - Postulado 2: Cada observable de un sistema físico, o magnitud física susceptible de ser medida experimentalmente sobre el sistema (la entropía, por ejemplo, no es un observable), se representa en el formalismo matemático de la Mecánica Cuántica mediante un operador lineal autoadjunto que actúa en el espacio de Hilbert
del sistema físico considerado.
-Nota: la recíproca no es cierta: no todo operador lineal autoadjunto representa un observable; pueden operar reglas de superselección (véase [GAL-89]). - Cada estado puro, correspondiente a una preparación maximal del sistema físico, es autoestado de un C.C.O.C. o «conjunto completo de observables compatibles«, un conjunto no redundante integrado por todos los observables independientes compatibles que se pueden medir sobre el sistema, es decir, que conmutan entre sí dos a dos:
, donde
y
son los operadores autoadjuntos que representan a los dos observables en el formalismo.
-Se trata, en consecuencia, de observables medibles simultáneamente sobre el sistema con precisión arbitraria, por no estar ligados por una relación de indeterminación. La reunión de todos estos autoestados, bajo determinadas condiciones, permite construir una base ortonormal del espacio.
-En términos matemáticos, los operadores de un C.C.O.C. admiten diagonalización simultánea. Asumiremos que en el correspondiente espacio de Hilbert existe una base ortonormal numerable generalizada, integrada por vectores propios y, en su caso, vectores propios generalizados, comunes a todos los operadores autoadjuntos y compatibles integrantes del C.C.O.C. En consecuencia, cualquier estado del Hilbert admitirá expresión desarrollo en términos de los vectores de cualquiera de estas bases. - Postulado 3: El resultado de medir un observable, representado por el operador autoadjunto A, es necesariamente un elemento del espectro de A.
-Nota: Recuérdese que el espectro de un operador autoadjunto es siempre real (véanse los temas de operadores lineales sobre espacios de Hilbert y su teoría espectral). - Postulado 4 o postulado del colapso: Sobre los cambios de los estados puros tras las medidas:
-Si un sistema físico se halla preparado en el estado descrito por el ket, de expresión en la correspondiente base de autofunciones del operador
(cuyo espectro suponemos ahora puramente discreto) dada por
,
donde cadaes autoestado del observable
con autovalor
, con degeneración
, entonces tras una medida sobre él del observable
con resultado («filtrante«)
, el sistema pasa al estado descrito por el vector normalizado
.
-Ejemplo: sies un autovalor no degenerado del espectro discreto de
, tras una medida filtrante sobre
con resultado
, el sistema pasaría a ser descrito por el ket
, siendo
una constante de normalización.
-El cumplimiento de esta condición resume el concepto de «medida ideal» sobre un estado puro: la que se atiene a lo postulado. Porque no todas las medidas, en el sentido más amplio de intervención experimental sobre el sistema, respetarán este postulado; piénsese, por ejemplo, en una medida que «destruya» el sistema. Por ello, se suelen definir las «medidas ideales» como aquellas medidas de segunda especie que «respetan» este postulado 4 (pues sí, quizás hay algo de circular en todo esto). Digamos que una medida ideal es aquella en la que el aparato de medida afecta «lo mínimo posible» al sistema sobre el que se mide: la que determina unos observables sin afectar el resto de observables compatibles con los medidos.
-El cambio producido en el estado tras una medida ideal se suele denominar como reducción o colapso de la función de onda, y se trata de un cambio estocástico e irreversible. Una vez producido, en posteriores medidas (ideales) repetidas del observablesobre el sistema se tiene certeza de obtener siempre el resultado
obtenido la primera vez.
-Nota: en notación de Dirac y para un observable general, cuyo espectro no fuera puramente discreto, el anterior desarrollo del ket
en la correspondiente base de autofunciones del operador
se expresaría:
.
- Postulado 5: La ecuación de Schrödinger: Entre dos medidas consecutivas, y supuesto el sistema no experimenta interacción alguna en ese transcurso,, un estado puro sigue siendo estado puro, y en el rayo unidad representativo existe un ket o vector estado
representativo cuya evolución temporal viene determinada por la ecuación
,
la ecuación de Schrödinger, donderepresenta el Hamiltoniano del sistema y
es la constante de Planck
dividida por
.
-Cuando el sistema es conservativo, el Hamiltonianono depende explícitamente del tiempo y representa la energía total del sistema, si
representa un estado propio del operador
, correspondiente al valor propio
,
,
entonces se dice quees un estado estacionario, y su evolución temporal viene dada por:
.
- La función de onda: dado un sistema físico y un C.C.O.C.,
, la base ortonormal del espacio de Hilbert asociado,
, integrada por los correspondientes vectores propios comunes (
, etc.), permite expresar la «función de onda en la representación asociada a esa base»,
, cuyas variables recorren los sendos espectros de todos los operadores del C.C.O.C.:
.
Nota: obsérvese que, conocido el C.C.O.C. y su base ortonormal asociada, construir una función de onda requiere fijar las fases de los vectores de la base. - El vector de estado
y la función de onda en representación de posiciones
(cf. [GAL-89]) :
- Para una sola partícula sin espín, el vector de posición
determina su estado, de forma que una base ortonormal en el espacio está constituída por todos los autovectores simultáneos
(fases por fijar) de este operador (el espectro de cada
es continuo y llena
).
- La función de onda representativa del estado puro
en la anterior base ortonormal, o función de onda en representación de posiciones,
, viene dada por
().
- La densidad de probabilidad
se define según:
representa la probabilidad de que al medir la posición de la partícula en el instante
se encuentre como resultado su localización en un volumen
alrededor de la posición
.
- Normalización en el espacio de Hilbert
:
.
- Dimensiones de
: según la anterior condición de normalización, las dimensiones de la función de onda, en el caso de un sistema compuesto por una sola partícula, deben ser
, donde
simboliza longitud. En general, la función de onda para un sistema de
partículas, caso
dimensional, tiene dimensiones
.
- La función de ondas no es en general una función
del espacio usual tridimensional: es una función del espacio de configuración, que resulta ser isomorfo al espacio usual tridimensional sólo en el caso del sistema constituido por una partícula (espín aparte). En general, para un sistema de
partículas (sin incluir espín), la función de ondas
pertenece a un espacio de
dimensiones.
- Para una sola partícula sin espín, el vector de posición
- El vector de estado cuántico
:
- No representa las propiedades del sistema físico.
- No es una propiedad del sistema físico.
- No representa nuestro conocimiento subjetivo de las propiedades del sistema físico.
- Es la herramienta matemática que permite evaluar las distribuciones de probabilidad de los resultados de la medida de todos los observables o magnitudes físicas medibles sobre el sistema físico a que se asocia (medidas que no revelan en modo alguno valores preexistentes de esos observables: «los experimentos no realizados no tienen resultados»).
- Contextualidad de algunas propiedades:
-Se denomina «contextualidad» a la propiedad que poseen algunas variables cuánticas de un sistema (como espín, posición, momento, etc.), según la cual las predicciones de la teoría sobre los resultados de las medidas de determinados observables compatibles son inconsistentes con la suposición de que dichas variables poseen valores definidos o pre-existentes a) con anterioridad a que las medidas se lleven a cabo y b) independientemente de cuáles sean todas las mediciones concretas dispuestas.
-Por tanto, el valor resultante de la medida de una variable física u observable cuántico contextual depende de lo que se decida medir simultáneamente a él. En este sentido, puede concebirse como una propiedad del sistema conjunto que integra el aparato experimental (con lo que se mide) con el sistema cuántico (sobre el que se mide).
-Ejemplo: Imaginemos que tenemos un sistema compuesto por dos electrones, 1 y 2, y queremos medir la componente de espíndel primero. Montamos una experiencia A en la que medimos
junto con
y otros observables, todos compatibles entre sí y con los dos anteriores. Por otro lado, montamos también una segunda experiencia B en que medimos
y
, ahora con otro conjunto de observables compatibles entre sí y con estos dos, pero distinto al anterior. En cada experiencia, los observables que se miden son compatibles; en caso contrario, el experimento tendría una restricción fundamental en la precisión alcanzable, marcada por el principio de indeterminación. Pero obsérvese que los dos observables que acompañan a
en cada experiencia,
y
, son complementarios (y pudiera haber más incompatibilidades entre sendos observables en las dos experiencias A y B). Pues bien, en sistemas idénticos, preparados de forma idéntica, asociados por tanto con la misma función de onda, las dos experiencias pueden producir legítimamente, para determinadas elecciones de todos los observables que se van a medir, sendos resultados distintos para
.
-La contextualidad cuántica invalida la suposición de que este tipo de propiedades poseen valores determinados o pre-existentes con anterioridad a que sus medidas se lleven a cabo. Igualmente, hace depender el resultado de las medidas de cuáles sean todas las mediciones concretas dispuestas, es decir, de cuáles propiedades compatibles específicas van a ser medidas simultáneamente. De modo que un observable contextual puede concebirse como una propiedad del sistema conjunto que integra el aparato experimental (con lo que se mide) con el sistema cuántico (sobre el que se mide). Posición, momento y espín son ejemplos de variables contextuales. - Algunas lecturas interesantes al respecto:
-Entrevista con A. Cabello, de la Univ. de Sevilla:
 https://joanencunyat.wordpress.com/2011/11/23/adan-cabello-el-experimento-de-innsbruck/
https://joanencunyat.wordpress.com/2011/11/23/adan-cabello-el-experimento-de-innsbruck/
-Efectos observables del teorema de Bell-Kochen-Specker en el laboratorio:
 http://www.tendencias21.net/Para-las-mediciones-cuanticas-el-sentido-comun-no-es-suficiente_a3520.html
http://www.tendencias21.net/Para-las-mediciones-cuanticas-el-sentido-comun-no-es-suficiente_a3520.html - En algún sentido, pues, podría decirse que el vector de estado representa una preparación experimental del sistema físico más que a este mismo… Una buena referencia para ampliar puntos de vista:
 Lalöe, F.; «Do we really understand quantum mechanics? Strange correlations, paradoxes and theorems«, American Journal of Physics 69 (6), 2001.
Lalöe, F.; «Do we really understand quantum mechanics? Strange correlations, paradoxes and theorems«, American Journal of Physics 69 (6), 2001.
- El valor medio o esperado del observable representado por el operador lineal autoadjunto
en el estado normalizado
(esto es,
) se define como la media de los resultados obtenidos al efectuar un gran número
de medidas de este observable en sendos
sistemas idénticos, todos ellos preparados en el mismo estado
. Es decir:
.
-Este valor esperado es un concepto estadístico: es la media de los resultados obtenidos, y en general no tiene por qué pertenecer siquiera al espectro del operador. Es decir, siendo siempre real, no tiene por qué coincidir con el resultado de una de las medidas realizadas (aunque pueda suceder, en particular); tampoco tiene por qué coincidir con el valor más probable.
-Sies normalizable, pero no está normalizado, la expresión para el valor esperado es:
.
- Algunos teoremas (cf. [GAL-89]):
- Principio de superposición: dada la estructura lineal del espacio de Hilbert
, cada superposición de vectores de estado del sistema, o combinación lineal
con coeficientes escalares arbitrarios
, representa otro estado puro del sistema (en ausencia de reglas de superselección, según notas anteriores).
- Principio de indeterminación: Dado un sistema físico en un estado caracterizado por el ket
, y dados dos observables
y
, entonces
, donde
es el conmutador de los dos operadores y
,
representa la desviación típica o dispersión cuadrática media (la raíz cuadrada de la varianza) de un conjunto de medidas, realizadas sobre una colección de sistemas idénticos entre sí e igualmente preparados en el mismo estado puro, o indeterminación en la medida del observable
sobre el sistema en el estado
.
- Principio de superposición: dada la estructura lineal del espacio de Hilbert
- Todo lo anterior forma parte del núcleo de la frecuentemente denominada «interpretación de Copenhague de la Mecánica Cuántica«, la (en denominación más adecuada) «interpretación ortodoxa«. Una relación más amplia de postulados básicos se encuentra en el apartado Axiomática fundamental de la Mecánica Cuántica.
Referencias
[COH-89] Cohen-Tannoudji, C., Diu, B. and Lalöe, F; Quantum Mechanics, 2 volúmenes, Wiley-VCH, New York.
[GAL-89] Galindo, A. y Pascual, P.; Mecánica Cuántica, Eudema, 1989
[JAM-74] Jammer, M.; The philosophy of Quantum Mechanics, Wiley, 1974.
[MEH-82] Mehra,J., Rechenberg,H.; The Historical Development of Quantum Mechanics, 6 vol., Springer-Verlag, Nueva York, 1982.
[NEU-91] Neumann, J. von; Fundamentos matemáticos de la Mecánica Cuántica, CSIC, Raycar, Madrid, 1991.
[WHE-83] Wheeler, J.A. y Zurek,W.H., ed.; Quantum Theory and measurement, Princenton Univ., Princenton, 1983.
Páginas complementarias
Bombal, F.; Los modelos matemáticos de la Mecánica Cuántica, La Ciencia en el siglo XX,
Seminario Orotava de Historia de la Ciencia, pp. 115-146, Consejería de Educación del Gobierno de Canarias, 1999.
Lalöe, F.; «Do we really understand quantum mechanics? Strange correlations, paradoxes and theorems«, American Journal of Physics 69 (6), 2001.
http://la-mecanica-cuantica.blogspot.com.es/2009/08/interpretacion-probabilista-de.html
http://la-mecanica-cuantica.blogspot.com.es/2009/08/interpretacion-probabilista-de-ii.html
APPS
excelente información
Super completa