Desarrollo histórico

Desarrollo histórico del formalismo cuántico

Diversidad original de formalismos

Una mirada a los manuales usuales nos proporcionará, en general, la siguiente cronología para el desarrollo del formalismo cuántico:

1925: Mecánica de Matrices: Born, Heisenberg, Jordan.
1926: Mecánica Ondulatoria: Schrödinger.
1926: Shrödinger establece la equivalencia entre ambas mecánicas:
E. Schrödinger,»Über das Verhältnis des Heisenberg-Born-Jordanschen Quantenmechanik zu der meinen», Annalen der Physik 79 (1926) 734-756.

En realidad, no serían plenamente equivalentes hasta 1932, en que von Neumann culminó su trabajo de formalización:
F.A. Muller, «The Equivalence Myth of Quantum Mechanics. I», Studies in Theory and Philosophy of Modern Physics, 28B,1 (1997) 35-61.Ref 2-2: F.A. Muller, «The Equivalence Myth of Quantum Mechanics. II», Studies in Theory and Philosophy of Modern Physics, 28B,2 (1997) 219-247.
La equivalencia matemática entre los distintos formalismos quedará plenamente demostrada, pues, cuando von Neumann presente la M.C. formalizada como un cálculo de operadores autoadjuntos en un espacio de Hilbert $H$ :
J. von Neumann, Mathematische Grundlagen der Quantenmechanik, Springer, Berlín, 1932:
-trad. española: Fundamentos matemáticos de la Mecánica Cuántica; Instituto de Matemáticas “Jorge Juan”; CSIC, 1949.
-trad. inglesa: Mathematical Foundations of Quantum Mechanics, Princenton Univ., Princenton, 1955.
-reimp. española: [NEU-91], J. von Neumann, Fundamentos matemáticos de la Mecánica Cuántica, Consejo Superior de Investigaciones Científicas, Madrid, 1991.

La equivalencia definitiva:

mecánica matricial: representación espacio l² de las secuencias de números complejos tales que Σ |x|² converge.
mecánica ondulatoria: representación espacio L²(R³) de las funciones complejas de cuadrado Lebesgue-integrable.
isomorfismo: resolver el problema de autovalores de un operador en L² es equivalente a diagonalizar la correspondiente matriz en l².
Si añadimos a este formalismo la interpretación probabilística de Born para |Ψ|² y el correspondiente conjunto de postulados, obtenemos el «core» de la denominada «interpretación de Copenhague de la M.C.«, denominada usualmente como «interpretación ortodoxa»:
[GAL-89]: A. Galindo y P. Pascual, Mecánica Cuántica, Eudema, Madrid, 1989.

¿Se trató de un proceso de desarrollo continuo, sin disensiones ni confrontamientos? NO.

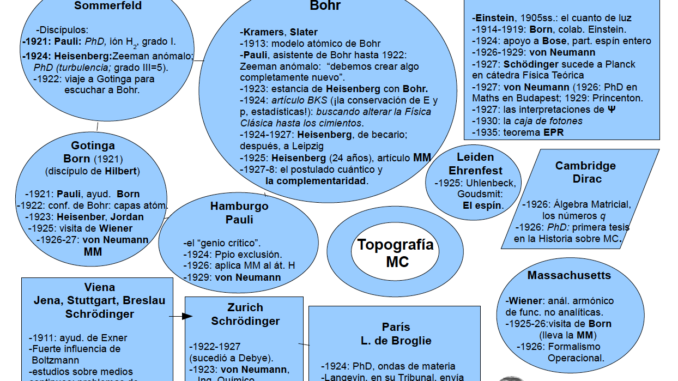
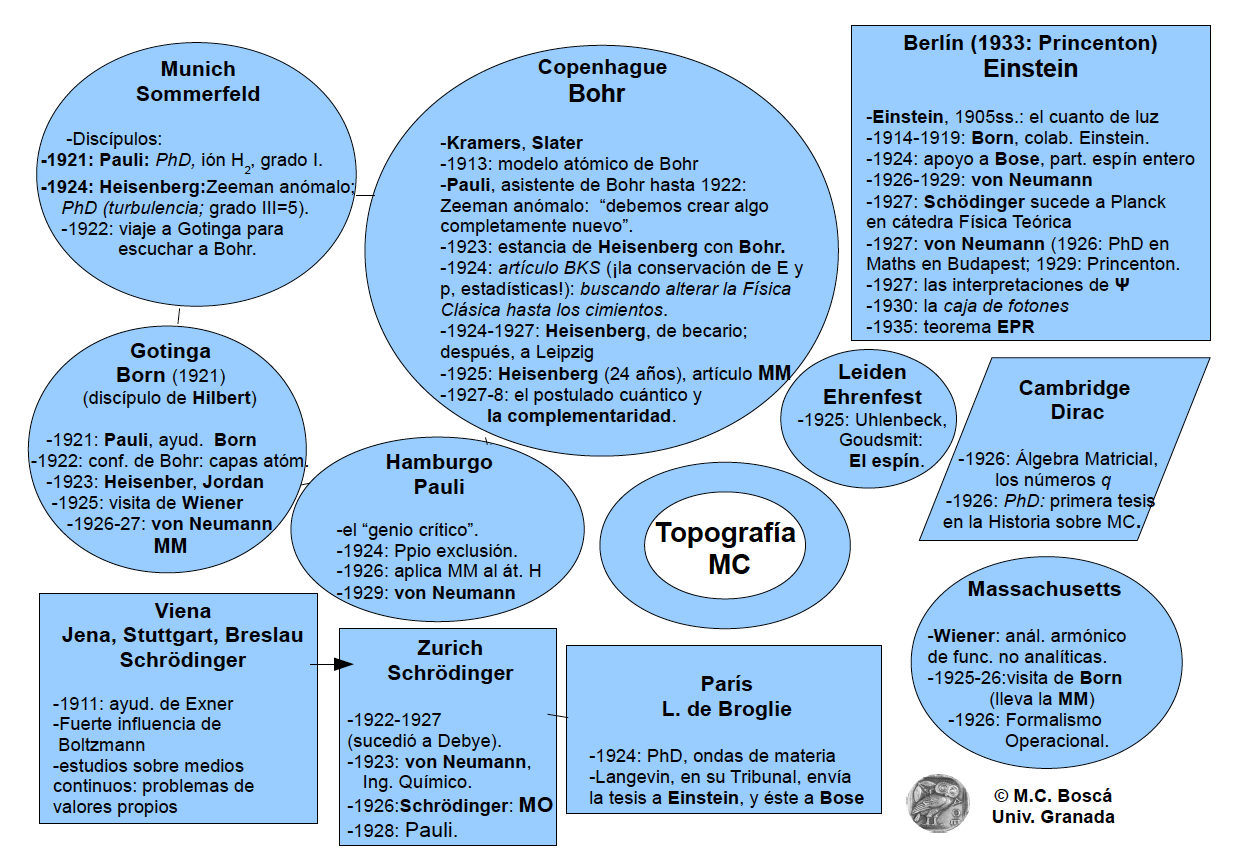
Geografía cuántica

Mecánica de Matrices y formalismo operacional de Born-Weiner

En 1925 Heisenberg publicó un artículo pionero, «Sobre la interpretación cuántica de las relaciones cinématicas y dinámicas»:
Heisenberg,W.; “Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen”, Zeitschrift für Physik 33 (1925) 879-893.

Se trata de la primera teoría consistente de los fenómenos cuánticos. Heisenberg hace intervenir sólo magnitudes observables, en una adhesión a los puntos de vista de Mach, inspirada en Einstein:
Heisenberg,W.; Encuentros y conversaciones con Einstein y otros ensayos, Alianza Editorial, Madrid, 1980.
Así pues, elige magnitudes ópticas determinadas experimentalmente, como la frecuencia y la amplitud, en sustitución de las variables orbitales, efectuándose la traducción de las expresiones clásicas al lenguaje cuántico mediante una aplicación del principio de correspondencia.
En el trabajo, vía este principio, el cual permite asociar a cada transición del átomo un término del desarrollo de Fourier de la trayectoria clásica, Heisenberg encontró para la probabilidad de una transición leyes cualitativamente similares a las de la intensidad de dichas componentes de Fourier.
Icaza, J.J.; La construcción de la Mecánica Cuántica, Univ. del País Vasco, Bilbao, 1991, pp. 22-29.
El papel de las coordenadas del electrón es asumido por un conjunto de parámetros correspondientes a los coeficientes de Fourier del movimiento clásico a lo largo de una trayectoria, viniendo a estar asociados con dos estados estacionarios del átomo y siendo una medida de la probabilidad de transición entre ellos.
Cada variable se representa en el formalismo de Heisenberg por un conjunto de amplitudes de transición, siendo el álgebra correspondiente no conmutativo.
1925: Los trabajos de Heisenberg, Born y Jordan, configuran la primera formulación rigurosa de la nueva Mecánica Matricial:
Born, M. and Jordan, P.; “Zur Quantenmechanik”, Zeitschrift für Physik 34 (1925) 858-888.
Born, M., Heisenberg ,W. and Jordan, P.; “Zur Quantenmechanik. II”, Zeitschrift für Physik 35 (1926) 557-615.[ICA-91], pp. 44-58.

Enuncian la relación mecánico-cuántica básica: $pq - qp=-i\frac{h}{2\pi} I$ , «misteriosa ecuación cuántica», donde $p$ y $q$ representan «conjuntos de números cuyo producto depende del orden» (posteriormente identificados como matrices; $I$ será la matriz identidad).
Las ecuaciones de la mecánica clásica hamiltoniana se sustituyen por equivalentes matriciales, jugando la energía un papel principal.
Los elementos diagonales de cada matriz solución de un problema de dinámica atómica se identifican con los valores medios en el tiempo de las magnitudes representadas, calculadas en los estados estacionarios.
Los elementos no diagonales se asocian con con transiciones cuánticas del sistema entre diferentes estados estacionarios.
1926, Pauli: aplicación al espectro de emisión del átomo de hidrógeno.
Pauli, W.; “Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik”, Zeitschrift für Physik 36 (1926) 336-363.
Sus resultados reproducían los del modelo de Bohr; además, obtenía, por medios matriciales, el efecto Stark, desarrollaba un cálculo perturbativo para la energía del átomo de hidrógeno en campos eléctrico y magnético cruzados, situación sin tratamiento posible para la vieja teoría cuántica.
La mecánica matricial se consolida como un método válido para los fenómenos atómicos.
1926, Born y Wiener: nueva formulación de las leyes de cuantización para fenómenos periódicos u aperiódicos, partiendo de un tratamiento operacional:
Born, M. and Wiener, N.; “A new formulation of the laws of quantization of periodic and aperiodic phenomena”, Journal of Mathematics and Physics (M.I.T.) 5 (1925-26) 84-98; “Eine neue Formulierung der Quantengesetze für periodische und nichtperiodische Vorgänge”, Zeitschrift für Physik 36 (1926) 174-187.
Interpretan las relaciones de conmutación y las ecuaciones canónicas de la mecánica matricial como ecuaciones entre operadores, introduciendo el concepto de hermiticidad para operadores.
Curiosidad: de la comparación entre las ecuaciones
$pq - qp=-i\frac{h}{2\pi} I$ , de un lado, y $\frac{d}{dt} \cdot t - t \frac{d}{dt}=I$ , de otro, podrían haber llegado a $p = -i\frac{h}{2\pi} \frac{\partial}{\partial q}$ . Pero no lo hicieron. Posteriormente, Born comentaría:
Nunca me perdonaré, porque, de haber hecho esto, habríamos obtenido, a partir de la mecánica cuántica, y unos meses antes que Schrödinger, toda la mecánica ondulatoria.
-Nota: en ese momento, la denominada «mecánica cuántica» era la «mecánica matricial» de Born y Heisenberg, mientras que el formalismo rival de Schrödinger era denominado como «mecánica ondulatoria».
Icaza, J.J.; La construcción de la Mecánica Cuántica, Univ. del País Vasco, Bilbao, 1991.
También disponemos del siguiente testimonio de Condon, que visitó Gotinga en 1926:
Hilbert se rió mucho de Born y Heisenberg porque, cuando descubrieron la Mecánica de Matrices, se encontraron con el mismo tipo de dificultades que, por supuesto, todo el mundo encuentra al manipular y tratar de resolver problemas con matrices [infinitas]. Cuando fueron a pedir ayuda a Hilbert, éste les dijo que las únicas veces que había tenido que ver con matrices fue cuando éstas aparecían como subproducto del estudio de autovalores de una ecuación diferencial con condiciones de contorno. Les sugirió que si encontraban la ecuación diferencial que originaba esas matrices, probablemente obtendrían más información. Heisenberg y Born pensaron que era un comentario para salir del paso, y que Hilbert no sabía realmente de lo que estaba hablando. Así que más tarde Hilbert se divirtió mucho, indicándoles que podían haber descubierto la Mecánica Ondulatoria de Schrödinger seis meses antes que éste, si le hubieran hecho caso.
Cit. en M. Jammer, The Conceptual Development of Quantum Mechanics, Tomash Publishers, American Institute of Physics, 1989.

Método algebraico de Dirac

En 1926 Dirac, sólo 5 días después que la referencia antes dada de Pauli, en la que se aplicó con éxito el formalismo matricial al átomo de Hidrógeno, publicó dos importantes artículos:
Dirac, P.A.M.; “The fundamental equations of Quantum Mechanics”, Proceedings of the Royal Society (London) A109 (1925) 642-653, al que seguirá: Dirac, P.A.M.; “Quantum Mechanics and a Preliminary Investigation of the Hydrogen Atom”, Proceedings of the Royal Society (London) A110 (1926) 561-579.
En ellos, Dirac desarrolla un nuevo método que, en esencia, traslada directamente la teoría de Hamilton-Jacobi a la mecánica cuántica, obteniendo la fórmula de Bohr del átomo de hidrógeno. Dirac, de hecho, no se percató de la equivalencia entre su nueva «extraña álgebra no conmutativa» y el álgebra matricial, y su método fue considerado como distinto al de Heisenberg.
Inspirado en los trabajos anteriores de Heisenberg, Born y Jordan, Dirac consiguió relacionar las nuevas variables cuánticas y su álgebra no conmutativa con las variables clásicas angulares y de acción de la teoría de Hamilton-Jacobi, a través de los corchetes de Poisson:
Principio de correspondencia de Dirac: La correspondencia entre las teorías clásica y cuántica no está tanto en el acuerdo en el límite en que h→0, sino más bien en el hecho de que las operaciones matemáticas en ambas teorías obedecen las mismas leyes.
Por tanto, toda ley de la mecánica clásica podía trasladarse a la mecánica cuántica mediante la sustitución del corchete de Poisson [x,y] por el corchete de Poisson cuántico $-i \frac{2\pi}{h}(xy-yx)$ , o «producto de Heisenberg».
Dirac propone distinguir entre variables de la física clásica, «números c», y variables de la física cuántica, «números q», de los que lo importante no es saber qué son realmente, sino representarlos mediante los c, a fin de obtener resultados contrastables con los experimentales:
P:A.M. Dirac en ref. 2-10, ver [WAE-67], pp. 418-419:
At present one can form no picture of what a q-number is like […] In order to be able to get results comparable with experiments, we must have some way of representing q-numbers by means of c-numbers, so that we can compare these c-numbers with experimental values. The representation must satisfy the condition that one can calculate the c-numbers that represent x+y, xy and yx when one is given the c-numbers that represent x and y.
El trabajo de Dirac, «versión mecánico-cuántica de la teoría clásica de las variables angulares y de acción», o «técnica de los números q», pasó inadvertido prácticamente, no consiguiendo casi ninguna atención, a diferencia de las mecánicas matricial y ondulatoria.

Lecturas interesantes:

http://www.lsr.ph.ic.ac.uk/~jrogel/write/essays/dirac.pdf
Entrevista con Dirac.

Ondas de materia de L. de Broglie

Precedentes:
- a) La analogía de Hamilton: En 1833, Hamilton había propuesto dotar a la óptica de un formalismo semejante al de la mecánica analítica, vía la analogía entre:1.
  La cantidad mecánica 1/p = 1/√2m(E – V) , en la expresión del principio de Maupertuis para una partícula de masa m y energía total E en un campo de fuerzas de energía potencial V, o principio de mínima acción: la trayectoria seguida por una partícula es la que hace estacionaria la acción.2. La cantidad óptica λ del principio de Fermat: la trayectoria seguida por un rayo de luz monocrómatico es la que hace estacionario el camino óptico.
  -Se establece, pues, una correspondencia entre cada magnitud de la mecánica y de la óptica geométrica: trayectoria de la partícula/rayo de luz; superficie de acción constante/superficie de onda. Si la óptica geométrica es una aproximación de la óptica ondulatoria, se intuye que la mecánica clásica es una aproximación a una «mecánica ondulatoria».
- b) Los trabajos de M. Brillouin:M. Brillouin en sus estudios sobre el movimiento vibracional de una partícula en un medio elástico había realizado una comparación con el modelo atómico de Bohr, caracterizando las propiedades discontinuas por números enteros:
  Brillouin, M.; «Actions mécaniques à hérédité discontinue par propagation; essai de théorie dynamique de l’atom à quanta», Comptes Rendus 171 (1919) 1318-1320; «Actions à hérédité discontinue et raies spectrales», Comptes Rendus 171 (1920) 1000-1002.
La tesis de L. de Broglie:
- En 1924 L. de Broglie presenta su tesis doctoral:
  Broglie, L. de; «Recherches sur la théorie des quanta», Annales de Physique 10,3 (1925) 22-128.
- La tesis es una versión integrada de diversos artículos aparecidos entre 1922 y 1924, y en ella de Broglie establece la dualidad onda corpúsculo para las partículas materiales.
- Hipótesis: la idea básica de la teoría cuántica el la imposibilidad de considerar «una porción aislada de energía» sin asignarle una frecuencia ν: relación de Einstein E = hν para los cuantos de luz (fotones).
- Tesis: las partículas materiales, también «porciones aisladas de energía», debería ser tratadas análogamente, asociándoles una longitud de onda λ: → relación de de Broglie λ = h/p para las partículas materiales (ondas de fase o materia).
- Esquema de la tesis:
  1. Cap. 1: Justificación de la introducción de la onda de fase y discusión de sus propiedades, demostrándose la igualdad entre la velocidad de grupo y la de la partícula.
  2. Cap. 2: Análisis de los principios de Fermat y Maupertuis, aplicados a la descripción de la partícula cuántica:
    «El principio de Fermat aplicado a la onda de fase es idéntico al principio de Mauterpuis aplicado a la partícula; las trayectorias dinámicamente posibles para la partícula son idénticas a los rayos posibles para la onda».
  3. Cap. 3: Estudio de las condiciones cuánticas de la estabilidad de las órbitas electrónicas en los átomos; se impone la condición de resonancia longitud de la órbita = n·λ y se obtienen las condiciones de cuantización de Bohr-Sommerfeld.
  4. Cap. 4: Aplicación de la condición de resonancia al átomo de hidrógeno relativista.
  5. Cap. 5: Mediante los cuantos de luz, supuestos de masa extraordinariamente pequeña, se justifican con la teoría corpuscular de la luz los efectos Dopplery otros.
  6. Cap. 6: Estudio de la dispersión de rayos X y γ por la materia; análisis del efecto Compton.
  7. Cap. 7: Desarrollo de una mecánica estadística de los cuantos de luz y átomos.
Hay que destacar que en 1923 de Broglie ya había sugerido la posibilidad de observar fenómenos de difracción con sus ondas de fase. Asimismo, en la lectura de su tesis, a preguntas de Perrin, miembro del tribunal, afirmó que podría realizarse mediante la difracción de electrones por cristales. Tales experimentos serían llevados a cabo en 1927 por Davisson y Germer e, independientemente, por Thomson.
Comentemos, finalmente, que Langevin, miembro también del tribunal, haría llegar una copia de la tesis a Einstein, quien comentaría muy favorablemente su contenido al propio Langevin y a Lorentz.

Mecánica ondulatoria de Schrödinger

Con anterioridad a la publicación de sus comunicaciones, Schrödinger se había familiarizado en la Univ. de Viena con las ecuaciones de onda y los problemas de valores propios.
En 1926 aparecerán 4 artículos, las 4 «comunicaciones», en que desarrollará el formalismo ondulatorio de la M.C.:
Icaza, J.J.; La construcción de la Mecánica Cuántica, Univ. del País Vasco, Bilbao, 1991, pp. 90ss.
Nota: Sin embargo, la primera publicación de un formalismo continuo para la mecánica cuántica corresponde a Lanczos, quien, un mes antes de aparecer la primera comunicación de Schrödinger, publicó un desarrollo de la teoría en términos de ecuaciones integrales:
Ref. 2-20: Lanczos, K.; «Über eine feldmässige Darstellung der neuen Quantenmechanik», Zeitschrift für Physik 35 (1926) 812-830.
Las cuatro comunicaciones de Schrödinger:
1. Primera comunicación:
  Schrödinger, E.; «Quantisierung als Eigenwertproblem (Erste Mitteilung)», Annalen de Physik 79 (1926) 361-376.
  -Plantea un problema variacional. Partiendo de la ecuación de Hamilton-Jacobi para un sistema cuyo hamiltoniano sea constante del movimiento y coincida con la energía, introduce una función desconocida ψ, relacionada con la función característica del sistema, consiguiendo expresar H = E como una forma cuadrática F en ψ y sus derivadas primeras,
  F = 0.
  -A continuación, introduce una condición variacional de «búsqueda de ψ real, unívoca, finita, continua, con derivadas primeras continuas, que haga extremal la integral de F extendida a todo el espacio de configuración»:
  -Reemplazo de las condiciones cuantización por un problema variacional que conduce a la obtención de la ecuación de Schrödinger independiente del tiempo.
  -Resuelta la ecuación, con ayuda de Weyl, Schrödinger obtuvo el espectro del átomo de hidrógeno, partes discreta y continua, con la adición de la condición «δψ → constante» a largas distancias.
  -Finalizaba con las siguientes observaciones:
  Schrödinger, en su primera comunicación, cit. en [ICA-91], p. 97:
  Se puede, por tanto, intentar asociar la función ψ con un proceso vibratorio en el átomo, proceso posiblemente más real que las órbitas electrónicas, cuya existencia está siendo muy cuestionada actualmente […]. El misterioso requisito de los números enteros no entra ya en las reglas de cuantización, sino que ha retrocedido, por así decir, un paso atrás, al demostrar que es el resultado de la finitud y univocidad de una cierta función espacial […]. No hace falta decir cuánto más agradable sería concebir una transición cuántica como un intercambio de energía de un modo de vibración a otro, que considerarla como un salto de electrones.
  Schrödinger → deshacerse de las reglas de cuantización para recuperar lo esencial: la continuidad.
2. Segunda comunicación:
  Schrödinger, E.; «Quantisierung als Eigenwertproblem (Zweitte Mitteilung)», Annalen de Physik 79 (1926) 489-527.
  -Plantea un problema de valores propios.
  -Se inicia con una disquisición sobre la analogía de Hamilton, claramente inspirada en de Broglie; a continuación establece la ecuación de Hamilton-Jacobi como la expresión del principio de Huyguens, identificando los principios de Maupertuis y Fermat.
  -Afirma la necesidad de desarrollar una mecánica ondulatoria, ante el fallo de la mecánica clásica en «dimensiones muy pequeñas y con curvaturas orbitales muy pronunciadas».
  -El desarrollo del tal mecánica ondulatoria se inicia a partir de la ecuación de ondas para una función ψ sinusoidal, para la que se ha establecido la velocidad de propagación mediante las relaciones de de Broglie: Reemplazo de las condiciones cuantización por un problema de valores propios que conduce a la obtención de la ecuación de Schrödinger independiente del tiempo.
  -Resuelta la ecuación, de la multiplicidad de soluciones obtenidas se escogen las correspondientes a los procesos estacionarios, imponiendo las apropiadas condiciones de contorno, exigiendo a la función ψ ser unívoca, finita y continua en todo el espacio de configuración.
  -A continuación se realiza la aplicación al oscilador armónico lineal y algunos sistemas atómicos simples, obteniéndose los mismos resultados que con la mecánica matricial de Born, Heisenberg y Jordan.
3. Tercera comunicación:
  Schrödinger, E.; «Quantisierung als Eigenwertproblem (Dritte Mitteilung)», Annalen de Physik 80 (1926) 436-490.
  -Desarrollo de la teoría de perturbaciones independiente del tiempo, extendiendo el método de Strutt para vibraciones acústicas a la mecánica cuántica, incorporando el tratamiento de casos degenerados.
4. Cuarta comunicación:
  Schrödinger, E.; «Quantisierung als Eigenwertproblem (Vierte Mitteilung)», Annalen de Physik 81 (1926) 109-139.
  -Desarrollo de la teoría de perturbaciones dependiente del tiempo.
  -Obtención de la ecuación de Schrödinger dependiente del tiempo, verdadera ecuación de ondas, pues contiene ∂ψ/∂t; la ψ es ya compleja.

Interpretaciones matricial y ondulatoria frente a frente

Comparación entre las características de los formalismos matricial y ondulatorio:

Mecánica Ondulatoria	Mecánica Matricial
-tratamiento analítico -se destaca la continuidad -onda como concepto básico	-tratamiento algebraico -se destaca la discontinuidad -corpúsculo como concepto básico*

* Aunque Heisenberg no creía necesario emplear términos como «partícula» u «onda» para abordar los fenómenos cuánticos, y prefería suponer a la teoría como meramente proveedora de un esquema matemático consistente que nos diga todo lo que puede ser observado, algo que le llevaría a la confrontación con Bohr; en cambio, Born y Jordan defendían el mantenimiento del concepto de partícula. Escuchemos la opinión de Heisenberg, expresada en 1967:

Heisenberg, W., “Quantum theory and its interpretation”, en Niels Bohr-His Life and Work as seen by his Friends and Colleagues, ed. Por Rozental, North-Holland, Amsterdam, 1967, p. 98, cit. en [JAM-74]:

“We have a consistent mathematical scheme and this consistent mathematical scheme tell us everything which can be observed. Nothing is in nature which cannot be described by this mathematical scheme”.

Equivalencia entre formalismos y teoría de las transformaciones

1926: entre la publicación de las dos primeras comunicaciones, Schrödinger publicó un artículo donde establecía como, desde el punto de vista puramente matemático, la mecánica matricial y la mecánica ondulatoria son completamente equivalentes, afirmando que la prioridad de una u otra podría, desde este punto de vista, reducirse a la conveniencia de cálculo:
Schrödinger, E.; «Über das Verhältnis des Heisenberg-Born-Jordanschen Quantenmechanik zu der meinen», Annalen der Physik 79 (1926) 734-756.
Desde un punto de vista positivista, pues, en que se identifican equivalencia matemática y física, mecánica matricial y mecánica ondulatoria eran la misma teoría.
Eckart, de forma independiente, publicó unos artículos donde resolvía la ecuación de Schrödinger del oscilador armónico con el tratamiento operacional de Born y Wiener, estableciendo la equivalencia de las leyes de cálculo de ambas mecánicas y calculando las amplitudes de transición del átomo de hidrógeno incluyendo en su tratamiento el espín electrónico:
Eckart,C.; «The solution of the problem of the simple oscillator by a combination of the Schröndiger and the Lanczos theories», Proceedings of the National Academy of Sciences 12 (1926) 473-476.
Eckart,C.; «Operator calculus and the solution of the equations of the quantum dynamics», Physical Review 28,2 (1926) 711-726.
Eckart,C.; «The hydrogen spectrum in the new quantum theory», Physical Review 28,2 (1926) 927-935.
Teoría de las transformaciones: 1927: Dirac desarrolla la teoría de las transformaciones, método matemático para el tratamiento de los problemas cuánticos semejante al de las transformaciones canónicas de la Dinámica clásica:
Dirac, P.A.M.; «The Physical Interpretation of the Quantum Dynamics», Proceedings of the Royal Society (London) A113 (1927) 621-641:
«Las funciones propias de la ecuación de Schrödinger son precisamente los elementos de la matriz de transformación, o las funciones de transformación, que permiten transformar el esquema de la representación matricial a un esquema en que el hamiltoniano es una matriz diagonal» (es en este artículo donde Dirac introdujo la función delta que lleva su nombre).
Establecimiento de la equivalencia entre las mecánicas matricial y ondulatoria: 1927: Jordan, casi simultáneamente a Dirac, llevó a cabo otro desarrollo de la teoría de las transformaciones, afirmando en su artículo:
Jordan,P.; «Über eine neue Begründung der Quantenmechanik», Zeitschrift für Physik 40 (1927) 809-838.
Las cuatro forrmas de la Mecánica Cuántica: la teoría matricial, la teoría de Born y Wiener, la mecánica ondulatoria y la teoría de los números q, son casos particulares de la misma teoría formal general.
Estos trabajos de Dirac y Jordan se publicaron después de que Born hubiera expuesto su interpretación probabilística para ψ, y en ellos se señala la conveniencia de situar en la base del formalismo y del contenido conceptual de la mecánica cuántica las consideraciones estadísticas, abandonando el principio de correspondencia, que es considerado ya como artificioso.

Formalismo de von Neumann: Mecánica Cuántica en el espacio de Hilbert

1927: Hilbert, von Neumann y Nordheim llevan a cabo un estudio profundo de los fundamentos matemáticos de la mecánica cuántica, basado en el desarrollo de la teoría de las transformaciones de Jordan:
Hilbert, D., Von Neumann, J., Nordheim, L.; «Über die Grundlagen der Quantenmechanik», Mathematische Annalen 98 (1927) 1-30.

Partiendo de un conjunto de axiomas de contenido físico, se construye un formalismo matemático consistente en un cálculo operacional general, derivándose las ecuaciones de Schrödinger como las ecuaciones funcionales para las amplitudes de probabilidad relativa.
1927-1932: von Neumann establece el marco matemático para la M.C. que se establecería como definitivo:
von Neumann, J.; «Mathematische Begründung der Quantenmechanik», Götinger Nachrichten (1927) 1-57; «Wahrscheinlichkeitstheoretischer Aufbau der Quan-tenmechanik», Göttinger Nachrichten (1927) 245-272; «Thermodynamik quantenmechanischer Gesamtheiten», Göttinger Nachrichten (1927) 273-29; «Allgemeine Eigenwerttheorie Hermitescher Funk-tionaloperatoren», Mathematische Annalen 102 (1929) 49-131; «Beweis des Ergodensatzes und des H-Theorems in der neuen Mechanik», Zeitschrift für Physik 57 (1929) 30-70.
von Neumann, J.; Mathematische Grundlagen der Quantenmechanik, Springer, Berlín, 1932; trad. al inglés como Mathematical Foundations of Quantum Mechanics, Princenton Univ., Princenton, 1955; trad. al español como Fundamentos Matemáticos de la Mecánica Cuántica, Publicaciones del Instituto de Matemáticas «Jorge Juan», Consejo Superior de Investigaciones Científicas, Madrid, 1949; 2ª edición en 1991, ver [NEU-91].
Formalismo de la Mecánica Cuántica en el espacio de Hilbert:
Galindo, A. y Pascual, P.; Mecánica Cuántica, Eudema, Madrid, 1989 (y la mayoría de los manuales de mecánica cuántica).
F. Bombal, «Los modelos matemáticos de la Mecánica Cuántica«, La Ciencia en el siglo XX; Seminario “ Orotava” de Historia de la Ciencia, pp. 115-146.

Curiosidad: con posterioridad, von Neumann se declararía disconforme con su formalismo, debido a la insatisfacción generada por el problema de la interpretación de la probabilidad cuántica: von Neumann, cit. en Birkhoff, G.; «Lattice Theory», American Mathematical Society Colloquium Publications 25 (1966): «I would like to make a confession which may seem immoral: I do not believe absolutely in Hilbert space any more»; cf. Rèdei, Miklós; «Why John von Neumann did not Like the Hilbert Space Formalism of Quantum Mechanics (and What he Liked Instead)», Studies in History and Philosophy of Modern Physics 27, 4 (1996) 493-510.

Referencias

Lecturas sugeridas:http://www-history.mcs.st-andrews.ac.uk/HistTopics/The_Quantum_age_begins.html http://mooni.fccj.org/~ethall/quantum/quant.htm Sobre los premios Nobel http://www.faqs.org/docs/qp/chap05.html http://www-inst.eecs.berkeley.edu/~cs191/lectures/lecture7.pdf
Una buena relación de links:
–http://www.aip.org/history/heisenberg/p08r.htm

Bibliografía

[ABR-51] Abro, d’, The rise of the new Physics, Dover, 1951.
[GAL-89] Galindo, A. y Pascual, P.; Mecánica Cuántica, Eudema, Madrid, 1989.
[ICA-91] Icaza, J.J.; La construcción de la Mecánica Cuántica, Univ. del País Vasco, Bilbao, 1991.
[JAM-66] Jammer, M.; The Conceptual Development of Quantum Mechanics, McGraw-Hill, Nueva York, 1966.
[MEH-82] Mehra, J., Rechenberg, H.; The Historical Development of Quantum Mechanics, 6 vol., Springer-Verlag, Nueva York, 1982.
[NEU-91] Neumann, J. von; Fundamentos Matemáticos de la Mecánica Cuántica, Consejo Superior de Investigaciones Científicas, Madrid, 1991.
[WAE-67] Waerden, B.L. van der; Sources of Quantum Mechanics, Dover, Nueva York, 1967.
[WHE-83] Wheeler, J.A. y Zurek, W.H., eds.; Quantum Theory and measurement, Princenton Univ., Princenton, 1983.

Física cuántica en la red

Un sitio para adentrarse en la física cuántica