El teorema de Bell-Kochen-Specker

Contextualidad: El teorema Bell-Kochen-Specker

Se denomina contextualidad cuántica a la propiedad que poseen algunas variables cuánticas de un sistema (como espín, posición, momento, etc.), según la cual:

Las predicciones de la teoría sobre los resultados de las medidas de algunos observables (que se agrupan para su medida en distintos subconjuntos compatibles) son inconsistentes con la suposición de que dichas variables poseen valores definidos o pre-existentes: a) con anterioridad a que las medidas se lleven a cabo, y b) independientes de cuáles sean todas las mediciones concretas dispuestas.

-Dichos observables se denominan como «contextuales«.

La propiedad fue establecida de forma teórica en el denominado teorema de Bell / Kochen-Specker, que escribimos ahora así para remarcar que fue derivado, de forma independiente, de un lado por J.S. Bell, y, de otro lado, por S. Kochen y E. Specker:

«On the problem of hidden variables in quantum mechanics», Reviews of Modern Physics 38 (1966) 447-452; trad. en [BEL-90], pp. 25-40; reproducido en [WHE-83], pp. 396-402; véase también archivo de Mermin sobre el tema: Mermin-Bellvo.pdf.

S. Kochen and E. P. Specker, The problem of hidden variables in Quantum Mechanics; J. Math. Phys. 17 (1967) 59-87; The Logico-Algebraic Approach to Quantum Mechanics, pp 293–328, Springer.

-En realidad, ha sido señalado que el teorema puede considerarse como un caso especial del teorema de Gleason (véase más adelante, en esta misma entrada; también en el apartado de variables ocultas).

Teorema Bell / Kochen-Specker:

«There is no non-contextual model with hidden variables in quantum mechanics».

En 1993 D. Mermin publicó un artículo en el que revisaba a fondo tanto el teorema de Bell como el de Bell-Kochen-Specker, con la virtud de introducir demostraciones mucho más sencillas (usando sistemas compuestos en vez de un solo sistema individual):

N. D. Mermin, Hidden variables and the two theorems of John Bell, Rev. Mod. Phys. 65 (1993) 803; erratum 985 (2013) 819.

En este caso, a diferencia de la situación EPR-Bell que condujo al abandono del realismo local, no se involucran medidas en dos partes de un sistema en regiones EPR separadas, sino que se refiere en general a medidas compatibles realizadas en una misma región:

Un observable dado se mide varias veces, como integrante de distintos subconjuntos internamente compatibles, pero que pudieran integrar sendos observables incompatibles entre sí.

Estos subconjuntos son pues «contextos« alternativos para la medida del observable en cuestión; cada contexto consiste en un conjunto de experimentos elementales, compatibles, cuyos resultados, bajo una hipótesis de no-contextualidad, tienen probabilidades bien definidas con independencia del orden en que se hagan.

Kochen y Specker demostraron la existencia de un conjunto de experimentos de resultado dicotómico, que especificaron, en los cuales es imposible realizar una asignación de valores pre-existentes para sus resultados, y ello con independencia del estado en que esté preparado el sistema cuántico: «un contexto Kochen-Specker«.

Fuentes: La exposición siguiente sigue tanto el artículo antes referido de D. Mermin como el de F. Lalöe, Do we really understand quantum mechanics? Strange correlations, paradoxes, and theorems, American Journal of Physics 69, 6 (2001); pp. 671-672.

Sea una partícula de espín 1 y sea $\{|1-1>,|10>,|1+1>\}$ una base ortonormal del correspondiente Hilbert, compuesta por autofunciones simultáneas de los observables compatibles $(\vec{S}^2, S_z)$ ; se considera el conjunto de observables compatibles dos a dos $(S_x^2,S_y^2,S_z^2)$ , correspondientes al valor del número cuántico de momento angular $S=1$ , y que satisfacen $S_x^2 +S_y^2+S_z^2=2\hbar^2$ .

-Al ser observables compatibles, podemos concebir una medida simultánea de dichas tres componentes (al cuadrado), sobre cualesquiera tres direcciones ortogonales $\{x,y,z\}$ integrantes de un sistema dado de ejes cartesianos OXYZ. Estas medidas NO pueden hacerse midiendo los tres $S_i \ ,\ i=x,y,z$ , y elevando al cuadrado (entre otros inconvenientes, como el de encerrar menos información, se tienen tres autovalores para las componentes y dos para sus cuadrados, las componentes sí son observables complementarios entre sí dos a dos).

-Supóngase que, hechas las medidas, se asocia un elemento de realidad objetivo al resultado de la medida de $S_x^2$ , que representaremos por una variable adicional $\lambda_x$ que puede tomar los dos valores 0 o $\hbar^2$ ; análogamente y por simetría surgen dos variables adicionales $\lambda_y$ y $\lambda_z$ con el mismo espectro de resultados.

-De entrada, las tres variables dicotómicas $\lambda_i$ , $i=x,y,z$ , proporcionarían $2^3=8$ posibilidades de resultados para los tres operadores, pero la ligadura $\lambda_x + \lambda_y +\lambda_z=2\hbar^2$ las reduce a tres: quedan eliminadas las combinaciones de valores en que hay o dos variables $\lambda_i$ nulas o las tres iguales.

-Se procede entonces a marcar de rojo las dos direcciones en que las variables $\lambda_i$ y $\lambda_j\,,\,j\ne i$ son no nulas; la restante, $\lambda_k\,,\,k\ne i \,,\, k\ne j$ , nula, se colorea en azul.

-El procedimiento se quiere continuar cambiando la elección de conjunto de tres direcciones ortogonales, y la pregunta que surge es: ¿puede SIEMPRE colorearse una dirección arbitraria de un color dado (asunción como elemento de realidad objetivo del valor de la variable $\lambda_i$ correspondiente) con independencia de los colores que tomen los correspondientes dos ejes ortogonales restantes («el contexto«)?.

-Por ejemplo: se fija OZ y se rotan OX y OY alrededor de él: ¿puede OZ conservar su color?

Lo que demostraron Kochen&Specker es que la respuesta es negativa: si el ángulo entre dos vectores de diferente color es menor que 26,565º, pueden localizarse vectores adicionales que, conjuntamente con los iniciales, constituyan un conjunto no coloreable según lo requerido.

Se trata, en definitiva, de una aplicación particular a la cuántica de un antiguo problema de geometría:

Planteamiento del clásico problema de Geometría «coloración ternaria de las direcciones de un espacio«:

¿Es posible colorear todos los puntos (o direcciones) del espacio tridimensional con 3 colores de tal manera que no existan tres puntos colineales a una distancia específica con colores distintos, o que se eviten configuraciones monocromáticas?

-Muy en breve: el problema geométrico original plantea asignar uno de entre tres colores a cada posible dirección (o línea que pasa por el origen) en un espacio tridimensional, de manera que cumpla con ciertas restricciones de consistencia geométrica.
-La restricción fundamental es la ortogonalidad: que si tres direcciones son mutuamente perpendiculares (forman un triedro ortogonal), deben tener colores distintos entre sí.
-y la solución al problema así planteado es que es imposible realizar tal coloración ternaria en el espacio tridimensional de forma continua o consistente sin incurrir en contradicciones.

Aplicado a la física cuántica, un problema relacionado es el contenido del teorema de Kochen-Specker, que demuestra que es imposible asignar uno de dos valores (0 o 1) a un conjunto de direcciones en $\mathbb{R}^3$ de forma que, para cualquier tríada de direcciones mutuamente ortogonales, exactamente sólo una tenga el valor 0.

Localizar un conjunto de direcciones con la propiedad de que sea imposible, usando sólo dos colores, colorearlas todas de tal manera que cada subconjunto de tres direcciones mutuamente ortogonales contenga sólo un eje de un color y dos ejes del otro.

Así pues, tanto Bell como Kochen y Specker establecieron (independientemente) que ese tipo de conjuntos de observables (compatibles) existen en física cuántica.

Un punto muy importante es, de cara a la prueba experimental, es que Kochen y Specker dieron un paso más respecto a la abstracta (y muy complicada) demostración matemática general y especificaron un conjunto de experimentos elementales, que convierten en innecesaria la parte estadística dependiente del estado particular inherente en teoría cuántica (algo que no hizo Bell en su publicación). Esto es: concretaron un conjunto específico de direcciones, vectores tridimensionales, para las cuales es imposible asignar la coloración dual. Bell no dio este paso, estableciendo sólo que había un ángulo mínimo que lo hacía imposible; Kochen y Specker fueron capaces de ir más allá y proporcionar un conjunto de 117 observables (los análogos de las direcciones en geometría), estableciendo que la inconsistencia que conlleva la introducción de VO objetivas es inherente a la propia estructura general de la teoría y por completo independiente del carácter especial de algunos estados cuánticos que pudieran entonces concebirse como «especiales».

El artículo de Mermin antes referido, tras realizar una exposición general de la prueba original del teorema (ver p. 807), presenta dos nuevas versiones, con demostraciones mucho más fáciles que las originales BKS, debido a que en vez de realizarlas en el espacio tridimensional, las desarrolla en un espacio de 4 dimensiones para un sistema de dos partículas, 9 observables (sección V, p. 810), y 8 dimensiones para un sistema de 3 partículas, 10 observables (sección VI, pp. 810-811; ésta es muy similar al razonamiento GHZ y lo emparenta así con el teorema de Bell):

Prueba en 4 dimensiones: considera dos partículas de espín $\frac{1}{2}$ y los 9 observables dicotómicos $\sigma_i^j=\pm 1\;,\;i=x,y,z\;,\;j=1,2$ , con sendos autovalores posibles $+1$ y $-1$ , dispuestos en una matriz 3×3:

$\begin{array}{ccc} \sigma_x^1 & \sigma_x^2 & \sigma_x^1\sigma_x^2 \\ \sigma_y^2 & \sigma_y^1 & \sigma_y^1\sigma_y^2 \\ \sigma_x^1\sigma_y^2 & \sigma_y^1\sigma_x^2 & \sigma_z^1\sigma_z^2 \end{array}$

todos ellos de espectro dicotómico con autovalores $\pm 1$ y tales que satisfacen:

a) Cada dos que pertenecen a la misma fila o columna conmutan entre sí.

b) Cada producto de los tres operadores en la misma fila o columna produce +1, rojo, excepto el producto de los tres en la última columna, que produce -1, amarillo (recuérdese: $\sigma_x^j \sigma_y^j=i\sigma_z^j$ , donde $j$ representa el índice de partícula).

-Es decir, se han sustituido los infinitos tripletes de direcciones en un espacio tridimensional, por seis grupos de tres operadores (3 filas + 3 columnas), sobre los que se plantea el mismo problema: ¿pueden colorearse de rojo (resultado +1) y amarillo (resultado -1) los 9 elementos de la matriz anterior en una forma que sea consistente con las predicciones mecano-cuánticas?

-El caso es que se requiere que cada fila, y cada columna, contenga o tres rojos, o un rojo y dos amarillos, excepto la tercera columna, que ha de contener tres amarillos o sólo uno. Y ¡es imposible encontrar solución entonces!

-Otra forma de verlo (ver Mermin, p. 810): ya que el producto de los valores en cada fila es rojo (+1), el producto de los nueve valores en la matriz es también rojo; pero el producto de las tres columnas es amarillo (es rojo , +1, para las dos primeras columnas, pero es amarillo, -1, para la tercera): ¡imposible!

Prueba en 8 dimensiones: considera tres partículas de espín $\frac{1}{2}$ y los 10 observables dispuestos según:

$\begin{array} {ccccccc}.&.&.&P_1=\sigma_y^1&.&.&. \\ P_2=\sigma_x^1\sigma_x^2\sigma_x^3&.&C_1=\sigma_y^1\sigma_y^2\sigma_x^3&.&C_2=\sigma_y^1\sigma_x^2\sigma_y^3&.&P_3=\sigma_x^1\sigma_y^2\sigma_y^3\\ .&C_3=\sigma_x^3&.&.&.&C_4=\sigma_y^3&.\\.&.&.&.&.&.&.\\ .&.&. &C_5=\sigma_x^1&.&.&. \\ .&.&.&.&.&.&. \\.&P_4=\sigma_y^2&.&.&.&P_5=\sigma_x^2&. \end{array}$

-Se dibuja la siguiente estrella, en la que los cinco puntos $P$ se corresponden con las puntas y los cinco operadores $C$ se corresponden con las intersecciones entre dos lados:

$\equiv \begin{array}{ccccccc}.&.&.&P_1&.&.&. \\.&.&.&.&.&.&.\\ P_2&.&C_1&.&C_2&.&P_3\\ .&C_3&.&.&.&C_4&.\\ .&.&. &C_5&.&.&. \\ .&.&.&.&.&.&.\\P_4&.&.&.&.&.&P_5 \end{array}$

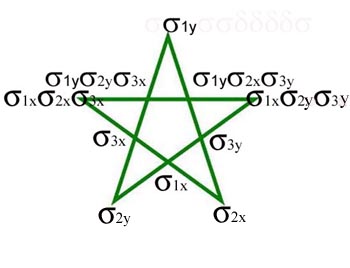
-Los 10 observables se dividen así en 5 grupos de 4, por prolongación de las 5 líneas de los lados del pentágono que forman los puntos $C$ en la segunda matriz, dibujando así la anterior estrella de 5 puntas P, forzando a que sobre cada línea caigan cuatro operadores.

-Se satisface:
a) Los 4 operadores en cada grupo son compatibles.
b) Cada observable está en dos de esos grupos.
c) El producto de los cuatro operadores en cada grupo, excepto para la horizontal, produce +1.
d) El producto de los cuatro operadores en la línea horizontal (los 4 operadores con tres $\sigma$ ) produce -1.

-Entonces, a partir de las dos últimas condiciones, el producto de todos los operadores, sobre las 5 líneas (los 10 observables), ha de ser $-1$ .

$\Rightarrow$ Se produce por tanto una inconsistencia, ya que lo anterior es imposible, porque cada observable pertenece a dos de los 5 grupos (líneas), o sea, aparece dos veces en el producto global de todos, aportando un resultado $+1$ .

Por tanto: el suponer que el resultado de la medida de un observable es independiente de qué otros observables (compatibles) se miden simultáneamente con él, la hipótesis de no contextualidad, conduce a la inconsistencia.

Hipótesis de no-contextualidad: El resultado de la medida de un observable A cuando se realiza su medida simultánea con otros observables B, C… compatibles con él, es siempre el mismo, sean cuáles sean estos otros operadores.

-Obsérvese que distintas elecciones de conjuntos de operadores a medir simultáneamente con A, todos ellos que conmuten con él, pueden incluir operadores que, estando en distintos conjuntos, no conmutan entre sí.

Contextualidad cuántica: La consistencia del formalismo hace imposible asumir la hipótesis de no-contextualidad.

Un buen resumen del contenido y significado del teorema:

C. Saulder: Contextuality and the Kochen-Specker Theorem; Enciclopedia Stanford de Filosofía: The Kochen-Specker Theorem:

Let H be a Hilbert space of QM state vectors of dimension $x \ge 3$ . There is a set M of observables on H, containing y elements, such that the following two assumptions are contradictory:

(KS1) All y members of M simultaneously have values, i.e. are unambiguously mapped onto real numbers (designated, for observables A, B, C,…, by v(A), v(B), v(C),…).

(KS2) Values of observables conform to the following constraints:

(a) If A, B, C are all compatible and C = A+B, then v(C) = v(A)+v(B);

(b) if A, B, C are all compatible and C = A·B, then v(C) = v(A)·v(B).

The heart of statement is much more than a simple theorem about the geometrical structure of the quantum mechanical Hilbert-space. It forbids a certain class of hidden variable theories that isn’t prohibited by Bell’s theorem by showing that realism and non contextuality cause a contradiction. Furthermore some arithmetic rules for measured values of systems of several observables follow out of the Kochen-Specker theorem.

-Assumption KS1 of the theorem obviously is an equivalent of VD = value definiteness = «All observables defined for a QM system have definite values at all times».

-Assumptions KS2 (a) and (b) are called the Sum Rule and the Product Rule, respectively, in the literature. (The reader should again note that, in opposition to von Neumann’s implicit premise [véase postulado 4 en teorema de von Neumann, más adelante, en esta misma entrada], these rules non-trivially relate the values of compatible observables only).

-In the original KS proof x=3 and y=117. More recently proofs involving less observables have been given by (among many others) Peres (1991, 1995) for x=3 and y=33, by Kernaghan (1994) for x=4 and y=20 and by Cabello et al. (1996) for x=4 and y=18.

Obsérvese: una hipótesis de VD = Valor definido asume:

VD = «All observables defined for a QM system have definite values at all times»,

mientras que una hipótesis de NC = No Contextualidad establece:

NC = «If a QM system possesses a property (value of an observable), then it does so independently of any measurement context, i.e. independently of how that value is eventually measured».

Ambas hipótesis VD («determinación del valor») + NC («no contextualidad») vienen a incorporar la idea de la objetividad (clásica) del proceso de medida: la independencia de la realidad física, exterior al observador, respecto al proceso de medida («independence of physical reality from its being measured»).

Mermin: A Kochen-Specker Theorem for Imprecisely Specified Measurement:

Abstract: A recent claim that finite precision in the design of real experiments «nullifies» the impact of the Kochen-Specker theorem, is shown to be unsupportable, because of the continuity of probabilities of measurement outcomes under slight changes in the experimental configuration.

A. Cabello: Comment on «Non-contextual hidden variables and physical measurement»

Abstract: Kent’s conclusion that «non-contextual hidden variable theories cannot be excluded by theoretical arguments of the Kochen-Specker type once the imprecision in real world experiments is taken into account» [véase Phys. Rev. Lett. 83, 3755 (1999)], is criticized. The Kochen-Specker theorem just points out that it is impossible even conceive a hidden variable model in which the outcomes of all measurements are pre-determined; it does not matter if these measurements are performed or not, or even if these measurements can be achieved only with finite precision.

Sobre conjuntos mínimos de contextos cuánticos: A. Cabello, «El teorema Kochen-Specker llega al laboratorio», Investigación y Ciencia 461 (2015) 8-9:

El teorema de Kochen-Specker complementa el resultado de Bell, ya que demuestra que la imposibilidad de reproducir las predicciones cuánticas mediante variables ocultas no se circunscribe a sistemas entrelazados, sino que ocurre también en sistemas individuales y con independencia de cómo preparemos el estado cuántico.

La existencia de conjuntos de Kochen-Specker (conjuntos de experimentos elementales cuyos resultados tienen probabilidades bien definidas con independencia de en que orden se hagan y en los que resulta imposible preasignar resultados) demuestra que en el Universo no admite descripciones que cumplan la hipótesis de no contextualidad.

Pero una forma que encuentro más adecuada de expresarlo sería:

En el Universo se producen situaciones (fenómenos) que no admiten descripciones que cumplan cualquier hipótesis de no contextualidad.

Tras el sistema físico determinado en 1967 por Kochen y Specker, con 117 observables dicotómicos a los que resultaba imposible «colorear» con dos solos colores (0 o 1) de manera que en un conjunto de 118 contextos, o experimentos alternativos en que intervenían los 117 observables, se verificasen las predicciones de resultados de la mecánica cuántica, el físico A. Peres (Instituto Technion, en Haifa) propuso en 1991 dos demostraciones diferentes (cf. siguiente referencia), una con 33 observables y otra con 24. En 1994, M. Kernaghan (Univ. de Western Ontario) encontró una demostración del mismo tipo con sólo 20 observables, y ya en 1996, A. Cabello, en colaboración con J.M. Estebaranz y G. García Alcaine, Universidad Complutense de Madrid, encontraron una demostración con solo 18 observables:
A. Cabello, «Los experimentos no realizados no tienen resultados», Misterios de la física cuántica, Investigación y Ciencia, Temas 10, 1997, pp. 65-67; Prensa Científica, Barcelona, 1997; ISBN: 84-411-35566-10.

Las 33 direcciones BKS de Peres, 1991 — *Fuente: https://upload.wikimedia.org/wikipedia/commons/6/68/Variables_ocultas_y_los_teoremas_de_Bell.pdf*

-Para la demostración de A. Cabello, que fue récord en su momento en la utilización del más pequeño número de observables:
A. Cabello y G. García Alcaine, «Bell-Kochen-Specker theorem for any finite dimensions $n \ge 3$ «, J. Phys. A29, 5, 1025-1036 (1996), DOI: 10.1088/0305-4470/29/5/016.

Avances en la competición por descubrir el contexto Kochen-Specker (KS) más pequeño (búsquedas con IA, a fecha marzo de 2026):

–Para el espacio tridimensional: Un conjunto de 31 vectores y fue descubierto por John Conway y Simon Kochen alrededor de 1990. Consta de 31 vectores (o direcciones) de inmersión en 3D, a menudo referidos como el sistema de 31 vectores de Conway-Kochen. Aunque han existido búsquedas exhaustivas para encontrar conjuntos más pequeños, el conjunto de 31 mantiene el récord de ser el mínimo conocido en tres dimensiones.
-En dimensiones superiores: más allá de 3D, se ha demostrado que el conjunto de KS con la cardinalidad mínima ocurre en dimensión 4 (4D) y consta de 18 vectores.
-Límite teórico: Aunque se han establecido límites inferiores computacionales, el conjunto de 31 (3D) sigue siendo la realización concreta más pequeña actualmente reconocida. Aunque el conjunto de Peres de 33 vectores es más simétrico, el sistema de 31 es más pequeño en número total de vectores.

Li, Zhengyu & Bright, Curtis & Ganesh, Vijay; «A SAT Solver + Computer Algebra Attack on the Minimum Kochen-Specker Problem«; 10.21203/rs.3.rs-2279231/, 2023.

El contexto de Kochen-Specker (KS) más pequeño conocido actualmente, en términos de número de contextos de medición, consta de 7 contextos. Este conjunto fue hallado por investigadores de la Universidad de Sevilla y constituye el límite teórico para una prueba de paridad simétrica del teorema de KS en cualquier dimensión. Detalles clave de este conjunto mínimo: integra 7 bases o contextos de medición, y contiene 21 experimentos elementales (vectores). Cada vector pertenece exactamente a dos bases, lo que genera una contradicción lógica (paridad) que demuestra que los resultados de las mediciones no pueden estar predefinidos antes de la observación:
P. Lison, P. Badzia, J.R. Portillo and A. Cabello; «Kochen-Specker set with seven contexts«.

Otros récords de «tamaño» en el teorema de KS:
Dependiendo de cómo se defina «más pequeño» (por dimensión o por número de vectores), existen otros hitos importantes:
-Dimensión 3 (Qutrits): El sistema de vectores más pequeño conocido tiene 31 vectores, descubierto por Conway y Kochen. El límite inferior computacional actual indica que debe tener al menos 23 vectores.
-Dimensión 4: El conjunto de cardinalidad mínima (menos vectores totales) ocurre en esta dimensión y tiene 18 vectores.
-Pruebas de estado independiente: Recientemente se ha propuesto un conjunto KS simétrico con solo 14 bases en sistemas de dos qutrits, superando récords anteriores de 16 bases.

F. Arends, J. Ouaknine and C.W. Wampler, «On Searching for Small Kochen-Specker Vector Systems»
Abstract: Kochen-Specker (KS) vector systems are sets of vectors in $R^3$ with the property that it is impossible to assign 0s and 1s to the vectors in such a way that no two orthogonal vectors are assigned 0 and no three mutually orthogonal vectors are assigned 1. The existence of such sets forms the basis of the Kochen-Specker and Free Will theorems. Currently, the smallest known KS vector system contains 31 vectors. In this paper, we establish a lower bound of 18 on the size of any KS vector system. This requires us to consider a mix of graph-theoretic and topological embedding problems, which we investigate both from theoretical and practical angles. We propose several algorithms to tackle these problems and report on extensive experiments. At the time of writing, a large gap remains between the best lower and upper bounds for the minimum size of KS vector systems.

El teorema BKS y los teoremas anteriores de imposibilidad de VO

Desde 1932, el teorema de imposibilidad de VO de von Neumann, demostrado en su texto fundacional:

J. von Neumann, J., Mathematische Grundlagen der Quantenmechanik, Springer, Berlín, 1932; Mathematical Foundations of Quantum Mechanics, Princenton Univ., Princenton, 1955; Fundamentos matemáticos de la Mecánica Cuántica, C.S.I.C., Madrid, 1991,

había abordado, y descartado, la posibilidad de construir una teoría de VO que permitiera una descripción más completa y profunda que la Mecánica Cuántica.

-Desde el abandono del determinismo, ése es un anhelo que no ha desaparecido nunca. En la siguiente cita del filósofo Adler de 1992, recogida también por Mermin en el artículo antes indicado, podemos comprobar cómo la situación es difícil de comprender para los especialistas de campos ajenos a la Física, algunos de los cuáles no llegan a comprender en profundidad el alcance de la revolución cuántica como configuradora de una nueva manera de concebir el mundo, sus objetos y las relaciones involucradas:

M.J. Adler, Natural Theology, Chance, and God:

Most theoretical physicists are guilty of… fail[ing] to distinguish between a measurable indeterminacy and the epistemic indeterminability of what is in reality determinate. The indeterminacy discovered by physical measurements of subatomic phenomena simply tell us that we cannot know the definite position and velocity of an electron at one instant of time. It does not tell us that the electron, at any instant of time, does not have a definite position and velocity. [Physicists] (…) convert what is not measurable by them into the unreal and the nonexistent.

Estructura del teorema de von Neumann:

[ICA-91]: J.J. Icaza; La construcción de la Mecánica Cuántica, Univ. del País Vasco, Bilbao, 1991, pp. 238ss.

1. Premisas:

-Postulado 1: Si un observable es representado por el operador P, entonces una función f de ese observable es representado por f(P).

-Postulado 2: Si se consideran observables representados por los operadores P,S,…, entonces la suma de observables se representa por la suma de operadores P+S+…, conmuten o no entre sí dichos operadores.

-Postulado 3: Si la magnitud P es no-negativa, entonces el observable P es positivo ( $<P> \ge 0$ ).

–Postulado 4 (sobre el que Bell dirigirá su crítica): Se establece un isomorfismo entre la estructura de espacio vectorial de los observables cuánticos y la de los observables de la teoría de V.O., de forma que se tiene que si P,Q,…, son observables arbitrarios y a, b,…€ R, entonces
<aP + bQ + …> = a<P> + b<Q> + …

2. Conclusión:

No existen estados libres de dispersión $\Rightarrow$ No es posible una descripción con V.O.

En otras palabras:

Cf. [GAL-89], vol. I, pp. 459-460:

El aspecto estocástico de la M.C. no puede reproducirse bajo la hipótesis de que existen unos parámetros cuyo conocimiento fije un microestado de un sistema, libre de dispersión para todo observable y en términos de los cuales un estado cuántico puro ordinario $\Psi$ no sea más que un macroestado mezcla incoherente de aquéllos.
Partiendo del contexto ordinario de la M.C., en que los observables se identifican con los operadores autoadjuntos de un espacio de Hilbert complejo y separable, y los estados cuánticos convencionales son simplemente funcionales lineales positivos sobre los observables acotados, y haciendo la hipótesis de que los microestados o estados libres de dispersión son igualmente funcionales lineales positivos sobre los observables acotados, se concluye que no existen estados libres de dispersión o microestados, o sea, que no es posible una descripción por V.O.

La autoridad de von Neumann era tan considerable y considerada que, durante dos décadas, tras la publicación de su teorema, las V.O. fueron abandonadas como tema de investigación. Dos ejemplos ilustrativos:

1. Cuando en 1952 Bohm publicó su teoría de V.O., fue completamente ignorada, a pesar de que su mera existencia como teoría de V.O. determinista (no local) capaz de reproducir los resultados de la M.C. (no relativista) debiera haber suscitado la atención, al menos sobre cómo era posible su misma existencia.

2. Bell ha narrado como, atraído fuertemente por el argumento EPR y la posibilidad relacionada de elaborar una descripción teórica más completa que la de la M.C., en cuanto tuvo conocimiento de que von Neumann había demostrado su imposibilidad abandonó el tema. Posteriormente, sin embargo, «al ver lo imposible realizado», decidió analizar cómo era posible, es decir, analizar la posibilidad de que el teorema de von Neumann fuera erróneo.

J.S. Bell, On the impossible pilot wave, Foundations of Physics, 12 (1982) 989-999.

Existen otros teoremas de imposibilidad además del de von Neumann. Entre ellos, con parecidas consecuencias negativas para las V.O., pueden citarse como más conocidos el de Jauch y Piron,

J.M. Jauch and C. Piron, Helv. Phys. Acta 36 (1963) 827,

y el de Gleason,

A.M. Gleason, J. Math. Mech., 6 (1957) 885,

este último considerado en su momento como definitivo:

Fuente: http://www.fisicafundamental.net/misterios/bell.html#gleason:

Teorema de Gleason:

Si $P_{a}$ es un proyector que proyecta sobre un cierto $|\psi_a>\equiv |a>$ (podemos pensar en $P_{a}$ como $|a><a|$ o como una cierta expansión $\sum_{\alpha} |a,\alpha><a,\alpha|$ ) y $\rho$ es un estado mezcla arbitrario (un estado puro $\rho=|\Psi><\Psi|$ o una mezcla estadística $\sum_i |\Psi_i>p_i<\Psi_i|$ , con $0 \le p_i \le 1\,\,, \sum_i p_i=1$ ), la única función posible que define la probabilidad de obtener el resultado r es esencialmente $Prob(a)=Tr(P_a\rho)$ .

Como la función $Prob(a)$ es continua sobre la esfera unidad como función de $\rho$ , es imposible que adopte los valores 0 y 1 sobre la misma. Con la esfera unidad aquí nos referimos a una esfera de estados de espín, es decir, a todos los $|\Psi>$ tales que $\rho=|\Psi><\Psi|$ en la ecuación anterior, y donde $\vec{\sigma} \cdot \vec{n}|\Psi>=\pm \Psi>$ , y $\vec{n}$ es una dirección arbitraria sobre la 2-esfera espacial de radio 1. Una función continua sobre este conjunto no puede tomar los valores 0 y 1 sin tomar todos los valores intermedios posibles.

La consecuencia de esto es que es imposible resolver todas las proposiciones de espín posibles con unas variables deterministas adicionales que fijen sus valores. Podríamos decir que este es un teorema de tipo ontológico: los valores definidos del espín no pueden ser la imagen o recorrido de un cierto conjunto matemático en una correspondencia punto a punto.

-Difieren del de von Neumann, esencialmente, en que relajan el postulado 4, exigiéndolo sólo para operadores que conmutan, y añaden hipótesis varias sobre valores esperados de determinados proyectores, hipótesis cuya validez, siendo clara para los estados de la M.C., es también supuesta para los microestados.

El teorema BKS, de hecho, es considerado un caso especial del de Gleason.

En 1966 Bell publicó un artículo en que exponía un resultado fundamental, que de hecho había demostrado antes que su célebre teorema de 1964, aunque lo publicara después:

J. S. Bell, On the problem of hidden variables in quantum mechanics, Reviews of Modern Physics 38 (1966) 447-452.

-En la introducción de este artículo, Bell afirmaba que, aunque los teoremas de imposibilidad eran mayoritariamente considerados hasta entonces como universales e invulnerables,

La conciencia de que la prueba de von Neumann es de relevancia limitadada ha ido ganando terreno desde el trabajo de Bohm de 1952. Sin embargo, se halla lejos de ser universal. Además, quien escribe no ha encontrado en la literatura ningún análisis de qué era incorrecto en dicha prueba.

-Además, Bell señalaba la existencia de un debate sobre si la cuestión de las V.O. es interesante o no. Pero él, nos dice, no se propone contribuir a tal debate, sino sólo «clarificar lo que realmente demostraron von Neumann y sus continuadores«, haciendo hincapié en que esos análisis «dejan intacta la cuestión real«.

-Nota: sin embargo, ya en 1935, según señaló M. Jammer ([JAM-74], p.273), G. Herman había criticado la prueba de imposibilidad de VO de von Neumann, aunque su trabajo fue ignorado.

-Esencialmente, en su trabajo Bell señala el postulado 4 como inaceptable para los microestados (los estados que, incorporando las VO, refinan la predicción cuántica), en concreto:

Contra von Neumann: El hecho de que el valor esperado de una combinación lineal de observables sea la combinación lineal de los valores esperados de los correspondientes valores esperados, cierto para los estados cuánticos, no tiene por qué requerirse para los microestados. Es decir: si C=A+B, y [A,B]=0 , entonces sí se puede requerir a los valores v asignados a dichos observables que v(C)=v(A)+v(B), pero cuando A y B no conmutan, caso en el que, de hecho, mecano-cuánticamente no se pueden medir simultáneamente, es absurdo imponer el mismo requisito.

Contra von Neumann y Gleason: Para los microestados, los valores esperados de los observables pueden depender no sólo del observable a medir, sino también del aparato particular, es decir, del montaje experimental concreto, con el que se va a realizar la medición (i.e.: de qué otros observables se decide medir también): la denominada contextualidad cuántica.

Es decir, Bell establece que los teoremas de von Neumann (1932), Gleason y similares, anteriores al suyo de 1964, lo que fijaron fue sólo que:

«Existe un tipo de V.O. inconsistentes con las predicciones de la Mecánica Cuántica: las V.O. no-contextuales» (que son todas locales, aunque puede haber también VO locales que sean contextuales; sobre tipos de variables ocultas ver el apartado Tipología de VO).

El teorema de Bell: Este famoso teorema, formulado en 1964, vendría a establecer por su parte que:

Las V.O. locales, todas, son inconsistentes con la M.C.

En otras palabras:

http://www.fisicafundamental.net/misterios/bell.html:

Así como el teorema de Bell se interpreta como la demostración de que no es posible la coexistencia del realismo local con la MC, el teorema de [Bell-]Kochen-Specker se interpreta como la demostración de que no es posible la coexistencia del realismo no contextual o intrínseco, si se quiere, con la MC. En otras palabras: Hay ciertos observables en el espacio interno del espín que, aun siendo compatibles, no pueden tener definitud simultánea; no pueden por tanto considerarse propiedades intrínsecas del sistema.

Es imposible que una teoría de Variables Ocultas no contextuales sea predictivamente equivalente a la Mecánica Cuántica.

Teorema de Hardy y contextos Kochen-Specker:
El contexto de Hardy (la paradoja de Hardy) a menudo no se clasifica estrictamente como un contexto de Kochen-Specker (KS) clásico porque está diseñado para violar el realismo local, la no-localidad de Bell, utilizando probabilidades, en lugar de demostrar una contradicción lógica pura e independiente del estado en un conjunto de mediciones, que es el sello distintivo del teorema de Kochen-Specker.
-Aunque ambos conceptos demuestran la «contextualidad cuántica», esto es, la imposibilidad de asignar valores preexistentes a las propiedades físicas independientemente del contexto de medición, existen diferencias clave:
1. La naturaleza de la paradoja misma involucrada:
Las situaciones Hardy involucran un par de partículas entrelazadas para mostrar que ciertas mediciones, basadas en una lógica contrafactual, proposiciones tipo «si… entonces», conducen a una contradicción probabilística: La probabilidad de éxito de este escenario no es cero según la mecánica cuántica, mientras que cualquier teoría de variables ocultas locales predice que debería ser cero.
2. Independencia del estado en los contextos KS vs. estricta dependencia del estado en el deasarrollo de Hardy:
El teorema original de Kochen-Specker demuestra que, para sistemas de dimensión 3 o mayor, es imposible asignar valores a todos los observables compatibles de una manera no contextual, lo que resulta independiente del estado cuántico particular del sistema.Por contra, la paradoja de Hardy depende críticamente del estado entrelazado específico utilizado.
-Nota: sin embargo, a pesar de estas diferencias atendiendo a la formulación original de las situaciones Hardy, investigaciones recientes han mostrado que el escenario Hardy puede ser reformulado como una prueba de contexto, conduciendo a un tipo de prueba o test denominado como «un test Hardy de contextualidad», que funciona para un solo sistema de dimensión 3 o superior. Esta reformulación conecta la paradoja de Hardy con la contextualidad, siendo por tanto un vínculo directo entre la no-localidad a la Bell y el teorema de Kochen-Specker.
A. Cabello et al «Simple Hardy-Like Proof of Quantum Contextuality»

Bibliografía

-[GAL-89]: A. Galindo y P. Pascual; Mecánica Cuántica, Eudema, Madrid, 1989.

-[ICA-91]: J.J. Icaza; La construcción de la Mecánica Cuántica, Univ. del País Vasco, Bilbao, 1991.

-[JAM-74] Jammer, M.; The philosophy of Quantum Mechanics,Wiley, 1974.

-A. Cabello, «Los experimentos no realizados no tienen resultados», Misterios de la física cuántica, Investigación y Ciencia, Temas 10, 1997, pp. 65-67; Prensa Científica, Barcelona, 1997; ISBN: 84-411-35566-10.

-A. Cabello y G. García Alcaine, «Bell-Kochen-Specker theorem for any finite dimensions $n \ge 3$ «, J. Phys. A29, 5, 1025-1036 (1996), DOI: 10.1088/0305-4470/29/5/016.

-A. Cabello, J. M. Estebaranz and G. García Alcaine, «Bell-Kochen-Specker theorem: A proof with 18 vectors»; quant-ph/9706009, DOI: 10.1016/0375-9601(96)00134-X.

-A. Cabello: A State-Specific Proof of the Bell-Kochen-Specker Theorem Using Only 5 Propositions

-A. Cabello: Tesis doctoral: Pruebas algebraicas de imposibilidad de variables ocultas en mecánica cuántica.

-A. Cassinello and A. Gallego, The quantum mechanical picture of the world, American Journal of Physics 73, 3 (2005); pp. 273-281.

-S. Kochen, E. Specker, «The problem of hidden variables in Quantum Mechanics»; J. Math. Phys. 17 (1967) 59-87; The Logico-Algebraic Approach to Quantum Mechanics, pp 293–328, Springer.

-C. Saulder: Contextuality and the Kochen-Specker Theorem.

-Straumann: A simple proof of the BKS theorem