
Advertencia: entrada en construcción: está incompleta y todavía con errores de sintaxis y (puede ser) en fórmulas, figuras…
Sobre secretos…
«Tres pueden guardar un secreto si dos de ellos están muertos» (Benjamin Franklin)
«Lo que no quieras que sepan muchos no lo digas a nadie» (Juan Eusebio Nieremberg)
«El que confía sus secretos a otro hombre se hace esclavo de él» (Baltasar Gracián)
«En España la mejor manera de guardar un secreto es escribir un libro» (Manuel Azaña)
Criptografía
El diccionario de la Real Academia define “criptología” como el “estudio de los sistemas, claves y lenguajes ocultos o secretos”. la convención es distinguir en esta disciplina entre la esteganografía o comunicación secreta, mediante un mensaje oculto, y la criptografía, que por ahora podemos definir como la ciencia de cifrar cierta información para que se pueda transmitir preservando su secreto. De modo que la diferencia esencial entre ellas es que la primera pretende ocultar el mismo mensaje –por ejemplo, usando tinta invisible; o, como hacían los antiguos chinos, recubriendo con cera tiras de seda enrolladas, sobre las que se había escrito un mensaje; o con imágenes ocultas en los bits que componen otras…-, mientras que la segunda pretende sobre todo ocultar el significado del mensaje, codificándolo –de manera que, aunque sea interceptado, no pueda ser leído. A ellas se añade el criptoanálisis, que es el encargado de intentar romper los sistemas o códigos usados en criptografía, con el fin de tener acceso a la información que se ha pretendido reservar.
Como vamos a ver, la física cuántica va a permitir aumentar la seguridad de las comunicaciones secretas, porque nos va a proporcionar garantía respecto a si nuestro mensaje ha sido interceptado, es decir, sometido a criptoanálisis, antes de llegar a nosotros.
La criptografía clásica y su seguridad
Algunos cifrados clásicos primitivos
La Criptografía comenzó siendo considerada un arte, que se transformaría en disciplina científica al imbricarse con la matemática y la computación. Su objetivo es la transformación de cierta información, usualmente encerrándola en un pictograma que ha de poder ser transmitido preservando su integridad y confidencialidad, garantizando tanto el origen de los datos como la dificultad de su desciframiento para terceros diferentes de su destinatarios. El arte de la criptografía se resume en el significado de la palabra que nos proporciona el diccionario de la Real Academia: “arte de escribir con clave secreta o de un modo enigmático”. Puede remontarse hasta al menos el siglo V a.C., cuando los espartanos utilizaron la escítala, un primer sistema de criptografía por transposición, es decir, que oculta el significado de un texto alterando el orden de las letras. En palabras de Plutarco, en su obra “Vida de Lisandro”:
![]() “Cuando los éforos [magistrados] mandan a alguno de comandante de la armada o de general, cortan dos trozos de madera redondos, y enteramente iguales en el diámetro y en el grueso, de manera que los cortes se correspondan perfectamente entre sí. De estos guardan el uno, entregando el otro al nombrado, a estos trozos los llaman escítalas. Cuando quieren, pues, comunicar una cosa secreta e importante, toman una tira de cuero, larga y estrecha como un listón, y la acomodan al trozo o escítala que guardan, sin que sobre ni falte, sino que ocupan exactamente con el cuero todo el hueco; hecho esto, escriben en el cuero lo que quieren, estando arrollado en la escítala. Luego que han escrito, quitan el cuero, y sin el trozo de madera lo envían al general. Recibido por éste, nada puede sacar de unas letras que no tienen unión, sino que están cada una por su parte; pero tomando su escítala, extiende en ella la cortadura de cuero, de modo que, formándose en orden el círculo, y correspondiendo unas letras con otras, las segundas con las primeras, se presente todo lo escrito seguido a la vista”.
“Cuando los éforos [magistrados] mandan a alguno de comandante de la armada o de general, cortan dos trozos de madera redondos, y enteramente iguales en el diámetro y en el grueso, de manera que los cortes se correspondan perfectamente entre sí. De estos guardan el uno, entregando el otro al nombrado, a estos trozos los llaman escítalas. Cuando quieren, pues, comunicar una cosa secreta e importante, toman una tira de cuero, larga y estrecha como un listón, y la acomodan al trozo o escítala que guardan, sin que sobre ni falte, sino que ocupan exactamente con el cuero todo el hueco; hecho esto, escriben en el cuero lo que quieren, estando arrollado en la escítala. Luego que han escrito, quitan el cuero, y sin el trozo de madera lo envían al general. Recibido por éste, nada puede sacar de unas letras que no tienen unión, sino que están cada una por su parte; pero tomando su escítala, extiende en ella la cortadura de cuero, de modo que, formándose en orden el círculo, y correspondiendo unas letras con otras, las segundas con las primeras, se presente todo lo escrito seguido a la vista”.
Por tanto, si una escítala se interceptaba, hacía falta un bastón de las mismas características para descifrar el mensaje: se trata de un método de transposición simple, que no sustituye los símbolos usados, sino que los desordena, al disponerlos en fila y luego leerlos en columna.
La figura siguiente nos muestra como podemos fabricar una muy básica, correspondiente a 12 filas de 10 columnas, que se correspondería con una frase de 120 caracteres:

La criptografía primitiva usó frecuentemente procedimientos de sustitución de unos caracteres por otros, como en el denominado cifrado César, en el que cada letra se sustituye por la que le sigue en el correspondiente alfabeto un número establecido de posiciones, número que fija a su vez las últimas letras que han de sustituirse por las primeras, respetando su orden. Hay tantas llaves posibles como letras del alfabeto que se emplee, la de llave 3 (desplazamiento de tres posiciones) fue la usado por Julio César, correspondiendo a la siguiente tabla de sustituciones (construida con el alfabeto latino moderno, para el que son posibles 26 llaves; se podría en su caso modificar el número de caracteres, por ejemplo para incorporar caracteres especiales de las distintas lenguas, como nuestra ñ):
En estas tablas, cada letra de la primera fila se sustituye por la que está justo debajo en la segunda fila (ejemplo, la g, que ocupa la posición 6, se sustituye por la letra que ocupa la posición 9, la J).

Este sencillo método, cuyo criptoanálisis conduce rápidamente a su ruptura o descifrado, corresponde a la fórmula matemática Y=C(x) ≡ x + 3 (mod 26), que nos indica que el carácter C(x) que va a sustituir al carácter x del texto plano para formar el criptograma va a ser el que ocupa en un alfabeto de 26 caracteres (este número es lo que indica la sigla “mod”, el “módulo”) la posición de x (posiciones numeradas empezando por la cero) aumentada en tres unidades; si resulta un número mayor que 25, se le resta 26. La expresión se lee “Y es congruente con x, módulo 26”. Se trata de una expresión de matemática modular (veáse el apartado B del apéndice de ampliación al final de esta entrada), en la que se está representando el hecho de que
,
donde n es un número natural.
Así pues, aplicando la fórmula Y ⁄ 26=(n∙26)+3 es posible obtener de forma directa la codificación de cualquier mensaje. Por ejemplo, vamos a obtener el criptograma de “ya vive oculta”; usaremos minúsculas para las letras del mensaje original, a codificar, y mayúsculas para su expresión codificada. No tenemos sino que aplicar la fórmula a cada letra:
C(y) ≡ 24 + 3=27 ≡ Y
(ya que 27 es mayor que 26, se resta 26, obteniendo 1 que es la posición de la letra b en la tabla);
C(a) ≡ 0 + 3=4 ≡ E
(ya que e ocupa la posición 4 en la tabla);
C(v) ≡ 21 + 3=24 ≡ Y ;
C(i) ≡ 8 + 3=11 ≡L ; etc.,
de manera que resulta el criptograma BDYLYHRFXOWD.
Para desencriptarlo, basta usar la fórmula inversa D(x) ≡ x – 3 (mod 26), que aplicada a este criptograma con ayuda de la tabla anterior proporciona:
D(B)=1-3=-2 D(B) ≡ 1 – 3=-2 ≡ Y (ya que -2 es negativo, se suma 26, obteniendo 24 que es la posición de la letra y en la tabla);
C(D) ≡ 3 – 3=0 ≡ a (ya que “a” ocupa la posición 0 en la tabla).
El método se puede refinar añadiéndole una “clave”: una palabra o frase que se añade sin repetir letras en una posición determinada de la tabla de sustituciones, por ejemplo, “VIVEOCULTO”, desplazando y alterando la serie de sustituciones, de manera que ya no opera una llave común a todos los caracteres:
En definitiva, lo que se está usando son distintas ordenaciones de las diferentes letras del alfabeto (26). Pero hay 26!=26 x 25 x … x 3 x 2 x 1 maneras distintas de ordenar 26 caracteres –sus permutaciones, sin respetar el orden alfabético-, un número muy grande (del orden de 10 elevado a 26), lo cual quiere decir que son posibles 26! tablas diferentes de sustitución. Ello ofrece una nueva posibilidad, mucho más segura, de cifrado: escoger al azar una cualquiera de esas 26! permutaciones para cifrar el texto; su lectura exigirá entonces conocer cuál se ha empleado y aplicar la permutación inversa.
Dado el gran número de posibilidades, en principio podría parecer que el criptoanálisis del cifrado sería casi imposible. Pero, de la mano del matemático Al-Kindi, autor en el siglo IX del primer tratado de criptoanálisis, el método del análisis de frecuencias proporcionó un eficaz método de desencriptado para estos métodos de sustitución. Como explica Edgar Allan Poe en su cuento “El escarabajo de oro”, si se incorporan las características específicas de la lengua que se está usando, tales como las frecuencias de aparición de las distintas letras, y las apariciones obligadas de algunas letras seguidas, puede romperse el cifrado, siempre que el texto tenga una longitud suficiente. Y ello incluso aunque se incorporen “los nulos”, o caracteres no asociados a ninguna letra y que se reparten aleatoriamente para modificar las frecuencias; los “homófonos”, que son distintos caracteres asociados a una misma letra de elevada frecuencia; los “códigos”, que sustituyen algunas palabras o varias por símbolos –requiriéndose entonces libros de códigos-…. La debilidad del cifrado subsiste. Como datos de muestra, en español (un alfabeto de módulo 27) las letras más frecuentes son la e y la a, con frecuencias respectivas del 13-16% y 10-12%, dependiendo del sistema de medición, mientras que las seis letras menos frecuentes son las letras ‘k’, ‘w’, ‘x’, ‘ñ’, ‘j’ y ‘z’, que no suelen ocupar en conjunto más del 1-3% de cualquier texto, mientras que artículos y preposiciones como ‘el’, ‘la’, ‘de’, ‘en’, etc., ocuparán alrededor del 30% del texto; además, se presentan dígrafos como ‘qu’, es decir, la ‘q’ debe ir siempre seguida de la ‘u’.
Para resistir mejor el criptoanálisis del método de las frecuencias, se desarrollaron los cifrados que recurrían a más de un alfabeto. En el siglo XV, Leon Alberti no sólo usó varios alfabetos de cifrado, para distintas partes de un mismo mensaje, sino que, además, ideó un sistema de discos móviles que hacían posible un eficaz uso de este sistema de sustitución polialfabética: probablemente el primer mecanismo automático de cifrado. Su artilugio se componía de dos discos concéntricos, representados en la figura 4.2. El exterior es fijo y su borde estaba dividido en 24 celdas iguales, sobre las que se disponía el alfabeto latino clásico (23 letras, el moderno añade ‘j’, ‘v’, ‘w’), a excepción de sus tres letras ‘h’, ‘k’ e ‘y’, y los cuatro primeros números, todos los carácter con su orden usual (en el mecanismo original, en mayúsculas, pero como van a corresponder al texto “plano” o sin cifrar, en la figura se han usado las minúsculas, según la convención actual). El disco interior puede girar, y se dividía a su vez en otras 24 celdas iguales, sobre las que se grababa el alfabeto latino completo, en un orden cualquiera dado, añadiendo el símbolos ‘&’. Este alfabeto se usará para el texto cifrado y en la figura se ha representado en mayúsculas.
Si para codificar un mensaje se decide, en la aplicación más sencilla del mecanismo, usar para todo el cifrado una posición fija de las posibles, la elección puede hacerse entre 24 posibilidades de alineación entre las respectivas celdas de los dos discos, o sea, entre 24 llaves o alfabetos de sustitución distintos, para un disco interno dado. Pero se puede también hacer uso, para cifrar distintas partes de un mismo mensaje, de distintas alineaciones, y también recurrir al uso de distintos discos internos, con los símbolos escritos en otra ordenación, es decir, 24! posibilidades diferentes… Todo ello va incrementando la complejidad tanto del criptoanálisis requerido para descifrar un mensaje interceptado como la de la clave, que no olvidemos también ha de ser conocida por el receptor que ha de leer el mensaje.
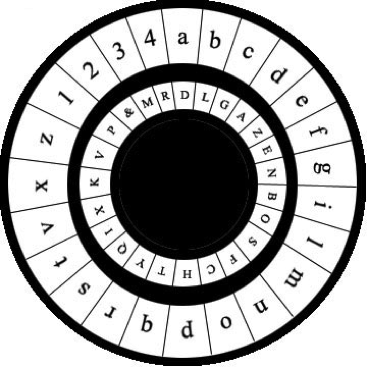
Los discos de Alberti son el primer artilugio mecánico de cifrado de una larga de serie de ellos como, por ejemplo, el cilindro formado por varios discos coaxiales ideado por Thomas Jefferson en 1790; los discos concéntricos de Charles Wheatstone, de 1860; los cilindros con discos cifradores de Étienne Bazeries, 1891… Hasta llegar a las máquinas cifradoras electro-mecánicas a rotor del siglo XX, indispensables para los diferentes servicios secretos, como Enigma y Lorenz (Alemania); Sigaba (Estados Unidos), de funcionamiento similar al de Enigma; Purple (Japón).
En el siglo XVI nació un sistema muy conocido de criptografía por sustitución polialfabética, el sistema de cifrado Belaso-Vigenère, método que, por ejemplo, puede ejecutarse haciendo uso de una clave preacordada y un cuadrado de Tritemio –inspirados por Johannes Trithemius-, o tabla en que se muestran todos los alfabetos de sustitución o llaves que se van a emplear. La figura siguiente muestra el correspondiente cuadrado para el alfabeto latino moderno (26 llaves):
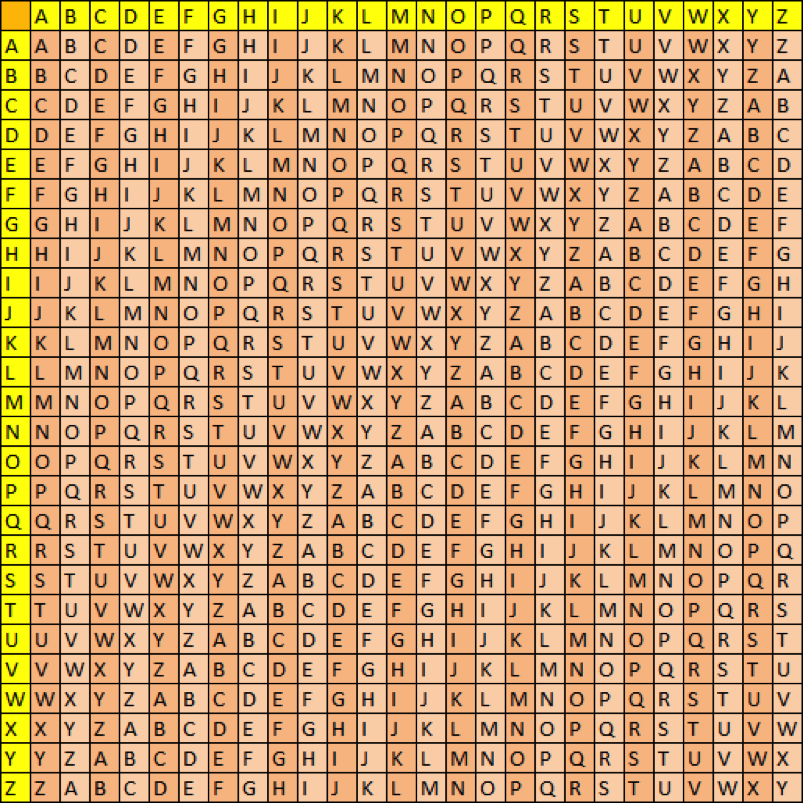
Una vez acordada la palabra clave, por ejemplo, “VIVEOCULTO”, se procede a escribirla repetitivamente debajo del mensaje a codificar, en este ejemplo “líbrate de la rutina”:
A continuación, se procede al cifrado utilizando el cuadrado de Tritemio (figura anterior), siendo posibles distintos métodos, por ejemplo:
-cifrado Vigenère (atribuido con frecuencia a Blaise de Vigenère, pero parece que en realidad debido a Giovan Belaso): cada par de letras alineados en columna constituyen las coordenadas de la letra que va a sustituir esa del mensaje, siendo indiferente su orden. Así, el anterior mensaje y clave definen una serie de coordenadas (l,V), (i,I), (b,V)… que, yendo al cuadrado permiten obtener el criptograma: GQWVOVYOXZVZPXWPU.
-cifrado Beaufort, s. XVIII, inverso al anterior: se busca dentro de la columna de cada letra del mensaje a cifrar la letra de la clave que le corresponde, cuyo índice de fila proporciona la letra a emplear en la cifra. Es decir: KAUNOJQIPDVUBLGPU.
Estos tipos de cifrados polialfabéticos fueron considerados inviolables, ya que al usar símbolos distintos para una misma letra se consiguen frecuencias de aparición más homogéneas, tanto más cuanto más larga sea la clave, por lo que el cifrado es inmune al análisis de frecuencias. Parecía, pues, que el secreto de la clave garantizaba la confidencialidad del mensaje, y así se creyó durante casi tres siglos, hasta que, a mediados del s. XIX, Charles Babbage logró romper este tipo de cifrado, con un método publicado poco después por Friedrich Kasiski y que conseguía una gran tasa de éxito. Esencialmente, el criptoanálisis se centra en averiguar la longitud de la clave usada, a partir de la localización y análisis estadístico de grupos de tres o más símbolos seguidos que se repitan en el criptograma, lo cual suele indicar casi siempre que dichas palabras eran la misma antes del cifrado y que la clave coincidió en la misma posición en ambas ocurrencias. Sabiendo entonces que la distancia entre palabras repetidas es un múltiplo de la longitud de la clave, se busca el máximo común divisor entre las distintas distancias localizadas. La longitud de la clave será este número o algún factor primo del mismo; a partir de ese dato, se consigue romper el cifrado mediante el análisis de frecuencia y, finalmente, averiguar la clave. En 1922, William Friedman desarrollaría otro método de violación para este cifrado, complementario al de Kasiski, a partir de la introducción de los “índices de coincidencia” o probabilidades de que se repitan dos símbolos sacados al azar del criptograma, lo que supuso un temprano trabamiento de la matemática y la estadística con la criptología.
Cifrados clásicos inviolables: el secreto perfecto
Por lo expuesto hasta aquí, está claro que la principal debilidad de los cifrados clásicos primitivos es la naturaleza repetitiva de su clave. En 1918, Gilbert Vernam declaró que sólo serían inviolables si se utilizara una clave que fuera completamente al azar, para evitar las peculiaridades de cada lenguaje natural, y como mínimo tan larga como el texto encriptado. Como es fácil imaginar, usar claves tan largas no resulta muy práctico, pero veamos un ejemplo.
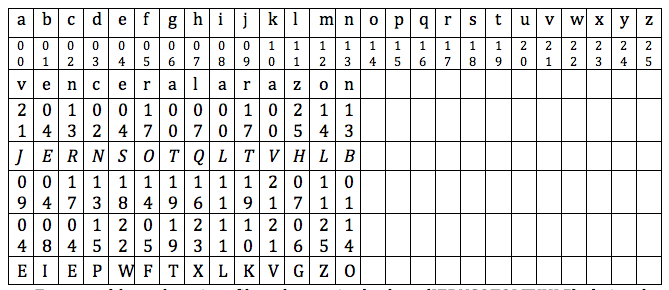
Un cifrado Vernam, sistema desarrollado por el mismo Vernam antes citado y perfeccionado por Joseph Mauborgne, al introducir claves aleatorias, representa el caso límite del cifrado de Vigenère. Fue originariamente ideado para emplear un alfabeto binario, pues se utilizó para comunicaciones telegráficas haciendo uso del código Baudot (representa los caracteres del alfabeto con cinco elementos que pueden ser el espacio o la marca -el cero o el uno, en digital-; fue diseñado para transmisiones telegráficas). Pero es posible realizar un cifrado tipo Vernam de manera sencilla, simplemente recurriendo a una tabla de equivalencia caracteres-números y usando una clave de longitud igual al texto a cifrar y generada aleatoriamente. Por ejemplo, supongamos que queremos cifrar el texto plano “vencerá la razón”, para ello generamos una clave aleatoria de 14 caracteres, y construimos la siguiente tabla, que nos va a servir para realizar “una suma de módulo 26” (es decir, similarmente a como hicimos antes en el cifrado César, si al sumar sale un número mayor que 25, restamos 26):
En esta tabla, en la quinta fila se ha escrito la clave (JERNSOTQLTVHLB), de igual longitud que el texto a cifrar y supuesta aleatoria; la penúltima fila corresponde a la suma en módulo 26 de las tercera y cuarta, constituye una hilera de números de dos dígitos que nos proporcionan el criptograma de la última fila, EIEPWFTXLKVGZO, sin más que sustituir los números por las letras correspondientes a esas posiciones (indicadas en la segunda fila).
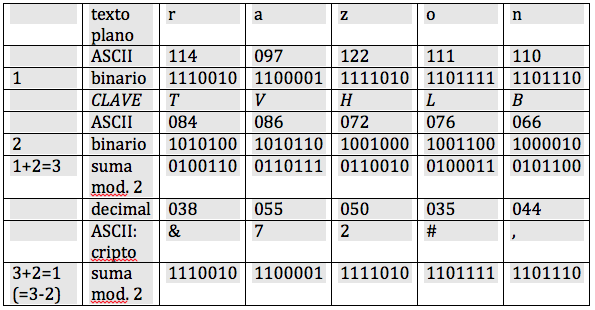
Es posible también realizar un cifrado Vernam imbatible digital, haciendo uso de la operación aritmética suma con módulo 2 (véase apartado B de las notas de ampliación, al final de esta entrada). En este cifrado, la clave, si es que queremos seguridad total, debe ser entonces una secuencia binaria aleatoria de la misma longitud que el texto plano o texto a cifrar. Por ejemplo, vamos a cifrar la palabra “razón”. Primero la escribimos en binario, haciendo uso de una tabla ASCII -sigla para American Standard Code for Information Interchange- de caracteres,
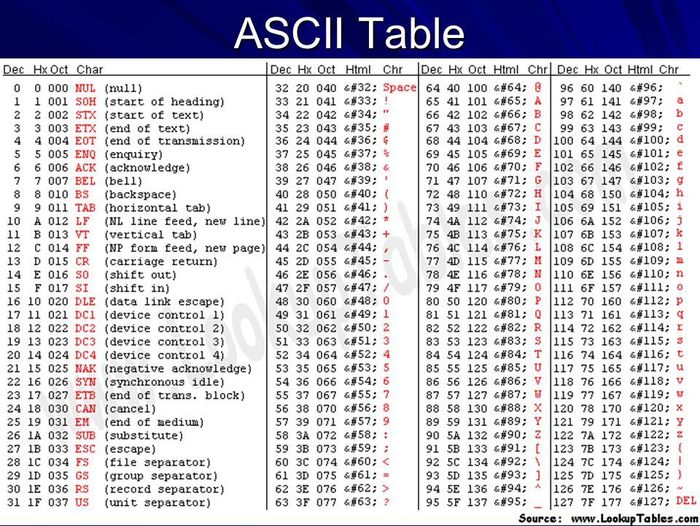
Aplicando la tabla ASCII, «razón» se codifica como 114-097-122-111-110; a continuación escribimos cada uno de estos números en binario, 1110010-1100001-1111010-1101111-1101110; introducimos una clave aleatoria de igual longitud, TVHLB, con la que procedemos de igual forma; sumamos en módulo 2 -operación lógica XOR, véase apartado B de las notas de ampliación, al final de esta entrada- los números binarios en cada columna y empleamos su conversión ASCII, lo que produce finalmente el criptograma: “&-7-2-#-, “. La tabla siguiente ilustra estos pasos:
Claude Shannon demostró matemáticamente en 1949, en su trabajo “Teoría de las comunicaciones secretas”, que el cifrado Vernam es en efecto inviolable, pero a condición de que la clave, de igual longitud que el texto a cifrar, se utilice solo una vez, un proceder que se encuadra en un tipo de sistemas criptográficos que se denominan “de libreta de un solo uso” (en inglés, one-time-pad). Lograr lo que Shannon definió como “secreto perfecto”, o mensaje cuyo cifrado es seguro frente a tiempo y recursos ilimitados, ya que el criptograma no proporciona absolutamente ninguna información acerca del texto original (o plano), requiere pues el uso de un gran cuaderno secreto de claves, del que se tiene que usar una “página” o clave distinta cada vez, destruyéndose a continuación, lo que resulta engorroso y complicado. A partir de las últimas décadas del siglo XX se propusieron muchos sistemas criptográficos de clave privada , también denominados como “simétricos”, más prácticos que el Vernam, con claves más breves que el mensaje a cifrar y reutilizables. Aunque algunos de ellos permanecen todavía sin ser violados, el caso es que tampoco se ha logrado establecer matemáticamente su invulnerabilidad.
Fortaleza de los cifrados clásicos
El esquema general de un sistema de cifrado simétrico se representado en la siguiente figura:
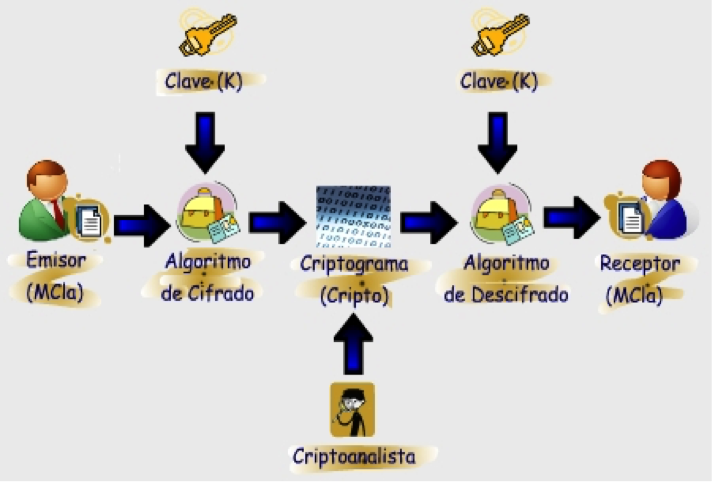
¿Qué aspectos deben considerarse para juzgar la fortaleza de un sistema de cifrado de mensajes? En su trabajo “La criptografía militar” de 1883, Auguste Kerckhoffs, estableció que los sistemas criptográficos deben cumplir varias reglas, entre ellas: debe ser imposible en la práctica descifrar el criptograma generado, es decir, que para ello se requiera de ingentes recursos; su seguridad debe ser independiente de que se conozca o no el sistema criptográfico usado; deben estar compuestos por dos tipos de información, la pública, relativa a la familia de algoritmos que definen el sistema criptográfico, y la privada, o clave secreta usadas en el cifrado, que debe ser conocida solo por los que aplican el sistema, preferiblemente una sola persona; la forma de escoger la clave debe ser fácil de recordar y modificar; el criptograma debe admitir transmisión vía los recursos de comunicación estándares; debe satisfacerse una proporcionalidad entre la importancia del secreto y la complejidad de lectura del criptograma.
La Historia da cuenta de muchos más ingeniosos métodos de criptografía clásica, hoy englobados, con sus correspondientes métodos de criptoanálisis, bajo la denominación usual de “criptología pre-científica”, y fueron numerosos los hechos históricos fundamentales, como las guerras, en que esos sistemas criptográficos jugaron un papel decisivo. Como ejemplo, el muy popular del artilugio de cifrado antes citado Enigma, usado por los alemanes en la II Guerra Mundial; las claves de los criptogramas que producía se lograron averiguar gracias a la construcción de la máquina Colossus, diseñada por un equipo de investigadores liderado por Max Neuman Alan Turing, uno de los padres de la informática y de la inteligencia artificial. Esta primera etapa se suele considerar que se extiende hasta mediados del siglo XX, cuando Shannon, también fundador de la teoría de la información, desarrolló su trabajo de fundamentación matemática de la criptografía, publicando en 1949 su trabajo “La Teoría de las Comunicaciones Secretas”, en el que sugería utilizar operaciones múltiples que mezclaran transposiciones y sustituciones y que se suele considerar marca el inicio de la etapa científica de la criptología.
A partir de entonces, el desarrollo de la informática y los avances matemáticos permitieron que los nuevos algoritmos de cifrado fueran cada día más complejos y eficaces. En 1973, los organismos oficiales estadounidenses hicieron una convocatoria pública para promover el desarrollo de sistemas criptográficos, fruto de la cual fue el complejo sistema DES (data encryption standard), presentado la compañía IBM dos años después. Se trata de un sistema de cifrado simétrico, de llave secreta o privada; opera sobre bloques de datos de 64 bits y utiliza una clave de 56 bits. Adoptado por muchos países, fue finalmente descifrado en varios ataques distintos, el definitivo en 1998, en un tiempo récord de 56 horas vía un ataque de simple fuerza bruta o búsqueda exhaustiva de la clave probando una tras otra, algo que por supuesto involucra ingentes recursos informáticos. De modo que se convocó otro concurso, que promovió el desarrollo de su sucesor AES (advanced encryption standard), cuyos creadores fueron Joan Daemen y Vincent Rijmen. Se trata de otro cifrado simétrico, pero ahora operando sobre bloques de datos de 128 bits y con clave que puede ser de 128, 192 o 256 bits: fue adoptado oficialmente en 2002. Sometido a criptoanálisis continuo, ninguno de los ataques exitosos publicados a fecha de hoy se considera lo suficientemente eficaz como para considerarlo realmente quebrado, lo que en criptoanálisis significa que se puede romper con un método más rápido que la simple fuerza bruta; si esa rapidez es suficiente, el cifrado se considera “comprometido”, lo que a día de hoy todavía no ha ocurrido para el AES. Pero en su horizonte acecha la amenaza de la computación cuántica, ya que, como vimos en el capítulo anterior, en 1996 Lov Grover publicó un algoritmo, destinado a ser aplicado por un ordenador cuántico, que optimizaba la búsqueda de un dato en una lista o secuencia de N elementos, requiriendo un tiempo de orden N1/2, mientras que el mejor algoritmo clásico requiere un tiempo de orden N; una consecuencia es que se mejora considerablemente la eficacia de resolución del problema, relacionado de la inversión de una función. Precisamente el tipo de procesos que se necesita implementar para romper la seguridad de cifrados del tipo DES y AES.
Debe considerarse que si bien en sus primeros usos un algoritmo de cifrado puede suponerse desconocido, con el tiempo se difundirá, de modo que la seguridad de un cifrado no puede depender de la mayor o menor difusión del algoritmo usado, sino que debe radicar en el secreto de la clave y, en caso de ser interceptada, de su fortaleza frente al criptoanálisis, así que con frecuencia una clave se usa para cifrar otras, en una jerarquía progresiva. Mientras que todos los sistemas hasta 1976 eran simétricos, haciendo uso de claves que han de mantenerse como un secreto adicional al del mensaje entre emisor y receptor, ese año Whitfield Diffie y Martin Hellman propusieron en su trabajo “Nuevas direcciones en criptografía” desarrollar sistemas criptográficos asimétricos, idea novedosa a la que también contribuyeron Ralph Merkle y Clifford Cocks. La idea consiste en añadir a la clave privada una clave pública, de forma que el esquema de la anterior figura se ampliaría para incuir dos claves distintas:
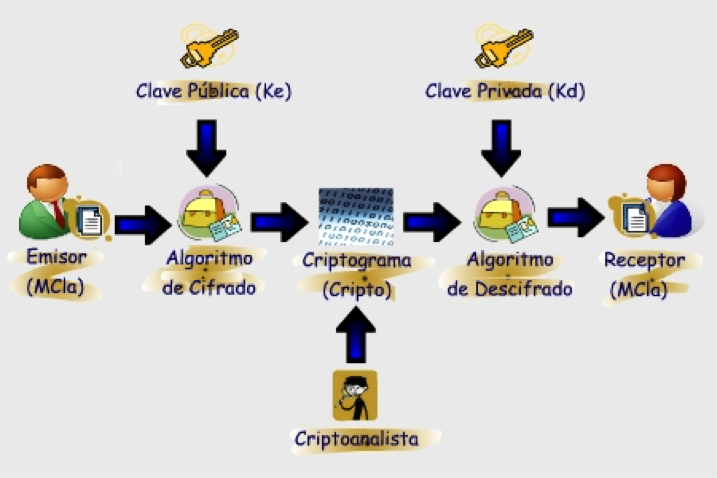
Conocidos como sistemas CSCP, uno de los primeros fue el RSA, sigla formada con las iniciales de sus creadores, Ron Rivest, Adi Shamir y Leonard Adleman, publicado en 1977 y considerado muy seguro, por lo que suele utilizarse sólo para temas trascendentales -como por ejemplo la generación de firmas digitales- por su elevada complejidad y coste asociados.
El algoritmo RSA: la garantía actual de muchas comunicaciones
Bautizado con las iniciales de sus creadores, Rivest, Shamir y Adleman, el algoritmo RSA es un algoritmo asimétrico, que involucra dos claves, una privada y otra pública, a partir del producto de dos números primos suficientemente grandes como para que el tiempo que se tardaría en averiguarlos con los actuales ordenadores (“clásicos”) sea muy elevado. A partir del resultado fundamental de que todo número natural puede descomponerse de forma única como producto de sus factores primos, la encriptación, usando dos sencillos números de un dígito sigue los pasos:
-Alicia elige los dos números primos n1=3 y n2=5, y calcula N=3×5=15.
-Calcula el valor de la función f(n1,n2)=(n1-1)(n2-1)=2×4=8, y elige un tercer número que carezca de divisores en común con 8, por ejemplo, n3=7.
-Calcula un cuarto número n4 tal que satisfaga n3xn4 mod [(n1-1)(n2-1)]=1, es decir, 7xn4 mod [2×4]=1, por ejemplo, n4=7 , ya que 7×7 mod (8)=49 mod (8)=1.
-Alicia hace públicos los números N y n3, pero se reserva n1, n2 y n4, tres números que van a ser su clave privada.
-Blas, para mandar el mensaje cuyo contenido es un número, digamos m=6<N (si es mayor, subdivide el mensaje y lo envía en varias partes), lo encripta como otro número M, que obtiene a partir de la operación M=m^(n_3 ) mod (N), es decir M=67 mod 15 = 279936 mod (15) =6.
-Cuando Alicia recibe M, lo descifra mediante m=M^(n_4 )mod (N) = 67 mod (15) =6.
-Alicia elige los dos números primos n1=3 y n2=5, y calcula N=3×5=15.
-Calcula el valor de la función f(n1,n2)=(n1-1)(n2-1)=2×4=8, y elige un tercer número que carezca de divisores en común con 8, por ejemplo, n3=9.
-Calcula un cuarto número n4 tal que satisfaga n3xn4 mod [(n1-1)(n2-1)]=1, es decir, 9xn4 mod [2×4]=1, por ejemplo, n4=1 , ya que 9×1 mod (8)=9 mod (8)=1.
-Alicia hace públicos los números N y n3, pero se reserva n1, n2 y n4, tres números que van a ser su clave privada.
-Blas, para mandar el mensaje cuyo contenido es un número, digamos m=4<N (si es mayor, subdivide el mensaje y lo envía en varias partes), lo encripta como otro número M, que obtiene a partir de la operación M=m^(n_3 ) mod (N), es decir M=49 mod 15 = 1024 mod (15) =4.
-Cuando Alicia recibe M, lo descifra mediante m=M^(n_4 )mod (N) = 41 mod (15) =4.
La siguiente figura esquematiza este proceder:
Para la seguridad del procedimiento es crucial que Eva, nuestra espía, aunque pueda acceder a N –se transmite de forma pública o insegura-, si éste es suficientemente grande no pueda, en un tiempo computacionalmente razonable, por muchos medios que de que disponga, descomponerlo en sus factores primos, para hacerse así con el número secreto n4 , a partir de los dos números primos n1 y n2 que descomponen N: sus dos factores primos. Y es que se trata de un problema cuya resolución crece en términos de demanda de recursos de forma exponencial; así pues, lleva mucho tiempo de computación conseguirlo, especialmente cuando los dos factores son muy grandes y de tamaño similar. Jorge Ramió Rodríguez, de la Universidad Politécnica de Madrid, nos presenta en su web la siguiente gráfica para el consumo de recursos sobre un ordenador con CPU Intel Core i7-2600, CPU a 3.40 GHz y RAM de 8.0 GB, en un sistema operativo de 64 bits: RSA-640, un número más pequeño, conteniendo 193 dígitos decimales (640 bits) el 4 de noviembre de 2005. Ambas factorizaciones requirieron varios meses de tiempo de computadoras, utilizando el poder combinado de 80 CPUs Opteron AMD.
 En RSA, como en todo sistema de clave pública, cada usuario posee dos claves de cifrado: una pública y otra privada, creadas a partir de una pareja respectiva de números primos grandes (un número primo es aquel número natural mayor que la unidad que solo admite división exacta por él mismo y por la unidad: 2, 3, 5, 7, 11 ,13…), que constituyen ahora los secretos a preservar con celo. Por ejemplo, imaginemos dos amigos, Alicia y Blas, que quieren disponer de un canal de información mutuo secreto. Si, por ejemplo, Alicia quiere enviar un mensaje a Blas, busca la clave pública de ella, cifra su mensaje con esa clave, y cuando Blas reciba ese criptograma así generado, lo descifrará usando su clave privada. Por tanto, no realizan ningún intercambio de claves, y está garantizado que sólo Blas podrá descifrar el mensaje, ya que ella ha generado sus dos claves a partir de su pareja de números primos -que sólo ella conoce-, mediante operaciones matemáticas muy complejas que involucran funciones del tipo “de un sentido”, fáciles de calcular en una dirección pero muy difíciles de invertir (algoritmo cuántico de Grover al margen).
En RSA, como en todo sistema de clave pública, cada usuario posee dos claves de cifrado: una pública y otra privada, creadas a partir de una pareja respectiva de números primos grandes (un número primo es aquel número natural mayor que la unidad que solo admite división exacta por él mismo y por la unidad: 2, 3, 5, 7, 11 ,13…), que constituyen ahora los secretos a preservar con celo. Por ejemplo, imaginemos dos amigos, Alicia y Blas, que quieren disponer de un canal de información mutuo secreto. Si, por ejemplo, Alicia quiere enviar un mensaje a Blas, busca la clave pública de ella, cifra su mensaje con esa clave, y cuando Blas reciba ese criptograma así generado, lo descifrará usando su clave privada. Por tanto, no realizan ningún intercambio de claves, y está garantizado que sólo Blas podrá descifrar el mensaje, ya que ella ha generado sus dos claves a partir de su pareja de números primos -que sólo ella conoce-, mediante operaciones matemáticas muy complejas que involucran funciones del tipo “de un sentido”, fáciles de calcular en una dirección pero muy difíciles de invertir (algoritmo cuántico de Grover al margen).
Los algoritmos CSCP son mucho más lentos de ejecutar, en general, que los simétricos, por lo que en la práctica se recurre a combinarlos. Por ejemplo, puede recurrirse al mecanismo del “sobre digital”, en el que Alicia cifra el mensaje con un sistema o protocolo simétrico, cuya clave secreta es cifrada asimétricamente vía la clave pública de Blas; ambos mensaje (con cifra simétrica), y clave simétrica (con cifra asimétrica), son transmitidos a Blas, quien, cuando los recibe, descripta primero la clave simétrica con su clave privada asimétrica y la aplica luego a descifrar el criptograma del mensaje.
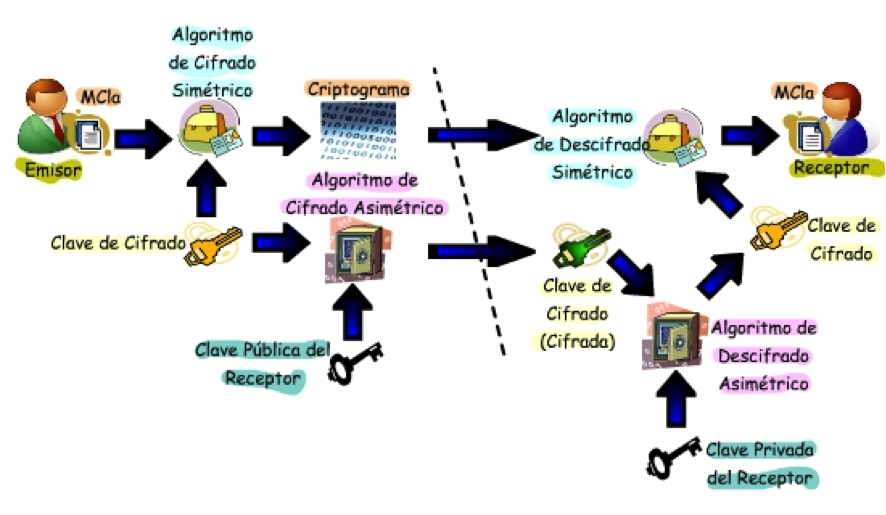
El criptoanálisis de los métodos asimétricos ha establecido que su seguridad, supuesta una clave pública lo suficientemente larga, depende, en última instancia y esencialmente, de cuán rápido y eficaz pueda resolverse el problema matemático de la descomposición de un número grande en factores primos (un teorema fundamental de la aritmética establece que cualquier entero mayor que 1 puede escribirse de forma única como un producto de números primos). En consecuencia, protocolos como el RSA podrán considerarse como seguros mientras que no se conozcan algoritmos eficaces para abordar esa tarea de descomposición. Sin embargo, en 1994 Peter Shor publicó un eficaz algoritmo ideado para proceder a la factorización de números grandes en factores primos, lo que supuso una amenaza teórica seria para la seguridad del cifrado RSA. Pero su aplicación requiere un ordenador cuántico operativo con una memoria estable de un tamaño todavía muy lejos por alcanzar, de forma que hoy por hoy el algoritmo RSA sigue siendo seguro en la práctica, ya que la factorización en primos sigue siendo inabordable en tiempos sensatos para los computadores clásicos. De hecho, aunque se han publicado rupturas para claves por debajo de los mil bits, conseguidas vía muchas horas de computación en miles de ordenadores cooperando en sus horas libres a lo largo del mundo -la compañía RSA establece golosos premios para los que consigan tales éxitos criptoanalíticos-, el descifrado de claves de unos 2000 a 4000 bits –como las que se usan hoy en las altas instancias- se supone imposible, pues se cree conllevaría millones de años de proceso. Pero, seamos prudentes, siempre cabe pensar que se podrían ir desarrollando mejores algoritmos de factorización implementables en ordenadores clásicos que van también siendo de manera progresiva mucho más potentes.
El problema de la gestión de claves y su interceptación
Siempre cabe también la posibilidad de acceder a las claves vía el espionaje. Sorprendentemente, en 2013 unos investigadores israelitas –Daniel Genkin, Eran Tromer y el propio Shamir, uno de los inventores del RSA, publicaron un artículo en que explicaban cómo habían logrado hacerse con la clave de un tipo de cifrado RSA vía un criptoanálisis acústico: analizando los sonidos emitidos por la CPU de varios modelos de ordenador. En palabras del sumario de un artículo suyo de 2016, publicado en la revista “Journal of Cryptology”:
“El ataque puede extraer la clave completa de 4096 bits para el descifrado RSA de los ordenadores personales, de varios modelos, en un tiempo de en torno a una hora, usando el sonido generado por el computador durante el descifrado de algunos criptogramas seleccionados. Hemos demostrado experimentalmente que este tipo de ataques puede realizarse usando bien un simple teléfono móvil colocado cerca del ordenador, bien un micrófono situado a unos 10 metros”.
De manera que ¡la seguridad RSA requiere también aislamiento acústico de los ordenadores empleados!
Para todos los cifrados simétricos, es obvio que es muy importante para su seguridad el sistema de intercambio de claves que se adopte. En cambio, podría pensarse que en un sistema asimétrico la buena gestión de claves ya no va a ser crucial, puesto que no se procede a ningún intercambio de claves. Sin embargo, no es así, el problema de cómo gestionar las claves subsiste, aunque la seguridad se relaciona en este caso no con cómo se distribuyen las claves públicas, sino con cómo autentificar a los intervinientes en un intercambio de información, ante la posibilidad de sufrir una interceptación y consiguiente ataque de los denominados “de respuesta”. Veamos en qué consisten con un ejemplo.
Supongamos que una tercera parte, Eva, nuestra espía, quiere interceptar la comunicación entre Alicia y Blas, y consigue publicar claves de un modo hacen que Alicia las interprete erróneamente como pertenecientes a Blas. Si Eva es capaz de interceptar los criptogramas que Alicia envía a Blas, además de leerlos sin problemas –puesto que están generados con la clave pública de Eva y no con la de Alicia, así que sólo tiene que aplicarle su clave privada-, también puede ocultar su espionaje, enviándole a Alicia un criptograma respuesta de Blas espúreo, elaborado a partir de esa falsa clave pública- la que Alicia ha tomado engañada como de Blas- y su clave privada (las dos de Eva). Es decir, en estas condiciones Eva puede no sólo descifrar cualquier mensaje de Alicia que intercepte, sino también cifrarlo con la clave pública auténtica de Blas y su propia clave secreta (de Eva), enviándolo después así modificado –no necesariamente en cuanto a su contenido plano, sí en su encriptación- a Blas, quien creerá que procede de Alicia. Por tanto, Alicia y Blas creen que se están comunicando en secreto, pero en realidad los mensajes de Alicia están siendo leídos por Eva, sin que ni Alicia ni Blas se den cuenta. Es contra este tipo de ataques contra los que se desarrollaron los certificados de firma digital, que acreditan la autenticidad de los emisores de un mensaje.
La cuestión de la gestión de claves fue el entorno teórico en que se produjo la primera propuesta de aplicación de la física cuántica a la criptología. Se trata del protocolo BB84, que describiremos más adelante, tras una corta introducción a la criptología cuántica.
La criptografía cuántica y su seguridad
Introducción
Después del breve recorrido hecho por la criptología clásica, parece claro que se presentan dos problemas. Por un lado, el hecho de que la seguridad completa, aunque demostrada matemáticamente como posible para un cifrado simétrico con clave aleatoria, de un solo uso y tan larga como el mensaje a cifrar, resulta poco práctica y requiere intercambio secreto de la clave que se ha de compartir; en esa distribución, podría interceptarse la clave sin que se dejara rastro alguno. De otro, que los sistemas de clave pública o asimétrica, que eliminan la necesidad de compartir una clave y por tanto de distribuirla, aparte de que no se haya establecido matemáticamente su seguridad completa, plantean el problema de la suplantación o ataques tipo “respuesta”. Pues bien, vamos a ver como la aplicación de la física cuántica a la criptología remueve estos obstáculos, puesto que hace posible métodos seguros de generación y distribución de claves, en la forma de secuencias aleatorias de bits, que se transmiten por un canal cuántico, un canal cuántico, esto es, implementadas sobre sistemas cuánticos, como átomos o fotones, que garantizan que cualquier vulneración de la seguridad o espionaje que se produzca será irremediablemente detectado, gracias a la acción de los principios de indeterminación, no clonado y colapso cuánticos.
El origen de la criptología cuántica suele asociarse con Stephen Wiesner, quien a principio de los 60 concibió la idea de aplicar el principio de indeterminación para conseguir billetes imposibles de falsificar, así como para transmitir por un mismo canal dos mensajes, de forma que sólo uno de ellos pudiera ser leído. Estas ideas sonaron tan extravagantes por aquel entonces que no logró publicarlas hasta 1970; de hecho, no sería hasta los 80 cuando estos temas empezaron a considerarse en serio, de manera que Charles Bennet y Gilles Brassard, ambos de IBM, iniciaron un trabajo que daría como fruto el famoso protocolo BB84, una aplicación cuántica a la criptografía de clave secreta pública? que implementa un protocolo seguro de distribución –generación en concreto en este caso- de la clave (en jerga criptológica, un mecanismo de QKD: quantum key distribution), en el sentido de que cualquier interceptación del mensaje por terceros será detectada por los interlocutores.
El protocolo BB84
Antes de explicar los protocolos cuánticos, hay que señalar que, en criptografía cuántica, los bits clásicos que se van a generar e intercambiar han de sustituirse por qubits, y estos corresponden al estado general de superposición cuántica |ψ> = α|0> + β|1> de los dos estados básicos ortonormales {|0> ,|1> } de un sistema, los análogos del bit clásico. El soporte físico puede ser, por ejemplo, los estados de polarización de un fotón, representados de forma convencional bien en la base horizontal-vertical, {H≡|↔> ,V≡|↑> }, bien en la diagonal {DD≡|↗> , DI≡|↖> }. De manera que la expresión de un qubit en una de ellas, por ejemplo la primera, se corresponde con el estado cuántico superpuesto |ψ> = α|↔|↔> + β|↕> , donde α y β son dos complejos que satisfacen |α|^2 + |β|^2=1 , representando cada uno de los sumandos en esta última expresión las sendas probabilidades de que al medir la polarización del fotón se encuentre como resultado el horizontal H, |↔> , o el vertical V, |↕>. La relación entre los estados de estas dos bases viene dada por el usual conjunto de ecuaciones del cambio de base: H=1⁄√2 (DD-DI) V (=1)⁄√2 (DD+DI) DD=1⁄√2 (H+V) DI (=1)⁄√2 (-H+V). Un bit clásico o es |0> o es |1> , nunca los dos a la vez; un qubit es un estado en general superpuesto de las dos posibilidades de una variable contextual dicotómica, como la polarización, lineal o circular, de un fotón. Convenimos en que vamos a asociar el bit clásico |0> con los estados cuánticos H y DD, y el bit clásico |1> con los estados cuánticos V y DI; un qubit es una superposición con coeficientes complejos –en particular, pueden ser reales- de cualesquiera dos estados de la misma base. La idea sobre la que se basa el protocolo es conjugar el envío de un mensaje por un canal tradicional –clásico- con un envío adicional de una serie de qubits -canal cuántico-, implementados sobre fotones polarizados. De esta manera, dos comunicantes –nuestros Alicia y Blas- se van a intercambiar una clave secreta aleatoria, que luego se supone usarán para cifrar sus comunicaciones con un cifrado clásico como, por ejemplo, el Vernam. La seguridad que conlleva la incorporación del canal cuántico va a ser que, en virtud del principio de indeterminación y las superposiciones cuánticas, si cualquier espía –nuestra Eva- intercepta el canal cuántico –la clave secreta-, inapelablemente dejará una huella de su acción que será detectada por Alicia y Blas, quienes entonces desecharán esa clave. Comencemos el protocolo. Alicia, por ejemplo, envía a Blas una radiación de pulsos monofotónicos cuyos integrantes han sido forzados a determinar su estado de polarización a uno de entre los cuatro {H≡|↔> ,V≡|↕> ,DD≡|↗> ,DI≡|↖> } ; para ello, como ya hemos visto, basta por ejemplo hacer pasar un fotón despolarizado por un cristal de calcita orientado en modo recto –Modo HV, salidas H o V al 50% -o en modo girado un ángulo de 45° -modo DID, salidas DD o DI, al 50%-, distribuyéndose así los fotones al azar entre cuatro estados de polarización lineal, asociados a los cuatro ángulos respectivos para la serie de estado anterior {0°,90°,45°,135°}, respecto a una dirección del espacio que establecemos como la horizontal H o eje X; el eje Z se asigna convencionalmente a la dirección de propagación. Para conseguir una secuencia aleatoria de polarizaciones, basta ir eligiendo entre las dos modos de la calcita al azar, cambiándolos en su caso antes de la llegada de cada fotón. Alicia, pues, codifica sobre los fotones una serie de bits clásicos, según –por ejemplo- la siguiente secuencia, determinada por completo al azar:
Apéndice: notas de ampliación
A) Aritmética básica en binario
Estamos acostumbrados a manejar el sistema decimal, en las operaciones aritméticas cotidianas… pero también el sistema binario: lo hacemos cada vez que, por ejemplo, manejamos un ordenador. Este sistema es de base dos, lo que quiere decir que maneja solo dos caracteres (el decimal emplea 10), llamados “bits” (contracción de «binary digits»). Para representar un número natural x –esto es, la serie de enteros positivos 1, 2, 3…, más el cero-, en un sistema binario “posicional” se procede a indicar sus componentes n_i, de valor 0 o 1 y en el orden establecido (n_N,n_(N-1)⋯n_1,n_0), que permiten expresarlo como:
x=n_N∙2^N+n_(N-1)∙2^(N-1)+⋯+n_1∙2^1+n_0∙2^0 ,
donde N es otro número natural, que define el bit “n_N” o bit “más significativo”. Así, por ejemplo, los primeros 10 números (0,1,2,…,9) se codificarían en un sistema binario posicional de 4 bits como:
Para codificar los números naturales entre 0 y 255, se necesitarán 8 bits (un “byte”), ya que . Por lo general, el empleo de N bits (N posiciones) permite codificar los números naturales entre
y
.
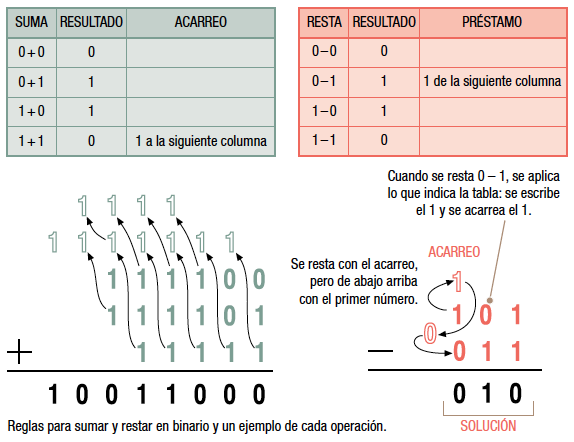
Para sumar o restar dos números binarios, se empieza sumando o restando los bits menos significativos, produciendo bits de suma y bits de acarreo. Se continúa operando con los sucesivos bits de derecha a izquierda, incorporando en su caso el acarreo, según las reglas de la tabla de suma en la figura adjunta. La resta binaria se realiza de manera similar, pero empleando acarreos negativos o “préstamos” a una columna desde la columna anterior cuando el minuendo de esa columna sea un 0 y el sustraendo sea un 1. Así, para restar dos números binarios se restan primero los bits menos significativos, produciendo bits de resta y bits de préstamo en su caso. Se continúa procesando bits de derecha a izquierda, restando cada bit de préstamo, si lo hubiere, de la siguiente columna a la izquierda, de modo que cada vez que hay un préstamo la correspondiente posición del minuendo que presta pasa de 1 a 0; si ya era cero, pasa a 1, y se tomaría de la siguiente posición, que pasaría a ser 0 si fuera 1 (si fuera cero, se pone a 1 y se pediría a la siguiente, y así hasta que se tope con un 1).
En la figura siguiente se representan reglas y ejemplos:
B) Aritmética modular: suma modular y la operación lógica XOR
Consideremos un cifrado César de dos caracteres, 0 y 1, esto es, se aplicaría el módulo 2 para sustituir las letras de un mensaje, de forma que, por ejemplo, la palabra “una” se encriptaría según la fórmula:
,
o sea, «101», ya que:
;
y
;
análogamente, «oculta» se cifraría como «111001», etc.
Para visualizarlo, podemos imaginar un reloj con solo dos números, 0 y 1, y tomar el mod 2 de cualquier entero n de la siguiente manera: empezando a partir de la posición 0, realizar la secuencia de movimientos 0⇒1⇒0⇒…, dando n pasos; la posición final, bien 0, bien 1, nos indicará el valor de “n mod 2”. Así que, de forma obvia, las letras con índice de posición cero o par en el alfabeto irían a cero y las de índice impar a 1.
Para calcular otros módulos, se puede usar el mismo procedimiento; por ejemplo, en módulo 8 pondríamos 8 horas o posiciones en el reloj, numeradas de 0 a 7, e iríamos saltando sucesivamente de una a otra. Otro ejemplo, 9 (mod 8) = 1 (ya que 9 = 8 · 1 + 1, con un residuo de 1 = 9 – 8 en la correspondiente división de 9 entre 8 para dar 1); 14 (mod 8) = 6 (ya que 14 = 8 · 1 + 6, con residuo 6 = 14 – 8 en la división de 14 entre 8 para dar 1); etc.
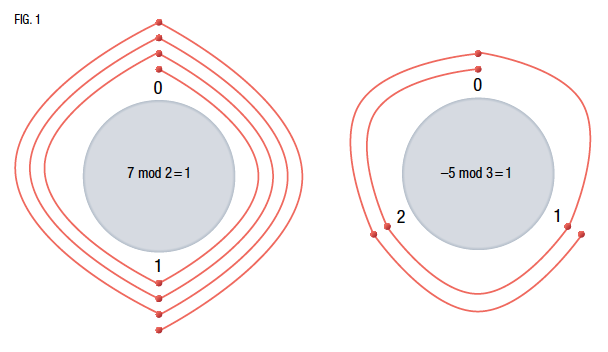
Para un número entero negativo, daríamos los pasos en sentido antihorario, como se muestra a la derecha en la siguiente figura, que nos ayuda a representarnos este tipo de operaciones:
En la matemática binaria de módulo 2, simplemente se ignoran los acarreos, de forma que la suma y la resta en módulo 2 se igualan a la operación lógica denominada XOR, cuya “tabla de verdad”, es decir, el valor de la suma en módulo 2 de los dos números, se muestra a continuación, junto con un ejemplo de suma y resta modular de tres bits:
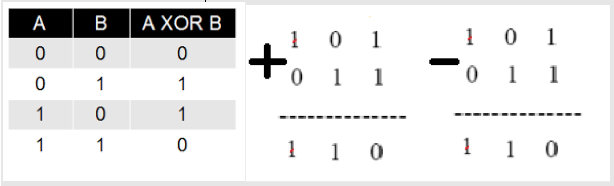
En el ejemplo, se están sumando los números 5 (en binario, 101) y 3 (011), obteniéndose en módulo 2 el binario 110, es decir, el decimal 6, que tomado en módulo 2 conduce al resultado final 0. Por lo tanto:
.
La puerta lógica XOR, o disyunción exclusiva lógica, se corresponde con la suma aritmética binaria de módulo 2; su símbolo como operador es + dentro de un círculo, , y realiza la función booleana
,
donde la prima (‘) simboliza la negación y el signo positivo + la disyunción no exclusiva (OR).
Enlaces
(¡enlaces no comprobados!)
https://www.dhushara.com/book/quantcos/aq/qcrypt.htm
http://www.criptored.upm.es/
criptored.es
criptored.upm.es
https://mappingignorance.org/2013/05/06/satellite-based-quantum-cryptography/ https://www.wired.com/2013/06/quantum-cryptography-hack/
Quantum Cryptography May Not Be as Secure as Previously Thought
https://www.extremetech.com/extreme/228095-nist-report-says-we-urgently-need-more-work-in-post-quantum-cryptography
https://arstechnica.com/information-technology/2012/09/quantum-cryptography-yesterday-today-and-tomorrow/
https://www.welivesecurity.com/la-es/2016/06/14/computacion-cuantica-armagedon-criptografico/
https://revista.seguridad.unam.mx/numero-19/criptograf%C3%AD-cu%C3%A1ntica-%E2%80%93-parte-ii https://physics.aps.org/articles/v9/s119
|α|^2 + |β|^2=1
{H≡|⬌> ⬍ , V≡|↕> }|↔↔↑↓→←↔↕↘>|↔↔↑↓→←↔↕↘>↔↔↔ -Son imágenes: ![]()
![]()
![]() , -Diagonales azules {DD≡|↗> ,DI≡|↖> }.
, -Diagonales azules {DD≡|↗> ,DI≡|↖> }.
-Aquí van los 9: ← ↑ → ↓ ↔ ↕ ↖ ↗ -Aquí van los azules:↕↔ ↔ ↕ ↖ ↗ ↔ FIN 1 ⟷ ↔ ⬍ Fin2 -Polarizaciones circulares: ↺ ↻ -Nombre: ↔ ↕
LECTURAS RECOMENDADAS
-Hernández Encinas, L.; La criptografía». CSIC, Los libros de la Catarata; Madrid, 2016.
-Khan, D.; The Codebreakers: The Comprehensive History of Secret Communication from Ancient Times to the Internet. Scribner; New York, 1996.
-Loepp, S. and Wootters, W.K.; Protecting Information: From Classical Error Correction to Quantum Cryptography. Cambridge University Press, Cambridge, 2006.
-Nielsen, M.A. and Chuang, I.L.; Quantum Computation and Quantum Information; Cambridge University Press, 2000. ISBN 0-521-63503-9.
-Singh, S.; Los códigos secretos. Biblioteca Buridán; Barcelona, 2011.




Dejar una contestacion