El teorema de imposibilidad de Hardy

Teorema de Hardy: imposibilidad realismo local.

Introducción

«La Mecánica Cuántica viola el realismo local» y «variados resultados experimentales fiables parecen violar definitivamente el realismo local, mientras que concuerdan con las predicciones mecano-cuánticas» son dos proposiciones que a partir de 1993, cada vez con más convencimiento, parecían haberse establecido como ciertas para la mayoría de la comunidad científica. Ese mismo año, un desarrollo teórico de Hardy vino a corroborarlo:

L. Hardy, Nonlocality for two particles without inequalities for almost all entangled states, Phys. Rev. Lett. 71 (1993) 1665-1668.

Como para el teorema de Bell, existen numerosas demostraciones del resultado en la bibliografía, es muy recomendable la exposición de Laloë en el marco de un formidable artículo sobre fundamentos de la Mecánica Cuántica:

F. Laloë, Do we really understand Quantum Mechanics?; American Journal of Physics 69 (2001) 655 – 701; http://arxiv.org/abs/quant-ph/0209123v2

-Otra buena referencia es el addendum que D. Styer publicó para su texto sobre Mecánica Cuántica:

D. Styer: Hardy’s test of quantum mechanics; www.oberlin.edu/physics/dstyer/StrangeQM/Hardy.pdf

-Y como no, una buena divulgación, a cargo del mismo Hardy en colaboración con Kwiat:

The mystery of the quantum cakes

Esencialmente, lo que diferencia el teorema de Hardy de los teoremas tipo Bell es que, mientras estos últimos involucran relaciones entre ratios de resultados de medidas correlacionadas, Hardy logra establecer la imposibilidad de que se produzca un resultado experimental concreto, y sin involucrar desigualdades, si se incorpora la hipótesis del realismo local:

The best version of Bell’s theorem (Mermin):

N. D. Mermin, The best version of Bell’s theorem, en Fundamental Problems in Quantum Theory, Ann. Acad. Sci. 755, New York, 1995, pp. 616-623.

Desarrollo teórico

Fuente: la exposición siguiente se basa en la exposición de Laloë antes indicada:

F. Laloë, Do we really understand Quantum Mechanics?; American Journal of Physics 69 (2001) 655 – 701; http://arxiv.org/abs/quant-ph/0209123v2

Consideremos dos partículas, partícula A, $PaA$ , y partícula B, $PaB$ , sobre las cuales se van a realizar dos tipos de medidas, correspondientes a sendas disposiciones experimentales $Ex1$ y $Ex2$ para la medida de un observable dicotómico dado, cuya medida sobre cada partícula sólo puede arrojar uno de los dos resultados $+1$ o $-1$ ; representaremos los valores obtenidos para el segundo experimento con primas (‘).

-Nos aseguramos de que las medidas realizadas sobre cada partícula se hagan en regiones separadas einsteinianamente (medidas separadas por un intervalo de género espacio), de forma que no puedan invocarse influencias mutuas.

-Por ejemplo, podemos imaginar que $PaA$ y $PaB$ son dos electrones, y los experimentos $Ex1$ y $Ex2$ son montajes que miden la componente de espín (de forma equivalente, la matriz de Pauli, $\vec{\sigma}=\frac{2}{\hbar}\vec{S}$ , para que los autovalores de la tercera componente sean $\pm1$ ) de una de las partículas respecto a sendas direcciones formando ángulos dados $\theta_1$ y $\theta_2$ con respecto a una dirección fijada como eje $OZ$ .

-Así, podemos someter la partícula $PaA$ al test experimental $Ex1$ , y denominamos el correspondiente resultado obtenido como $A$ (que puede ser +1 o -1). O podemos someterla al test $Ex2$ , que arrojará un resultado $A'$ (que puede ser +1 o -1).

-Análogamente, podemos someter la partícula $PaB$ al test experimental $Ex1$ , obteniendo el resultado $B$ (que puede ser +1 o -1); o podemos someterla al test $Ex2$ , que arrojará un resultado que notamos $B'$ (y que también puede ser +1 o -1).

-Es decir: se va a usar una notación en que los resultados sin (con) prima (‘) corresponden a medidas con la disposición experimental $Ex1$ ( $Ex2$ ); los resultados con la letra A (B) corresponden a la partícula $PaA$ ( $PaB$ ).

Planteemos a continuación la posibilidad de que se produzcan tres situaciones:

1. Proposición Hardy 1: Se someten ambas partículas al experimento $Ex1$ .

$\bullet$ SÍ puede obtenerse la pareja de resultados $A=1$ y $B=1$ .

2. Proposición Hardy 2: Se someten las partículas a sendos tests distintos: o bien $PaA$ al test $Ex1$ y $PaB$ al test $Ex2$ , o intercambiados (esto es, $PaA$ al test $Ex2$ y $PaB$ al test $Ex1$ ).

$\bullet$ NUNCA se obtiene el resultado conjunto $A=+1=B'$ y $A'=+1=B$ .

3. Proposición Hardy 3: Se someten ambas partículas al mismo experimento $Ex2$ .

$\bullet$ NUNCA se obtiene la pareja de resultados $A'=-1$ y $B'=-1$ .

La pregunta que se plantea es: «¿podemos preparar las dos partículas en un estado en el que las tres proposiciones Hardy puedan satisfacerse?»

Discusión con hipótesis realista (local): La lógica clásica muestra que si asumimos elementos de realidad (variables ocultas) objetivos, responsables de los resultados establecidos, las tres situaciones resultan incompatibles:

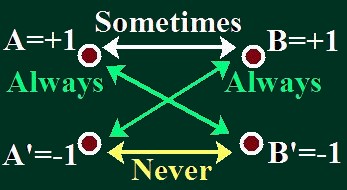
-En efecto: la situación 1 implica que, si $A=+1$ , entonces necesariamente por la situación 2 ha de ser $B'=-1$ (primera diagonal en la figura). Simétricamente, al ser $B=+1$ , se implica $A'=-1$ (segunda diagonal). Entonces, se tiene que el evento que ha producido $A=+1=B$ (situación 1), implica que $A'=-1=B'$ , lo que hace imposible que se cumpla la proposición 3. Luego queda establecedida la situación Hardy como imposible en un marco teórico que incorpore el realismo local:

La lógica clásica concluye que las tres situaciones son incompatibles: no puede existir un estado de las dos partículas que permita un evento en que las tres situaciones se presenten a la vez.

Discusión mecano-cuántica: consideremos dos electrones y el observable espín, y construyamos el estado (puro)

$|\left.\Psi \right\rangle$ $=\alpha \,| \left. +_A \, -_B\right\rangle +\beta \,| \left. -_A \, +_B\right\rangle + \gamma \,| \left. +_A \, +_B\right\rangle$ ,

que es claramente una superposición de estados de la base

$\{ | \left. +_A \, +_B\right\rangle \,,\, | \left. +_A \, -_B\right\rangle \,,\, | \left. -_A\, +_B\right\rangle \,,\, | \left. -_A \, -_B\right\rangle \}$ .

-Este estado puro es entrelazado:

$|\Psi> \ne |A> \otimes |B>$ ,

y su normalización corresponde a la ecuación

$\alpha^2 + \beta^2 + \gamma^2=1$ ,

donde $|+>$ y $|->$ son los respectivos autoestados monoparticulares correspondientes a los autovalores $+$ (up, $\uparrow$ , «hacia arriba») y $-$ (down, $\downarrow$ , «hacia abajo») de la tercera componente de espín:

$S_z |+>=+\frac{\hbar}{2}|+> \; ; \quad S_z |->=-\frac{\hbar}{2}|->$

-Sean los ángulos $\theta_1=2\theta$ y $\theta_2=0$ ; esto es: $Ex1$ mide la componente de espín sobre una dirección en el plano OXZ que forma un ángulo $2\theta$ con el eje OZ ; $Ex2$ mide la componente $S_z$ .

-La situación 3 se cumple de entrada, ya que no hay un sumando del tipo $|-_A\,-_B>$ :

$|-_A\,-_B><-_A\,-_B|\Psi>=0$

-El autoestado de una partícula correspondiente al autovalor $+\frac{\hbar}{2}$ para la componente de espín sobre una dirección $\hat{n}=(sen \vartheta cos \varphi , sen \vartheta sen \varphi , cos \vartheta )$ en el plano $OXZ$ , esto es, la dirección con componente $n_y=0$ ( $\varphi=0$ ), que forma un ángulo $\vartheta=2\theta$ con el eje $OZ$ es:

$S_{\hat{n}} | \phi>=\frac{\hbar}{2}| \phi> \, , \, \sigma_{\hat{n}} | \phi>=| \phi>$ ,

$S_{\hat{n}}=\hat{n}\cdot\vec{S}=S_x\, sen\ 2\theta + S_z\, cos\ 2\theta$ .

-La situación 2 excluye:

$\bullet$ NO $A'=+1=B \Rightarrow$

NO el estado $|\Phi_1>=|+_A>\,|\phi_B> =\cos \theta \, |+_A +_B > \, +\, \sin \theta \, |+_A -_B >$

$\bullet$ NO $A=+1=B' \Rightarrow$

-Es decir, $\Psi$ no puede contener las anteriores componentes, de forma que se deriva:

$<\Psi | \Phi_1 >=0 \Rightarrow \alpha \, \sin \theta + \gamma \cos \theta =0$

$<\Psi | \Phi_2 >=0 \Rightarrow \beta \, \sin \theta + \gamma \cos \theta =0$
por lo que debe ser

$\alpha = \beta = -\gamma \, \cot \theta$

-Por lo tanto, el estado $|\Psi>$ , con la elección $\gamma=\sin \theta$ , queda:

$|\left.\Psi \right\rangle$ $=-\cos \theta \, (| \left. +_A \, -_B\right\rangle +\,| \left. -_A\, +_B\right\rangle ) + \sin \theta \,| \left. +_A \, +_B\right\rangle$

con norma al cuadrado

$<\Psi | \Psi >=$ $2 \cos ^2 \theta + \sin ^2 \theta$

-A continuación, se realiza el producto escalar entre el anterior estado $|\Psi>$ y el
$|\Phi>=|\phi_A \, \phi_B>$ , a fin de indagar la probabilidad de cumplimiento de la situación 1:

$<\Phi | \Psi>=-\sin \theta \, \cos^2 \theta$

-Y, finalmente, normalizando probabilidades:

$P(\mbox{evento satisfaciendo situaciones 1, 2 y 3})$

$=\frac{|<\Phi | \Psi >|^2}{< \Psi | \Psi >}=\frac{\sin^2 \theta \cos^4 \theta}{2\cos^2 \theta + \sin^2 \theta}$ ,

función que presenta un máximo de valor $(\frac{\sqrt{5}-1}{2})^2 \approx 0.09017$ .

Por tanto:

Se tiene una probabilidad no nula de que se produzca un evento de medida que satisfaga las tres situaciones Hardy a la vez: un evento con hasta un 9.0169944% de probabilidad de ser observado, pese a su imposibilidad de ocurrir en un contexto realista local.

Es más: el desarrollo expuesto admite generalización a un número arbitrario de medidas, lo que redunda en un incremento de la probabilidad de eventos imposibles para el realismo local, llegándose a alcanzar porcentajes próximos al 50% para la probabilidad de observación.

La generalización involucra una cadena que, conservando en el inicio los requisitos 1 y 2 originales, reconvierte el 2 en una cadena recurrente (cf. Laloë, ibid. p.37).

En conclusión: la Mecánica Cuántica permite construir un estado en el que las tres proposiciones (los tres tipos de medidas conjuntas que la pareja de experimentadores decide acometer) pueden coexistir, pero no es correcto asumir que los cuatro resultados A,A’,B y B’, pueden ponerse en correspondencia con unos elementos de realidad (locales), incluso si estos elementos, ajenos a la MC, se consideran variables ocultas a determinar en futuras compleciones de la teoría.

Implementación experimental

La realización experimental pionera de la propuesta de Hardy fue llevada a cabo en 1999 por Kwiat et al, en el Laboratorio Nacional de Los Alamos, quienes encontraron una rotunda desviación respecto a la predicción del realismo local:

A.G. White, D.F. V. James, P.H. Eberhard y P.G. Kwiat, Nonmaximally Entangled States: Production, Characterization, and Utilization, Physical Review Letters 83,16(1999)3103-3107.

Es interesante reseñar, finalmente, la realización experimental que publicaron Carlson, Olmstead y Beck, por ser una ilustración del abaratamiento de la tecnología requerida para esta clase de experiencias: un experimento acometido por estudiantes de Física en un laboratorio del Whitman College, en Washington, U.S.A.:

J.A. Carlson, M.D. Olmstead and M. Beck, Quantum mysteries tested: An experiment implementing Hardy’s test of local realism; Am. J. Phys. 74 (3), 2006, 180-186.

Guo, W., Fan, D. & Wei, L.; Sci. China Phys. Mech. Astron. (2015) 58: 1; https://doi.org/10.1007/s11433-014-5495-0: https://link.springer.com/article/10.1007/s11433-014-5495-0:

Bell’s theorem argues the existence of quantum nonlocality which goes basically against the hidden variable theory (HVT). Many experiments have been done via testing the violations of Bell’s inequalities to statistically verify the Bell’s theorem. Alternatively, by testing the Hardy’s ladder proofs we experimentally demonstrate the deterministic violation of HVT and thus confirm the quantum nonlocality. Our tests are implemented with non-maximal entangled photon pairs generated by spontaneous parametric down conversions (SPDCs). We show that the degree freedom of photon entanglement could be significantly enhanced by using interference filters. As a consequence, the Hardy’s ladder proofs could be tested and Bell’s theorem is verified robustly. The probability of violating the locality reach to 41.9%, which is close to the expectably ideal value 46.4% for the photon pairs with degree of entanglement ɛ = 0.93. The higher violating probability is possible by further optimizing the experimental parameters.

Como señalan todos los autores, aunque en pura teoría la observación de una simple ocurrencia del suceso imposible bastaría para demostrar la violación del realismo local, en la práctica los laboratorios reales son imperfectos, de manera que en la práctica el test se reconvierte a una desigualdad (aunque un solo evento positivo, por sí mismo, viola el realismo local).

La conexión con la propiedad de la contextualidad cuántica:

A. Cabello, P. Badziąg, M. Terra Cunha y M. Bourennane, «Simple Hardy-like proof of quantum contextuality», Phys. Rev. Lett. 111, 18, 180404 (2013); arXiv:1310.8330 [quant-ph]; DOI: 10.1103/PhysRevLett.111.180404.
Contextuality and nonlocality are two fundamental properties of nature. Hardy’s proof is considered the simplest proof of nonlocality and can also be seen as a particular violation of the simplest Bell inequality. A fundamental question is: Which is the simplest proof of contextuality? We show that there is a Hardy-like proof of contextuality that can also be seen as a particular violation of the simplest noncontextuality inequality. Interestingly, this new proof connects this inequality with the proof of the Kochen-Specker theorem, providing the missing link between these two fundamental results, and can be extended to an arbitrary odd number n of settings, an extension that can be seen as a particular violation of the n-cycle inequality.

Nota: curiosidad matemática

A. Cabello relata la siguiente anécdota en relación al desarrollo de Hardy: consultado A. Galindo sobre un artículo que habían redactado al respecto, éste les dio la siguiente opinión:

I haven’t had time to read it … However, your result is correct» […] because the final result is the fifth power of the inverse of the golden ratio, and such a beautiful number cannot happen by chance.

A. Cabello, «Examples of mathematical beauty when comparing classical and quantum worlds», en R. F. Álvarez-Estrada, A. Dobado, L. A. Fernández, M. A. Martín-Delgado and A. Muñoz Sudupe (eds.), Fundamental Physics Meeting «Alberto Galindo», Aula Documental de Investigación, Madrid, 2004, 209-218.

Esto también lo advierte D. Styer en su exposición sobre el resultado:

One thing that intrigues me about Hardy’s test is the mathematical origin of the probability $0.09017\ldots$ The number is $g^5$ , where the constant $g$ is equal to $(\sqrt{5}-1)/2=0.6180\ldots$ and is called «the golden mean» […] It is the first time I’ve ever seen it appear in quantum mechanics.

D. Styer: Hardy’s test of quantum mechanics.

Referencias

J.A. Carlson, M.D. Olmstead and M. Beck, Quantum mysteries tested: An experiment implementing Hardy’s test of local realism; Am. J. Phys. 74 (3), 2006, 180-186.

T. Fritz, Quantum analogues of Hardy’s nonlocality paradox; http://arxiv.org/pdf/1006.2497.pdf

http://www.sciencedirect.com/science/article/pii/037596019290619W

L. Hardy, Nonlocality for two particles without inequalities for almost all entangled states, Phys. Rev. Lett. 71 (1993) 1665-1668.

L. Hardy, A quantum optical experiment to test local realism, Phys. Lett. A167(1)(1992)17-23.

F. Laloë, Do we really understand Quantum Mechanics?; American Journal of Physics 69 (2001) 655 – 701; http://arxiv.org/abs/quant-ph/0209123v2.

D. Styer: Hardy’s test of quantum mechanics; www.oberlin.edu/physics/dstyer/StrangeQM/Hardy.pdf

José L. Cereceda, «A simple proof of the converse of Hardy’s theorem», http://cds.cern.ch/record/396514/files/9908039.pdf; en ArXiv: https://arxiv.org/abs/quant-ph/9907094.

Bell’s theorem with easy math

Bell’s Theorem: An Overview with Lotsa Links, by David R. Schneider;
www.DrChinese.com

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

El teorema de imposibilidad de Hardy

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta