El efecto Compton

*Imagen de http://imagine.gsfc.nasa.gov.*

Dispersión Compton

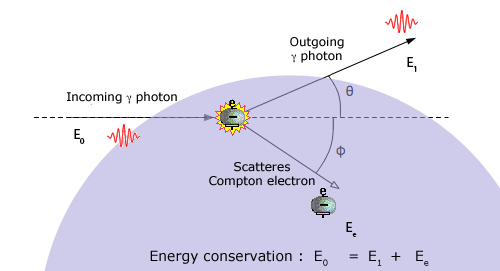
*Efecto Compton: colisión de un fotón y un electrón atómico; imagen tomada de la URL: http://www.laradioactivite.com/fr/site/pages/Effet_Compton.htm.*

Otro de los experimentos fundamentales que muestra aspectos corpusculares en la radiación es el denominado efecto Compton, observado por A.H. Compton en 1923 en la dispersión de rayos $X$ por electrones atómicos. El efecto consiste en que, bajo determinadas circunstancias, se presenta radiación dispersada con una longitud de onda mayor a la incidente (corrimiento Compton).
La teoría electromagnética clásica no es capaz de justificar este fenómeno. Según la predicción clásica, la radiación difundida debe tener la misma longitud de onda que la incidente: se excitan los electrones del blanco y oscilan emitiendo energía con la misma frecuencia. Pero el hecho es que experimentalmente se observa, además del esperado pico clásico o pico Thomson, correspondiente a una longitud de onda $\lambda$ igual a la incidente, un segundo pico, el pico Compton, para cada ángulo de dispersión, a otro valor distinto $\lambda' > \lambda$ . El pico Compton se observa de forma más nítida cuanto más dura (de mayor frecuencia) es la radiación incidente, constituyendo una discrepancia con la predicción clásica, unas anomalías que ya fueron observadas de forma temprana a partir de 1906 por Barkla, en sus experimentos de difusión de rayos X , en los que estudió la dispersión Thomson. Dada la poca resolución manejada en sus experimentos, las anomalías se interpretaron como simples errores experimentales.
En 1921-23 Compton estudió con suficiente precisión el fenómeno, estableciendo la presencia real de esa segunda longitud de onda, diferente a la incidente, en la radiación difundida; posteriormente, Compton y Debye, independientemente, justificaron teóricamente el fenómeno recurriendo a la hipótesis del cuanto de luz de A. Einstein (que empezaría a denominarse como fotón a partir de 1926, en denominación acuñada por G.N. Lewis), esto es, mediante, podría decirse, el «tratamiento corpuscular» de la radiación. Compton recibiría por ello el Premio Nobel en 1927 (Debye sería premiado a su vez con el Nobel de Química de 1936, por sus estudios sobre estructuras moleculares).
En el experimento correspondiente, un haz de rayos $X$ de longitud de onda $\lambda$ se hace incidir sobre un blanco de Carbono y la radiación difundida se analiza con un espectroscopio:
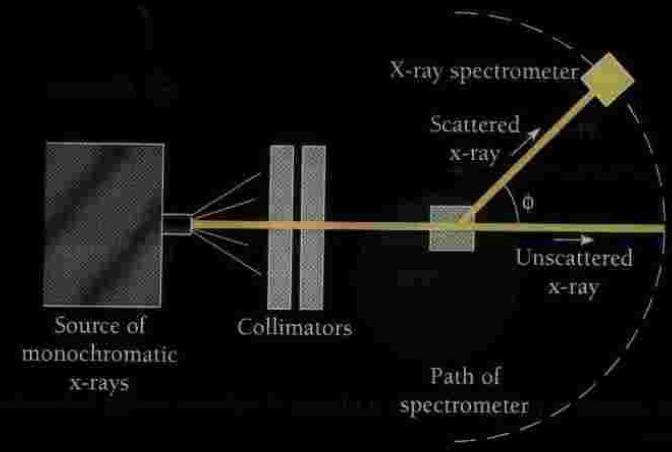
Dispositivo experimental para dispersión Compton (imagen de http://fismoderna.wikispaces.com/Efecto+Compton).
Las figuras siguientes muestran los resultados obtenidos para la correspondiente distribución espectral de intensidad, para algunos ángulos de dispersión:
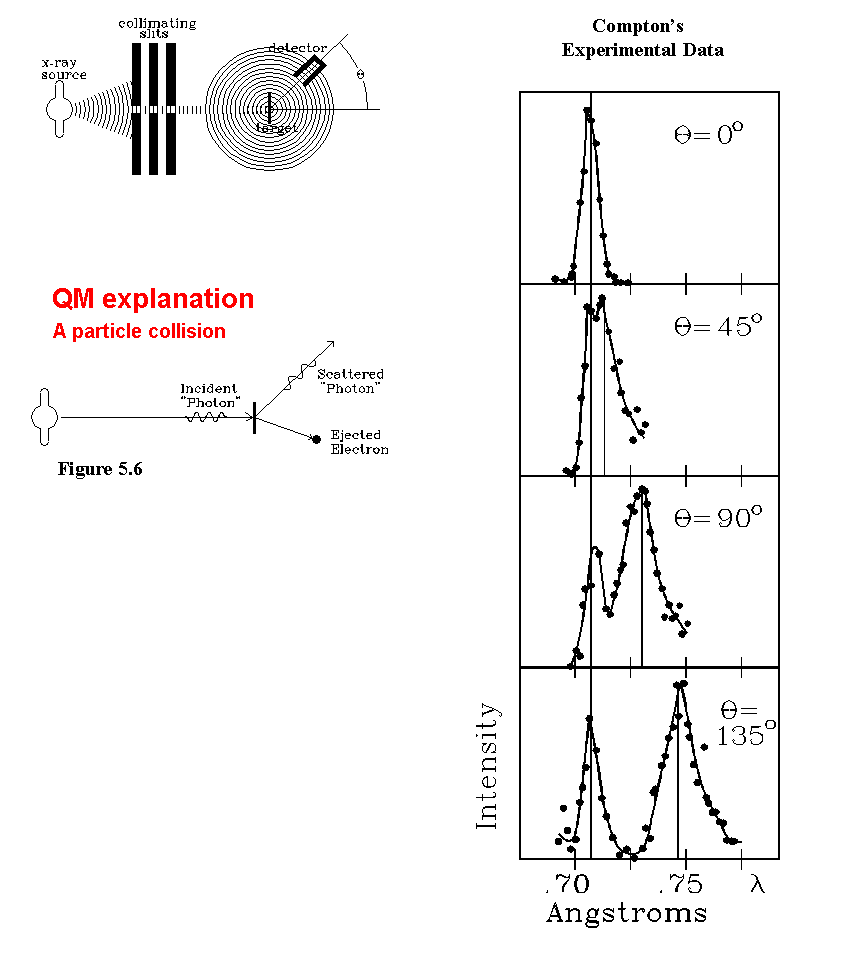
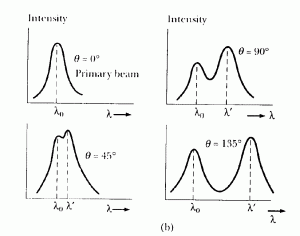
Las características principales de los resultados medidos en diferentes experimentos, involucrando distintos materiales como blanco y variando la energía de los rayos incidentes, son:
1. Para ángulos a partir de cierto valor, se observan dos picos o máximos; uno de ellos corresponde siempre a la longitud de onda incidente, el otro a un valor mayor.
2. La magnitud del desplazamiento entre ellos, denominado corrimiento Compton, $\Delta \lambda =\lambda' - \lambda$ (en la notación de la gráfica anterior, $\lambda' - \lambda_0$ ), depende del ángulo de dispersión $\theta$ , aumentando al hacerlo él; por el contrario, no depende del material utilizado en el blanco, ni de la $\lambda$ incidente.
3. La intensidad asociada al máximo no desplazado (pico Thomson), esto es, la altura del máximo, disminuye al aumentar el ángulo de dispersión $\theta$ ; por el contrario, la intensidad asociada al máximo desplazado (pico Compton) aumenta al hacerlo $\theta$ (¡las gráficas para los distintos ángulos no están todas a la misma escala!).
4. La intensidad asociada al máximo no desplazado (pico Thomson) crece al hacerlo en número atómico $Z$ del material blanco, sucediendo lo opuesto para el pico desplazado o Compton, que disminuye.
Todos estos resultados serían justificados por Compton y Debye, de forma independiente, planteando en primer lugar el problema de una colisión elástica entre un fotón incidente y un electrón ligado atómico:

Justificación teórica del pico Compton

Planteemos el problema del choque elástico entre un un fotón incidente de frecuencia $\nu$ y un electrón ligado atómico, supuesto en las capas más externas y, por ello, tratado aproximadamente como libre (se desprecia la energía de ligadura atómica frente al valor muy superior de energía del fotón incidente; se justificó al observar que, en general, los resultados no dependían del material utilizado como blanco):
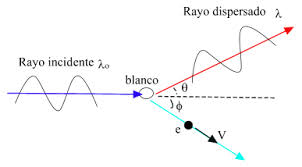
Esquema:
Esquema de un proceso de difusión Compton.

Tabla ecuaciones cinemáticas (relativistas) de la colisión elástica fotón-electrón libre y en reposo:

Antes de la colisión, fotón	Antes de la colisión, electrón	Comentarios
$E_{\gamma 0}=h\nu_0$	$E_{e0}=m_{0}c^2$	-electrón supuesto inicialmente como libre y en reposo.
$\vec{p_{\gamma 0}} \, , \,p_{\gamma 0}=\frac{E_{\gamma 0}}{c}=\frac{h\nu_ 0}{c}=\frac{h}{\lambda_0}$	$p_{e0}=0$
Tras la colisión, fotón (ángulo $\theta$ )	Tras la colisión, electrón (ángulo $\phi$ )
$E_{\gamma 1}=h\nu_1$	$E_{e1}=+\sqrt{m_0^2c^4+p_{e1}^2c^2}=mc^2=K_{e1}+m_0c^2$
$\vec{p_{\gamma 1}} \, , \, p_{\gamma 1}=\frac{E_{\gamma 1}}{c}=\frac{h}{\lambda_1}$	$\vec{p}_{e1}=m\vec{v}=\frac{m_0\vec{v}}{\sqrt{1-\frac{v^2}{c^2}}} \ne 0$
ECUACIONES:
Conservación de la energía:	Conservación del momento:
$h\nu_0 + m_{0}c^2=h\nu_1 + \sqrt{m_0^2c^4+p_{e1}^2c^2}$ $E_{e1}=h(\nu_0 - \nu_1) + m_{0}c^2$	$\vec{p}_{\gamma 0}=\vec{p}_{\gamma 1}+\vec{p}_{e1}$ $\vspace{0,30cm}$ -Eje $OX$ : $\frac{h\nu_0}{c}=\frac{h\nu_1}{c}cos \theta + p_{e1}cos \phi$ -Eje $OY$ : $0=\frac{h\nu_1}{c}sen \theta - p_{e1}sen \phi$	-la conservación del momento es una ecuación vectorial.
Desplazamiento Compton:	$\Delta \lambda=\lambda_1 - \lambda_0=\frac{h}{m_0c}(1-cos \theta)$
Longitud de onda Compton del electrón:	$\lambda_C=\frac{h}{m_0c}=0,02426\,\AA$	$m_0c^2=511\,keV$
Desplazamiento Compton:	$\Delta \lambda=\lambda_1 - \lambda_0=\lambda_C (1-cos \theta)=2\lambda_C sen^2 \frac{\theta}{2}$
Energía cinética del electrón tras la colisión:	$K_{e1}=E_{e1}-m_0c^2=h(\nu_0 - \nu_1)=c(\|\vec{p}_{\gamma 0}\|-\|\vec{p}_{\gamma 1}\|)$
Relación entre ángulos:	$cotan\phi = (1+ \frac{\lambda_C \nu_0}{c})\, tan \frac{\theta}{2}$

La expresión para el corrimiento Compton $\Delta \lambda$ proporciona un ajuste excelente para la longitud de onda desplazada, mayor que la incidente, medida experimentalmente.
Obsérvese que el desplazamiento Compton aumenta con el ángulo $\theta$ , alcanzando su valor máximo para el caso de colisión frontal, esto es, $\theta=\pi$ , en cuyo caso el fotón regresa por la misma dirección de incidencia, teniéndose $\Delta \lambda(\theta=\pi)=2\lambda_C$ .
Además, el corrimiento Compton $\Delta \lambda$ resulta ser independiente de la longitud de onda $\lambda_0$ incidente, por lo que se va haciendo relativamente más pequeño al crecer la $\lambda$ incidente, esto es, conforme la radiación incidente es más blanda. De esta forma, para una radiación en la zona del espectro de los rayos $X$ , por ejemplo, $\lambda \approx 0,5\,\AA$ , el desplazamiento es del $10$ %, por completo apreciable. Más ejemplos: para $\theta =\pi$ se observa radiación difundida de $200\, KeV$ para incidencia de $1\,MeV$ , una reducción en energía del $80$ %, mientras que para incidencia de $1000\,eV$ se difunden fotones de $996\,eV$ , una reducción energética sólo del $0,4$ % (en ambos casos, el desplazamiento Compton es de unos $0,050\,\AA$ ).
En la deducción de la fórmula del corrimiento Compton $\Delta \lambda$ se ha supuesto que la energía de ligadura del electrón atómico es despreciable frente a la energía del fotón incidente, pero si se considera un electrón fuertemente ligado (energía de ligadura del orden del $keV$ ) , de los más internos en el átomo, entonces en el choque habría de considerarse la masa de todo el átomo, de forma que en la conservación del momento sería el átomo completo el que intervendría. Dada su gran masa, la transferencia de energía al átomo es despreciable y el fotón apenas modifica su frecuencia (energía): el corrimiento Compton producido será despreciable, indetectable experimentalmente. Ésta es la situación correspondiente al pico Thomson, que refleja la radiación dispersada sin cambio en la $\lambda$ , y que se explica entonces como una colisión elástica fotón-átomo en bloque.
Análogamente, no se observa pico Compton cuando la radiación incidente tiene una longitud de onda larga, como es el caso del visible, ya que en este caso la hipótesis de energía de ligadura atómica despreciable frente a energía fotón incidente tampoco se cumple, ni siquiera para los electrones menos ligados.
En resumen: a) los fotones que son dispersados por electrones fuertemente ligados, que permanecen tras la colisión ligados, no experimentan cambio apreciable en su $\lambda$ , y se recogen en el pico Thomson (dispersión clásica o Rayleigh); b) los electrones que son expulsados del átomo por la colisión con el fotón incidente, se convierten en electrones libres o de retroceso, y se liberan simultáneamente a la radiación difundida con cambio apreciable en su $\lambda$ , que se recoge en el pico Compton, con un cambio en la longitud de onda dado por el desplazamiento Compton.
Respecto a la dependencia con el material usado de la intensidad de las radiaciones dispersadas, o altura de los picos, para materiales pesados (altos $Z$ ) habrá muchos electrones fuertemente ligados y pocos, sólo los más externos, débilmente. En consecuencia, en idénticas condiciones de observación, será más probable que se produzca dispersión Thomson, siendo la altura del pico no desplazado mayor que para un material de bajo $Z$ , en el cual serán más probables los sucesos de colisión Compton.
La observación de los electrones de retroceso que intervienen en la explicación teórica del efecto Compton tuvo lugar por primera vez en 1923, por W. Bothe y C.T.R. Wilson; en 1925 Bothe y H. Geiger demostraron que el electrón de retroceso y el fotón dispersado aparecen simultáneamente. Finalmente, en 1927, A.A. Bless logró medir la energía del electrón de retroceso, resultando un valor también de acuerdo con los cálculos anteriores del efecto Compton (cf. [BRA-00], p. 19).

Nota 1: repárese que en el límite clásico, $h \rightarrow 0$ , la longitud de onda Compton $\lambda_C$ se anula, de forma que no hay corrimiento Compton y sólo tiene lugar dispersión Rayleigh o clásica. En este sentido, cuando $\nu \rightarrow 0$ , o $\lambda \rightarrow \infty$ , esto es, cuando la radiación incidente se va haciendo blanda, el pico Thomson domina; para radiación cada vez más dura, irá predominando el pico Compton (por ejemplo, para radiación $\gamma$ ).
Nota 2: La radiación Compton difundida a distintas frecuencias es incoherente entre sí.
Nota 3: A muy altas energías, puede ocurrir el denominado Compton inverso, en el que una partícula cargada transfiere parte de su energía a un fotón, de forma que éste disminuye su longitud de onda. En Astrofísica, se relaciona con ciertas observaciones de emisiones de rayos $X$ .