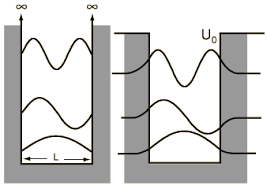
Cuantización de la energía: ejemplos generales
- A continuación, se expondrá una discusión general que ilustrará como, a partir de la resolución de la ecuación de autovalores de la energía, o ecuación de Schrödinger independiente del tiempo, incorporando las adecuadas condiciones de contorno, la cuantización de la energía de algunos sistemas emerge del formalismo.
-Por lo tanto, todo el apartado refiere a sistemas conservativos: el Hamiltoniano no tiene dependencia temporal y representa la energía total del sistema.
Pozo finito continuo unidimensional
-Nota bibliográfica: este punto es en gran parte un resumen hecho sobre el apartado 3.6, pp. 104-115 del libro [BRA-00].
-
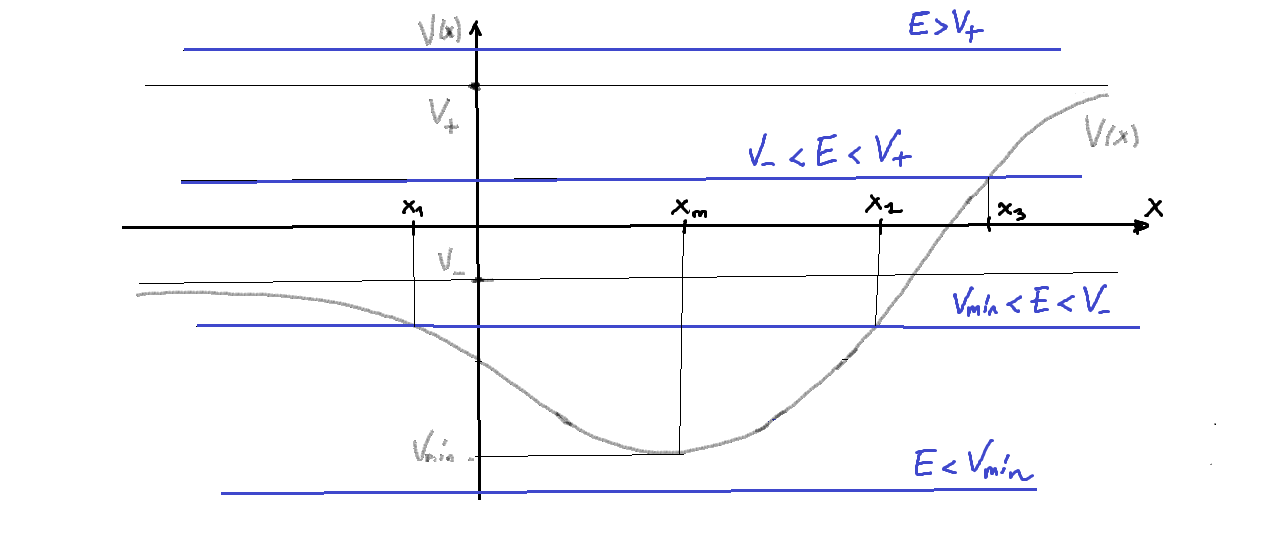
- Sea el siguiente problema de contorno general (pozo finito continuo, caso unidimensional) (véase [BRA-00], pp. 104ss.):
,
equivalente a la resolución de la ecuación diferencial ordinaria (EDO)
,
dondees una función real y continua
, de expresión según la figura:
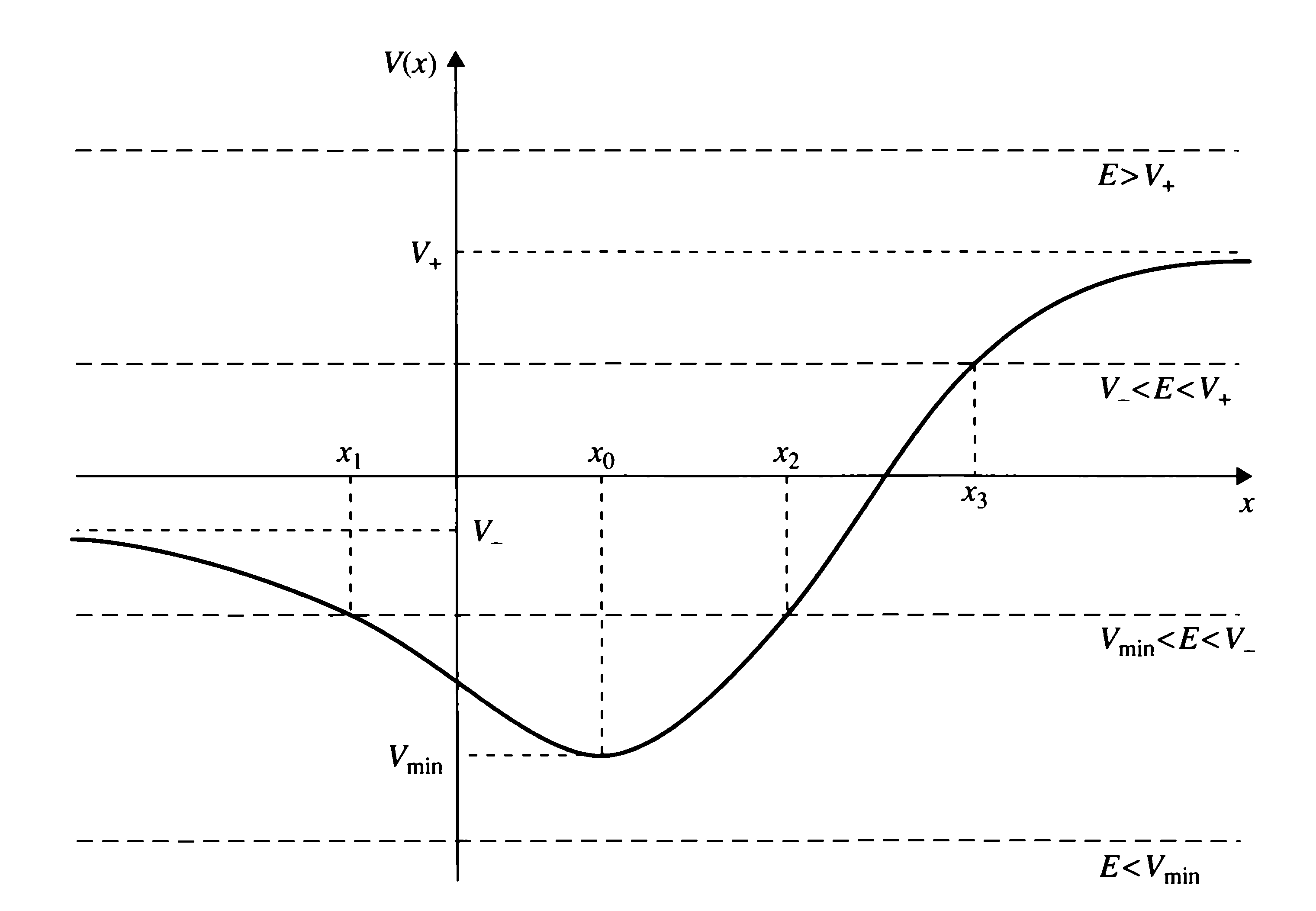
- Se requieren soluciones físicamente aceptables, para lo que deben ser soluciones unívocas y finitas
que cumplan que
y su derivada primera
sean funciones continuas
(lo que no implica que
); además, alternativamente:
- Para obtener funciones
, es decir,
, que representarán estados ligados del sistema, se requerirá
(aunque, en rigor, esta condición de anulación a largas distancias no garantice que las soluciones obtenidas estén en el Sóbolev
, en la práctica suele llevar a ello) .
- Para obtener funciones
, que representarán estados no ligados o de difusión del sistema, se impondrá sólo
,
.
-Nota: pueden existir estados de difusión que cumplan: estados oscilatorios que tienden a cero a largas distancias y que sin embargo no son de cuadrado integrable, pues oscilan demasiado lentamente; un ejemplo de estos estados aparece para el potencial coulombiano).
- Para obtener funciones
- En el límite
, puesto que se tiene
,
la forma asintótica de la EDO (ahora de coeficientes constantes) planteada es:
, de forma que se presentan dos casos:
, donde
,
,
.
-En este caso, la solución general de la EDO es de la forma:
; con
escalares arbitrarios.
, donde
,
,
.
-En este caso la solución general de la EDO tendrá la expresión:
; con
escalares arbitrarios.
- El problema general planteado para cada
es, en concreto, responder a la pregunta fundamental: ¿para qué valores del parámetro real
el problema de contorno
con las condiciones especificadas posee solución (única o no )?
- La respuesta depende del valor de
, del que depende el signo de la función coeficiente
de
en la EDO:
.
- Primer caso:
:
- Clásicamente, la región
, corresponde a la zona en que la energía cinética clásica es negativa,
, de forma que, clásicamente, este tramo de valores de energía está prohibido para la partícula.
- Mecano-cuánticamente:
Luegoy
tienen el mismo signo
.
- Por lo tanto, dado
:
-si: función cóncava hacia arriba en un entorno de
.
-si: función convexa hacia arriba en un entorno de
.
-si: la función posee un punto de inflexión en
(se produce un cambio de signo de la función en el entorno de
).
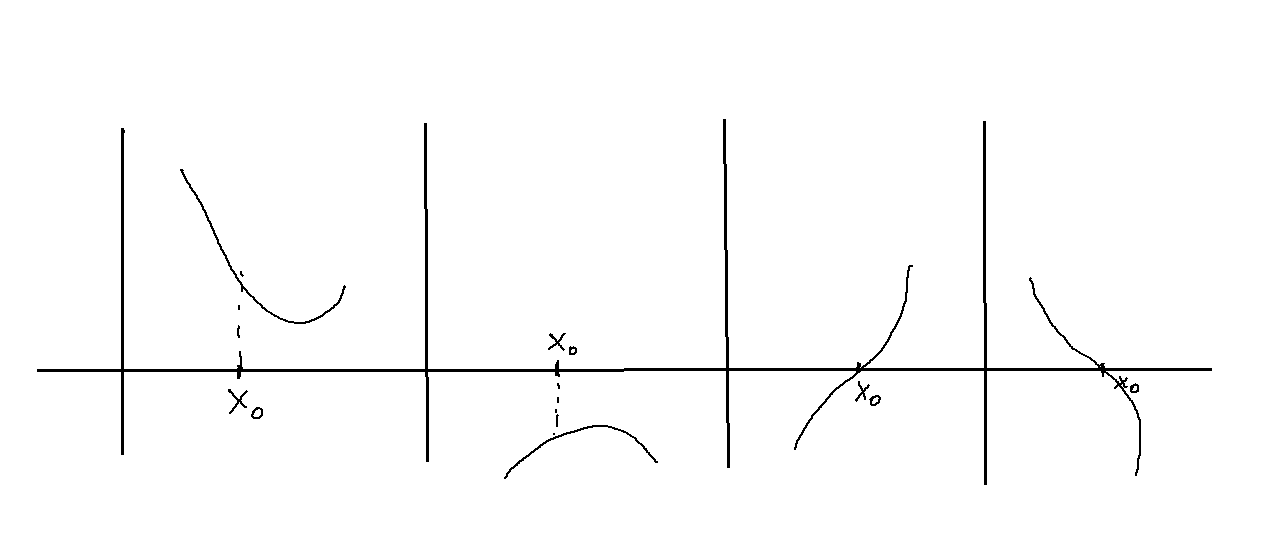 -como se observa en las figuras, es imposible realizar en cada caso el cambio de curvatura necesario para controlar el comportamiento adecuado -no «explosivo»- de la función a largas distancias, puesto que se involucraría un cambio de signo de la derivada segunda
-como se observa en las figuras, es imposible realizar en cada caso el cambio de curvatura necesario para controlar el comportamiento adecuado -no «explosivo»- de la función a largas distancias, puesto que se involucraría un cambio de signo de la derivada segunda que es imposible, debido a que debe conservar el mismo signo que
.
- Puesto que
, toda solución de la EDO en este caso o bien diverge para
, o bien lo hace para
, o para ambos: no hay solución físicamente aceptable.
- Y, en efecto, en el límite
, puesto que se tiene
,
la forma asintótica de la EDO planteada es:
, de forma que la solución general de la EDO es de la forma:
; con
escalares arbitrarios. Como para largas distancias, en cada uno de los dos límites
hay que conservar la función acotada, resulta también evidente que es imposible la conexión analítica requerida:
- Se concluye por tanto que no existen soluciones físicamente aceptables del problema de autovalores de energía (o ecuación de Schrödinger independiente del tiempo) cuando
.
- Clásicamente, la región
- Segundo caso:
:
- Existen dos puntos
y
en los que
, que se corresponden con los dos puntos clásicos de retroceso, ya que en las regiones
y
se tiene
, esto es, la energía cinética se hace negativa. Son por tanto regiones del espacio (recta real) inaccesibles a la partícula clásica con estos valores de energía; en esos puntos se anula su energía cinética y se invierte el sentido de su movimiento, confinado por tanto a la región
.
- Estos dos puntos
y
marcan las regiones en que se dividirá el estudio mecánico-cuántico del problema:
- Región interna II:
: en esta región
, luego
, de manera que
y
tienen signo opuesto
:
- Por lo tanto, dado
:
-si: función convexa hacia arriba en un entorno de
.
-si: función cóncava hacia arriba en un entorno de
.
-si: la función posee un punto de inflexión en
.
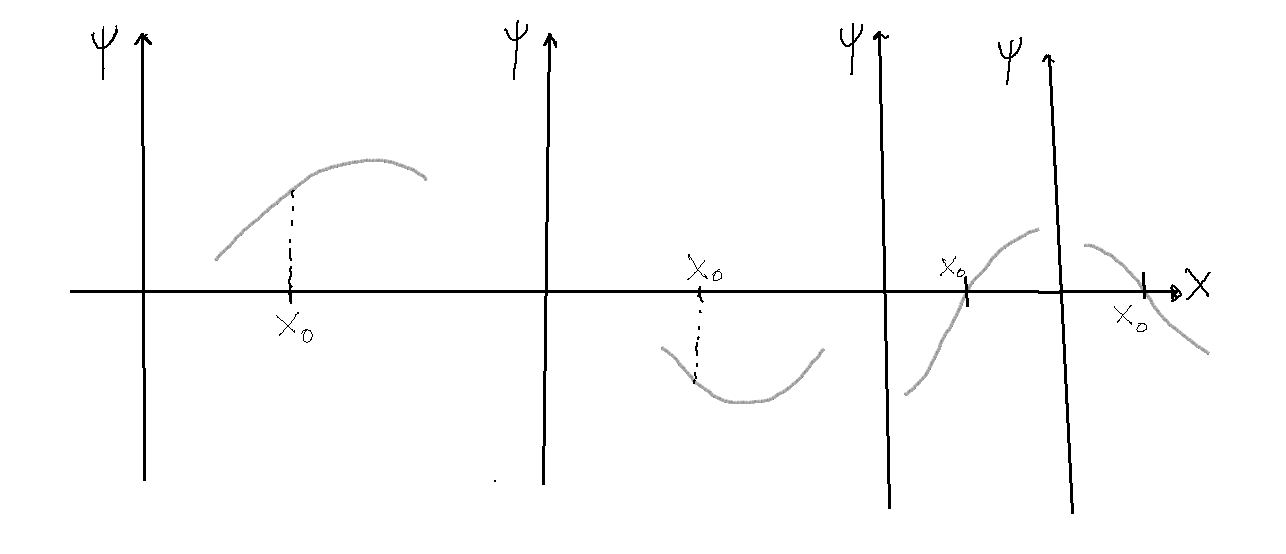
- En esta región cada solución presenta en general un carácter oscilatorio, como por ejemplo el mostrado en la siguiente figura:
 Aunque habrá también una solución del tipo
Aunque habrá también una solución del tipo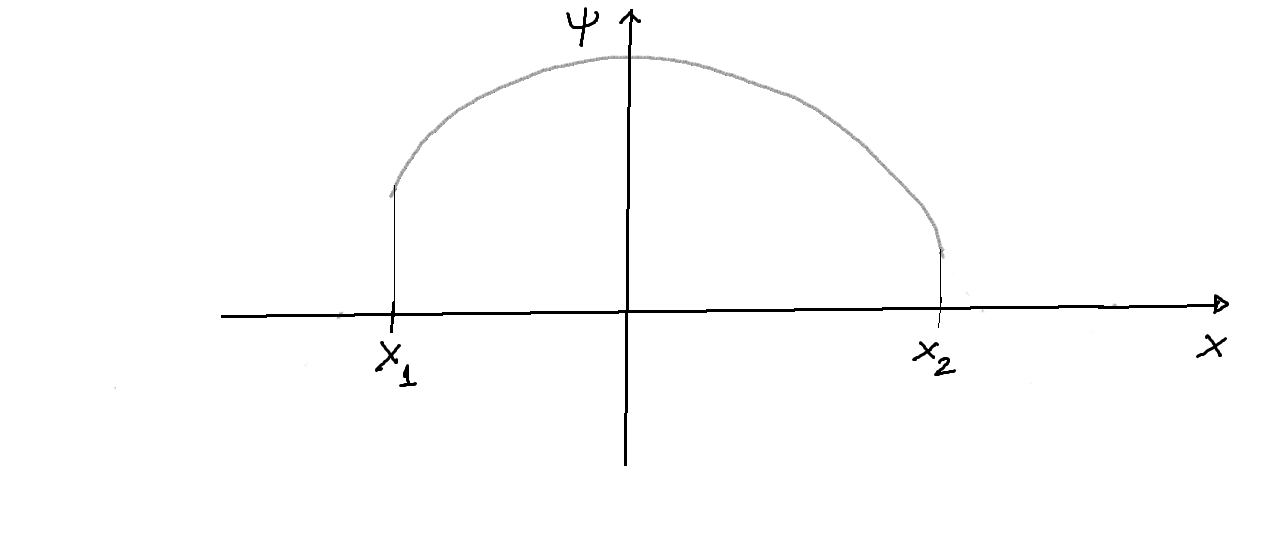 que no posee ningún nodo entre
que no posee ningún nodo entre y
.
- Por lo tanto, dado
- Región I:
: en esta región
, luego
, por lo que
y
tienen igual signo
:
- Dado
:
-si: función cóncava hacia arriba en un entorno de
.
-si: función convexa hacia arriba en un entorno de
.
- Sea ahora en particular
, de forma que la EDO toma la expresión
, donde
,
,
,
cuya solución general es de la forma:
; con
escalares arbitrarios.
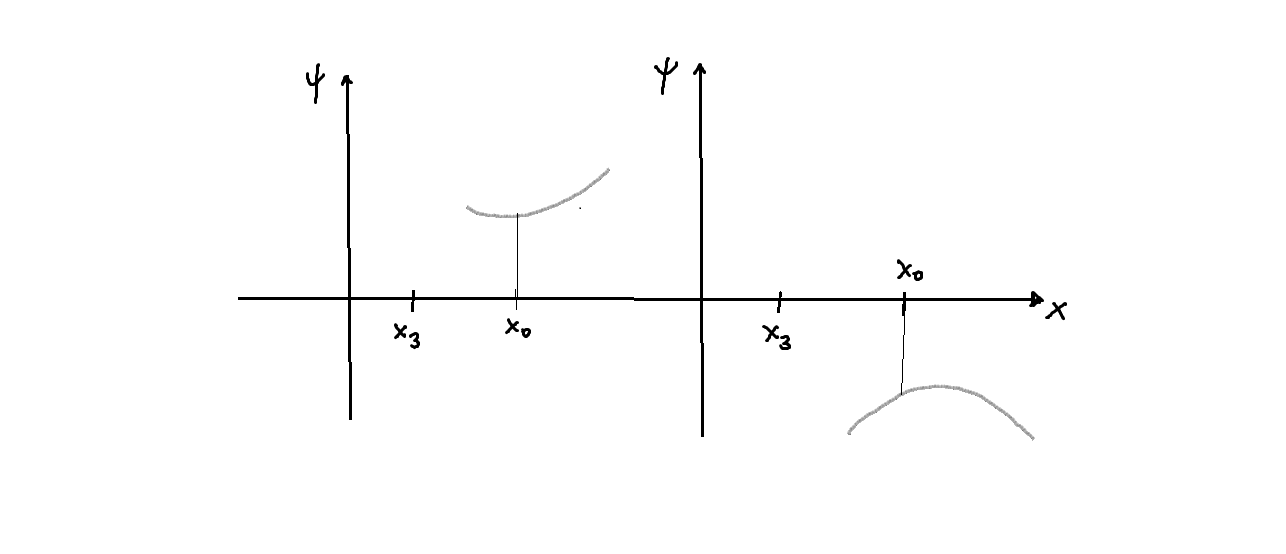
- Hay por lo tanto dos tipos de soluciones particulares:
-las, que divergen para
y tienden a cero para
.
-las, que divergen para
y tienden a cero para
.
- Es evidente pues que la única solución físicamente aceptable en esta región como función de onda es la
.
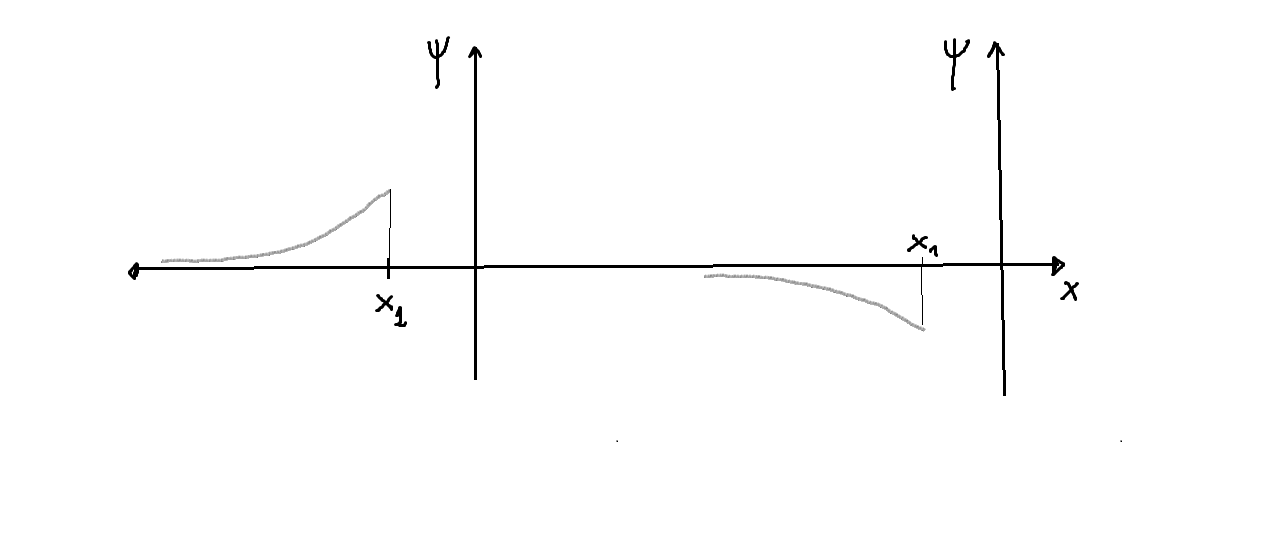
- Y esta solución es única, aparte de una constante multiplicativa global, puesto que el problema de contorno planteado, integrado por la EDO más condiciones de contorno sobre
(por ejemplo,
) , es un problema de Cauchy para el que el correspondiente teorema garantiza la existencia y unicidad de la solución.
- La solución en la zona
muestra el comportamiento asintótico de las soluciones en la región
.
- Dado
- Región III:
: en esta región
, luego
, por lo que
y
tienen igual signo
:
- Dado
:
-si: función cóncava hacia arriba en un entorno de
.
-si: función convexa hacia arriba en un entorno de
.
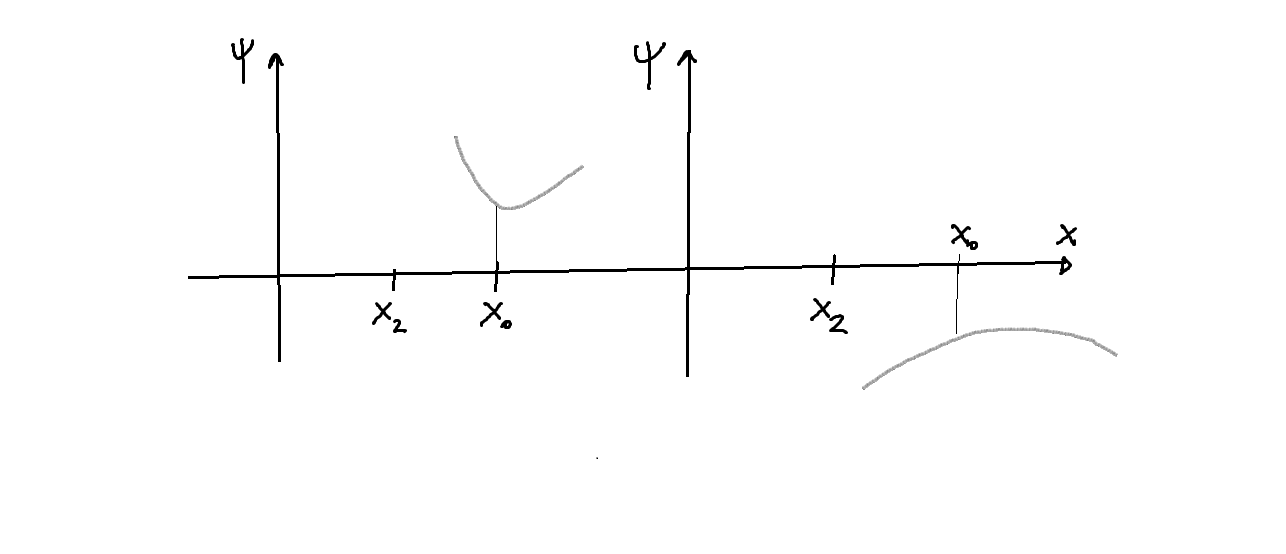
- Sea ahora en particular
, de forma que la EDO toma la expresión
, donde
,
,
,
cuya solución general es de la forma:
; con
escalares arbitrarios.
- Hay por lo tanto dos tipos de soluciones particulares:
-las, que divergen para
y tienden a cero para
.
-las, que divergen para
y tienden a cero para
.
- Es evidente pues que la única solución físicamente aceptable en esta región como función de onda es la
.
- Y esta solución es única, puesto que el problema de contorno planteado, integrado por la EDO más las condiciones de contorno sobre
(por ejemplo,
) , es un problema de Cauchy para el que el correspondiente teorema garantiza la existencia y unicidad de la solución (constante global aparte).
- La solución en la zona
muestra el comportamiento asintótico de las soluciones en la región
.
- Dado
- Conexión entre las regiones:
- Requerimos funciones
continuas, de forma que se han de imponer las condiciones adecuadas de empalme o conexión de las soluciones en cada zona en los puntos divisorios
y
:
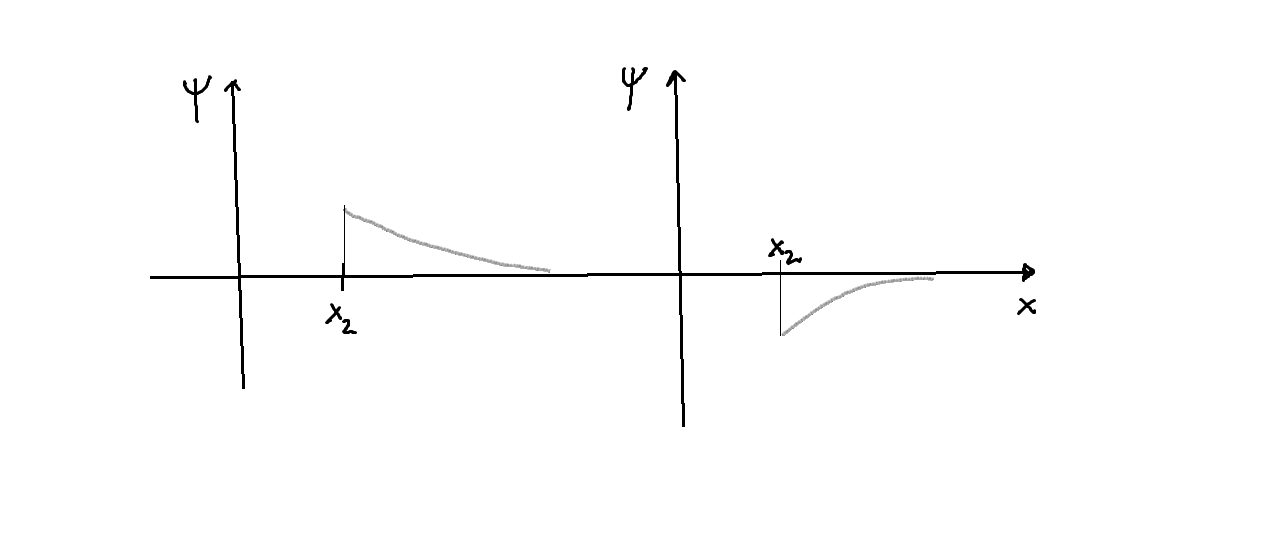
- Estas condiciones servirán para fijar los valores de los parámetros
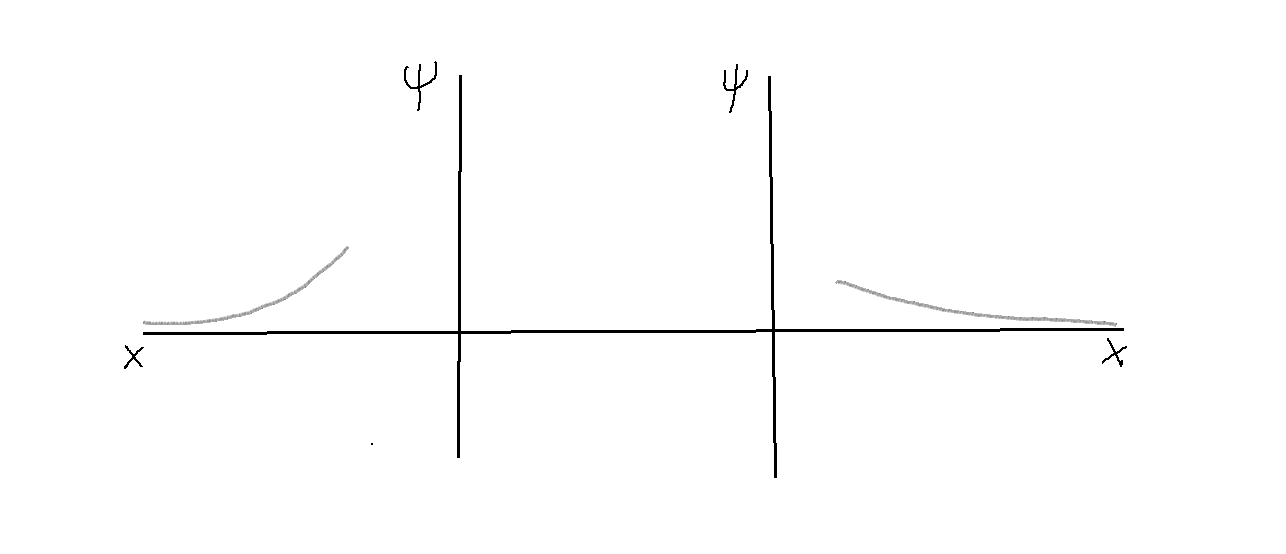
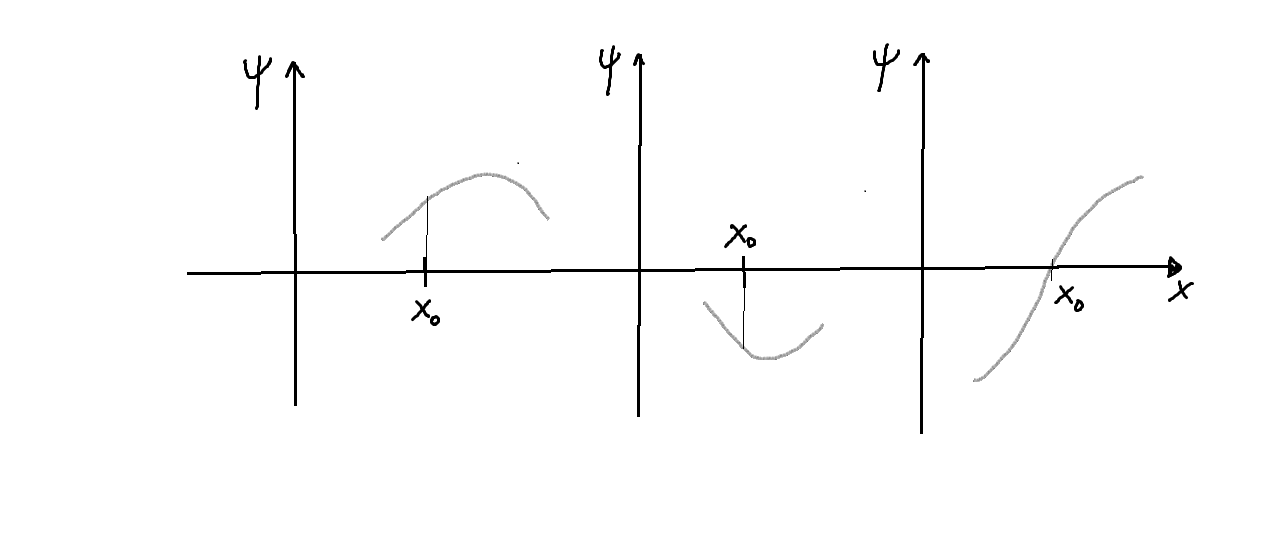
que figuran en las soluciones generales, y extraer así la solución particular de la familia de soluciones que constituye la solución general de la EDO. La cuestión que se plantea muy a menudo, sin embargo, es que el conjunto global de condiciones antes especificadas conduce a una solución nula como la única compatible.
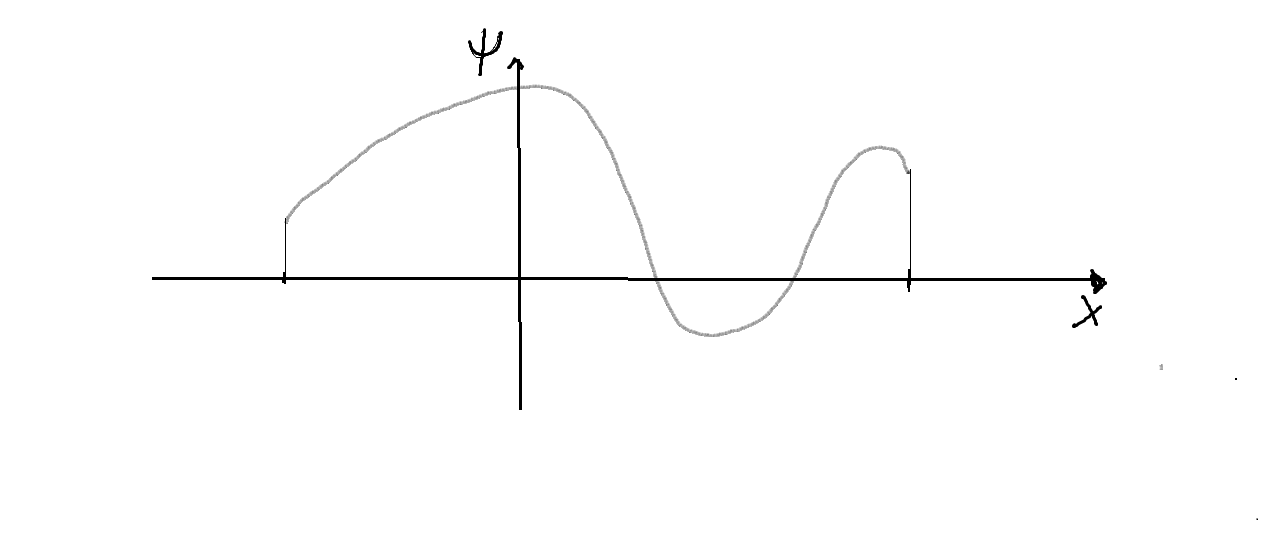
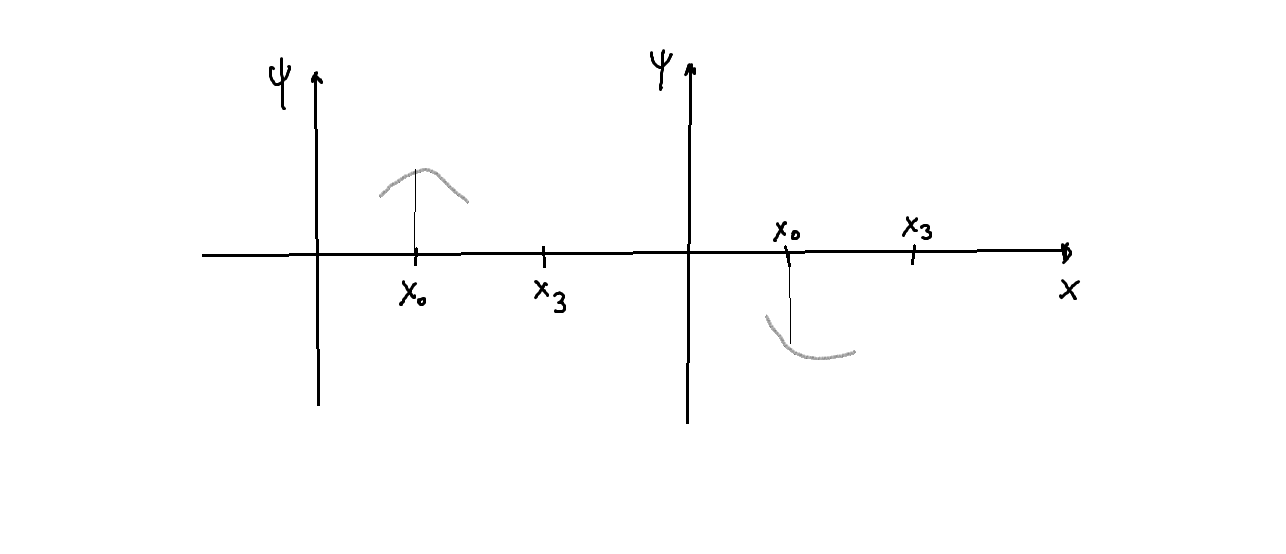
- Es decir, que para ese valor dado
,
, la solución que no diverge para
, sino que cumple
, resulta que contiene en la región
una componente que diverge para
, o sea, es físicamente inadmisible; y lo mismo intercambiando las regiones
y
. Un ejemplo se dibuja en la siguiente figura:
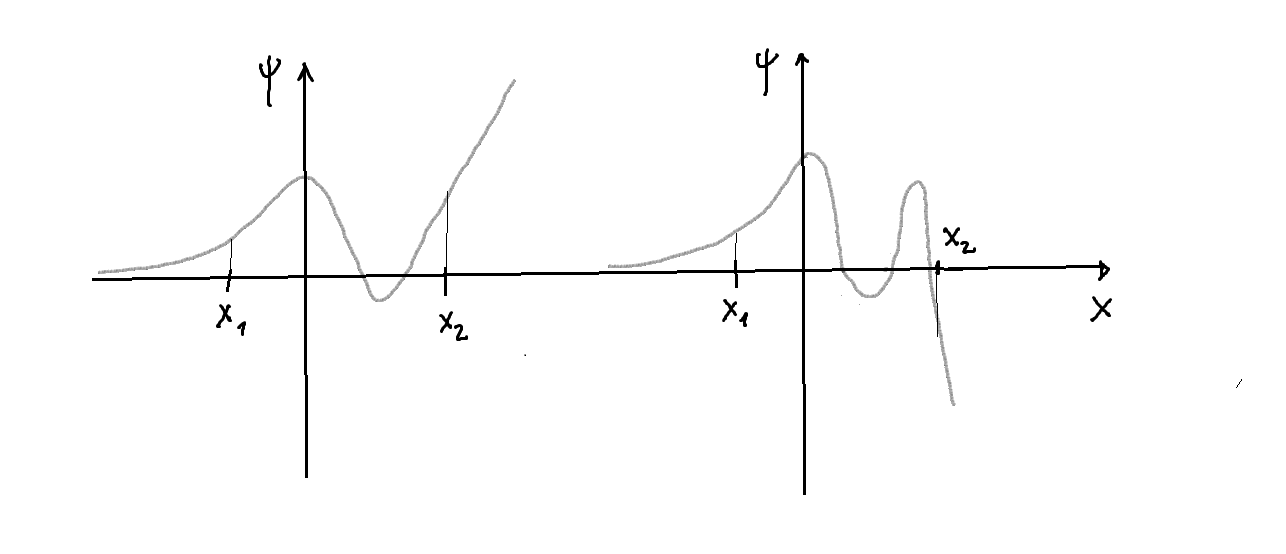
- Sin embargo, existen unos pocos valores específicos del autovalor
para los cuales el problema tiene solución no nula, que es además siempre única, es decir, existe una función
que es físicamente aceptable: puede ser tomada como función de onda (independiente del tiempo) del problema de autovalores planteado, ya que satisface la ecuación
y, además, se tiene
continuas
,
. A estas soluciones se les denomina autofunciones de energía, para el autovalor
,y la siguiente figura ilustra este comportamiento:
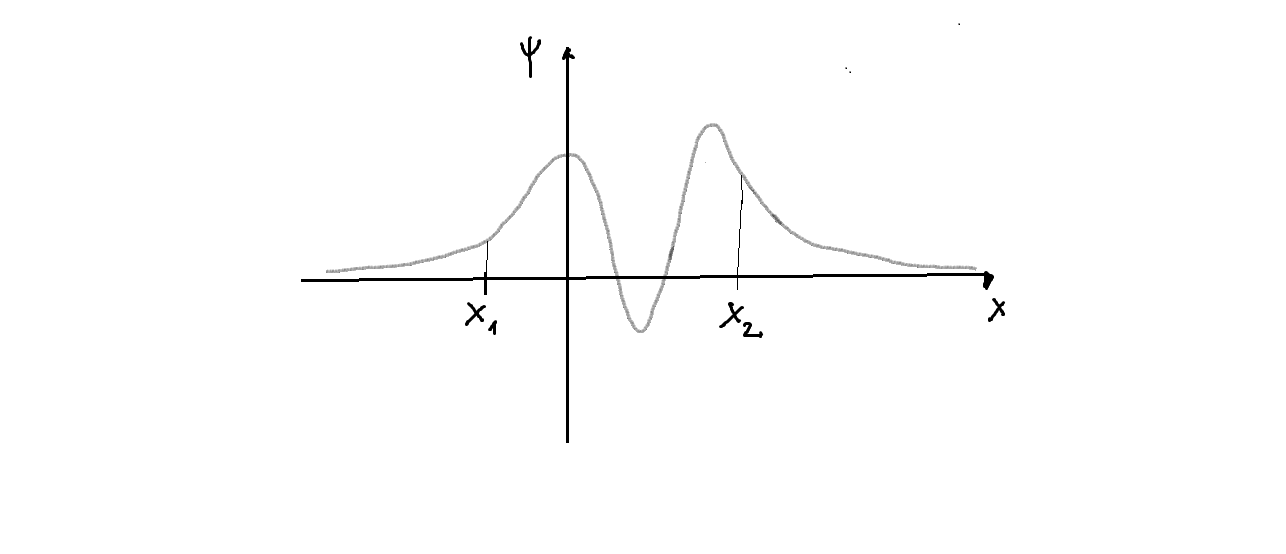
- Requerimos funciones
- Las autofunciones de energía se dice que representan estados ligados (bound-states), y a los valores discretos de
para los que existen esas soluciones se les denomina energías de estados ligados.
- Los estados ligados de un potencial
continuo o continuo a trozos (y, por lo tanto, finito)
:
- Son autofunciones del Hamiltoniano correspondientes a puntos espectrales pertenecientes a la parte puntual del espectro:
, donde
es autovalor en sentido estricto (es decir, no sólo en sentido generalizado).
- Ambas
son continuas
.
.
- Son de cuadrado integrable Lebesgue, es decir,
, y lo mismo para su derivada primera
. Por lo tanto, están en el Sóbolev
.
.
- Son autofunciones del Hamiltoniano correspondientes a puntos espectrales pertenecientes a la parte puntual del espectro:
- Se ha obtenido pues un resultado fundamental: Los valores de energía están cuantizados: sólo son posibles determinados valores. Su número depende del potencial concreto
, pudiendo ser finito o no.
- Obsérvese que, en contraste con los resultados clásicos, que establecen en el caso
el confinamiento del movimiento de la partícula en la región
, la función de onda de cada estado ligado se extiende fuera de los puntos de retroceso clásicos, anulándose estrictamente sólo en los límites
: existe una probabilidad no nula de encontrar a la partícula fuera de la zona
(más pequeña cuanto más lejos).
- La unicidad de las autofunciones de energía de los estados ligados es fácil de comprobar: dados dos autoestados ligados
y
, correspondientes al mismo autovalor
, que se suponen linealmente independientes, se satisfará
,
integrando se obtiene la expresión del wronskiano,
,
y aplicando las condicionesse implica que la constante que aparece es nula,
, es decir,
,
en contra de su inicialmente supuesta independencia lineal. Por tanto: los autovalores de energía correspondientes a los estados ligados no presentan degeneración.
-Nota: este resultado ya no será cierto en tres dimensiones.
- Región interna II:
- Existen dos puntos
- Tercer caso:
:
- En este caso la partícula no está ligada, pues puede moverse en la región de infinita extensión
. En
hay un punto de retroceso clásico, en el que
, y que establece dos regiones:
- Región
:
, correspondiente a la zona clásicamente permitida;
y
tienen signo opuesto
, de forma que, dado
:
-si: función convexa hacia arriba en un entorno de
.
-si: función cóncava hacia arriba en un entorno de
.
 La solución en esta zona tiene pues un carácter oscilatorio:
La solución en esta zona tiene pues un carácter oscilatorio: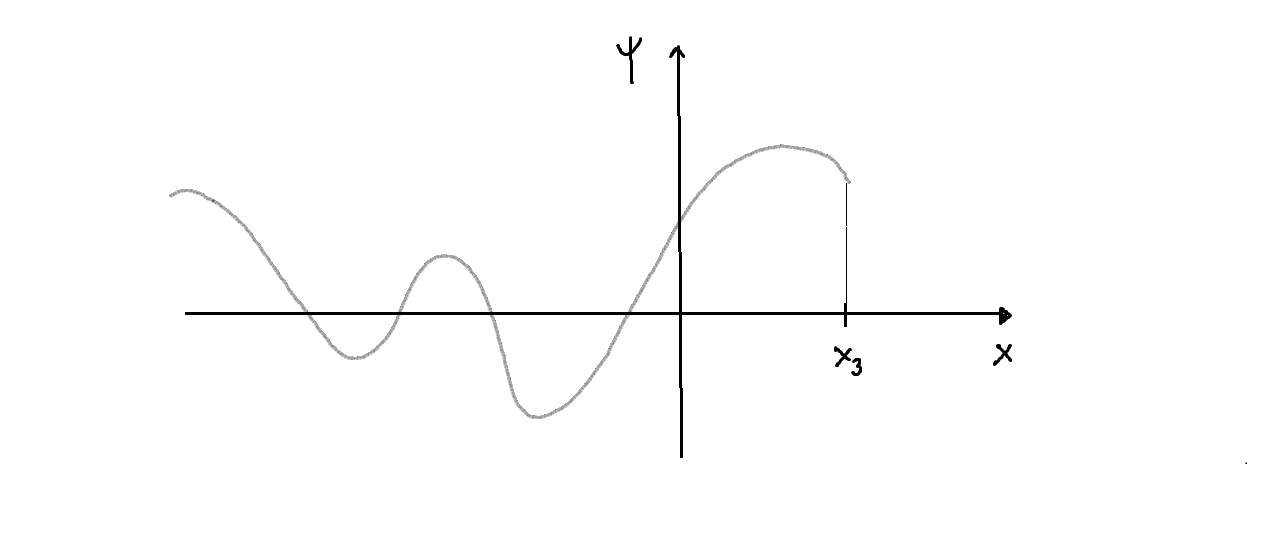 -En el límite
-En el límite , la EDO es
, donde
,
,
.
-En este caso límite, la solución general de la EDO tiene la expresión:
; con
escalares arbitrarios.
-Ninguna de las soluciones particulares se anula a larga distancia,: se trata de funciones no normalizables de forma estándar,
.
- Región
:
, correspondiente a la zona clásicamente prohibida;
y
tienen igual signo
, de forma que, dado
:
-si: función cóncava hacia arriba en un entorno de
.
-si: función convexa hacia arriba en un entorno de
.
 La solución general en esta zona es la combinación de dos soluciones particulares, una de las cuales diverge en el límite
La solución general en esta zona es la combinación de dos soluciones particulares, una de las cuales diverge en el límite , mientras que la otra converge, anulándose.
-En el límite, la EDO es
, donde
,
,
.
-En este caso límite, la solución general de la EDO es de la forma:
; con
escalares arbitrarios.
-la solución físicamente aceptable es la que cumple, solución que es única (factor fase global aparte, una vez normalizada la función).
- Región
- Conexión entre las dos regiones
y
: Por continuidad:
Estas ecuaciones determinan la única solución físicamente aceptable para el problema de valores propios planteado. - La figura siguiente presenta el aspecto de este tipo de solución:
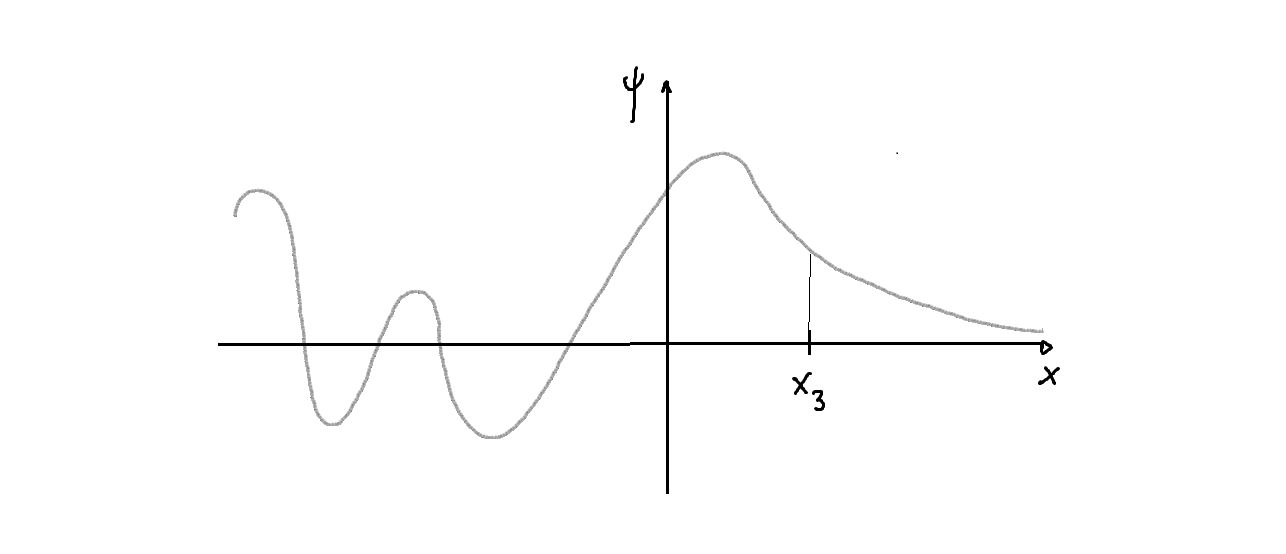
- La solución única anterior aparece para cada autovalor
en el intervalo
, de forma que, en este intervalo de la recta real, las energías permitidas forman un continuo; además, estos autovalores, puesto que se corresponden con una única autofunción, ya que la solución es única, son no degenerados.
- Las soluciones de este tipo, que surgen asociadas a autovalores de energía (en sentido generalizado) en la parte continua del espectro del operador,
, cumplen las condiciones de contorno:
,
,
de forma que son funciones acotadas pero no son funciones de cuadrado integrable Lebesgue,. Representan estados no ligados o de difusión del sistema; en este caso, la partícula sólo puede acercarse a la zona del potencial, «incidir», desde la izquierda.
-Nota 1: pueden existir estados de difusión que cumplan: estados oscilatorios que tienden a cero a largas distancias y que sin embargo no son de cuadrado integrable, pues oscilan demasiado lentamente; un ejemplo de estos estados aparece para el potencial coulombiano.
-Nota 2: recuérdese que el espectro de un operador autoadjunto consta sólo de dos partes, la puntual y la continua. Los autovalores pertenecen a la puntual, mientras que los autovalores generalizados se sitúan en la parte continua. - De nuevo en contraste con los resultados clásicos, la función de onda de cada estado de difusión se extiende fuera del punto de retroceso clásico, anulándose estrictamente sólo en el límite
: existe una probabilidad no nula de encontrar a la partícula fuera de la zona
(más pequeña cuanto más lejos).
- En este caso la partícula no está ligada, pues puede moverse en la región de infinita extensión
- Cuarto caso:
:
- En este caso clásicamente la partícula no está ligada, pues su energía cinética es siempre positiva, y puede moverse a lo largo de toda la recta real
, existiendo dos sentidos posibles de acercamiento a la zona del potencial o de incidencia: desde la derecha y desde la izquierda.
- Mecano-cuánticamente, ahora
, luego
y
tienen signo opuesto
, de forma que, dado
:
-si: función convexa hacia arriba en un entorno de
.
-si: función cóncava hacia arriba en un entorno de
.
-si: la función posee un punto de inflexión en
.
La solución general en esta zona combina soluciones particulares linealmente independientes, ambas con carácter oscilatorio y por tanto físicamente aceptables, y ello para cualquier valor deen el intervalo
.
- En el límite
, la EDO es
, donde
,
,
, cuya solución general tiene la expresión:
; con
escalares arbitrarios.
- Las soluciones en este caso son pues finitas pero no nulas a largas distancias:
,
,
de forma que no son funciones de cuadrado integrable Lebesgue,. Representan estados no ligados o de difusión del sistema, de aspecto:
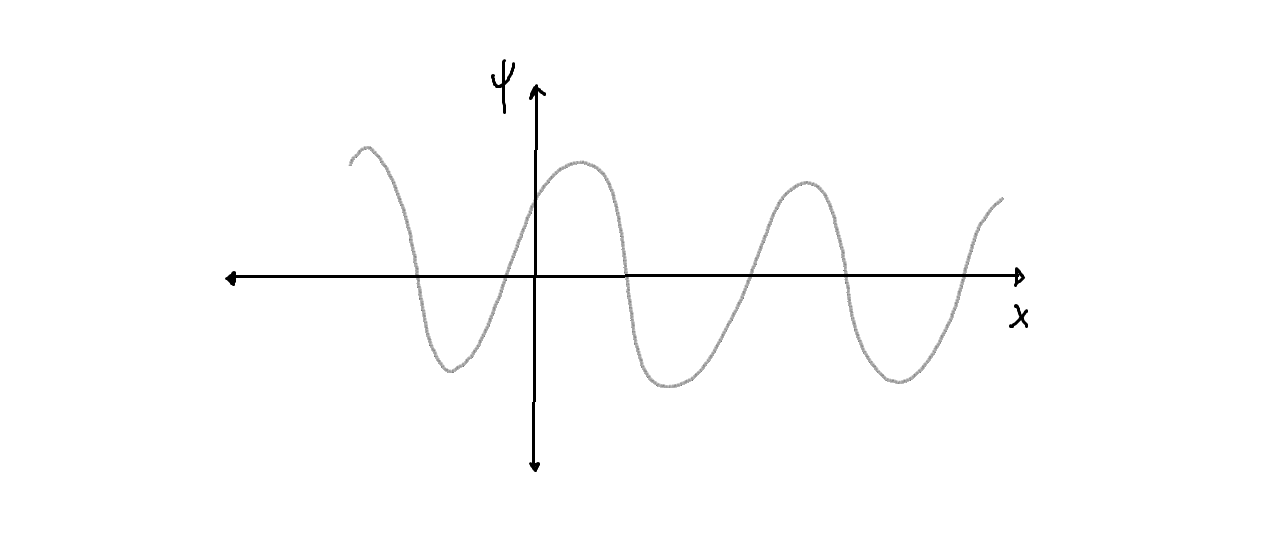
- Aparecen dos soluciones linealmente independientes para cada autovalor generalizado
en esta parte continua del espectro del operador,
, correspondiente a un valor
. De esta forma, en este intervalo de valores, las energías permitidas forman un continuo de autovalores (generalizados) doblemente degenerados.
- En este caso clásicamente la partícula no está ligada, pues su energía cinética es siempre positiva, y puede moverse a lo largo de toda la recta real
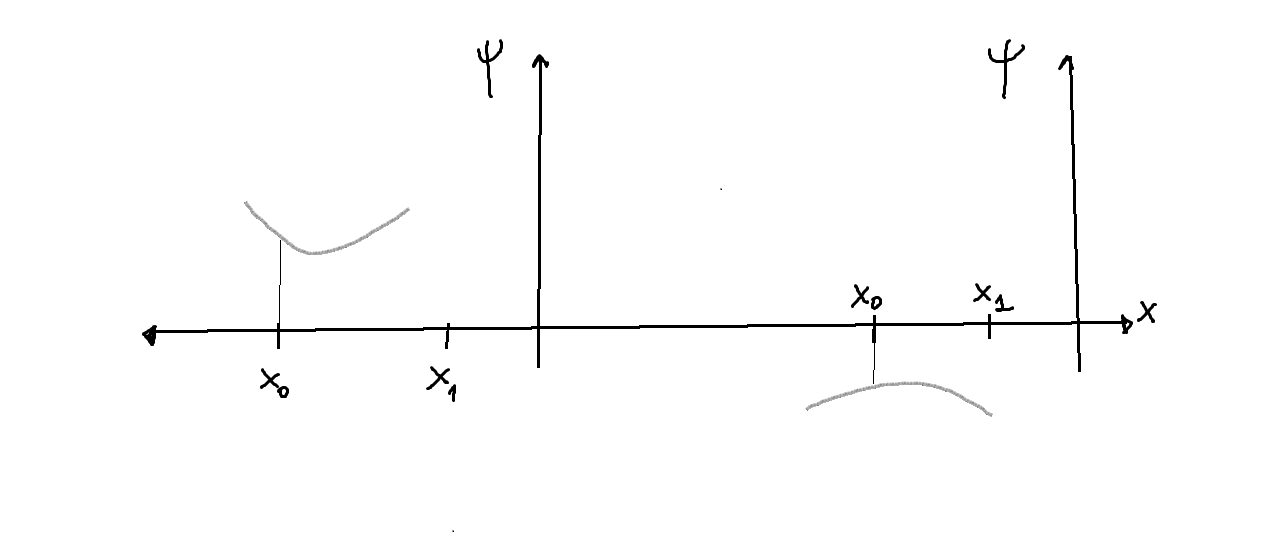
- La siguiente figura ilustra las posibilidades analizadas:
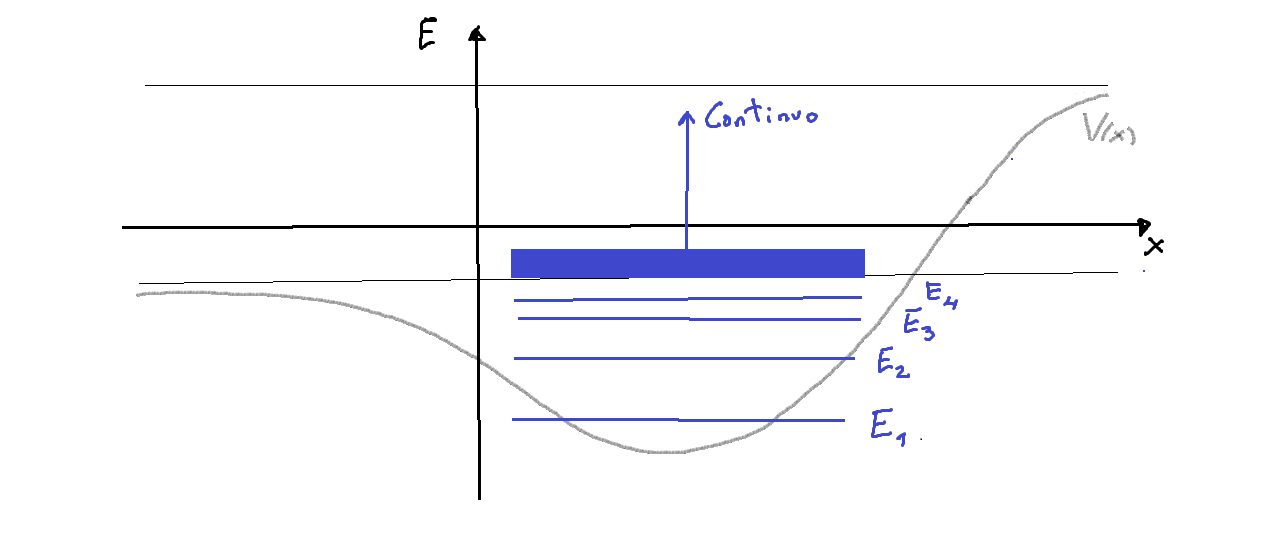
- En resumen:
- Solamente para algunos valores del autovalor
se obtienen autofunciones de energía físicamente aceptables del correspondiente problema de autovalores o ecuación de Schrödinger independiente del tiempo
.
De esos valores se dice que constituyen el espectro energético asociado al potencial:
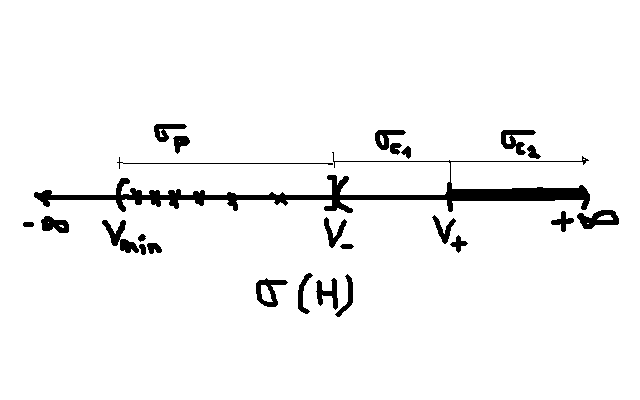
- Las soluciones del problema de autovalores de energía pueden:
-representar los denominados estados ligados de energía (bound-states), que son funciones de onda tales que ella y su primera derivada son de cuadrado integrable,, normalizables por tanto de forma estándar y que se anulan a largas distancias,
. Los valores de
a que se asocian estas autofunciones constituyen la parte discreta del espectro de energías del correspondiente potencial
. Mientras que en Física Clásica todos los valores de energía están permitidos, en un continuo, en Física Cuántica sólo algunos valores discretos son posibles, un fenómeno denominado como cuantización de la energía. Al estado más bajo en energía del espectro discreto de estados ligados se le denomina estado fundamental (ground state); a los restantes estados ligados se les denomina como estados excitados.
-alternativamente, representar los estados de difusión o scattering, funciones que no son de cuadrado integrable,, que no son normalizables de forma estándar y que no se anulan bien en uno de los dos límites
, bien en los dos. Los valores de
a que se asocian estas autofunciones generalizadas constituyen la parte continua del espectro de energías del correspondiente potencial
, que se extiende hasta el infinito.
- Respecto a los estados ligados:
-los estados ligados de un potencial monodimensional no son degenerados y, cuando el potencial es simétrico respecto al origen,, presentan paridad definida.
-si, entonces el espectro del correspondiente Hamiltoniano,
, es puramente discreto, con un número infinito de estados ligados (cf. [GAL-89], I, p. 175).
-para cualquier potencial monodimensionalque cumpla la condición
,
se tiene, al menos, un estado ligado de energía negativa si y sólo si el potencial encierra un área no positiva, es decir,
(cf. [GAL-89], p. 176).
-el valorno pertenece al espectro puntual del Hamiltoniano,
, para todo potencial unidimensional
de soporte compacto, cumpliéndose:
(puede ser vacío), cf. [GAL-89], I, pp. 174 y 181).
- Por debajo del mínimo absoluto en todas direcciones del potencial
, no se obtienen soluciones físicamente aceptables.
- Solamente para algunos valores del autovalor
- Sea el siguiente problema de contorno general (pozo finito continuo, caso unidimensional) (véase [BRA-00], pp. 104ss.):
- Obsérvese que:
- En todos los casos a considerar, se va a requerir a las funciones
al menos su acotación a largas distancias (en general, en cualquier dirección):
,
constante real, positiva y finita,
.
- Puesto que en la EDO obtenida tanto
como
son reales, para cualquier solución
se cumplirá que su parte real
y su parte imaginaria
son por separado también soluciones de la EDO, y son ambas funciones reales, de forma que podemos reducirnos a considerar sólo soluciones reales del problema de valores propios planteado, sin pérdida de generalidad.
- En todos los casos a considerar, se va a requerir a las funciones
- Si se cambia el potencial
mediante la adición de una constante,
, constante finita real con dimensiones de energía, las autofunciones no se alteran, mientras que los correspondientes autovalores de energía son desplazados (shifted) en un valor igual a esa constante
(es lo que pasaría al sumar la constante
al potencial ejemplo inicial de esta entrada). Es decir, la adición de una constante al potencial carece de efectos físicos, más allá de un corrimiento en el origen (arbitrario) de las energías.
-Una práctica frecuente respecto a la elección de origen de energías es desplazar el potencial de manera que, si existen estados de difusión y estados ligados, los segundos se correspondan con valores negativos de energía, comenzando la parte continua del espectro en el origen de energía: la semirrecta real positiva como parte continua del espectro del correspondiente potencial (convenientemente desplazado para que ello suceda mediante la adición de una constante; en el ejemplo hecho, habría que sumar al potencialuna constante
, con dimensiones de energía).
- En el caso de un potencial tridimensional similar
, finito
, los resultados son análogos: en general, el espectro energético de un potencial finito
contiene siempre un rango de energías continuo, correspondiente a estados de difusión, y puede contener a veces un rango de energía discreto, correspondiente a estados ligados; ninguno de los dos tipos de autovalores puede ser inferiores al mínimo absoluto del potencial.
-Los estados ligados son los análogos de las órbitas cerradas de las Mecánicas Clásica y pre-Cuántica; su número puede ser finito o infinito; podrán también en algunos casos presentar degeneración. Los estados de difusión, por su parte, son los análogos de las órbitas abiertas; sus energías se extienden sobre un continuo hasta el infinito.
Potenciales con discontinuidades de primera y segunda especie
- Sea un potencial
que presenta discontinuidades finitas, por ejemplo la función representada en la siguiente figura:
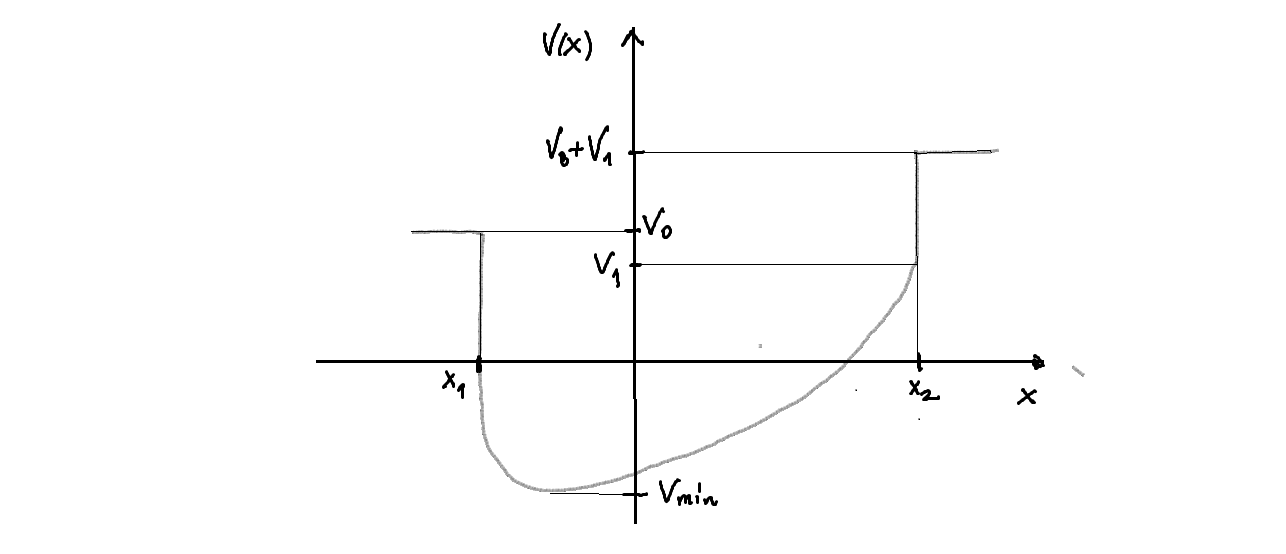
Este potencial presenta discontinuidades de primera especie en los puntosy
, ambas con un salto finito de valor
.
La resolución del problema de autovalores para este tipo general de potenciales (como se comprobará detalladamente más adelante) produce los siguientes resultados:- No existen soluciones físicamente aceptables del problema de autovalores de energía (o ecuación de Schrödinger independiente del tiempo) cuando
, es decir,
.
- Para
aparece un fenómeno de cuantización de la energía, teniéndose soluciones correspondientes a estados ligados (en general: si
estuviese demasiado próximo a
, el potencial podría no ligar).
- Para
aparecen soluciones en la forma de estados de difusión, correspondientes a valores del autovalor
de energía en un continuo.
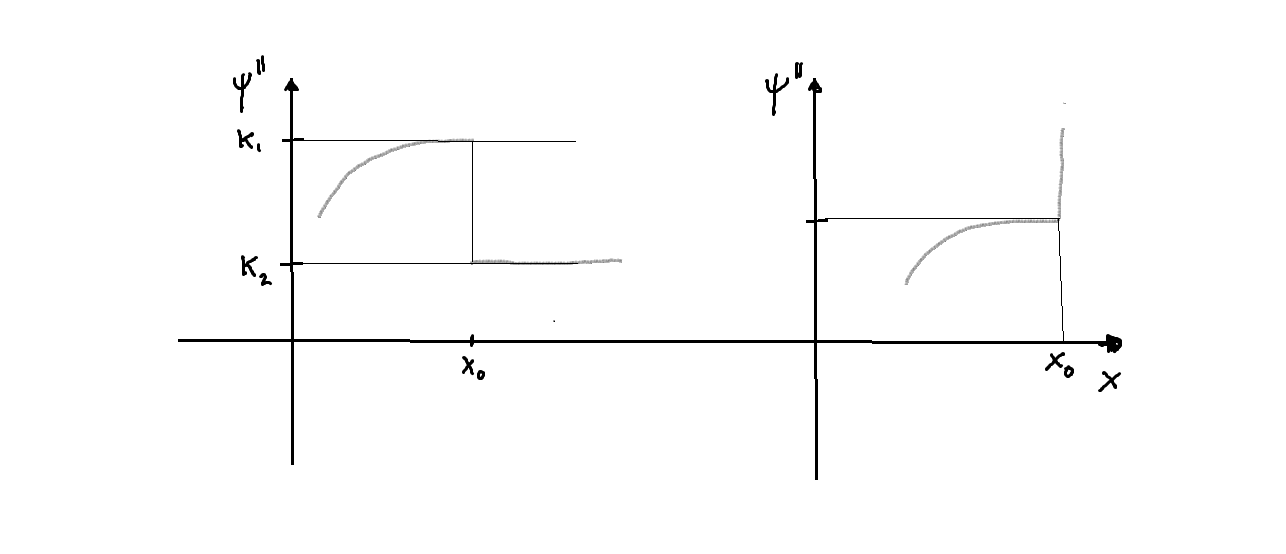
- Es obvio que, puesto que
es una función continua a trozos,
también lo será, presentando discontinuidades de primera especie (saltos finitos) en algunos puntos
, es decir, se satisfará
y
,
dondey
representan constantes reales finitas y distintas,
.
-Repárese en que si la situación fuera la correspondiente a una discontinuidad de segunda especie (como se dará para otro tipo de potenciales, como los que consideraremos a continuación), el salto sería infinito y entoncessería indeterminado, de manera que sería ya ineludible imponer la anulación de la solución el el punto del salto.
- La siguiente figura ilustra los anteriores comentarios:
- No existen soluciones físicamente aceptables del problema de autovalores de energía (o ecuación de Schrödinger independiente del tiempo) cuando
- Sea un potencial
que presenta discontinuidades infinitas, por ejemplo la función representada en la siguiente figura (obsérvese que el potencial en la siguiente figura puede considerarse el límite cuando
del caso anterior):
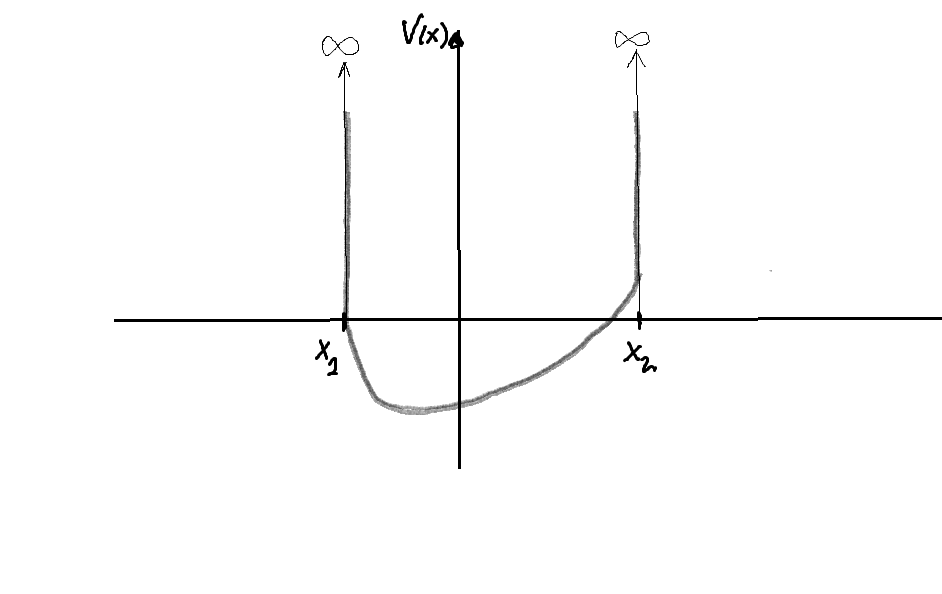 -Este potencial presenta discontinuidades de segunda especie en los puntos
-Este potencial presenta discontinuidades de segunda especie en los puntos y
, con un salto infinito.
-La resolución del problema de autovalores para este tipo general de potenciales (como se comprobará detalladamente también más adelante) produce los siguientes resultados:- El espectro de energías es exclusivamente discreto, con un número infinito de estados ligados: la energía está totalmente cuantizada (la parte continua del espectro del Hamiltoniano es en este caso vacía) .
- Es evidente que en este caso, como el potencial presenta discontinuidades de segunda especie en los puntos
y
, lo mismo ocurrirá para
, de forma que las condiciones de contorno requeridas impondrán la anulación de
en esos puntos: el valor infinito del potencial en ellos actúa como una barrera impenetrable y la función de ondas se anula en ellos.
- La derivada primera de la función de onda,
, presentará una discontinuidad de primera especie en los puntos en que el potencial se hace infinito.
- Considerado este potencial como el caso límite
del anterior (i.e., el que presenta discontinuidades finitas en los puntos
y
) , puede interpretarse el proceso del paso al límite como un proceso en que la parte continua del espectro va disminuyendo hasta desaparecer.
- El resultado es generalizable al caso en tres dimensiones: Un sistema físico encerrado en una caja tridimensional de paredes impenetrables (esto es, sobre la superficie de las paredes de la caja hay un potencial infinito) posee un espectro de energías totalmente cuantizado: compuesto exclusivamente por un número infinito de valores discretos, a los que corresponden estados ligados determinables a partir de la imposición de la condición de contorno que anula la función de onda sobre la superficie de las paredes de la caja.
- Ejemplo prototipo de este tipo de potenciales: el oscilador armónico.
- Para un potencial como el de la figura siguiente,
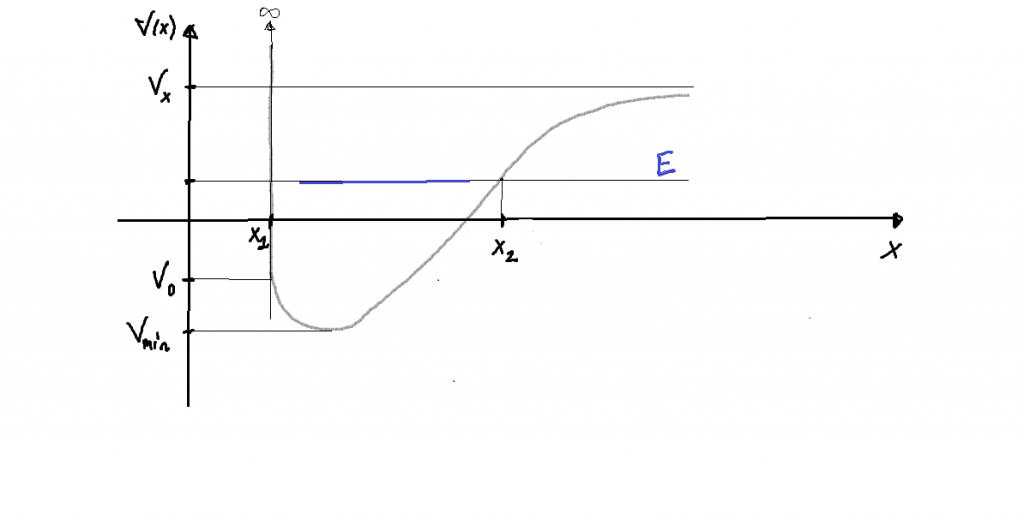 que presenta sólo una pared infinita, el espectro de energías se compone de dos partes:
que presenta sólo una pared infinita, el espectro de energías se compone de dos partes:
- Para
aparece un fenómeno de cuantización de la energía, apareciendo soluciones correspondientes a estados ligados (parte discreta del espectro).
- Para
aparecen soluciones en la forma de estados de difusión, correspondientes a valores del autovalor
de energía en un continuo (parte continua del espectro, sin degeneración).
- Todos los autoestados, ligados y de difusión, cumplen las condiciones de contorno:
;
continua en
;
continuas en
; la derivada primera
presentará una discontinuidad de primera especie en el punto en que el potencial se hace infinito,
.
- Para
Potenciales sin estados ligados
- Finalmente, para un potencial como el de la figura siguiente,
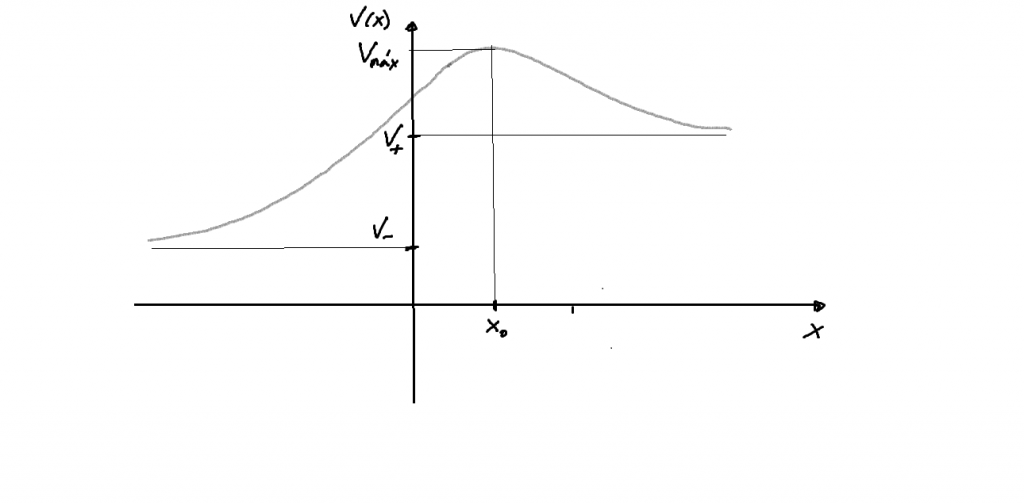
el resultado de la resolución del correspondiente problema de valores propios de energía es que sólo aparecen estados de difusión: sólo hay parte continua en el espectro del operador (no aparecen estados ligados:).
- Nota: para un potencial
tal que
, donde
, el espectro discreto del Hamiltoniano es siempre vacío.
Teorema de oscilación de Sturm para los estados ligados
- Sea una función potencial
, con valor finito
, y tal que
, es decir, existe un conjunto no vacío
de autofunciones de la energía,
. Entonces, si se ordenan los autovalores discretos de energía en orden creciente, esto es,
,
siendo las respectivas autofunciones de energía
,
,
…,
se tiene que:- La autofunción
se anula al menos una vez
.
- Las autofunciones de energía poseen un número creciente de ceros, de manera que la autofunción
ésima
posee
nodos o ceros finitos (los estados ligados se anulan además todos en los límites
).
- Entre cada dos nodos consecutivos de
, la anterior autofunción
posee un nodo.
- La autofunción
- Para potenciales que posean discontinuidades de segunda especie, donde por tanto las autofunciones se deben anular, el anterior teorema de oscilación se satisface de forma que los
ceros de la autofunción
ésima,
se producen adicionalmente a los nodos en los puntos en los que el potencial se hace infinito.
-Por ejemplo: en un caso monodimensional como el del anterior potencial de paredes infinitas o infranqueables
 la autofunción ligada
la autofunción ligada posee un total de
nodos o ceros en el intervalo
.
Nota matemática (repetición)
- Consideremos el espacio de Hilbert
de las funciones complejas de cuadrado Lebesgue-integrable, integrado por funciones que obviamente podrán ser siempre ser normalizadas dividiéndolas por su norma
.
- Dentro de este Hilbert, nos restringiremos en ocasiones a funciones de onda
en el subespacio de Hilbert de Sóbolev,
, integrado por aquellas funciones de
que cumplan que también
y
pertenezcan al Hilbert.
- Puede demostrarse que se satisface el siguiente teorema:
-Teorema 1: Dadacon derivadas primeras y segundas también en
, se implica que
es continua y satisface
.
-Nota: Más generalmente (cf. R.D. Richtmyer; Principles of Advanced Mathematical Physics, Springer-Verlag, 1997, p. 97), se tiene:
Dadacon todas sus derivadas hasta orden
también en
, donde
es el entero menor que satisface
, se implica que
es continua y satisface
.
Referencias
[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.
[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.
[SCH-68] Schiff, L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.
Páginas complementarias
http://la-mecanica-cuantica.blogspot.com.es/2009/08/solucion-matematica-de-la-ecuacion-de.html
APPS
Dejar una contestacion