Potenciales periódicos

Potenciales periódicos

Un potencial $V(x)$ es periódico cuando satisface una condición $V(x+a)=V(x)$ , de forma que repite su forma con período $a$ . Los potenciales periódicos se producen asociados a estructuras reticulares, siendo muy importantes en el estudio del estado sólido.
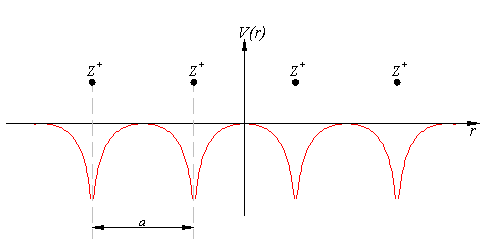
Imagen de la Wikipedia.
A continuación se presenta el estudio de los potenciales periódicos monodimensionales $V(x) \in L^2[(0,a=l)]$ . El rasgo característico de estos potenciales, frente a los expuestos anteriormente (no periódicos), va a ser la presencia de una estructura de bandas en un espectro que además va a carecer de parte discreta, $\sigma_p(H)=\emptyset$ .
-Es decir, los estados del continuo se agrupan en intervalos de energías permitidas, o zonas de estabilidad, separados por zonas de de energías prohibidas, las zonas de inestabilidad. Esta estructura se presenta siempre que el potencial $V(x)$ no sea una constante; frecuentemente, ocurre también que desaparecen muchas de las zonas prohibidas.
-En todo caso, siempre las anchuras de las zonas prohibidas tienden a cero en el límite $E \rightarrow +\infty$ , asemejándose entonces el espectro al del operador energía cinética.
–En cada banda permitida, las energías $E$ son doblemente degeneradas, teniendo asociadas las dos soluciones linealmente independientes (teorema de Bloch):
$\psi_1=e^{ikx}u_{1k}(x) \quad , \quad \psi_2=e^{-ikx}u_{2k}(x) \quad , \quad u_{jk}(x)= u_{jk}(x+nl)\;,\;j=1,2\,$ ,
donde $k$ representa una constante real que satisface
$-\frac{\pi}{l} < k \le \frac{\pi}{l}$
y siendo $n=0,\pm 1,\pm 2 \ldots$
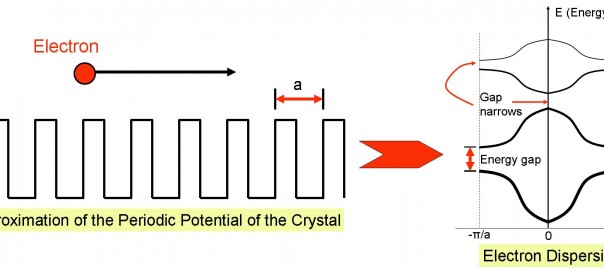
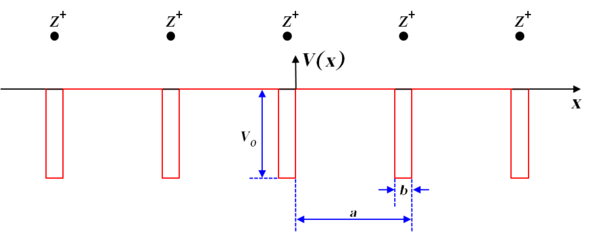
Por ejemplo, un potencial de este tipo es el potencial de Kronig-Penney:
$V(x) = \left \{ \begin{matrix} -V_o < 0 \quad \mbox{si } \quad -b < x \le 0 \;,\; b>0 \;,\; b\in \mathbb{R}\\ 0 \quad \mbox{si } \quad 0 < x \le a-b \;,\; a>b \;,\; a\in \mathbb{R} \\ V(x+a)=V(x) \;,\; \forall x \in \mathbb{R}\end{matrix}\right.$
-Este potencial constituye un modelo sencillo para aproximar la interacción a la que se halla sometido un electrón en una red cristalina unidimensional. Como ilustra la figura, consiste en una secuencia de pozos cuadrados finitos de potencial, periódicamente distribuidos; el período $a$ representa la distancia internuclear de los átomos en la hilera infinita que constituye la red, aproximando cada pozo la interacción atractiva que ejercen los núcleos sobre los electrones:

Propiedades generales de las soluciones de la ecuación de Schrödinger independiente del tiempo para potenciales periódicos

Teorema de Bloch:
Para un potencial periódico, , continuos en todo , en cada banda de valores de energía permitidos los autovalores son doblemente degenerados, de forma que a cada uno de ellos están asociadas dos soluciones linealmente independientes, denominadas como ondas de Bloch, que tienen la forma de sendas ondas planas moduladas por un factor que es una función de período el mismo () del potencial:
,
donde es una constante real que satisface
-Nota: pueden aparecer también autovalores discretos de energía con otro tipo de autofunciones asociadas, pero resultan irrelevantes en la práctica; véase [GAL-89], pp. 225 y 227.
1. Sea la ecuación de autovalores de la energía o ecuación de Schrödinger (ES) independiente del tiempo:
  $\frac{-\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}+V(x)\psi(x)=E\psi(x)$
  y supongamos un autovalor $E$ de la misma con una autofunción $\psi(x)$ asociada.
  -La ES en $x'=x+l$ tiene la expresión
  $\frac{-\hbar^2}{2m}\frac{d^2\psi(x')}{dx'^2}+V(x')\psi(x')=E\psi(x')$
  $\Rightarrow \psi(x+l)=\psi(x')$ es también autofunción para ese autovalor dado $E$ , ya que $V(x'=x+l)=V(x)$ .
  -Dado que la ES es una EDO lineal, de segundo orden, cualquier solución de la misma puede expresarse como combinación lineal de dos soluciones particulares linealmente independientes entre sí, $\psi_1$ y $\psi_2$ , estando garantizada la existencia de ese par de soluciones particulares linealmente independiente (denominado conjunto fundamental) por la continuidad de $V(x)$ y su primera derivada $V'(x)$ en cada intervalo $[x_o,x_o+l] \;,\;x_o \in \mathbb{R}$ .
  -Por tanto, cualquier solución de la ES admite expresión:
  $\psi(x)=e_1\psi_1(x) + e_2\psi_2(x)$ , con $e_1$ y $e_2$ constantes dadas.
2. Puesto que $\psi_1(x+l)$ y $\psi_2(x+l)$ son a su vez también soluciones particulares linealmente independientes de la misma ES, se tendrá:
  $\left \{ \begin{matrix} \psi_1(x+l)=a_{11}\psi_1(x)+a_{21}\psi_{2}(x) \\ \psi_2(x+l)=a_{12}\psi_1(x)+a_{22}\psi_{2}(x) \end{matrix}\right.$ [sistema ***] ,
  cumpliéndose además para cualquier solución que
  $\psi(x+l)=d_1\psi_1(x)+d_2\psi_2(x)=c_1\psi_1(x+l)+c_2\psi_2(x+l)$
  -Consecuentemente:
  $\psi(x+l)=d_1\psi_1(x)+d_2\psi_2(x)$
  $=c_1[a_{11}\psi_1(x)+a_{21}\psi_{2}(x)]+c_2[a_{12}\psi_1(x)+a_{22}\psi_{2}(x)]$
  $\Rightarrow \left \{ \begin{matrix} d_1=c_1a_{11}+c_2a_{12} \\ d_2=c_1a_{21}+c_2a_{22}\end{matrix}\right.$
  -En forma matricial:
  $\left( \begin{array}{c} d_1 \\ d_2 \end{array} \right) = \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right) \cdot \left( \begin{array}{c} c_1 \\ c_2 \end{array} \right)=A\left( \begin{array}{c} c_1 \\ c_2 \end{array}\right)$ [ecuación $$$]
  donde se ha introducido la matriz $A$ de coeficientes,
  $A= \left( \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right)$
3. La matriz $A$ es no singular, $det(A)=|A|=a_{11}a_{22}-a_{21}a_{12} \ne 0$ , ya que, si fuera cero, las dos soluciones $\psi_1\,,\,\psi_2$ serían linealmente dependientes, por tenerse la relación entre wronskianos:
  $W[\psi_1(x+l),\psi_2(x+l)]= \left| \begin{array}{cc} a_{11}\psi_1(x)+a_{21}\psi_{2}(x) & a_{12}\psi_1(x)+a_{22}\psi_{2}(x) \\ a_{11}\psi_1'(x)+a_{21}\psi_{2}'(x) & a_{12}\psi_1'(x)+a_{22}\psi_{2}'(x) \\ \end{array} \right|$
  $=|A|\ W[\psi_1(x),\psi_2(x)]$
  donde los dos wronskianos han de ser no nulos por la independencia lineal de las funciones involucradas.
  -Nota: el wronskiano de dos soluciones linealmente independientes de la EDO general $\psi''+f(x)\psi=0\;,\; f\$ función continua, correspondientes a la misma energía $E$ , ha de ser no nulo y constante (si es nulo, lo es $\forall x$ , y corresponde al caso en que las dos soluciones son linealmente dependientes):
  $\frac{\psi_1''}{\psi_1}=\frac{\psi_2''}{\psi_2}=-f(x)\;,\;\forall x$
  $\Rightarrow \psi_1''\psi_2-\psi_2''\psi_1=(\psi_1'\psi_2)'-(\psi_2'\psi_1)'=0$
  $\Rightarrow \psi_1'\psi_2-\psi_2'\psi_1=\mbox{constante}$
  $=-W[\psi_1,\psi_2]=- \left| \begin{array}{cc} \psi_1(x) & \psi_{2}(x) \\ \psi_1'(x) & \psi_{2}'(x) \\ \end{array} \right| \ne 0$
  -Por lo tanto, $|A| \ne 0$ y $A$ es diagonalizable:
  $A\varphi=\lambda \varphi \Rightarrow (A-\lambda I)\varphi=0$
  o sistema homogéneo de ecuaciones lineales
  $\left. \begin{matrix} (a_{11}-\lambda)f_1 +a_{12}f_2=0 \\ a_{21}f_1 +(a_{22}-\lambda)f_2=0 \end{matrix}\right \}$ ,
  donde $\varphi=\left( \begin{array}{c} f_1 \\ f_2 \end{array} \right)$
  -El sistema tendrá solución no trivial si y sólo si $|A-\lambda I|=0$ , condición que constituye la ecuación de autovalores de la matriz:
  $(a_{11}-\lambda)(a_{22}-\lambda)-a_{12}a_{21}=0$
  $\Rightarrow \lambda^2-(a_{11}+a_{22})\lambda-(a_{11}a_{22}-a_{21}a_{12})=0$
4. Sean $\lambda_1 \,,\lambda_2\;,\;\lambda_1 \ne \lambda_2$ , dos raíces de la anterior ecuación, y sean $\varphi^{(i)}\,,\,i=1,2$ sendos vectores propios asociados, de forma que se satisface
  $A\varphi^{(i)}=\lambda_i \varphi^{(i)}=\lambda_i \left( \begin{array}{c} f_1^{(i)} \\ f_2^{(i)} \end{array} \right)=\left( \begin{array}{c} d_1^{(i)} \\ d_2^{(i)} \end{array} \right)$
  donde se ha incorporado la expresión anterior ($$$) y a partir de la cual se derivan los valores:
  $\left. \begin{matrix} d_1^{(i)}=a_{11}f^{(i)}_1+a_{12}f^{(i)}_2=\lambda_if^{(i)}_1 \\ d_2^{(i)}=a_{21}f^{(i)}_1+a_{22}f^{(i)}_2=\lambda_if^{(i)}_2 \end{matrix}\right \}$
  $\Rightarrow \left. \begin{matrix} a_{11}=\lambda_i \quad , \quad a_{12}=0 \\ a_{21}=0 \quad , \quad a_{22}=\lambda_i \end{matrix}\right \}$ ,
  conjunto de valores que sustituido en el anterior sistema (***) conduce al resultado:
  $\Rightarrow \left. \begin{matrix} \psi_1(x+l)=\lambda_i \psi_1(x) \\ \psi_{2}(x+l)=\lambda_i \psi_2(x) \end{matrix}\right \}$
  -Es decir: entre las soluciones particulares $\psi$ de la ES planteada, correspondiente a un potencial periódico genérico $V(x)=V(x+l)$ , continuo y con derivada primera continua, existen dos linealmente independientes entre sí que cumplen:
  $\psi(x+l)=\lambda \psi(x)\;,\; \lambda =constante$
  expresión que constituye el teorema de Floquet.
5. La ecuación anterior implica la siguiente:
  $\psi(x+nl)=\lambda^n \psi(x)=|\lambda|^n e^{i n \chi } \psi(x)\;,\;\chi \in \mathbb{R}$ ,
  con $n=0,\pm 1,\pm 2\ldots$ ,
  que expresa la invariancia translacional: la solución es una función periódica, con el mismo período $l$ que el potencial $V(x)$ .
  -Si se tiene $|\lambda| \ne 1$ , entonces o bien $\lim_{x \rightarrow +\infty}|\psi(x)|\rightarrow +\infty$ (por lo que surge la condición $|\lambda| \le 1$ ), o bien $\lim_{x \rightarrow -\infty}|\psi(x)|\rightarrow +\infty$ (surge la condición $|\lambda| \ge 1$ ). En consecuencia, se requiere $|\lambda| = 1$ para obtener una solución físicamente aceptable.
6. La acotación de las soluciones a largas distancias requiere, por tanto, $|\lambda|=1$ , que permite escribir
  $\lambda=e^{i\chi}\;,\;\chi \in \mathbb{R}$ ,
  por lo que se implica
  $\Rightarrow \psi(x+l)=e^{i\chi}\psi(x)$
  $\Rightarrow \psi(x+nl)=e^{in\chi}\psi(x)$
  con $n=0,\pm 1,\pm 2 \ldots$ .
7. En resumen: dadas dos soluciones particulares linealmente independientes $\psi_{\lambda_1}$ y $\psi_{\lambda_2}$ , correspondientes ambas al mismo autovalor $E$ , han de verificar
  $\psi_{\lambda_1}(x+l)=\lambda_1 \psi_{\lambda_1}(x)$
  $\psi_{\lambda_2}(x+l)=\lambda_2 \psi_{\lambda_2}(x)$
  donde $\lambda_1\,,\,\lambda_2$ representan constantes de módulo unidad que supondremos en general distintas.
8. Según lo expuesto anteriormente para los wronskianos involucrados, para las dos soluciones consideradas se ha de tener:
  $W[\psi_{\lambda_1}(x+l),\psi_{\lambda_2}(x+l)]= \mbox{constante}$
  $=\left| \begin{array}{cc} \psi_{\lambda_1}(x+l) & \psi_{\lambda_2}(x+l) \\ \psi_{\lambda_1}'(x+l) & \psi_{\lambda_2}'(x+l) \\ \end{array} \right|$
  $=\psi_{\lambda_1}(x+l)\psi_{\lambda_2}'(x+l)-\psi_{\lambda_2}(x+l)\psi_{\lambda_1}'(x+l)$
  $=\lambda_1 \lambda_2 W[\psi_{\lambda_1}(x),\psi_{\lambda_2}(x)]=\lambda_1 \lambda_2 \cdot \mbox{constante}$
  $\Rightarrow \lambda_1 \lambda_2=1=det(A)$
  -Es decir: en primer lugar, la matriz $A$ es unitaria; en segundo, como además, según se vio anteriormente, para que las soluciones sean físicamente aceptables se ha de tener $|\lambda_1|=| \lambda_2|=1$ , entonces las dos soluciones $\psi_{\lambda_1}$ y $\psi_{\lambda_2}$ , correspondientes ambas al mismo autovalor $E$ , han de satisfacer:
  $\psi_{\lambda_1}(x+l)=\lambda_1 \psi_{\lambda_1}(x)=e^{i\chi}\psi_{\lambda_1}(x)$
  $\psi_{\lambda_2}(x+l)=\lambda_2 \psi_{\lambda_2}(x)=e^{-i\chi}\psi_{\lambda_2}(x)$
  (expresión de las denominadas ondas de Bloch), con $\chi \in \mathbb{R}$ , implicándose
  $\psi_{\lambda_1}(x+nl)=e^{in\chi}\psi_{\lambda_1}(x)$
  $\psi_{\lambda_2}(x+nl)=e^{-in\chi}\psi_{\lambda_2}(x)$
  con $n=0,\pm 1,\pm 2 \ldots$ .
9. Puesto que $e^{in2\pi}=1\;,\; n=0,\pm 1,\pm 2 \ldots$ , puede restringirse $\chi$ a tomar valores en cualquier intervalo de longitud $2\pi$ , por ejemplo fijando $-\pi < \chi \le +\pi$ . Tomando entonces $\chi=kl$ , donde $k$ es una constante real, se tiene
  $-\frac{\pi}{l} < k \le \frac{\pi}{l}$
  ecuación que define la denominada zona de Brillouin.
  -Las soluciones físicamente admisibles, esto es, las que satisfacen el requisito de invariancia traslacional, han pues de verificar:
  $\psi(x+l)=e^{ikl}\psi(x) \Rightarrow \psi(x+nl)=e^{ikln}\psi(x)$
  con $-\frac{\pi}{l} < k \le \frac{\pi}{l}$ y $n=0,\pm 1,\pm 2 \ldots$ , ecuación que constituye la denominada condición de Bloch, que no es sino una ecuación de invariancia traslacional que nos indica que es imposible distinguir el pozo concreto de la hilera en que se encuentra la partícula.
10. Introduciendo para la función de onda $\psi(x)$ la expresión
  $\psi(x)=e^{ikx}u_k(x)$
  se deriva finalmente:
  $\psi(x+l)=e^{ik(x+l)}u_k(x+l)=e^{ikl}\psi(x)=e^{ikl}e^{ikx}u_k(x)$
  donde se ha usado la condición de Bloch; análogamente:
  $\psi(x+nl)=e^{ik(x+nl)}u_k(x+nl)=e^{ikln}e^{ikx}u_k(x)$
  $\Rightarrow u_k(x+l)=u_k(x)=u_k(x+nl)$
  resultado conocido como teorema de Bloch (también como teorema de Floquet) y que establece las soluciones estacionarias para un potencial periódico:
  La ecuación de Schrödinger independiente del tiempo para un potencial periódico $V(x)=V(x+l)$ posee dos soluciones linealmente independientes que tienen la forma de una onda plana modulada por una función periódica con período $l$ igual al del potencial:
  $\psi_1(x)=e^{ikx}u_{1k}(x)\;,\; \psi_2(x)=e^{-ikx}u_{2k}(x)$
  cumpliéndose $u_{jk}(x+nl)=u_{jk}(x)\;,\;j=1,2$ ,
  donde $-\frac{\pi}{l} < k \le \frac{\pi}{l}$ y $n=0,\pm 1,\pm 2 \ldots$
  (soluciones que se denominan ondas de Bloch).
  -Cada onda de Bloch $\psi(x)=e^{\pm ikx}u_{k}(x)$ representa una onda plana viajera con longitud de onda $\lambda =\frac{2\pi}{k}$ y función amplitud $u_k(x)$ de período $l$ igual al de la correspondiente red cristalina.
11. Nota: puede suceder que la ecuación de autovalores de la matriz $A$ posea sólo una raíz doble, $\lambda_1=\lambda_2$ . Estos casos son irrelevantes a efectos del estudio de la parte continua del espectro del correspondiente Hamiltoniano, cf. [GAL-89], p. 225.

Estructura espectral del Hamiltoniano para potenciales periódicos

El espectro del Hamiltoniano correspondiente a un potencial periódico presenta las siguientes características (cf. [GAL-89], pp. 224-226):
1. Carece de partes discretas; es decir, no aparecen estados ligados al resolver el problema de autovalores de la energía: $\sigma_P(H)=\emptyset$ .
2. Teorema de oscilación de Birkhoff :
  -Sea la matriz de coeficientes $B(E)$ definida por la ecuación
  $\left( \begin{array}{c} \psi(l) \\ \psi'(l) \end{array} \right) =B(E)\left( \begin{array}{c} \psi(0) \\ \psi'(0) \end{array}\right)$
  donde $\psi(x)$ es la solución del problema de contorno especificada por las condiciones iniciales $\psi(0)\,,\,\psi'(0)$ y la matriz $B$ cumple $det(B)=1$ , de forma que es diagonalizable cuando las raíces de su ecuación de autovalores son distintas, lo que sucede siempre cuando $Traza(B) \ne \pm 2$ .
  -Sea la secuencia de valores de energía $E_0,E_1,E_2,E_3 \cdots$ constituida por las raíces de la ecuación $Tr[B(E)]=+2$ ordenadas en sentido creciente, repitiendo en la ordenación cada raíz múltiple un número de veces igual a su multiplicidad; análogamente, sea la secuencia de valores de energía $E_0',E_1',E_2',E_3' \cdots$ constituida por las raíces de la ecuación $Tr[A(E)]=-2$ , también ordenadas en sentido creciente y repitiendo en la ordenación cada raíz múltiple un número de veces igual a su multiplicidad.
  -Entonces, se tiene:
  $E_0<E_0' \le E_1' < E_1 \le E_2 < E_2' \le E_3' < \cdots$
  viniendo dada la parte continua del Hamiltoniano por
  $\sigma_C(H)=[E_0,E_0']\cup [E_1',E_1]\cup [E_2,E_2']\cup \cdots$
3. El espectro tiene estructura de bandas: está compuesto por intervalos continuos de energías permitidas, denominadas como zonas de estabilidad, separadas por intervalos continuos de energías prohibidas, o zonas de inestabilidad.

Ejemplo 1: Potencial periódico con deltas de Dirac

Sea el potencial de período $l$ y expresión
$V(x)=V_o \cdot l\sum_{n=-\infty}^{+\infty} \delta(x-nl)$
-Representado en un intervalo en torno al origen de longitud menor que $2l$ para $V_o>0$ sería:

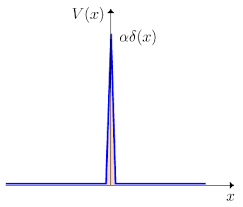
Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html.

-Introducir la periodicidad consiste en añadir deltas en todos los puntos $x=nl\;,\;n=\pm l$ a lo largo del eje OX:

Tren («comb») de deltas; $T$ es el período, representado por $l$ en el presente texto (imagen de la Wikipedia).
Problema de autovalores de energía:
$\frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}[E-V(x)]\psi(x)=0$ ,
ecuación diferencial ordinaria a la que habrán de añadirse las condiciones de contorno adecuadas que permitan obtener las soluciones físicamente aceptables del problema planteado.
Sólo habrá soluciones físicamente aceptables en el rango ; buscamos soluciones que cumplan:
1. Según el teorema de Bloch, de expresión dada por una onda de Bloch:
  $\psi(x)=e^{ikx}u_{k}(x)$
  $u_{k}(x+nl)=u_{k}(x)$
  con $n=0,\pm 1,\pm 2 \ldots$
  y $-\frac{\pi}{l} < k \le \frac{\pi}{l}$ (zona de Brillouin).
  -En todos los sitios donde el potencial es nulo, es decir, en las regiones $x \ne nl\;,\;n=0,\pm 1,\pm 2 \ldots$ , respondiendo a la expresión general
  $\psi(x)=Ae^{i\beta x}+Be^{-i\beta x}\; , \; \beta =\frac{\sqrt{2mE}}{\hbar} \; , \; \beta\in \mathbb{R} \; , \; \beta >0$ .
2. Reuniendo ambos resultados anteriores, en una zona de longitud $l$ , que fijamos como, por ejemplo, $0 < x\le l$ (zona II), se tendrá:
  $\psi^{II}(x)=Ae^{i\beta x}+Be^{-i\beta x}=e^{ikx}u_k(x)$
  $\Rightarrow u_k(x)=Ae^{i(\beta -k) x}+Be^{-i(\beta +k)x}$
  que ha de cumplir la periodicidad dada, por lo que será:
  $u_k(x\pm nl)=u_k(x) \Rightarrow u_k(x)=Ae^{i(\beta -k) (x\pm nl)}+Be^{-i(\beta +k)(x\pm nl)}$
3. A continuación hemos de escribir la expresión de la función de onda para $-l < x \le 0$ , que denominaremos como zona I. Para ello, dada la periodicidad de $u_k(x)$ , basta observar que un punto dado $x$ perteneciente a la región I se corresponde con el punto $x+l$ perteneciente a la región II:
  $\psi^{I}(x)=e^{ikx}u_k(x)$
  $\psi^{II}(x)=Ae^{i\beta x}+Be^{-i\beta x}=e^{ikx}u_k(x)$
  $u_k(x+l)=u_k(x)$
  $\Rightarrow \psi^{II}(x+l)=Ae^{i\beta (x+l)}+Be^{-i\beta (x+l)}$
  $=e^{ik(x+l)}u_k(x+l)=e^{ik(x+l)}u_k(x)$
  $\Rightarrow u_k(x)=Ae^{i\beta (x+l)-ik(x+l)}+Be^{-i\beta(x+l)-ik(x+l)}$
  $\Rightarrow \psi^{I}(x)=e^{ikx}u_k(x)=e^{-ikl}[Ae^{i\beta (x+l)}+Be^{-i\beta (x+l)}]$
4. Reuniendo resultados, la función de onda en el intervalo $-l < x\le l$ tiene la expresión:
  $\psi(x) = \left \{ \begin{matrix} Ae^{i[\beta (x+l)-kl]}+Be^{-i[\beta (x+l)+kl)]} \quad \mbox{si } \quad -l < x \le 0 \;,\;\mbox{zona I} \\ Ae^{i\beta x}+Be^{-i\beta x} \quad \mbox{si } \quad 0 < x \le l \;,\;\mbox{zona II}\end{matrix}\right.$
5. A continuación se imponen las condiciones de contorno requeridas; dada la periodicidad, bastará imponerlas en uno de los puntos $x= nl\;,\;n=0,\pm 1,\pm 2 \ldots$ ; elegimos el punto $x=0$ en el intervalo en el que ya tenemos escrita la función de onda, esto es, en $-l < x\le l$ :
  – $\psi(x)$ continua:
  $\psi(0^+)=\psi(0^-) \Rightarrow A+B=Ae^{i(\beta -k)l}+Be^{-i(\beta +k)l}$
  – $\psi'(x)$ con salto de primera especie en $x=0$ dado por:
  $\psi'(0^+)-\psi'(0^-)= \frac{2m}{\hbar^2}V_o \cdot l\ \psi(0)$
  $\Rightarrow i\beta (A-B)-i\beta (Ae^{i(\beta -k)l}-Be^{-i(\beta +k)l})=\frac{2m}{\hbar^2}V_o \cdot l\ (A+B)$
  $\Rightarrow A(1-e^{i(\beta -k)l})-B(1-e^{-i(\beta +k)l})=-i\frac{2mV_ol}{\hbar^2 \beta }(A+B)$
  $\Rightarrow A(1-e^{i(\beta -k)l}+i\frac{2mV_ol}{\hbar^2 \beta } )-B(1-e^{-i(\beta +k)l}-i\frac{2mV_ol}{\hbar^2 \beta })=0$
6. Las dos ecuaciones anteriores constituyen un sistema lineal homogéneo de ecuaciones que, para que posea solución no trivial, ha de tener determinante de coeficientes nulo,
  $0=\left| \begin{array}{cc} 1-e^{i(\beta -k)l} & 1- e^{-i(\beta +k)l} \\ 1-e^{i(\beta -k)l}+i\frac{2mV_ol}{\hbar^2 \beta } & -1+e^{-i(\beta +k)l}+i\frac{2mV_ol}{\hbar^2 \beta } \\ \end{array} \right|$
  lo que permite derivar finalmente la ecuación de autovalores:
  $F(\beta l)=cos \beta l +\frac{mV_ol}{\hbar^2 \beta } sen \beta l = cos kl$
  -Aparece así una estructura de bandas continuas de valores de energía permitidos, cuyos extremos vienen dados por:
  $|cos \beta l +\frac{mV_ol}{\hbar^2 \beta } sen \beta l| = 1$
  $\Rightarrow \beta l=n\pi\;,\;n >0 (\mbox{ya que }\beta>0 \;,\; kl=n\pi \Rightarrow cos kl=\pm 1)$
  
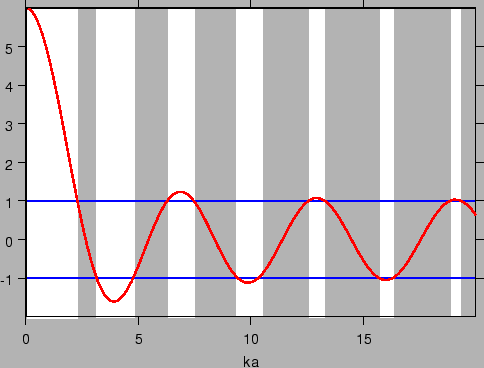
  Representación de $F(\beta l)$ como función de $\beta l$ para $mV_ol/ \hbar ^2 =5$ (imagen de http://people.physik.hu-berlin.de/~sokolov/QM1/QMall/node46.html).
  
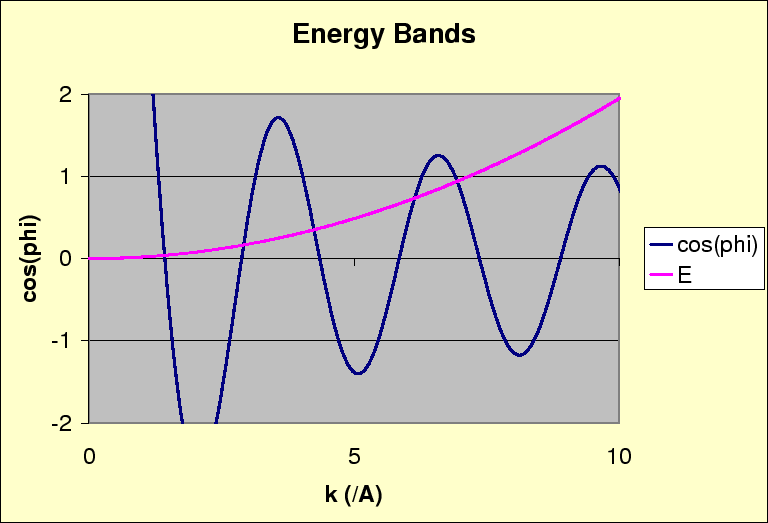
  En la figura, $\phi=\beta l$ y $k=\beta$ del presente texto (imagen de http://quantummechanics.ucsd.edu/ph130a/130_notes/node156.html).

Ejemplo 2: Pozos periódicos de deltas de Dirac

Sea el potencial de período $l$ y expresión
$V(x)=V_o \cdot l\sum_{n=-\infty}^{+\infty} \delta(x-nl)$
-Representado en un intervalo en torno al origen de longitud menor que $2l$ para $V_o<0$ sería:

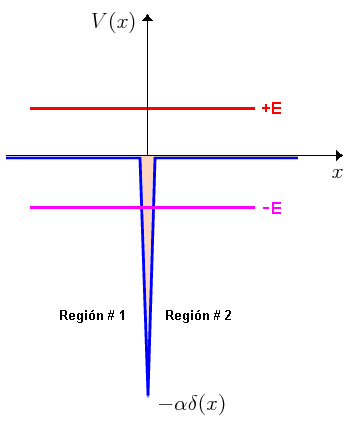
Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2009/08/el-potencial-delta-de-dirac.html.

-Introducir la periodicidad consiste en añadir deltas en todos los puntos $x=nl\;,\;n=0, \pm 1,\pm2 \ldots$ a lo largo del eje OX.

Potencial-periodico-pozos-Dirac_comb_Wikipedia — *Hilera de pozos deltas de Dirac.*

Problema de autovalores de energía:
$\frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}[E-V(x)]\psi(x)=0$ ,
ecuación diferencial ordinaria a la que habrán de añadirse las condiciones de contorno adecuadas que permitan obtener las soluciones físicamente aceptables del problema planteado.
Resolución en el rango de energías negativas, : Buscamos soluciones que cumplan:
1. Según el teorema de Bloch, de expresión dada por ondas de Bloch:
  $\psi(x)=e^{ikx}u_{k}(x)$
  $u_{k}(x+nl)=u_{k}(x)$
  con $n=0,\pm 1,\pm 2 \ldots$
  y $-\frac{\pi}{l} < k \le \frac{\pi}{l}$ (zona de Brillouin).
  -En todos los sitios donde el potencial es nulo, es decir, en las regiones $x \ne nl\;,\;n=0,\pm 1,\pm 2 \ldots$ , respondiendo a la expresión general
  $\psi(x)=Ae^{\beta x}+Be^{-\beta x}\;,\;\beta=\frac{\sqrt{2m|E|}}{\hbar}$
2. Reuniendo ambos resultados anteriores, en una zona de longitud $l$ , que fijamos como, por ejemplo, $0 < x\le l$ (zona II), se tendrá:
  $\psi^{II}(x)=Ae^{\beta x}+Be^{-\beta x}=e^{ikx}u_k(x)$
  $\Rightarrow u_k(x)=Ae^{(\beta -ik) x}+Be^{-(\beta +ik)x}$
  que ha de cumplir la periodicidad dada, por lo que será:
  $u_k(x\pm l)=u_k(x) \Rightarrow u_k(x)=Ae^{(\beta -ik) (x\pm l)}+Be^{-(\beta +ik)(x\pm l)}$
3. A continuación hemos de escribir la expresión de la función de onda para $-l < x \le 0$ , que denominamos como zona I. Para ello, dada la periodicidad de $u_k(x)$ , basta observar que un punto dado $x$ perteneciente a la región I se corresponde con el punto $x+l$ perteneciente a la región II:
  $\psi^{I}(x)=e^{ikx}u_k(x)$
  $\psi^{II}(x)=Ae^{\beta x}+Be^{-\beta x}=e^{ikx}u_k(x)$
  $u_k(x+l)=u_k(x)$
  $\Rightarrow \psi^{II}(x+l)=Ae^{\beta (x+l)}+Be^{-\beta (x+l)}$
  $=e^{ik(x+l)}u_k(x+l)=e^{ik(x+l)}u_k(x)$
  $\Rightarrow u_k(x)=Ae^{\beta (x+l)-ik(x+l)}+Be^{-\beta(x+l)-ik(x+l)}$
  $\Rightarrow \psi^{I}(x)=e^{ikx}u_k(x)=e^{-ikl}[Ae^{\beta (x+l)}+Be^{-\beta (x+l)}]$
4. Reuniendo resultados, la función de onda en el intervalo $-l < x\le l$ tiene la expresión:
  $\psi(x) = \left \{ \begin{matrix} Ae^{[\beta (x+l)-ikl]}+Be^{-[\beta (x+l)+ikl)]} \quad \mbox{si } \quad -l < x \le 0 \;,\;\mbox{zona I} \\ Ae^{\beta x}+Be^{-\beta x} \quad \mbox{si } \quad 0 < x \le l \;,\;\mbox{zona II}\end{matrix}\right.$
5. A continuación se imponen las condiciones de contorno requeridas; dada la periodicidad, bastará imponerlas en uno de los puntos $x= nl\;,\;n=0,\pm 1,\pm 2 \ldots$ ; elegimos el punto $x=0$ en el intervalo en el que ya tenemos escrita la función de onda, esto es, en $-l < x\le l$ :
  – $\psi(x)$ continua:
  $\psi(0^+)=\psi(0^-) \Rightarrow A+B=Ae^{(\beta -ik)l}+Be^{-(\beta +ik)l}$
  – $\psi'(x)$ con salto de primera especie en $x=0$ dado por:
  $\psi'(0^+)-\psi'(0^-)= \frac{2m}{\hbar^2}V_o \cdot l \psi(0)$
  $\Rightarrow \beta (A-B)-\beta (Ae^{(\beta -ik)l}-Be^{-(\beta +ik)l})=\frac{2m}{\hbar^2}V_o \cdot l\ (A+B)$
  $\Rightarrow A(1-e^{(\beta -ik)l})+B(-1+e^{-(\beta +ik)l})=\frac{2mV_ol}{\hbar^2 \beta }(A+B)$
  $\Rightarrow A(1-e^{(\beta -ik)l}-\frac{2mV_ol}{\hbar^2 \beta } )+B(-1+e^{-(\beta +ik)l}-\frac{2mV_ol}{\hbar^2 \beta })=0$
6. Las dos ecuaciones anteriores constituyen un sistema lineal homogéneo de ecuaciones que, para que posea solución no trivial, ha de tener determinante de coeficientes nulo,
  $0=\left| \begin{array}{cc} 1-e^{(\beta -ik)l} & 1- e^{-(\beta +ik)l} \\ 1-e^{(\beta -ik)l}-\frac{2mV_ol}{\hbar^2 \beta } & -1+e^{-(\beta +ik)l}-\frac{2mV_ol}{\hbar^2 \beta } \\ \end{array} \right|$
  lo que permite derivar finalmente la ecuación de autovalores:
  $F(\beta l)=cosh \beta l -\frac{mV_ol}{\hbar^2 \beta } senh \beta l = cos kl$
  -Aparece así una estructura de bandas continuas de valores de energía permitidos, cuyos extremos vienen dados por:
  $|cosh \beta l +\frac{mV_ol}{\hbar^2 \beta } senh \beta l| = 1$
  -Cuando $\beta=0=\frac{+\sqrt{2m|E|}}{\hbar}$ :
  $\Rightarrow cos kl=1-\frac{mV_ol}{\hbar^2}$
  -Cuando $\beta \rightarrow \infty$ :
  $\lim_{\beta \rightarrow \infty} \frac{cos kl}{cosh \beta l}=1-\frac{mV_ol}{\hbar^2 \beta} \Rightarrow 1-0=0$
  de forma que no existen soluciones.
7. Obsérvese que no se han obtenido estados ligados: las soluciones del potencial periódico para $E<0$ son ondas de Bloch, esto es, ondas planas por una función amplitud con período igual al del potencial (los estados ligados reaparecerán si se toma el límite $l \rightarrow +\infty$ ).
La resolución para $E>0$ es por completo análoga a la hecha en el caso de $V_o>0$ , sin más que cambiar el signo de este parámetro en el desarrollo.
Las siguientes gráficas presentan ejemplos de resolución numérica:
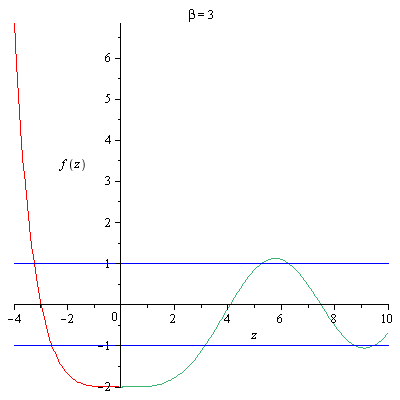
Imagen de http://physicspages.com/2013/06/01/band-structure-of-solids-negative-energies/.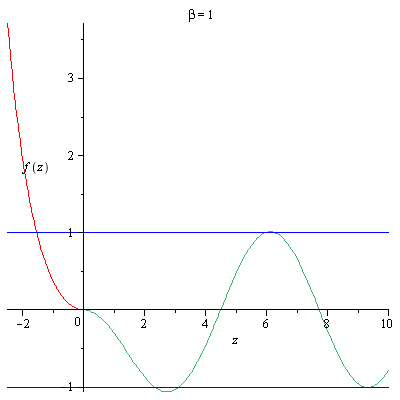

Imagen de http://physicspages.com/2013/06/01/band-structure-of-solids-negative-energies/.

Potencial de Kronig-Penney

$V(x) = \left \{ \begin{matrix} -V_o < 0 \quad \mbox{si } \quad -b < x \le 0 \;,\; b>0 \;,\; b\in \mathbb{R}\\ 0 \quad \mbox{si } \quad 0 < x \le l-b \;,\; l>b \;,\; l\in \mathbb{R} \\ V(x+l)=V(x) \;,\; \forall x \in \mathbb{R}\end{matrix}\right.$
Imagen de la Wikipedia.
Problema de autovalores de energía:
$\frac{d^2\psi}{dx^2}+\frac{2m}{\hbar^2}[E-V(x)]\psi(x)=0$ ,
ecuación diferencial ordinaria a la que habrán de añadirse las condiciones de contorno adecuadas que permitan obtener las soluciones físicamente aceptables del problema planteado.
-Para la resolución, consideramos un intervalo del eje $OX$ de longitud un período $l=a$ :
Zona I: $-b < x \le 0$
Zona II: $0 < x \le l-b$
Resolución en el rango de energías negativas, $-V_o < E < 0$ :
-En cada una de las dos zonas elegidas la anterior EDO tiene la expresión:
$\left\{ \begin{matrix} \frac{d^2\psi}{dx^2}+\alpha^2\psi(x)=0 \quad \alpha=\frac{+\sqrt{2m(E+V_o)}}{\hbar} \quad \mbox{si } \quad -b < x \le 0 \\ \frac{d^2\psi}{dx^2}-\beta^2\psi(x)=0 \quad \beta=\frac{+\sqrt{-2mE}}{\hbar} \quad \mbox{si } \quad 0 < x \le l-b \end{matrix}\right.$
Buscamos soluciones que cumplan:
1. Según el teorema de Bloch, de expresión dada por las ondas de Bloch:
  $\psi(x)=e^{ikx}u_{k}(x)$
  $u_{k}(x+nl)=u_{k}(x)$
  en la zona de Brillouin,
  $-\frac{\pi}{l} < k \le \frac{\pi}{l}\;,\;n=0,\pm 1,\pm 2 \ldots$
  -Es decir, puesto que $|\psi(x)|^2=|u_k(x)|^2=|\psi(x+l)|^2$ , la interpretación asociada es que, en una red cristalina, cada electrón tiene igual probabilidad de ser localizado en la vecindad de cualquiera de los átomos individuales en la red.
2. En la celda de longitud $l=a$ considerada, y en cada una de sus dos subzonas I y II, con sendas expresiones generales:
  Zona I: $\psi_I(x)=Ae^{i\alpha x}+Be^{-i\alpha x}$
  Zona II: $\psi_{II}(x)=Ce^{\beta x}+De^{-\beta x}$
3. Reuniendo ambos resultados anteriores, en la celda de longitud $l$ elegida, $-b < x \le l-b$ , se tendrá, para cada subzona:
  Zona I:
  $\psi^{I}(x)=e^{ikx}u_{k}^{I}(x)=Ae^{i\alpha x}+Be^{-i\alpha x}$
  $\Rightarrow u_{k}^{I}(x)=Ae^{i(\alpha -k) x}+Be^{-i(\alpha +k)x}$
  Zona II:
  $\psi^{II}(x)=e^{ikx}u_{k}^{II}(x)=Ce^{\beta x}+De^{-\beta x}$
  $\Rightarrow u_{k}^{II}(x)=Ce^{(\beta -ik) x}+De^{-(\beta +ik)x}$
  -Nota: la notación $u_{k}^{I}(x)$ quiere representar la función $u(x)$ cuando x toma valores en el intervalo $-b < x \le 0$ , y análogamente para otros supraíndices, siempre para la misma $u(x)$ .
  -Se ha de satisfacer la periodicidad dada,
  $V(x)=V(x+l) \Rightarrow \psi(x+nl)=e^{ink}\psi(x) \;,\;u(x+nl)=u(x)$
  por lo que la dos expresiones anteriores proporcionan la función de onda en cualquiera de las celdas, sin más que realizar la traslación oportuna.
  -Por ejemplo, en la región $l-b<x\le l$ , que denominamos zona III, dentro de la celda $(l-b,2l-b]$ , la expresión de la función de onda sería, a partir de la expresión en la zona I (un punto $x$ en la celda $(l-b,2l-b]$ se corresponde con el punto $x-l$ perteneciente a la celda $(-b,l-b]$ :
  $\psi^{III}(x)=e^{ikx}u_k(x)\quad (x\in III)$
  $\psi^{I}(x)=Ae^{i\alpha x}+Be^{-i\alpha x}=e^{ikx}u_k(x)\quad (x\in I)$
  $\Rightarrow \psi^{I}(x-l)=Ae^{i\alpha (x-l)}+Be^{-i\alpha (x-l)}=e^{ik(x-l)}u_k(x-l)$
  $u_k(x-l)=u_k(x)$
  $\Rightarrow \psi^{I}(x-l)=Ae^{i\alpha (x-l)}+Be^{-i\alpha (x-l)}=e^{ik(x-l)}u_k(x)$
  $\Rightarrow u_k(x)= \psi^{I}(x-l)e^{-ik(x-l)}=Ae^{i\alpha (x-l)-ik(x-l)}+Be^{-i\alpha(x-l)-ik(x-l)}$
  $\Rightarrow \psi^{III}(x)=e^{ikx}u_k(x)=e^{ikl}[Ae^{i\alpha (x-l)}+Be^{-i\alpha (x-l)}]$
  $\Rightarrow u_k^{III}(x)=e^{-ikx}\psi^{III}(x)=e^{-ik(x-l)}[Ae^{i\alpha (x-l)}+Be^{-i\alpha (x-l)}]=Ae^{i(\alpha -k)(x-l)}+Be^{-i(\alpha +k)(x-l)}$
4. A continuación se imponen las condiciones de contorno requeridas sobre $\psi$ que, por ser $\psi=e^{ikx}u$ , deberán ser también cumplidas por la función $u$ . Y, dada la periodicidad de $u(x)$ , $u(x)=u(x+nl)$ , bastará imponerlas sobre $u(x)$ , tanto en el borde $x=0$ del pozo de potencial en la celda elegida como en el punto $x=l-b$ , el correspondiente al otro extremo del pozo en la celda considerada, $-b < x \le l-b$ , para que se propaguen a todos los pozos en la red:
  – $u(x)$ continua en $x=0$ :
  $u^{II}(0^+)=u^{I}(0^-) \Rightarrow C+D=A+B$
  – $u'(x)$ continua en $x=0$ : $u^{II}(0^+)=u^{I}(0^-)$
  $\Rightarrow (\beta -ik)C-(\beta +ik)D=i(\alpha -k)A-i(\alpha +k)B$
  – $u(x)$ continua en $x=l-b$ : $u^{III}((l-b)^+)=u^{II}((l-b)^-)$
  $\Rightarrow Ae^{i(\alpha -k)(-b)}+Be^{-i(\alpha +k)(-b)}=Ce^{(\beta -ik) (-b)}+De^{-(\beta +ik)(-b)}$
  – $u'(x)$ continua en $x=l-b$ : $u^{III}((l-b)^+)=u^{II}((l-b)^-)$ $\Rightarrow Ai(\alpha -k)e^{i(\alpha -k)(-b)}-B(\alpha +k)e^{-i(\alpha +k)(-b)}=C(\beta -ik)e^{(\beta -ik) (-b)}-D(\beta +ik)e^{-(\beta +ik)(-b)}$
  -Se obtiene así un sistema de cuatro ecuaciones lineales homogéneas para las cuatro incógnitas $A,B,C,D$ .
5. El anterior sistema tendrá solución distinta de la trivial sólo cuando la matriz de coeficientes tenga determinante nulo, requisito que proporciona la condición de existencia de autoestados de energía:
  $0=\left| \begin{array}{cccc} 1 & 1 & 1 & 1 \\ i(\alpha -k) & -i(\alpha +k) & (\beta -ik) & -(\beta +ik) \\ e^{i(\alpha -k)(-b)} & e^{-i(\alpha +k)(-b)} & e^{(\beta -ik) (-b)} & e^{-(\beta +ik)(-b)} \\ i(\alpha -k)e^{i(\alpha -k)(-b)} & -(\alpha +k)e^{-i(\alpha +k)(-b)} & (\beta -ik)e^{(\beta -ik) (-b)} & -(\beta +ik)e^{-(\beta +ik)(-b)}\\ \end{array} \right|$
  lo que permite derivar finalmente la ecuación de autovalores:
  $F(E)=F(\alpha,\beta)$
  $=\cos \alpha b \ \cosh \beta (l-b)-\frac{\alpha^2-\beta^2}{2 \alpha \beta} \sin \alpha b \ \sinh \beta (l-b) = \cos kl$
La resolución para $E>0$ es por completo análoga a la hecha en el caso anterior: basta considerar que ahora $\beta$ pasa a ser imaginario puro, por lo que haciendo la sustitución
$\beta=\frac{+\sqrt{-2mE}}{\hbar}=i\sigma \;,\; \sigma \in \mathbb{R}\;,\; \sigma >0$
todo el desarrollo anterior sigue siendo válido.
-En este caso, por tanto, la correspondiente ecuación para los autovalores de energía es:
$F(E)=F(\alpha,\sigma)$
$= \cos \alpha b \ \cos \sigma (l-b)-\frac{\alpha^2 + \sigma^2}{2 \alpha \sigma } \sin \alpha b \ \sin \sigma (l-b) = \cos kl$
Reuniendo resultados, para todo el rango de valores de $E$ se obtiene una ecuación implícita de la forma general $F(E)=cos kl$ , de expresión
$F(E) = \left \{ \begin{matrix} \cos \alpha b \ \cosh \beta (l-b)-\frac{\alpha^2 - \beta^2}{2 \alpha \beta } \sin \alpha b \ \sinh \beta (l-b) = \cos kl \quad \mbox{si } \quad 0 < E < V_o \\ \cos \alpha b \cos \sigma (l-b)-\frac{\alpha^2 + \sigma^2}{2 \alpha \sigma } \sin \alpha b \ \sin \sigma (l-b) = \cos kl \quad \mbox{si } \quad E>0 \end{matrix}\right.$
-Esta función $F(E)$ es continua:
$\lim_{\eta \rightarrow 0}F(E-\eta)=\lim_{\eta \rightarrow 0}F(E+\eta)\; \forall E$
-En particular, es continua en el origen:
$\lim_{E \rightarrow 0^+}F(E)=\lim_{E \rightarrow 0^-}F(E)$
Puesto que debe ser $|F(E)|=|\cos kl| \le 1$ , aparecen bandas alternas de valores de energía $E$ permitidos y prohibidos.
-Cada valor $E$ permitido, en el espectro $\sigma_C(H)$ , es doblemente degenerado, pues lleva asociadas dos autofunciones linealmente independientes: las sendas ondas de Bloch con factores $e^{ikx}$ y $e^{-ikx}$ .
-En la figura siguiente se presenta un ejemplo de resolución numérica para la función $F(E)$ :

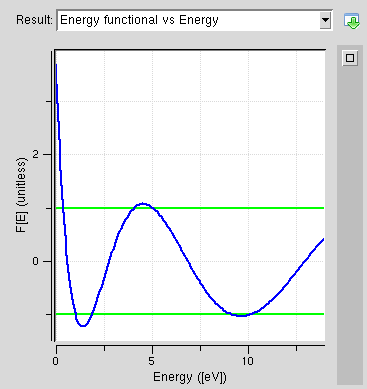
Image by Abhijeet Paul; Junzhe Geng; Gerhard Klimeck (2008), «Periodic Potential Lab,» https://nanohub.org/resources/kronig_penney. (DOI: 10.4231/D3VT1GQ74).
La siguiente figura es una captura de pantalla de una URL donde se pueden ver los resultados para el caso análogo de un potencial periódico con barreras (en la correspondiente página indicada a pie de figura se proporcionan apps para la resolución):
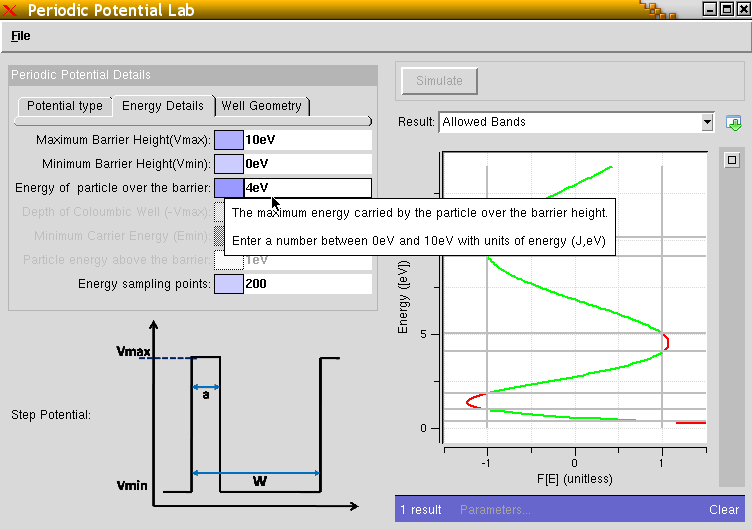
Image by Abhijeet Paul; Junzhe Geng; Gerhard Klimeck (2008), «Periodic Potential Lab,» https://nanohub.org/resources/kronig_penney. (DOI: 10.4231/D3VT1GQ74).
Si en la ecuación obtenida la anchura $b$ de la barrera se hace tender a cero y su altura $V_o$ se hace tender a $+\infty$ , manteniendo su producto $bV_o$ constante, el potencial se convierte en un tren de deltas de Dirac (comb de deltas) situadas en el punto $x = a$ y en todos los $x=nl$ , o sea, $bV_o \delta(x - b - na)$ con $n$ entero, de forma que se recuperan las anteriores ecuaciones correspondientes al tren de deltas de Dirac.
Y si, manteniendo $V_o$ y $b$ constantes, se va incrementando el período $l=a$ , es decir, los pozos se van separando entre sí manteniendo su forma constante, las bandas de energía para $0<E<V_o$ se van progresivamente estrechando, hasta que en el límite $\lim_{x\rightarrow +\infty}$ se recuperan los niveles discretos del pozo finito aislado.
-En definitiva, conforme el espaciado entre los átomos (iones) en la red aumenta, el movimiento de cada electrón en el cristal se va viendo menos afectado por la presencia de los átomos más alejados, y en el límite la solución corresponde al problema matemático para un átomo aislado.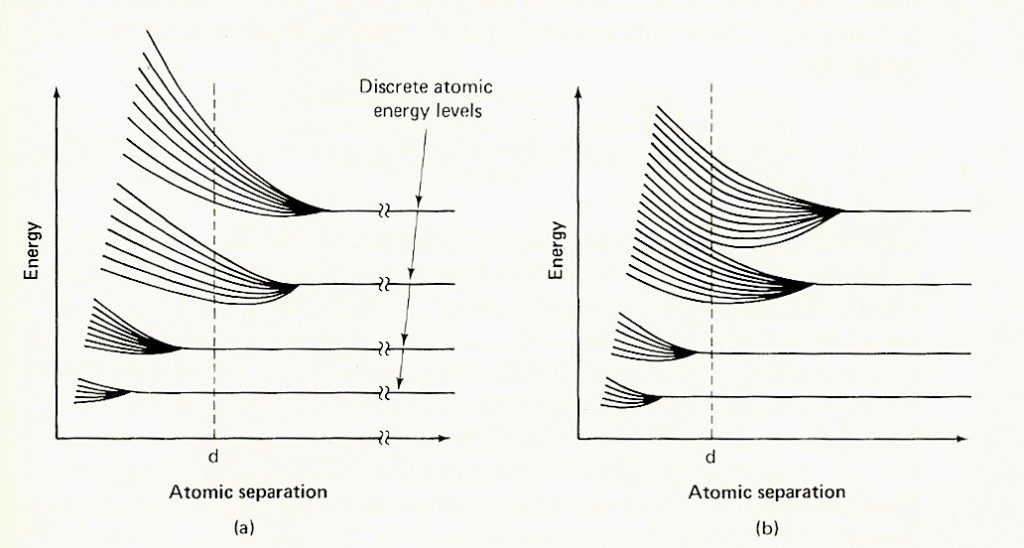

Above (Ref. 1, copyright: M.A. Green, UNSW): In the material of figure (a) we see that there is a relatively large gap between the uppermost energy bands, as opposed to (b), where at the atomic separation d the bands overlap and there is no forbidden region between the valence and conduction band (imagen y texto de http://solarwiki.ucdavis.edu/).
Efectos de frontera:
-Si se incorpora el hecho de que todo cristal tiene un tamaño finito $L$ , habría que incorporar las inherentes condiciones de frontera $\psi(x)=0$ en los extremos de la red, para establecer la imposibilidad para los electrones de escapar del cristal. La incorporación de estas condiciones complica mucho la resolución del problema, pues requiere construir paquetes de superposiciones de ondas de Bloch a fin de permitir las exigidas ondas estacionarias.
-El procedimiento al que se suele recurrir con frecuencia es imponer condiciones del tipo periódico $\psi(-\frac{L}{2})=\psi(+\frac{L}{2})$ , despreciando así los efectos de borde del cristal. Es decir, se trata el problema matemáticamente como si un electrón al salirse del material por uno de sus extremos reentrara inmediatamente por el opuesto.
-Otro procedimiento posible para incorporar condiciones periódicas es, para una hilera con $N$ átomos, cerrarla sobre sí misma, esto es, convertirla en un anillo, de forma que se impone
$\psi(x+Nl)=\psi(x) \Rightarrow e^{ikNl}=1 \Rightarrow k=\frac{2\pi n}{Nl}\;,\;n=0,\pm 1,\pm 2 \ldots$
obteniéndose entonces una discretización del espectro continuo, que contiene $N$ autovalores discretos en cada banda permitida.

Imagen de www.molpit.com.
Las siguientes figuras ilustran un material de Ge/SiGe:

Pot-period_Band-profile1_nano-cnr-it — Band profile at the L point of a [001]-Ge/SiGe quantum cascade structure under an applied electric field of 7kV/cm. The squared modulus of the wavefunctions for L electrons are also reported. The band profile and the energy position of the first confined level in each barrier are also shown (imagen de http://www.nano.cnr.it/index.php?mod=men&id=230).

Pot-period_Band-profile2_nano-cnr-it — *Ge/SiGe quantum cascade structure grown by chemical vapor deposition on a SiGe buffer (imagen de http://www.nano.cnr.it/index.php?mod=men&id=230)*

Nota: La La distribución delta de Dirac

En el enlace Funcionales y distribuciones se encuentra una introducción a las funciones generalizadas y distribuciones, incluyendo una lista de propiedades básicas de la delta de Dirac.

Referencias

[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.

[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.

[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.

[GRI-06] Griffiths, D. J. ; «Introduction to Quantum Mechanics», 2nd Edition; Pearson Education, 2006.

[SCH-68] Schiff,L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.

Páginas complementarias

http://www.uco.es/hbarra/index.php/fc/apuntesfc/179-fc0604

http://www.ugr.es/~bosca/WebFCenRed/indexFC_archivos/c10-s6.pdf (apuntes de E. Buendía).

http://www.sc.ehu.es/sbweb/fisica/cuantica/lineal/lineal.htm

http://www.nucleares.unam.mx/~vieyra/node39.html

http://quantummechanics.ucsd.edu/ph130a/130_notes/node156.html