SPDC: conversión paramétrica, descendente y espontánea

Producción de fotones entrelazados por SPDC

Conversión óptica descendente, paramétrica y espontánea (SPDC)

La forma más eficiente y accesible hoy en día de producir fotones entrelazados y estados monofotónicos (estados de Fock) es el mecanismo conocido como conversión óptica descendente, paramétrica y espontánea (SPDC: spontaneous optical parametric down-conversion) o fluorescencia paramétrica, un fenómeno de óptica no-lineal (el vector polarización eléctrica no depende linealmente del vector intensidad del campo eléctrico) que se ha desarrollado enormemente debido a la consecución de láseres de gran poder y en el cual, a partir de un fotón que incide sobre un cristal no lineal, se generan instantáneamente dos (casi siempre) fotones correlacionados.

-El fenómeno fue predicho teóricamente, y observado, a partir de los años sesenta:

I.W.H. Louisell, A. Yariv and A.E. Siegman; «Quantum Fluctuations and Noise in Parametric Processes»; Phys. Rev. 124 (1961) 1646,

S. E. Harris, M. K. Oshman and R. L. Byer; «Observation of Tunable Optical Parametric Fluorescence»; Phys. Rev. Lett. 18 (1967) 732

-La primera observación de la simultaneidad en la emisión del par correlacionado es de 1970:

D.C. Burnham and D.L. Weinberg; Observation of simultaneity in parametric production of optical photons pairs; Phys. Rev. Lett. 25, 84 (1970).

-La denominación «paramétrica» refiere a que el estado del cristal permanece inalterado durante el proceso, derivándose en consecuencia la estricta conservación de energía y momento entre los fotones involucrados, ya que existe una relación de fase entre los campos incidente y saliente. Por tanto, es un proceso «a la baja» o «descendente», en el sentido de que se producen fotones con menor energía que el incidente.

-Un ejemplo de cristal no lineal muy usado en las nuevas tecnologías cuánticas es el «beta-borato de bario», BBO, que presenta alta birrefringencia, o capacidad de desdoblar un haz de luz incidente en dos rayos polarizados ortogonalmente entre sí (véase nota al final de esta entrada). Otros cristales birrefringentes son la calcita o espato de Islandia (carbonato cálcico, CaCO3) y el cristal de LN (niobato de litio): para todos ellos su índice de refracción cambia con el plano de polarización de la luz que lo atraviesa.

-El proceso SPDC es espontáneo, y se considera estimulado por las fluctuaciones cuánticas aleatorias del vacío, de manera que el par de fotones entrelazados se crea sólo en algunas ocasiones, al azar, y con una eficiencia de conversión generalmente muy baja: la ratio de pares producidos por fotón incidente que se observa suele ser del orden de $10^{-10}$ , de modo que la mayoría de los fotones del haz de bombeo atravesarán el cristal sin que se presente el efecto.

-Su uso es hoy muy frecuente en muchos ámbitos, habiendo sustituido a otros mecanismos de producción de pares de fotones entrelazados empleados anteriormente, como el efecto de cascada atómica en el Ca que se aplicó en los experimentos de Aspect sobre la desigualdad de Bell.

Sabemos que el índice de refracción de un cristal birrefrigente cambia con la frecuencia y polarización de la radiación incidente que lo atraviesa, por lo que el requisito de satisfacer la conservación de energía y momento en el proceso de emisión de un par de fotones, a partir del bombardeo del cristal con radiación, seleccionará ciertos tripletes de frecuencias. El siguiente texto, extraído de la publicación indicada a continuación, en la que se presenta el diseño e implementación de un método óptico para la medición directa de la distribución angular de fotones producto de un proceso SPDC, resume las bases de este fenómeno; las figuras intercaladas no corresponden al texto, sino que están extraídas según se indica en cada una:

E. A. Martínez, L. Rebón, A. E. Luna, S. A. Ledesma, Métodos simples de caracterización de cristales no lineales para Conversión Paramétrica Espontánea Descendente, ANALES AFA 22, 1 (2011) 56-62:

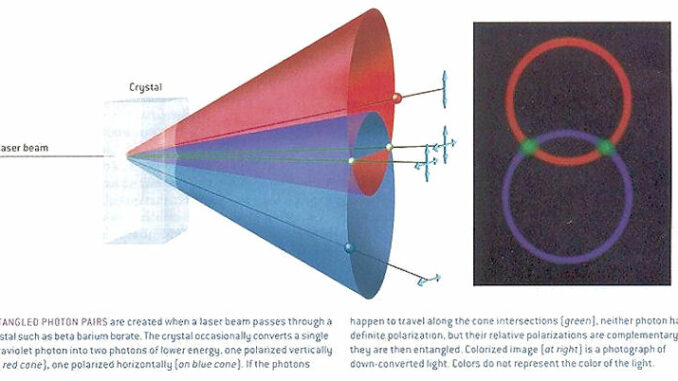
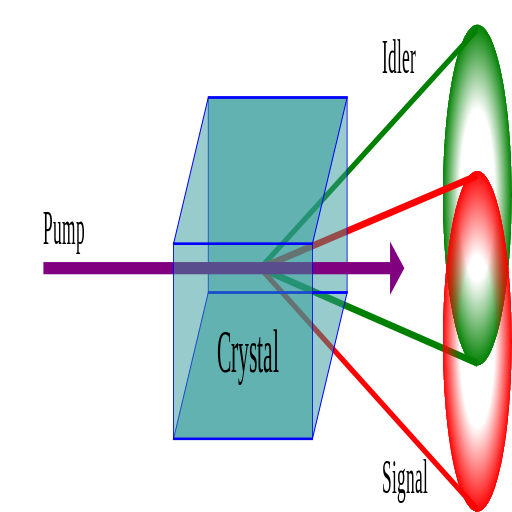
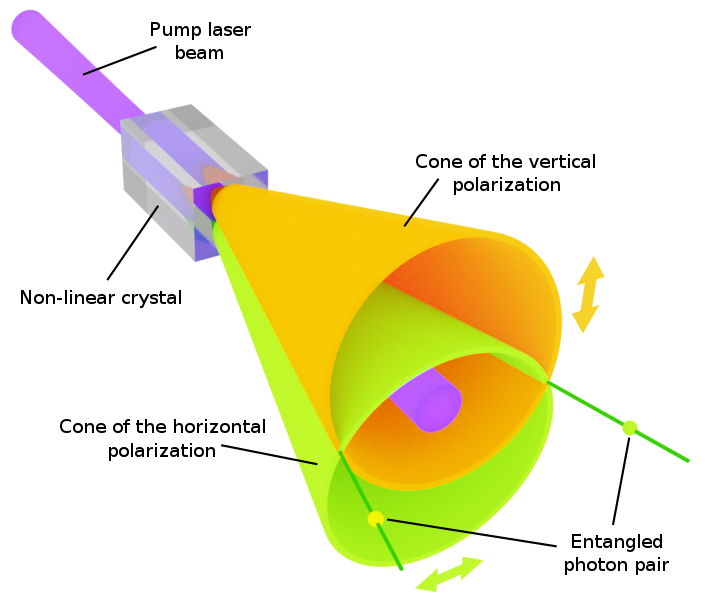
El fenómeno tiene lugar cuando una onda monocromática de gran intensidad atraviesa el adecuado medio no lineal, generalmente un cristal. Para ello se incide sobre el cristal con un láser de bombeo y se obtienen a la salida pares de fotones de menor energía, que dependiendo del corte del cristal, forman dos conos coaxiales, en el caso de cristales de tipo I, o dos conos desplazados, para cristales de tipo II. El ángulo de salida de estos pares de fotones, para cada longitud de onda, depende del ángulo de incidencia del haz de bombeo, respecto de la dirección del eje óptico del cristal. Conocer esta dependencia es crucial para ubicar correctamente los detectores de fotones necesarios en cualquier experimento.

El proceso de Conversión Paramétrica Espontánea Descendente (SPDC por sus siglas en inglés, Spontaneous Parametric Down Conversion) en un medio no lineal, es uno de los más utilizados en la construcción de fuentes de pares de fotones entrelazados. Con ellos se pueden realizar numerosos experimentos que permiten testear aspectos fundamentales de la mecánica cuántica, como la no localidad y la no separabilidad. Por otra parte, es de sumo interés la capacidad de generar y manipular este tipo de estados cuánticos, que son la base para los procesos de información cuántica, tales como comunicación cuántica, teleportación, criptografía cuántica y computación cuántica.

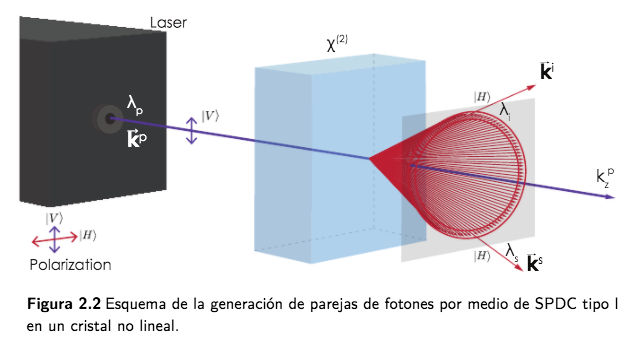
Durante el proceso de SPDC, un fotón proveniente del haz de bombeo de frecuencia angular $\omega_p$ (fotón pump) que incide sobre un cristal no lineal, tiene una cierta probabilidad de generar dos fotones de más baja frecuencia, $\omega_s$ y $\omega_i$ (habitualmente llamados signal y idler), como se esquematiza:

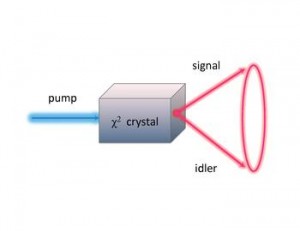
Fotones incidente (pump) y convertidos (signal e idler) en un cristal tipo I (imagen de la Wikipedia). — Fotones incidente (pump) y convertidos (signal e idler («señal» y «acompañante») en un cristal **tipo I**. En este caso, todos los fotones producidos delimitan una superficie cónica. Se producen a pares correlacionados en frecuencia (energía) y espacialmente (momento angular orbital), sobre sendas generatrices opuestas del cono y ambos con polarización **ortogonal a la del fotón de bombeo** (imagen de la Wikipedia; autor: Denysbondar; Creative Commons Attribution-Share Alike 3.0 Unported license).

SPDC tipo II — Fotones incidente (pump) y convertidos (signal e idler: «señal» y «acompañante») en un cristal **tipo II**. En este caso, todos los fotones se producen a pares correlacionados en frecuencia (energía) y espacialmente (momento angular orbital), sobre sendas superficies cónicas que comparten vértice; para cada par, sus sendas polarizaciones son **una paralela a la del fotón de bombeo y otra ortogonal** (imagen de la Wikipedia; autor: Cholloway; CC BY-SA 3.0, vía Wikimedia Commons).

La conservación de la energía y el impulso requiere que

$\omega_p=\omega_s + \omega_i$

$\vec{k}_p=\vec{k}_s + \vec{k}_i$

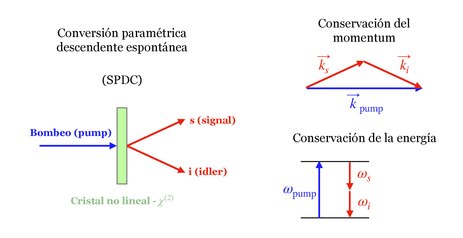
Phase-matching en SPDC — Condiciones de ajuste de fase en SPDC; las leyes de conservación se asumen con respecto a la energía y el momento dentro del cristal (imagen y texto de la Wikipedia; autor: Juanra31a; licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional).

y por lo tanto, para una dada frecuencia y dirección de incidencia del bombeo, cada fotón producto de la conversión se encuentra correlacionado tanto en frecuencia como espacialmente respecto de su par. Estas ecuaciones se conocen como condiciones de phase-matching, y para un cristal birrefringente, sólo existen dos formas de satisfacerlas:

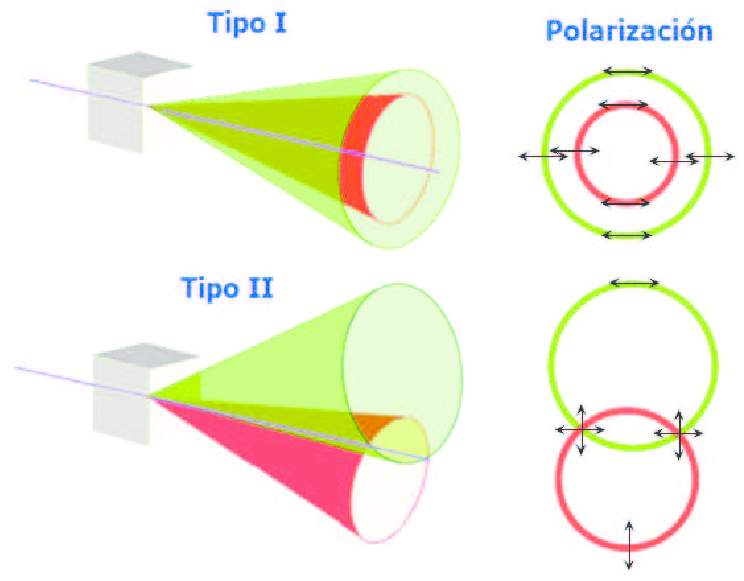
(i) los fotones convertidos tienen polarizaciones paralelas entre sí y ortogonales al bombeo (phase-matching tipo I); en este caso todos los fotones de una misma longitud de onda son emitidos formando un cono coaxial con la dirección de propagación del haz de bombeo;

SPDC tipo I; imagen por Axel Heuer, Universidad de Potsdam; en «Complementarity in single photon interference – the role of mode functions and vacuum fields», https://www.researchgate.net/publication/287687124_Complementarity_in_single_photon_interference_-_the_role_of_mode_functions_and_vacuum_fields.

(ii) uno de los fotones, signal o idler, tiene la misma polarización que el bombeo, y ortogonal a la de su compañero (phase-matching tipo II); en este caso hay dos conos (no coaxiales) por cada longitud de onda, uno por cada polarización.

https://commons.wikimedia.org/wiki/File:Spdc_II_3D_model_EN.svg — Se producen fotones a pares correlacionados en frecuencia (energía) y espacialmente (momento angular orbital), sobre sendas generatrices en cada uno de los dos conos (imagen de la Wikipedia: https://commons.wikimedia.org/wiki/File:Spdc_II_3D_model_EN.sv).

Una de las mayores dificultades en toda experiencia que emplee fotones de SPDC está en seleccionar pares de fotones convertidos y poder distinguir esta señal del ruido de fondo, debido a las coincidencias accidentales. Dado que la eficiencia de conversión en este proceso es muy baja, típicamente del orden de $10^{-10}$ a las frecuencias de interés, es fundamental para el éxito del experimento prealinear los detectores y los componentes ópticos como lentes y diafragmas. El primer paso entonces es conocer con precisión la dirección de salida de cada fotón del par, en función de su longitud de onda, y de la longitud de onda y del ángulo de incidencia del bombeo. Existen programas de acceso libre que permiten calcular numéricamente estos parámetros, para distintos tipos de cristales y distintas condiciones de phase-matching. En todos los casos, se necesita conocer la dirección del eje óptico del cristal y el espesor del mismo.

Las siguientes figuras ilustran con más detalle los dos tipos de proceso SPDC:

Condiciones de ajuste de fase (phase-matching) en SPDC — **Condiciones de ajuste de fase** (phase-matching) en SPDC; imagen de: «Discriminación de estados cuánticos no ortogonales», Thesis de máster de X.J. Sánchez Lozano, Univ. Iberoamericana de León.

**SPDC tipo I:** en este tipo los pares de fotones correlacionados **no constituyen un estado entrelazado en polarización**. Imagen de: D.G. Gutiérrez López; «Estudio experimental del control de parejas de fotones generadas por un haz Bessel Gauss de orden cero».

SPDC tipo II (imagen de la Wikipedia) — **SPDC tipo II**: en este caso, de todos los pares de fotones correlacionados producidos, **sólo el par que comparten conos constituye un par entrelazado en polarización.**

https://iopscience.iop.org/article/10.1088/2058-7058/15/11/38: Physics World 15,11 (2002) 37.

–Nota: existe un tercer tipo de mecanismo SPDC, el tipo-0, en el que los fotones signal e idler tienen la misma polarización, coincidente también con la del fotón incidente.

Procesos SPDC como fuente de preparación de fotones entrelazados en polarización

Con los procesos SPDC es posible preparar los estados de la base de Bell para dos fotones, entrelazados en polarización, como se describe en las siguientes figuras para cada tipo de proceso. Una detallada referencia al respecto es la siguiente:

Tesis doctoral de J. Catalano, Universidad de Portland, 2014: Spontaneous Parametric Down-Conversion and Quantum Entanglement; especialmente ver figuras en pp. 15-16 (se reproducen a continuación).

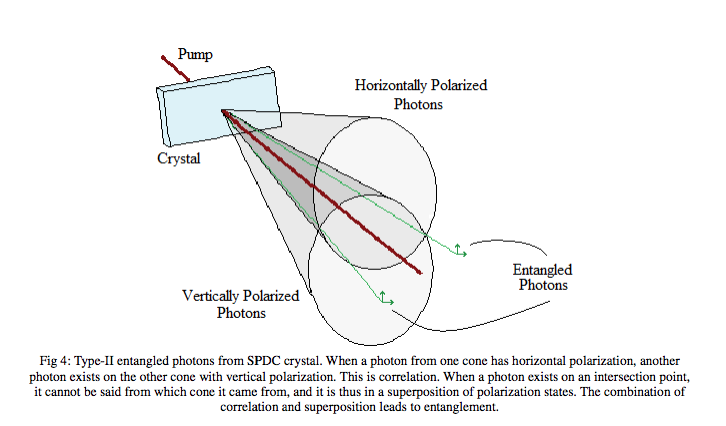
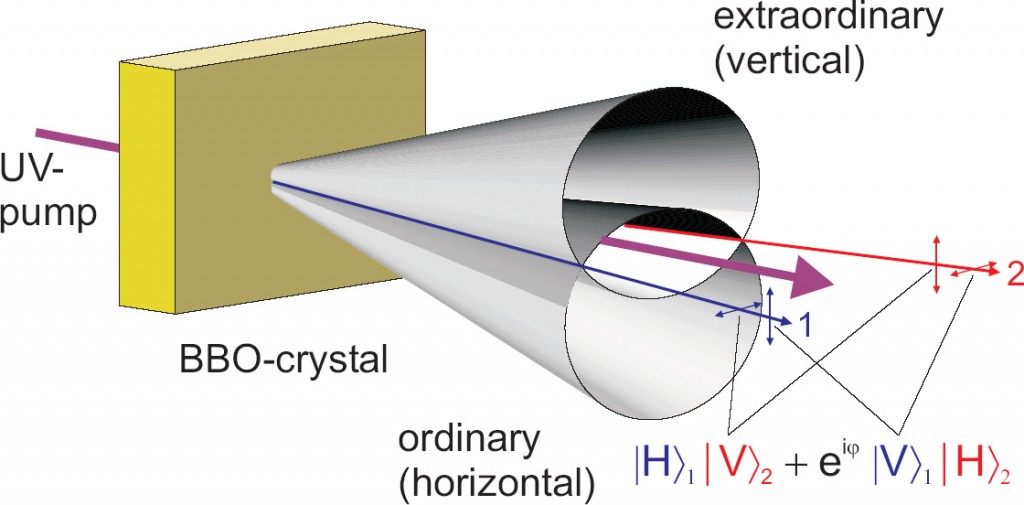
Proceso SPDC tipo II:

Figura de: Jesse L. Catalano, University Honor Thesis, Univ. de Portland: "Spontaneous Parametric Down-Conversion and Quantum Entanglement". — Figura de: Jesse L. Catalano, University Honor Thesis, Univ. de Portland: «Spontaneous Parametric Down-Conversion and Quantum Entanglement».

"Schematic — –**SPDC tipo II**: el par de fotones que comparten conos constituyen un par entrelazado en polarización; ajustando fases, se producen los estados entrelazados de Bell $|\Psi^{\pm}>$ (anticorrelacionados en polarización). Figura de: Jesse L. Catalano, University Honor Thesis, Univ. de Portland: «Spontaneous Parametric Down-Conversion and Quantum Entanglement».

–**SPDC tipo II**: el par de fotones que comparten conos constituyen un par entrelazado en polarización; ajustando fases, se producen los estados entrelazados de Bell $|\Psi^{\pm}>$ (anticorrelacionados en polarización). Figura de: Jesse L. Catalano, University Honor Thesis, Univ. de Portland: «Spontaneous Parametric Down-Conversion and Quantum Entanglement».

Para imágenes de fotones entrelazados producidos a partir de SPDC tipo-II, véase:

M. Reck: Imagen de dos fotones entrelazados; http://home.ustc.edu.cn/~gongsiqiu/_book/2-Single-photon%20sources/New%20High-Intensity%20Source%20of%20Polarization-Entangled%20Photon%20Pairs.html

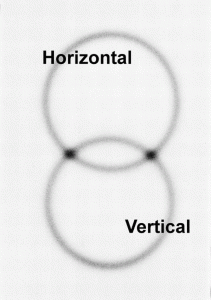
Photograph taken perpendicular to the propagation direction. Photons are produced in pairs. A photon on the top circle is horizontally polarized while its exactly opposite partner in the bottom circle is vertically polarized. At the intersection points their polarizations are undefined; all that is known is that they have to be different, which results in entanglement (imagen by M. Reck; véase también en IOP; texto de Nature en red). — **SPDC** **tipo II:** Imagen tomada en el plano perpendicular a la dirección de propagación; se producen fotones a pares y los puntos de intersección señalados representan fotones de polarización superpuesta y anticorrelacionada: dos fotones entrelazados en polarización; imagen de M. Reck.

Véase también en IOP: https://iopscience.iop.org/article/10.1088/2058-7058/15/11/38

https://www.researchgate.net/figure/A-photograph-of-the-down-conversion-photons-taken-with-different-interference-filters_fig3_317630056 :

Proceso SPDC tipo I:

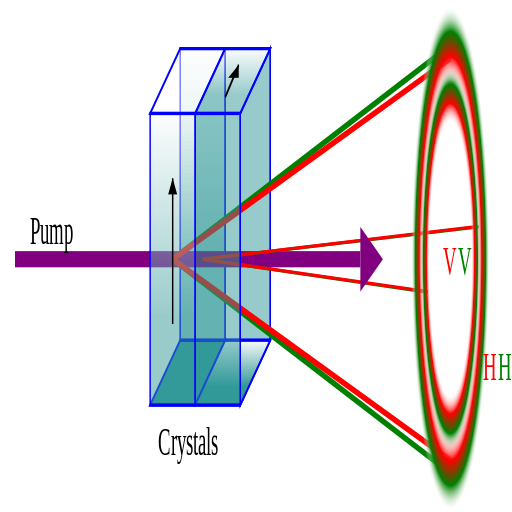
Phase-matching tipo I: a sandwich source of entangled photons, created by stacking two nonlinear crystals with type-I spontaneous parametric down-conversion at 90 degrees to each other (imagen y texto de la Wikipedia). — Posibles dos situaciones de ajuste de fase en un proceso **SPDC tipo I** configurado para generar fotones entrelazados en polarización: el uso de dos cristales empaquetados con los sendos ejes ópticos orientados perpendicularmente entre sí constituye una situación en la que **es imposible distinguir de cuál cristal procede el par fotónico en cada evento SPDC**. De esta forma, la combinación de correlación con superposición permite generar un par fotónico (¡un solo par en cada evento!; la figura muestra dos a la vez y puede inducir a confusión) en los estados entrelazados de Bell $|\Phi^{\pm}>$ (correlacionados en polarización).

Posibles dos situaciones de ajuste de fase en un proceso **SPDC tipo I** configurado para generar fotones entrelazados en polarización: el uso de dos cristales empaquetados con los sendos ejes ópticos orientados perpendicularmente entre sí constituye una situación en la que **es imposible distinguir de cuál cristal procede el par fotónico en cada evento SPDC**. De esta forma, la combinación de correlación con superposición permite generar un par fotónico (¡un solo par en cada evento!; la figura muestra dos a la vez y puede inducir a confusión) en los estados entrelazados de Bell $|\Phi^{\pm}>$ (correlacionados en polarización).

Tipos I y II de SPDC — Producción de fotones entrelazados con Tipos I y II mediante SPDC. Figura de: Li Yuan, Ding Fei, Schmidt Oliver, «Entangled-photons generation with quantum dots», Chinese Physics B, 27(2), 2018, 020307, http://cpb.iphy.ac.cn/article/2018/1924/cpb_27_2_020307.html

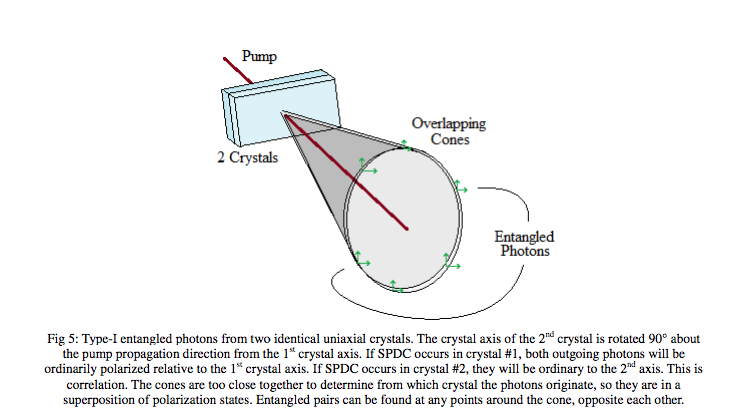
Es importante que se garantice la indistinguibilidad entre los sendos pares de fotones correspondientes a cada cristal: es decir, que, para cada evento SPDC-I, para cada par de fotones correlacionados producidos, se tenga 50% de probabilidad de corresponder a uno u otro cristal. De esa forma, se genera un estado entrelazado en polarización de expresión general:

$| \Psi(A,B)>=\frac{1}{\sqrt{2}}( | H_A H_B > +e^{i\varphi} | V_A V_B > )\ne |\psi(A)> \otimes \; | \psi(B)>$

-Este método, que requiere que los cristales sean lo suficientemente delgados como para que se conserve la indistinguibilidad (sea imposible conocer en qué cristal ha tenido lugar la emisión del par), fue propuesto en 1999:

P. G. Kwiat, E. Waks, A. G. White, I. Appelbaum, and P. H. Eberhard; Phys. Rev. A 60 (1999) R773.

[In SPDC type-II ]…the source brightness is still very limited because the photons are polarization entangled only along two special directions […] Using a two-crystal geometry, we have constructed a source in which all pairs of a given color are entangled, and we expect that this should extend to most, if not all, of the spectral down-conversion output, i.e., to cones corresponding to different colors. […]A 45°- polarized pump photon will be equally likely to downconvert in either crystal ~neglecting losses from passing through the first!, and these two possible down-conversion processes are coherent with one another, as long as the emitted spatial modes for a given pair of photons are indistinguishable for the two crystals.

-Otro método es recurrir a la postselección (rotar la polarización de uno de los dos fotones producidos en SPDC I, o II, y luego recombinarlos en un divisor de haz); en las siguientes referencias se usan fotones entrelazados así producidos para nuevas formas de obtener violaciones de las desigualdades de Bell:

Y.H. Shih and C.O. Alley; Phys. Rev. Lett. 61 (1988) 2921; Z.Y. Ou and L. Mandel; Phys. Rev. Lett. 61 (1988) 50.

-Puede consultarse también la tesis de Licenciatura de :

Martin Schäffer, Bachelor Thesis, Univ. de Múnich: Two-Photon Polarization Entanglement in Type I SPDC Experiment

SPDC y estados mecano-cuánticos de Bell

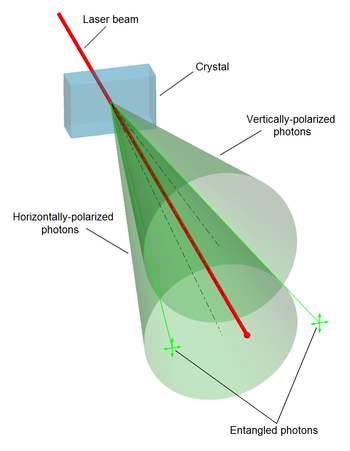
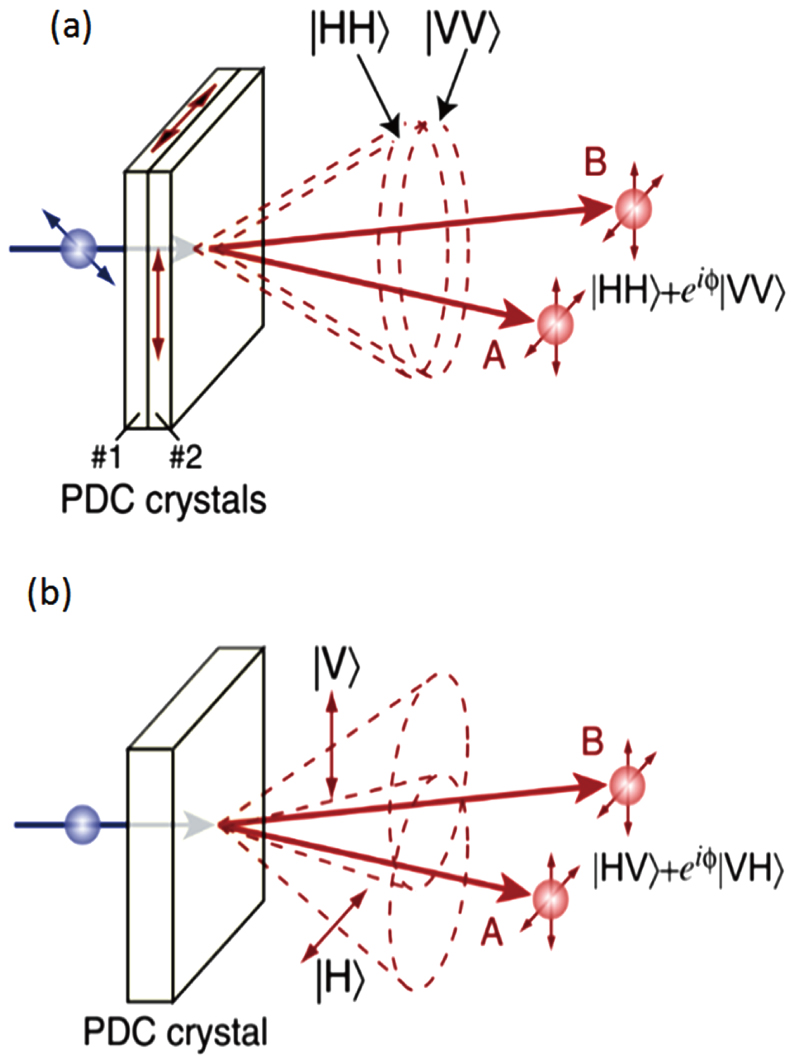
En un proceso de SPDC con type II de ajuste de fases (phase-matching II) los dos fotones entrelazados emergen sobre la superficie de dos conos coaxiales y con polarizaciones opuestas, de forma que el par de fotones correspondientes a los puntos de intersección de las dos superficies salen entrelazados, ya que pueden presentar cualquiera de las dos polarizaciones (horizontal H o vertical V) con igual probabilidad.

-Es decir, el estado correspondiente a este par entrelazado tiene la expresión:

$| \Psi(A,B)>=\frac{1}{\sqrt{2}}( | H_A V_B > +e^{i\varphi} | V_A H_B > )\ne |\psi(A)> \otimes \; | \psi(B)>$

donde $\varphi$ es una fase óptica que puede después ajustarse a conveniencia usando los dispositivos adecuados (desplazadores de fase). Fijándola a los valores $0$ y $\pi$ se consigue que el par entrelazado producido se corresponda con uno de los estados de la denominada base de Bell.

Análogamente, a aprtir de procesos SPDC tipo-I se pueden generar otros dos estados de Bell, a partir del estado entrelazado generado, de expresión

$| \Psi(A,B)>=\frac{1}{\sqrt{2}}( | H_A H_B > +e^{i\varphi} | V_A V_B > )\ne |\psi(A)> \otimes \; | \psi(B)>$ .

Fijando en las anteriores expresiones los valores de $\varphi$ como $0$ o $\pi$ se consigue que el par entrelazado en polarización producido se corresponda con uno de los estados de la denominada base de Bell, integrada por los cuatro vectores base conocidos como los 4 estados de Bell (que son mutuamente ortogonales):

Los 4 estados de Bell:

$| \Psi^{\pm};A,B)>=\frac{1}{\sqrt{2}}( | H_A V_B > \pm | V_A H_B > )\ne |\psi(A)> \otimes \; | \psi(B)>$

$| \Phi^{\pm};A,B)>=\frac{1}{\sqrt{2}}( | H_A H_B > \pm | V_A V_B > )\ne |\phi(A)> \otimes \; | \phi(B)>$

Otras referencias sobre SPDC y fotones entrelazados

SPDC-I aplicada a la creación de pares de fotones entrelazados en momento angular orbital (OAM):

Characterisation of a spontaneous parametric down-conversion source for spatially-entangled photon pairs

La investigación en nuevos métodos de producción de pares entrelazados sigue avanzando:

Scientists in the UK have been able to generate pairs of entangled photons from a nanoscale crystal of semiconductor known as a «quantum dot» far more efficiently than was possible before.

SPDC y entrelazamiento en posición (noticia de 2017):

Estados entrelazados por SPDC procedentes de diferentes posiciones:

Kayn A. Forbes, Jack S. Ford, and David L. Andrews, Journal Physical Review Letters, «Nonlocalized generation of correlated photon pairs in degenerate down-conversion«, PRL 118, 133602 (2017):

The achievement of optimum conversion efficiency in conventional spontaneous parametric down- conversion requires consideration of quantum processes that entail multisite electrodynamic coupling, actively taking place within the conversion material. The physical mechanism, which operates through virtual photon propagation, provides for photon pairs to be emitted from spatially separated sites of photon interaction; occasionally pairs are produced in which each photon emerges from a different point in space. The extent of such nonlocalized generation is influenced by individual variations in both distance and phase correlation. Mathematical analysis of the global contributions from this mechanism provides a quantitative measure for a degree of positional uncertainty in the origin of down-converted emission.

Aplicaciones de los fotones entrelazados:

A. Zeilinger, «Light for the quantum. Entangled photons and their applications: A very personal perspective», Physica Scripta 92,7 (2017) 072501, DOI: 10.1088/1402-4896/aa736d.

2019: «Retrato» de dos fotones entrelazados:

«Fotografía» de dos fotones entrelazados

Observando la violación del realismo local con fotones entrelazados: Paul-A. Moreau, E. Toninelli, T. Gregory, R.S. Aspden, P.A. Morris and M.J. Padgett, Science Advances 5,7(2019), DOI: 10.1126/sciadv.aaw2563.

Nota: Sobre la birrefrigencia

Una forma de obtener luz polarizada linealmente es hacer uso de los cristales birrefringentes, como la calcita o espato de Islandia (carbonato cálcico, CaCO3), que tienen la propiedad de desdoblar la luz incidente, en general, en dos rayos linealmente polarizados de manera perpendicular entre sí, como si el material tuviera dos índices de refracción distintos.

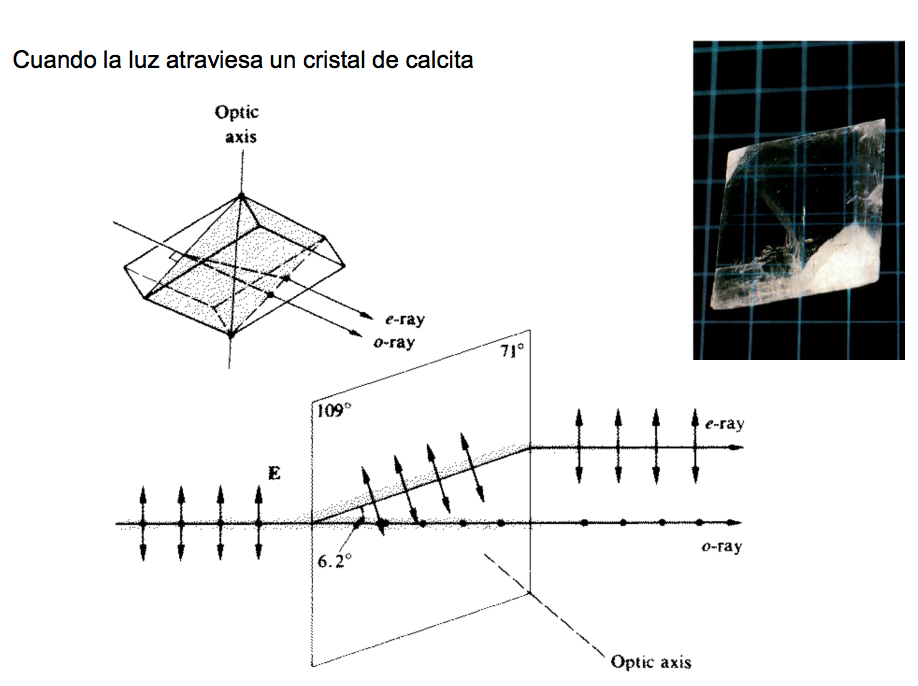
-La birrefringencia, o doble refracción, se produce porque el correspondiente material, debido a su estructura atómica, es anisótropo, esto es, la velocidad de la luz no es la misma en todas las direcciones. En consecuencia, un rayo de luz incidente puede separarse en dos rayos, denominados con frecuencia como «rayo ordinario» y «rayo extraordinario», que resultan con sendas polarizaciones perpendiculares entre sí.

-Existe una dirección particular en un material birrefringente en que ambos rayos se propagan con la misma velocidad, la cual define el eje óptico del cristal; si la incidencia es según esa dirección, no se observa desdoblamiento. Pero cuando la luz incide según una dirección diferente a la que marca ese eje, se producen dos rayos que emergen según diferentes direcciones, determinadas por la del eje óptico; si entonces se hace girar el cristal, el rayo extraordinario gira en el espacio en torno al ordinario.

Calcita, espato de Islandia, "ala de ángel": un mineral birrefringente. — Calcita, espato de Islandia, «ala de ángel»: un mineral birrefringente.

–La calcita posee una birrefringencia acusada, fácil de constatar al advertir que a su través se forman dos imágenes distintas de cualquier punto situado detrás. Al incidir luz según una dirección distinta a la del eje óptico, la luz se descompone en dos haces, polarizados siempre de forma perpendicular entre sí y según sendas direcciones determinadas por la dirección del eje óptico del cristal. El rayo que apenas se desvía es el denominado como rayo ordinario, que es transmitido con polarización perpendicular al plano del cristal que contiene al eje óptico y a la dirección de incidencia; el rayo muy desviado, o rayo extraordinario, resulta con polarización ortogonal al ordinario y paralela a dirección del eje óptico. La acción de este tipo de cristales se ilustra en las figuras siguientes; para que se dé este efecto, el eje óptico del cristal no debe estar contenido en la cara tallada del cristal sobre la que se produce la incidencia, ni ser perpendicular a ella. Una ventaja adicional frecuente en ellos es que la absorción de la radiación que los atraviesa suele ser mínima.

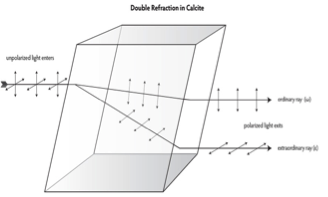
Doble refracción en la calcita; imagen de: http://materias.df.uba.ar/f2bygaa2016c1/files/2012/07/RESUMEN_POLARIZACION2.pdf

Serie anterior de figuras:

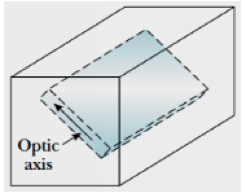
-Arriba: desdoblamiento de la luz despolarizada al atravesar un cristal de calcita. Cuando la dirección de incidencia no es según el eje óptico, la luz se descompone en dos haces polarizados siempre de forma ortogonal entre sí y según sendas direcciones determinadas por la dirección del eje óptico del cristal. En las figuras, el rayo indicado como ordinario es el que no se desvía en incidencia específica (la primera figura) y es transmitido con polarización horizontal, esto es, perpendicular al plano del cristal que contiene el eje óptico y la dirección de incidencia; el rayo desviado se denomina como extraordinario y resulta con polarización vertical, perpendicular a la del rayo ordinario.

-Abajo: imagen doble de un lápiz a través de un cristal de calcita y dirección del eje óptico en el cristal.

Curiosidad: Los vikingos y la calcita, noticia en ABC:
El misterioso artefacto con el que los vikingos navegaron el Atlántico Norte.

Un divisor de haz o espejo semirreflector (sigla en inglés BS, beam-splitter) es un dispositivo en el que un haz de luz incidente es en parte reflejado y en parte transmitido, usualmente al 50%, en un BS entonces denominado como de tipo 50:50, según se muestra en la figura siguiente:

-Hay diversas maneras de implementar este dispositivo; por ejemplo, es muy frecuente hacer uso de un cubo compuesto por dos prismas de vidrio triangulares que están pegados por la base. En particular, en la figura siguiente se muestra un prisma de Wollaston, que constituye un divisor de haz y un polarizador a la vez: consta de dos prismas triangulares rectos de calcita unidos por la hipotenusa y con sus ejes ópticos perpendiculares, de forma que la luz se divide en dos rayos con sendas polarizaciones ortogonales que divergen al salir:

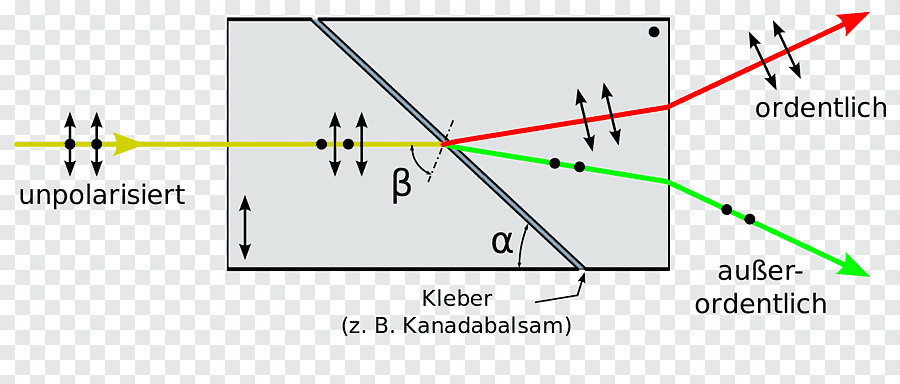
Prisma Wollaston, birrefringencia (imagen de : https://www.pngegg.com/es/png-wjdzf).

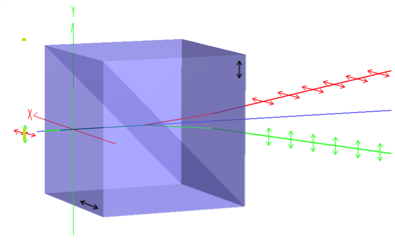
En el caso de que se hagan incidir pulsos de luz monofotónica, esto es, fotones de uno en uno, no hay manera de conocer de antemano cuál de las dos posibilidades, reflexión o transmisión, va a ser observada para cada fotón individual, y lo mismo para un divisor polarizador, siempre que la luz incidente no hubiese sido ya polarizada en uno de los dos posibles estados de salida. Es decir, centrándonos en un divisor de haz de tipo 50:50 genérico, si no añadimos detectores de radiación a ambos lados del dispositivo la función de onda del sistema es una superposición de dos posibilidades, sendos sumandos que describen uno el fotón transmitiéndose y otro el fotón reflejándose.

Bibliografía

-David C. Burnham and Donald L. Weinberg. Observation of simultaneity in parametric production of optical photon pairs. Physical Review Letters, 25(2):84–87, julio 1970.

-Una presentación sobre SPDC: Gallivan, S. and Olivier, K., Spontaneous Parametric Down Conversion, University of Oregon,[http://hank.uoregon.edu/experiments/spdc/SPDC%20final%20presentation.pdf , accesible en 2017, parece que retirado]; ahora disponible en: https://pdxscholar.library.pdx.edu/cgi/viewcontent.cgi?article=1588&context=honorstheses

– Métodos simples de caracterización de cristales no lineales para Conversión Paramétrica Espontánea Descendente, ANALES AFA 22, 56-62 (2010) Malargüe, 56.

-Universidad de Leiden: Characterisation of SPDC (type I).

-Dalia Gutiérrez López, Dalia; Estudio experimental de control de parejas de fotones generadas por un haz Bessel Gauss de orden cero , PY – 2019/11/20; DO 10.13140/RG.2.2.20711.60324.

-Tesis doctoral de J. Catalano, Universidad de Portland, 2014 (DOI: 10.15760/honors.474): Spontaneous Parametric Down-Conversion and Quantum Entanglement

-Martin Schäffer, Bachelor Thesis, Univ. de Múnich: Two-Photon Polarization Entanglement in Typ I SPDC Experiment

–SPDC systems in Quantum Information.

-Aplicaciones para la producción de fotones individuales de alta fidelidad para su uso en redes de fibra óptica: SPIE newsroom

-Lin Yin, Jianjun Li, Wenchao Zhai, Maopeng Xia, Youbo Hu and Xiaobing Zheng; Analysis of the Spatial Properties of Correlated Photon in Collinear Phase-Matching.

-C. Couteau, «Spontaneous parametric down-conversion», en ArXiv: https://arxiv.org/pdf/1809.00127.pdf.

-K. Edamatsu, «Entangled Photons: Generation, Observation, and Characterization»; Japanese Journal of Applied Physics, Volume 46, 11R (2007) 7175; DOI 10.1143/JJAP.46.7175.

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

SPDC: conversión paramétrica, descendente y espontánea

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta