Divisores de haz e interferómetros

Divisores de haz no absorbentes

Fuentes: esta entrada se basa principalmente en:

-cap. 6, Introductory Quantum Optics, de Gerry y Knight ([GER-05]).

-cap. 8, Quantum Optics, de Chiao y Garrison ([GAR-08]).

Un divisor de haz puede obtenerse superponiendo capas sucesivas de material dieléctrico, escogiéndose los índices de refracción de cada capa según los parámetros de reflexión y transmisión del haz incidente que se quieran obtener. Con un diseño cuidadoso, estos coeficientes pueden igualarse para las dos caras del divisor, que se caracteriza entonces como divisor de haz simétrico.

De la Wikipedia: Por ejemplo, una forma común de divisor de haz es la de un cubo compuesto por dos prismas de vidrio triangulares que están pegados por la base usando bálsamo de Canadá. El grosor de la capa de resina es ajustado para que —a una cierta longitud de onda— la mitad de la luz incidente en una «puerta» (es decir, una cara del cubo) sea reflejada y la otra mitad sea transmitida. Los beam splitter polarizadores, tales como el prisma de Wollaston, usan materiales birrefringentes, dividiendo la luz en rayos de diferente polarización.
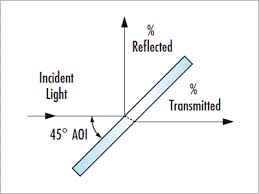
Otro diseño es mediante el uso de espejos semitransparentes. Consiste en una lámina de vidrio con un delgado revestimiento de aluminio (normalmente depositado mediante vapor de aluminio) con un grosor tal que, para un rayo de luz que incida con un ángulo de 45 º, la mitad es transmitida y la otra mitad es reflejada. En lugar de un revestimiento metálico, también puede usarse un revestimiento óptico dieléctrico.

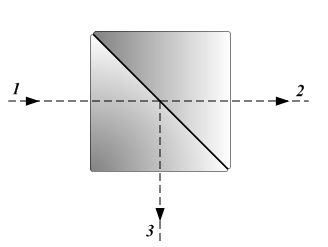
-En un divisor de haz (en inglés, «beam-splitter», BS), la radiación incidente es parcialmente reflejada y parcialmente transmitida; si el material es (supuesto ideal) no absorbente, los correspondientes porcentajes de intensidad suman a 100: un dispositivo óptico denominado en inglés como «lossless beam splitter»:

Descripción teórica

Sea un haz clásico de radiación, de amplitud compleja $E_i$ , que incide sobre un divisor de haz no absorbente, y sean $E_r=rE_i$ y $E_t=tE_i$ las amplitudes reflejada y transmitida, cumpliendo

$|E_i|^2=|E_r|^2+|E_t|^2 \quad \Leftrightarrow \quad 1=r^2 + t^2$ ,

ya que no hay absorción de intensidad.

-Si a partir de esta descripción clásica tratamos de introducir sin más la cuantización del campo, introduciríamos unos operadores escalón $\hat{a}_i$ asociados a los tres canales $(i,r,t)$ involucrados en la imagen clásica expuesta, definidos satisfaciendo:

$\hat{a}_r=r\hat{a}_i \quad , \quad \hat{a}_t=t\hat{a}_i$

$\rightarrow$ Pero el resultado es erróneo: no se alcanza una descripción cuántica satisfactoria (en particular, los operadores de campo no satisfacen la conmutación requerida: por ejemplo, resulta $[ \hat{a}_r, \hat{a}^{\dagger}_t] \ne 0$ ).

-El porqué es evidente si uno recuerda, por ejemplo, el simple estudio mecano-cuántico de una barrera de potencial monodimensional: la resolución de la correspondiente ecuación de Schrödinger independiente del tiempo, o problema de autovalores de energía, proporciona dos soluciones linealmente independientes, que pueden elegirse en particular de forma que se asocien a las denominadas «onda incidente desde la izquierda» y «onda incidente desde la derecha».

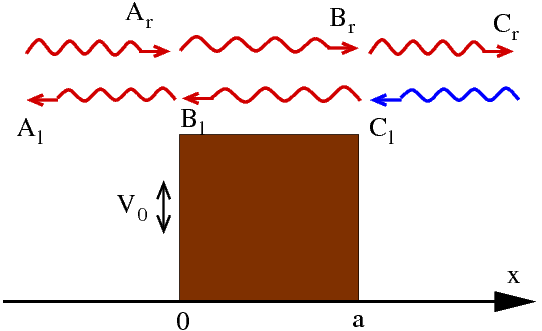
Barrera de potencial (imagen de la Wikipedia).

-Se han de tener en cuenta pues las dos soluciones posibles al problema: incorporar los operadores cuánticos que permitan obtener la solución completa mecano-cuántica.

-Visualmente, se ha de sustituir, en definitiva, la imagen clásica inicial de entrada a través de un solo canal por una más fiel a la situación matemática cuántica, que añade un segundo canal o modo de radiación en la entrada:

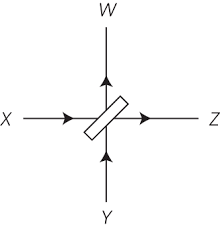
-Y es que el proceso de incidencia en el canal X, con reflexión en el canal W y transmisión en el Z, necesita poder suceder de forma reversa en el tiempo, esto es, una onda incidente en W que es reflejada en X y transmitida en Y. Por tanto, hay que considerar un formalismo matemático que incorpore 4 puertos o canales: en la imagen revertida temporalmente, X e Y son canales de salida, mientras que ambos son canales de entrada en la imagen directa. En la descripción clásica, el segundo canal de entrada Y no se usa, pero la descripción matemática cuántica necesita que la acción del divisor de haz se corresponda con la acción de un operador unitario, lo que implica manejar cuatro canales, dos de entrada (estado incidente) y dos de salida (canales reflejado y transmitido).

-La razón física profunda que se suele aducir radica en las tantas veces invocadas fluctuaciones del vacío, que vienen a requerir ese segundo canal o modo de radiación de incidencia, incorporado mediante el operador $a_o$ y con el que se garantiza que se satisfagan las relaciones de conmutación correctas entre los operadores de cuantización del campo electromagnético.

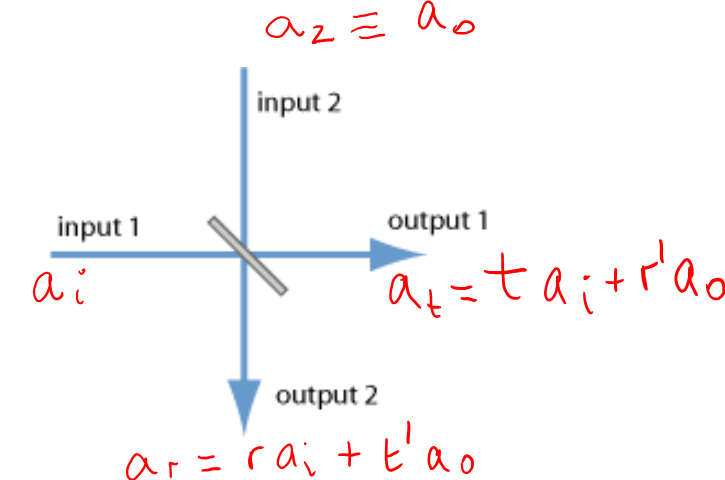
En definitiva, se necesitan cuatro operadores $a$ de campo, relacionados según la transformación lineal $R$ que convierte un estado incidente en otro de salida:

$\left( \begin{array}{c} \hat{a}_r \\ \hat{a}_t \end{array} \right) = R$ $\left( \begin{array}{c} \hat{a}_o \\ \hat{a}_i \end{array} \right) =$ $\left( \begin{array}{cc} t' & r \\ r' & t \end{array} \right)$ $\left( \begin{array}{c} \hat{a}_o \\ \hat{a}_i \end{array} \right)$ $\rightarrow \left\{ \begin{array}{l} \hat{a}_r = t' \ \hat{a}_0 + r \ \hat{a}_i \\ \hat{a}_t = r' \ \hat{a}_0 + t \ \hat{a}_i \end{array} \right\}$

-La adecuada conmutación entre los operadores de campo así introducidos

$[ \hat{a}_j ,\hat{a}^{\dagger}_k]=\delta_{jk} \quad , \quad [\hat{a}_j,\hat{a}_k]=0=[\hat{a}_j^{\dagger},\hat{a}_k^{\dagger}]$

$(j,k=o,i,r,t)$

implica las relaciones (cf. [GER-05] pp. 138-139):

$|r'|=|r| \;,\;|t'|=|t| \;,\;|r|^2 + |t|^2=1 \;,\;r^*t'+r't^*=0=r^*t+r't'^*$

(que garantizan la conservación de la energía).

-La transformación unitaria entre modos de entrada y salida admite la expresión en términos de un operador lineal $\hat{U}$ actuando sobre los modos de entrada:

$|out> = \hat{U} |in>$

siendo $\hat{U}$ el correspondiente operador unitario.

Un divisor de haz es un dispositivo óptico pasivo de cuatro puertos o canales: ni crea ni destruye fotones, tan sólo transforma los estados.

En general, los divisores de haz se fabrican superponiendo capas de diferentes materiales dieléctricos, y se nombran indicando la relación reflexión-transmisión; por ejemplo, un «BS 50:50» es un divisor de haz (idealmente no absorbente, lossless) que refleja y transmite al 50%, también denominado como divisor de haz simétrico.

-Para un BS con una sola capa de material dieléctrico, se introduce una diferencia de fase entre los haces reflejado y transmitido del orden de $e^{\pm i\frac{\pi}{2}}=\pm i$ ; si además se trata de un BS simétrico, los operadores de campo $\hat{a}$ asociados a los distintos modos se relacionan según:

$\hat{a}_r=\frac{1}{\sqrt{2}}(\hat{a}_o + i \hat{a}_i)$

$\hat{a}_t=\frac{1}{\sqrt{2}}(i\hat{a}_o + \hat{a}_i)$

$\hat{a}_0=\frac{1}{\sqrt{2}}(\hat{a}_r - i \hat{a}_t)$

$\hat{a}_o^{\dagger}=\frac{1}{\sqrt{2}}(\hat{a}_r^{\dagger}+ i\hat{a}_t^{\dagger})$

$\hat{a}_i=\frac{1}{\sqrt{2}}(-i\hat{a}_r+ \hat{a}_t)$

$\hat{a}_i^{\dagger}=\frac{1}{\sqrt{2}}(i\hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger})$

-Expresiones para los operadores de la transformación unitaria asociada para un BS simétrico, supuesto introduce un desfase de $\frac{\pi}{2}$ en el haz reflejado:

$R=\frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & i \\ i & 1 \end{array} \right)$

$\hat{U}=e^{i\frac{\pi}{4}(\hat{a}_o^{\dagger}\hat{a}_i +\hat{a}_o\hat{a}_i^{\dagger} )}$

Ejemplos de aplicación: foton(es) sobre un BS

Dado un BS simétrico y supuesto se introduce una diferencia de fase entre los haces reflejado y transmitido del orden de $e^{\pm i\frac{\pi}{2}}=\pm i$ , aplicando las anteriores relaciones entre los distintos operadores de campo se puede, en un desarrollo en imagen de Schrödinger en que se construyen los estados salida a partir de la acción de los correspondientes operadores de creación sobre los estados vacíos de los canales de salida, teniéndose que el vacío en la entrada lleva al vacío en la salida:

$|0_o>|0_i> \rightarrow |0_r>|0_t>$

Estado fotónico incidente de un fotón $|0_o>|1_i>$ :

-El BS actuará según:

$|in>\equiv \hat{a}_i^{\dagger}|0_o>|0_i>$

$\quad \rightarrow |out>\equiv \frac{1}{\sqrt{2}}(i\hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger})|0_r>|0_t>$

$=\frac{1}{\sqrt{2}}(i|1_r>|0_t> +|0_r>|1_t>) \equiv \frac{1}{\sqrt{2}}(i|1_r0_t> +|0_r1_t>)$

-Y para su alternativa equivalente, incidencia en el otro modo de entrada, la diferencia será una fase relativa: $|1_o>|0_i>$ :

$|in>\equiv \hat{a}_0^{\dagger}|0_o>|0_i>$

$\quad \rightarrow |out>\equiv \frac{1}{\sqrt{2}}(\hat{a}_r^{\dagger} + i \hat{a}_t^{\dagger})|0_r>|0_t>$

$=\frac{1}{\sqrt{2}}(|1_r>|0_t> +\ i|0_r>|1_t>) \equiv \frac{1}{\sqrt{2}}(|1_r0_t> +\ i|0_r1_t>)$

-Este estado de salida es un estado puro «entrelazado» (aquí el entrelazamiento es entre ambos modos de salida, el sistema incidente no tiene partes), que se corresponde con el operador densidad:

$\hat{\rho}_{rt}=|out><out|=\frac{1}{2}(i|1_r0_t> +|0_r1_t>)(-i<1_r0_t| +<0_r1_t|)$

$=\frac{1}{2}( |1_r0_t><1_r0_t|-i |0_r1_t><1_r0_t|$

$+i|1_r0_t><0_r1_t| +|0_r1_t><0_r1_t|)$

para el que

$Tr (\hat{\rho}_{rt})^2=1$

Igual probabilidad, 50%, de reflexión y transmisión.

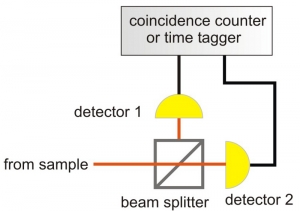
No habrá detección en coincidencia: detectores preparados para recoger los pulsos reflejado y transmitido detectarán anticoincidencia.
El que así se observe experimentalmente, será una confirmación de que la luz incidente es verdaderamente monofotónica.

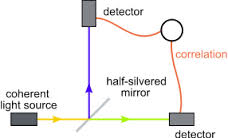
$\rightarrow$ Éste fue el procedimiento que utilizaron Grangier et al en su artículo de 1986:

En 1986 Grangier et al, empleando fotones entrelazados de la desintegración en cascada del Ca, publicaron los primeros experimentos de interferencia que defienden como primeros realizados con luz auténticamente monofotónica:

P. Grangier, G. Roger and A. Aspect, Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences, Europhys. Lett. 1 (4), 1986, 173-179.

Abstract: We report on two experiments using an atomic cascade as a light source, and a triggered detection scheme for the second photon of the cascade. The first experiment shows a strong anticorrelation between the triggered detections on both sides of a beam splitter. This result is in contradiction with any classical wave model of light, but in agreement with a quantum description involving single-photon states. The same source and detection scheme were used in a second experiment, where we have observed interferences with a visibility over 98%.

Se produce un estado de salida entrelazado («entrelazamiento» definido ahora entre dos modos diferentes, y no entre dos partes de un sistema compuesto).

-Si sólo se coloca detección en uno de los dos canales de salida, «output 2», r (o bien «output 1», t,) intervendrá el correspondiente operador traza parcial , que producirá el operador densidad reducido que contiene toda la información presente en $\hat{\rho}_{rt}$ relativa al canal medido:

$\hat{\rho}_r=Tr_t\hat{\rho}_{rt}= \sum_{n_t=0}^{\infty}<n_t|\hat{\rho}_{rt}|n_t>$

$=\frac{1}{2}(|0_r><0_r| +|1_r><1_r|)$

que es un estado mezcla:

$Tr (\hat{\rho}_{r})^2<1$

Indiferentemente de en qué canal se sitúe, el detector señalará radiación sólo en el 50% de las veces.

Trabajando con estados monofotónicos: cómo detectar si la luz es verdaderamente monofotónica: Single Photon sources; Observation of photon antibunching with only one standard single-photon detector.

Apps: Interference experiments with single photons.

Estado fotónico incidente de dos fotones en el mismo canal: $|0_o>|2_i>$

-En este caso hay un solo modo de radiación incidente, y la actuación del BS se corresponde con la ecuación:

$|in>\equiv \hat{a}_i^{\dagger} \hat{a}_i^{\dagger}|0_o>|0_i>$

$\rightarrow \quad |out>\equiv \frac{1}{2}(i\hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger})(i\hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger})|0_r>|0_t>$

$=\frac{1}{2}(-\hat{a}_r^{\dagger} \hat{a}_r^{\dagger} + i \hat{a}_r^{\dagger} \hat{a}_t^{\dagger} + i \hat{a}_t^{\dagger} \hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger} \hat{a}_t^{\dagger})|0_r>|0_t>$

$=\frac{1}{2} \ (-|2_r0_t> +2i|1_r1_t> + \ |0_r2_t>)$ ,

un estado de salida normalizado:

$|out> =\sqrt{\frac{2}{3}} \ (-|2_r0_t> +2i|1_r1_t> + \ |0_r2_t>)$

Habrá detección en coincidencia

Cuando sólo se ocupa uno de los dos canales o modos de entrada, y el número de fotones es mayor a la unidad, es cuando, en realidad, el término «divisor de haz» cobra su sentido.

Estado fotónico incidente de N fotones en el mismo canal: $|0_o>|N_i>$

-En este caso hay un solo modo de radiación incidente, y la actuación del BS se corresponde con la ecuación:

$|in>\equiv (\hat{a}_i^{\dagger})^N |0_o>|0_i>$

$\rightarrow \quad |out>\equiv \frac{1}{2^{\frac{N}{2}}} (i\hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger})^N |0_r>|0_t>$

$=\frac{1}{2^{\frac{N}{2}}} \; \sum_{k=0}^{k=N} \left(\begin{smallmatrix} N\\ k \end{smallmatrix}\right) i^{N-k} ( \hat{a}_r^{\dagger})^{N-k} ( \hat{a}_t^{\dagger})^{k} |0_r>|0_t>$

$=\frac{1}{2^{\frac{N}{2}}} \ \; \sum_{k=0}^{k=N} \left(\begin{smallmatrix} N\\ k \end{smallmatrix}\right) i^{N-k} |(N-k)_rk_t>$ ,

un estado de salida (sin normalizar) compuesto por N estados N-fotónicos entrelazados.

Habrá detección en coincidencia

Cuando sólo se ocupa uno de los dos canales o modos de entrada, y el número de fotones es mayor a la unidad, es cuando, en realidad, el término «divisor de haz» cobra su sentido.

Estado fotónico incidente en un estado coherente: $|0_o>|\alpha_i>$

(homodyne detection)

Montaje experimental (imagen de la Wikipedia).

-El BS actuará, en términos del correspondiente operador desplazamiento

$\hat{d}(\alpha)=e^{\alpha \hat{a}^{\dagger}-\alpha^*\hat{a}}=e^{\frac{1}{2}|\alpha|^2}e^{-\alpha^*\hat{a}}e^{+ \alpha \hat{a}^{\dagger}}=e^{-\frac{1}{2}|\alpha|^2}e^{+\alpha\hat{a}^{\dagger}}e^{-\alpha^* \hat{a}}$

que actúa sobre el vacío del canal $i$ dando lugar al estado coherente:

$\hat{d}_i(\alpha)|0_i>=|\alpha_i>\equiv |\alpha>_i$

donde $|\alpha_i>\equiv$ estado en el canal incidente $i$ igual a un estado coherente $|\alpha>$ , autoestado del operador destrucción $\hat{a}_i$ con autovalor $\alpha$ .

-Por tanto, se tiene:

$|in>\equiv \hat{d}_i(\alpha)|0_o>|0_i>=e^{\alpha \hat{a}_i^{\dagger}- \alpha^* \hat{a}_i}|0_o>|0_i>$

$\rightarrow \quad |out>\equiv e^{\alpha\frac{1}{\sqrt{2}}(i\hat{a}_r^{\dagger} + \hat{a}_t^{\dagger})-\alpha^* \frac{1}{\sqrt{2}}(-i\hat{a}_r + \hat{a}_t) } |0_r>|0_t>$

$=e^{\alpha\frac{1}{\sqrt{2}}( i\hat{a}_r^{\dagger} + \hat{a}_t^{\dagger}) -\alpha^* \frac{1}{\sqrt{2}}(-i \hat{a}_r +\hat{a}_t)}|0_r>|0_t>$

$=e^{(\frac{i\alpha}{\sqrt{2}})\hat{a}_r^{\dagger}-(\frac{-i\alpha^*}{\sqrt{2}}) \hat{a}_r} e^{(\frac{\alpha}{\sqrt{2}})\hat{a}_t^{\dagger}-(\frac{\alpha^*}{\sqrt{2}}) \hat{a}_t}|0_r>|0_t>$

$=|(\frac{i\alpha}{\sqrt{2}})_r>|(\frac{\alpha}{\sqrt{2}})_t>$

La intensidad incidente se divide por la mitad entre los dos canales de salida (con sendos detectores en sus extremos), emergiendo el 50% de los fotones por cada uno, con un desfase entre los dos haces dado por $e^{i\frac{\pi}{2}}=i$ . Se trata de un resultado clásico, y el entrelazamiento está ausente.

El caso monofotónico NO se puede derivar del caso para el estado coherente $|\alpha>$ tomando el límite para $|\alpha |$ muy pequeño.

-Introduciendo la expresión normalizada del estado coherente,

$|\alpha>=e^{-\frac{1}{2}|\alpha|^2}\sum_n \frac{\alpha^n}{\sqrt{n!}}|n>$

se comprueba el resultado indicado:

-Para el estado de entrada, $|in>$ :

$|in>\equiv |0_o>|\alpha_i>=e^{-\frac{1}{2}|\alpha|^2}\sum_n \frac{\alpha^n}{\sqrt{n!}}|0_o>|n_i>$

donde $|n_i>\equiv |n>_i$ representa el estado en el canal incidente $i$ igual a un estado número $|n>$ , autoestado del operador número $\hat{n}$ con autovalor $n$ ;

-Para el estado de salida $|out>$ :

$|out> \equiv |(\frac{i\alpha}{\sqrt{2}})_r>|(\frac{\alpha}{\sqrt{2}})_t>$

$=e^{-|\alpha|^2} \sum_l \frac{(\frac{i\alpha}{\sqrt{2}})^l}{\sqrt{l!}} \sum_s \frac{(\frac{\alpha}{\sqrt{2}})^s}{\sqrt{s!}}|l_r>|s_t>$

$=e^{-|\alpha|^2}\sum_n \frac{\alpha^n}{\sqrt{n!}}\cdot (\frac{1}{2^{\frac{n}{2}}}\sum_{m=0}^{n} i^m(\frac{n!}{m!(n-m)!})^{\frac{1}{2}}\ |m_r>|(n-m)_t>)$

expresión que indica una distribución binomial de los fotones entre los dos modos, estando poblados cada uno de ellos por la mitad del número medio total de fotones, $\frac{|\alpha|^2}{2}$ , y poseyendo el modo asociado al modo de salida r («reflexión») un desfase $i=e^{\frac{i\pi}{2}}$ .

-En este caso no se obtiene a la salida un estado entrelazado.

Situación HOM: Estado fotónico incidente de dos fotones en sendos canales de entrada: $|1_o>|1_i>$

(los dos modos de entrada ocupados; Hong-Ou-Mandel -HOM- interference)

-La actuación del BS se corresponde con la ecuación:

$|in>\equiv \hat{a}_o^{\dagger} \hat{a}_i^{\dagger}|0_o>|0_i>$

$\rightarrow \quad |out>\equiv \frac{1}{2}(\hat{a}_r^{\dagger}+ i\hat{a}_t^{\dagger})(i\hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger})|0_r>|0_t>$

$=\frac{1}{2}(\hat{a}_r^{\dagger} \hat{a}_r^{\dagger} +\hat{a}_t^{\dagger} \hat{a}_t^{\dagger})|0_r>|0_t>$ ,

un estado de salida normalizado:

$|out> =\frac{i}{\sqrt{2}} \ (|2_r0_t> + \ |0_r2_t>)$

-Por lo tanto, siempre se produce detección de los dos fotones en el mismo detector (¡supuesto que el dispositivo ha conseguido la indistinguibilidad requerida!): nunca se produce detección en coincidencia (HOM dip). A este fenómeno se le conoce como interferencia bifotónica, o efecto de agrupamiento («bunching») fotónico en un divisor de haz, que no ocurre si las correspondientes amplitudes de Feynman son distinguibles.

No habrá detección en coincidencia: nunca los dos detectores señalarán a la vez.

–Advertencia: ¡cuidado con la notación! En el caso de dos fotones incidentes, en los sendos canales «i» y «o», los dos canales o modos de salida se suelen seguir notando como «r» (lleva al detector «output 2») y «t» (conduce al detector «output 1» ), pero ahora, por tanto, la interpretación de un estado, como por ejemplo el $|2_r0_t>$ , no es la de que se corresponde con reflexión para ambos fotones, sino con la llegada conjunta de ambos fotones al detector «output 2», correspondiente al canal de salida modo «r»:

-El mecanismo que subyace es la interferencia entre las sendas amplitudes dce probabilidad asociadas a las dos posibles situaciones que pueden producir un resultado de un fotón en cada modo de salida, $|1_r1_t>$ , esto es, los dos posibles procesos: uno en el que ambos fotones transmiten (proceso 2 en la figura siguiente) y otro, distinto pero indistinguible (si así se ha preparado) del anterior, en que ambos reflejan (proceso 3), procesos ambos en que los fotones llegarían a sendos detectores distintos:

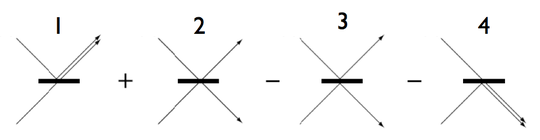
HOM interferencia fotónica — Imagen de la Wikipedia, por P. Kok.

$\rightarrow$ Las amplitudes de probabilidad de ambos procesos 2 y 3 se cancelan: puesto que el canal de reflexión dota de un desfase $e^{i\frac{\pi}{2}}=i$ al fotón reflejado, las amplitudes de probabilidad asociadas son $\mathcal{A}_{refl}=\frac{i}{\sqrt{2}}$ y $\mathcal{A}_{trans}=\frac{1}{\sqrt{2}}$ , de forma que la probabilidad para reflexión de ambos fotones resulta $P_{2refl}=|\mathcal{A}_{refl}|^2=-\frac{1}{2}$ , mientras que para transmisión conjunta es $P_{2trans}=|\mathcal{A}_{trans}|^2=+\frac{1}{2}$ , de forma que el cálculo de la probabilidad conjunta de ambos eventos (los dos fotones se reflejan, o los dos se transmiten) es nulo:

$P_{\mbox{2refl+2trans}}=| \mathcal{A}_{refl1}\mathcal{A}_{refl2}+\mathcal{A}_{trans1}\mathcal{A}_{trans2}|^2=| \frac{i}{\sqrt{2}}\frac{i}{\sqrt{2}}+ \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}|^2 =0$

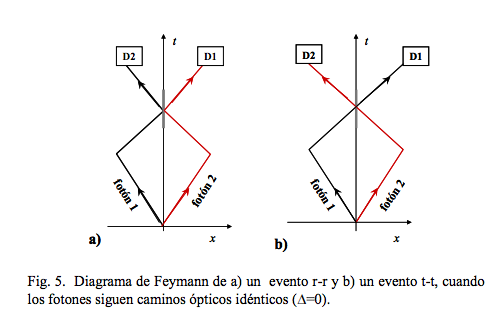
HOM_caminos-opticos-iguales — Imagen de A. Ibarra-Durán, Interferencias bifotónicas en un divisor de haces, Tecnociencia 8, 1, 2006, pp. 167-181 . Se ilustran los sendos procesos en que ambos fotones a) reflejan y b) transmiten, cuyas amplitudes de Feynman se cancelan si los caminos ópticos se configuran experimentalmente como indistinguibles.

Al igual que en la doble rendija, el hecho de que haya dos vías alternativas posibles (caminos o procesos de Feynman) indistinguibles para llegar al mismo resultado, necesita ser incorporado: la amplitud de probabilidad total $\mathcal{A}$ para el evento es la suma de las amplitudes de probabilidad para cada proceso, $\mathcal{A}=\sum_i \mathcal{A}_i$ , de forma que en el cálculo de la probabilidad del evento,

$P=|\mathcal{A}|^2=|\sum_i \mathcal{A}_i|^2$ ,

pueden ocurrir cancelaciones entre las amplitudes:

$\rightarrow$ Experiencia de Hong, Ou y Mandel

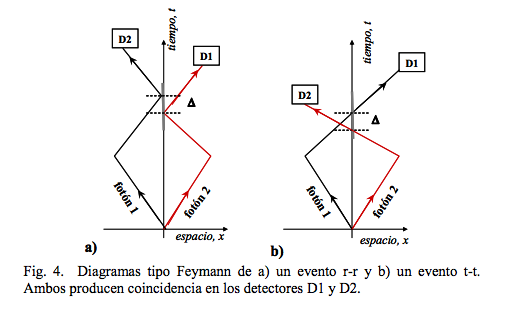
Pero si hay distinguibilidad entre las vías alternativas, entonces las probabilidades se suman directamente:

$P=\sum_i P_i=\sum_i |\mathcal{A}_i|^2$

y desaparecen las interferencias entre las amplitudes, de modo que se registran coincidencias en los detectores: no hay efecto de agrupamiento o «bunching» fotónico.

canales r-r y t-t en coincidencia — Caso de caminos ópticos diferentes; imagen de A. Ibarra-Durán, Interferencias bifotónicas en un divisor de haces, Tecnociencia 8, 1, 2006, pp. 167-181 .

Cuando se ocupan los dos canales o modos de entrada, el divisor de haz puede denominarse más bien como un «combinador» de modos.

Estado fotónico incidente con dos fotones en un estado de Bell y en sendos canales de entrada:

$|in> = | \Psi^{\pm}(A,B)>=\frac{1}{\sqrt{2}}( | 0_A 1_B > \pm \; | 1_A 0_B >)$

$\equiv \frac{1}{\sqrt{2}}( | H_A V_B > \pm \; | V_A H_B >)$

$\ne |\psi(A)> \otimes \; | \psi(B)>$

Aclaración sobre la notación introducida para tratar este ejemplo: de nuevo se tienen los dos canales o modos de entrada ocupados, pero ahora hemos de distinguir los operadores de creación $\hat{a}_i^{\dagger}$ en términos de la polarización, para los dos valores posibles, horizontal H y vertical V. Por ello, desdoblamos:

$\hat{a}_{o}^{\dagger} \rightarrow \; (\hat{a}_{oH}^{\dagger} \; ; \; \hat{a}_{oV}^{\dagger} )$ ; $\quad \hat{a}_{i}^{\dagger} \rightarrow \; (\hat{a}_{iH}^{\dagger} \; ; \; \hat{a}_{iV}^{\dagger} )$

$\hat{a}_{r}^{\dagger} \rightarrow \; (\hat{a}_{rH}^{\dagger} \; ; \; \hat{a}_{rV}^{\dagger} )$ ; $\quad \hat{a}_{t}^{\dagger} \rightarrow \; (\hat{a}_{tH}^{\dagger} \; ; \; \hat{a}_{tV}^{\dagger} )$

-En este caso, la actuación del BS se corresponde con la ecuación:

$|in>\equiv \frac{1}{\sqrt{2}} \; ( \hat{a}_{oH}^{\dagger} \hat{a}_{iV}^{\dagger} \pm \; \hat{a}_{oV}^{\dagger} \hat{a}_{iH}^{\dagger} ) |0_o>|0_i>$

$= \frac{1}{\sqrt{2}} \; \hat{a}_{oH}^{\dagger} \hat{a}_{iV}^{\dagger} |0_o>|0_i> \pm \; \hat{a}_{oV}^{\dagger} \hat{a}_{iH}^{\dagger} |0_o>|0_i>$

$\rightarrow \quad |out>\equiv (\frac{1}{\sqrt{2}})^3 ( \hat{a}_{rH}^{\dagger} + i \hat{a}_{tH}^{\dagger} ) ( i\hat{a}_{rV}^{\dagger} + \hat{a}_{tV}^{\dagger} ) |0_r>|0_t>$

$\pm \; (\frac{1}{\sqrt{2}})^3 ( \hat{a}_{rV}^{\dagger} + i \hat{a}_{tV}^{\dagger} ) ( i\hat{a}_{rH}^{\dagger} + \hat{a}_{tH}^{\dagger} ) |0_r>|0_t>$

$=\frac{1}{2\sqrt{2}} \; [( i| H_r V_r >) + | H_r V_t > - | V_r H_t> + i | H_t V_t >)$

$\pm (i | V_r H_r > + | V_r H_t > - | H_r V_t > +i | H_t V_t >)]$ ,

de modo que a cada uno de estos dos estados de la base de Bell le corresponden los sendos estados de salida:

$|in> = | \Psi^{+}(H,V)> \quad \rightarrow \quad |out> \frac{i}{\sqrt{2}} \; ( | H_r V_r > + \; | H_t V_t > )$

$=\frac{i}{\sqrt{2}} \ (|1_{Hr}1_{Vr}> + \ |1_{Vt}1_{Ht}>)$

$\equiv \frac{i}{\sqrt{2}} \ (|2_{r}0_{t}> + \ |0_{r}2_{t}>)$ ;

produciéndose un fenómeno de agrupamiento o «bunching» fotónico, mientras que, para el estado de Bell antisimétrico, se tiene un efecto de antiagrupamiento, «antibunching», resultando que el estado permanece inalterado:

$|in> = | \Psi^{-}(H,V)> \quad \rightarrow \quad |out> \frac{1}{\sqrt{2}} \; ( | H_r V_t> -\; | V_r H_t > )$

$=\frac{1}{\sqrt{2}} \ (|1_{Hr}1_{Vt}> - \ |1_{Vr}1_{Ht}>) = | \Psi^{-}(H,V)>$ .

Esta es la razón de que, por ejemplo, en la medida de Bell que se hace en el experimento de teletransporte de Innsbruck, la teleportación se sepa como efectivamente realizada en el 25% de los casos en que se produce detección en coincidencia, esto es, los respectivos detectores de los canales r y t señalan detección fotónica simultánea.

Interferometría: algunos tipos de interferómetros y experimentos asociados

A) Interferometría HOM (estados incidentes con dos fotones)

Interferometría HOM.

Y.-H. Kim; Two-photon interference without bunching two photons; Physics Letters A 315 (2003) 352-357:

Abstract: We report an experiment which conclusively demonstrates that the two-photon entangled state interference cannot be pictured as the overlap and ‘bunching’ of two individual photons on a beamsplitter. We also demonstrate that photon ‘bunching’ does not occur if the two-photon Feynman amplitudes are distinguishable, even though individual photons do overlap on a beamsplitter.

We report a novel interference experiment in which the two-photon entangled state interference cannot be pictured in terms of the overlap and bunching of two individual down-converted photons on a beamsplitter. Experimentally, this is accomplished by choosing the arrival time difference between the two photons at the beamsplitter much bigger than the coherence time of the pump pulse as well as the coherence times of the individual photons. We also experimentally demonstrate that two-photon interference, or photon bunching effect on a beamsplitter, does not occur if the twophoton Feynman amplitudes are distinguishable, even though individual photons do overlap on a beamsplitter. Therefore, two-photon interference cannot be viewed as interference of two individual photons, rather it should be viewed as two-photon or biphoton interfering with itself. The results may also be useful for studying decoherence management in entangled two-qubit systems as we observe near complete restoration of quantum interference after the qubit pairs, generated by a femtosecond laser pulse, went through certain birefringent elements.

M. Horne, A. Shimony and A. Zeilinger: Nature: Two particle interferometry

Interferometría bifotónica: artículo divulgativo de A. Ibarra (en el repositorio de la Univ. de Panamá).

Entrada en el blog de Dan Jackson: Quantum Beam Splitters & The Hong-Ou-Mandel Effect

B) Interferómetro de Mach-Zehnder

B.1) Interferometría Mach-Zehnder: estudio general

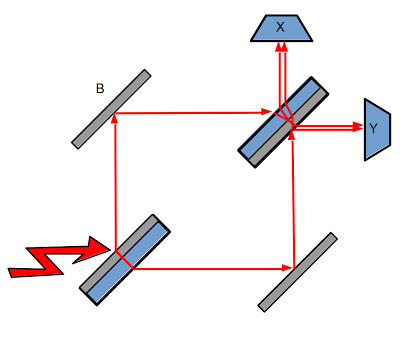
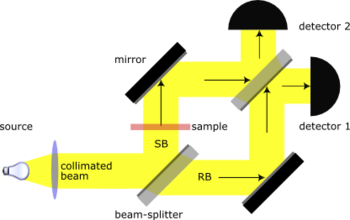
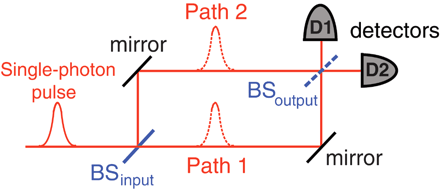
Un interferómetro de Mach-Zehnder consta de dos divisores de haz y dos espejos perfectamente reflectantes, dispuestos según la figura.

L. Zehnder, Z. Instrumentenkunde 11 (1891) 275; L. Mach, Z. Instrumentenkunde 12 (1892) 89.

-Una configuración así no permite distinguir con los detectores entre los dos caminos de Feynman posibles, de forma que se producirán interferencias entre ellos.

-Es conveniente introducir en uno de los dos caminos un desplazador de fase (ps, phase shifter), de forma que se pueda ajustar la fase mutua entre los fotones que recorren diferentes caminos:

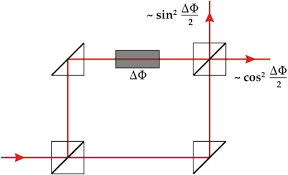
Interferómetro de Mach-Zender con retardador de fase.

-La acción del desfasador se expresa por la acción del correspondiente operador

$\hat{ps}=e^{i\theta \hat{n}}$

donde $\hat{n}$ representa el operador número en la cuantización del campo en la correspondiente región y $\theta$ es el desfase relativo añadido entre los dos caminos ópticos posibles en la figura superior para la radiación a partir del primer divisor de haz (en la figura inferior, el desfasador actúa a partir del primer divisor de haz introduciendo un desfase $\phi$ entre los fotones incidentes por el canal 1 y «reflejados», e incidentes por el canal 2 y «transmitidos», de un lado, y los fotones incidentes por el canal 1 y «transmitidos», e incidentes por el canal 2 y «reflejados», de otro).

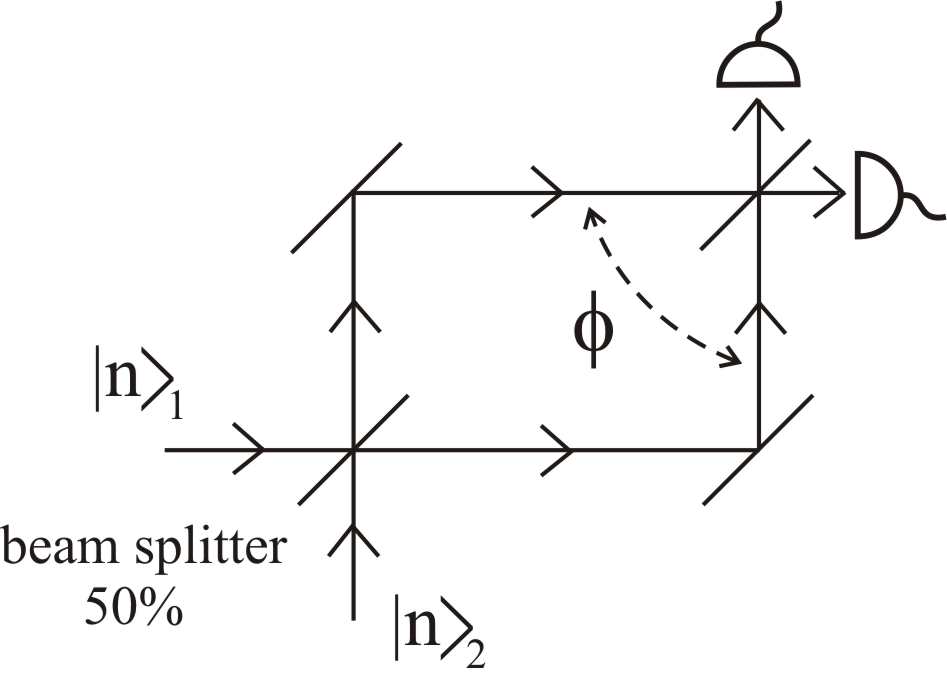
Fotones en interferómetro de Mach-Zender.

Emily Marshman and Chandralekha Singh, Interactive tutorial to improve student understanding of single photon experiments involving a Mach-Zehnder Interferometer; European Journal of Physics 37-2 (2016).

Light Trans; Observation of Complementary Interference Pattern in a Mach-Zehnder Interferometer with Prism Beam Splitter.

B.2) Interferometría Mach-Zehnder con estados de un solo fotón

Descripción matemática del proceso interferencial en el caso de incidencia monofotónica y divisores de haz simétricos y no absorbentes:

Interferómetro de Mach-Zehnder con desfasador.

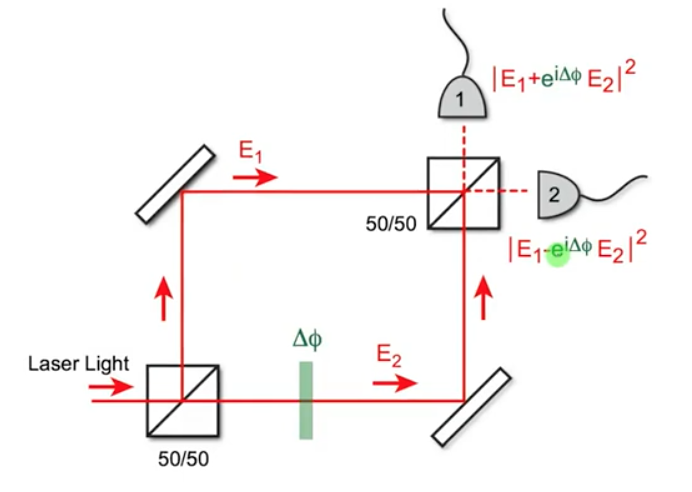
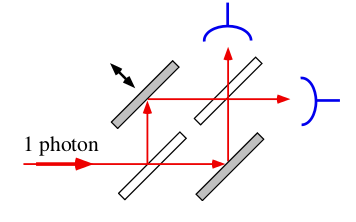
Estado monofotónico en un interferómetro de Mach-Zender — Estado monofotónico en un interferómetro de Mach-Zehnder; imagen de: http://cuentoscuanticos.com/2013/12/25/soledad-foton/

-Estado inicial o incidente: $|in>= |0>|1_i>$

-Transformación en el divisor de haz del camino con ajustador de fase (que supondremos, por ejemplo, que desfasa el modo transmitido en el primer divisor de haz):

$|in>\equiv |0_o>|1_i>=\hat{a}_i^{\dagger}|0_o>|0_i>$

$\rightarrow |out>\equiv \frac{1}{\sqrt{2}} (i\hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger})|0_r>|0_t>$

$=\frac{1}{\sqrt{2}} (i|1_r>|0_t>+|0_r>|1_t>)$

antes de llegar al ajustador de fase, y

$\rightarrow \frac{1}{\sqrt{2}}(i|1_r>|0_t>+e^{i\theta}|0_r>|1_t>)$

tras salir de él.

-Análogamente, en el segundo divisor de haz se produce para cada fotón entrante la transformación

1. Para estado incidente $|in>\equiv |r>$ :

$|in>\equiv |0_t>|1_r>= \hat{a}_r^{\dagger}|0_{o'}>|0_{i'=r}>$

$\rightarrow |out>\equiv \frac{1}{\sqrt{2}}(i\hat{a}_{r'}^{\dagger}+ \hat{a}_{t'}^{\dagger})|0_{r'}>|0_{t'}>$

$=\frac{1}{\sqrt{2}}(i|1_{r'}>|0_{t'}>+|0_{r'}>|1_{t'}>)$

2. Para estado incidente $|in>\equiv e^{i\theta}|t>$ :

$|in>\equiv e^{i\theta}|0_{o'}>|1_{i'=t}>= \hat{a}_t^{\dagger}e^{i\theta}|0_{o'}>|0_{i'=t}>$

$\rightarrow |out>\equiv \frac{1}{\sqrt{2}}e^{i\theta}(i\hat{a}_{r''}^{\dagger}+ \hat{a}_{t''}^{\dagger})|0_{r''}>|0_{t''}>$

$=\frac{1}{\sqrt{2}}e^{i\theta}(i|1_{r''}>|0_{t''}>+|0_{r''}>|1_{t''}>)$

-Reuniendo todos los resultados, para el estado incidente inicial , $|in>\equiv |0>|1_i>$ , se produce una transformación dada por:

$|in>= |0_o>|1_i>$

$\underrightarrow{BS_1} \quad \frac{1}{\sqrt{2}} (i|1_r>|0_t>+|0_r>|1_t>)$

$\underrightarrow{ps} \quad \frac{1}{\sqrt{2}}(i|1_r>|0_t>+e^{i\theta}|0_r>|1_t>)$

$\underrightarrow{BS_2} \quad \frac{1}{2}[i(i|1_{r'}>|0_{t'}>+|0_{r'}>|1_{t'}>)$

$+e^{i\theta}(i|1_{r''}>|0_{t''}>+|0_{r''}>|1_{t''}>) ]$

$=\frac{1}{2}[-|1_{r'}>|0_{t'}> +e^{i\theta}(|0_{r''}>|1_{t''}>]$

$+\frac{1}{2}[i\ |0_{r'}>|1_{t'}> +ie^{i\theta} \ |1_{r''}>|0_{t''}>]$

$=\frac{1}{2} (e^{i\theta}-1) |1>_1|0>_2 \, + \, \frac{1}{2} \ i \ (e^{i\theta}+1) |0>_1|1>_2$ ,

con expresión final:

$|out>=\frac{1}{2} [(e^{i\theta}-1) |1>_1|0>_2 \, + \, i \ (e^{i\theta}+1) |0>_1|1>_2]$ ,

donde se ha incorporado la indistinguibilidad entre los procesos $r',t''$ , de un lado, y $r'',t'$ , de otro; $|>_j\;,\; j=1,2$ , indica proceso o camino hacia el detector $D_j$ (hacia $D_1$ van $r', t''$ , mientras que hacia $D_2$ van $t',r''$ ).

Por tanto, las amplitudes de probabilidades respectivas de detección en cada uno de los dos detectores, $A(D_i)\, i=1,2$ , bajo incidencia monofotónica, tienen la expresiones:

$A(D_1)= \frac{1}{2} \ (e^{i\theta}-1)$

$A(D_2)= \frac{1}{2} \ i \ (e^{i\theta}+1)$ ,

de modo que las ratios de contaje de cada detector varían con $\theta$ según:

-detección del estado $|1>_1|0>_2$ : se activa el detector $D_1$ , con probabilidad de detección:

$P_1=|A(D_1)|^2=| \frac{1}{2} (e^{i\theta}-1)|^2=\frac{1}{2} \ (1-\cos \theta)\quad \rightarrow P_1=\sin^2 (\frac{\theta}{2})$

-detección del estado $|0>_1|1>_2$ : se activa el detector $D_2$ , con probabilidad de detección:

$P_2=|A(D_2)|^2=| \frac{1}{2} i \ (e^{i\theta}+1)|^2=\frac{1}{2} \ (1+\cos \theta)\quad \rightarrow P_2=\cos^2 (\frac{\theta}{2})$ .

Para un desfase fijo de $\theta=0 , 2\pi ...$ se activa, para todos los eventos, sólo el detector $D_2$ .

Para un desfase fijo de $\theta=\pi , 3\pi ...$ se activa, para todos los eventos, sólo el detector $D_1$ .

Para un desfase fijo de $\theta=\frac{3\pi}{2} , \frac{5\pi}{2} ...$ se activan, para todos los eventos, los dos detectores, al 50% de ratio final y nunca los dos a la vez: sin coincidencias.

Para un valor general de $\theta$ se activará, para cada evento, uno u otro detector, con ratios individuales dependientes del valor concreto de $\theta$ y siempre complementarias a 100.

Para un evento individual, nunca se activarán los dos detectores a la vez: ratio 0 de detección en coincidencia.

The University of St Andrews Quantum Mechanics Visualisation project:

-Apps: Step by step explanation, desde la Univ. of St. Andrew:

Mach-Zehnder I ,

Mach-Zehnder II (con phase shifter).

B.2.1) Experimento de Grangier et al

$\rightarrow$ Grangier et al en su artículo de 1986:

P. Grangier, G. Roger and A. Aspect, Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences, Europhys. Lett. 1 (4), 1986, 173-179.

Abstract: We report on two experiments using an atomic cascade as a light source, and a triggered detection scheme for the second photon of the cascade. The first experiment shows a strong anticorrelation between the triggered detections on both sides of a beam splitter. This result is in contradiction with any classical wave model of light, but in agreement with a quantum description involving single-photon states. The same source and detection scheme were used in a second experiment, where we have observed interferences with a visibility over 98%.

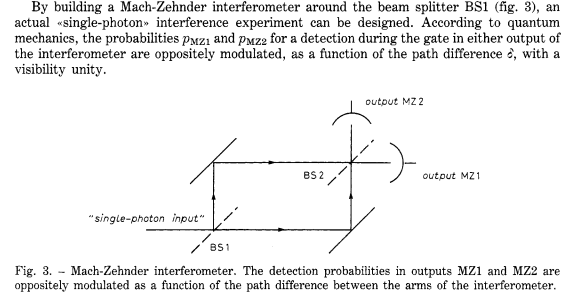
-Trabajan con un interferómetro de Mach-Zehnder, con un dispositivo en el que el segundo BS puede desplazarse, de forma que varían la diferencia de camino entre los dos haces (entre los brazos del interferómetro), midiendo las interferencias correspondientes: registran una visibilidad de éstas del $98,7 \pm 0,5$ % .

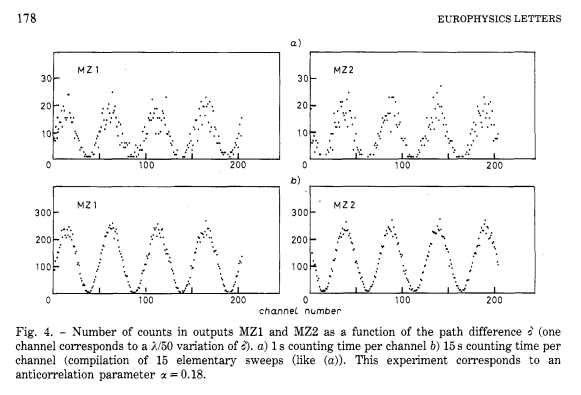
-Gráfica de resultados (Europhys. Lett. 1 (4), 1986, 173-179):

B.2.2) Experimento de Wheleer et al

$\rightarrow$ Experimento de Wheeler (primera parte):

V. Jacques, E. Wu, F. Grosshans, F. Treussart, P. Grangier, A. Aspect, J.-F. Roch, Experimental realization of Wheeler’s delayed-choice Gedanken Experiment, Science 315, 5814 (2007) 966; DOI: 10.1126/science.1136303; https://arxiv.org/abs/quant-ph/0610241.

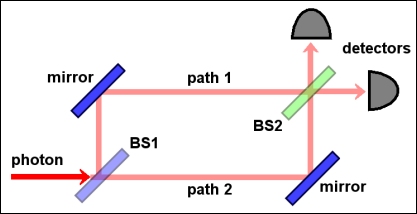
-La inclinación del segundo divisor de haz BS2 puede variarse, de manera que su acción equivale a la de un desfasador; además, su acción también puede anularse por completo (o sea: suprimirlo en el montaje, aplicándole un voltaje nulo), lo que equivale a tener sólo un divisor de haz: supresión de las interferencias.

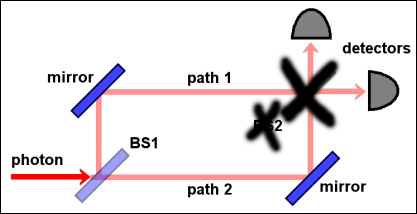
Modificación sobre la imagen del experimento de Wheeler — (modificación sobre la imagen anterior)

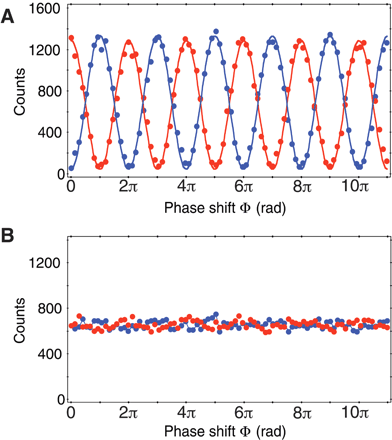
$\rightarrow$ En el montaje con los dos divisores de haz presentes, variando el desfase $\theta$ , se obtienen oscilaciones en las ratios de contaje de los dos detectores (gráfica A).

$\rightarrow$ En el montaje con un solo divisor de haz (BS1) presente, no se producen oscilaciones en las ratios de contaje de los dos detectores: cada uno señala en el 50% de las ocasiones, y nunca en coincidencia (gráfica B).

$\rightarrow$ Cuando se mantiene la acción del segundo BS, el montaje es equivalente a una doble rendija sin «detección de camino»: observación de interferencia (gráfica A), que se manifiesta en las oscilaciones de las ratios de contaje de los detectores.

$\rightarrow$ Cuando se anula la acción del segundo BS, el montaje es equivalente a una doble rendija con «detección de camino»: no se produce interferencia (gráfica B).

Resultados en el experimento de Wheeler: The phase shift (indicated with arbitrary origin) is varied by tilting BS’. Each point, recorded with acquisition time of 1.9 s, corresponds to the detection of about 2600 photons. The detector dark counts, 59 s^{-1} for D1 (blue points) and 70 s^{-1} for D2 (red points), have been subtracted from the data. (A) Cases when V is applied on the EOM (closed configuration); interference with 94% visibility is obtained. (B) Cases when no voltage is applied on the EOM (open configuration); no interference is observed and equal detection probabilities (0.50 ± 0.01) on the two output ports are measured, corresponding to full knowledge of the complementary which-way information (I parameter greater than 99%); imagen y texto de: http://www.sciencemag.org/content/315/5814/966.full ;http://www.sciencemag.org/content/315/5814/966/F2.expansion.html

$\rightarrow$ cuando no actúa el segundo BS (experimento con «detección de camino»), los dos detectores clickean con igual frecuencia (¡y nunca a la vez!): equivalente a una doble rendija con «observación de camino»: proceso no interferencial (conducta corpuscular).

$\rightarrow$ cuando el desfase se ajusta a $\theta=0$ sólo da señal uno de los dos detectores ( $D_2$ ; sería $D_1$ para un desfase de $\theta=\pi$ ): equivalente a una doble rendija «sin observación de camino»: con proceso interferencial («conducta ondulatoria«).

La doble rendija a la Mach-Zehnder

Con segundo divisor de haz BS2: el fotón produce interferencia (dependiendo de la diferencia de fase entre los dos caminos, diferencia que se puede ajustar introduciendo un retardador en uno de los dos caminos); se puede conseguir que siempre registre sólo uno y el mismo de los dos detectores, el detector-luz; el otro, el detector-oscuridad, no registra nunca (o bien, cualquier resultado intermedio con diferentes, o iguales, ratios de contaje en los dos detectores). Suele decirse que «se observan interferencias porque no hay determinación de camino» (no which-way information).

$\rightarrow$ Hay interferencia porque hay indistinguibilidad de «caminos» (¡de posibilidades!).

Sin segundo divisor de haz BS2: el fotón alcanza aleatoriamente uno u otro detector (nunca los dos a la vez): decimos que «no se observan interferencias porque hay determinación de camino» (which-way information).

¡Advertencia!: cuando hablamos de «camino» del fotón, y de su determinación o no, hay que tener claro que se trata, una vez más, de un recurso a la retórica clásica, porque no existe el observable «camino del fotón» (ni de ninguna partícula cuántica). Así que ese «camino» es el concepto clásico que, una vez que un un detector específico ha hecho «clic», utilizamos para elaborar una narración a posteriori de los hechos: «puesto que lo ha detectado el detector 1, es como si el fotón hubiera llegado a él «recorriendo» el camino óptico 1: camino en retrodicción. Un concepto ajeno a la matemática cuántica, pero útil para la narración de los fenómenos observados con el lenguaje clásico de los humanos racionales.

$\rightarrow$ No hay interferencia porque los dos caminos (¡las dos posibilidades!) son distinguibles.

Pulsos monofotónicos en el experimento de Wheeler; imagen de:
http://www.sciencemag.org/content/315/5814/966/F1.expansion.html

El experimento de la doble rendija a la Mach-Zehnder (imagen by P.E. Moran, en la Wikipedia).

C) Otros tipos de interferómetros

Una presentación de la U. de Toronto:

http://www.physics.utoronto.ca/~aephraim/2206/2206-12-lect4.pdf

De Hong-Ou-Mandel.

De Franson.

De doble cristal o Zou-Wang-Mandel.

Una reseña de interferometría con efectos no-separables, por Franson:

http://arxiv.org/pdf/0707.0475.pdf

Interferencias con tres fotones

Interferómetrometría y ondas gravitacionales

Febrero, 2016: primera detección experimental de ondas gravitacionales:

The First Sounds of Merging Black Holes

Actualización 2017: Las ondas gravitacionales anticipadas por Einstein le dan el Premio Nobel de Física a los investigadores Rainer Weiss, Barry C. Barish y Kip S. Thorne:

La noticia en la BBC.

Bibliografía

[GER-05] Gerry, C. C. and Knight, P. L., Introductory Quantum Optics, Cambridge Univ. Press, Cambridge, 2005.

G. Weihs and A. Zeilinger, Photon statistics at beam splitters: an essential tool in quantum information and teleportation.

C. H. Holbrow, E. Galvez and M. E. Parks, Photon quantum mechanics and beam splitters, Am. J. Phys. 70, 3 (2002) 260.

Splitting a Light Beam in Two: http://physics.aps.org/story/v18/st14

Vídeos en Youtube por Immanuel Bloch:

–Single photon on BS

–Homodyne detection

-The quantum Mach-Zehnder interferometer

Divisores de haz y muchos mundos:
–The Many Worlds of the Quantum Beam Splitter

Prácticas en un laboratorio de Óptica avanzada.