Experimento de Hong-Ou-Mandel

Hong-Ou-Mandel dip — Experimento de Hong-Ou-Mandel: interferometría HOM (imagen: Wikipedia).

Experiencia Hong-Ou-Mandel

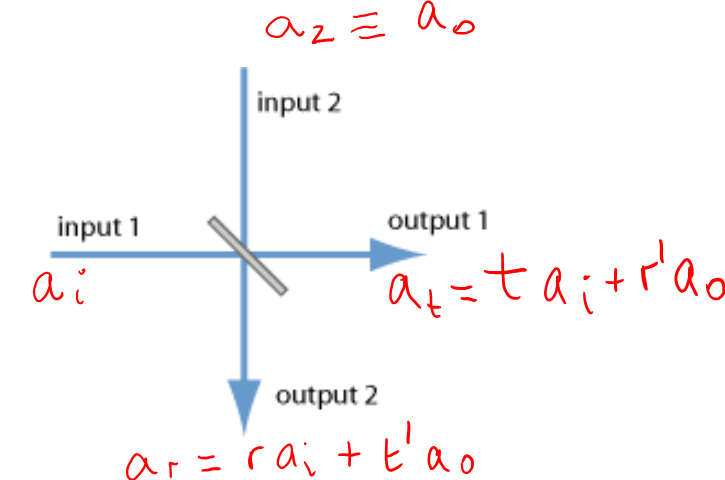
Cuando sobre un divisor de haz simétrico (50:50) e idealmente no absorbente inciden por los dos puertos o canales de entrada sendos fotones, de forma que el estado incidente es $|1_o>|1_i>$ , no se produce detección en coincidencia, contra lo que podría esperarse de un esquema como el siguiente:

HOM_caminos-opticos-iguales — Imagen de A. Ibarra-Durán, *Interferencias bifotónicas en un divisor de haces*, Tecnociencia 8, 1, 2006, pp. 167-181; http://www.up.ac.pa/ftp/2010/f_ciencias/tecnociencias/volumen8-1/Articulo11.pdf)

Experiencia Hong-Ou-Mandel (HOM): Estado fotónico incidente de dos fotones en sendos canales de entrada: $|1_o>|1_i>$

-La actuación del BS se corresponde con la ecuación:

$|in>\equiv \hat{a}_o^{\dagger} \hat{a}_i^{\dagger}|0_o>|0_i>$

$\rightarrow \quad |out>\equiv \frac{1}{2}(\hat{a}_r^{\dagger}+ i\hat{a}_t^{\dagger})(i\hat{a}_r^{\dagger}+ \hat{a}_t^{\dagger})|0_r>|0_t>$

$=\frac{1}{2}(\hat{a}_r^{\dagger} \hat{a}_r^{\dagger} +\hat{a}_t^{\dagger} \hat{a}_t^{\dagger})|0_r>|0_t>$ ,

un estado de salida normalizado:

$|out> =\frac{i}{\sqrt{2}} \ (|2_r0_t> + \ |0_r2_t>)$

-Por lo tanto, siempre se produce detección de los dos fotones en el mismo detector (¡supuesto que el dispositivo ha conseguido la indistinguibilidad requerida!): nunca se produce detección en coincidencia (HOM dip). A este fenómeno se le conoce como interferencia bifotónica, o efecto de agrupamiento («bunching») fotónico en un divisor de haz, que no ocurre si las correspondientes amplitudes de Feynman son distinguibles.

No habrá detección en coincidencia: nunca los dos detectores señalarán a la vez.

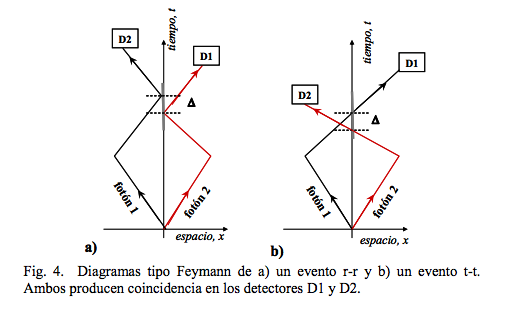
–Advertencia: ¡cuidado con la notación! En el caso de dos fotones incidentes, en los sendos canales «i» y «o», los dos canales o modos de salida se suelen seguir notando como «r» (lleva al detector «output 2») y «t» (conduce al detector «output 1» ), pero ahora, por tanto, la interpretación de un estado, como por ejemplo el $|2_r0_t>$ , no es la de que se corresponde con reflexión para ambos fotones, sino con la llegada conjunta de ambos fotones al detector «output 2», correspondiente al canal de salida modo «r»:

Divisor de haz — Operadores cuánticos en un divisor de haz

-El mecanismo que subyace es la interferencia entre las sendas amplitudes dce probabilidad asociadas a las dos posibles situaciones que pueden producir un resultado de un fotón en cada modo de salida, $|1_r1_t>$ , esto es, los dos posibles procesos: uno en el que ambos fotones transmiten (proceso 2 en la figura siguiente) y otro, distinto pero indistinguible (si así se ha preparado) del anterior, en que ambos reflejan (proceso 3), procesos ambos en que los fotones llegarían a sendos detectores distintos:

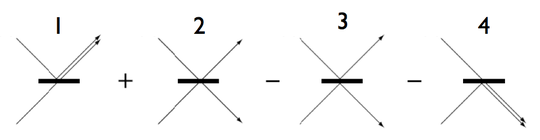
HOM interferencia fotónica — Imagen de la Wikipedia, por P. Kok.

$\rightarrow$ Las amplitudes de probabilidad de ambos procesos 2 y 3 se cancelan: puesto que el canal de reflexión dota de un desfase $e^{i\frac{\pi}{2}}=i$ al fotón reflejado, las amplitudes de probabilidad asociadas son $\mathcal{A}_{refl}=\frac{i}{\sqrt{2}}$ y $\mathcal{A}_{trans}=\frac{1}{\sqrt{2}}$ , de forma que la probabilidad para reflexión de ambos fotones resulta $P_{2refl}=|\mathcal{A}_{refl}|^2=-\frac{1}{2}$ , mientras que para transmisión conjunta es $P_{2trans}=|\mathcal{A}_{trans}|^2=+\frac{1}{2}$ , de forma que el cálculo de la probabilidad conjunta de ambos eventos (los dos fotones se reflejan, o los dos se transmiten) es nulo:

$P_{\mbox{2refl+2trans}}=| \mathcal{A}_{refl1}\mathcal{A}_{refl2}+\mathcal{A}_{trans1}\mathcal{A}_{trans2}|^2=| \frac{i}{\sqrt{2}}\frac{i}{\sqrt{2}}+ \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}|^2 =0$

Al igual que en la doble rendija, el hecho de que haya dos vías alternativas posibles (caminos o procesos de Feynman) indistinguibles para llegar al mismo resultado, necesita ser incorporado: la amplitud de probabilidad total $\mathcal{A}$ para el evento es la suma de las amplitudes de probabilidad para cada proceso, $\mathcal{A}=\sum_i \mathcal{A}_i$ , de forma que en el cálculo de la probabilidad del evento,

$P=|\mathcal{A}|^2=|\sum_i \mathcal{A}_i|^2$ ,

pueden ocurrir cancelaciones entre las amplitudes:

$\rightarrow$ Experiencia de Hong, Ou y Mandel

Pero cuando hay distinguibilidad entre las vías alternativas, entonces las probabilidades se suman directamente:

$P=\sum_i P_i=\sum_i |\mathcal{A}_i|^2$ ,

por lo que desaparecen las interferencias entre las amplitudes, de modo que se registran coincidencias en los detectores: no hay efecto de agrupamiento o «bunching» fotónico.

canales r-r y t-t en coincidencia — Caso de caminos ópticos diferentes; imagen de A. Ibarra-Durán, Interferencias bifotónicas en un divisor de haces, Tecnociencia 8, 1, 2006, pp. 167-181 .

Cuando se ocupan los dos canales o modos de entrada, el divisor de haz puede denominarse más bien como un «combinador» de modos: la actuación del BS se corresponde pues con la ecuación:

$|in>\equiv \hat{a}_o^{\dagger} \hat{a}_i^{\dagger}|0_o>|0_i>$

$\rightarrow \quad |out>\equiv =\frac{i}{\sqrt{2}}(|2_r0_t> +|0_r2_t>)$

Emergencia de los dos fotones juntos: por las interferencias que ocurren, no se produce detección en coincidencia.

Los detectores colocados en los dos canales de salida nunca señalarán eventos de detección simultáneamente, una indicación clara de que los dos fotones están realmente incidiendo simultáneamente.

En 1987, Hong, Ou y Mandel realizaron la comprobación experimental de este resultado (ausencia de coincidencias):

Hong, C. K., Ou, Z. Y. and Mandel, L.; Measurement of subpicosecond time intervals between two photons by interference; Phys. Rev. Lett. 59, 18 (1987) 2044-2046.

We wish to report an experiment in which the time interval between signal and idler photons, and by implication the length of a subpicosecond wave packet, produced in parametric down-conversion was measured. The technique is based on the interference of two two-photon probability amplitudes in two-photon detection, and is easily able to measure a time interval of 50 fs, with an accuracy that could be 1 fs or better.

-Su dispositivo (interferómetro de Hong-Ou-Mandel) tenía como propósito medir la separación temporal entre una pareja de fotones, producidos por conversión paramétrica a la baja en un cristal no lineal, SPDC tipo I, que se hacían incidir sobre un divisor de haz (BS), que se podía desplazar ajustando así la diferencia de camino entre los dos haces o, en términos de fotones, su retardo temporal:

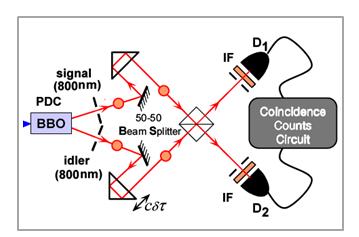
Dispositivo HOM — Un láser operando a 351,1 nm incide sobre un cristal KDP; imagen de: http://smos.sogang.ac.kr/wiki/index.php/Quantum_optics

-Si el BS se sitúa de manera que hay un retraso entre el tiempo de incidencia de uno de los fotones respecto al otro, los fotones se reflejarán o transmitirán de forma independiente, y los detectores irán señalando a un ritmo en el que la razón de coincidencia puede demostrarse sigue la fórmula:

$R_{coinc}\approx (1-e^{-(\Delta \omega)^2(\tau_s-\tau_i)^2})$

(cf. [GER-05] , p. 218), donde $\Delta \omega$ es la anchura espectral, que se asume como gaussiana, y $c\tau_s \,,\, c\tau_i$ son las distancias que los fotones signal e idler, respectivamente, han recorrido desde el cristal hasta el BS; $\tau_{corr}=\frac{1}{\Delta \omega}$ es el tiempo de correlación o coherencia, que es del orden de unos pocos nanosegundos.

$\rightarrow$ Con caminos de longitud diferente, cuando la diferencia entre ellos es mayor que el tiempo de coherencia, no hay interferencia y cada fotón sale aleatoriamente al 50% por cada puerto, de manera que se produce detección en coincidencia en el 50% de los eventos.

Para una posición del BS en que los dos caminos son iguales, y su diferencia es entonces menor que el tiempo de correlación, esto es, no hay retraso de un fotón respecto al otro, $\tau_s=\tau_i$ , y se ha de tener $R_{coinc}\approx 0$ .

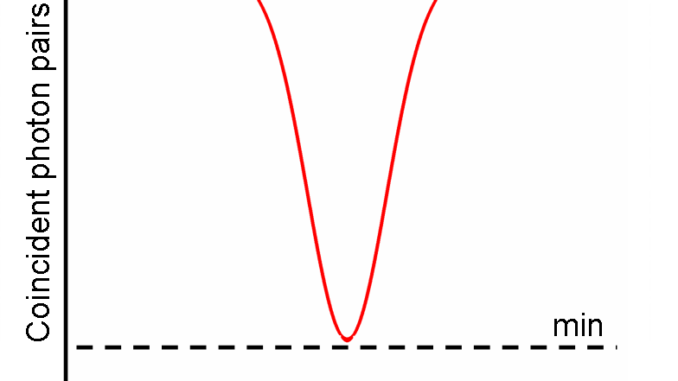
-Los resultados del experimento se muestran en la siguiente figura:

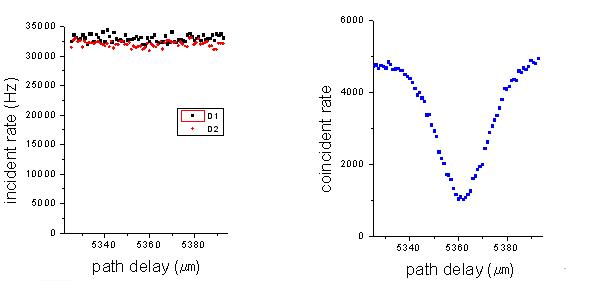
Resultados HOM — La ratio de coincidencias muestra un pico de bajada muy acusado cuando los caminos ópticos de los dos fotones se hacen idénticos (véase http://smos.sogang.ac.kr/wiki/index.php/Quantum_optics).

La razón de coincidencias es máxima cuando $|\tau_s -\tau_i| \gg \tau_{corr}$ .

It will be seen that for a certain symmetric position of the beam splitter, the two-photon coincidence rate falls to a few percent of its value in the wings, by virtue of the destructive interference of the two two-photon probability amplitudes. The width of the dip in the coincidence rate provides a measure of the length of the photon wave packet.

La detección en coincidencia prácticamente desaparece cuando los dos caminos se igualan en longitud, esto es, los dos fotones inciden simultáneamente (no es cero estrictamente ya que la simultaneidad nunca es totalmente perfecta).

Interferometría HOM o bifotónica

Al igual que en la doble rendija, el hecho de que haya dos vías alternativas posibles (caminos o procesos de Feynman) indistinguibles para llegar al mismo resultado, provoca que se produzcan cancelaciones entre las amplitudes.

Si hay distinguibilidad entre las vías alternativas, entonces las probabilidades se suman directamente y desaparecen las interferencias entre las amplitudes, de modo que se registran coincidencias en los detectores: no hay efecto de agrupamiento o «bunching» fotónico.

Y.-H. Kim; Two-Photon Interference without Bunching Two Photons;

Y.-H. Kim; Two-photon interference without bunching two photons; Physics Letters A 315 (2003) 352-357:

Abstract: We report an experiment which conclusively demonstrates that the two-photon entangled state interference cannot be pictured as the overlap and «bunching» of two individual photons on a beamsplitter. We also demonstrate that photon «bunching» does not occur if the two-photon Feynman amplitudes are distinguishable, even though individual photons do overlap on a beamsplitter.

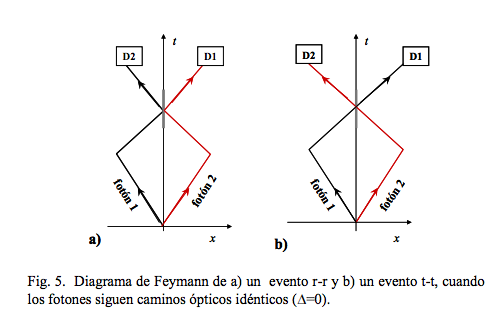
This effect, which we refer to as SA/HOM effect, has the following interpretation: because the two two-photon (or biphoton) amplitudes leading to a coincidence count (both photons are reflected at the beamsplitter, r-r, or both photons are transmitted at the beamsplitter, t-t) become indistinguishable, even in principle, when the photons arrive at the beamsplitter simultaneously from the different input ports, fourth-order two-photon quantum interference occurs. Due to the destructive nature of the interference (each photon accumulates i phase shift upon reflection at the beam splitter) between r-r and t-t amplitudes, zero coincidence counts are expected.

Abstract del preprint: We report a novel interference experiment in which the two-photon entangled state interference cannot be pictured in terms of the overlap and bunching of two individual down-converted photons on a beamsplitter. Experimentally, this is accomplished by choosing the arrival time difference between the two photons at the beamsplitter much bigger than the coherence time of the pump pulse as well as the coherence times of the individual photons. We also experimentally demonstrate that two-photon interference, or photon bunching effect on a beamsplitter, does not occur if the two photon Feynman amplitudes are distinguishable, even though individual photons do overlap on a beamsplitter. Therefore, two-photon interference cannot be viewed as interference of two individual photons, rather it should be viewed as two-photon or biphoton interfering with itself. The results may also be useful for studying decoherence management in entangled two-qubit systems as we observe near complete restoration of quantum interference after the qubit pairs, generated by a femtosecond laser pulse, went through certain birefringent elements.

Análisis del experimento de Kim et al: A. Ibarra-Durán, Interferencia bifotónica en un divisor de haces (artículo de divulgación).

Otros experimentos

Correlaciones, indistinguibilidad y entrelazamiento en experimentos de Hong-Ou-Mandel a frecuencias de microondas:

Lang, C., Eichler, C., Steffen, L. et al., Correlations, indistinguishability and entanglement in Hong–Ou–Mandel experiments at microwave frequencies, Nature Phys 9, 345–348 (2013); https://doi.org/10.1038/nphys2612

Zou, X. Y., Wang, L. J. and L. Mandel, Induced coherence and Indistinguishability in Optical Interference, Phys. Rev. Lett. 67 (1991) 318:

Interferometría HOM con partículas materiales:

-Una propuesta de experimento con ondas de materia:

Lewis-Swan & Kheruntsyan; Proposal for demonstrating the Hong-Ou-Mandel effect with matter waves, Nature Communications (2014), DOI: 10.1038/ncomms4752.

-Y una realización con átomos:

R. Lopes et al; Atomic Hong-Ou-Mandel experiment, Nature Letter 520 (2015)66 , DOI: https://doi.org/10.1038/nature14331.

Otros artículos sobre interferometría HOM:

Macroscopic Hong-Ou-Mandel interference

A. Aspect, Hanbury Brown and Twiss, Hong Ou and Mandel effects and other landmarks in quantum optics: from photons to atoms.

Bibliografía

[FOX-06] Fox, M.; «Quantum Optics. An introduction». Oxford Univ. Press; Oxford, 2006 (pp. 301-303).

[GER-05] Gerry, C. C. and Knight, P. L., «Introductory Quantum Optics», Cambridge Univ. Press, Cambridge, 2005 (pp. 217-219).

G. Armendáriz, J. Cravioto-Lagos, V. Velázquez, M. Grether, E. López-Moreno and E. J. Galvez Teaching quantum mechanics with the Hong-Ou-Mandel interferometer , Proceedings of SPIE – The International Society for Optical Engineering, July 2013, 9289; OSA Publishing; DOI: 10.1117/12.2070280.

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

Experimento de Hong-Ou-Mandel

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta