Fuentes: esta entrada se basa principalmente en:
- Caps. 5 y 7, Introductory Quantum Optics, de Gerry y Knight ([GER-05]).
- Cap. 5, Quantum Optics, de Garrison y Chiao ([GAR-08]).
- Caps. 5 y 6, Quantum Optics. An introduction, de M. Fox ([FOX-04]).
Estadísticas fotónicas
Luz poissoniana
![]() Los estados coherentes de luz, o estados Glauber, siguen una estadística de Poisson, de forma que, sobre un estado de Glauber (autoestado del operador destrucción
Los estados coherentes de luz, o estados Glauber, siguen una estadística de Poisson, de forma que, sobre un estado de Glauber (autoestado del operador destrucción ):
-Valor medio del operador número y su cuadrado; indeterminación:
expresión característica de la distribución estadística de Poisson.
-Probabilidad de que el resultado de la medida del número de fotones en el campo, sobre un estado coherente , sea
:
probabilidad correspondiente a una distribución de Poisson:
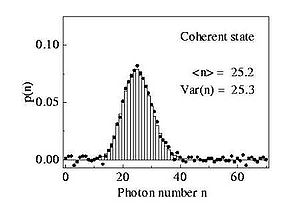
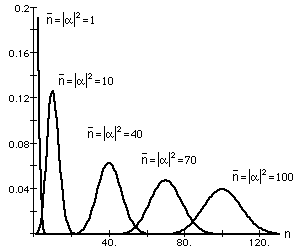
![]() La luz asociada a la distribución de Poisson es luz cuasi-clásica: la luz perfectamente coherente de un haz de intensidad constante, o la mayoría de la luz procedente de fuentes astronómicas, por ejemplo, pertenece a este tipo.
La luz asociada a la distribución de Poisson es luz cuasi-clásica: la luz perfectamente coherente de un haz de intensidad constante, o la mayoría de la luz procedente de fuentes astronómicas, por ejemplo, pertenece a este tipo.
-Un histograma de los fotones detectados por intervalo de tiempo sigue en este caso la distribución estadística de Poisson:
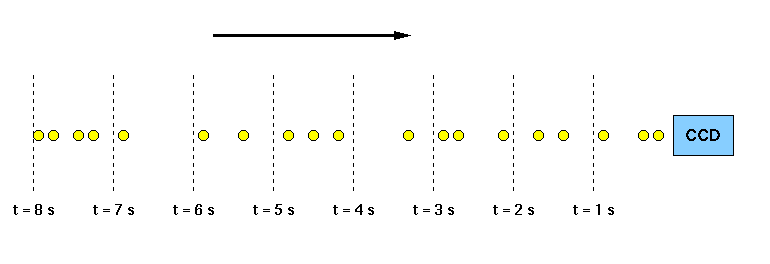
-Esta luz está compuesta por fotones distribuidos al azar sobre grandes distancias, de manera que los fotones van siendo detectados con grandes variaciones en el contaje (CCD=Charge Coupled Device):
Clasificación de la luz por estadística
![]() Existen más estadísticas fotónicas, además de la de Poisson:
Existen más estadísticas fotónicas, además de la de Poisson:
Junto con el valor
, el denominado parámetro
, definido como
,
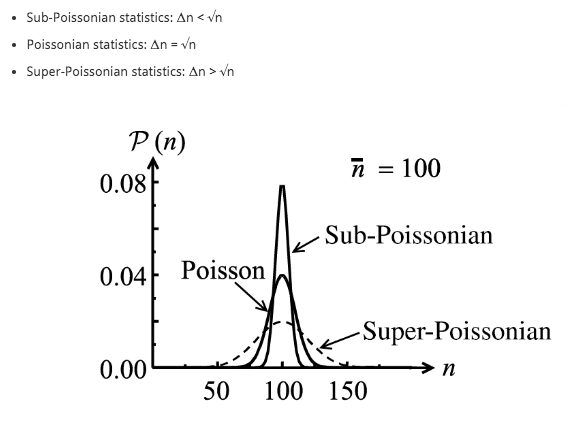
permite clasificar las distintas estadísticas fotónicas:
- Luz poissoniana o coherente:
.
- Luz super-poissoniana:
.
- Luz sub-poissoniana:
.
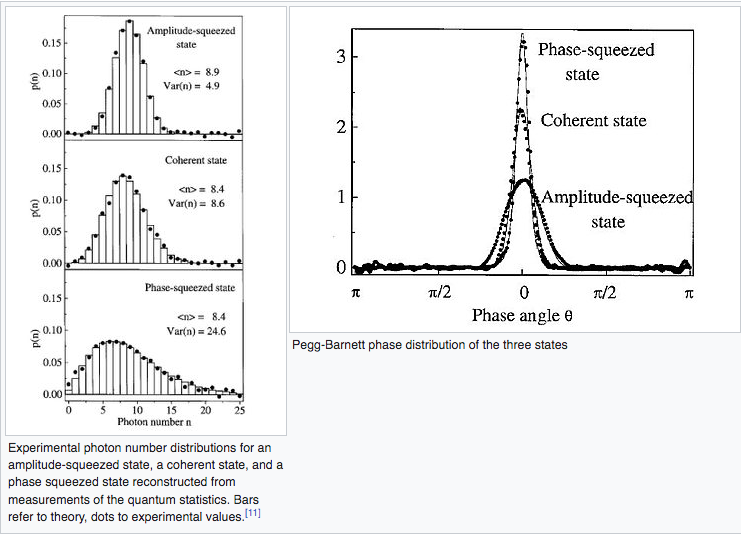
![]() Presentación por M. Krottenmüller: Estadísticas fotónicas
Presentación por M. Krottenmüller: Estadísticas fotónicas
![]() Estadísticas fotónicas en Wolfram
Estadísticas fotónicas en Wolfram
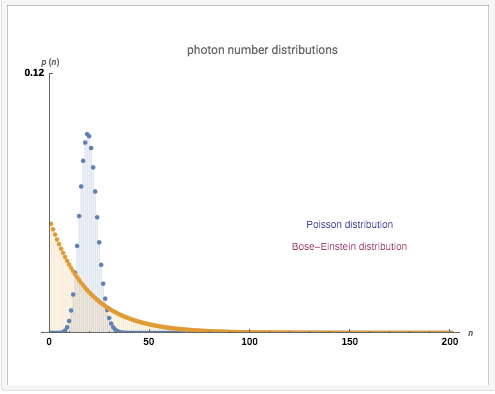
Luz super-poissoniana
![]()
![]() Esta estadística corresponde a una luz en la que se producen fluctuaciones de intensidad, por ejemplo, luz clásica en que la intensidad no se mantiene constante.
Esta estadística corresponde a una luz en la que se producen fluctuaciones de intensidad, por ejemplo, luz clásica en que la intensidad no se mantiene constante.
-Ejemplos: la radiación térmica o negra; la luz parcialmente coherente (caótica) de las rayas espectrales producidas en un tubo de descarga: el flujo de fotones no es constante debido a las fluctuaciones en la intensidad de la luz sobre una escala de tiempos de orden de magnitud del tiempo de coherencia.
-Es decir, medidas en un intervalo temporal recogerán luz super-poissoniana (efecto HBT); medidas en
recogerán en cambio luz poissoniana, ya que las variaciones de intensidad en esta escala temporal no se apreciarán.
-Es una luz con más ruido que la perfectamente coherente: en el sentido clásico de presentar variaciones de intensidad, y en el sentido cuántico de presentar mayores fluctuaciones en el número de fotones.
-Es un efecto clásico.
Luz sub-poissoniana
![]()
![]() Esta estadística corresponde a una luz sin análogo clásico, en la que la intensidad también se mantiene constante.
Esta estadística corresponde a una luz sin análogo clásico, en la que la intensidad también se mantiene constante.
-En algún sentido, se trata de luz más estable que la perfectamente coherente: una conceptualización sería la de un haz en que todos los fotones poseen una misma separación temporal constante , de forma que el contaje en un tiempo
sería siempre el mismo número entero de fotones
, y
.
![]() Los estados de Fock
Los estados de Fock , autoestados del operador número, responden a esta estadística, constituyendo la forma más pura de luz sub-poissoniana.
Clasificación de la luz por la función de coherencia
![]() Las funciones de correlación temporal de segundo orden, clásica y cuántica, se definen:
Las funciones de correlación temporal de segundo orden, clásica y cuántica, se definen:
,
dondeindica promedio sobre un intervalo de tiempo
suficientemente largo;
y
representan, respectivamente, la intensidad del campo eléctrico y de la radiación en el instante
,
-Mientras quecuantifica las fluctuaciones temporales del campo eléctrico
, la de segundo orden
cuantifica las fluctuaciones temporales de la intensidad de la radiación
.
,
representando la probabilidad condicional de que se detecte, en una posición dada, un fotón eny también otro en
, esto es, con un retardo
.
-Si , entonces los fotones van llegando de forma independiente.
-Puede esperarse que para cualquier estado del campo, es decir, que, transcurrido un intervalo de tiempo suficientemente grande, la memoria del primer fotón detectado desaparezca.
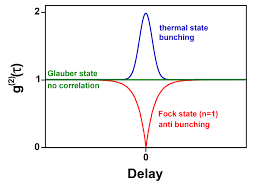
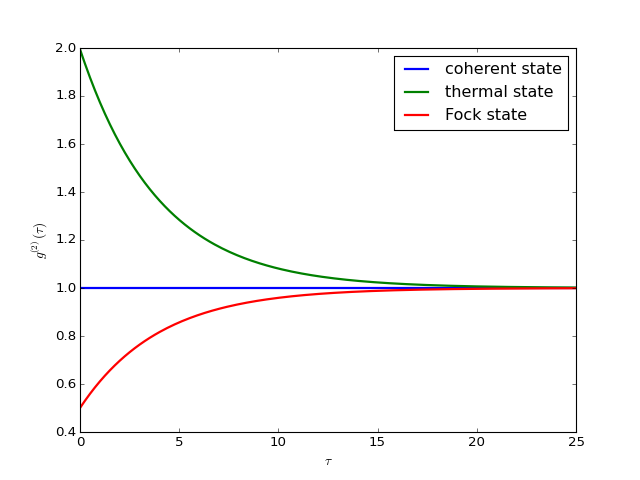
![]() En función del valor que tome la función de correlación cuántica temporal de segundo orden,
En función del valor que tome la función de correlación cuántica temporal de segundo orden, , la luz se clasifica como:
A) Primer criterio de clasificación:
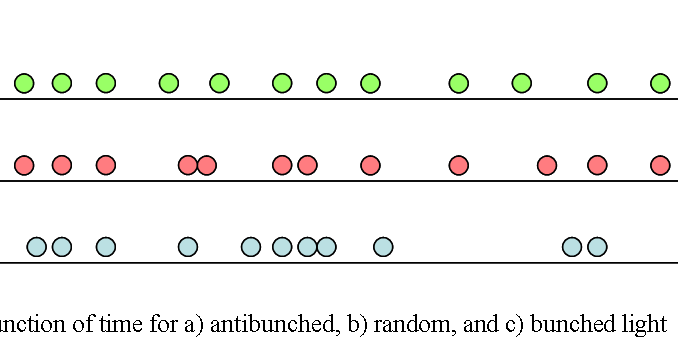
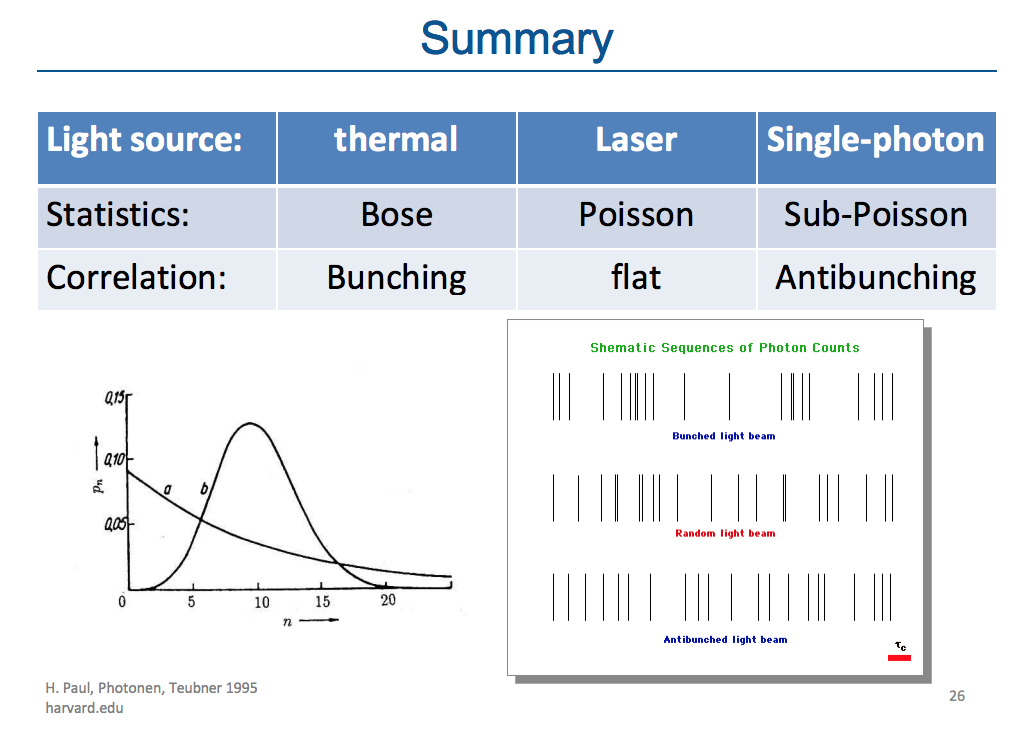
-Por el valor respecto a su valor en el origen: clasificación por bunching:
- A1:
: Luz agrupada o aglutinada (bunched light, photon bunching):

-Los fotones tienden a aparecer juntos, agrupados en paquetes: hay alta probabilidad de que se produzcan detecciones en coincidencia de fotones.
-La probabilidad de que se produzca la detección de un segundo fotón después de un retardodecrece con
-El efecto no es posible sobre un estado de un solo modo de campo.
-Se trata de luz parcialmente coherente, caótica.
-Es un efecto clásico. - A2:
: Luz anti-agrupada (photon antibunching):

-Los fotones tienden a aparecer separados, llegando con intervalo temporal de separación fijo.
-La probabilidad de que se produzca la detección de un segundo fotón después de un retardocrece con
.
-La probabilidad de que se produzcan detecciones en coincidencia de fotones en un intervaloes menor que en el caso de estado coherente.
-El efecto no es posible sobre un estado de un solo modo de campo.
-Luz totalmente incoherente.
–Luz no clásica.
-Empieza a estudiarse experimentalmente sobre todo a partir de 1977: H. Paul, Photon antibunching: «Nonlinear interaction mechanisms like multiphoton absorption and parametric three-wave interaction are suited to change the photon statistical properties of incident (in most cases coherent) light such that the output field will be endowed with antibunching properties».
- A3:
:Luz aleatoria (random) o desagrupada: ni agrupada ni anti-agrupada:

-Los fotones se presentan aleatoriamente.
-Ejemplo: la luz perfectamente coherente.
–Efecto clásico.
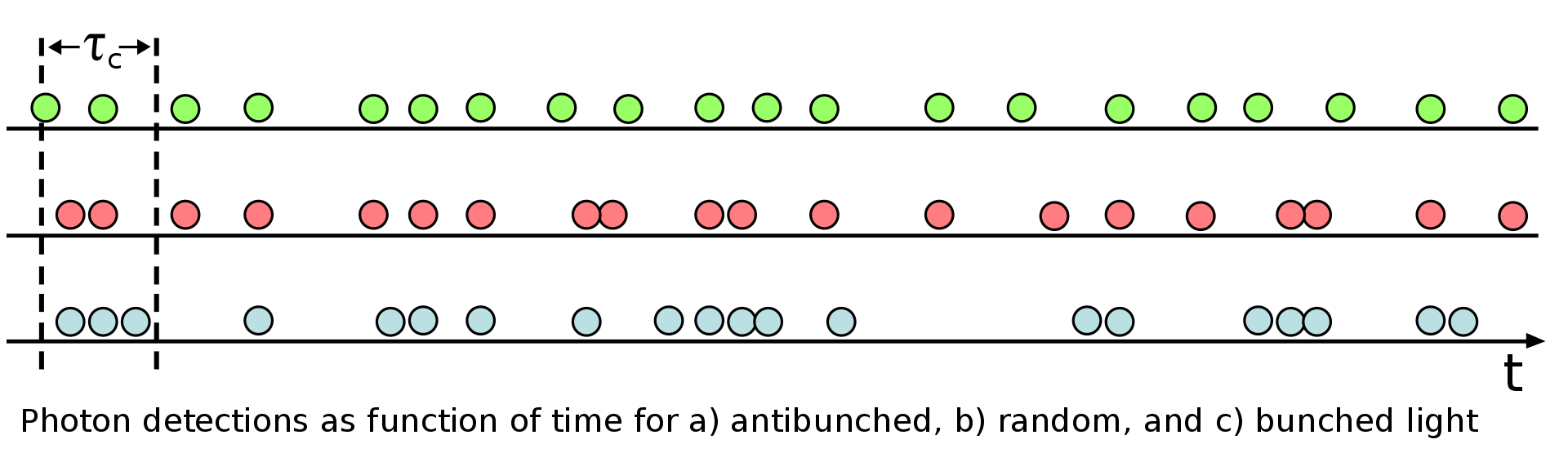
B) Segundo criterio de clasificación:
-Por el valor respecto a la unidad (resurge la clasificación por estadística):
B1: Cuando : luz no sub-poissoniana.
B1.1: Cuando : Luz perfectamente coherente, poissoniana.
-Ejemplo: campo en uno de los estados coherentes de Glauber, .
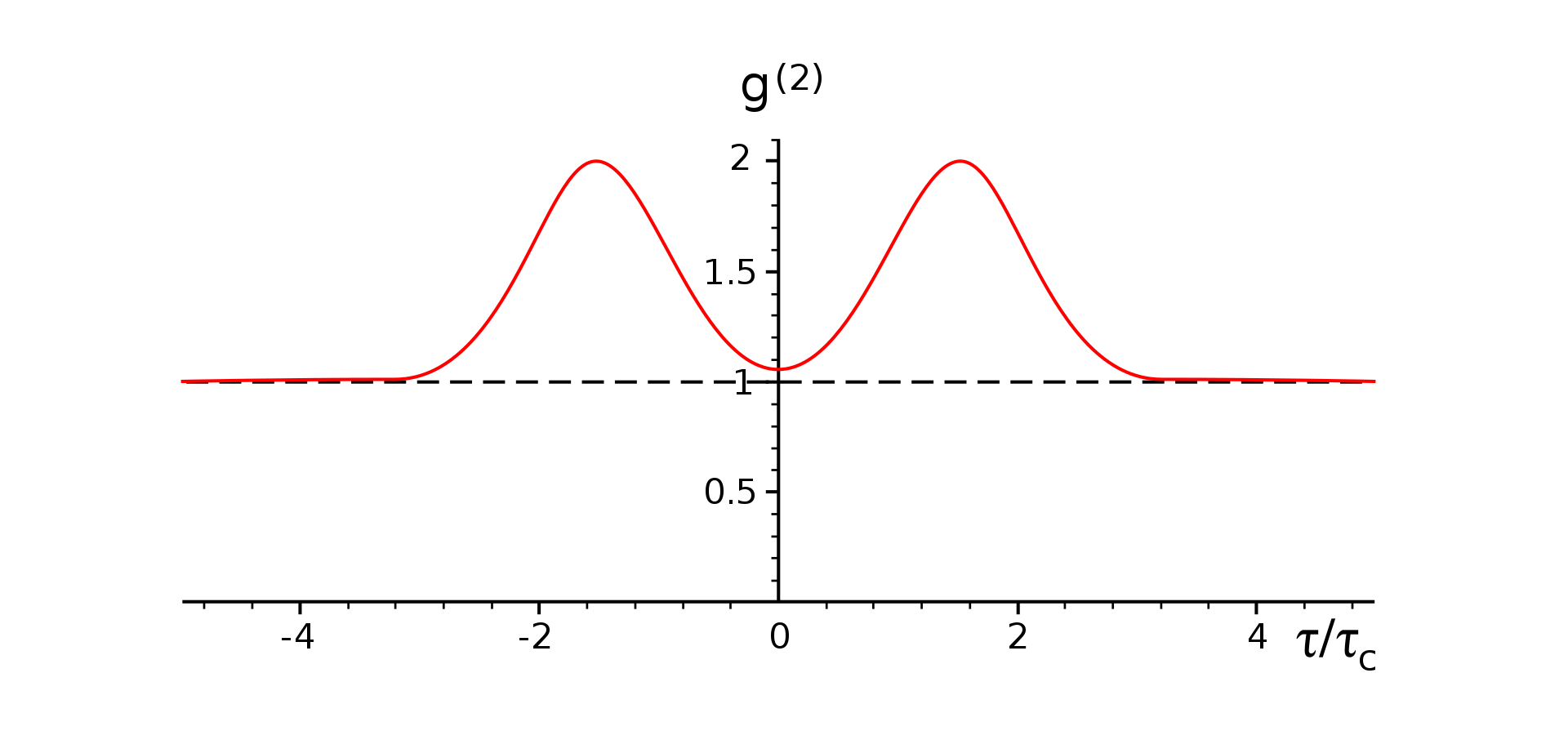
B1.2: Cuando : Luz parcialmente coherente o caótica, agrupada.
-Ejemplo: Para un campo en un modo monocromático térmico: (alta probabilidad de detección de fotones en coincidencia).
-Ejemplo: Toda la luz clásica (poissoniana y super-poissoniana).
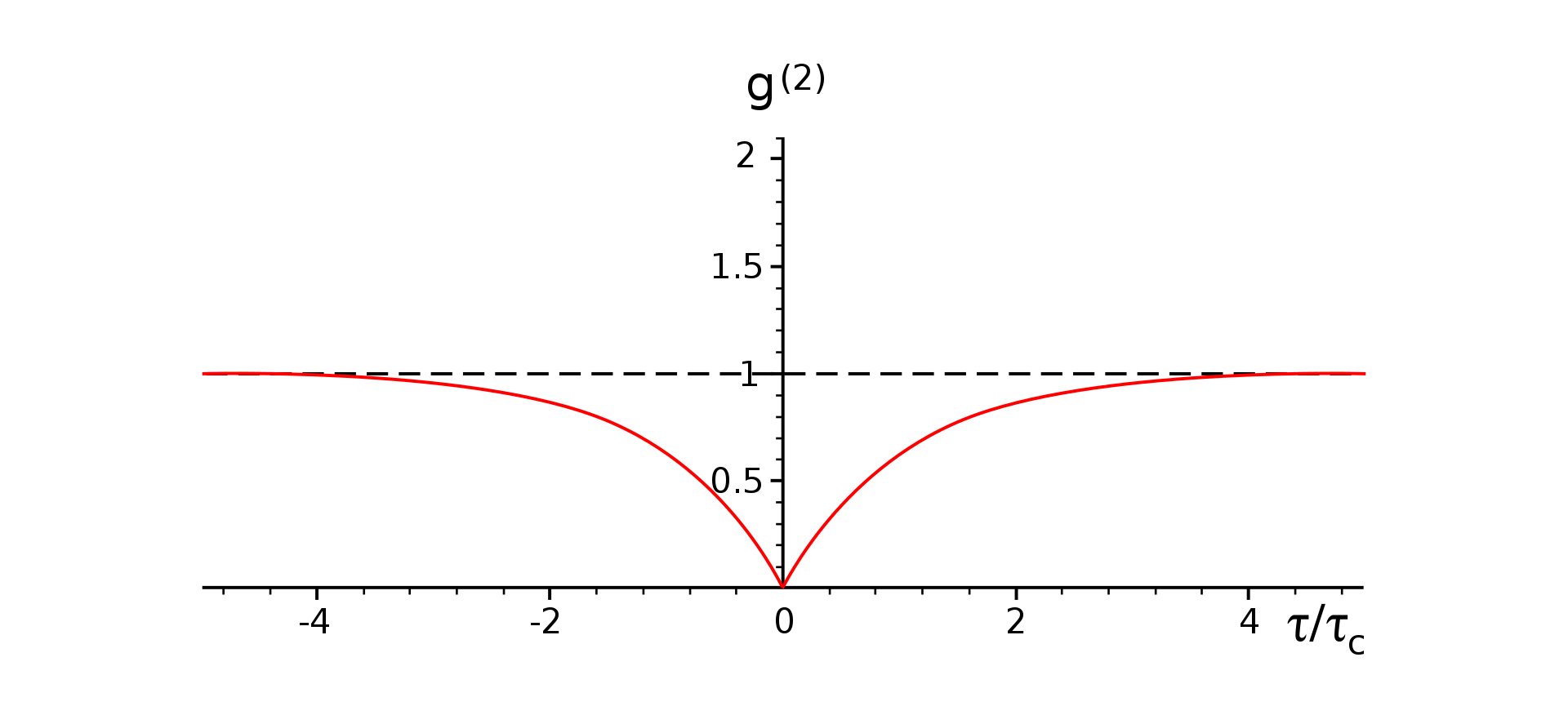
B2: Cuando : luz sub-poissoniana.
-Ejemplo: Sobre un estado de Fock , autoestado del operador número:
-En particular, para un estado de Fock de un solo fotón, , se tiene
.
-La condición puede ser simultánea con la de antibunching o no: son efectos diferentes:
![]() X. Y. Zou and L. Mandel, ‘‘Photon-antibunching and subPoissonian photon statistics’’, Phys. Rev. A 41, 475-476(1990).
X. Y. Zou and L. Mandel, ‘‘Photon-antibunching and subPoissonian photon statistics’’, Phys. Rev. A 41, 475-476(1990).
-La condición indica también anti-bunching cuando, siempre que no sea constante, se tenga
-Por ejemplo, para el caso de un solo modo de excitación de campo, se tiene , constante, y no hay anti-bunching.
-Es luz no clásica.
Luz coherente y luz comprimida o squeezed
![]() Un estado de luz se define como cuadráticamente comprimido (cuadrature squeezed state) cuando: bien
Un estado de luz se define como cuadráticamente comprimido (cuadrature squeezed state) cuando: bien , bien
.
-Por lo tanto, los estados squeezed no son en general estados MUS, o estados de mínima indeterminación (minimum uncertainty state), ya que sobre ellos no necesariamente se satura el principio de indeterminación, alcanzándose el mínimo producto de indeterminaciones:
,
donde , representan los operadores de cuadratura del campo electromagnético:
![]() Los operadores hermíticos cuadratura del campo,
Los operadores hermíticos cuadratura del campo, y
, se definen según:
y cumplen:
-Estos operadores se asocian a sendas amplitudes de oscilación en cuadratura, esto es, desfasadas entre sí radianes.
-En la representación número de fotones:
de manera que el principio de indeterminación satura sobre el vacío, ya que:
,
esto es, el vacío es un estado MUS.
-También los estados coherentes (estados de Glauber) son estados MUS:
![]() Los estados comprimidos
Los estados comprimidos son estados sobre los que la indeterminación de uno de las dos operadores cuadratura del campo
es menor que
, por lo que la del otro,
ha de ser mayor que
, de forma que sobre ellos las indeterminaciones de los dos operadores cuadratura son diferentes.
![]() Los estados comprimidos
Los estados comprimidos son estados sobre los que uno de los dos operadores cuadratura posee menos ruido que sobre un estado MUS como el vacío o como cualquier estado coherente; el otro, en cambio, posee más ruido.
-Algunos estados comprimidos pueden también saturar la desigualdad del principio de indeterminación, es decir, pueden ser estados MUS, pero en general no lo son.
-La compresión o squeezing no es un fenómeno clásico.
![]() Clasificación de la luz en términos de su compresión o squeezing:
Clasificación de la luz en términos de su compresión o squeezing:
- Luz no comprimida:
-Ejemplo: toda la luz clásica. - Luz comprimida:
Luz cuasi-clásica (cuántica) y no-clásica (radicalmente cuántica)
-Sea el parámetro:
.
Entonces:
A) Luz clásica (¡también cuántica!):
.
–Perfectamente coherente cuando ;
(fotones al azar).
–Parcialmente coherente o caótica cuando
-Superpoissoniana: (fotones agrupados).
-Nunca subpoissoniana.
-Nunca anti-agrupada.
-Nunca comprimida.
B) Luz no clásica (o radicalmente cuántica):
–Sub-poissoniana cuando ;
.
–Anti-agrupada cuando .
–Comprimida cuando .
-Nota: un criterio claro de clasicidad/no-clasicidad para un estado de luz puede darse en términos de la distribución de cuasi-probabilidad , o función de Glauber-Sudarshan, definida como la función tal que
Se consideran cuasi-clásicos los estados de luz para los cuales
es positiva o «no más singular que una función delta» (cf. [GER-05], p. 60).
———
Bibliografía
[FOX-04] Fox, M.; Quantum Optic. An introduction. Oxford Univ. Press; Oxford, 2004. ISBN: 0?19?856672?7, 978?0?19?856672?4.
[GAR-08] Garrison, J. C. and R. Y. Chiao, Quantum Optics, Oxford Univ. Press, Oxford, 2008. ISBN: 978-0-19-850886-1.
[GER-05] Gerry, C. C. and Knight, P. L., Introductory Quantum Optics, Cambridge Univ. Press, Cambridge, 2005. ISBN: 0-521-82035-9.
![]() Daniel Adam Steck, notes in Quantum and Atom Optics
Daniel Adam Steck, notes in Quantum and Atom Optics
![]() L. Scheel, Lecture notes in Quantum Optics:
L. Scheel, Lecture notes in Quantum Optics:
Lehre_Scheel/quantenoptik/Quantenoptik-Vorlesung3.pdf
Lehre_Scheel/quantenoptik/Quantenoptik-Vorlesung5.pdf
![]() Representaciones gráficas del campo cuántico en cavidades: Cavity Quantum Electrodynamics
Representaciones gráficas del campo cuántico en cavidades: Cavity Quantum Electrodynamics
![]() Carlos Navarrete-Benlloch; Lectures notes: Introduction to quantum optics
Carlos Navarrete-Benlloch; Lectures notes: Introduction to quantum optics
![]() Representaciones en el espacio de fases: funciones
Representaciones en el espacio de fases: funciones y de Wigner:
http://www.physics.miami.edu/~curtright/TimeDependentWignerFunctions.html
![]() http://journals.aps.org/rmp/abstract/10.1103/RevModPhys.54.1061
http://journals.aps.org/rmp/abstract/10.1103/RevModPhys.54.1061
![]() Estudios sobre luz antiagrupada (antibunched light):
Estudios sobre luz antiagrupada (antibunched light):
-https://www.picoquant.com/applications/category/metrology/antibunching
![]() SPDC y anti-bunching:
SPDC y anti-bunching:
https://opg.optica.org/josab/fulltext.cfm?uri=josab-14-10-2417&id=35141
–M.C. Teich and B.E.A. Saleh, Squeezed and Antibunched Light, Physics Today 43(6), 1990,26-34; DOI:10.1063/1.881246.
-O.S. Magaña-Loaiza, Single emitters and photon antibunching.
Dejar una contestacion