El efecto fotoeléctrico

foton_elec_teleformacion-ayto-corun%cc%83a

Efecto fotoeléctrico

En 1887 H. Hertz observó que era más fácil establecer una descarga eléctrica entre dos electrodos metálicos si uno de ellos se iluminaba con luz ultravioleta.
Investigaciones posteriores de J.J. Thomson, W. Hallwachs y, principalmente, P.L.A. Lenard, demostraron que la luz ultravioleta provocaba la emisión de electrones desde la superficie del metal en el cátodo, con energía suficiente para alcanzar el ánodo.
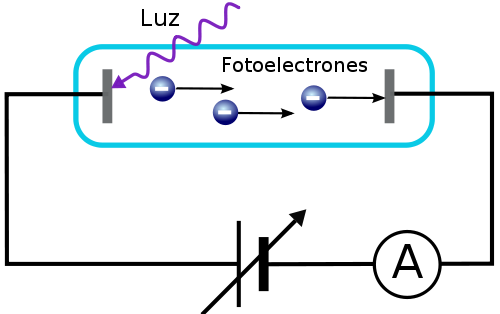
Los resultados experimentales observados son:
1. Respecto a la intensidad de la corriente generada en función de la diferencia de potencial aplicada entre los electrodos, para unas frecuencia fija e intensidad variable de la luz incidente:
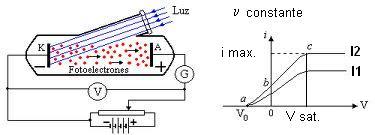
  - Cuando $V$ aumenta, $i$ aumenta; pero a partir de cierto valor suficientemente grande del potencial $V$ (denominado «potencial de saturación» $V_{sat}$ ), la corriente $i$ se mantiene ya estable en un valor máximo $i_{max}$ .
  - Al variar la intensidad $I$ de la luz incidente, cambia $i_{max}$ , manteniéndose $V_{sat}$ constante para $\nu$ constante. Este hecho ya había sido observado por J.J. Thomson en sus experimentos con rayos catódicos en tubos de descarga.
  - Al invertir la polaridad de $V$ , convirtiéndolo en potencial retardador, existe un valor de corte $V_{0}$ a partir del cual la corriente $i$ desaparece; para este valor se tiene la ecuación $e \cdot |V_{0}|=\frac{1}{2}mv_{max}^2$ , de forma que la constancia de $V_{0}$ indica que la distribución energética de los fotoelectrones es independiente de la intensidad $I$ de la luz incidente.
2. Respecto a la frecuencia de la luz incidente:
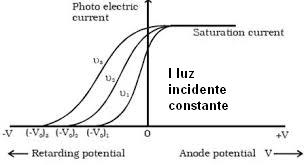
  - Al variar la frecuencia $\nu$ de la luz incidente, varía el potencial de corte $V_{0}$ , es decir, la energía cinética máxima de los fotoelectrones es directamente proporcional a la frecuencia de la luz incidente: una débil luz azul produce fotoelectrones más energéticos que una intensa luz roja (¡pero en menor número!). Esto ya había sido también observado por Thomson: una radiación de mayor frecuencia producía la emisión de partículas con mayor energía cinética.
  - Existe una frecuencia umbral $\nu_{0}$ , distinta y característica para cada metal, por debajo de la cual no se emiten fotoelectrones:
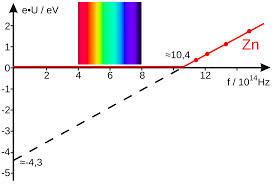
    Diagram of the maximum kinetic energy as a function of the frequency of light on zinc (Zn). x: frequency of light; y: kinetic energy of the electrons With the spectrum of visible light the electrons aren’t emitted (autor de imagen y pie: Klaus-Dieter Keller; Creative Commons Attribution 3- Unported license).
  - La energía máxima de los fotoelectrones depende de la frecuencia $\nu$ de la luz incidente, para cada metal, según la ley $e \cdot |V_{0}|=\frac{1}{2}mv_{max}^2=\text{constante} \cdot (\nu-\nu_{0})$ , determinándose que la constante era universal: no dependía del material utilizado en el cátodo.
3. Dentro de los límites de precisión accesibles, no se produce un retardo temporal entre la incidencia de la luz sobre la superficie y la emisión fotoeléctrica.

Explicación teórica

Explicación clásica:
La explicación clásica no consigue dar cuenta de todos los hechos experimentales observados:
1. La energía cinética de los fotoelectrones debería ser proporcional a la intensidad $I$ de la onda electromagnética incidente, aumentando con ésta aunque la frecuencia $\nu$ se mantuviese constante (algo que no ocurre).
2. El efecto fotoeléctrico debería producirse para cualquier valor de la frecuencia $\nu$ , siempre que la intensidad $I$ de la onda electromagnética incidente se aumentase lo suficiente: no se explica pues la aparición de la frecuencia umbral $\nu_{0}$ específica para cada metal.
3. Debido a que la energía en una onda se supone uniformemente distribuida a lo largo de todo el frente de onda, para una luz débil debería observarse un cierto retardo temporal en la emisión fotoeléctrica, de magnitud apreciable con los límites de precisión en medición de tiempos accesibles experimentalmente (no observado nunca).

Explicación por Einstein: en 1905, en un artículo titulado «Un punto de vista heurístico sobre la producción y transformación de la luz«, disponible también en Universo Einstein, mostró como la hipótesis de un cuanto de luz podía explicar el efecto fotoeléctrico y la presencia de una frecuencia característica para cada material por debajo de la cual no se producía ningún efecto:
«In spite of the complete experimental confirmation of the theory as applied to diffraction, reflection, refraction, dispersion, etc., it is still conceivable that the theory of light which operates with continuous spatial functions may lead to contradictions with experience when it is applied to the phenomena of emission and transformation of light.
It seems to me that the observations associated with blackbody radiation, fluorescence, the production of cathode rays by ultraviolet light, and other related phenomena connected with the emission or transformation of light are more readily understood if one assumes that the energy of light is discontinuously distributed in space. In accordance with the assumption to be considered here, the energy of a light ray spreading out from a point source is not continuously distributed over an increasing space but consists of a finite number of energy quanta which are localized at points in space, which move without dividing, and which can only be produced and absorbed as complete units.
In the following I wish to present the line of thought and the facts which have led me to this point of view, hoping that this approach may be useful to some investigators in their research».
-Por esta explicación «heurística», expuesta con tanta precaución y con la que resolvería el efecto fotoeléctrico, recibiría el premio Nobel de Física en 1921. Aunque lo cierto es que, en su momento, más bien se usó este tema como pretexto, porque no hubo coraje para dárselo por su también revolucionaria teoría de la relatividad general, publicada en 1915.
Por otra parte, el mismo Einstein no atribuiría «realidad» a los cuantos de luz hasta casi 1916, cuando logró derivar con ellos la fórmula de Planck para la radiación del cuerpo negro. Fue entonces cuando estableció que el cuanto de luz posee momento (¡una cantidad vectorial!), y afirmó que había tres procesos elementales para describir la interacción materia-radiación: uno espontáneo (Ausstrahlung), en el que las moléculas emiten sin estímulo exterior, y dos inducidos por la radiación (Einstrahlung), uno de emisión estimulada (germen del láser) y otro de absorción, en ambos casos con probabilidad proporcional a la densidad de radiación presente. Además, encuentra que las correspondientes probabilidades de transición son espontáneas: el azar comienza a insinuarse como un ingrediente ineludible e inherente a la teoría cuántica (cf. Einstein, “Sobre la teoría cuántica de la radiación”, Mitt. Phys. Ges. Zürich 18, 1916).
Suele afirmarse que Einstein conceptualizó la radiación como compuesta de paquetes indivisibles de energía o «cuantos de luz» («fotones» a partir de 1926, en terminología introducida por Lewis), que se desplazan localizadamente a velocidad $c$ (vacío); para una frecuencia $\nu$ , la energía del cuanto es $E = h \nu$ . Con esta hipótesis, se consigue dar cuenta de todos los hechos experimentales observados:

1. Los cuantos de luz penetran en el material, comunicando toda su energía a algún electrón atómico (absorción completa: requiere electrón ligado), que es expulsado con energía cinética variable, $\frac{1}{2}mv^2=h \cdot \nu-W$ , que será máxima para el caso de un electrón superficial (para el que la función de trabajo $W$ del material, o energía mínima necesaria para arrancarlo, variable en general para cada electrón, toma el valor $W=W_0$ , característico de cada material):
  $\frac{1}{2}mv_{max}^2=h \cdot \nu-W_{0}$ , donde $h$ es la constante de Planck, $h = 6.626 \times 10^{-34}J \cdot s = 41.357 \times 10^{-16} eV \cdot s$ , y $W_{0}$ representa la función de trabajo del material específico, o trabajo mínimo necesario para arrancar un electrón desde la superficie de ese metal (depende del metal específico, es igual para todos los electrones de la superficie y suele ser del orden de algunos pocos $eV$ ).
2. Por lo anterior, queda justificado que la energía cinética máxima de los fotoelectrones no dependa de la intensidad de la luz incidente: al tratarse de una interacción de cada fotoelectrón con un cuanto, importa la frecuencia de este último, no el número de ellos presente.
3. Y, por lo mismo, a mayor intensidad $I$ de luz incidente (esto es, a mayor número de cuantos de luz), mayor intensidad $i$ de corriente producida, al producirse mayor número de procesos de interacción fotoelectrón-cuanto de luz.
4. Según la correspondiente fórmula anterior, $\frac{1}{2}mv_{max}^2=h \cdot \nu-W_{0}$ , y podemos calcular el potencial de corte $V_{0}$ experimental, o potencial retardador a partir del cual cesa la corriente, dependiente de la frecuencia de la luz incidente: $e \cdot |V_{0}|=\frac{1}{2}mv_{max}^2=h \cdot \nu-W_{0}$ .
5. La frecuencia de corte característica $\nu_{0}$ para ese material corresponderá al caso de energía cinética cero: $h \nu_{0} = W_{0}$ ; por debajo de esta frecuencia umbral no se producirá corriente, incluso sin potencial retardador, porque no se produce la emisión de fotoelectrones: los cuantos de luz con frecuencia inferior a la umbral, según Einstein, no han sido absorbidos por los fotoelectrones, y tampoco un electrón podía absorber más de un cuanto de luz con $\nu < \nu_0$ y acumular energía para convertirse así en fotoelectrón (electrón emitido y que sale del material hacia el ánodo).
6. El carácter localizado e indivisible del cuanto de luz (carácter corpuscular, en suma), justifica la instantaneidad del proceso y la subsiguiente ausencia de retardo observable en la emisión de los fotoelectrones.
Obsérvese que, obtenida la curva experimental $e \cdot |V_{0}|= h \cdot (\nu-\nu_{0})$ , a partir de la pendiente de esta recta se puede estimar el valor de la constante $h$ de Planck (conocida la carga $e$ del electrón).
Durante los años 1912-1916, tras haber obtenido la masa del electrón con su experimento de la gota de aceite, R. Millikan comprobó en una serie de experimentos sucesivos como la ecuación $e \cdot |V_{0}|=h \cdot \nu-W_{0}$ se ajustaba a los datos experimentales, lo cual le permitió determinar el valor de la constante $h$ de Planck. Hay que destacar que estos experimentos eran muy difíciles de realizar, sobre todo por las dificultades prácticas que presentaba la medida del potencial de contacto o Volta entre los electrodos, fuente de numerosos errores experimentales. Por todo su trabajo, recibiría el Premio Nobel en 1923. En su discurso de aceptación del Nobel, en 1924, como una muestra de la desconfianza general que persistía por aquel entonces respecto al cuanto de luz, declaró:
“La concepción de los cuantos de luz localizados, a partir de la cual Einstein obtuvo su ecuación [efecto fotoeléctrico] debe considerarse todavía lejos de estar establecida”.
Nota: Hoy en día, se ha observado que, cuando la intensidad de la luz es muy elevada (luz láser, por ejemplo), puede suceder que un solo electrón absorba dos fotones, esto es, una energía $2 h \nu$ . Entonces, es como si se estuviese iluminando con luz de frecuencia doble. Igualmente, también son posibles procesos más complicados, por ejemplo, en los que un mismo fotón interactúa con varios electrones de un mismo átomo… (véase, por ejemplo, Cohen-Tannoudji, 1998, pp. 98ss.). La óptica cuántica, a través de la teoría cuántica de campos, dará cumplida cuenta de todos ellos.

Notas históricas

La observación de que la diferencia entre los conceptos de energía discreta y continua lleva a contradicciones con la experiencia en la interacción radiación-materia llevó a Einstein en 1905 a introducir el “cuanto de luz”:
A. Einstein, “Sobre un punto de vista heurístico concerniente a la producción y la transformación de la luz”, Ann. Phys. 17, 1905, 132-148:
«La energía de un rayo de luz […] no está distribuida de forma continua sobre un espacio creciente, sino que consiste en en un número finito de cuantos de energía que se localizan en puntos del espacio, se mueven sin dividirse, y pueden ser sólo producidos y absorbidos como unidades completas».
«Concluimos que la la radiación monocromática de baja densidad (dentro del rango de validez de la fórmula de Wien para la radiación) se comporta termodinámicamente como si consistiese de un número de cuantos de energía independientes».
Conviene señalar, por rigor histórico, que Einstein afirmó en 1909, en carta a Lorentz, respecto a su cuanto de luz:
«I must have expressed myself unclearly in regard to the light quanta. That is to say, I am not at all of the opinion that one should think of light as being composed of mutually independent quanta localized in relatively small spaces. This would be the most convenient explanation of the Wien end of the radiation formula. But already the division of a light ray at the surface of refractive media absolutely prohibits this view. A light ray divides, but a light quantum indeed cannot divide without change of frequency».
«As I already said, in my opinion one should not think about constructing light out of discrete, mutually independent points. I imagine the situation somewhat as follows: […] I conceive of the light quantum as a point that is surrounded by a greatly extended vector field, that somehow diminishes with distance. Whether or not when several light quanta are present with mutually overlapping fields one must imagine a simple superposition of the vector fields, that I cannot say. In any case, for the determination of events, one must have equations of motion for the singular points in addition to the differential equations for the vector field».
En 1911, en el I Congreso Solvay, afirmó: «Insisto en el carácter provisional de este concepto (quanta de luz) que no parece reconciliable con las consecuencias experimentales verificadas de la teoría ondulatoria».
Pero en 1918 afirma ya, en carta a M. Besso: «No dudo ya de la realidad de los cuantos de radiación, aunque todavía permanezco bastante solo en esta convicción»
Son variadas las razones que motivaban que la mayoría de los físicos se resistieran a aceptar el cuanto de luz. Entre ellas:
1. Einstein era un completo desconocido en la Física de 1905. Y su «hipótesis heurística» introducía una oscura noción que sugería, nada más y nada menos, reconsiderar las ecuaciones de Maxwell.
2. Así que, como ejemplos, Poincaré afirmó en el primer Congreso Solvay, 1911: “La implantación del cuanto de luz podría significar el fin de las ecuaciones diferenciales como herramienta matemática para expresar las leyes de la física. El cálculo con diferencias finitas ocuparía su lugar, tal vez”. Y Planck, en 1913, afirmó, en la misma línea: “En suma, puede afirmarse que entre los problemas importantes, tan abundantes en la física moderna, no existe alguno ante el que Einstein no adoptara una posición de forma notable. Que, a veces, errara en sus especulaciones, como por ejemplo en su hipótesis acerca del quantum de luz, no puede esgrimirse realmente demasiado en su contra. Porque sin correr un riesgo de vez en cuando es imposible, incluso en la ciencia natural de mayor exactitud, introducir verdaderas innovaciones”.
3. Un ejemplo más, especialmente significativo: R. Millikan, 1916: “La ecuación fotoeléctrica de Einstein parece predecir exactamente en todos los casos los resultados observados. Pero la teoría semicorpuscular mediante la cual Einstein llegó a su ecuación parece hoy completamente insostenible. […] A pesar del éxito aparentemente completo de la ecuación de Einstein [para el efecto fotoeléctrico], la teoría física, de la que estaba destinada a ser expresión simbólica, se halló tan insostenible que el mismo Einstein, según creo, ya no la mantiene”. Y en 1924, en su discurso de recepción del Premio Nobel: “La concepción de los cuantos de luz localizados, a partir de la cual Einstein obtuvo su ecuación [efecto fotoeléctrico] debe considerarse todavía lejos de estar establecida”.
4. De modo que la oposición al cuanto de luz era casi unánime por aquellos años, y ni siquiera los resultados experimentales del efecto Compton (1923-25) lograron constituirse como una justificación suficiente para su aceptación unánime.