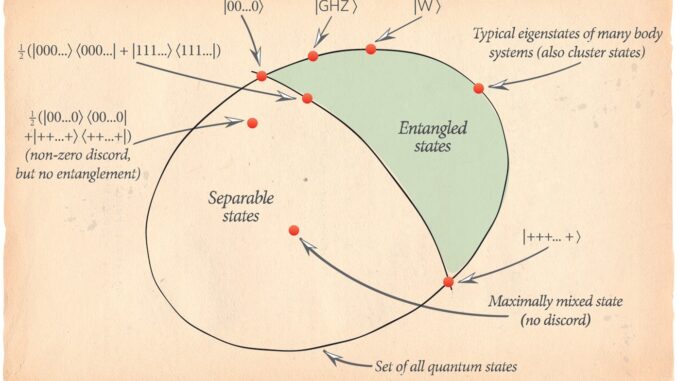
El entrelazamiento o enredo cuántico
![]() La propiedad cuántica del entrelazamiento (entanglement; «Verschränkung» originariamente en alemán) es una propiedad de algunos estados cuánticos que fue señalada por primera vez por Schrödinger en 1935:
La propiedad cuántica del entrelazamiento (entanglement; «Verschränkung» originariamente en alemán) es una propiedad de algunos estados cuánticos que fue señalada por primera vez por Schrödinger en 1935:
![]() Discussion of probability relations between separated systems, Proceedings of the Cambridge Philosophical Society 31 (1935) 555-562.
Discussion of probability relations between separated systems, Proceedings of the Cambridge Philosophical Society 31 (1935) 555-562.
![]() La función de onda del sistema de dos partículas, que se han separado después de una interacción temporal, no puede expresarse posteriormente como producto de funciones de onda separadas y, por tanto, el conocimiento de
La función de onda del sistema de dos partículas, que se han separado después de una interacción temporal, no puede expresarse posteriormente como producto de funciones de onda separadas y, por tanto, el conocimiento de [la función de onda del sistema de dos partículas entrelazadas] no permite adscribir a cada una de las dos partículas una función de onda individual; en otras palabras, el mejor conocimiento de un todo no incluye el mejor conocimiento de sus partes.
![]() Schrödinger consideró esta característica cuántica como profundamente insatisfactoria, pero a la vez también como la característica esencial y más radical del nuevo formalismo:
Schrödinger consideró esta característica cuántica como profundamente insatisfactoria, pero a la vez también como la característica esencial y más radical del nuevo formalismo:
![]() It is rather discomforting that the theory should allow a system to be steered or piloted into one or the another type of state at the experimenter’s mercy in spite of his having no access to it (ibid).
It is rather discomforting that the theory should allow a system to be steered or piloted into one or the another type of state at the experimenter’s mercy in spite of his having no access to it (ibid).
![]() I would not call [entanglement] one but the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought.
I would not call [entanglement] one but the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought.
![]() Einstein, Podolsky y Rosen la considerarían como no razonable:
Einstein, Podolsky y Rosen la considerarían como no razonable:
![]() A. Einstein, B. Podolsky and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Physical Review 47 (1935) 777-780:
A. Einstein, B. Podolsky and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Physical Review 47 (1935) 777-780:
![]() This makes the reality of P and Q depend upon the process of measurement carried out on the first system, which does not disturb the second system in any way. No reasonable definition of reality could be expected to permit this.
This makes the reality of P and Q depend upon the process of measurement carried out on the first system, which does not disturb the second system in any way. No reasonable definition of reality could be expected to permit this.
![]() Entrelazamiento o entanglement (definición de G.G. Alcaine):
Entrelazamiento o entanglement (definición de G.G. Alcaine):
![]() G. García Alcaine, «Enredo cuántico«, Revista Española de Física 19 (1), 2000, 17-29:
G. García Alcaine, «Enredo cuántico«, Revista Española de Física 19 (1), 2000, 17-29:
![]() Propiedad de aquellos estados de un sistema compuesto (calificados como verwickelten en alemán, entangled en inglés, enredados, entrelazados, etc. en español) que contienen correlaciones cuánticas clásicamente inalcanzables.
Propiedad de aquellos estados de un sistema compuesto (calificados como verwickelten en alemán, entangled en inglés, enredados, entrelazados, etc. en español) que contienen correlaciones cuánticas clásicamente inalcanzables.
[…] Si el sistema total se encuentra en un estado puro (es decir, máximamente determinado), el enredo se manifiesta en que el estado total no puede expresarse como producto de estados para cada una de sus partes (desde el punto de vista matemático), y en que ninguna de dichas partes por separado se encuentra en un estado puro (desde el punto de vista físico).
[…] El enredo cuántico es responsable de algunas de las propiedades más llamativas de la Mecánica Cuántica: contradicción con las teorías de Variables Ocultas deterministas Locales, teleportación del estado para variables discretas o continuas, borrado cuántico con elección retardada, interferencia de varias partículas, enredo entre dos cavidades con un sólo fotón, aplicaciones en metrología, espectroscopía, litografía interferométrica, mejora de la relación señal-ruido (en relojes atómicos, detección de ondas gravitacionales, etc.), etc. Mención especial merecen las aplicaciones del enredo en el campo de la información cuántica, incluyendo codificación densa, comunicación cuántica, superaditividad en la comunicación, criptografía cuántica, corrección de errores cuánticos, computación cuántica…
–Pero:
 Advertencia: correlaciones cuánticas sin entrelazamiento:
Advertencia: correlaciones cuánticas sin entrelazamiento:
![]() Correlaciones cuánticas clásicamente inalcanzables en sistemas sin entrelazamiento:
Correlaciones cuánticas clásicamente inalcanzables en sistemas sin entrelazamiento:
![]() Una demostración experimental de la violación de las desigualdades de Kochen y Specker para un único sistema cuántico, un fotón que puede viajar a lo largo de tres caminos posibles donde se realizan diferentes medidas cuyos resultados deben ser compatibles entre sí:
Una demostración experimental de la violación de las desigualdades de Kochen y Specker para un único sistema cuántico, un fotón que puede viajar a lo largo de tres caminos posibles donde se realizan diferentes medidas cuyos resultados deben ser compatibles entre sí:
![]() R. Lapkiewicz et al, «Experimental non-classicality of an indivisible quantum system», Nature 474 (2011) 490-493.
R. Lapkiewicz et al, «Experimental non-classicality of an indivisible quantum system», Nature 474 (2011) 490-493.
![]() En análisis de A. Cabello:
En análisis de A. Cabello:
![]() A. Cabello, «»Correlations without parts», Nature 474 (2011) 456-458:
A. Cabello, «»Correlations without parts», Nature 474 (2011) 456-458:
![]() Kochen and Specker noticed that quantum mechanics is in conflict with classical physics even for non-composite systems. This conflict can be converted into experimentally testable violations of classical correlation inequalities and into experiments showing that quantum correlations occur for any quantum state, not necessarily just for entangled ones.
Kochen and Specker noticed that quantum mechanics is in conflict with classical physics even for non-composite systems. This conflict can be converted into experimentally testable violations of classical correlation inequalities and into experiments showing that quantum correlations occur for any quantum state, not necessarily just for entangled ones.
![]() (Lapkiewicz and colleagues´) findings are therefore of fundamental importance, because they confirm that quantum correlations also occur in system in which entanglement, which is supposed to be the most emblematic feature of quantum mechanics, cannot be defined.
(Lapkiewicz and colleagues´) findings are therefore of fundamental importance, because they confirm that quantum correlations also occur in system in which entanglement, which is supposed to be the most emblematic feature of quantum mechanics, cannot be defined.
![]() It seems that Bell experiments, composite systems and entangled states are not enough to provide a complete understanding of the physical principles behind quantum mechanics: quantum correlations exist without them.
It seems that Bell experiments, composite systems and entangled states are not enough to provide a complete understanding of the physical principles behind quantum mechanics: quantum correlations exist without them.
![]() Divulgado en el blog de Francisco R. Villatoro.
Divulgado en el blog de Francisco R. Villatoro.
Estados puros y estados mezcla; operador densidad
![]() Estado puro: Sea un sistema cuántico y sea
Estado puro: Sea un sistema cuántico y sea el correspondiente espacio de Hilbert complejo y separable asociado para su descripción en el formalismo cuántico.
-Cuando sobre ese sistema se tiene información maximal, entonces el sistema se encuentra en un estado descrito matemáticamente por el vector de estado o ket , autoestado simultáneo de un C.C.O.C. (conjunto completo de observables compatibles, existiendo en el Hilbert una base ortonormal numerable común a todos ellos, esto es, en la que todos admiten expresión diagonal). En este caso, se dice que el sistema se halla en un estado puro, representado por el correspondiente ket del Hilbert.
![]() Operador densidad para un estado puro:
Operador densidad para un estado puro:
-El operador densidad para un estado puro se define como el producto externo o ket-bra:
,
que representa, en este caso, el proyector sobre el espacio monodimensional del correspondiente ket.
-La matriz densidad se define como la matriz cuadrada de elementos
, donde
representa una base ortonormal dada del correspondiente espacio de Hilbert.
![]() En términos del operador densidad para el estado puro
En términos del operador densidad para el estado puro ,
, se escriben:
-El valor esperado de un observable
sobre el estado puro normalizado
:
,
donde simboliza la operación matemática «traza».
-La probabilidad de obtener como resultado de su medida sobre dicho estado el autovalor
(supuesto por simplicidad perteneciente a su espectro puntual y no degenerado), correspondiente a la autofunción
,
, viene dada por:
donde representa el correspondiente proyector.
-El nuevo estado del sistema tras la medida de A con resultado
(no degenerado):
-La ecuación de Schrödinger (un postulado cuántico) adquiere la forma de la ecuación de von Neumann (el «análogo cuántico» a la ecuación de Liouville clásica):
![]() Un estado puro es la herramienta matemática que proporciona las distribuciones de probabilidad para los resultados de las medidas de todos los observables del sistema preparado en ese estado.
Un estado puro es la herramienta matemática que proporciona las distribuciones de probabilidad para los resultados de las medidas de todos los observables del sistema preparado en ese estado.
![]() Estado mezcla: es la descripción matemática de un sistema cuántico que se halla en un estado sobre el que no existe información maximal, esto es, el sistema se encuentra en una mezcla estadística de estados puros,
Estado mezcla: es la descripción matemática de un sistema cuántico que se halla en un estado sobre el que no existe información maximal, esto es, el sistema se encuentra en una mezcla estadística de estados puros,
(normalizados pero no necesariamente ortogonales entre sí),
con probabilidades normalizadas respectivas
;
en este caso, la descripción matemática del estado del sistema en el formalismo cuántico se corresponde con un operador densidad general.
![]() Operador densidad para un estado mezcla:
Operador densidad para un estado mezcla:
-Un estado mezcla se describe matemáticamente en el formalismo mecano-cuántico como el siguiente operador densidad general:
,
para el que, supuesto que las probabilidades están normalizadas, se tiene que (en general, cada estado
no tiene por qué ser autoestado de
).
-El valor esperado de un observable
sobre el estado mezcla del sistema representado por el operador densidad
viene dado:
![]() Un estado puro
Un estado puro es un caso particular de estado mezcla en que todas las probabilidades
son nulas excepto la que corresponde precisamente al estado puro en cuestión, que es la unidad; el operador densidad entonces, para un estado puro, satisface
(es idempotente).
![]() Propiedades generales del operador densidad:
Propiedades generales del operador densidad:
![]() Es acotado, autoadjunto, positivo, con traza unidad y cumpliendo
Es acotado, autoadjunto, positivo, con traza unidad y cumpliendo (por lo tanto, compacto, de modo que su espectro es puramente puntual y discreto, salvo, a lo sumo y en su caso, con el cero como punto de acumulación).
![]() El cuadrado de un operador densidad tiene la expresión:
El cuadrado de un operador densidad tiene la expresión:
.
![]() Para un estado puro, el operador densidad es idempotente, esto es,
Para un estado puro, el operador densidad es idempotente, esto es, .
![]() Sea, en particular, la expresión de un operador densidad en términos de la base ortonormal
Sea, en particular, la expresión de un operador densidad en términos de la base ortonormal del Hilbert asociada al operador compacto densidad
, esto es, su base propia, en la que su expresión es diagonal:
con
(análoga a la definición anterior pero integrada ahora sí por proyectores ortogonales dos a dos); su expresión en otra segunda base ortonormal del Hilbert sería (cf. [GAL-89], pp. 88ss.):
donde la transformación es unitaria, esto es, se cumple
donde
(¡matriz no diagonal!)
-Supuestas las dos bases como integradas por estados físicamente realizables, se tiene que:
El elemento diagonal de la matriz densidad en la base,
, representa la probabilidad de hallar al sistema en el estado
de la base, denominándose población de dicho estado
.
El término no diagonal de la matriz densidad,
con
, da cuenta de las interferencias entre los estados
y
que surgen al expresar
en la nueva base
, cumpliéndose que
; asimismo,
implica
.
Los escalares complejos
con
se denominan como coherencias, representando la coherencia residual en
de los vectores
y
tras el promedio estadístico; en un estado puro, se cumple la condición de coherencia máxima:
para todo par de índices
.
Cuando en un estado mezcla al menos un par de elementos no diagonales
de la matriz densidad (o coherencias) cumple
, se dice que el estado mezcla está sólo parcialmente mezclado.
Cuando en un estado mezcla al menos un par de elementos no diagonales de la matriz densidad satisfacen las dos condiciones
y
, se dice que el estado mezcla está totalmente mezclado.
![]() Ejemplos: sean los siguientes operadores densidad, dados también en su representación matricial, en el espacio de espín
Ejemplos: sean los siguientes operadores densidad, dados también en su representación matricial, en el espacio de espín :
Ejemplo 1:
-Representa el estado puro , cumpliéndose
.
Ejemplo 2:
-Representa el estado puro , cumpliéndose
.
Ejemplo 3:
-Representa un estado mezcla, parcialmente mezclado, ya que se cumple .
-Esto es, no existe ningún tal que
.
Ejemplo 4:
-Representa un estado mezcla, totalmente mezclado, ya que se cumple
y
.
Trazas
![]() La traza de un operador densidad
La traza de un operador densidad ,
es independiente de la base elegida para su cálculo, y satisface las siguientes propiedades:
-Es igual a la unidad si el operador densidad representa un estado puro normalizado:
-Es igual a la unidad si el operador densidad representa un estado mezcla (siempre que todos los estados puros de la mezcla estadística y sus probabilidades estén normalizados):
![]() La traza es una operación que convierte operadores (matrices) en escalares:
La traza es una operación que convierte operadores (matrices) en escalares:
![]() La traza del cuadrado de un operador densidad tiene un valor diferente para estados puros y estados mezcla:
La traza del cuadrado de un operador densidad tiene un valor diferente para estados puros y estados mezcla:
,
por lo que:
-para un estado puro: y
-para un estado mezcla: y
Sistemas compuestos
![]() Si un sistema cuántico está compuesto por
Si un sistema cuántico está compuesto por subsistemas idénticos, cuyos respectivos espacios de Hilbert (complejos y separables) asociados para sus sendas descripciones en el formalismo cuántico son
, el espacio de Hilbert para el sistema compuesto es el producto tensorial
, de dimensión
.
![]() Por ejemplo, en el caso de un sistema cuántico compuesto por dos subsistemas idénticos A y B con sendos Hilberts asociados de dimensión 2 (por ejemplo: un sistema de 2 qubits), el espacio de Hilbert para el sistema compuesto es el producto tensorial
Por ejemplo, en el caso de un sistema cuántico compuesto por dos subsistemas idénticos A y B con sendos Hilberts asociados de dimensión 2 (por ejemplo: un sistema de 2 qubits), el espacio de Hilbert para el sistema compuesto es el producto tensorial , de dimensión 4, cuya base general suele representarse como:
![]() El qubit o qbit: en información cuántica, se denomina así a la superposición general
El qubit o qbit: en información cuántica, se denomina así a la superposición general
,
donde y
son los dos estados cuánticos de una base ortonormal en un Hilbert de dimensión 2, los análogos de los bits clásicos; los
y
son escalares (complejos) arbitrarios.
Traza parcial
Sea un sistema bipartito compuesto por dos partes A y B.
![]() Por ejemplo, puede ser el caso de dos átomos, cada uno de los cuales se asocia con sendos Hilberts
Por ejemplo, puede ser el caso de dos átomos, cada uno de los cuales se asocia con sendos Hilberts , de dimensiones respectivas 2 y 3, de forma que el Hilbert del sistema que componen sería
, de dimensión 6 .
-Notando los vectores de los sendos espacios de Hilbert como
,
,
un vector general del Hilbert del sistema compuesto sería
-Los operadores C y D, actuando sobre y refiriendo sólo respectivamente a cada subsistema A y B, serán de la forma
y
, con expresión matricial:
![]() La traza parcial de un operador
La traza parcial de un operador , actuando sobre
, se define entonces según:
expresiones que proporcionan sendos operadores actuando sólo sobre y
.
-al «tracear» un subsistema sobre el estado de un sistema compuesto, es como si lo elimináramos.
![]() En el ejemplo, serían:
En el ejemplo, serían:
;
,
donde el primer paréntesis representa un escalar y el segundo un operador, de forma que representa un operador que actúa sobre
, cumpliéndose:
![]() De manera que la traza parcial convierte el operador original sobre
De manera que la traza parcial convierte el operador original sobre en un operador sobre el correspondiente espacio no traceado del subsistema implicado.
![]() Todo operador actuando sobre el espacio de Hilbert
Todo operador actuando sobre el espacio de Hilbert asociado a un sistema compuesto puede escribirse como combinación lineal de operadores actuando sólo sobre cada uno de los subsistemas componentes. Por ejemplo, para un sistema bipartito A-B:
,
de forma que las definiciones de traza parcial pueden extenderse por linealidad a todos los operadores actuando en el Hilbert del sistema compuesto.
-Por ejemplo: dado el operador
,
se tiene:
de forma que el resultado es un operador actuando sólo sobre .
![]() La traza parcial de un operador densidad
La traza parcial de un operador densidad , en el caso de un sistema bipartito A y B , define los denominados operadores densidad reducidos:
que son sendos operadores sobre los espacios de Hilbert y
.
![]() Sea un sistema bipartito A-B que se halla en el estado representado por el operador densidad
Sea un sistema bipartito A-B que se halla en el estado representado por el operador densidad
,
donde son dos kets arbitrarios del espacio de Hilbert
y
dos kets arbitrarios del espacio de Hilbert
. Entonces, el correspondiente operador reducido obtenido traceando sobre B tendrá la expresión:
,
donde
y es un operador actuando en
.
![]() Propiedades:
Propiedades:
-la traza parcial convierte el producto externo de
,
, en producto interno,
, que no es, en general, igual a la unidad (y análogamente para
).
-puede demostrarse que:
,
donde y
representan, respectivamente, un conjunto de estados de los espacios de Hilbert de los subsistemas A y B.
-el coeficiente constante , el solapamiento entre
y
, representa el peso específico con que la matriz
aparecerá en el resultado final, tras la suma.
-y, como el coeficiente es una constante, la traza parcial
(
) es un algoritmo que elimina toda referencia al sistema B (A): «tracea», anula, todas las amplitudes pertenecientes al subsistema traceado, proporcionado la estadística de resultados de la medida de los observables sobre el subsistema A (B) y cuantificando la ignorancia o ausencia de información sobre el subsistema traceado B (A):
![]() La operación de traza parcial sobre un subsistema es una operación que reduce el espacio de Hilbert
La operación de traza parcial sobre un subsistema es una operación que reduce el espacio de Hilbert del sistema compuesto al espacio de Hilbert del subsistema no traceado: proyecta los estados del sistema compuesto sobre los estados del correspondiente subsistema no traceado.
![]() Los operadores densidad reducidos encierran toda la información contenida en el operador densidad
Los operadores densidad reducidos encierran toda la información contenida en el operador densidad relativa sólo al correspondiente subsistema.
-Por ejemplo, sea el operador , relativo sólo al subsistema A. Entonces, una extensión trivial suya al Hilbert
viene dada por el operador
y su valor esperado en el estado del sistema compuesto representado por el operador densidad
es:
-es decir: es posible calcular el valor esperado de un operador que actúa solamente sobre el subsistema A como si estuviese aislado y descrito por : el operador
, obtenido traceando el subsistema B, describe el estado del subsistema A.
![]() Por lo tanto: La operación de traza parcial sobre uno de los subsistemas que componen un sistema compuesto reduce el espacio de Hilbert global al espacio de Hilbert correspondiente al subsistema concreto: se ignoran las otras partes del sistema, anulando las correspondientes amplitudes de probabilidad.
Por lo tanto: La operación de traza parcial sobre uno de los subsistemas que componen un sistema compuesto reduce el espacio de Hilbert global al espacio de Hilbert correspondiente al subsistema concreto: se ignoran las otras partes del sistema, anulando las correspondientes amplitudes de probabilidad.
![]() A partir de las dos matrices densidad reducidas del sistema bipartito A-B, en el estado
A partir de las dos matrices densidad reducidas del sistema bipartito A-B, en el estado , puede definirse el operador
, que en general no coincide con
, sino que describe un estado en que las variables de los dos subsistemas no presentan correlación mutua. Es decir:
![]() El operador densidad
El operador densidad sobre
corresponde a la descripción de un sistema donde las respectivas variables de cada subsistema presentan correlación nula.
![]() En general, para un estado del sistema compuesto
En general, para un estado del sistema compuesto , de forma que el operador densidad
describe un estado en que las variables de los dos subsistemas presentan alguna correlación.
![]() Las trazas parciales de la matriz densidad de un estado puro de un sistema bipartito sobre cada uno de los dos espacios de Hilbert involucrados proporcionan como resultado, en general, un estado mezcla.
Las trazas parciales de la matriz densidad de un estado puro de un sistema bipartito sobre cada uno de los dos espacios de Hilbert involucrados proporcionan como resultado, en general, un estado mezcla.
![]() Ejemplo 1: sea un sistema compuesto bipartito A-B en el estado puro
Ejemplo 1: sea un sistema compuesto bipartito A-B en el estado puro
,
donde y
representan estados de sendas bases de los espacios de Hilbert
y
.
-Entonces:
,
expresión última que contiene sólo los elementos diagonales y las correspondientes probabilidades en la base del espacio .
![]() Ejemplo 2: sea un sistema de dos qubits, de forma que el Hilbert
Ejemplo 2: sea un sistema de dos qubits, de forma que el Hilbert del sistema compuesto es de dimensión 4, con base
y sea el estado puro del Hilbert correspondiente al estado de Bell :
,
cuya matriz densidad es:
-Finalmente, puede calcularse:
.
-Análogamente:
, estado mezcla.
-Finalmente, pues, concluimos que para este estado de Bell:
.
![]() Es decir: aunque el estado de un sistema bipartito de dos qubits sea puro, cada qubit puede hallarse en un estado mezcla.
Es decir: aunque el estado de un sistema bipartito de dos qubits sea puro, cada qubit puede hallarse en un estado mezcla.
![]() Poseer información maximal sobre el estado del sistema compuesto puede no proporcionar información maximal sobre sus partes: es lo que sucede en los estados entrelazados.
Poseer información maximal sobre el estado del sistema compuesto puede no proporcionar información maximal sobre sus partes: es lo que sucede en los estados entrelazados.
![]() Poseer los operadores densidad reducidos de las sendas partes del sistema bipartito entrelazado no da acceso a toda la información sobre el sistema compuesto: está ausente la información sobre las correlaciones entre sus partes.
Poseer los operadores densidad reducidos de las sendas partes del sistema bipartito entrelazado no da acceso a toda la información sobre el sistema compuesto: está ausente la información sobre las correlaciones entre sus partes.
Purificación
![]() Dado un sistema cuántico A en un estado mezcla descrito por el operador densidad
Dado un sistema cuántico A en un estado mezcla descrito por el operador densidad , el proceso de purificación consiste en introducir un segundo sistema B en un sistema existente A, de tal manera que se extienda el espacio de Hilbert original y el sistema compuesto resultante A-B esté en un estado puro
, que satisface
.
-La purificación representa, en cierta manera, la operación inversa a la de traza parcial o traceado de un subsistema de un sistema compuesto.
![]() Es un proceso siempre posible.
Es un proceso siempre posible.
Entrelazamiento en estados puros de sistema bipartitos
![]() Sea un sistema cuántico compuesto por dos subsistemas A-B, de forma que el espacio de Hilbert para el sistema compuesto es el producto tensorial
Sea un sistema cuántico compuesto por dos subsistemas A-B, de forma que el espacio de Hilbert para el sistema compuesto es el producto tensorial , de dimensión
.
![]() Un estado puro de expresión general
Un estado puro de expresión general se denomina separable cuando admite expresión en forma factorizable, esto es, como un producto tensorial de sendos vectores de cada uno de los Hilberts:
con ,
.
![]() Los estados puros separables, o estados puros producto, corresponden a estados puros del sistema en los que la información es maximal, tanto para el sistema compuesto como para cada uno de los subsistemas que lo componen.
Los estados puros separables, o estados puros producto, corresponden a estados puros del sistema en los que la información es maximal, tanto para el sistema compuesto como para cada uno de los subsistemas que lo componen.
![]() Un estado estado puro de expresión general
Un estado estado puro de expresión general se denomina entrelazado (entangled) cuando no admite expresión en forma factorizable, esto es, como un producto de factores separados:
.
-Dado un estado cuántico arbitrario, en general es muy difícil establecer si es separable o no.
![]() Los estados puros no-separables, o estados puros entrelazados, son estados puros del sistema para los que los operadores densidad reducidos de los subsistemas componentes (al menos para uno de ellos) no describen estados puros, sino estados mezcla.
Los estados puros no-separables, o estados puros entrelazados, son estados puros del sistema para los que los operadores densidad reducidos de los subsistemas componentes (al menos para uno de ellos) no describen estados puros, sino estados mezcla.
![]() Para los estados puros entrelazados, disponer de información maximal sobre el sistema compuesto no conlleva disponer de información maximal sobre todos los subsistemas componentes.
Para los estados puros entrelazados, disponer de información maximal sobre el sistema compuesto no conlleva disponer de información maximal sobre todos los subsistemas componentes.
![]() Mientras que la dimensión del subespacio integrado por los estados separables es
Mientras que la dimensión del subespacio integrado por los estados separables es , la dimensión del Hilbert es mucho mayor en general, viniendo dada por
![]() Ejemplos:
Ejemplos:
-el singlete de espín:
–los 4 estados de Bell o pares EPR:
,
de los que se dice que poseen un entrelazamiento máximo (rango de Schmidt máximo, véase apartado siguiente), ya que las correspondientes matrices densidad reducidas corresponden a una mezcla uniforme de los estados y
. Para ellos,
, es decir,
no da cuenta de las correlaciones cuánticas entre A y B.
-Como ya vimos antes para el estado de Bell , en estos estados puros entrelazados del sistema de los dos qubits, cada qubit individual se encuentra en un estado mezcla: no se dispone de información maximal sobre él.
La descomposición de Schmidt: un criterio de entrelazamiento
![]() Para los sistemas bipartitos la descomposición de Schmidt proporciona un criterio para determinar si un estado puro del sistema es separable o entrelazado (pero no una medida precisa del grado de entrelazamiento).
Para los sistemas bipartitos la descomposición de Schmidt proporciona un criterio para determinar si un estado puro del sistema es separable o entrelazado (pero no una medida precisa del grado de entrelazamiento).
![]() Teorema de descomposición biortonormal de Schmidt (1907):
Teorema de descomposición biortonormal de Schmidt (1907):
![]() Dado un estado puro
Dado un estado puro de un sistema cuántico bipartito A-B, existe al menos un par de sendas bases ortonormales
dependientes del estado particular y tales que se satisface:
,
donde , son números reales positivos, denominados como pesos o coeficientes de Schmidt, que satisfacen la ligadura
.
El real positivo que satisface
,
se denomina número o rango de Schmidt del estado puro ; representa el número de amplitudes no nulas en la correspondiente descomposición de Schmidt.
-Obsérvese que la potencia del teorema es que aparezca en su expresión una sola sumatoria: es trivial que cualquier estado puro del Hilbert admite expresión en sendas bases y
de
y
, de la forma
,
donde los representan escalares (complejos).
-La descomposición de Schmidt implica una correlación perfecta entre entre los autovalores y
correspondientes a cada pareja de autoestados
y
.
-Cuando el rango de Schmidt es máximo, , y los módulos de todos los coeficientes son iguales,
,
se dice que el estado es máximamente entrelazado (por ejemplo, el singlete de espín y los cuatro estados de Bell lo son).
![]() Propiedades: Para un estado puro de un sistema bipartito:
Propiedades: Para un estado puro de un sistema bipartito:
-La descomposición de Schmidt es única en el sentido de que el rango y, hasta cierto orden, los pesos, son únicos; también, en el de que, dado un coeficiente no degenerado , los estados asociados
y
son únicos salvo factores de fase recíprocos. Pero si el espectro de
presenta degeneración, las bases de Schmidt no son únicas.
-Las bases y
de un par de Schmidt están integradas por autovectores de los operadores densidad reducidos
y
,
correspondientes respectivamente a los dos subsistemas que componen el sistema bipartito: son sus bases propias.
-Las matrices densidad reducidas y
son autoadjuntas, positivas y de traza unidad (como corresponde a todo operador densidad).
-Las matrices densidad reducidas son diagonales en una base de Schdmidt, y tienen un número de autovalores positivos igual al rango de Schmidt , que proporciona entonces su dimensión.
-Los autovalores de las matrices densidad reducidas son precisamente los coeficientes o pesos de Schmidt , de forma que los espectros de los dos operadores densidad reducidos coinciden (salvo a lo sumo en la degeneración del autovalor nulo, en su caso), por lo que poseen los mismos autovalores
.
-El número de Schmidt no cambia si se hacen operaciones unitarias sobre alguno de los subsistemas.
–Un estado puro de un sistema bipartito es separable si y sólo si su número de Schmidt es 1.
–Un estado puro de un sistema bipartito es entrelazado si y sólo si su número de Schmidt es mayor que 1.
-Si el estado puro es entrelazado (numero de Schmidt mayor que 1) y, además, todos los coeficientes son distintos, la descomposición es única.
-Si el estado puro es entrelazado (numero de Schmidt mayor que 1) y, además, al menos dos coeficientes son iguales, existen infinitas descomposiciones de Schmidt distintas, y el estado se denomina «máximamente entrelazado» (cf. G. Alcaine, op. cit., p. 9).
![]() La medida de Schmidt para el entrelazamiento de estados puros se define como:
La medida de Schmidt para el entrelazamiento de estados puros se define como:
expresándose en la unidad e-bit: los 4 estados de Bell poseen cada uno un e-bit de entrelazamiento.
-Se han introducido muchas definiciones de medidas de entrelazamiento, en términos de los coeficientes de Schmidt; dependiendo de las aplicaciones se usarán unas u otras.
-También se han introducido testigos de entrelazamiento, que son observables que presentan valores esperados distintos para estados separables y entrelazados, y que pueden expresarse en términos de operadores autoadjuntos positivos. Un ejemplo: la magnetización, en ciertos sistemas.
Entrelazamiento en estados de un sistema bipartito
![]() En general, los estados de un sistema bipartito se clasifican en:
En general, los estados de un sistema bipartito se clasifican en:
1. Estados puros separables, o estados puros producto o no correlacionados: cuando el operador densidad tiene la estructura:
–Todo estado producto es puro y trivialmente separable (pero no todo estado puro es estado producto o separable).
![]() Los estados puros separables de un sistema bipartito satisfacen todas las desigualdades del tipo Bell y admiten una descripción en términos de elementos de realidad EPR locales.
Los estados puros separables de un sistema bipartito satisfacen todas las desigualdades del tipo Bell y admiten una descripción en términos de elementos de realidad EPR locales.
2. Estados puros no separables:
–Todo estado puro entrelazado de un sistema bipartito viola una desigualdad de Bell.
3. Estados mezcla separables: cuando el operador densidad total admite expresión (no única en general) como una suma lineal convexa con más de un término de operadores densidad de la forma (Alcaine, op.cit., p. 10):
donde y
y la cardinalidad del estado se define como el menor número de sumandos presente en el conjunto de todas las sumas convexas anteriores posibles.
-A estos estados (mezcla) se les denomina a veces como clásicamente correlacionados (cf. R.F. Werner, Physical Review A40 (1989) 4277; cit. en Alcaine, op. cit., p. 10).
-Si la suma anterior tuviera un solo término, se trataría del primer caso anterior: un estado puro separable o estado puro producto.
4. Estados entrelazados o no-separables: todo estado que no es separable (puro o mezcla).
-También se denominan como estados cuánticamente correlacionados.
![]() Sin embargo, un estado mezcla separable también puede exhibir correlaciones no clásicas, aunque sólo los estados mezcla entrelazados presentan correlaciones similares a las vistas en los estados puros entrelazados. Y es que, para estados no puros, la distinción entre separabilidad y entrelazamiento no está resuelta (véase G. Alcaine, op. cit., p. 10, donde se pueden encontrar las referencias específicas para las siguientes afirmaciones):
Sin embargo, un estado mezcla separable también puede exhibir correlaciones no clásicas, aunque sólo los estados mezcla entrelazados presentan correlaciones similares a las vistas en los estados puros entrelazados. Y es que, para estados no puros, la distinción entre separabilidad y entrelazamiento no está resuelta (véase G. Alcaine, op. cit., p. 10, donde se pueden encontrar las referencias específicas para las siguientes afirmaciones):
![]() G. García Alcaine, «Enredo cuántico«, p. 10:
G. García Alcaine, «Enredo cuántico«, p. 10:
![]() Para estados no-puros la distinción entre estados separables (clásicamente correlacionados) y estados no-separables (cuánticamente correlacionados, es decir enredados) no está totalmente resuelta. Se conocen diversas condiciones necesarias para que un estado sea separable, pero sólo para los espacios de dimensión más baja (4 ó 6) se conocen condiciones suficientes. Voy a analizar brevemente alguno de estos criterios de separabilidad.
Para estados no-puros la distinción entre estados separables (clásicamente correlacionados) y estados no-separables (cuánticamente correlacionados, es decir enredados) no está totalmente resuelta. Se conocen diversas condiciones necesarias para que un estado sea separable, pero sólo para los espacios de dimensión más baja (4 ó 6) se conocen condiciones suficientes. Voy a analizar brevemente alguno de estos criterios de separabilidad.
–Verificación de las desigualdades de Bell: Una condición necesaria para la separabilidad y para la existencia de un modelo de VO Locales es que se satisfagan todas las desigualdades de Bell, y en particular las de CHSH para cualquier conjunto de observables A, A’ , B, B’ . En ciertos casos se conocen condiciones necesarias y suficientes para que dichas desigualdades se verifiquen. La verificación de las desigualdades de CHSH no es suficiente para la separabilidad: existen operadores estado que las cumplen, y sin embargo contienen correlaciones cuánticas, que pueden utilizarse para fenómenos específicamente cuánticos como la teleportación. Estas correlaciones dan lugar a violaciones del realismo local si se consideran secuencias de mediciones.
![]() Una condición necesaria para la separabilidad de un estado mezcla es que se satisfagan todas las desigualdades de Bell, y en particular las de CHSH, para cualquier conjunto de 4 observables A, A’ , B y B’ , pero no es condición suficiente (cf. G. García Alcaine, Enredo cuántico, p. 22, cita previa).
Una condición necesaria para la separabilidad de un estado mezcla es que se satisfagan todas las desigualdades de Bell, y en particular las de CHSH, para cualquier conjunto de 4 observables A, A’ , B y B’ , pero no es condición suficiente (cf. G. García Alcaine, Enredo cuántico, p. 22, cita previa).
![]() Para la medida de entrelazamiento de los estados mezcla se han desarrollado numerosos métodos, entre ellos: las entropías de von Neumann (1927), de Renyi, de Tsallis…
Para la medida de entrelazamiento de los estados mezcla se han desarrollado numerosos métodos, entre ellos: las entropías de von Neumann (1927), de Renyi, de Tsallis…
![]() G. Vidal and R. F. Werner, «Computable measure of entanglement», Phys. Rev. A 65 (2002) 032314; DOI=10.1103/PhysRevA.65.032314.
G. Vidal and R. F. Werner, «Computable measure of entanglement», Phys. Rev. A 65 (2002) 032314; DOI=10.1103/PhysRevA.65.032314.
![]() Véase: G. García Alcaine, Enredo cuántico, pp. 22ss.
Véase: G. García Alcaine, Enredo cuántico, pp. 22ss.
Sistemas tripartitos: estados GHZ
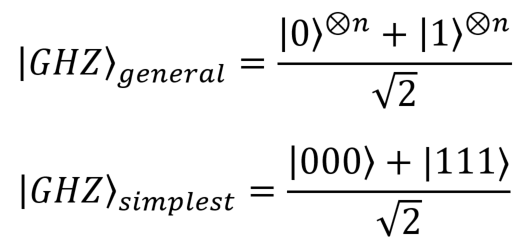
![]() Un estado general GHZ es un estado mecano-cuántico entrelazado para más de dos subsistemas; para
Un estado general GHZ es un estado mecano-cuántico entrelazado para más de dos subsistemas; para subsistemas de dos dimensiones (qubits) tiene la expresión general:
-Una expresión muy simple es la del estado GHZ de 3 partículas, que presenta además entrelazamiento máximamente no trivial, en el sentido de que, para muchas formas introducidas de cuantificación del entrelazamiento, resulta con un valor máximo. Su expresión es:
.
![]() En general, para tres partículas son posibles 8 estados GHZ:
En general, para tres partículas son posibles 8 estados GHZ:
-Considerado el siguiente conjunto de observables compatibles dos a dos:
(que es redundante, ya que ) , todos sus integrantes son diagonalizados por los 8 estados GHZ.
![]() Los estados GHZ son estados entrelazados, y han sido ya creados en el laboratorio, a partir de fotones (las componentes de espín
Los estados GHZ son estados entrelazados, y han sido ya creados en el laboratorio, a partir de fotones (las componentes de espín se sustituyen por polarizaciones: H/V si se elige la base Horizontal / Vertical, o + / – para polarización dextrógira / levógira).
-Los estados GHZ presentan diversas propiedades como, por ejemplo, la de que producen un estado mezcla cuando se toma la traza de uno de los subsistemas, por ejemplo:
Entrelazamiento GHZ a tres en el laboratorio
![]() En el año 2000, se publicó la primera realización experimental del entrelazamiento a tres, un experimento realizado en Innsbruck , que se considera el primer test del realismo local sobre un estado entrelazado de tres partículas sin involucrar desigualdades:
En el año 2000, se publicó la primera realización experimental del entrelazamiento a tres, un experimento realizado en Innsbruck , que se considera el primer test del realismo local sobre un estado entrelazado de tres partículas sin involucrar desigualdades:
![]() J.-W. Pan, D. Bouwmeester, M. Daniell, H. Weinfurter & A. Zeilinger, Experimental test of quantum nonlocality in three -photon Greenberger±Horne±Zeilinger entanglement , Nature, 403 (2000) 515-519.
J.-W. Pan, D. Bouwmeester, M. Daniell, H. Weinfurter & A. Zeilinger, Experimental test of quantum nonlocality in three -photon Greenberger±Horne±Zeilinger entanglement , Nature, 403 (2000) 515-519.
![]() Abstract: Bell’s theorem states that certain statistical correlations predicted by quantum physics for measurements on two-particle systems cannot be understood within a realistic picture based on local properties of each individual particle -even if the two particles are separated by large distances. Einstein, Podolsky and Rosen first recognized the fundamental significance of these quantum correlations (termed ‘entanglement’ by Schrödinger) and the two-particle quantum predictions have found ever-increasing experimental support. A more striking conflict between quantum mechanical and local realistic predictions (for perfect correlations) has been discovered; but experimental verification has been difficult, as it requires entanglement between at least three particles. Here we report experimental confirmation of this conflict, using our recently developed method to observe three-photon entanglement, or ‘Greenberger±Horne±Zeilinger’ (GHZ) states. The results of three specific experiments, involving measurements of polarization correlations between three photons, lead to predictions for a fourth experiment; quantum physical predictions are mutually contradictory with expectations based on local realism. We find the results of the fourth experiment to be in agreement with the quantum prediction and in striking conflict with local realism.
Abstract: Bell’s theorem states that certain statistical correlations predicted by quantum physics for measurements on two-particle systems cannot be understood within a realistic picture based on local properties of each individual particle -even if the two particles are separated by large distances. Einstein, Podolsky and Rosen first recognized the fundamental significance of these quantum correlations (termed ‘entanglement’ by Schrödinger) and the two-particle quantum predictions have found ever-increasing experimental support. A more striking conflict between quantum mechanical and local realistic predictions (for perfect correlations) has been discovered; but experimental verification has been difficult, as it requires entanglement between at least three particles. Here we report experimental confirmation of this conflict, using our recently developed method to observe three-photon entanglement, or ‘Greenberger±Horne±Zeilinger’ (GHZ) states. The results of three specific experiments, involving measurements of polarization correlations between three photons, lead to predictions for a fourth experiment; quantum physical predictions are mutually contradictory with expectations based on local realism. We find the results of the fourth experiment to be in agreement with the quantum prediction and in striking conflict with local realism.
![]() Otras realizaciones experimentales relacionadas con estados GHZ:
Otras realizaciones experimentales relacionadas con estados GHZ:
![]() A. Cabello, Stronger Two-Observer All-Versus-Nothing Violation of Local Realism, Phys. Rev. Lett. 95 (2005) 210401.
A. Cabello, Stronger Two-Observer All-Versus-Nothing Violation of Local Realism, Phys. Rev. Lett. 95 (2005) 210401.
![]() http://www.nature.com/srep/2012/121210/srep00942/full/srep00942.html
http://www.nature.com/srep/2012/121210/srep00942/full/srep00942.html
![]() Experimental three-photon quantum nonlocality under strict locality conditions
Experimental three-photon quantum nonlocality under strict locality conditions
![]() Una noticia más reciente (Universidad de Waterloo, Canadá, 2014): producción de un estado entrelazado de tres fotones con la misma polarización, y aplicación en otro test del realismo local con separaciones de más de medio kilómetro:
Una noticia más reciente (Universidad de Waterloo, Canadá, 2014): producción de un estado entrelazado de tres fotones con la misma polarización, y aplicación en otro test del realismo local con separaciones de más de medio kilómetro:
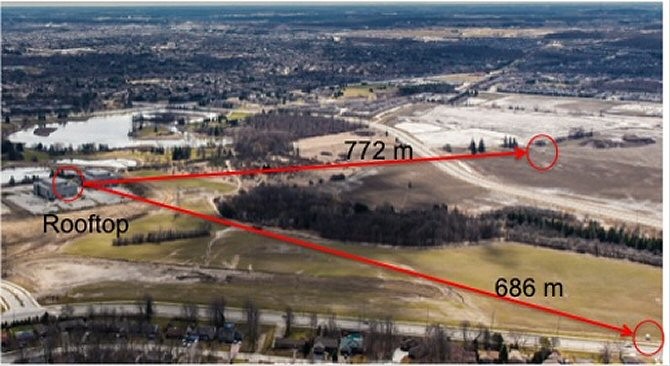
![]() Realización experimental del entrelazamiento de tres fotones: Three’s a Charm: NIST Detectors Reveal Entangled Photon Triplets
Realización experimental del entrelazamiento de tres fotones: Three’s a Charm: NIST Detectors Reveal Entangled Photon Triplets
![]() Direct generation of three-photon polarization entanglement
Direct generation of three-photon polarization entanglement
![]() Espectacular entrelazamiento a tres
Espectacular entrelazamiento a tres
![]() Cuando lo cuántico supera a la razón
Cuando lo cuántico supera a la razón
![]() Estados GHZ y tres jugadores contra un Casino: «Greenberger-Horne-Zeilinger-like proof of Bell’s theorem involving observers who do not share a reference frame«, A. Cabello, Physical Review A68 (2003) 042104.
Estados GHZ y tres jugadores contra un Casino: «Greenberger-Horne-Zeilinger-like proof of Bell’s theorem involving observers who do not share a reference frame«, A. Cabello, Physical Review A68 (2003) 042104.
![]() Sobre el entrelazamiento en sistemas tripartitos, pueden consultarse también los siguientes trabajos de investigación:
Sobre el entrelazamiento en sistemas tripartitos, pueden consultarse también los siguientes trabajos de investigación:
![]() Entrelazamiento cuántico en sistemas de muchos cuerpos (tesis doctoral de J.M. Matera, Univ. de La Plata).
Entrelazamiento cuántico en sistemas de muchos cuerpos (tesis doctoral de J.M. Matera, Univ. de La Plata).
![]() A quantitative witness for Greenberger-Horne-Zeilinger entanglement
A quantitative witness for Greenberger-Horne-Zeilinger entanglement
Desarrollos recientes
![]() 2012: Entanglement Between Photons that have Never Coexisted ; The first quantum entanglement of photons through space and time ; la noticia en Science.
2012: Entanglement Between Photons that have Never Coexisted ; The first quantum entanglement of photons through space and time ; la noticia en Science.
![]() 2013: nuevo test para determinar entrelazamiento en sistemas cuánticos
2013: nuevo test para determinar entrelazamiento en sistemas cuánticos
![]() 2016: entrelazamiento de hasta 5 fotones: I. Schwartz, D. Cogan, E. R. Schmidgall, Y. Don, L. Gantz, O. Kenneth, N. H. Lindner and D. Gershoni, «Deterministic generation of a cluster state of entangled photons», Science 354, 6311 (2016) 434-437; DOI: 10.1126/science.aah4758.
2016: entrelazamiento de hasta 5 fotones: I. Schwartz, D. Cogan, E. R. Schmidgall, Y. Don, L. Gantz, O. Kenneth, N. H. Lindner and D. Gershoni, «Deterministic generation of a cluster state of entangled photons», Science 354, 6311 (2016) 434-437; DOI: 10.1126/science.aah4758.
![]() 2018: Entrelazamiento energía-tiempo entre dos fotones: https://physicsworld.com/a/energy-time-entanglement-detected-in-photons/
2018: Entrelazamiento energía-tiempo entre dos fotones: https://physicsworld.com/a/energy-time-entanglement-detected-in-photons/
![]() 2019: Entrelazamiento posición-momento (radiales) entre dos fotones: Physicsworld.com
2019: Entrelazamiento posición-momento (radiales) entre dos fotones: Physicsworld.com
![]() 2022: Entrelazamiento en la estación espacial internacional: «NASA is launching a new quantum entanglement experiment in space», «The Space Entanglement and Annealing QUantum Experiment (or SEAQUE)», artículo por C. Hu en Popular Science.
2022: Entrelazamiento en la estación espacial internacional: «NASA is launching a new quantum entanglement experiment in space», «The Space Entanglement and Annealing QUantum Experiment (or SEAQUE)», artículo por C. Hu en Popular Science.
![]() 2023: Entrelazamiento entre dos partículas distinguibles: «Physicists just discovered a new type of quantum entanglement», in ZME-Science; in Brookhaven National Laboratory; Sciences Advances 9-1 (2023); DOI: 10.1126/sciadv.abq39.
2023: Entrelazamiento entre dos partículas distinguibles: «Physicists just discovered a new type of quantum entanglement», in ZME-Science; in Brookhaven National Laboratory; Sciences Advances 9-1 (2023); DOI: 10.1126/sciadv.abq39.
Ejercicio final
El teorema EPR, revisitado a la luz del formalismo del operador densidad y los estados entrelazados:
![]() Density-Matrix Description of the EPR Paradox
Density-Matrix Description of the EPR Paradox
Bibliografía
- [GAL-89] A. Galindo y P. Pascual, Mecánica Cuántica I, Eudema, Madrid, 1989.
- A. Einstein, B. Podolsky and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Physical Review 47 (1935) 777-780.
- G. García Alcaine, Enredo cuántico (también en Enredo cuántico).
- E. Schrödinger, Discussion of probability relations between separated systems, Proceedings of the Cambridge Philosophical Society 31 (1935) 555-562.
- Density Matrix Formalism:
- https://cds.cern.ch/record/1555700/files/978-3-642-24070-6_BookBackMatter.pdf
- http://ocw.mit.edu/courses/chemistry/5-74-introductory-quantum-mechanics-ii-spring-2009/lecture-notes/MIT5_74s09_lec12.pdf
- K.T. McDonald: Density-Matrix Description of the EPR «Paradox«
- V. Vedral, «Quantum entanglement«, Nature Physics 10 (2014) 256-258, https://doi.org/10.1038/nphys2904.
- K. Edamatsu, «Entangled Photons: Generation, Observation, and Characterization»; Japanese Journal of Applied Physics, Volume 46, 11R (2007) 7175; DOI 10.1143/JJAP.46.7175.
Críticas respecto de las desigualdades tipo Bell:
https://repositoriodeconfusiones-comentarios.blogspot.com/2018/03/eistein-vs-bohr.html#DB.Sintesis