El fotón como excitación del campo

Cuantización del campo electromagnético en cavidades
Fuentes: esta entrada se basa principalmente en los cap. 2 de los manuales:
–Introductory Quantum Optics, de Gerry y Knight ([GER-05]).
–Quantum Optics, de Garrison y Chiao ([GAR-08]).
(la cuantización del campo electromagnético se desarrolla similarmente en multitud de fuentes; se sigue la notación y orden del primero).

Cavidad con un modos de oscilador

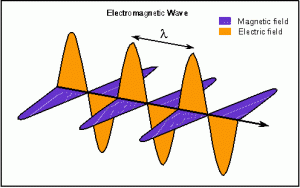
Onda electromagnética polarizada linealmente.

Sea un campo de radiación confinado en una cavidad monodimensional (eje $OZ$ ) de paredes perfectamente conductoras y de anchura $L$ . Suponiendo ausencia de fuentes y sumideros de radiación en la caja, y polarización según el eje $OX$ del campo,

$\vec{E}(\vec{r},t)=\vec{e_x}E_x(z,t)$ ,

donde $\vec{e_x}$ es un vector unitario de polarización, las ecuaciones de Maxwell toman la forma:

$\nabla \cdot \vec{E}=0$ (no cargas libres)
$\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}$
(ley de Faraday)
$\nabla \cdot \vec{B}=0$ (no monopolos magnéticos)
$\nabla \times \vec{B}=\varepsilon_0 \mu_0\frac{\partial \vec{E}}{\partial t}$ (ley de Ampère)

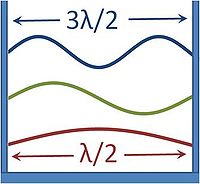
-Las condiciones de frontera, nodos sobre las paredes de la caja, cuantizan los valores de frecuencia permitidos:

$\omega_n= c(\frac{n\pi}{L})\;,\;n=1,2\ldots$

-Un modo individual de campo, solución de las ecuaciones de Maxwell y cumpliendo las condiciones de contorno, viene dado por:

$E_x(z,t)=(\frac{2\omega^2}{V\varepsilon_0})^{\frac{1}{2}} q(t)\sin(kz)$ ,

donde $\omega$ es una de las frecuencias permitidas y $k$ el número de ondas.

-El campo magnético en la cavidad,

$\vec{B}(\vec{r},t)=\vec{e_y}B_y(z,t)$

viene dado por:

$B_y(z,t)=(\frac{\varepsilon_0 \mu_0}{k})(\frac{2\omega^2}{V\varepsilon_0})^{\frac{1}{2}}p(t)\cos(kz)$

donde $V$ es el volumen efectivo de la cavidad, $q(t)$ es un función temporal con dimensiones de longitud y $p(t)=\frac{dq}{dt}$ el momento canónico, para masa unidad.

El Hamiltoniano clásico, representando la energía electromagnética $U_{em}$ (correspondiente pues a un solo modo de radiación) es:

$H=U_{em}=\frac{1}{2}\int [\varepsilon_0\vec{E}^2(\vec{r},t)+\frac{1}{\mu_0}\vec{B}^2(\vec{r},t)]dV$

$=\frac{1}{2}\int [\varepsilon_0E^2_x(z,t)+\frac{1}{\mu_0}B_y^2(z,t)]dV$

$=\frac{1}{2}(p^2+\omega^2q^2)$

equivalente al Hamiltoniano de un oscilador armónico monodimensional de masa unidad, reemplazando los operadores mecano-cuánticos posición y momento por, respectivamente, las intensidades de campo eléctrico $E$ y magnético $B$ , con los correspondientes factores de escala, y donde:

$p=\dot{q}=\frac{\partial U_{em}}{\partial p}$

$\dot{p}=-\frac{\partial U_{em}}{\partial q}=-\omega^2q$

Cuantización: Realizando las sustituciones convencionales (cf. principio de correspondencia)

$q \rightarrow \hat{q}$

$p \rightarrow \hat{p}$

donde $\hat{q}$ y $\hat{p}$ representan los operadores autoadjuntos cuánticos posición y momento, de conmutador

$[\hat{q},\hat{p}]=i\hbar\hat{I}$ ,

se obtienen finalmente las expresiones operatoriales para las intensidades de campo del modo de radiación:

$\hat{E_x}(z,t)=(\frac{2\omega^2}{V\varepsilon_0})^{\frac{1}{2}}\hat{q}(t)\sin(kz)$

$\hat{B_y}(z,t)=(\frac{\varepsilon_0 \mu_0}{k})(\frac{2\omega^2}{V\varepsilon_0})^{\frac{1}{2}}\hat{p}(t)\cos(kz)$ ,

en términos de las cuales el Hamiltoniano (operador) se expresa:

$\hat{H}=\frac{1}{2}(\hat{p}^2+\omega^2\hat{q}^2)$

Operadores escalera y número

A continuación se introducen los operadores creación $\hat{a^+}$ , destrucción $\hat{a}$ (no autoadjuntos: no observables) y número $\hat{n}$ :

$\hat{a}=(2\hbar\omega)^{-\frac{1}{2}}(\omega \hat{q}+i\hat{p})$

$\hat{a}^+=(2\hbar\omega)^{-\frac{1}{2}}(\omega \hat{q}-i\hat{p})$

$\hat{n}=\hat{a}^+\hat{a}$

$\leftrightarrow \hat{q}=\sqrt{\frac{\hbar}{2\omega}}(\hat{a}+\hat{a^+}) \quad , \quad \hat{p}=-i\sqrt{\frac{\hbar \omega}{2}}(\hat{a}-\hat{a^+})$

$[\hat{a},\hat{a}^+]=1\quad \Rightarrow$

$\hat{E_x}(z,t)=\mathcal{E}_0(\hat{a}+\hat{a^+})\sin(kz)$

$\hat{B_y}(z,t)=-i\mathcal{B}_0\varepsilon_0(\hat{a}-\hat{a}^+)\cos(kz)$

donde

$\mathcal{E}_0=(\frac{\hbar\omega}{V\varepsilon_0})^{\frac{1}{2}} \quad y \quad \mathcal{B}_0=(\frac{\mu_0}{k})(\frac{\varepsilon_0 \hbar \omega^3}{V})^{\frac{1}{2}}$

representando, respectivamente, los campos eléctrico y magnético «por fotón» (pero, en rigor, el campo medio por cada conjunto con número definido de fotones es cero, de manera que lo que representan son fluctuaciones del campo).

-En términos de los operadores creación y destrucción el Hamiltoniano se expresa:

$\hat{H}=(\hat{a}^+\hat{a}+\frac{1}{2})\hbar \omega=(\hat{n}+ \frac{1}{2})\hbar \omega$

En la imagen de Heisenberg, para un operador $\hat{O}$ , sin dependencia explícita del tiempo, se tiene

$\frac{d\hat{O}}{dt}=\frac{i}{\hbar}[\hat{H},\hat{O}]$

fórmula que, aplicada a los operadores creación y destrucción genera

$\frac{d\hat{a}}{dt}=\frac{i}{\hbar}[\hat{H},\hat{a}]$

$=\frac{i}{\hbar}[\hbar \omega (\hat{a}^+\hat{a}+\frac{1}{2}),\hat{a}]$

$=i\omega(\hat{a}^+\hat{a}\hat{a}-\hat{a}\hat{a}^+\hat{a})$

$=i\omega[\hat{a},\hat{a}^+]\hat{a}=-i\omega\hat{a}$

ecuación diferencial cuya solución es:

$\hat{a}(t)=\hat{a}(0)e^{-i\omega t}$ ;

análogamente,

$\hat{a}^+(t)=\hat{a}^+(0)e^{+i\omega t}$

El operador número $\hat{n}=\hat{a}^+\hat{a}$ , introduciendo la notación de Dirac $|n>$ para el autoestado de energía $E_n$ de un modo de radiación del campo, satisface:

$\hat{H}|n>=\hbar \omega (\hat{a}^+\hat{a}+\frac{1}{2})|n>=E_n|n>$

-Multiplicando por $\hat{a}^+$ a la izquierda:

$\hat{a}^+\hat{H}|n>=\hbar \omega (\hat{a}^+\hat{a}^+\hat{a}+\frac{1}{2}\hat{a}^+)|n>=E_n\hat{a}^+|n>$ ;

usando la relación de conmutación

$[\hat{a},\hat{a}^+]=1=\hat{a}\hat{a}^+ -\hat{a}^+\hat{a}$

$\Rightarrow \hbar\omega[(\hat{a}^+\hat{a}-1)\hat{a}^++\frac{1}{2}\hat{a}^+]|n>=E_n\hat{a}^+|n>$

$\Rightarrow \hbar \omega (\hat{a}^+\hat{a}+\frac{1}{2})(\hat{a}^+|n>)=(E_n+\hbar\omega)(\hat{a}^+|n>)$

$\rightarrow (\hat{a}^+|n>)$ es autoestado de $\hat{H}$ con autovalor de energía $(E_n+\hbar\omega)$ ;

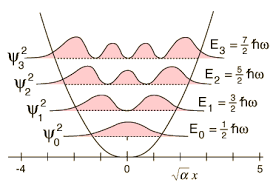
análogamente,

$\hbar \omega (\hat{a}^+\hat{a}+\frac{1}{2})(\hat{a}|n>)=(E_n-\hbar\omega)(\hat{a}|n>)$

$\rightarrow (\hat{a}|n>)$ es autoestado de $\hat{H}$ con autovalor de energía $(E_n-\hbar\omega)$ :

Los operadores escalera $\hat{a^+}$ y $\hat{a}$ , respectivamente, crean y destruyen un cuanto de energía de tamaño $\hbar\omega$ (un fotón).

El fotón, pues, se introduce al cuantizar el campo electromagnético como el cuanto de energía de excitación de un modo monocromático en una cavidad: no tiene sentido concebirlo como una partícula (¡no existe un operador posición fotónico: el cuanto de energía, de hecho, está repartido por toda la cavidad!).

Representación número de fotones: espacio de Fock

Si representamos el estado fundamental del oscilador, de energía $E_{GS}\equiv E_0$ , como $|0>$ , y cada estado $n$ -fotónico como el estado número $|n>$ , se tendrá:

$\hat{H}(\hat{a}|0>)=0$

$\hat{H}|0>=(\hat{a}^+\hat{a}+\frac{1}{2})\hbar \omega|0>= \frac{1}{2}\hbar\omega |0>$

denominándose $E_0$ como la energía del punto cero; $|0>$ representa el vacío electromagnético.

El espacio de Hilbert $\mathscr{H}$ para un solo modo de radiación es el espacio generado por todos los vectores número, esto es, su envolvente lineal, integrado pues por vectores de la forma

$|\Psi>=\sum_{n=0}^{\infty}c_n|n>$

donde $c_n$ representan escalares.

-Este espacio de Hilbert se denomina espacio de Fock (monomodal).

Los estados número se normalizan a la unidad y constituyen un sistema ortonormal, satisfaciéndose:

$<n|n'>=\delta_{nn'}$

$\Rightarrow |\Psi>=\sum_{n=0}^{\infty}|n><n|\Psi>$

( $|n><n|$ es un proyector ortogonal)

$\sum_n|n><n|=I$ (relación de cierre o clausura)

$\hat{a}|n>=\sqrt{n}|n-1>$

$\hat{a}^+|n>=\sqrt{n+1}|n+1>$

$\hat{n}|n>=\hat{a}^+\hat{a}|n>=n|n>$

$|n>=\frac{(\hat{a}^+)^n}{\sqrt{n!}}|0>$

$n\ne m \Rightarrow <m|\hat{a}|n>=c_{m}\delta_{m,n\pm 1}$

$<n-1|\hat{a}|n>=\sqrt{n}(n-1)|n-1>=\sqrt{n}$

$<n+1|\hat{a}^+|n>=\sqrt{n+1}(n+1)|n+1>=\sqrt{n+1}$

Incluyendo explícitamente la dependencia temporal en la expresión para el operador campo eléctrico, se obtiene:

$\hat{E_x}(z,t)=\mathcal{E}_0(\hat{a}(0)e^{-i\omega t}+\hat{a^+}(0)e^{+i\omega t})\sin(kz)$ ,

teniéndose que

$[\hat{n},\hat{E}_x(z,t)]=\mathcal{E}_0(\hat{a}^+-\hat{a})\sin (kz)$

En la representación número de fotones el estado $|n>$ representa un campo monocromático cuantizado, de frecuencia $\omega$ y conteniendo $n$ fotones excitados desde el vacío (se abandona la representación de posiciones: el ket representa sólo un número de cuantos de excitación de energía).

Cada estado $|n>$ es un autoestado de autoenergía $E_n$ sobre el que el valor medio del campo eléctrico es nulo:

$<n|\hat{E}_x(z,t)|n>=\mathcal{E}_0\sin(kz)<n|\hat{a}+\hat{a}^+|n>=0$

-Pero el valor medio del cuadrado del campo no es nulo:

$<n|\hat{E}_x^2(z,t)|n>=\mathcal{E}_0^2\sin^2(kz)<n|\hat{a}^2+\hat{a}^{+2}+2\hat{a}^+\hat{a}+1|n>$

$=2\mathcal{E}_0^2\sin^2(kz)(n+\frac{1}{2})$

Fluctuaciones del campo

Las fluctuaciones en el campo eléctrico se caracterizan por la varianza

$\sigma^2 (E_x(z,t))=|<E_x^2(z,t)>-<E_x(z,t)>^2|$

que sobre un estado fotónico $|n>$ se convierte en la indeterminación mecano-cuántica (raíz):

$\Delta_n \hat{E}_x(z,t)=|<n|(\hat{E}_x-<n|\hat{E}_x|n>)^2|n>|^{\frac{1}{2}}$

$=|<n|\hat{E}_x^2|n>-<n|\hat{E}_x|n>^2|^{\frac{1}{2}}$

$=\sqrt{2\mathcal{E}_0}\sin(kz)(n+\frac{1}{2})^{\frac{1}{2}}$

-El campo presenta fluctuaciones en el vacío:

$\Delta_0 \hat{E}_x(z,t)=\sqrt{\mathcal{E}_0}\sin(kz)$

-El principio de indeterminación:

$\Delta \hat{A} \ \Delta \hat{B} \ge \frac{1}{2}|<[\hat{A},\hat{B}]>|$

-El principio de indeterminación en el oscilador armónico monodimensional:

$\Delta \hat{q}=\left\langle \hat{q}^2 -\left\langle \hat{q} \right\rangle^2 \right\rangle^{\frac{1}{2}}=(n+\frac{1}{2})^{\frac{1}{2}}(\frac{\hbar}{\omega m})^\frac{1}{2}$
$\Delta \hat{p}=\left\langle \hat{p}^2 -\left\langle \hat{p} \right\rangle^2 \right\rangle^{\frac{1}{2}}= (n+\frac{1}{2})^{\frac{1}{2}}(\hbar \omega m)^\frac{1}{2}$
$\Rightarrow \Delta \hat{q} \cdot \Delta \hat{p}=(n+\frac{1}{2})\hbar \ge \frac{\hbar}{2}$

$\rightarrow$ La igualdad se tiene para el estado fundamental, $n=0$ : $\psi_o(x)$ es una gaussiana.

-El principio de indeterminación sobre el vacío de Fock:

$<0|\hat{q}|0>=0 \quad \Rightarrow \quad <0|\hat{q}^2|0>=\frac{\hbar}{2\omega}\ne 0$

$<0|\hat{p}|0>=0 \quad \Rightarrow \quad <0|\hat{p}^2|0>=\frac{\hbar \omega}{2}\ne 0$

$\rightarrow \Delta_0 \hat{q}=\sqrt{\frac{\hbar}{2\omega}} \quad , \quad \Delta_0 \hat{q}=\sqrt{\frac{\hbar \omega}{2}}$

$\Delta_0 \hat{q} \Delta_0 \hat{p}=\frac{\hbar}{2}$

(saturación de la desigualdad sobre el vacío: el vacío como estado en el que el producto de indeterminaciones es mínimo: estado de mínima indeterminación).

-El principio de indeterminación para los dos operadores complementarios $\hat{n}$ y $\hat{E}_x$ :

$\Delta \hat{n} \Delta \hat{E}_x \ge \frac{\mathcal{E}_0}{2} |\sin(kz)| \cdot |<\hat{a}^+-\hat{a}>|$

( $\Delta_n \hat{n}=0=<n|\hat{a}^+-\hat{a}|n>$ ; pero $\Delta \hat{E}_x=0 \Rightarrow$ número de fotones indeterminado).

Operadores cuadratura del campo

Los operadores hermíticos cuadratura del campo, $\hat{X}_1$ y $\hat{X}_2$ , se definen según:

$\hat{X}_1=\frac{1}{2}(\hat{a}+\hat{a}^+) = (2\hbar\omega)^{-\frac{1}{2}} \, (\omega \hat{q}) = \sqrt{ \frac{\omega}{2\hbar}} \, ( \hat{q})$

$\hat{X}_2=\frac{1}{2i}(\hat{a}-\hat{a}^+) = (2\hbar\omega)^{-\frac{1}{2}} \, ( \hat{p}) = \frac{1}{\sqrt{2\hbar\omega}} \, ( \hat{p})$

y cumplen:

$[\hat{X}_1,\hat{X}_2]=\frac{i}{2}$ $\Rightarrow \Delta \hat{X}_1\Delta \hat{X}_2\ge \frac{1}{4}$ ,

pudiendo expresarse

$\hat{E}_x(z,t)=2\mathcal{E}_0\sin(kz)(\hat{X}_1\cos \omega t +\hat{X}_2\sin \omega t )$

-Estos operadores se asocian a sendas oscilaciones de las amplitudes de campo en cuadratura, esto es, desfasadas entre sí $\frac{\pi}{2}$ radianes.

–Estados MUS, estados de mínima indeterminación (minimum uncertainty state):

$\Rightarrow (\Delta_{MUS}\hat{X}_1)(\Delta_{MUS} \hat{X}_2)= \frac{1}{4}$

-En la representación número de fotones:

$<n|\hat{X}_1|n>=<n|\hat{X}_2|n>=0$

$<n|\hat{X}_1^2|n>=<n|\hat{X}_2^2|n>=\frac{1}{4}(2n+1)$

de manera que

$\Delta_{n}\hat{X}_1=\Delta_{n} \hat{X}_2$ ;

además, el principio de indeterminación satura sobre el vacío, que es un estado MUS, ya que:

$(\Delta_0 \hat{X}_1)=(\Delta_0 \hat{X}_2)=\frac{1}{2}$

Cavidad con infinitos modos de radiación

Sea una cavidad cúbica de lado $L$ muy grande en comparación con las dimensiones atómicas involucradas; volumen $V=L^3$ ; con paredes perfectamente reflectantes; sin fuentes ni sumideros en su interior (se satisfacen pues las ecuaciones de Maxwell en la forma indicada al principio). En su interior se supone un campo electromagnético para el que todas las longitudes de onda presentes cumplen $\lambda \ll L$ .

-Sea $\vec{\mathrm{A}}(\vec{r},t)$ el potencial vector del campo, que satisface la ecuación de ondas

$\nabla^2\vec{\mathrm{A}}-\frac{1}{c^2}\frac{\partial^2\vec{\mathrm{A}}}{\partial t^2}=0$ ;

se impone gauge de Coulomb,

$\nabla \cdot \vec{\mathrm{A}}(\vec{r},t)=0$ ;

se satisface:

$\vec{E}(\vec{r},t)=-\frac{\partial \vec{\mathrm{A}}(\vec{r},t)}{\partial t}$

$\vec{B}(\vec{r},t)=\nabla \times \vec{\mathrm{A}}(\vec{r},t)$

-Sobre las ondas planas en la cavidad se imponen condiciones de frontera periódicas,

$e^{ik_jx}=e^{ik_j(x+L)} \Rightarrow k_j=\frac{2\pi}{L}m_j\;,\;m=0,\pm 1,\pm 2\ldots \;,\; j=x,y,z$

$\Rightarrow \vec{k}=\frac{2\pi}{L}(m_x,m_y,m_z)\;,\; k=|\vec{k}|=\frac{\omega_k}{c}$

-Es decir, cada modo de oscilación (con dos polarizaciones posibles) de los infinitos (numerable) posibles viene determinado por una tríada de coordenadas enteras $(m_x,m_y,m_z)$ , siendo el número total de modos con sendas coordenadas $j$ en el intervalo $\Delta m_j$ :

$\Delta m=\prod_{j=x,y,z}\Delta m_j=2(\frac{L}{2\pi})^3\prod_{j=x,y,z}\Delta k_j$

-Puesto que para todas las longitudes de onda se cumple $\lambda \ll L$ , puede realizarse el paso al continuo, obteniéndose el número de modos, en el ángulo sólido $d\Omega=\sin \theta d\theta d\phi$ , con $k$ entre $k$ y $k+dk$ (coordenadas esféricas):

$\vec{k}=k(\sin \theta \cos \phi,\sin \theta \sin \phi,\cos \theta)$

$dm=2(\frac{V}{8\pi^3})k^2dkd\Omega$ ;

$d\Omega=\sin \theta d\theta d\phi$ ,

o elemento de ángulo sólido alrededor de la dirección $\vec{k}$ .

-Usando $\omega_k=kc$ se obtiene el número de modos, con $k$ entre $k$ y $k+dk$ :

$dm=2(\frac{V}{8\pi^3})k^2dkd\Omega$ ;

finalmente, integrando sobre $\Omega$ , se obtiene la densidad $\rho(\omega_k)$ de modos en la cavidad , por unidad de volumen, en todas direcciones y con frecuencia $\omega_k$ entre $\omega_k$ y $\omega_k+d\omega_k$ :

$\rho(\omega_k)=\frac{\omega_k^2}{\pi^2c^3}$ ;

$\rho(\omega_k)\ d\omega = \rho(k)\ dk$ .

-El potencial vector $\vec{\mathrm{A}}$ admite expresión como superposición de ondas planas:

$\vec{\mathrm{A}}(\vec{r},t)=\sum_{\vec{k},s}\vec{e}_{\vec{k}s}[A_{\vec{k}s}(t)e^{i\vec{k}\cdot\vec{r}}+A_{\vec{k}s}^*(t)e^{-i\vec{k}\cdot\vec{r}}]$

donde $A_{\vec{k}s}$ representa la amplitud de cada modo $({\vec{k}s})$ del campo (compleja); $\vec{e}_{\vec{k}s}$ es el vector polarización; la coordenada $s$ suma sobre las dos polarizaciones ortogonales posibles, $\vec{e}_{\vec{k}s}\vec{e}_{\vec{k}s'}=\delta_{s,s'}$ (en el libre espacio la suma sobre los modos en la cavidad se convertiría en una integral $\frac{V}{\pi^2}\int k^2dk$ ).

-Por la condición de Gauge impuesta, se satisface $\vec{k}\cdot\vec{e}_{\vec{k},s}=0$ , condición de transversalidad: el gauge de Coulomb conlleva que los modos de polarización son ortogonales a la dirección de propagación. De esta forma, los tres vectores $\vec{\kappa}=\frac{\vec{k}}{k},\vec{e}_{\vec{k}1},\vec{e}_{\vec{k}2}$ , resultan ortogonales dos a dos: $\vec{\kappa}=\vec{e}_{\vec{k}1}\times \vec{e}_{\vec{k}2}$

-Sustituyendo después en la ecuación de onda e incorporando el gauge, se deriva la ecuación del oscilador armónico para cada amplitud del campo:

$\frac{d^2A_{\vec{k}s}}{dt^2}+\omega_k^2A_{\vec{k}s}=0\;,\;\omega_k=kc$ ,

cuya solución es

$A_{\vec{k}s}(t)=A_{\vec{k}s}(0)e^{-i\omega_kt}$

-A partir de la anterior expresión los campos resultan:

$\vec{E}(\vec{r},t)=i\sum_{\vec{k},s}\omega_k\vec{e}_{\vec{k}s}[A_{\vec{k}s}(0)e^{i(\vec{k}\cdot\vec{r}-\omega_k t)}-A_{\vec{k}s}^*(0)e^{-i(\vec{k}\cdot\vec{r}-\omega_k t)}]$

$\vec{B}(\vec{r},t)=\frac{i}{c} \sum_{\vec{k},s} \omega_k(\vec{\kappa}\times \vec{e}_{\vec{k}s})[A_{\vec{k}s}(0)e^{i(\vec{k}\cdot\vec{r}-\omega_k t)}-A_{\vec{k}s}^*(0)e^{-i(\vec{k}\cdot\vec{r}-\omega_k t)}]$

-La energía clásica del campo viene dada por:

$H=\frac{1}{2}\int_V (\epsilon_0\vec{E}\cdot \vec{E}+\frac{1}{\mu_0}\vec{B}\cdot \vec{B})dV$

-Imponiendo las condiciones de contorno periódicas,

$\int_0^L e^{\pm ik_jr_j}dr_j=L\delta_{k_j0}\;;\:j=x,y,z$

$\equiv \int_Ve^{\pm i(\vec{k}-\vec{k}')\cdot \vec{r}}dV=V\delta_{\vec{k}\vec{k}'}$

-Y sustituyendo las expresiones de los campos en términos de las amplitudes $A$ :

$H=2\epsilon_0V\sum_{\vec{k},s}\omega_k^2A_{\vec{k}s}(t)A_{\vec{k}s}^*(t)$

$=2\epsilon_0V\sum_{\vec{k},s}\omega_k^2A_{\vec{k}s}(0)A_{\vec{k}s}^*(0)$

-A continuación se expresan las amplitudes del campo en términos de las variables canónicas:

$A_{\vec{k}s}(0)=\frac{1}{2\omega_k(\epsilon_0V)^{\frac{1}{2}}}[\omega_kq_{\vec{k}s}+ip_{\vec{k}s}]$

$A_{\vec{k}s}^*(0)=\frac{1}{2\omega_k(\epsilon_0V)^{\frac{1}{2}}}[\omega_kq_{\vec{k}s}-ip_{\vec{k}s}]$

$\Rightarrow H=\frac{1}{2}\sum_{\vec{k},s} (p_{\vec{k},s}^2+\omega_k^2q_{\vec{k},s}^2)$

esto es, una suma de términos energéticos de oscilador (masa $m=1$ ).

Cuantización: se asumen las reglas de cuantización para los operadores autoadjuntos $\hat{q}_{\vec{k},s}$ y $\hat{p}_{\vec{k},s}$ que representan los observables cuánticos,

$[\hat{q}_{\vec{k},s},\hat{q}_{\vec{k}',s'}]=0$

$[\hat{p}_{\vec{k},s},\hat{p}_{\vec{k}',s'}]=0$

$[\hat{q}_{\vec{k},s},\hat{p}_{\vec{k}',s'}]=i\hbar \delta_{\vec{k}\vec{k}'}\delta_{ss'}$

y se definen unos operadores escalera (no hermíticos) y número, por modo de radiación $(\vec{k}s)$ :

$\hat{a}_{\vec{k},s}=\frac{1}{(2\hbar\omega_k)^{\frac{1}{2}}}[\omega_k\hat{q}_{\vec{k},s}+i\hat{p}_{\vec{k},s}]$

$\hat{a}_{\vec{k},s}^+=\frac{1}{(2\hbar\omega_k)^{\frac{1}{2}}}[\omega_k\hat{q}_{\vec{k},s}-i\hat{p}_{\vec{k},s}]$

$\hat{n}_{\vec{k},s}=\hat{a}_{\vec{k},s}^+\hat{a}_{\vec{k},s}$

que satisfacen las reglas de conmutación

$[\hat{a}_{\vec{k},s},\hat{a}_{\vec{k}',s'}]=0$

$[\hat{a}_{\vec{k},s}^+,\hat{a}_{\vec{k}',s'}^+]=0$

$[\hat{a}_{\vec{k},s},\hat{a}_{\vec{k}',s'}^+] =\delta_{\vec{k}\vec{k}'}\delta_{ss'}$

-El operador Hamiltoniano se expresa:

$\hat{H}=\sum_{\vec{k},s}(\hat{a}_{\vec{k},s}^+\hat{a}_{\vec{k},s}+\frac{1}{2})\hbar\omega_k$

$=\sum_{\vec{k},s}(\hat{n}_{\vec{k},s}+\frac{1}{2})\hbar\omega_k$

Espacio de Fock multimodal: Cada modo de radiación $(\vec{k}s)\equiv (j)$ es independiente de los demás, de forma que se asocia con un conjunto de estados número de fotones $|n_{\vec{k},s}>\equiv |n_j>$ para los que:

$\hat{n}_{\vec{k},s}|n_{\vec{k},s}>=n_{\vec{k},s}|n_{\vec{k},s}>$

$\equiv \hat{n}_j|n_j>=n_j|n_j>$

-El Hamiltoniano del campo se puede expresar entonces como:

$\hat{H}=\sum_{j}(\hat{n}_{j}+\frac{1}{2})\hbar\omega_j$

-Los estados número multifotónicos, con fotones pertenecientes a distintos modos de radiación $(\vec{k}s)\equiv (j)$ , pueden notarse como:

$|n_1>|n_2>\ldots \equiv |n_1n_2\ldots> \equiv |\{n_j\}>$

representando autoestados simultáneos del Hamiltoniano $\hat{H}$ ,

$\hat{H}|\{n_j\}>=E|\{n_j\}>\quad , \quad E=\sum_{j}(n_{j}+\frac{1}{2})\hbar\omega_j$ ,

y de todos los operadores números $\hat{n}_j$ asociados a cada modo,

$\hat{n}_j|n_j>=n_j|n_j>$

-Los estados número constituyen una base ortonormal del correspondiente Hilbert:

$<n_1n_2\ldots |n_1'n_2'\ldots>=\delta_{n_1n_1'}\delta_{n_2n_2'}\ldots$

-Actuación de los operadores escalera:

$\hat{a}_{j}|n_1n_2\ldots n_j\ldots>=\sqrt{n_j}|n_1n_2\ldots n_j-1\ldots>$

$\hat{a}_{j}^+|n_1n_2\ldots n_j\ldots>=\sqrt{n_j+1}|n_1n_2\ldots n_j+1\ldots>$

-El operador número total de fotones $\hat{n}$ se define:

$\hat{n}=\sum_{\vec{k},s} \hat{n}_{\vec{k},s} =\sum_{\vec{k},s}\hat{a}_{\vec{k},s}^+\hat{a}_{\vec{k},s}$

$\equiv \sum_j\hat{n}_j$

$\Rightarrow \hat{n}|\{n_j\}>=(\sum_j \hat{n}_j)|\{n_j\}>=(\sum_j n_j)|\{n_j\}>$

-Estado vacío:

$|0>|0>\ldots \equiv |00\ldots> \equiv |\{0\}>$

$\hat{a}_{j}|\{0\}>=0\;,\;\forall j$

-Generación de estados sobre el vacío:

$|\{n_j\}>=\prod_j\frac{(\hat{a}_{j}^+)^{n_j}}{\sqrt{n_j!}}|\{0\}>$

-Algunos estados monofotónicos:

$|1_j>\equiv |00\ldots 0\overbrace{1}^{j} 0\ldots 0>=\hat{a}_j^+|00\ldots 0>\quad (j) \equiv (\vec{k}_js_j)$

$|1_m> \equiv |00\ldots 0\overbrace{1}^{m} 0\ldots 0>=\hat{a}_m^+|00\ldots 0>\quad (m) \equiv (\vec{k}_ms_m)$

$|\Psi>=\frac{1}{\sqrt{2}}(|1_j>+|1_m>)=\frac{1}{\sqrt{2}}(\hat{a}_j^++\hat{a}_m^+)|0>$

(ya que $\hat{n}|\Psi>=|\Psi>$ ).

Un estado de Fock monofotónico es en general una superposición de modos y no está asociado con un modo individual clásico: un paquete de ondas para un fotón individual es preparable.

Nota: recuérdese que no existe hoy una función de onda aceptada para el fotón, constituyendo un tema de investigación abierto en que han sido publicados numerosos y diferentes enfoques. Lo que está claro es que una interpretación probabilística para $\left|E(\vec{r};t)\right|^2$ como una densidad de probabilidad de posición, siendo $E(\vec{r};t)$ el paquete de ondas (por ejemplo, gaussiano), esto es, una suma de ondas, todas con igual velocidad de fase $v_f=\omega/k=c$ , no es aplicable al fotón. Feynmann dijo que a la pregunta «¿Dónde está el fotón?«, la respuesta es «nadie lo sabe, y lo mejor es que no se intente pensar sobre ello«. Desde luego, si acudimos al concepto de fotón como un modo de excitación normal del campo, y no como una partícula, la pregunta se difumina… Información amplia y actual sobre todo esto puede encontrarse en la referencia:

Optics and Photonic news, OPN Trends, octubre 2003: ¿Qué es un fotón?

Operadores amplitudes del campo, potencial vector y campos:

$\hat{A}^o_{\vec{k}s}\equiv\hat{A}_{\vec{k}s}(0)=(\frac{\hbar}{2\omega_k\epsilon_0V})^{\frac{1}{2}}\hat{a}_{\vec{k},s}(0)\equiv(\frac{\hbar}{2\omega_k\epsilon_0V})^{\frac{1}{2}}\hat{a}^o_{\vec{k},s}$

$\hat{A}^{o+}_{\vec{k}s}\equiv\hat{A}_{\vec{k}s}^+(0)=(\frac{\hbar}{2\omega_k\epsilon_0V})^{\frac{1}{2}}\hat{a}_{\vec{k},s}^+(0)\equiv(\frac{\hbar}{2\omega_k\epsilon_0V})^{\frac{1}{2}}\hat{a}^{o+}_{\vec{k},s}$

$\hat{a}^o_{\vec{k},s}\equiv\hat{a}_{\vec{k},s}(0)$

$\hat{a}^{o+}_{\vec{k},s} \equiv\hat{a}_{\vec{k},s}^+(0)$

$\hat{a}_{\vec{k},s}(t)=\hat{a}_{\vec{k},s}(0)e^{-i\omega_k t}=\hat{a}^o_{\vec{k},s}e^{-i\omega_k t}$

$\hat{a}_{\vec{k},s}^+(t)=\hat{a}^+_{\vec{k},s}(0)e^{+i\omega_k t}=\hat{a}^{o+}_{\vec{k},s}e^{+i\omega_k t}$

(imagen de Heisenberg)

$\hat{\vec{\mathrm{A}}}(\vec{r},t)=\sum_{\vec{k},s} (\frac{\hbar}{2\omega_k\epsilon_0V})^{\frac{1}{2}} \vec{e}_{\vec{k}s}[\hat{a}^o_{\vec{k}s}e^{i(\vec{k}\cdot\vec{r}-\omega_k t)}+\hat{a}^{o+}_{\vec{k}s}e^{-i(\vec{k}\cdot\vec{r}-\omega_k t)}]$

$\hat{\vec{E}}(\vec{r},t)=i\sum_{\vec{k},s}(\frac{\hbar\omega_k}{2\epsilon_0V})^{\frac{1}{2}}\vec{e}_{\vec{k}s}[\hat{a}^o_{\vec{k}s}e^{i(\vec{k}\cdot\vec{r}-\omega_k t)}-\hat{a}^{o+}_{\vec{k}s}e^{-i(\vec{k}\cdot\vec{r}-\omega_k t)}]$

$=i\sum_{\vec{k},s}(\frac{\hbar\omega_k}{2\epsilon_0V})^{\frac{1}{2}}\vec{e}_{\vec{k}s}[\hat{a}_{\vec{k}s}(t)e^{i\vec{k}\cdot\vec{r}}-\hat{a}^{+}_{\vec{k}s}(t)e^{-i\vec{k}\cdot\vec{r}}]$

$=\hat{\vec{E}}^{(+)}(\vec{r},t)+\hat{\vec{E}}^{(-)}(\vec{r},t)$

donde $\hat{\vec{E}}^{(+)}(\vec{r},t)$ se denomina la parte de frecuencia positiva del campo, que contiene los términos que oscilan como $e^{-i\omega t}$ , para $\omega >0$ ; $\hat{\vec{E}}^{(-)}(\vec{r},t)=(\hat{\vec{E}}^{(+)}(\vec{r},t))^{\dagger}$ se denomina la parte de frecuencia negativa del campo (dependen respectivamente de operadores destrucción y creación).

-Para el operador campo magnético:

$\hat{\vec{B}}(\vec{r},t)=\frac{i}{c} \sum_{\vec{k},s} (\vec{\kappa}\times \vec{e}_{\vec{k}s})(\frac{\hbar\omega_k}{2\epsilon_0V})^{\frac{1}{2}} [\hat{a}^o_{\vec{k}s}e^{i(\vec{k}\cdot\vec{r}-\omega_k t)}-\hat{a}^{o+}_{\vec{k}s}e^{-i(\vec{k}\cdot\vec{r}-\omega_k t)}]$

$=\frac{i}{c} \sum_{\vec{k},s} (\vec{\kappa}\times \vec{e}_{\vec{k}s})(\frac{\hbar\omega_k}{2\epsilon_0V})^{\frac{1}{2}} [\hat{a}_{\vec{k}s}(t)e^{i\vec{k}\cdot\vec{r}}-\hat{a}^+_{\vec{k}s}(t)e^{-i\vec{k}\cdot\vec{r}}]$

La cuantización de la radiación en la cavidad se resume en la hipótesis de que el campo de radiación se asimila a un conjunto de osciladores armónicos cuánticos.

Bibliografía

[FOX-06] M. Fox, Quantum Optics. An Introduction, Oxford Univ. Press, Oxford, 2006. ISBN: 0-19-856672-7.
[GAR-08]: Garrison, J. C. and R. Y. Chiao, Quantum Optics, Oxford Univ. Press, Oxford, 2008. ISBN: 978-0-19-850886-1.
[GER-05] C. C. Gerry and P. L. Knight, Introductory Quantum Optics, Cambridge Univ. Press, Cambridge, 2005. ISBN: 0-521-82035-9.
Cuentos cuánticos: un curso de introducción a la QFT
Representaciones gráficas del campo cuántico en cavidades: http://www.cqed.org/spip.php?article254

Curiosidad hipotética
-Las fluctuaciones y los viajes en el tiempo: Browne, Malcolm W. (21 de agosto de 1990), New Direction in Physics: Back in Time, The New York Times, consultado el 22 de mayo de 2010:
«According to quantum theory, the vacuum contains neither matter nor energy, but it does contain ‘fluctuations’, transitions between something and nothing in which potential existence can be transformed into real existence by the addition of energy.(Energy and matter are equivalent, since all matter ultimately consists of packets of energy.) Thus, the vacuum’s totally empty space is actually a seething turmoil of creation and annihilation, which to the ordinary world appears calm because the scale of fluctuations in the vacuum is tiny and the fluctuations tend to cancel each other out. But experiments using giant particle accelerators have shown that every conceivable kind of subnuclear particle (along with its antimatter equivalent particle) is constantly popping into existence in the vacuum only to be immediately reunited with its antiparticle in mutual annihilation.
These short-lived ‘virtual’particles can be converted into a real particle by supplying it with the needed energy a task made possible by modern particle accelerators.
Fluctuations Observed In 1948 a Dutch physicist, Hendrick B. G. Casimir, theorized that if two electrically conductive metal plates are held close enough together in a vacuum, they distort the normal quantum fluctuations in the vacuum between them, and the result is a measurable attraction between the plates. Experiments in the 1950’s confirmed the Casimir prediction. Theorists have since concluded that because of the distortion in fluctuations, the vacuum between the conducting plates contains negative energy.»

-Texto que acompaña al artículo en el The New York Times:
THE possibility of traveling through time, of creating something out of nothing and even of spawning a new universe in a laboratory are notions ordinarily reserved to fiction rather than science. But a rash of articles in some of the most prestigious scientific publications suggests that theoretical physicists have begun to take such outlandish ideas seriously.
Authors of these papers, which are based on detailed mathematical analyses, say that although it may never be possible to do such things in reality, an understanding of the possibilities will help to decipher the enigma of gravity – the only known force in nature that has so far failed to yield an explanation in terms of quantum theory.
Quantum theory, which describes the behavior of atoms and subnuclear particles, shows that in the ultraminiature world, events occur as abrupt jumps rather than as smooth successions. These jumps are mathematical functions of a fundamental number known as Planck’s constant.
Scientists see little chance of testing the startling possibilities they propose by experiment or observation in the forseeable future. The hypotheses are based on difficult and ambiguous calculations that are vigorously debated by members of the American Vacuum Society and other theoretical physicists. Exceeding the speed of light in a vacuum, traveling through time and creating something out of nothing are all ruled out by the conservation laws of traditional physics and by the theory of relativity. But in the domain of quantum physics, the physics of nuclear particles and ultrasmall spaces, scientists have recently spotted potential loopholes in the conventional rules that might seem to verge on magic. Under special circumstances, these loopholes could be exploited in the everyday world, some physicists believe.

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

El fotón como excitación del campo

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta