Interferómetro de Franson

Interferómetro de Franson

Fuente: [GAR-08], cap. 10, pp. 328ss.

Experimento de Franson: propuesta y realización

En 1989, Franson estableció un nuevo y sorprendente efecto de interferencia cuántico, en el que dos fotones (dos amplitudes de probabilidad Feynman) van a interferir sin que los fotones ocupen nunca un mismo entorno local:

J.D. Franson, «Bell inequality for position and time», Phys. Rev. Lett. 62 (1989), p. 2205:

Abstract: The quantum-mechanical uncertainty in the position of a particle or the time of its emission is shown to produce observable effects that are inconsistent with any local hidden-variable theory. A new experimental test of local hidden-variable theories based on optical interference is proposed.

J.D. Franson, «Violations of a simple inequality for classical fields» Phys. Rev. Lett. 67 (1991), p. 290:

Abstract: It has been shown that two correlated photons incident upon two distant interferometers can give a coincidence counting rate that depends nonlocally on the sum of the phases of the two interferometers. It is shown here that the results of existing experiments violate a simple inequality that must be satisfied by any classical or semiclassical field theory. The inequality provides a graphic illustration of the lack of objective realism of the electric field.

-Su realización experimental llegó al año siguiente:

Z. Y. Ou, X. Y. Zou, L. J. Wang, and L. Mandel; Observation of nonlocal interference in separated photon channels, Phys. Rev. Lett. 65 (1990) 321.

Abstract: A two-photon coincidence experiment of the kind recently proposed by J. D. Franson has been carried out with signal and idler photons produced in the process of parametric down-conversion. The coincidence rate registered by the two detectors is found to exhibit a cosine variation with the optical path difference, with periodicity equal to the wavelength.

Montaje

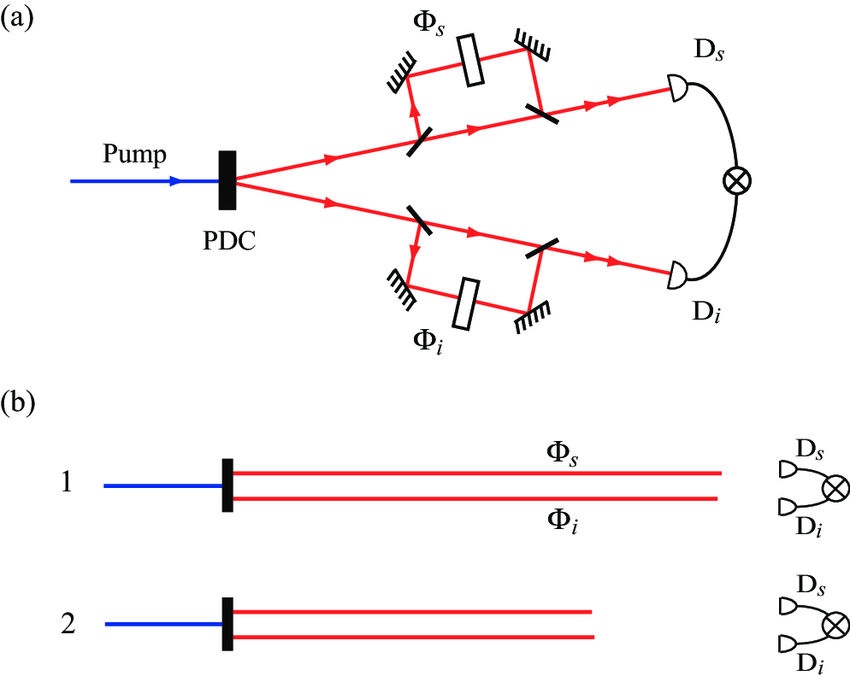
Mientras que en el experimento del doble cristal de Zou-Wang-Mandel dos fotones emitidos de forma simultánea por conversión paramétrica SPDC en un cristal no lineal inciden sobre un divisor de haz, produciéndose interferencias entre ellos porque el dispositivo experimental incluye dos cristales, siendo imposible determinar en cuál de ellos se ha producido la emisión SPDC (situación con dos posibles caminos o procesos de Feynman indistinguibles para su realización), en el efecto Franson nos encontramos con dos fotones que llegan a interferómetros distantes, separados espacialmente:

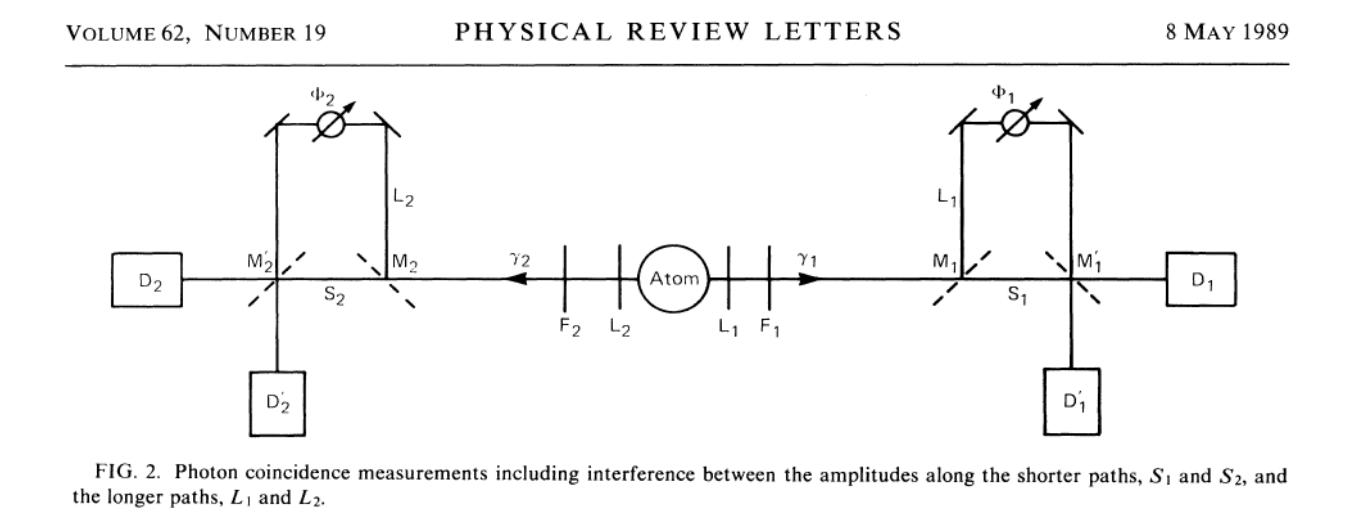
Efecto Franson, 1989 — Imagen original en J.D. Franson, Phys. Rev. Lett. 62 (1989), p. 2205.

-Es interesante señalar que en su artículo pionero de 1989 Franson empleaba una fuente fotónica consistente en un sistema atómico de tres niveles, que describía así en su artículo:

At time t=0 an atom is assumed to have been excited into the upper state $\psi_1$ , which has a relatively long lifetime $\tau_1$ . After emission of a photon $\gamma_1$ with wavelength $\lambda_1$ , the atom will be in the intermediate state $\psi_2$ , which has a relatively short lifetime $\tau_2 \ll \tau_1$ .Thus a second photon $\gamma_2$ with wavelength $\lambda_2$ will be emitted very soon after $\gamma_1$ , and a coincidence counting experiment would show a very narrow peak with a width $\sim \tau_2$ .The final state $\psi_3$ is assumed to either have a very long lifetime $\tau_3$ or to be the ground state. In principle, $\gamma_1$ and $\gamma_2$ could be any massless particles emitted by any quantum system, since the results do not depend on their properties. As a practical matter, atomic transitions frequently do satisfy the condition $\tau_2 \ll \tau_1$ .

-Es decir, el átomo propuesto es un átomo excitado a un estado muy estable, con larga vida media, y que cuando decae lo va a hacer vía la emisión casi simultánea de dos fotones, que han de ser considerados como emitidos en la misma ventana temporal dado el orden, respecto a la vida media involucrada, de la incertidumbre temporal que acompaña a la emisión.

-Los montajes actuales suelen usar como fuente de fotones correlacionados los producidos por SPDC en cristales no lineales, el tipo de fuente que de hecho incorporó ya Franson en su artículo de 1991.

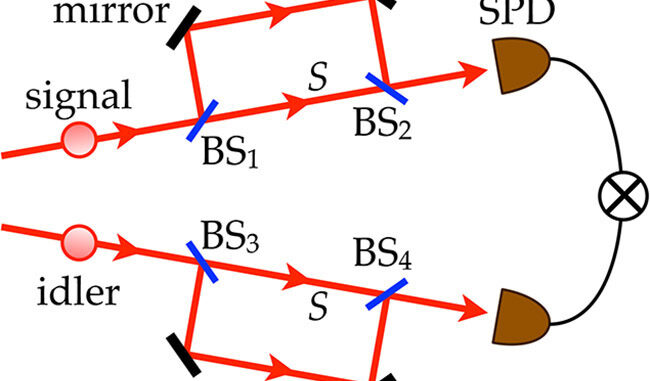
Un interferómetro de Franson es usual que presente un montaje en que se incluyen dos interferómetros de Mach-Zehnder sin balancear, es decir, en que los dos brazos ópticos tienen asociados caminos ópticos de longitud diferente.

-Bajo determinada configuración, jugando con los caminos ópticos en los dos interferómetros no balanceados, puede conseguirse la siguiente correlación estricta: que nunca se produzca un evento en que un fotón atraviesa su interferómetro por el brazo corto mientras que su acompañante en emisión lo hace por el brazo largo (siempre cada dos fotones compañeros acceden a interferómetros diferentes). El montaje permite también configurar una perfecta anticorrelación.

-Es decir, dos fotones que nunca interaccionan desde su emisión conjunta en el cristal realizan -por así decirlo- una elección al azar respecto al brazo del interferómetro que recorren (brazo largo o brazo corto), y las sendas elecciones aleatorias están correlacionadas.

Interferencias en un interferómetro de Franson

Los fotones signal e idler son monitorizados por los caminos largo L y corto S hacia los sendos segundos divisores de haz en cada interferómetro, BS2 y BS4; cada uno de ellos tiene dos puertos de salida, en uno se coloca un detector (detectores $D_{sig}$ y $D_{idl}$ ; el otro puerto en cada BS se denominará como puerto de salida (puertos salida S2 para BS2 y S4 para BS4) y podrá ser monitorizado o no.

-Sea la diferencia $\Delta C_j=L_j-S_j$ , con $j=s,l$ , que es ajustable y que jugará el papel del desfase óptico del que dependerá la interferencia, que se observará como una oscilación de la intensidad en los segundos divisores de haz. Como siempre, si este desfase óptico $\Delta C_j/c$ se hace mucho mayor que el tiempo de coherencia $\tau$ del fotón, no se observarán interferencias.

-Cuatro situaciones parece que podrían producir la detección de ambos fotones en coincidencia:

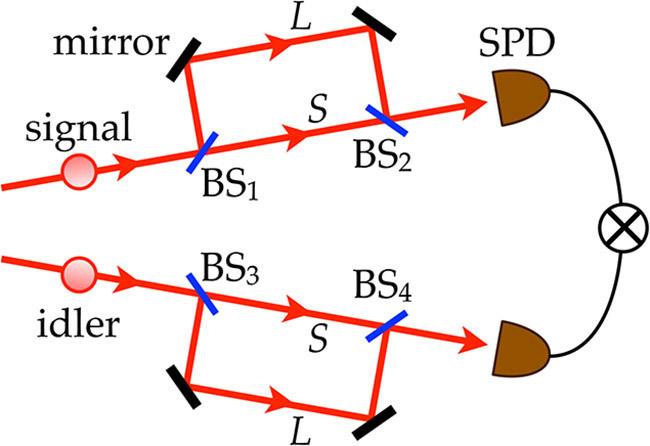
1) Ambos fotones siguen el camino largo: el fotón signal viaja por L (en el interferómetro signal) y alcanza el detector $D_{sig}$ ; análogamente para el fotón signal en el interferómetro idler.

2) Ambos fotones siguen el camino corto S en su interferómetro.

3) El fotón signal sigue el camino largo y el idler el corto.

4) El fotón signal sigue el camino corto y el idler el largo.

Sólo las posibilidades o procesos de Feynman indistinguibles de realización de un mismo resultado final pueden interferir.

-Si calculamos los tiempos de llegada de cada fotón a su respectivo detector, $t_j$ , con $j=i,s$ , dependerán del camino óptico según $t_j(L)=T+L/c$ y $t_j(S)=T+S/c$ , donde T representa la suma del tiempo invertido entre el cristal y el primer divisor de haz, más el tiempo invertido entre el segundo divisor de haz y el detector, que son los dos iguales para ambos fotones.

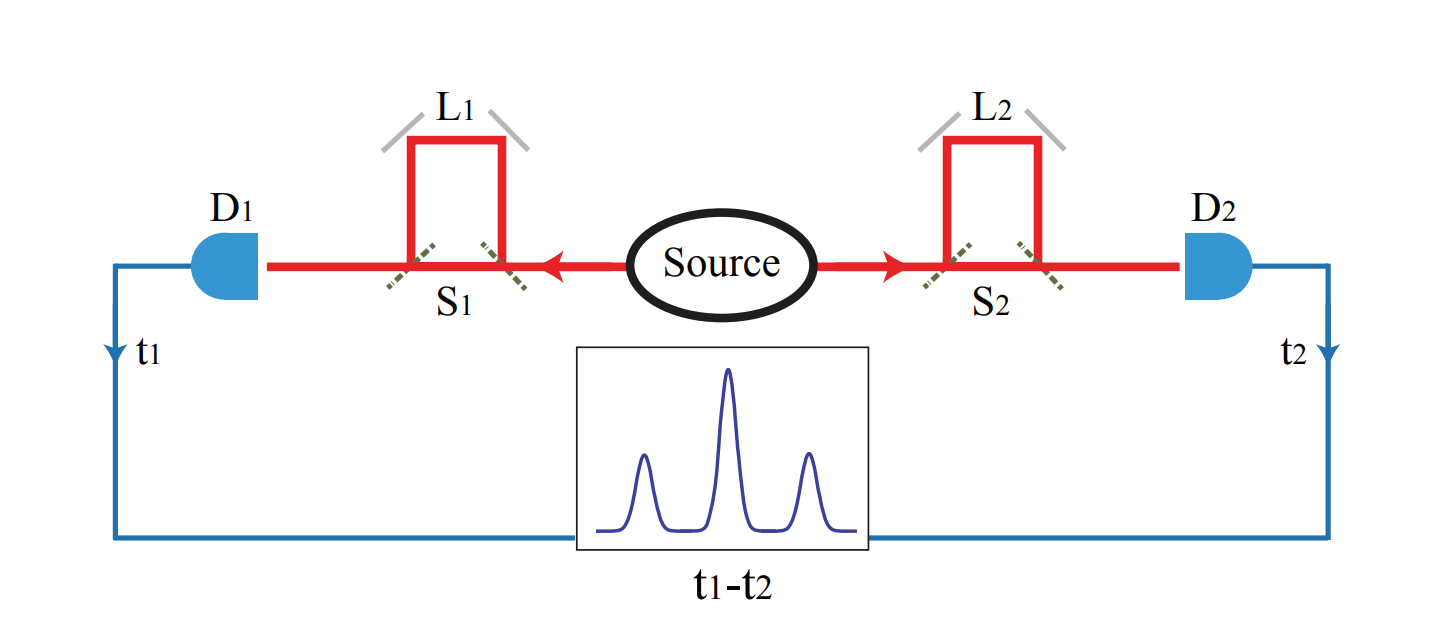
Los cuatro procesos posibles se asocian con las respectivas diferencias temporales:

1) Ambos fotones 1 y 2 (o idler y signal) siguen el camino largo: $\Delta T(L_1,L_2)=\frac{|L_1-L_2|}{c}$

2) Ambos fotones siguen el camino corto S en su interferómetro: $\Delta T(S_1,S_2)=\frac{|S_1-S_2|}{c}$

3) El fotón $\gamma_1$ sigue el camino corto y el otro, $\gamma_2$ , el largo: $\Delta T(S_1,L_2)=\frac{|S_1-L_2|}{c}$

4) El fotón $\gamma_1$ sigue el camino largo y el otro, $\gamma_2$ , el corto: $\Delta T(L_1,S_2)=\frac{|L_1-S_2|}{c}$

Los dos posibles caminos o procesos de Feynman no interferirán si la diferencia temporal $\Delta T(1,2)$ es mayor que el tiempo de coherencia asociado a los dos fotones, $\tau(1,2)=\frac{2}{\Delta \omega}$ .

-Por ejemplo, puede establecerse que:

$\Delta T(L_1,S_2)-\Delta T(S_1,L_2) =\frac{(L_1-S_1)+(L_2-S_2)}{c} \gg \tau_{1,2}$ ,

ya que $\Delta C_j/c \gg \tau$ y $\tau \sim \tau(1,2)$ ; análogamente, puede demostrase que los procesos L-S y S-L son distinguibles de los L-L y S-S.

-La conclusión es (véase [GAR-08], capítulo 10, p. 331) que la única interferencia posible puede ocurrir entre los procesos L-L y S-S, cuando efectivamente resulten indistinguibles. Como se tiene que:

$\Delta T(L_1,L_2)-\Delta T(S_1,S_2) =\frac{(L_1-S_1)-(L_2-S_2)}{c}$ ,

la interferencia entre estos dos procesos ocurrirá cuando se cumpla la condición:

$\frac{|\Delta C_1 - \Delta C_2|}{c} \ll \tau_{1,2}$ .

Es decir, para observar las interferencias hay que controlar cuidadosamente que los dos interferómetros sean casi idénticos, lo que no resulta fácil en el laboratorio.

Cuando se consigue la indistinguibilidad entre los dos procesos LL y SS, se está en las condiciones de aplicación de la suma de amplitudes a la Feynman, de modo que las correspondientes amplitudes de probabilidad se suman según $|\mathcal{A}_{LL} + \mathcal{A}_{SS}|^2$ , proporcionando la probabilidad de coincidencia en los detectores, que resulta dada por la expresión general ([GAR-08], p. 333):

$P=\cos^2 (\frac{\Delta \Phi}{2})$ :

donde $\Delta \Phi$ representa la diferencia de fase óptica,

$\Delta \Phi=\Phi_{LL}-\Phi_{SS}=\frac{\omega_o}{c}(C_1+C_2)$

(siendo $\lambda_o=\frac{2\pi c}{\omega_o}$ la longitud de onda común de los dos fotones, a partir de $\omega_{1(2)}=\omega_o +(-)\nu$ ).

Interferencia Franson, figura del artículo en Phys. Rev. Letter de Ou, Zou, Wang y Mandel, 1990: https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.65.321

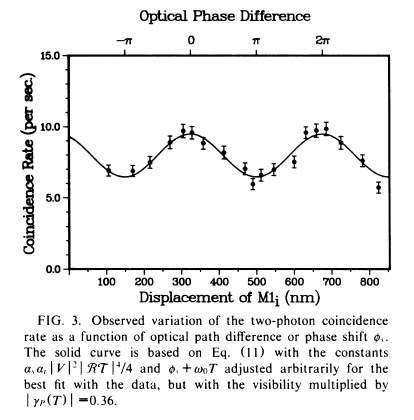
A partir de estos resultados, se confirmó la violación de las desigualdades de Bell, en una nueva y hermosa demostración de la imposibilidad teórica del realismo local.

Se constata la correlación entre dos eventos macroscópicos, las sendas detecciones en los dos detectores, que están separados suficientemente (a la EPR).

La interferencia se origina por la indistinguibilidad de los dos procesos que dan como resultado, de producirse, el mismo fenómeno observado.

Algunos enlaces:

Sven Aerts, Paul Kwiat, Jan-Ake Larsson and Marek Zukowski; Two-photon Franson-type experiments and local realism.

https://qutools.com/qued/qued-sample-experiments/sample-experiments-franson-interference/

https://www.researchgate.net/publication/348741037_The_Franson_experiment_revisited

Two-photon Franson-type experiments and local realism

Bibliografía

[GAR-08] Garrison, J. C. and R. Y. Chiao, Quantum Optics, Oxford Univ. Press, Oxford, 2008.

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

Interferómetro de Franson

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta