

Rayos X: descubrimiento y origen
- En 1895, W.C. Roentgen encontró que al hacer pasar una corriente eléctrica a través de un gas altamente enrarecido contenido en un tubo de descarga de vidrio, cubierto con una cartulina negra, una pantalla tratada para detectar radiación, colocada a alguna distancia del tubo, fluorecía emitiendo luz. Sus investigaciones trataban en principio de determinar si los rayos catódicos podían escapar a través de las paredes del tubo, por lo que, a fin de evitar la fluorescencia que se producía siempre en el vidrio tras el ánodo, provocada por el impacto contra él de los rayos catódicos (electrones), envolvió el tubo en cartulina negra, que sabía era capaz de frenarlos. Su sorpresa fue que observó otra fluorescencia, producida sobre otra pantalla, lo suficientemente alejada del tubo como para estar seguro de que los rayos catódicos no la podían estar alcanzando.
- En definitiva, había descubierto que una radiación altamente penetrante se producía cuando electrones muy rápidos incidían sobre materia, una «nueva clase de rayos» que, a diferencia de todos los conocidos hasta ese momento, atravesaban la cartulina sin ser absorbidos. Dado lo desconocido del fenómeno hasta ese momento, los denominó rayos «X».
- Roentgen, pues, observó por vez primera estos rayos estudiando fenómenos de descargas en tubos catódicos con gases enrarecidos. Realizó numerosas experiencias:
- Aplicando altos voltajes, del orden de decenas de
, encontró que sal de bario colocada cerca del tubo se volvía fluorescente, aunque nada visible se emitía desde el tubo.
- El fenómeno persistía aunque el tubo se envolviese en cartón negro; pronto se determinó que el origen estaba en la zona del tubo tras el ánodo en que chocaban los electrones.
- Aplicando altos voltajes, del orden de decenas de
- J.J. Thomson postuló pronto los rayos
como radiación electromagnética de corta longitud de onda
: de acuerdo con la teoría electromagnética clásica, aplicada a la dispersión de estos rayos por un material, los átomos en éste vibrarían con la misma frecuencia del campo eléctrico oscilante de la radiación incidente; subsiguientemente, se produciría la emisión de ondas electromagnéticas de la misma frecuencia. Es decir: la radiación incidente sobre los átomos en el material del blanco es dispersada sin sufrir ningún cambio en su
(dispersión Thomson).
- Investigaciones posteriores determinaron que:
- Se propagaban en línea recta, incluso si se aplicaban campos magnéticos o eléctricos: no experimentaban desviaciones en su seno.
- Eran capaces de atravesar materiales opacos (a la luz visible), como madera o carne; en cambio, materiales de altos pesos atómicos sí presentaban cierta opacidad a ellos, como el plomo y, parcialmente, el hueso.
- Causaban brillo en las sustancias fosforescentes e impresionaban placas fotográficas.
- A mayor velocidad de los electrones incidentes, mayor poder de penetración de los rayos X producidos.
- A mayor intensidad de electrones incidentes, mayor intensidad de rayos producidos.
- En 1899, Haga y Wind realizaron un experimento de difracción de rayos
por una rendija, estableciéndolos como un fenómeno ondulatorio, de longitud de onda del orden de
.
- En 1900, Thomson estableció que eran dispersados por la materia sin sufrir cambios en su longitud de onda, de acuerdo con la predicción clásica.
- Posteriormente, en 1906, Barkla, además de comprobar los resultados anteriores de Thomson, los estableció como ondas transversales, al polarizarlos usando distintos materiales. Sin embargo, observó ciertas «discrepancias» en sus experimentos, anomalías que ocurrían para los rayos más duros, esto es, de longitudes de onda más cortas, en los que midió ocasionalmente algunos cambios en la longitud de onda de la radiación dispersada. Atribuido inicialmente a errores experimentales, Compton confirmaría después rigurosamente el fenómeno.
- En 1912 M. von Laue (Premio Nobel en 1914 por el descubrimiento de la difracción de rayos X por cristales) y, posteriormente, W.L. Bragg (Premio Nobel en 1915, con su padre, por sus análisis de estructuras cristalinas mediante la difracción de rayos X), llevaron a cabo las primeras mediciones precisas de la
de los rayos
, mediante experimentos de difracción de rayos
por redes cristalinas. Posteriores medidas fueron refinando la precisión, de manera que, en 1913, su
estaba ya establecida entre valores de
y
. En 1923, A. Compton, gracias a esta alta precisión lograda, pudo realizar su famoso experimento de dispersión, que supuso la confirmación definitiva del cuanto de luz de Einstein.
- Radiación de frenado o «bremsstrahlung»: en definitiva, y según predice la teoría electromagnética, cargas aceleradas deben radiar ondas electromagnéticas, de forma que los rayos
serían la radiación de frenado que emiten los electrones al frenarse bruscamente por su choque contra las paredes del tubo de descarga.
Dispersión de rayos X por cristales: ley de Bragg
- Una explicación detallada del mecanismo de la difracción de rayos
por una red cristalina, y las ecuaciones involucradas, puede estudiarse en el siguiente enlace de la UNED: http://www.uned.es/cristamine/cristal/drx_ec.htm ; en http://www.xtal.iqfr.csic.es/Cristalografia/parte_05_5.html puede verse una explicación más corta.
- Los átomos en un cristal definen familias de planos paralelos, teniéndose una distancia característica de separación
entre los planos integrantes de cada familia, en una configuración sugerida en 1912 por W.L. Bragg, y de ahí que se denominen «planos de Bragg» (él y su padre W.H. Bragg fueron Premio Nobel en 1915 por sus trabajos). La hipótesis principal de Bragg consistió en modelar la difracción de los rayos X como una reflexión en «espejos» imaginarios, esto es, en los planos de átomos de la red cristalina. Al incidir un haz de rayos
de longitud de onda
sobre un cristal formando un ángulo
con los planos de Bragg, siendo la distancia entre dos de ellos consecutivos
, la radiación secundaria difundida por el cristal, que es isótropa si la radiación incidente no está polarizada, debe satisfacer unas condiciones específicas para que se produzca interferencia constructiva entre las diferentes ondas y, por tanto, un máximo en la intensidad difundida. Y esas condiciones vienen estipuladas por la ecuación de Bragg, que establece que la diferencia de caminos ópticos debe ser un número entero de veces la longitud de onda de la radiación:

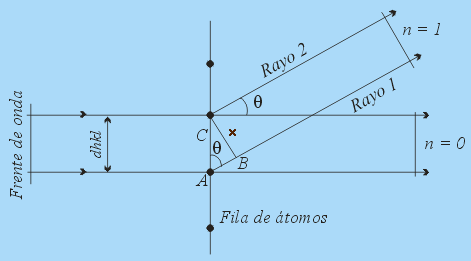
Imagen de la web: http://www2.uned.es/cristamine/cristal/drx_ec.htm. -Obsérvese en la figura anterior como el haz incidente sufre dispersión por un átomo en
y por otro en
, situados en dos planos consecutivos; ambos difunden el haz en todas direcciones. La interferencia constructiva se producirá sólo entre los haces secundarios elementales difundidos de forma paralela y cuyos caminos o recorridos difieran en un número entero de longitudes de onda,
(o nulo). Fuera de estas direcciones privilegiadas, la interferencia es destructiva y la intensidad del haz difundido resulta prácticamente nula. La figura adjunta a la izquierda ilustra la situación correspondiente a los dos primeros órdenes de difracción,
y
.
- Por tanto, si determinamos la distribución angular de la radiación difundida y conocemos el parámetro
que caracteriza la red cristalina, la ecuación proporciona un método de medida de la
de la radiación (o al revés: conocida
, podemos estudiar el parámetro
del cristal), a partir de un montaje como el de la siguiente figura:
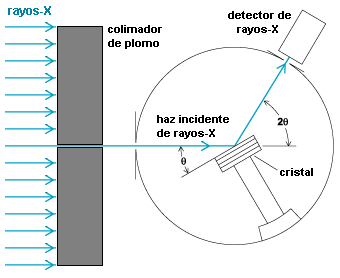
Imagen de: http://la-mecanica-cuantica.blogspot.com.es/2009/08/la-espectroscopia-de-rayos-x.html. - Según la figura, la condición de Bragg se cumple cuando ambos rayos incidentes tienen el mismo ángulo de dispersión, coincidente con el de incidencia del haz,
(análogo a la igualdad que sucede en la reflexión de un rayo luminoso); el entero
se denomina orden del haz difundido.
- Los espectrómetros de rayos
que usan redes cristalinas se basan en la ley de Bragg, permitiendo determinar la longitud de onda de la radiación incidente, a través de la medida de la intensidad de la radiación dispersada según las diferentes direcciones (ángulo
), que presentará máximos sucesivos en las direcciones que cumplan la ecuación de Bragg para los distintos órdenes (valores de
). Con ellos se puede tanto determinar la composición en longitudes de onda de una radiación como, conocida ésta, determinar la estructura de un cristal o molécula (i.e.: DNA) a estudiar.
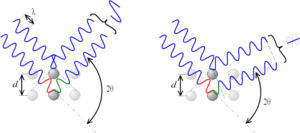
- Repárese en que el procedimiento tiene sentido cuando la longitud de onda de la radiación involucrada es de similar orden de magnitud al parámetro característico de la red de difracción o cristal utilizado,
, ya que
. Porque si la diferencia de orden de magnitud entre ellos es considerable, el procedimiento no es aplicable, bien porque los ángulos de dispersión son demasiado pequeños como para permitir su observación (
), bien porque no permite resolver entre los distintos planos de Bragg (
).
Rayos X: espectros continuo y discreto o característico
- Usando un espectrómetro con un cristal de propiedades conocidas apropiadas es posible obtener el espectro o composición en
de un haz dado de rayos
; para ello, se determina la intensidad del mismo, o energía contenida, por unidad de intervalo de longitud de onda. Por ejemplo, un resultado típico del análisis espectroscópico de los rayos
emitidos por ánodos blanco respectivos de Molibdeno y Cobre, bombardeados por electrones producidos al aplicar sendos voltajes
y
, produce una típica figura como la siguiente:

- El espectro observado muestra usualmente la superposición de un continuo (espectro blanco) y un conjunto de líneas discretas (espectro característico del material en el ánodo), con propiedades diferenciadas:
- Espectro continuo:
- Su forma depende principalmente de la energía de los electrones incidentes sobre el ánodo, siendo muy similar, a una energía dada de estos, para materiales diferentes.
- Aparece una longitud de onda mínima (predicha por Einstein en 1906), por debajo de la cual no hay radiación presente. Este valor mínimo es inversamente proporcional al valor del potencial de aceleración
aplicado, según la ecuación
(fórmula de Duane-Hunt), y es el mismo para todos los materiales.
- Espectro característico:
- Las longitudes de onda discretas presentes en el espectro dependen exclusivamente del material en el ánodo, específicamente de su número atómico
, siendo por completo independientes de la energía de los electrones incidentes.
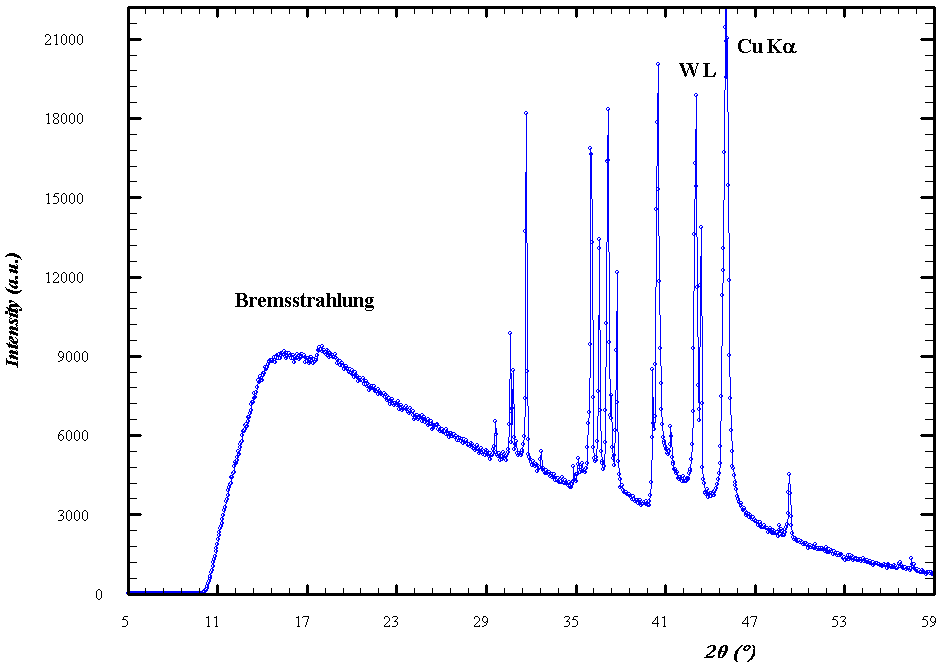
Espectro típico de rayos X (corresponde a Cu). - Una línea con una
específica no aparece en el espectro a no ser que satisfaga la relación
, siendo
la energía de los electrones incidentes.
- La intensidad de una línea
aumenta con la energía de los electrones incidentes, según la ecuación empírica
, donde
es un parámetro de valor aproximado
.
- Las longitudes de onda discretas presentes en el espectro dependen exclusivamente del material en el ánodo, específicamente de su número atómico
- Espectro continuo:
- Según la física clásica, el fenómeno de bremsstrahlung explica la presencia del espectro continuo, aunque no así la presencia de la longitud de onda mínima
, por debajo de la cual no hay radiación, ni mucho menos la presencia del espectro característico. Por ello, constituyó un éxito para la incipiente teoría cuántica lograr justificar la presencia de la longitud de onda mínima observada experimentalmente:
- Sea un electrón de energía cinética
que incide sobre un núcleo de un material determinado; al pasar por su cercanía se desvía, cambiando su velocidad y emitiendo radiación electromagnética (de frenado o bremsstrahlung), cuya
variará para cada electrón concreto, pues cada uno sufrirá un proceso de aceleración o variación de su velocidad distinto, obteniéndose así una distribución continua de frecuencias.
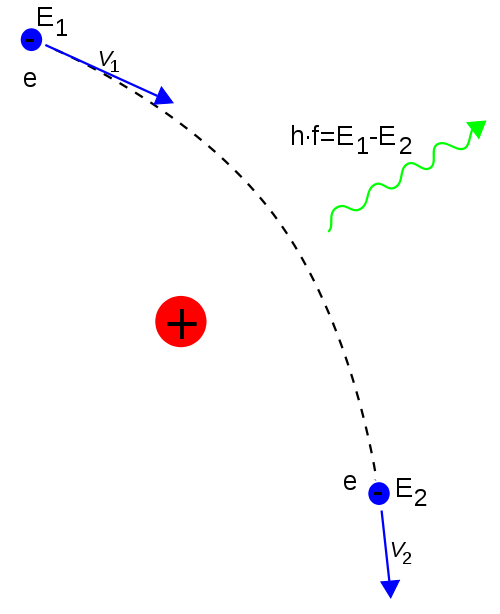
- Pero, como justificó Stark en 1909, incorporando el cuanto de luz se tendrá para la energía del fotón emitido la ecuación
, por lo que la frecuencia máxima emitida en cualquiera de los procesos, para electrones acelerados por un potencial
, será
, de acuerdo con la fórmula de Duane-Hunt, comprobada experimentalmente por estos autores en 1915.
- Sea un electrón de energía cinética
- Nota: obsérvese que la fórmula de Duane-Hunt proporciona otro método experimental para la determinación del valor de la constante
de Planck.
- Este proceso suele denominarse «efecto fotoeléctrico inverso»: aquí, en vez de convertirse la energía de un fotón incidente en energía cinética de un electrón que se emite, es la energía cinética de un electrón incidente la que se convierte en un fotón emitido.
Espectro característico de rayos X: ley de Moseley y número atómico Z

- En 1913, Moseley estudió los espectros de líneas de 39 elementos, comprendidos entre el
y el
, todos ellos muy similares en apariencia y mayoritariamente consistentes en dos grandes grupos de líneas, las series
y
, comenzando siempre la segunda a frecuencias inferiores que la primera.
- Moseley encontró que la frecuencia de la n-ésima línea de cada serie variaba suavemente con valor de
correspondiente al elemento usado en el blanco, siendo capaz de establecer la ley empírica
, o ley de Moseley, donde
es una constante independiente de
y
un parámetro con valores entre 1 y 2 para la serie
y entre 7.4 y 9.4 para la serie
.
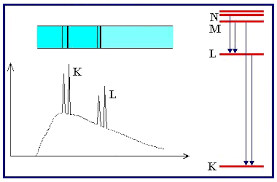
Imagen de: http://la-mecanica-cuantica.blogspot.com.es/2009/08/la-espectroscopia-de-rayos-x.html 
Ley de Moseley (imagen de: http://www.nt.ntnu.no/users/floban/ KJ%20%203055/KJ%203055.html#xray). - Hay que señalar que en 1913
tenía como único significado el de la localización de un elemento en la tabla periódica, en la que se ordenaban en general los elementos en orden creciente de pesos atómicos (salvo determinadas excepciones que se hacían para preservar la periodicidad de propiedades químicas).
- La aplicación del modelo de Bohr, como veremos, permitió a Moseley explicar todas estas regularidades observadas. Baste decir por ahora que ya que
se suponía entonces, aproximadamente, igual a la mitad del peso atómico del correspondiente elemento, y puesto que los experimentos de Geiger y Marsden de dispersión de partículas
habían mostrado que la carga nuclear tenía un valor de aproximadamente la mitad del peso atómico,
, Moseley sugirió identificar
con la carga nuclear, suponiendo entonces que la carga nuclear efectiva para los electrones más internos, debido a efectos de apantallamiento por los restantes electrones, podría expresarse en términos de
, donde
era una constante que incorporaba ese efecto.
- Es decir, Moseley fue capaz de identificar el número
de cada elemento, multiplicado por la carga en valor absoluto del electrón, con la carga nuclear
, mostrando que el modelo de Bohr podía, de forma aproximada, aplicarse a los electrones más internos, sujetos al campo coulombiano de núcleo de forma más dominante.
- Moseley también postuló la existencia de elementos desconocidos todavía, cuya existencia consideró necesaria para evitar algunas discontinuidades en sus gráficas (por ejemplo: los elementos con
y
, todos ellos posteriormente descubiertos). Y también procedió a la reordenación de algunos elementos en la tabla, para que tuvieran el
correcto que los acomodara sobre las rectas de sus gráficas.
- La explicación completa de las características de los espectros de rayos
, sin embargo, no se alcanzaría hasta la irrupción de la nueva mecánica cuántica, que permite tratar adecuadamente todos electrones del átomo, incluidos los más externos, sujetos a potenciales donde la interacción coulombiana nuclear no es tan dominante.
Descubrimiento de la radiactividad
- Algunos meses después del descubrimiento de Roentgen, y también en 1896, H. Becquerel, en un intento de producir rayos
a partir de sales de Uranio, encontró que compuestos químicos de este elemento eran capaces de impresionar una placa fotográfica envuelta en papel negro, independientemente del hecho de haber sido expuestos a la luz solar o no. Intentaba establecer si un proceso inverso al establecido por Roentgen tenía lugar: puesto que los rayos
, al incidir sobre determinados materiales, producían fluorescencia, se dispuso a indagar si una luz intensa podría estimular en un material fluorescente la emisión de rayos
. Así que colocó sal de Uranio (fluorescente) sobre una placa fotográfica cubierta con papel negro, la expuso al sol intenso y encontró en efecto oscurecimiento de la placa. Pero, fortuitamente, tras unos días de clima con intenso nublado, descubrió que la placa se oscurecía igualmente sin haber expuesto el montaje al sol. Pronto fue capaz de establecer que los nuevos rayos que impresionaban las placas eran independientes de la luminiscencia del compuesto usado; productores de ionizaciones en gases y, al menos algunos de ellos, compuestos de partículas cargadas.
- En 1897 M. Curie eligió como tema para su tesis doctoral el nuevo fenómeno, al que enseguida bautizó como «radioactividad» (también «radiactividad«); ayudada por P. Curie, en 1898 ya había determinado cuáles de todos los elementos conocidos emitían los rayos descubiertos por Becquerel; descubierto algunos nuevos fuertemente radioactivos, como el Radio y el Polonio, y encontrado asímismo que la sustancia radioactiva se reducía espontáneamente a la mitad en un tiempo característico.
- En 1899, E. Rutherford encontró que los rayos emitidos por el Uranio eran de dos tipos, distinguibles por sus diferentes razones de absorción por la materia; los denominó como rayos
y rayos
. Posteriormente, en 1900, P.V. Villard descubrió en el Radio la emisión de un tercer tipo de rayos, de mayor poder de penetración que los dos anteriores y similares en propiedades a los rayos
, sobre todo porque no sufrían desviaciones en presencia de campos eléctricos y magnéticos exteriores: se denominaron rayos
.
- Mientras que los rayos
fueron tempranamente identificados como rayos catódicos, esto es, como compuestos por electrones, la naturaleza de los rayos
tardaría más en ser establecida: en 1903 Rutherford demostró primero que estaban cargados positivamente, postulando que se trataba de átomos de Helio doblemente ionizados; lograría demostrarlo en 1909, en colaboración con Royds, en un experimento en que logró generar a partir suya el espectro del Helio (a partir de 1911: partículas
interpretadas como núcleos atómicos de Helio).
- En 1903, Rutherford y F. Soddy establecieron la teoría de las transmutaciones radioactivas, que explicaba el origen de las distintas radiaciones ya descubiertas, sugiriendo que algunos átomos se transformaban en otros, espontáneamente. Además, establecieron que el número de uno de ellos que se desintegra, en un intervalo de tiempo, está determinado por una fracción concreta de los átomos existentes al principio, fracción que establecieron como característica de cada clase de elemento radioactivo.
- En 1914, Rutherford y Andrade midieron la longitud de onda de los rayos
, que quedaron identificados como radiación electromagnética de frecuencia superior a la de los rayos
.
- Ley exponencial de la desintegración radiactiva: Se ha establecido por observación que todos los procesos radiactivos simples siguen una ley exponencial decreciente. Si
es el número de núcleos radiactivos («radionúclidos»), de una especie nuclear radioactiva determinada, presentes en un instante inicial
en una muestra de material radiactivo, después de un cierto tiempo
el número de esos núcleos radiactivos presentes en dicha muestra,
, se ha reducido según la ley exponencial:
, donde
es la denominada «constante de desintegración», característica de cada elemento radiactivo. La magnitud
representa el «período de semi-desintegración» del elemento, o intervalo de tiempo transcurrido el cual el número de radionúclidos presentes en la muestra se divide por dos. Y su inverso,
, la denominada «vida media» de ese elemento, representa a su vez el tiempo medio en que tardará un átomo de esa especie en presentar un fenómeno de desintegración. Se trata de un parámetro estadístico, resultado promedio de la observación de los tiempos de desintegración de muchos átomos individuales de esa especie concreta. El período de semidesintegración, por tanto, es aproximadamente el 69,31 % de la vida media, para cada especie nuclear radiactiva.
Referencias
[BEI-87] Beiser, A.; Concepts of Modern Physics, McGraw-Hill, Singapore, 1987.
[MEH-82] Mehra,J., Rechenberg,H.; The Historical Development of Quantum Mechanics, 6 vol., Springer-Verlag, Nueva York, 1982.
Páginas complementarias
https://www.uam.es/personal_pas/txrf/TXRF2.html
http://www.unac.edu.pe (en pdf: un manual de prácticas)
http://www.uned.es/cristamine/cristal/drx_ec.htm
http://www.uv.es/~cantarer/esol/p2.pdf
http://www.sar.org.ar/web/docs/dayrad/hisotria_radiologia.pdf
http://www.heurema.com/ApuntesFQ/AQuimica/Atomo/LEYMOSELEY.pdf
http://la-mecanica-cuantica.blogspot.com.es/2009/08/la-espectroscopia-de-rayos-x.html
Introducción a la difracción de rayos X
Introducción a la Cristalografía
La ley exponencial de desintegración radiactiva
APPS
-Convierte tu teléfono móvil en un detector de radiación:
https://desayunoconfotones.org/2014/01/28/convierte-tu-smartphone-en-un-detector-de-radiacion/
«Según la física clásica, el fenómeno de bremsstrahlung explica la presencia del espectro continuo, aunque no así la presencia de la frecuencia mínima \lambda_{min}, por debajo de la cual no hay radiación, ni mucho menos la presencia del espectro característico». Entiendo que donde se dice frecuencia mínima debe decir longitud de onda mínima, además una es inversamente proporcional a la otra, C=Long.onda*frecuencia, de manera que long. de onda mínima implica frec. máxima. Saludos!
¡Corregido! Muchas gracias: decía frecuencia y escribía lambda, ahora ya está bien. Un abrazo.
Hola.
Me gustaría saber quién es el autor de la imagen del espectro del Mo y del Cu