Los modelos atómicos primitivos

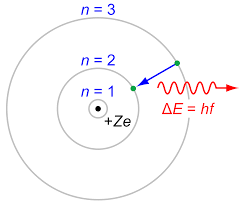
Modelos atómicos primitivos

Modelos de Thomson y Nagaoka (1904)

Nagaoka, 1904: modelo «saturnino»: «El sistema que voy a discutir consiste en un gran número de partículas de igual masa dispuestas en círculo a intervalos angulares iguales y repeliéndose entre sí con fuerzas inversamente proporcionales al cuadrado de la distancia; en el centro del círculo, se sitúa una gran masa que atrae las partículas de acuerdo con una fuerza que sigue la misma ley. Si esas partículas orbitan alrededor del centro atractivo con velocidades casi iguales, el sistema permanecerá en general estable, salvo pequeñas perturbaciones, siempre que la fuerza atractiva tenga la intensidad suficiente […] Nuestro caso caso se realizará como aproximación de forma evidente si sustituimos los satélites por electrones negativos y el centro atractor por una carga positiva. […] Las oscilaciones perpendiculares al plano de la órbita electrónica se demuestra llevan a un espectro que presenta una estructura con bandas, y las oscilaciones en el plano a una clase de espectro con líneas. Los rayos $\alpha$ y $\beta$ se emiten cuando el anillo de electrones se rompe a causa de perturbaciones mayores.» (Philosophical Magazine 7(1904)445; Nature 69(1904)332).
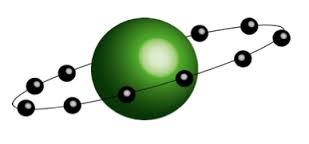
Modelo atómico de Nagoaka, 1904 (imagen de http://rle.dainf.ct.utfpr.edu.br/)
Thomson, 1904: un modelo (a veces denominado, quizás no muy acertadamente, como «del bollo de pasas»): electrones repartidos «a intervalos angulares iguales según la circunferencia de un círculo«, constituyendo un «anillo de $n$ partículas cargadas negativamente«, en movimiento «en el interior de una esfera» con una distribución uniforme de carga eléctrica positiva, que llena todo el volumen atómico. Desarrollado desde 1897, fue publicado en 1904 en el Philosophical Magazine:

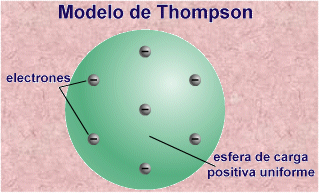
Modelo de átomo de Thomson: ver: http://www.gobiernodecanarias.org/educacion/3/usrn/lentiscal/1-cdquimica-tic/FlashQ/1-Estructura%20A/ExperienciaRutherford/Thomson-Rutherford.htm

Modelo de Rutherford: el núcleo atómico

La prueba concluyente de la inadecuación experimental de los modelos que asumían una distribución de carga positiva atómica con un radio de magnitud similar al atómico, como el modelo de Thomson, fue obtenida en 1911 por E. Rutherford, que fue su alumno, a partir del análisis de unos experimentos realizados desde 1909 en Manchester por H. Geiger y E. Marsden, a sugerencia suya, consistentes en la dispersión de partículas $\alpha$ (átomos de Helio doblemente ionizados: $He^{2+}$ , núcleos de helio, compuestos por dos protones y dos neutrones). En ellos, bombardearon finas láminas de oro con partículas $\alpha$ procedentes de un elemento radiactivo (Polonio), las cuales hacían atravesar una pantalla de plomo con un pequeño orificio, a fin de conseguir un estrecho haz que era dirigido contra la lámina blanco, observando mediante una pantalla fluorescente (sulfato de Zn) su dispersión.

Dispersión Rutherford de partículas alpha. — *Experimento de dispersión de partículas alfa por una lámina de oro.*

El experimento permite medir el número de partículas $\alpha$ dispersadas en un intervalo angular $(\theta, \theta + d\theta)$ , donde $\theta$ representa el ángulo con la dirección incidente. Los resultados observados fueron que, si bien muchas de ellas atravesaban la lámina metálica sin cambiar demasiado de dirección, había una estadística de partículas que sufrían deflexiones apreciables, e incluso había unas pocas que eran reflejadas hacia atrás con ángulos muy grandes, lo cual era un resultado completamente inesperado e incompatible por completo con el modelo de átomo de Thomson.
En efecto, un cálculo de dispersión bajo un potencial central (véase apartado siguiente), el potencial de Coulomb de interacción entre la carga en el blanco, para la que se supone una distribución esférica uniforme en el volumen atómico, y la carga incidente, ofrece como resultado desviaciones en torno a 1 grado o menos. Sin embargo, se encontró que, aunque la mayoría de las partículas incidentes apenas se desviaban, o no lo hacían en absoluto, unas pocas eran dispersadas con un ángulo muy grande (aproximadamente 1 cada $10^{4}$ es dispersada con un ángulo superior a los 90 grados), e incluso algunas pocas rebotaban hacia atrás: «It was as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you» (en expresión de Rutherford).
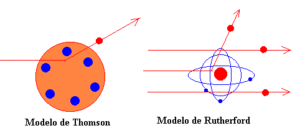
Comparativa dispersión en los modelos atómicos de Thomson y Rutherford (imagen: http://www.sc.ehu.es/sbweb/fisica/cuantica /rutherford/rutherford.html).

Puesto que las partículas $\alpha$ son relativamente pesadas (unas 7300 veces la masa del electrón), y puesto que las usadas en estos experimentos alcanzaban grandes velocidades (del orden de la vigésima parte de la velocidad de la luz $c$ ), un análisis matemático de las fuerzas involucradas le demostró a Rutherford que la dispersión sólo podía comprenderse si toda la carga positiva del átomo, y casi toda la masa, estuviese concentrada en un núcleo de dimensión muy inferior al radio atómico y situado en el centro de cada átomo de oro, permaneciendo los electrones fuera de él. Es decir, se concibe el denominado modelo nuclear atómico, en el que la mayor parte del átomo es espacio vacío.
Con este modelo de átomo, para el que se estimó un radio nuclear del orden del Fermi ( $1 \ fm=10^{-15}\ m$ ), frente al orden del Amstrong ( $1 \ \AA=10^{-10}\ m$ ) para el radio atómico, quedaba justificado, además de las grandes y esporádicas desviaciones observadas, el que la mayoría de las partículas atravesaran la lámina de oro sin desviarse: sólo unas pocas partículas pasan lo suficientemente cerca del núcleo.
Una magnífica referencia para comprender el experimento y sus resultados:
la-mecanica-cuantica.blogspot.com.es/2009/08/esparcimiento-clasico-de-particulas.html

Deducción teórica de la fórmula de difusión clásica por un potencial central

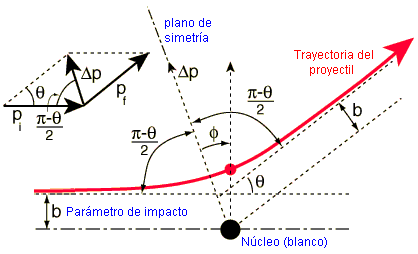
Dispersión Rutherford. — *Imagen de: la-mecanica-cuantica.blogspot.com.es /2009/08/esparcimiento-clasico-de-particulas.html*

Coordenadas polares $(r,\varphi)$ , plano $OZX$ : $z=r \cdot cos \varphi \; ; \, x=r \cdot sen \varphi$ ; $b$ es el denominado «parámetro de impacto»; $\theta$ es el ángulo de dispersión, con valores $0\le\theta\le\pi$ ; $r_0$ es la distancia de máximo acercamiento de la partícula incidente al centro difusor en el origen $O$ del sistema de ejes coordenados.
Se considera un campo central, esto es, el potencial de interacción depende sólo del módulo del vector de posición de la partícula incidente, o distancia al centro difusor en cada instante: ; consecuentemente, se tienen dos constantes del movimiento o magnitudes conservadas:
1. El momento angular a lo largo de cualquier trayectoria: $L=mr^2\dot{\varphi}=mv_0b=\text{constante}$ .
2. La energía cinética $E$ (supuesto que el blanco de número atómico $Z$ permanece en reposo en $O$ , es decir, se desprecia el retroceso del blanco en la dispersión, algo justificado por su masa mucho mayor que la de la partícula incidente): $E=\frac{1}{2}mv^2\, + \, V(r) = \frac{1}{2}m(\dot{r}^2 + r^2\dot{\varphi}^2)\, + \, V(r)=\text{constante}$ .

Ecuaciones generales para un potencial central arbitrario:
1. $\dot{r}=\frac{dr}{dt}=\pm (\frac{2}{m}[E-V(r)]-\frac{L^2}{m^2r^2})^{\frac{1}{2}}$ .
2. $\frac{d\varphi}{dr}=\frac{d\varphi}{dt}\frac{dt}{r}=\frac{L}{mr^2}(\frac{2}{m}[E-V(r)]-\frac{L^2}{m^2r^2})^{\frac{-1}{2}}$ , a integrar entre límites $(r_0, r)$ y $(\varphi_0 =\frac{\pi + \theta}{2}, \varphi)$ , pero donde la integración analítica es posible para muy pocos casos (entre ellos, el que interviene en la colisión estudiada: la interacción coulombiana).
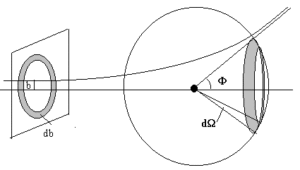
3. $dN' = I \, 2\pi \, b \, db = I \, 2\pi\, \frac{L}{(mv)^2}\,dL$ representa el número de partículas incidentes que atraviesan, por unidad de tiempo, un anillo de superficie $dS=2\pi b db$ , según figura adjunta.
4. $\frac{d\sigma}{d\Omega}=\frac{dN'}{Id\Omega}=-\frac{L}{mv^2sen\theta}\frac{dL}{d\theta}$ , expresión de la correspondiente «sección eficaz diferencial», $\frac{d\sigma}{d\Omega}$ , que representa el número de partículas difundidas por 1 centro difusor, por unidad de tiempo, dentro del ángulo sólido $d\Omega=2\pi sen\theta d\theta$ (el signo negativo tiene en cuenta que a un incremento positivo $db$ en el parámetro de impacto le corresponde una disminución en la fuerza ejercida sobre la partícula y, por tanto, una disminución en $\theta$ ).

Ecuaciones para un potencial de Coulomb, , para el que :
1. Ecuación de la trayectoria: $\frac{1}{r}=\frac{1}{b} sen \varphi + \frac{A}{b^2} (cos \varphi - 1)$ , donde $A=\frac{1}{4\pi \epsilon_0}\frac{1}{2E}$ .
2. Distancia de máximo acercamiento: $r_0=A \cdot (1 + \sqrt{1+\frac{b^2}{A^2}})$ .
3. Relación entre $b$ y $\theta$ : $b=Acotan(\frac{\theta}{2})$ .
4. Sección eficaz diferencial (la denominada «fórmula de Rutherford»): $\frac{d\sigma}{d\Omega}=(\frac{q_pq_Z}{4\pi \epsilon_0})^2 \frac{1}{16E^2sen^4(\frac{\theta}{2})}$ .
  -Es interesante resaltar que este resultado, obtenido usando la teoría clásica de la dispersión por un potencial central coulombiano, coincide con el que se obtiene cuando se aplica teoría cuántica moderna, contexto donde la interpretación de las secciones eficaces pasa a ser probabilística, y de ahí el ajuste espectacular con los datos de laboratorio que se logró; esta coincidencia no se da para otros potenciales.
5. Obsérvese que, si se realiza una integración sobre ángulo sólido, se tiene $\sigma=\int\frac{d\sigma}{d\Omega}d\Omega =2\pi\int_0^{\pi}sen \theta\frac{d\sigma}{d\Omega}d\theta \rightarrow \infty$ ; en la práctica, no obstante, el potencial de Coulomb se anula a larga distancia, de forma que la sección eficaz total $\sigma$ sí resulta definida.
6. No depende del signo del potencial; proporciona una distribución angular dependiente de $E^2$ a través de una función cuya forma no depende del valor de $E$ concreto.
7. La expresión anterior permite finalmente calcular el número $dN'$ de partículas dispersadas en el intervalo angular $(\theta, \theta + d\theta)$ al atravesar la lámina:
  $dN'=N(\theta)d\theta=(\frac{q_pq_Z}{4\pi \epsilon_0})^2 \cdot \frac{zZe^2}{2Mv^2} \cdot \frac{I\rho t 2\pi sen\theta d\theta}{sen^4(\frac{\theta}{2})}=\frac{d\sigma}{d\Omega}I\rho t d\Omega$ , fórmula que ajustaba a la perfección los datos experimentales obtenidos por Geiger y Marsden, quienes midieron dispersiones ocurridas entre 5 y 150 grados; con finas láminas de distintos espesores (en un intervalo de 10 pulgadas); con partículas $\alpha$ con energías difiriendo entre sí en un factor 3; con blancos de distinto número atómico $Z$ .
8. Sin embargo, la fórmula anterior falla, apareciendo discrepancias entre sus predicciones y los resultados experimentales, sobre todo cuando se consideran sobre átomos ligeros en el blanco y partículas incidentes con altas velocidades y dispersadas a ángulos próximos a 180 grados («backscattering»). Para corregir estas desviaciones puede comprobarse que no basta con incorporar la corrección debida al efecto de masa finita del núcleo en el blanco, sino que es preciso incorporar al análisis la interacción fuerte, o interacción de corto alcance y gran intensidad que mantiene ligados a los constituyentes del núcleo. En efecto, en las condiciones especificadas, la partícula incidente se ha aproximado mucho al núcleo, y no basta considerar la interacción de Coulomb para calcular la dispersión. Si en la fórmula anterior consideramos el caso límite de ángulo de dispersión $\theta=\pi$ , no consigue ajustar bien los resultados experimentales: se observan menos partículas dispersadas de las que predice, a partir de cierta velocidad que depende del material en el blanco. Este caso permite hacer una estimación del radio nuclear, a partir de la fórmula, correspondiente a $\theta=\pi$ , $r_0=\frac{zZe^2}{4\pi \epsilon_0 E}$ , obteniéndose, por ejemplo, un valor $R_{nuc}(Au)\leq 3 \times 10^{-14} \, m$ para el oro.

Dispersión Rutherford de partículas $\alpha$

La sección eficaz diferencial $\frac{d\sigma}{d\Omega}$ se define, para un proceso elástico (no se producen alteraciones en la estructura interna de las partículas que intervienen) como la razón entre el número de partículas difundidas en el ángulo sólido $d\Omega$ por unidad de tiempo, de centro difusor y de ángulo sólido, y el flujo de partículas incidentes sobre el
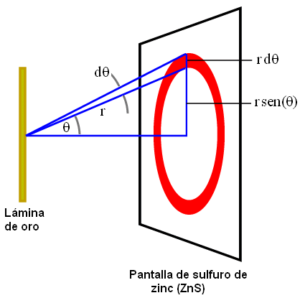
Imagen tomada de http://la-mecanica-cuantica.blogspot.com.es /2009/08/esparcimiento-clasico-de-particulas.html.

blanco: $(\frac{d\sigma}{d\Omega})=\frac{dN'}{I \cdot n \cdot d\Omega}$ , y representa cuánticamente la probabilidad de que una partícula sea dispersada dentro del ángulo sólido $d\Omega$ (según $\theta, \phi$ ), en un proceso elástico.
Notación:
1. $dN'$ es el número de partículas $\alpha$ dispersadas dentro de un elemento de ángulo sólido $d\Omega$ en la dirección $(\theta, \phi)$ por unidad de tiempo.
2. $I$ es el flujo de partículas incidentes, o número de partículas incidentes que atraviesan una unidad de área perpendicular al haz incidente, por unidad de tiempo; se supone uniforme y compuesto de partículas iguales y de la misma energía.
3. $n$ es el número de centros difusores en el blanco, que se supone lo suficientemente delgado como para que dichos centros difusores estén tan separados entre sí como para que cada proceso de colisión involucre sólo uno de ellos. De esta forma, no se consideran procesos de colisiones múltiples (de una partícula por varios centros difusores).
4. Supuesto el blanco a bombardear como una lámina de espesor de un material con densidad de átomos por unidad de volumen, se tendrá , donde:
  1. $\rho$ se expresa en átomos por unidad de volumen.
  2. $t$ tienen dimensiones de longitud.
  3. $n$ representa el número de átomos por unidad de superficie.

Fórmula de dispersión de Rutherford, en unidades M.K.S. y sistema laboratorio (o sistema en que el blanco está en reposo):
$\frac{d\sigma}{d\Omega} = (\frac{q_P \cdot q_Z}{4\pi \cdot \epsilon_0})^2 \frac{1}{16 \cdot E^2 \cdot sen^4(\theta/2)}$
Notación:
1. $\sigma=\int_{\Omega}\frac{d\sigma}{d\Omega}d\Omega$ es la sección eficaz total, con dimensiones de área; la unidad fundamental es el «barn«, $1\,barn=10^{-28}m^2$ .
2. $\frac{d\sigma}{d\Omega}$ es la sección eficaz diferencial, con dimensiones de área/estereorradián; la unidad fundamental es el $barn \cdot sr^{-1}$ .
3. $q_{P}$ es la carga de la partícula incidente, $z \cdot e$ ( $2e$ para el caso de partículas $\alpha$ ).
4. $q_{Z}$ es la carga del centro difusor, $Z \cdot e$ ( $Z$ es el número atómico del átomo en el blanco).
5. $E$ es la energía cinética de la partícula incidente.

El átomo de Rutherford

El modelo de Rutherford describe al átomo como un núcleo de carga positiva, con un radio 4 o 5 órdenes de magnitud inferior al del átomo, dotado de una gran masa en comparación con la de un electrón, y rodeado por los electrones en número suficiente como para mantener el conjunto con la carga adecuada. Estos últimos, por su parte, no pueden ser concebidos en reposo, sino que, para contrarrestar la atracción que el núcleo ejerce sobre ellos, han de moverse en órbitas dinámicamente estables alrededor de él.
Aplicando la mecánica newtoniana a este modelo, podemos deducir el radio, velocidad y energía total del electrón orbital del átomo de Hidrógeno: $\frac{1}{4\pi \epsilon_0}\frac{e^2}{r^2}=m\frac{v^2}{r}$ ; $v=\frac{e}{\sqrt{4\pi\epsilon_0 mr}}$ ; $E=K + V =-\frac{e^2}{8\pi\epsilon_0 r}$ , cumpliéndose el teorema del virial, que para un potencial culombiano establece $K=-\frac{1}{2}V$ . Estos resultados deberían corregirse incorporando el hecho de que la masa nuclear, aunque muy grande en comparación con la electrónica, es finita; la correspondiente corrección se denomina «de masa reducida», o de «centro de masas», y se detallará en el modelo de Bohr.
El problema inmediato de este modelo es que la teoría electromagnética, el otro gran pilar de la Física Clásica junto con la Mecánica de Newton, establece que una carga acelerada debe radiar energía en forma de radiación electromagnética, de manera que los electrones perderían continuamente energía, precipitándose sobre el núcleo: imposibilidad de justificar la estabilidad atómica observada.
Además, esa radiación de espectro continuo en absoluto se corresponde con la existencia bien conocida ya en la época de los variados y espectaculares espectros de líneas, característicos de cada elemento. Incluso admitiendo que, por algún mecanismo por establecer, el átomo consiguiese la estabilidad, no irradiando los electrones energía de forma continua, podría justificarse tan sólo, incorporando órbitas elípticas, la emisión de una sola frecuencia básica principal y todos sus múltiplos o armónicos sucesivos.

Modelo de Bohr

En 1913, N. Bohr combinó el modelo nuclear de Rutherford con unos postulados de cuantización del momento y de no radiación por los electrones atómicos en movimiento acelerado, en una completa síntesis que suponía un nuevo modelo atómico capaz de explicar, por primera vez en Ciencia, el espectro de líneas observado experimentalmente para el átomo de Hidrógeno, así como las diversas fórmulas para sus regularidades numéricas que habían sido publicadas en ese momento histórico.
Sus postulados fueron:
1. Un electrón ligado en un átomo se mueve a lo largo de una órbita circular alrededor del núcleo bajo la acción de la atracción de Coulomb entre el electrón y el núcleo, obedeciendo en este movimiento las leyes de la Mecánica Clásica.
2. De las infinitas órbitas posibles en Mecánica Clásica, el electrón sólo puede moverse a lo largo de las órbitas circulares en las que su momento angular orbital $L_e$ es un múltiplo entero de $\frac{h}{2\pi}=\hbar$ , donde $h$ es la constante de Planck: $L_e=n\hbar\, , \, n=1,2\ldots$ .
3. El postulado anterior se modificaría posteriormente, a fin de incorporar la corrección de masa reducida, que tiene en cuenta el hecho de que la masa nuclear, aunque muy grande en comparación con la electrónica, es finita, enunciándose entonces como: De las infinitas órbitas posibles en Mecánica Clásica, el electrón sólo puede moverse a lo largo de las órbitas en las que el momento angular orbital atómico $L$ sea un múltiplo entero de $\frac{h}{2\pi}=\hbar$ , donde $h$ es la constante de Planck: $L=n\hbar\, , \, n=1,2\ldots$ .
4. En su movimiento alrededor del núcleo en una de las órbitas estacionarias permitidas, el electrón lo hace sin emitir radiación electromagnética, de manera que su energía permanece constante. Este postulado rompía con la Teoría Electromagnética Clásica.
5. El electrón emite o absorbe radiación electromagnética cuando realiza un salto y pasa de moverse en una órbita donde su energía posee el valor constante $E_i$ a otra con valor constante $E_f$ , experimentando así un cambio discontinuo en su energía. La frecuencia $\nu$ de la radiación emitida ( $E_f<E_i$ ) o absorbida ( $E_f>E_i$ ) viene dada por $\nu=\frac{|E_f-E_i|}{h}$ («relación de frecuencia de Bohr»).
Los postulados constituían una combinación de Física Clásica y No-Clásica (Pre-Cuántica o Vieja Teoría de los Cuantos, decimos hoy), y su justificación radica en la comparación de las predicciones que permiten deducir con los resultados observados experimentalmente.

Radio orbital y niveles de energía de un átomo monoelectrónico

Supongamos en principio un núcleo infinitamente pesado (aproximación masa nuclear infinita frente al ligero electrón) y con carga y un electrón ligado orbitando según el modelo de Bohr; aplicando la Dinámica Clásica a este modelo, se obtiene ; incorporando la condición de cuantización , podemos obtener los valores posibles para la velocidad y radio orbitales, en función del número cuántico , denominado «número cuántico principal»:
1. $v\cdot r=\frac{n\hbar}{m}$ , de donde $v_n=\frac{Ze^2}{4\pi\epsilon_0 m}\frac{1}{vr}=\frac{Ze^2}{4\pi\epsilon_0}\frac{1}{n\hbar}=\alpha\frac{Z}{n\hbar}\hbar c$ ;
2. $r_n=\frac{Ze^2}{4\pi\epsilon_0 m}\frac{1}{v^2}=\frac{4\pi\epsilon_0}{Ze^2m}n^2\hbar^2=\frac{1}{\alpha}\frac{1}{\hbar c}\frac{1}{Zm}n^2\hbar^2$ , $n=1,2\ldots$
El radio de la primera órbita permitida, la más próxima al núcleo, viene dado para el Hidrógeno ( $Z=1$ ) por $a_0=r_1=\frac{4\pi\epsilon_0 \hbar ^2}{e^2 m}=\frac{\hbar}{\alpha mc}=5,292 \times 10^{-11}\,m=0.529177\, \AA$ , donde $\alpha$ es la constante de estructura fina, de valor $\alpha=\frac{e^2}{4\pi\epsilon_0 \hbar c}\approx \frac{1}{137}$ y adimensional; el valor correspondiente de la velocidad en esta la órbita más interna, es decir, la velocidad máxima para el electrón en el átomo de H. según el modelo de Bohr es: $v_{max}=v_1=\alpha c=2,2 \times 10^{6}\,m/s$ , lo que justifica el éxito de una aproximación no relativista.
Los distintos radios orbitales para un átomo monoelectrónico de número atómico $Z$ se expresan en función del de Bohr $a_0$ según: $r_n=\frac{n^2}{Z}a_0\,,\,n=1,2\ldots$
Las expresiones para las energías cinética, potencial y total en el modelo son:
1. $K_n=\frac{1}{2}mv^2=\frac{m}{2\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2\frac{1}{n^2}$ ;
2. $V_n=-\frac{Ze^2}{4\pi\epsilon_0 r}=-\frac{m}{\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2\frac{1}{n^2}$ ; obtenida a partir de $\int_{r_{ref}}^r \vec{F_C}\cdot d\vec{r}=\frac{Ze^2}{4\pi\epsilon_0}\int_{r_{ref}}^r \frac{1}{r^2}dr$ , con $F_C$ simbolizando fuerza de Coulomb y la elección $V(r_{ref})=0$ : origen de energía elegido cuando el electrón está en reposo e infinitamente separado del núcleo;
3. $E_n=K_n+V_n=-\frac{m}{2\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2\frac{1}{n^2}=-\frac{1}{2}mc^2(Z\alpha)^2 \frac{1}{n^2}$ , $n=1,2\ldots$
(Nota: aunque hayamos dado algunas de las expresiones anteriores en términos de la constante de estructura fina $\alpha$ , ésta es posterior al modelo de Bohr: aparecería en el contexto de las correcciones relativistas posteriores en el modelo de Sommerfeld).
Los valores $E_n$ de energía se denominan»niveles de energía» del átomo; si se fija el origen de la escala de energía en el umbral de ionización, cuando el electrón deja de estar ligado al núcleo y queda en reposo, tienen valores negativos, representando estados en que el electrón se encuentra ligado al núcleo. El primero de ellos, el más bajo en energía, se denomina «estado fundamental» o capa K ( $n=1$ ); los restantes, «estados excitados» ( $n=2,\ldots$ ): capa L ( $n=2$ ), capa M ( $n=3$ ), etc. La siguiente figura ilustra la situación de estos niveles discretos:
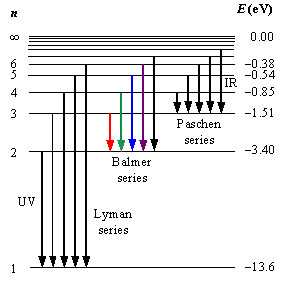
Series en el espectro del Hidrógeno atómico (imagen: http://iesdmjac.educa.aragon.es/).
Conforme aumenta $n$ , la correspondiente energía $E_n$ se aproxima al valor límite nulo, $E_n ({n \rightarrow \infty }) = 0$ , valor correspondiente a cuando el electrón ha dejado de estar ligado: el átomo neutro se ha convertido en un ión positivo $H^+$ . Por tanto, el trabajo necesario para separar un electrón de un átomo monolectrónico de número atómico $Z$ en su estado fundamental, denominado como potencial de ionización del mismo, $I_P$ , viene dado por: $I_P=-E_1=\frac{m}{2\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2=Z^2\cdot 2,17991 \times 10^{-18}\,J=Z^2\cdot 13,6058\,eV$ , con un grado de acuerdo experimental verificado muy alto para el átomo de Hidrógeno, para el que $Z=1\,, \, I_P(H)=13,5984\,eV$ .
Introduciendo la «constante de Rydberg» de energía, $R(\infty)=\frac{m}{2\hbar^2}(\frac{e^2}{4\pi\epsilon_0})^2=13,6058\,eV$ (expresión en aproximación de masa nuclear infinita), los potenciales de ionización para los átomos monoelectrónicos toman la expresión: $I_P=R(\infty)Z^2$ ; en términos de él se pueden expresar los distintos niveles de energía como $E_n=-I_P/n^2$ .
El modelo de Bohr logró la primera explicación teórica satisfactoria de las líneas espectrales observadas para el átomo de Hidrógeno y las fórmulas empíricas espectroscópicas (Balmer, etc.): según el postulado quinto del modelo, la frecuencia de la radiación emitida o absorbida por el átomo al realizarse una transición entre dos niveles de energía dados, $E_i$ y $E_f$ , viene dada por $\nu=\frac{|E_f-E_i|}{h}=\frac{m}{2\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2 |\frac{1}{n_f^2}-\frac{1}{n_i^2}|=R_{\nu}(\infty)Z^2 |\frac{1}{n_f^2}-\frac{1}{n_i^2}|$ , donde se ha introducido la constante de Rydberg de frecuencia, de valor $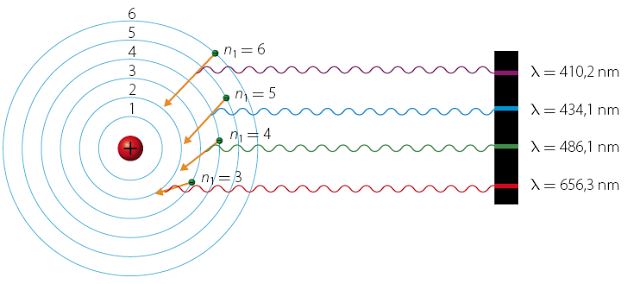R_{\nu}(\infty)=\frac{me^4}{8\epsilon_0^2h^3}=R(\infty)/h$ .
La siguiente figura ilustra los valores numéricos de algunas de estas líneas y su justificación teórica, con valores expresados en números de ondas: $\tilde{\nu}=\frac{1}{\lambda}=\frac{|E_f-E_i|}{hc}$ , donde aparece la constante de Rydberg de número de ondas, $\tilde{R}(\infty)=\frac{me^4}{8\epsilon_0^2h^3c}=\frac{R(\infty)}{hc}=109737\,cm^{-1}$ (valor experimental $\tilde{R}_H=109677,58\,cm^{-1}$ ; se reserva la notación con subíndice $H$ para los valores experimentales, los cuales deben compararse con los teóricos tras incorporar a estos correcciones como la de masa reducida y otras):
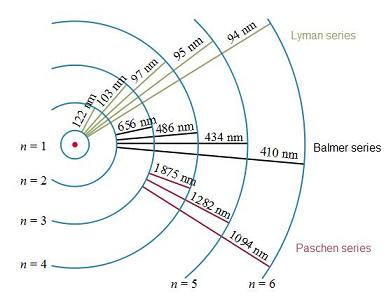
Líneas del espectro del Hidrógeno atómico. (Imagen por Szdory, licencia GNU).
En definitiva: en el estado normal o no excitado de un átomo, estado fundamental, el electrón ocupa la órbita más interna ( $n=1$ ); al producirse una excitación, por ejemplo, porque incide radiación electromagnética sobre el átomo susceptible de ser absorbida, el electrón realiza una transición hacia un estado de mayor energía, que puede ser también ligado, correspondiente a un valor entero $n>1$ . Posteriormente, y puesto que, como todo sistema físico, el átomo tiende a situarse en el nivel de energía más bajo posible, el átomo emite espontáneamente radiación, bien emitiendo un cuanto de energía (en lenguaje actual: un fotón) de la misma frecuencia que absorbió, bien emitiendo fotones de menor energía, avanzando mediante uno o varios «saltos» hacia una configuración de menor energía, hasta conseguir regresar al estado fundamental. Así que estos «saltos electrónicos» también son posibles entre dos estados excitados dados; por ejemplo, en condiciones en que los átomos que componen el gas están todos en el estado fundamental inicialmente, la única serie que se observa en el correspondiente espectro de absorción es la de Lyman, pero, si el gas se excita (aumentamos la temperatura $T$ , por ejemplo), comienza a haber suficientes átomos que están, inicialmente, en estados excitados, apareciendo las series adicionales.
Nota histórica: es interesante comentar que Bohr se opuso tajantemente a aceptar el concepto de «cuanto de luz», formulado por Einstein como una «hipótesis heurística» en 1905 y que tomó para él cuerpo real en 1916, cuando la aplicó a la derivación de la fórmula de Planck para la radiación del cuerpo negro. La oposición de Bohr al cuanto de luz, bautizado como «fotón» por Lewis en 1926, se mantendría hasta bien entrado 1925, por lo menos. El hecho es que, aunque la hipótesis del fotón es suficiente para explicar fenómenos fundamentales para el desarrollo de la conceptualización cuántica de la luz, como el efecto fotoeléctrico y el Compton, no es necesaria. Un modelo semiclásico, en que no se cuantiza el campo electromagnético, es capaz de explicar la fenomenología tradicional relacionada con estos fenómenos. Por supuesto, existen otros experimentos que sí son imposibles de explicar en un marco semi-clásico, que no cuantice el campo electromagnético.
En el caso de producirse ionización, el electrón deja de estar ligado, habiéndose convertido el sistema en el conjunto de un ión más un electrón libre, con energía positiva según la elección de origen hecha (para un electrón libre, no hay cuantización en la energía permitida: estamos ya en la parte continua del espectro, que se extiende a toda la parte positiva del eje de energía, desde cero hasta infinito). La parte continua del espectro, por tanto, corresponde a un electrón libre que describe un movimiento no periódico, según una trayectoria hiperbólica, alrededor del núcleo, estando permitidas todas las trayectorias de este tipo.
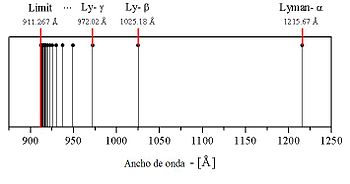
Serie de Lyman: la frecuencia límite en cada serie muestra el umbral de ionización para un electrón proveniente de ese nivel de energía, en esta serie el estado fundamental (n=1). (Imagen libre de Wikipedia).
El éxito del modelo de Bohr en la justificación teórica de las series espectrales incluyó además el de la predicción de las series de Lyman, Brackett y Pfund, que no se observarían experimentalmente hasta años después de su publicación. Y no se redujo sólo al átomo de Hidrógeno: fue aplicado también para otros átomos monoelectrónicos, como los iones $He^+\, , \,(Z=2)$ , $Li^{2+}\, , \,(Z=3)$ , etc. Estos iones pueden producirse, por ejemplo, mediante una descarga eléctrica suficientemente intensa a través del correspondiente gas de átomos neutros, en un tubo de descarga, detectándose su presencia por la observación de espectros diferentes a los correspondientes al átomo neutro. Así, en el caso del $He^+$ , su espectro es más simple que el de $He$ neutro, pareciéndose al de Hidrógeno.
Sobre el concepto precuántico de «salto cuántico» del electrón entre órbitas, conviene recordar las palabras de Max Born, el «padre» de la interpretación probabilística de la función de onda de Schrödinger:
Sin embargo, conforme la carga nuclear $Ze$ aumenta, para los iones más pesados, a partir de más o menos $Z \ge 20)$ , el modelo de Bohr comienza a fallar en la predicción de las correspondientes líneas espectrales del ión monoelectrónico. La razón principal es que las velocidades de los electrones comienzan a alcanzar el rango de velocidades donde la aproximación no relativista deja de ser válida: $v_1=\frac{Ze^2}{4\pi \epsilon_0}\frac{1}{\hbar}=\alpha\frac{Z}{hbar}\hbar c\approx Z \cdot 2,2 \times 10^{6}\,m/s$ , de forma que $\frac{v_1}{c}=Z \cdot 0,00733$ , que para los $Z$ indicados, $Z \ge 20$ , comienza ser significativo.

Corrección de masa reducida

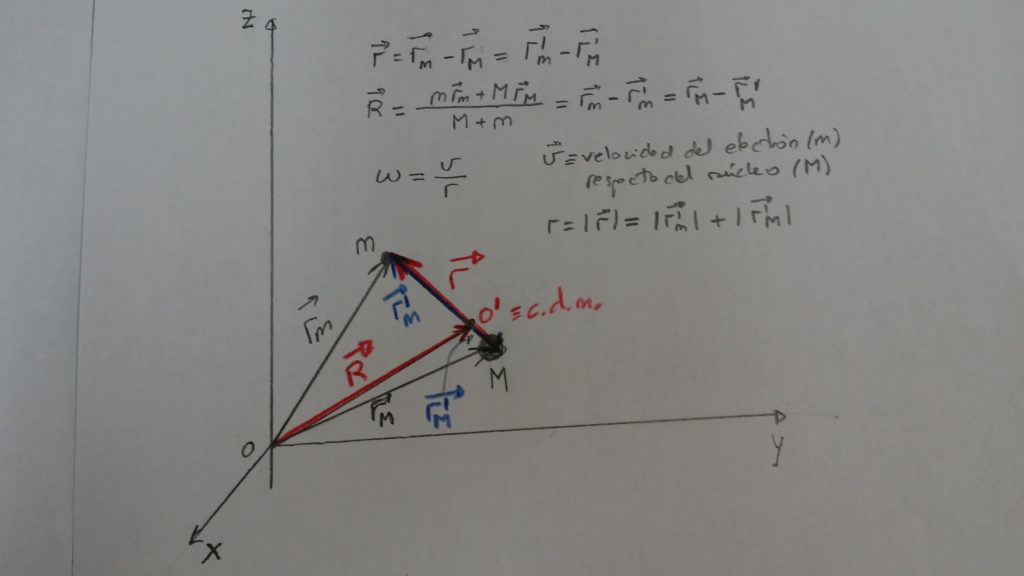
Las fórmulas anteriores deben corregirse incorporando el hecho de que la masa nuclear, aunque muy grande en comparación con la electrónica, es finita; la correspondiente corrección se denomina «de masa reducida», o de «centro de masas», y en ella en vez de concebir al núcleo en reposo con el electrón girando en torno a él, ambos electrón y núcleo giran en torno al centro de masas. Como hemos visto antes, incluso para el átomo monoelectrónico de núcleo más ligero, el Hidrógeno, la aproximación es buena, ya que $M_p\approx 1836 m_e$ . Pero conforme la precisión de las medidas espectroscópicas se incrementa, es más conveniente tener el cuenta el efecto de masa nuclear finita. Como no se ejercen fuerzas externas al átomo, el centro de masas permanecerá en reposo o en movimiento uniforme, lo que permitirá en todo caso suponerlo en reposo y tomarlo como origen del sistema de coordenadas (eliminando así su contribución a la energía cinética total).

Sean pues un electrón, de masa $m$ y carga $e$ , y un núcleo de masa $M$ y carga $Ze$ , con respectivos vectores de posición $\vec{r}_m$ y $\vec{r}_M$ ; el centro de masas del sistema ocupará la posición, en ese sistema de coordenadas exterior centrado en $O$ , dada por $\vec{R}=\frac{m\vec{r}_m+M\vec{r}_M}{M+m}=\vec{r}_m-\vec{r'}_m=\vec{r}_M-\vec{r'}_M$ ; notamos $\vec{r}=\vec{r'}_m-\vec{r'}_M=\vec{r}_m-\vec{r}_M$ ( $r=r'_{m}+r'_{M}$ ) como la coordenada relativa de posición; se cumple también $m\vec{r'}_m=-M\vec{r'}_M$ , de modo que se puede obtener: $\vec{r'}_M=-\frac{m\vec{r}}{m+M}$ y $\vec{r'}_m=\frac{M\vec{r}}{m+M}$ .
La lagrangiana del sistema se transforma entonces según: $\mathcal{L} = K-V$ $= \frac{1}{2} (m+M) \dot{\vec{R}}^2$ $+ \frac{1}{2}M \dot{\vec{r}'}_M^2$ $+\frac{1}{2}m \dot{\vec{r}'}_m^2 -V$ $=\frac{1}{2}(M+m) \dot{\vec{R}}^2$ $+\frac{1}{2} \frac{Mm}{M+m}$ $\dot{\vec{r}}^2-V$ : se ha reducido el problema de dos cuerpos a un problema de un cuerpo cuya masa es la reducida del sistema, $\mu=\frac{Mm}{M+m}$ .
Mientras que cuando se supone el núcleo en reposo en O el único momento angular orbital que aparece es el del electrón, con expresión $L_e=mvr$ , ahora ha de considerarse también el correspondiente al giro del núcleo en torno al centro de masas, de forma que el momento angular total del átomo viene dado por: $L_{at}=m \omega (r'_{m})^2 +M\omega (r'_{M})^2$ ; puesto que se tiene $M\cdot r'_{M}=m\cdot r'_{m}$ ( $r'_{m}$ y $r'_{M}$ representan, respectivamente, los vectores posición del electrón y el núcleo, respecto al centro de masas), se deriva finalmente $L_{at}=\mu \omega r^2=\mu v r$ , donde $\omega=v/r$ representa la velocidad angular de giro de ambos, electrón y núcleo, en torno a su común centro de masas, y $\mu=\frac{mM}{m+M}$ es la masa reducida del sistema electrón-núcleo.
Aplicando el tercer postulado del modelo de Bohr, se impone la cuantización: ; modificando consecuentemente las expresiones anteriores se obtienen las expresiones corregidas de centro de masas, o ecuaciones con corrección de masa reducida, ya que basta cambiar en ellas la masa del electrón por la masa reducida para obtenerlas, a partir de la cuantización de y la igualdad dinámica :
1. $v\cdot r=\frac{n\hbar}{\mu}$ , de donde $v_n=\frac{Ze^2}{4\pi\epsilon_0 \mu}\frac{1}{vr}=\frac{Ze^2}{4\pi\epsilon_0}\frac{1}{n\hbar}=\alpha\frac{Z}{n\hbar}\hbar c$ ;
2. $r_n=\frac{Ze^2}{4\pi\epsilon_0 \mu}\frac{1}{v^2}=\frac{4\pi\epsilon_0}{Ze^2\mu}n^2\hbar^2=\frac{1}{\alpha}\frac{1}{\hbar c}\frac{1}{Z\mu}n^2\hbar^2$ , $n=1,2\ldots$ ;
3. Radio de Bohr reducido: $a_{\mu}=\frac{m}{\mu}a_0$ ; $r_n=a_{\mu}\frac{n^2}{Z}$ , $n=1,2\ldots$ ;
4. $K_n=\frac{1}{2}m (v'_{m})^2$ $+ \frac{1}{2}M (v'_{M})^2$ $= \frac{1}{2}m\omega^2 (r'_{m})^2 + \frac{1}{2}M\omega^2 (r'_{M})^2$ $= \frac{1}{2}\mu v^2=\frac{\mu}{2\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2\frac{1}{n^2}$ , donde se ha suprimido el sumando de la energía cinética del c.d.m., $\frac{1}{2}(M+m)v_{c.d.m.}^2$ , al suponer a éste en reposo;
5. $V_n=-\frac{Ze^2}{4\pi\epsilon_0 r}=-\frac{\mu}{\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2\frac{1}{n^2}$ ; obtenida a partir de $\int_{r_{ref}}^r \vec{F_C}\cdot d\vec{r}=\frac{Ze^2}{4\pi\epsilon_0}\int_{r_{ref}}^r \frac{1}{r^2}dr$ , con $F_C$ simbolizando fuerza de Coulomb y la elección $V(r_{ref})=0$ : origen de energía elegido cuando el electrón está en reposo e infinitamente separado del núcleo;
6. $E_n=K_n+V_n=-\frac{\mu}{2\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2\frac{1}{n^2}=-\frac{1}{2}\mu c^2(Z\alpha)^2 \frac{1}{n^2}$ , $n=1,2\ldots$
7. Para las constantes de Rydberg: $R(M)=\frac{\mu}{m}R(\infty)=\frac{\mu}{2\hbar^2}(\frac{e^2}{4\pi\epsilon_0})^2=13,5984\,eV$ , teniéndose la igualdad cuando $M\rightarrow \infty$ ( $\mu \rightarrow m$ ). Con la corrección incorporada, para la constante en número de ondas se obtiene el valor $\tilde{R}(M)=\frac{\mu e^4}{8\epsilon_0^2h^3c}=109681\,cm^{-1}$ , en mejor acuerdo también con el valor experimental ( $\tilde{R}_H=109677,58\,cm^{-1}$ ).
A causa del efecto de masa nuclear finita existen diferencias entre las frecuencias de las líneas espectrales análogas de los diferentes isótopos de mismo átomo, un fenómeno conocido con el nombre de «desplazamientos isotópicos». Así, los espectros del Deuterio, isótopo del Hidrógeno cuyo núcleo contiene un protón y un neutrón, y del Tritio, con núcleo compuesto por un protón y dos neutrones, difieren levemente, entre sí y con el espectro del Hidrógeno normal (núcleo con un solo protón). De hecho, fue la observación de esta diferencia lo que en 1932 provocara el descubrimiento del Deuterio (alrededor de 1 cada 6000 átomos de hidrógeno es deuterio).
Otro éxito fue la justificación de la serie espectral de Pickering, que había sido descubierta antes de 1913 y para cuyas líneas se había determinado que sus valores de número de ondas satisfacían la expresión $\frac{1}{\lambda}=\tilde{\nu}=\frac{\nu}{c}=\frac{\mu e^4}{8\epsilon_0^2 h^3 c}(\frac{1}{2^2}-\frac{1}{k^2})$ , donde $k$ tomaba los valores $k=\frac{5}{2},3,\frac{7}{2},4 \ldots$ Para los valores enteros de $k$ los valores numéricos de las líneas eran muy próximos a los de la serie de Balmer, lo que provocó especulaciones (que luego se descartaron) sobre si el hidrógeno de las estrellas podría ser de naturaleza distinta al terrestre. Posteriormente, la serie se observó en los laboratorios, cuando se experimentaba con mezclas de hidrógeno y helio. Tras publicar su modelo, Bohr interpretó la serie haciéndola corresponder al ion de helio, $He^+$ , con número atómico $Z=2$ en sus fórmulas, lo que conducía a la expresión anterior: $\frac{1}{\lambda}=\tilde{\nu}=\frac{\nu}{c}=\frac{\mu e^4}{2\epsilon_0^2 h^3 c}(\frac{1}{n^2} - \frac{1}{k^2})=\frac{\mu e^4}{8\epsilon_0^2 h^3 c}(\frac{1}{(\frac{n}{2})^2} - \frac{1}{(\frac{k}{2})^2})$ , con $n=4$ y $k=5,6,7\ldots$ ; la masa reducida del sistema es $\mu=\frac{4M_pm}{4M_p+m}$ . Asimismo, Bohr logró mediante la aplicación de su modelo predecir y justificar la presencia de líneas de tipo hidrogenoide para el litio doblemente ionizado $Li^{++}$ y el berilio triplemente ionizado, $Be^{3+}$ , que fueron observadas en efecto en los espectros estelares.
Nota: Otra consecuencia de la finitud de la masa nuclear es que se debe considerar un retroceso del átomo en bloque al aplicar la ecuación de conservación del momento, lo que conlleva en procesos como el de la emisión de un fotón una pequeña modificación en la frecuencia (respecto a lo establecido por la relación de Bohr).

Espectro característico de rayos X: ley de Moseley y modelo atómico de Bohr

*Ley de Moseley (imagen de: historiayrevolucinesqcas.blogspot.com).*

En 1913, Moseley estudió los espectros de líneas de 39 elementos, comprendidos entre el $Al$ y el $Au$ , todos ellos muy similares en apariencia y mayoritariamente consistentes en dos grandes grupos de líneas, las series $K$ y $L$ , comenzando siempre la segunda a frecuencias inferiores que la primera.
Moseley encontró que la frecuencia de la n-ésima línea de cada serie variaba suavemente con el número atómico $Z$ del elemento usado en el blanco, siendo capaz de establecer la ley empírica $\sqrt{\nu_n} = C_{n}(Z - \sigma)$ , o ley de Moseley, donde $C_{n}$ es una constante independiente de $Z$ y $\sigma$ un parámetro con valores entre 1 y 2 para la serie $K$ y entre 7.4 y 9.4 para la serie $L$ .
Ley de Moseley (imagen de: http://www.nt.ntnu.no/users/floban/ KJ%20%203055/KJ%203055.html#xray).
Hay que señalar que en 1913 $Z$ tenía como único significado el de la localización de un elemento en la tabla periódica, en la que se ordenaban en general los elementos en orden creciente de pesos atómicos (salvo determinadas excepciones que se hacían para preservar la periodicidad de propiedades químicas).
La aplicación del modelo de Bohr permitió a Moseley explicar todas estas regularidades observadas:
- Cuando electrones con energía suficiente chocan contra un átomo, los electrones más internos, que son los más fuertemente ligados, se excitan hacia niveles superiores, creándose así huecos electrónicos en capa internas.
- La emisión de rayos $X$ se produce cuando otros electrones, también en capas muy internas pero menos intensamente ligados, realizan transiciones hacia los anteriores huecos, ocupándolos. Todos ellos, por estar en órbitas muy internas, sienten un potencial efectivo que es, esencialmente, el coulombiano creado por el núcleo, y estas transiciones involucran fotones (cuantos de luz en terminología de la época) cuyas frecuencias se corresponden con la parte del espectro que denominamos como rayos $X$ (transiciones que involucran electrones más externos, menos ligados, se corresponden con partes menos energéticas del espectro, como la parte visible). (Nota: otra posibilidad adicional de desexcitación, que no involucra emisión de radiación, es el efecto Auger, descubierto en 1920 por Lise Meitner, en el que un electrón es expulsado, acarreando la correspondiente energía).
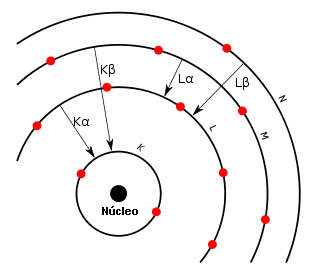
  Explicación por Moseley del espectro característico de rayos X (imagen de la-mecanica-cuantica.blogspot.com).
- Ya que $Z$ se suponía, aproximadamente, igual a la mitad del peso atómico del correspondiente elemento, y puesto que los experimentos de Geiger y Marsden de dispersión de partículas $\alpha$ habían mostrado que la carga nuclear tenía un valor de aproximadamente la mitad del peso atómico, $\frac{P}{2}$ , Moseley sugirió identificar $Ze$ con la carga nuclear, suponiendo entonces que la carga nuclear efectiva para los electrones más internos, debido a efectos de apantallamiento por los restantes electrones, podría expresarse como $(Z-\sigma)$ , donde $\sigma$ era una constante que incorporaba ese efecto.
- Usando entonces la fórmula de Bohr para los niveles de energía atómicos de átomos monoelectrónicos, Moseley expresó la frecuencia de las líneas espectrales para las transiciones aplicando las expresiones de Bohr modificadas para incorporar ese efecto de apantallamiento de la carga nuclear: $\nu_{i \rightarrow f}=\frac{R}{Z^2} (Z-\sigma)^{2}(|\frac{1}{n_i^2}-\frac{1}{n_f^2}|)\,,\,n_i>n_f$ , donde $R$ representa el correspondiente Rydberg.
- La serie $K$ de líneas se atribuye entonces a transiciones atómicas en las que uno de los dos niveles involucrados se fija como $n_1=1$ ; en ella, las sucesivas líneas $K_\alpha, K_\beta\ldots$ , ordenadas en orden decreciente de longitud de onda, corresponden a los valores crecientes $n_2=n_1+1, n_1+2\ldots$ . Se aplica una notación similar en las otras capas: $L\, (n_1=2)$ , $M\, (n_1=3)$ , $N\, (n_1=4)$ , etc.
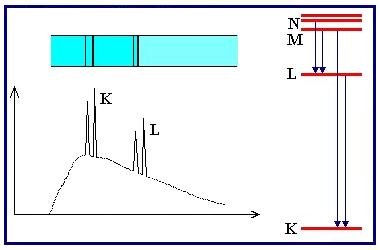
  Atribución de picos del espectro característico (imagen del blog: www.la-mecanica-cuantica.blogspot.com).
- Por lo tanto, Moseley fue capaz de identificar el número atómico $Z$ de cada elemento con la carga nuclear ( $Ze$ ), mostrando como el modelo de Bohr podía, de forma aproximada, aplicarse a los electrones más internos, sujetos al campo coulombiano de núcleo de forma más dominante.
- Moseley también postuló la existencia de elementos desconocidos todavía, cuya existencia consideró necesaria para evitar algunas discontinuidades en sus gráficas (por ejemplo: los elementos con $Z=43, 61, 72$ y $75$ , todos ellos posteriormente descubiertos). Y también procedió a la reordenación de algunos elementos en la tabla, para que tuvieran el $Z$ correcto que los acomodara sobre las rectas de sus gráficas.
La explicación completa de las características de los espectros de rayos $X$ , sin embargo, no se alcanzaría hasta la irrupción de la nueva mecánica cuántica, que permite tratar adecuadamente todos electrones del átomo, incluidos los más externos, sujetos a potenciales donde la interacción coulombiana nuclear no es tan dominante.

Insuficiencia del modelo

El enorme avance que supuso el modelo de Bohr en la explicación teórica del átomo no impide que adoleciera de graves limitaciones, entre ellas:
1. No es generalizable con éxito para átomos con más de un electrón.
2. No logra explicar los desdoblamientos de estructura fina, unos desdoblamientos adicionales observados en las líneas de los espectros atómicos, incluido el del átomo de Hidrógeno.
3. No aplicable a sistemas no periódicos; no incorpora correcciones relativistas.
4. Incorporó excepciones al cumplimiento de las leyes clásicas que se toman como axiomas sobre los que no se logra edificar por completo una nueva teoría que sustituyera al marco clásico, proporcionando justificación teórica para todos los datos experimentales conocidos ya en su época. Por ejemplo: no proporciona un marco teórico capaz de realizar cálculos para las probabilidades de las transiciones atómicas.
Todo ello motivaría que el modelo de Bohr quedara finalmente obsoleto y desterrado en Física a partir de 1925, con el desarrollo de la Física Cuántica (aunque se siga usando todavía como aproximación sencilla y herramienta rápida de cálculo allí donde ofrece buenos resultados numéricos). Y ello a pesar de que el modelo fuera corregido posteriormente para incorporar efectos relativistas por A. Sommerfeld y W. Wilson, logrando dar cuenta de esos desdoblamientos adicionales de estructura fina mencionados.

Modelo relativista de Bohr-Sommerfeld

Reglas de cuantización de Sommerfeld-Wilson-Ishiwara

En 1915-16 tres científicos, A. Sommerfeld, W. Wilson y J. Ishiwara, de forma independiente, llevaron a cabo una generalización de los postulados de cuantización que hasta ese momento se habían formulado, aplicándolos a sistemas periódicos con más de un grado de libertad. Para ello enunciaron unas reglas de cuantización aplicables a cualquier sistema físico cuyas coordenadas generalizadas fuesen funciones periódicas del tiempo, incluyendo las cuantizaciones hechas por Planck y Bohr como casos particulares.
Estas reglas fueron de gran aplicabilidad, permitiendo a Sommerfeld desarrollar un modelo atómico que logró, al incorporar correcciones relativistas, explicar la denominada «estructura fina» del átomo de Hidrógeno y, en algunos casos, el efecto Zeeman, o desdoblamientos de las líneas espectrales observados en presencia de campos magnéticos.
Las reglas de cuantización S-W-I se aplican a sistemas multiperiódicos con más de un grado de libertad: Sea un sistema físico con $m$ grados de libertad, descrito por las $m$ coordenadas generalizadas $q_1,\ldots,q_m$ , y sean $p_1,\ldots,p_m$ los correspondientes momentos generalizados, los cuales supondremos que, sobre cada trayectoria en el espacio de las fases, pueden expresarse como funciones que dependen exclusivamente de la coordenada $q_i$ correspondiente, esto es, $p_i=f(q_i)\,,\,i=1,2,\ldots ,m$ . Supongamos también que cada $q_i$ describe un movimiento periódico en el tiempo (sistema multiperiódico), de forma que la proyección del movimiento sobre el plano $(p_i,q_i)$ es una curva cerrada (libración) o periódica en $q_i$ (rotación).
Según las condiciones indicadas, la función Hamiltoniana del sistema puede escribirse en términos de las variables de acción $J_1,\ldots,J_m$ , definidas según $\oint p_idq_i$ , donde la integral se extiende a un período completo de la variable $q_i$ , de forma que $J_i$ sólo está definido si el sistema es en efecto periódico en la variable $q_i$ , teniéndose entonces $H=H(J_1,\ldots,J_m)$ .
Las variables de acción $J_i$ son constantes del movimiento, viniendo dada la frecuencia de cada movimiento por $\nu_i=\frac{\partial H}{\partial J_i}\,;\,i=1,\ldots,m$ .
Las reglas de cuantización S-W-I establecen que las variables de acción $J_i$ están cuantizadas: sólo pueden tomar los valores que cumplen la condición $J_i=\oint p_idq_i=n_ih\,,\,i=1,\ldots,m\,,\,n_i=0,1,2\ldots$ , donde los $n_i$ representan los distintos números cuánticos así introducidos.
Es decir: en una ruptura con la Física Clásica, donde las variables de acción toman valores sobre un rango continuo, según las reglas S-W-I sólo pueden tomar valores discretos, siendo la constante $h$ de Planck la que determina el tamaño de la discretización establecida, es decir, el cuanto elemental de acción.
Ejemplos de aplicación:
1. El oscilador armónico unidimensional:
  1. Sea una partícula de masa $m$ que se mueve bajo la acción de una fuerza $F=-kx\,,\,k=\text{constante}$ ; el potencial es $V=-\int Fdx=\frac{1}{2}kx^2$ y la coordenada $x$ toma la expresión $x(t)=x_0sen\omega t$ , donde $\omega$ es la frecuencia angular del movimiento, $\omega=\sqrt{\frac{k}{m}}$ , realizando la partícula un movimiento armónico simple de amplitud $x_0$ , frecuencia $\nu=\frac{\omega}{2\pi}$ y período $T=\frac{1}{\nu}$ .
  2. La variable de acción para este movimiento vendrá dada por $J=\oint p_xdx=\int_0^T p_x(t)dx(t)$ , con $p_x=\frac{\partial \mathcal{L}}{\partial \dot{x}}=m\frac{dx}{dt}=mx_0\omega cos\omega t$ ; la integral conduce al resultado $J=mx_0^2\omega \pi$ , de forma que la correspondiente regla de cuantización se expresa como:
    $J=mx_0^2\omega \pi=nh$ , donde $n$ es un entero no negativo.
  3. La regla, expresada en términos dela energía, conduce a:
    $E=K+V=\frac{p_x^2}{2m}+\frac{1}{2}kx^2=\frac{1}{2}x_0^2 \omega ^2m=\frac{J}{2\pi}\omega=nh\nu=n \hbar \omega\,,\,n=0,1,2,\ldots$ , recuperándose la cuantización de la energía de un oscilador en términos del cuanto de energía $h\nu$ (Planck; recuérdese que en teoría cuántica surge un sumando adicional constante de valor $\frac{1}{2}\hbar \omega$ ).
  4. Obsérvese que si se considera el plano de coordenadas $(x,p_x)$ , la gráfica para un valor constante de la energía $E$ corresponde a la elipse $\frac{p_x^2}{2mE}+\frac{x^2}{2Ek^{-1}}=1$ , de semiejes $a=\sqrt{\frac{2E}{k}}$ y $b=\sqrt{2mE}$ . La acción $J=\oint p_xdx$ representa el área $S=\pi a b=J$ de cada elipse, y la diferencia de área entre cada dos elipses permitidas ( $S_n=nh,\,n_i=0,1,2\ldots$ ) consecutivas proporciona $h$ .
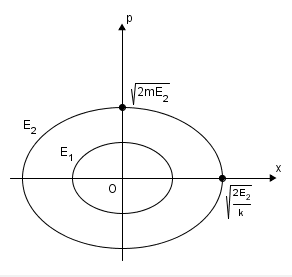
  5. Por tanto, sólo son posibles las trayectorias que describen elipses en el plano $(x,p_x)$ para las cuales el área encerrada es un múltiplo entero de la constante de Planck.
2. El átomo de Bohr:
  1. Sea un electrón de masa $m$ moviéndose en una órbita circular de radio $r_0$ . La posición de la partícula en cada instante puede especificarse por las coordenadas polares $(r,\theta)$ , con $x=rcos\theta,y=rsen\theta$ ; se tiene $r(t)=r_0\,, \,0 \le \theta (t) \le 2\pi$ . Las coordenadas generalizadas correspondientes $(p_r,p_{\theta})$ vienen dadas por $p_i=\frac{\partial \mathcal{L}}{\partial \dot{q}_i}\,,\,i=r,\theta$ , donde $\mathcal{L}$ representa la Lagrangiana del sistema.
  2. La correspondiente Lagrangiana del sistema vendrá dada por: $\mathcal{L}=T-V=\frac{1}{2}m(\dot{x}^2+\dot{y}^2) - V(r)$ $=T-V=\frac{1}{2}m(\dot{r}^2+r^2 \dot{\theta}^2) - V(r)=\frac{1}{2}mr^2 \dot{\theta}^2 - V(r)$ .
  3. Los momentos generalizados: $p_r=\frac{\partial \mathcal{L}}{\partial \dot{r}}=m\dot{r}=0$ ; $p_{\theta}=\frac{\partial \mathcal{L}}{\partial \dot{\theta}}=mr^2 \dot{\theta}=L=mr_0^2 \omega$ , donde $L=m| \vec{r}\times \dot{\vec{r}} |$ representa el módulo del momento angular orbital del electrón, constante en cada órbita ( $\theta$ es una coordenada cíclica y $p_{\theta}=L$ es una constante del movimiento).
  4. La aplicación de la regla de cuantización conduce a: $J_{\theta}=\oint p_{\theta}d\theta=\int_0^{2\pi} Ld\theta=2\pi L=nh \, \Rightarrow \, L=n\frac{h}{2\pi}=n\hbar$ , recuperándose el postulado de cuantización de Bohr para el momento angular del electrón en la órbita, del cual se derivan los valores discretos para la energía en el modelo.

Modelo atómico de Sommerfeld

A. Sommerfeld aplicó en 1916 las reglas de cuantización S-W-I al átomo de Hidrógeno. Para ello desarrolló un modelo que esencialmente coincide con el de Bohr, pues supone un núcleo positivo y al electrón orbitando a su alrededor, ligado por el potencial coulombiano de interacción, $V(r)=-\frac{Ze^2}{4\pi \epsilon_0 r}=-\frac{k}{r}\,,\,k>0$ .
Dinámicamente no es sino un problema típico de fuerzas centrales, el denominado «problema de Kepler», para el cual las trayectorias resultan ser elipses contenidas en un plano perpendicular al momento angular del sistema (véase Goldstein, cap. III, sec. 3-6); la energía total $E$ es una constante del movimiento, puesto que las fuerzas son conservativas, y con signo negativo por tratarse de órbitas cerradas; $\vec{L}$ es el momento angular orbital, teniéndose que $\vec{L}^2$ y $L_z$ son también constantes del movimiento.
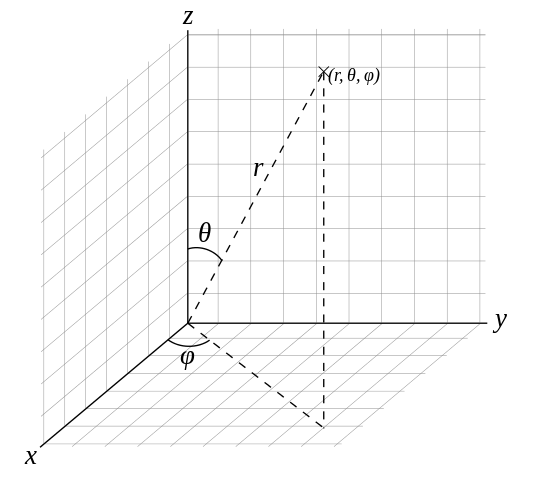
El sistema posee tres grados de libertad, por lo que vendrá descrito por tres coordenadas y tres correspondientes momentos generalizados; empleando coordenadas esféricas , definidas según:
1. Imagen de Adeggs, Wiki GNU licence.
  
  $x=rsen \theta \,cos \varphi \,,\,0\le r < +\infty \,,\,r=\sqrt{x^2+y^2+z^2}$ ,
2. $y=rsen \theta \,sen \varphi \,,\,0 \le \theta \le \pi \,,\,\theta =arc \,tan (\frac{\sqrt{x^2+y^2}}{z})$ ,
3. $z=rcos \varphi \,,\,0\le \varphi < 2\pi \,,\,\varphi =arc \, tan (\frac{y}{x})$ .
La Lagrangiana: $\mathcal{L}=T-V=\frac{1}{2}\mu ( \dot{r}^2 +r^2\dot{\theta}^2 +r^2sen^2\theta \dot{\varphi}^2) - V(r)$ .
Los momentos generalizados, representando la masa reducida del sistema electrón-núcleo:
1. $p_r=\frac{\partial \mathcal{L}}{\partial \dot{r}}=\mu \dot{r}$ ,
2. $p_{\theta}=\frac{\partial \mathcal{L}}{\partial \dot{\theta}}=\mu r^2 \dot{\theta}$ ,
3. $p_\varphi=\frac{\partial \mathcal{L}}{\partial \dot{\varphi}}=\mu r^2 sen^2 \theta \dot{\varphi}=L_z$ , la tercera componente del momento angular orbital $\vec{L}$ .
  -Esta componente, ya que la tercera coordenada $\varphi$ no aparece explícitamente ni en la energía cinética ni en la potencial, constituye una coordenada cíclica, de forma que su momento asociado $p_{\varphi}=L_z$ es una constante del movimiento (véase Goldstein, pp. 60ss. y 260ss.).
La Hamiltoniana:
$H=T+V=\frac{1}{2}\mu (\dot{r}^2 +r^2\dot{\theta}^2 +r^2sen^2\theta \dot{\varphi}^2) + V(r)$ y $\dot{p_{\varphi}}=-\frac{\partial H}{\partial \varphi}=0$ $\Rightarrow$ $p_\varphi=\mu r^2 sen^2 \theta \dot{\varphi} =L_z=\text{constante}$ .
El momento angular orbital: $\vec{L}=\mu r\times \dot{\vec{r}}=\mu r^2(-\dot{\theta} sen \varphi -\dot{\varphi}sen \theta cos \theta cos \varphi \,,\, \dot{\theta} cos \varphi -\dot{\varphi}sen \theta cos \theta sen \varphi \,,\,\dot{\varphi}sen^2 \theta)$ ;
$\vec{L}^2=\mu^2 r^4 (\dot{\theta}^2 + \dot{\varphi}^2 sen^2 \theta)=p_\theta^2 + \frac{p_{\varphi}^2}{sen^2 \theta}$ .
La Hamiltoniana: $H=\frac{1}{2\mu}(p_r^2 +\frac{p_\theta^2}{r^2} +\frac{p_{\varphi}^2}{r^2 sen^2 \theta}) +V(r)=\frac{1}{2\mu}(p_r^2 +\frac{\vec{L}^2}{r^2}) +V(r)$ ; en este caso $H$ es independiente del tiempo, representando una constante del movimiento.
-Además (¡no siempre es así!: lo uno no implica lo otro, véase Goldstein, p. 261), en este caso $H$ también representa la energía total del movimiento.
Se tienen pues tres constantes del movimiento: $L_z$ , $\vec{L}^2$ y $E$ .
Las variables de acción:
1. $J_r=\oint p_rdr=-2\pi(L-\frac{\sqrt{\mu}Ze^2}{4\pi \epsilon_0 \sqrt{2|E|}})=n_rh$ , donde $n_r$ es un entero no negativo;
2. $J_{\theta}=\oint p_{\theta}d\theta=2\pi(L-|L_z|)=n_{\theta}h$ , donde $n_{\theta}$ es un entero no negativo;
3. $J_{\varphi}=\oint p_{\varphi} d\varphi=2\pi|L_z|=n_{\varphi}h$ , donde $n_{\varphi}$ es un entero no negativo.
4. Para calcular estas tres integrales se puede recurrir a la ecuación de Hamilton-Jacobi para obtener su expresión en términos de una función característica $W(r,\theta,\varphi)$ , que permite realizar una separación de variables, vía la descomposición $W=W_r(r)+W_\theta(\theta)+W_\varphi(\varphi)$ (véase Goldstein, pp. 353-355).
Es usual realizar un cambio en la elección de los tres números cuánticos que aparecen, pasando a denominarlos y notarlos como:
1. Número cuántico principal: $n=n_r +n_\theta + n_\varphi$ , con $n=1,2\ldots$
2. Número cuántico azimutal: $n_\psi=n_\theta + n_\varphi$ , con $n_\psi=1,2,\ldots,n$ (el valor $n_\psi =0$ se descartó, pues correspondería a un movimiento rectilíneo; luego se sustituiría por $l=n_{\psi}-1=0,1,2,\ldots,n-1$ , o número cuántico de momento angular orbital moderno).
3. Número cuántico magnético: $m$ tal que $|m|=n_\theta \,,\, |m| \le n_\psi$ : $m=-n_\psi,-n_\psi + 1,-n_\psi+2,\ldots,-1,0,+1,\ldots,n_\psi$ .
  -Nota: Sin embargo, en realidad en cuántica moderna el número cuántico magnético tomará los $2l + 1$ valores $m=-l,-l + 1,-l+2,\ldots,-1,0,+1,\ldots,+l-1, +l$ , siendo $l$ el número cuántico de momento angular orbital, $l=0,1,2,\ldots,n-1$ .
4. En el modelo de Sommerfeld, pues, la degeneración $d$ de cada nivel $n$ es $d=n(n+2)$ (i.e.: $n=2 \rightarrow n_\psi=1\,,\, m=-1,0,+1\,;\,n_\psi=2\,,\, m=-2,-1,0,+1,+2$ $\Rightarrow d=3+5=8$ ). En cuántica moderna, sin embargo, pasará a ser $d=n^2$ .

En función de estos números cuánticos las expresiones para la energía total , el módulo del momento angular orbital y su tercera componente son:
1. $E=-\frac{2\pi^2 \mu Z^2e^4}{(J_r+J_\theta+J_\varphi)}=-\frac{Ze^4\mu}{32\pi^2 \epsilon_0^2 \hbar^2}\frac{1}{n^2}=-\frac{1}{2}\mu (Z\alpha c)^2\frac{1}{n^2}$ ;
2. $L=n_\psi \hbar$ ;
3. $L_z=m\hbar$ .
La ecuación $E=\frac{1}{2\mu}(p_r^2 +\frac{\vec{L}^2}{r^2}) -\frac{Ze^2}{4\pi \epsilon_0}$ representa una elipse en el plano de coordenadas $(r,p_r)$ , con semiejes mayor $a= \frac{Ze^2}{8\pi \epsilon_0 |E|}=-\frac{k}{2|E|}$ y menor $b=\frac{L}{\sqrt{2\mu |E|}}=a^{\frac{1}{2}}\sqrt{\frac{L^2}{\mu k}}$ , excentricidad $\epsilon=\frac{\sqrt{a^2-b^2}}{a}=(1+\frac{2EL^2}{\mu k^2})^{\frac{1}{2}}=(1+\frac{32\pi^2 \epsilon_o^2EL^2}{\mu Z^2 e^4})^{\frac{1}{2}}\,,\,\epsilon < 1\,,\,E<0$ ; sólo para $n=n_\psi$ se tiene un círculo, $a=b$ (órbita de Bohr). El período del movimiento resulta ser $T=\frac{Ze^2}{8\pi \epsilon_0}(\frac{\mu}{2|E|^3})^{\frac{1}{2}}$ .
En resumen, la energía, el módulo del momento angular orbital y su tercera componente han sido cuantizados. La energía depende sólo del número cuántico principal $n$ , y no lo hace explícitamente con el azimutal $n_\psi$ , de forma que todos los $n$ niveles correspondientes a los distintos $n_\psi$ posibles para un $n$ dado tienen la misma energía. A este hecho se le denomina degeneración accidental, y es característico del potencial coulombiano, no teniéndose en general para otro tipo de potenciales, centrales o no; lo que sí es común a todos los potenciales centrales es la no dependencia con $m$ de la energía.
Para cada órbita circular del modelo de Bohr, con una energía $E_n$ y radio $r_n$ dados, el modelo de Sommerfeld proporciona un conjunto de $n$ órbitas elípticas con igual semieje mayor $a$ pero con diferentes excentricidades. Éstas órbitas van a estar inicialmente degeneradas en energía en el modelo, pero van a dar lugar a desdoblamientos al introducir las correcciones relativistas, que les asociarán energías ligeramente diferentes.
Los valores de energía son los mismos que proporcionaba el modelo de Bohr (algo esperable dado el buen acuerdo de estos con el experimento), pero la mayor complejidad de este modelo, con la aparición de números cuánticos adicionales, va a permitir la explicación de observaciones experimentales para las que el modelo de Bohr se mostró incapaz.

Estructura fina del átomo de Hidrógeno

La estructura fina del espectro del átomo de Hidrógeno (ya descrita por Michelson en 1891), consiste en unos desdoblamientos observados para las líneas espectrales cuando se realizaban medidas espectroscópicas con mayor precisión. Es decir: experimentalmente se comprobó que cada uno de los niveles que denominamos de Bohr, salvo el fundamental, estaba compuesto en realidad por un conjunto de niveles muy próximos entre sí. Por ejemplo, la línea $H_{\alpha}$ de la serie de Balmer resultaba ser en realidad un par de líneas (en aquella época) separadas $0.33\, cm^{-1}$ entre sí, según se muestra en la figura adjunta:

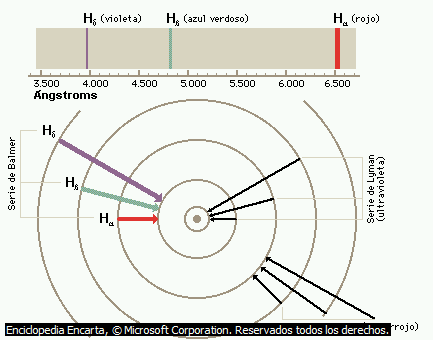
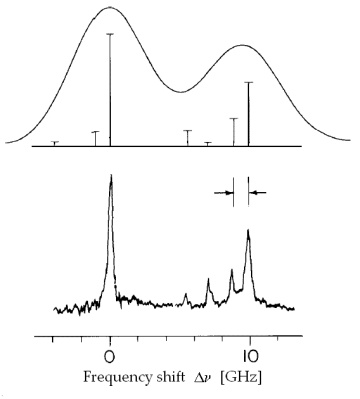
Estructura (datos modernos) de la raya H alfa del hidrógeno, que resulta estar compuesta por varias líneas, destacando dos separadas 0,33 cm^{-1} entre sí.
Para explicarla, Sommerfeld introdujo en su modelo correcciones relativistas, ya que aunque las velocidades electrónicas orbitales sean pequeñas, del orden de $v_n=\frac{Z\alpha c}{n}=\frac{Zc}{137n}$ , los efectos relativistas son capaces de romper la degeneración que se
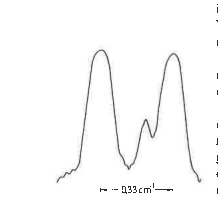
Estructura fina de la línea H sub-alfa del Hidrógeno.

obtiene cuando no se incorporan. Por lo tanto, Sommerfeld corrigió su modelo (era lógico que las órbita más excéntricas requirieran corrección relativista, puesto que la velocidad v crece al estar el electrón más cercano al núcleo), imponiendo las reglas de cuantización tomando como punto de partida la expresión relativista de la energía cinética, $K=\mu c^2 (\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}-1)$ , obteniendo (recuérdese que la lagrangiana relativista no es $T-V$ ) la fórmula relativista para la energía total $E(n,n_\psi)=\mu c^2([1 +Z^2\alpha^2(n -n_\psi +\sqrt{n_\psi^2 -Z^2\alpha^2})^{-2}]^{\frac{-1}{2}}-1)$ , que desarrollada en potencias de $(Z\alpha)$ y cortada hasta tercer orden incluido proporciona la expresión final siguiente: $E(n,n_\psi) \approx -\frac{1}{2}\mu(Z\alpha c)^2\frac{1}{n^2}[1+\frac{\alpha^2 Z^2}{n}(\frac{1}{n_\psi}-\frac{3}{4n})]\,,\,Z\alpha<<1$ ( $n=1,2\dots$ y $n_{\psi}=1,2, \ldots, n$ ).
La predicción es que, mientras el estado fundamental no se desdobla, los niveles de Bohr con $n > 1$ sí lo hacen: el primer estado excitado, $n=2$ , lo hará en dos subniveles, correspondientes a los valores $n_\psi=1$ y $n_\psi=2$ ; el siguiente, $n=3$ , lo hará en tres, correspondientes a los valores $n_\psi=1,2,3$ , y así sucesivamente.
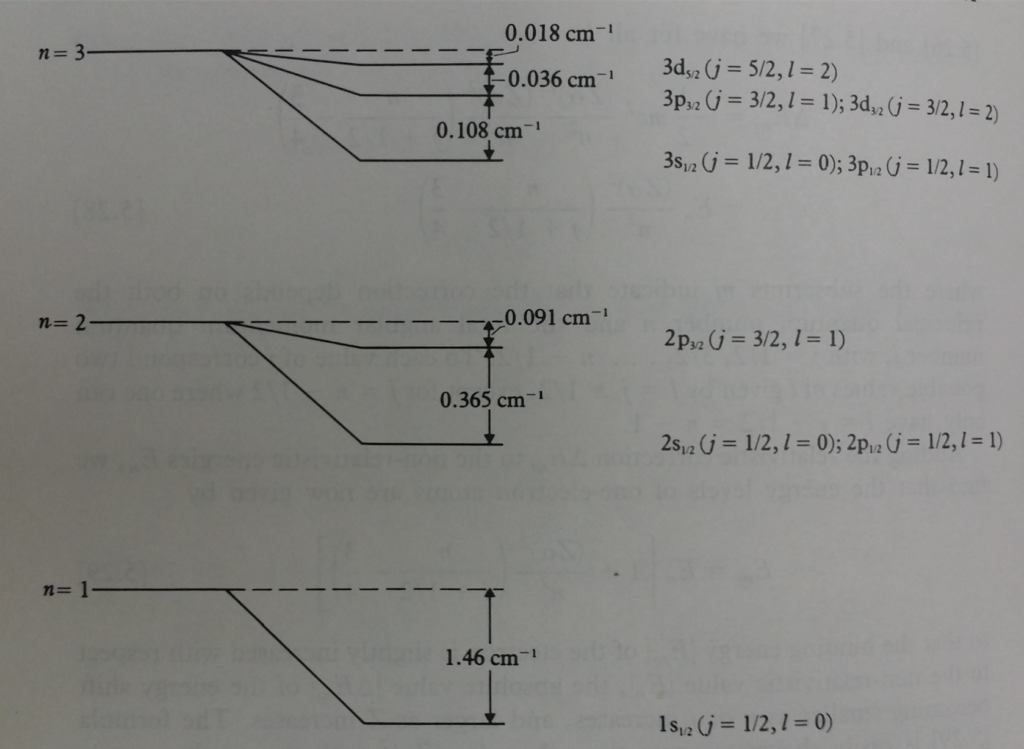
Orden de magnitud de la estructura fina en los primeros niveles del átomo de hidrógeno (valores modernos; véase Bransden-Joachain, p. 202).
El acuerdo de este modelo de Sommerfeld que incorpora corrección relativista con los espectros observados del Hidrógeno e ión Helio fue excelente, aunque de hecho las multiplicidad de los niveles resulta incorrecta, y tampoco logró explicar porque no se observaban todas las transiciones posibles; tampoco justificó correctamente las intensidades y polarizaciones de las líneas sí observadas (por ejemplo, entre los niveles con $n\le 3$ sólo se observan las líneas $(n=2, n_\psi=2) \rightarrow (n=1, n_\psi=1)$ , $(n=3, n_\psi=2) \rightarrow (n=1, n_\psi=1)$ , $(n=3, n_\psi=2) \rightarrow (n=2, n_\psi=1)$ , $(n=3, n_\psi)=1 \rightarrow (n=2, n_\psi=2)$ y $(n=3, n_\psi=3) \rightarrow (n=2, n_\psi=2)$ ). Se infiere de las observaciones que está actuando una regla de selección $\Delta n_\psi=\pm 1$ , sin justificación en el modelo.
En cualquier caso, se ha llegado a calificar este éxito como de fortuito, en el sentido de que la fórmula correcta necesita incorporar el espín electrónico, postulado por S. Goudmit y G.E. Uhlenbeck en 1925 (aunque la primicia de la concepción, por meses, se deba R. Kronig, quien desistiera sin embargo de su idea por la desfavorable opinión inicial de Pauli), para explicar el efecto Zeeman anómalo. Tras su desarrollo teórico-matemático riguroso por Pauli en 1927, Dirac lo incorporaría en 1928 en su ecuación mecánico-cuántica relativista para el electrón.

Cuantización espacial

El fenómeno de la cuantización espacial consiste en que la orientación del plano de las órbitas permitidas respecto a una dirección dada no puede ser arbitrario, sino que su normal (esto es, la dirección de $\vec{L}$ ) debe formar con el eje $OZ$ (en general, con cualquier dirección prefijada) un ángulo $\phi$ dado por $cos\phi=\frac{L_z}{L}=\frac{m}{n_\psi}$ . Puesto que el espacio es isótropo, esta cuantización que surge en el modelo carece de sentido físico hasta que no se marque experimentalmente una dirección en el espacio, por ejemplo aplicando un campo magnético.
Esta predicción sería confirmada experimentalmente en 1922 por O. Stern y W. Gerlach, vía la medida de momentos magnéticos atómicos, y carecería de interpretación correcta hasta la introducción del espín, un momento angular intrínseco sin análogo clásico.

Efecto Zeeman

Se conoce con el nombre de efecto Zeeman el desdoblamiento que sufren las líneas espectrales en presencia de campos magnéticos externos. Fue descubierto por P. Zeeman en 1896, quien observó que, al aplicar un campo magnético intenso uniforme (efecto Zeeman normal o clásico), algunas líneas espectrales se desdoblaban en un triplete (los denominados «tripletes de Lorentz»), conjunto de tres líneas igualmente espaciadas que presentan un espaciado dependiente de la intensidad del campo $B$ pero no del átomo concreto en cuestión (la primera observación histórica fue sobre la línea azul de Cadmio).
El efecto fue explicado clásicamente por Lorentz en 1897, poco después de su primera observación (Zeeman y Lorentz compartirían el Premio Nobel de 1902 por estos estudios), aplicando teoría electromagnética clásica. Basta considerar en el Hamiltoniano del sistema una interacción adicional de expresión $-\vec{\mu}\cdot \vec{B}$ , donde $B$ representa la intensidad del campo magnético y $\vec{\mu}$ el momento magnético dipolar del electrón, que clásicamente es proporcional a su momento angular: $\vec{\mu}= -\frac{|e|}{2m_e}\vec{L}$ ; $e$ es la carga del electrón y $m_e$ su masa.
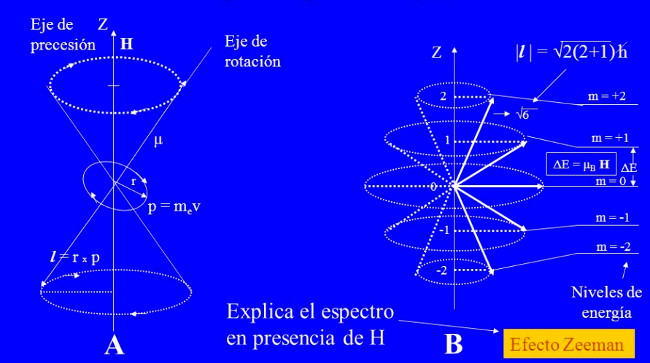
En efecto: si consideramos el electrón girando en una órbita circular de radio $r$ , el momento magnético dipolar es normal al plano de la corriente así constituida, de intensidad $I=\frac{|e|v}{2\pi r}$ , de forma que $\vec{\mu}=Id\vec{S}$ , donde $S=\pi r^2$ y $\mu=-\frac{|e|v\pi r^2}{2\pi r}=-\frac{|e|m_evr}{2m_e}=-\frac{|e|}{2m_e}L$ , según se representa en la siguiente figura:
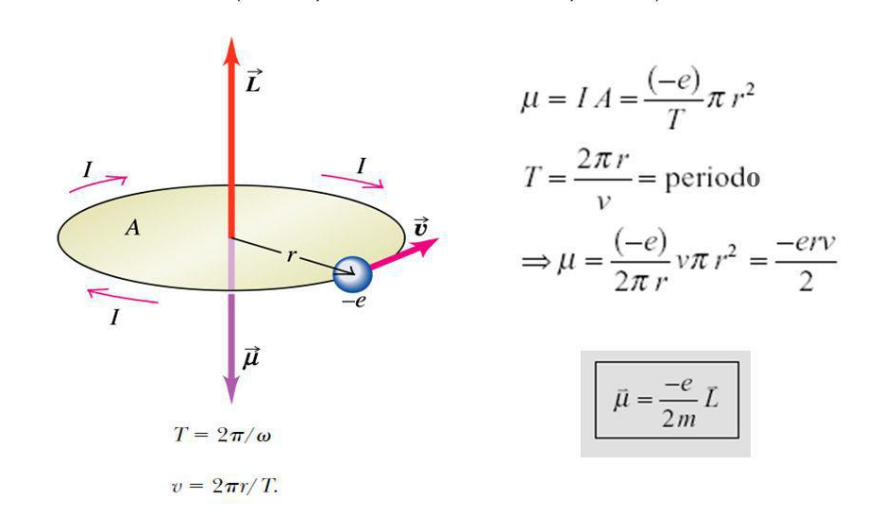
Obsérvese que el momento magnético dipolar tiene igual dirección que el momento angular orbital, y sentido opuesto.
Como estableció Lorentz en 1897, basta añadir al Hamiltoniano del sistema la interacción adicional de expresión $-\vec{\mu}\cdot \vec{B}$ , a partir del cual, supuesto el campo magnético uniforme de intensidad $B$ en la dirección positiva del eje $OZ$ , resulta un cambio en la energía $\Delta E=-\vec{\mu}\cdot \vec{B}= \frac{|e|}{2m_e}L_zB$ , que explica por qué las líneas espectrales se modifican en el seno del campo magnético aplicado.
En el contexto del modelo precuántico sin correcciones relativistas de Sommerfeld, y puesto que en este modelo aparece la cuantización de la tercera componente del momento angular orbital, $L_z=m\hbar$ , en términos de un número cuántico magnético $m$ , se tiene que la tercera componente del momento magnético adquiere la expresión cuantizada $\mu_z=-\mu_B \frac{L_z}{\hbar}$ , donde $\mu_B=\frac{|e|\hbar}{2m_e}=9,27408 \times10^{-24}\,JT^{-1}$ es una constante, denominada «el magnetón de Bohr» (unidades Julio/Tesla).
-Recuérdese que en el modelo de Sommerfeld aparecen tres números cuánticos: principal $n$ , azimutal, $n_\psi$ , y magnético $m$ . Mientras que $n$ toma valores enteros, $n=1,2\ldots$ , para cada $n$ el azimutal toma los valores $n_\psi=1,2,\ldots,n$ ; finalmente, el número cuántico magnético $m$ toma los $2n_\psi +1$ valores $m=-n_\psi,-n_\psi + 1,-n_\psi+2,\ldots,-1,0,+1,\ldots,n_\psi$ .
Por lo tanto, el cambio en la energía de los niveles provocado por el campo magnético resulta ser:
$\Delta E=\frac{|e|}{2m_e}L_zB=\frac{|e|}{2m_e}m\hbar B= \mu_B m B$ ,
de donde se deriva la siguiente fórmula para los niveles de energía de un átomo de hidrógeno en el seno de un campo magnético (fórmula del efecto Zeeman «normal», que es el que se observa para un campo uniforme intenso):
$E(n,m)=-\frac{1}{2}\mu (Z\alpha c)^2\frac{1}{n^2} + \mu_BBm$ .
-Se añade pues a la energía de cada nivel $E_n$ (energía sin corrección relativista o nivel de Bohr) una corrección independiente del nivel (independiente de $n$ ), que vino a coincidir con la predicción clásica de Lorentz, consiguiendo así reproducir su explicación del efecto Zeeman (normal).

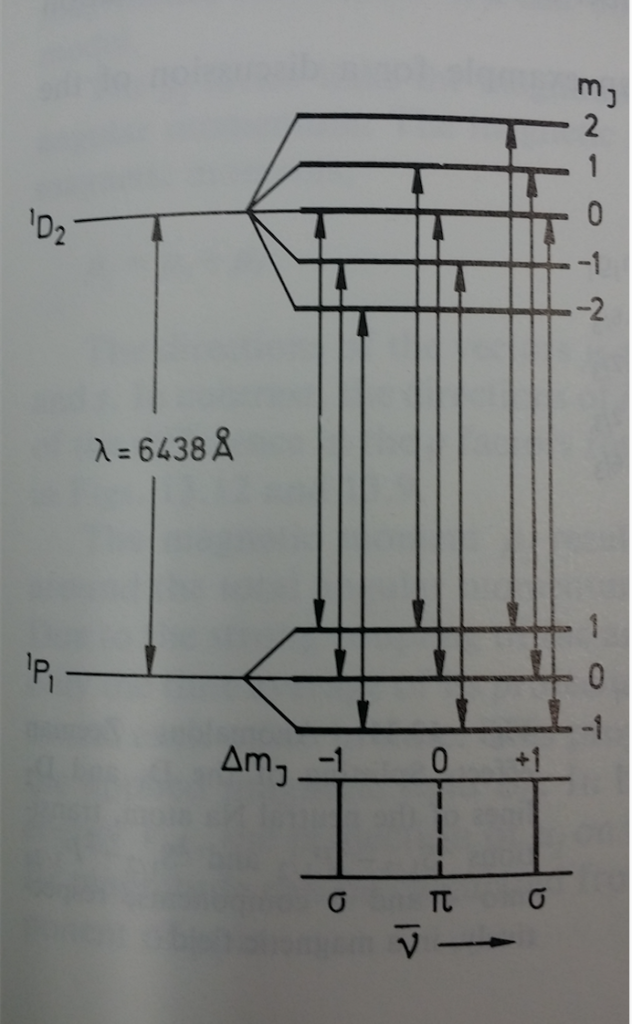
Efecto Zeeman normal en el Cd (¡un átomo que no es monoelectrónico!: téngase en cuenta). La figura es moderna y usa una notación para el momento angular no explicada en el texto (las J representan el momento angular total, suma de los momentos orbital y de espín).
En consecuencia, los valores de frecuencia para las transiciones resultan: $h\nu_{n_im\rightarrow n_fm'}=\frac{1}{2}\mu (Z\alpha c)^2 | \frac{1}{n_i^2} -\frac{1}{n_f^2}| + \mu_B B |m-m'|$ :
Efecto Zeeman normal (imagen de la-mecanica-cuantica.blogspot.com); el número cuántico orbital $l$ es igual al azimutal $n_\psi$ menos una unidad.
Nota: Aunque $|m-m'|$ puede ser cualquier entero entre $-(n_i+n_f)$ y $(n_i+n_f)$ , en la práctica las transiciones importantes son las que corresponden a $\Delta m=0,\pm 1$ , esto es, las dipolares eléctricas, para las que se demuestra la regla de selección $|\Delta m| \le 1$ . La línea correspondiente a $\Delta m=0$ se suele denominar como «línea $\pi$ «, mientras que las otras dos, $\Delta m=\pm 1$ , se denominan como líneas $\sigma^+$ y $\sigma^-$ , respectivamente.
Para intensidades menores del campo magnético, se producen desdoblamientos de naturaleza diferente en las líneas espectrales (efectos «Paschen-Back» para campos medios y «Zeeman anómalo» para campos débiles, éste descubierto por T. Preston), que sólo encontrarían justificación en la teoría plenamente cuántica moderna, en que se incorpora el espín electrónico, nueva magnitud cuántica sin análogo clásico y para cuyo descubrimiento la experimentación relacionada con los distintos efectos Zeeman fue decisiva.

Principio de correspondencia

En 1923 N. Bohr formuló el «principio de correspondencia», que establece que los resultados predichos por la nueva teoría cuántica en gestación, para cualquier sistema físico, deberían corresponderse con las predicciones de la Física Clásica en el límite en que los números cuánticos que especifican el sistema en cuestión se hacen muy grandes.
Su fundamento conceptual era la hipótesis de que la teoría cuántica, en su formalismo, contiene a la mecánica clásica como caso límite. En otras palabras, los resultados clásicos son «macroscópicamente correctos», debiendo ser considerados como casos límites de los resultados cuánticos cuando las discontinuidades cuánticas pueden, de forma aproximada, ignorarse.
Se consideraron manifestaciones de este principio-guía:
1. La convergencia de la teoría de la radiación de Planck para el cuerpo negro al límite clásico de Rayleigh-Jeans al hacerse el cuanto de radiación $h\nu$ infinitamente pequeño, esto es, en el límite $h \rightarrow 0$ , o límite de las frecuencias pequeñas, cuando $h\nu \, << \, K_BT$ y el teorema de equipartición de la energía clásico puede tomarse como válido.
2. La convergencia de los valores de la energía cuantizada para el oscilador armónico simple, $\epsilon =nh\nu\,,\, n=0,1,2\ldots$ , al continuo clásico cuando $h \rightarrow 0$ , límite de frecuencias muy pequeñas (tamaño de la discretización tendiendo a cero).
3. La convergencia en la relación de frecuencia de Bohr, $\nu=\frac{|E_f-E_i|}{h}=\frac{m}{2\hbar^2}(\frac{Ze^2}{4\pi\epsilon_0})^2 |\frac{1}{n_f^2}-\frac{1}{n_i^2}|$ , cuando el número cuántico principal se hace muy grande y se aproxima $|\frac{1}{(n-1)^2}-\frac{1}{n^2}|\approx \frac{2}{n^3}$ , de forma que se recupera la frecuencia radiada por un electrón en una órbita clásica, $\nu=v/2\pi r$ , cuando en esta última expresión se sustituyen el radio y velocidad del electrón en el modelo de Bohr: $\nu \approx \frac{\mu Z^2 e^4}{32\epsilon_0^2 \alpha^2 h^3}\frac{2}{n^3}$ .
Una aplicación inmediata de este principio fue la del estudio de las reglas de transición observadas entre los distintos niveles de energía atómicos: se determinó que los cálculos cuánticos, en el nuevo marco teórico, de frecuencias de transición, intensidades de líneas y polarizaciones, debían coincidir con los clásicos en el límite de grandes números cuánticos. El principio jugó un papel heurístico que ayudó a determinar, al menos a nivel cualitativo, nuevos resultados teóricos, teniendo un papel importante en el desarrollo de la fundamentación de la vieja teoría cuántica. Posteriormente su aplicación decayó, limitándose a garantizar el límite clásico correcto del nuevo formalismo cuántico.
Sin embargo, su importancia histórica es grande: de hecho, jugó un papel trascendental como principio guía de Heisenberg en el trabajo sobre Cinemática Cuántica que culminaría en su famosa publicación de 1925: nacimiento de la Mecánica Cuántica moderna, en su formulación matricial: Heisenberg,W.; «Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen», Zeitschrift für Physik 33 (1925) 879-893 («Sobre la interpretación cuántica de las relaciones cinématicas y dinámicas»).