El fotón y su necesidad

La hipótesis heurística del cuanto de luz

Fuente: esta entrada está basada en gran parte en el capítulo 1 del libro [GAR-08]: Garrison, J. C. and R. Y. Chiao, Quantum Optics, Oxford Univ. Press, Oxford, 2008.

Del diccionario de la RAE: «heurístico» (cuarta acepción): «En algunas ciencias, manera de buscar la solución de un problema mediante métodos no rigurosos, como por tanteo, reglas empíricas, etc.»

La naturaleza de la luz fue objeto de un largo debate científico, que se extendió durante siglos: chorro de corpúsculos para Newton pero onda para Huyguens (s. XVII); onda con Young y, parecía que definitivamente, Maxwell, en el s. XIX; vuelta a la teoría corpuscular con Einstein en el s. XX; naturaleza dual con el desarrollo de la Física Cuántica (¿vigente hoy?), y hasta la Electrodinámica Cuántica.

A principios del s. XX, los fenómenos experimentales como, por ejemplo, los relativos a la radiación del cuerpo negro, los espectros atómicos y el efecto fotoeléctrico (especialmente relacionados con la radiación electromagnética) provocaron una crisis científica, mostrando la insuficiencia de la Física Clásica y, en particular, de la Electrodinámica Clásica.

En 1905 Einstein, en un artículo titulado «Un punto de vista heurístico sobre la producción y transformación de la luz«, mostró que la idea de un «cuanto de luz» podía explicar la fenomenología observada del efecto fotoeléctrico:

Si la radiación monocromática de baja densidad se comporta en aspectos termodinámicos como un medio discreto que consistiera de quanta de energía mutuamente independientes de magnitud $\frac{R\beta \nu}{N} (\beta=\frac{h}{k},\, k=\frac{R}{N},\; \; \frac{R\beta \nu}{N}=h\nu \,$ , hipótesis del cuanto de luz), entonces esto sugiere como si las leyes de generación y conversión de la luz se dieran también como si la luz consistiera de cuantos de energía de esta clase.

(por esta explicación recibiría el Premio Nobel de Física en 1921).

-Einstein conceptualiza la radiación como compuesta de paquetes indivisibles de energía o cuantos de luz (o fotones, en controvertida terminología introducida por Lewis en 1926), que se desplazan localizadamente a velocidad $c$ (vacío); para una frecuencia $\nu$ , la energía del cuanto es $E = h \nu$ , donde $h$ es la constante de Planck; la intensidad de la radiación es proporcional al número (densidad) de cuantos de luz presentes.

La hipótesis del cuanto de luz es el hito teórico que inicia la conceptualización cuántica de la radiación electromagnética.

En ese momento histórico, la teoría electromagnética clásica se halla consolidada, contando como ingrediente principal con las ecuaciones de Maxwell del campo electromagnético, su resumen desde un punto de vista macroscópico.

Esas ecuaciones tienen la forma más general (unidades SI):
$\nabla \cdot \vec{D}=\rho$
$\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}$
$\nabla \times \vec{H}=\vec{J}+\frac{\partial \vec{D}}{\partial t}$
$\nabla \cdot \vec{B}=0$

en las que intervienen los parámetros:

$\vec{E}(\vec{r},t)$ : Campo eléctrico existente en el espacio, creado por las cargas.
$\vec{D}(\vec{r},t)$ : Campo dieléctrico que resume los efectos eléctricos de la materia.
$\vec{B}(\vec{r},t)$ : Campo magnético existente en el espacio, creado por las corrientes.
$\vec{H}(\vec{r},t)$ : Campo magnético que resume los efectos magnéticos de la materia.
$\rho(\vec{r},t)$ : Densidad de cargas existentes en el espacio.
$\vec{J}(\vec{r},t)$ : Densidad de corriente, mide el flujo de cargas por unidad de tiempo y superficie y es igual a: $\vec{J}=\rho\vec{v}$
$\varepsilon$ : Permitividad eléctrica, característica de los materiales dieléctricos.
$\mu$ : Permeabilidad magnética, característica de los materiales paramagnéticos.
Para el caso de que las cargas estén en medios materiales, y asumiendo que éstos son lineales, homogéneos, isótropos y no dispersivos, podemos encontrar una relación entre los vectores intensidad eléctrica e inducción magnética:
$\vec{D} = \varepsilon \vec{E} = \varepsilon_0 \varepsilon_r \vec{E}$
$\vec{B} = \mu \vec{H} = \mu_0 \mu_r \vec{H}$

La hipótesis del cuanto de luz resultó suficiente para acometer con éxito la explicación teórica de los citados fenómenos, ante los cuales la Física Clásica fracasaba:

El espectro de radiación de un cuerpo negro:
-En 1900, la fórmula de Planck, obtenida primero semi-empíricamente, realizando interpolaciones; luego, arduamente tratada de justificar relacionando la energía de un oscilador con su entropía, mediante argumentos termodinámicos y estadísticos; finalmente, deducible cuantizando la energía intercambiada por un oscilador, según $E=Nh\nu$ , consigue por fin ajustar los datos experimentales, renunciando al principio de equipartición de la energía:
$R(\nu,T) = \frac{2 \pi \nu^2}{c^2} \frac{h \nu}{exp{\frac{h\nu}{k_B T}}-1}\quad ,\quad R(\lambda,T) = \frac{2 \pi hc^2}{\lambda^5} \frac{1}{exp{\frac{hc}{\lambda k_B T}}-1}$
fórmula donde aparece por primera vez la constante $h$ , denominada por Planck como «constante auxiliar», que interviene en la subdivisión de la energía en «elementos» (Planck no aceptará públicamente el «cuanto» de energía hasta 1909, asumiéndolo hasta entonces tan sólo como una cuantización de los modos de los osciladores, de forma que la cuantización se reduce al intercambio de energía entre luz y materia).

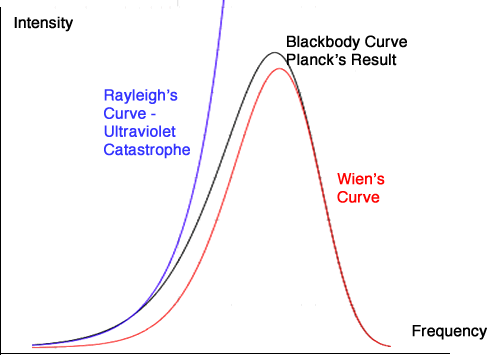
Comparativa entre fórmulas para la radiancia espectral del cuerpo negro.

-La fórmula permitía además la deducción de la ley del desplazamiento de Wien,
$R(\nu,T) = \frac{c}{4} \nu^{3}f(\frac{\nu}{T})$
(basta buscar el máximo de la función para una $T$ dada) y de la ley de Stefan-Boltzmann,
$R(\nu,T)=\sigma T^{4} \; ; \sigma=5.67\times10^{-8}W \cdot m^{-2} \cdot k^{-4}$
(integrando la intensidad emitida sobre el rango de frecuencias).
-Posteriormente, en 1917, Einstein mostró como la cuantización de la radiación en sí misma, es decir, considerando el campo electromagnético como compuesto de cuantos discretos, permitía la derivación de la fórmula para $R(\nu,T)$ .
-Si comparamos los dos caminos teóricos por los que Planck y Einstein logran la fórmula correcta para la radiación del cuerpo negro, podemos afirmar que, mientras que Planck abandona las leyes de la Mecánica Estadística (principio de equiparición de energía) como aplicables al campo electromagnético, incorporando una hipótesis ad hoc de cuantización del intercambio de energía pero conservando la teoría Electromagnética Clásica (ecuaciones de Maxwell), Einstein rompe con esta última.

–Planck, 1913:
En suma, puede afirmarse que entre los problemas importantes, tan abundantes en la física moderna, no existe alguno ante el que Einstein no adoptara una posición de forma notable. Aunque, a veces, errara en sus especulaciones, como por ejemplo en su hipótesis acerca del quantum de luz, no puede esgrimirse realmente demasiado en su contra. Porque sin correr un riesgo de vez en cuando es imposible, incluso en la ciencia natural de mayor exactitud, introducir verdaderas innovaciones.
El efecto fotoeléctrico:
-Los cuantos de luz penetran en el material, comunicando toda su energía a algún electrón atómico (absorción completa: requiere electrón ligado), que es expulsado con energía cinética variable, $\frac{1}{2}mv^2=h \cdot \nu-W$ , que será máxima para el caso de un electrón superficial (para el que la función de trabajo $W$ del material, o energía mínima necesaria para arrancarlo, variable en general para cada electrón, toma el valor $W=W_0$ , característico de cada material; $W_0=h\nu_0$ , donde $\nu_0$ es la frecuencia umbral de la radiación incidente, por debajo de la cual no se expulsan electrones del material).

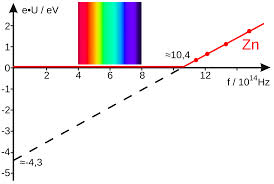
Diagram of the maximum kinetic energy as a function of the frequency of light on zinc (Zn). x: frequency of light; y: kinetic energy of the electrons With the spectrum of visible light the electrons aren?t emitted. Autor: Klaus-Dieter Keller. Creative Commons Attribution 3.0 Unported license.

-Durante los años 1912-1916, tras haber obtenido la masa del electrón con su experimento de la gota de aceite, R. Millikan comprobó en una serie de experimentos sucesivos como la ecuación del efecto fotoeléctrico, $e \cdot |V_{0}|=h \cdot \nu-W_{0}$ , se ajustaba a los datos experimentales, lo cual le permitió confirmar la dependencia lineal de la energía de los fotoelectrones con la frecuencia de la luz incidente y determinar un valor para la constante $h$ de Planck (recibiría el Premio Nobel en 1923).

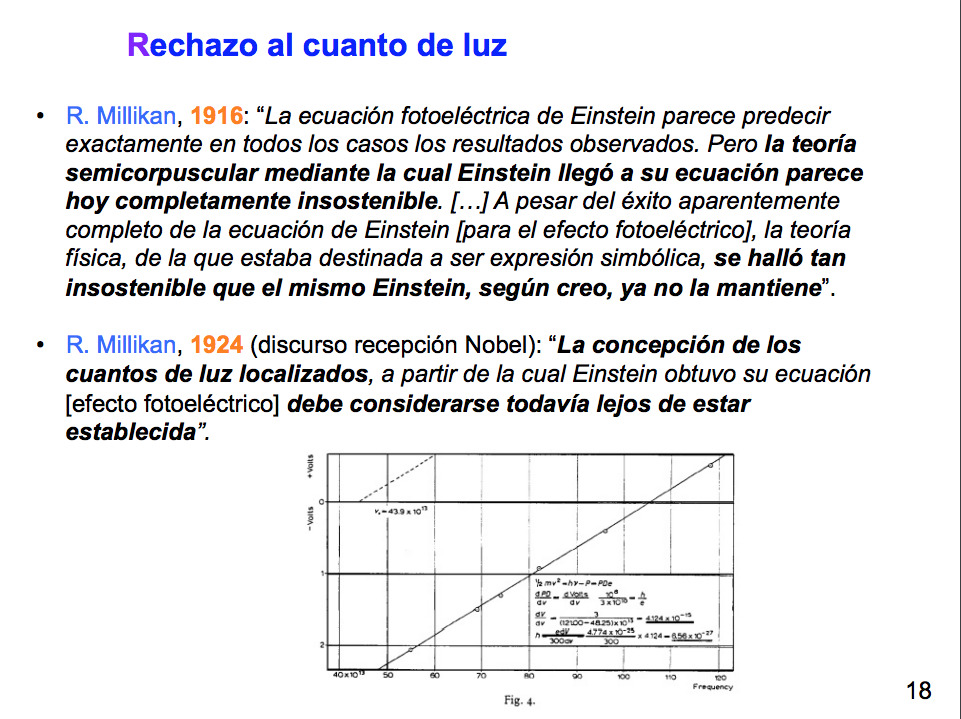
-Millikan inició sus mediciones sistemáticas sobre el efecto fotoeléctrico con el expreso propósito de mostrar que la ecuación de Einstein para tal efecto no era válida. Cuando sus mediciones mostraron la correción de la hipótesis de Einstein, aceptó que la ecuación de Einstein describe correctamente el fenómeno, pero ello no le llevó a aceptar la hipótesis del cuanto de luz:

Rechazo por Millikan del cuanto de luz, 1916-24.
El efecto Compton:
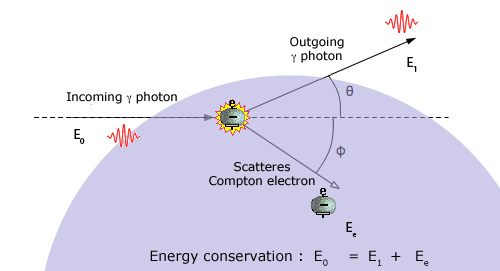
Efecto Compton: colisión de un fotón y un electrón atómico; imagen tomada de la URL: http://www.laradioactivite.com/fr/site/pages/Effet_Compton.htm.

-Todos los resultados experimentalmente observados en la dispersión de rayos $X$ por electrones atómicos, especialmente la presencia, bajo determinadas circunstancias, de radiación dispersada con una longitud de onda mayor a la incidente, serían justificados por Compton y Debye, de forma independiente, planteando en primer lugar el problema de una colisión elástica entre un fotón incidente y un electrón ligado atómico, que era supuesto en las capas más externas y, por ello, tratado aproximadamente como libre. Los fotones que son dispersados por electrones fuertemente ligados, que permanecen tras la colisión ligados, no experimentan cambio apreciable en su $\lambda$ , y se recogen en el pico Thomson; los electrones que son expulsados del átomo por la colisión con el fotón incidente, se convierten en electrones libres o de retroceso, y se liberan simultáneamente a la radiación difundida con cambio apreciable en su $\lambda$ , que se recoge en el pico Compton, con un cambio en la longitud de onda dado por el desplazamiento Compton,

$\Delta \lambda=\lambda_1 - \lambda_0=\frac{h}{m_0c}(1-cos \theta)$

-La observación de los electrones de retroceso que intervienen en la explicación teórica del efecto Compton tuvo lugar por primera vez en 1923, por W. Bothe y C.T.R. Wilson; en 1925 Bothe y H. Geiger demostraron que el electrón de retroceso y el fotón dispersado aparecen simultáneamente, y que la energía y el momento se conservaban en cada suceso individual (frente a la hipótesis BKS, Bohr-Kramers-Slater, 1924). Para ello Bothe ideó un dispositivo de detección en coincidencia, método introducido por él por primera vez y que se revelaría como enormemente fructífero (además de proporcionarle el premio Nobel en 1954): los rayos-X eran difundidos por una hoja metálica, con las condiciones adecuadas, y recogidos después por un detector Geiger; el electrón de retroceso era detectado por un segundo Geiger, cuidadosamente alineado en la dirección adecuada. La ventana de detección en coincidencia que manejaban hacía uso de la tecnología recién desarrollada en esos años de los tubos de vacío (tipo triodos), que permitían estipular un intervalo temporal en el transcurso del cual sendos pares recogidos en los dos Geiger se estipulaban como pertenecientes al mismo evento:

W. Bothe, Discurso de recepción del Premio Nobel, 1954:
The readings of both counters were recorded side by side on a moving paper chart. In this way we succeeded after a few failures to establish the accuracy of any temporal «coincidence» between the two pointer readings as being 10^-4 sec. Film consumption however was so enormous that our laboratory with the film strips strung up for drying sometimes resembled an industrial laundry.
The final result we obtained was that systematic coincidences do indeed occur with the frequency that could be estimated from the experimental geometry and the response probabilities of the counters on the assumption that, in each elementary Compton process, a scatter quantum and a recoil electron are generated simultaneously. -En un efecto Compton, el fotón difundido y el electrón de retroceso se producen en un estado entrelazado, lo que fuerza las correlaciones de los observables medidos para cada par fotón-electrón, adecuadamente detectados en coincidencia.

¿Contingencia teórica del cuanto de luz?

El hecho es que, aunque la hipótesis del fotón es suficiente para explicar los tres fenómenos expuestos, no es necesaria.

-Pese a su éxito explicativo, la hipótesis del cuanto de luz fue combatida con energía y tozudez por grandes físicos como Planck, Millikan, Bohr… hasta por lo menos 1926:

M.C. Boscá, «Notas historico-filosóficas sobre Mecánica cuántica, II«, pp. 12-32:

-De hecho, al mismo Einstein le costó tiempo asumir la realidad del cuanto de luz, más allá de su carácter inicial de «hipótesis heurística»:

Einstein sobre el cuanto de luz en 1909.

Einstein, 1916: el cuanto de luz comienza a ser real.

-Había muchas razones de peso para negarse al cuanto de luz:

Razones para un rechazo al cuanto de luz.

-Y era comprensible y lógica esta resistencia a aceptar el cuanto de luz, la cuantización de la radiación en sí misma, porque lo cierto es que:

Un modelo semiclásico, en que no se cuantiza el campo electromagnético, es capaz de explicar la fenomenología tradicional relacionada con los tres casos analizados.

Por ejemplo: para el efecto fotoeléctrico, en el contexto «estándar» que se suele considerar, un camino teórico alternativo de explicación, semi-clásico, puede consistir en adoptar el formalismo cuántico para la descripción de los electrones metálicos, pero conservar la descripción clásica del campo electromagnético:

-Sea $H_{int}=-\frac{e}{m}A(\hat{\vec{r}},t) \cdot \hat{\vec{p}}$ donde $\vec{A}=\nabla \times \vec{B}$ representa el potencial vector del campo, satisfaciendo $\nabla \cdot \vec{A}=0$ ; $\hat{\vec{r}}$ y $\hat{\vec{p}}$ representan los correspondientes operadores mecano-cuánticos posición y momento (autoadjuntos); el campo electromagnético de radiación viene determinado según:

$\vec{E}=-\frac{\partial \vec{A}}{\partial t}$

-Para un campo monocromático con frecuencia $\omega$ , el vector potencial clásico es

$\vec{A}(\vec{r},t)=\frac{1}{\omega}E_0 \vec{e}( e^{i \vec{k}\cdot \vec{r}-\omega t}+e^{-i \vec{k}\cdot \vec{r}-\omega t})$

donde $\vec{e}$ representa el vector unidad de polarización; $E_0$ es la amplitud del vector campo eléctrico $\vec{E}$ ; $|\vec{k}|=\frac{\omega}{c}$ es el vector número de ondas; se cumple $\vec{e}\cdot \vec{k}=0$ .

-Según la regla de oro de Fermi, obtenida mediante teoría de perturbaciones, si $P_{fi}(t)$ representa la probabilidad de transición desde el estado ligado $|i>$ hacia el de difusión $|f>$ la razón de transición , $W_{fi}=\frac{dP_{fi}}{dt}$ , viene dada por:

$W_{fi}=\frac{2\pi}{\hbar} |<f|H_{int}|i>|^2\delta(\epsilon_f-\epsilon_i-\hbar \omega)$

(resultado válido para observaciones en un intervalo de tiempo $t \gg \frac{1}{\omega}$ )

-Puesto que para los campos ópticos involucrados $\omega \approx 10^{15}s^{-1}$ , la expulsión del electrón se produce también en este cálculo semi-clásico sin retardo medible experimentalmente.

-Además, la presencia de la delta en la ecuación garantiza el valor correcto para el fotoelectrón; también, como el elemento de matriz $|<f|H_{int}|i>|$ es proporcional a la amplitud $E_0$ , la razón a que se emiten los fotoelectrones resulta proporcional a la intensidad de la radiación con que se ilumina el fotocátodo.

Sin necesidad de introducir el cuanto de luz, una teoría semiclásica, que no cuantiza el campo electromagnético, es capaz de explicar toda la fenomenología tradicional del efecto fotoeléctrico.

-El hecho fue ya advertido tempranamente por autores como G. Wentzel (1926: Z. Phys., 40, 574) y G. Beck (1927: Z. Phys., 41, 443); cf. Chiao & Garrison, op. cit. p. 22.

Sin necesidad de introducir el cuanto de luz, una teoría semiclásica, que no cuantiza el campo electromagnético, es capaz de explicar la fenomenología del efecto Compton.

-Y, por otra parte, también O. Klein e Y. Nishina (1929: Z. Phys., 52, 853; cf. Chiao & Garrison, op. cit. p. 23) derivaron una fórmula para la sección eficaz del efecto Compton en un contexto puramente semi-clásico, involucrando la ecuación relativista de Dirac y la teoría cuántica, con un cálculo de perturbaciones dependiente del tiempo, pero sin invocar la hipótesis del cuanto de luz. Su fórmula está en perfecto acuerdo con la obtenida en el marco de la Electrodinámica Cuántica.

Finalmente, la fórmula correcta para la radiación del cuerpo negro puede derivarse también en una teoría semi-clásica, reemplazando la hipótesis ad hoc de Planck por una descripción mecano-cuántica de los átomos en las paredes de la cavidad (y otras hipótesis tan ad hoc como ella, veáse [GAR-08], p. 21), sin cuantizar la propia radiación. Y lo mismo puede decirse para los procesos de emisión espontánea

Lo que sí aporta la explicación teórica vía el fotón es una incomparable y rotunda simplicidad en la resolución teórica de estos fenómenos.

¿Es entonces teóricamente contingente la hipótesis del cuanto de luz?
O, por el contrario, ¿existen experimentos imposibles de explicar en un marco semi-clásico que no cuantice el campo electromagnético?

Necesidad teórica del cuanto de luz

La teoría electromagnética clásica describe la luz en términos de los dos vectores intensidad $\vec{E}$ del campo eléctrico e intensidad $\vec{B}$ del campo magnético, tratándolos como variables continuas, mientras que la hipótesis fotónica postula una discretización de la energía de radiación cuyo unidad mínima, el cuanto, es indivisible.

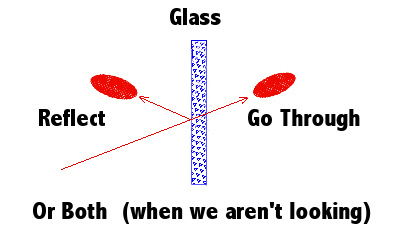
-Así, por ejemplo, en un divisor de haz una onda electromagnética clásica sufrirá una división continua, mientras que un fotón será siempre reflejado o transmitido al completo. Se trata obviamente de dos descripciones del fenómeno incompatibles

Los experimentos que involucren dispositivos o montajes donde la indivisibilidad del cuanto de luz intervenga son fenómenos para los cuales las predicciones de las teorías que no cuantizan el campo electromagnético, tanto clásicas como semi-clásicas, no coinciden con las predicciones teóricas que conlleva la cuantización del campo electromagnético.

Los experimentos que involucren dispositivos o montajes donde la indivisibilidad del cuanto de luz intervenga son fenómenos cruciales para aceptar la necesidad de la hipótesis del fotón.

En 1972 J.F. Clauser realizó un análisis de los datos de un experimento de Kocher y Commins de 1967 (Phys. Rev. Lett., 18, 575; véase [GAR-08], pp. 24ss), que involucraba la emisión en cascada en átomos de Ca (la fuente de fotones entrelazados que usaría después Aspect para su test de la desigualdad de Bell, a principios de los 80) .

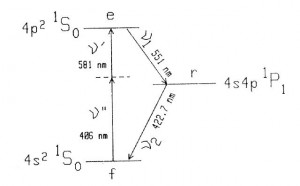
Cascada atómica en el experiemnto de Aspect — Imagen tomada de http://perso.wanadoo.fr/eric.chopin/epr/aspect.htm.

-Procedieron a realizar un experimento en que los dos fotones ópticos entrelazados, que son emitidos con momentos opuestos, eran sometidos a detección en coincidencia, mostrando polarizaciones correlacionadas (situación EPR). Los autores concluían que ninguna teoría semi-clásica es capaz de reproducir los datos experimentales (aquí la indivisibilidad fotónica no interviene directamente, al no incorporarse divisores de haz, pero subyace al tratamiento teórico; véase [GAR-08], pp. 24-25):

J.F. Clauser; Experimental Limitations to the Validity of Semiclassical Radiation Theories , Phys. Rev A (6) (1972) 49:

Abstract: The polarization correlation of photons emitted in an atomic cascade is treated in the framework of a general semiclassical radiation theory. The resulting predictions are contrasted with those of orthodox quantum-radiation theory. Experimental evidence is discussed which is in agreement with the latter theory, but excludes semiclassical theories in general.

En un contexto similar, con emisión en cascada en átomos de Hg, en 1974 Clauser llevó los fotones de cada par entrelazado producido a sendos divisores de haz, haciendo intervenir cuatro fotodetectores: encontró también ratios de detecciones en coincidencia inconsistentes con las predicciones semiclásicas:

J. F. Clauser, Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect , Phys. Rev D 9 (1974) 853; disponible también en otra versión en materias.df.uba.ar.

Abstract: We have measured various coincidence rates between four photomultiplier tubes viewing cascade photons on opposite sides of dielectric beam splitters. This experimental configuration, we show, is sensitive to differences between the classical and quantum field-theoretic predictions for the photoelectric effect. The results, to a high degree of statistical accuracy, contradict the predictions by any classical or semiclassical theory in which the probability of photoemission is proportional to the classical intensity.

En 1986 Grangier et al, empleando también fotones entrelazados de la desintegración en cascada del Ca, concluyen definitivamente lo mismo; además, publican los primeros experimentos de interferencia que defienden como ¡los primeros realizados con luz auténticamente monofotónica!:

P. Grangier, G. Roger and A. Aspect, Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences, Europhysics Lett. 1 (4), 1986, 173-179.

Abstract: We report on two experiments using an atomic cascade as a light source, and a triggered detection scheme for the second photon of the cascade. The first experiment shows a strong anticorrelation between the triggered detections on both sides of a beam splitter. This result is in contradiction with any classical wave model of light, but in agreement with a quantum description involving single-photon states. The same source and detection scheme were used in a second experiment, where we have observed interferences with a visibility over 98%.

During the past fifteen years, nonclassical effects in the statistical properties of light have been extensively studied from a theoretical point of view, and some have been experimentally demonstrated. All are related to second-order coherence properties, via measurements of intensity correlation functions or of statistical moments. However, there has still been no test of the conceptually very simple situation dealing with singlephoton states of the light impinging on a beam splitter. In this case, quantum mechanics predicts a perfect anticorrelation for photodetections on both sides of the beam splitter (a single-photon can only be detected once!), while any description involving classical fields would predict some amount of coincidences. In the first part of this letter, we report on an experiment close to this ideal situation, since we have found a coincidence rate, on both sides of a beam splitter, five times smaller than the classical lower limit.
When it comes to single-photon states of light, it is tempting to revisit the famous historical «single-photon interference experiments«. One then finds that, in spite of their denomination, none has been performed with single-photon states of light. As a matter of fact, all have been carried out with chaotic light, for which it is well known that quantum second-order coherence properties cannot be distinguished from classical ones, even with a strongly attenuated beam. This is why we have carried out an interference experiment with the same apparatus as used in the first experiment, i.e., with light for which we have demonstrated a property characteristic of single-photon states.

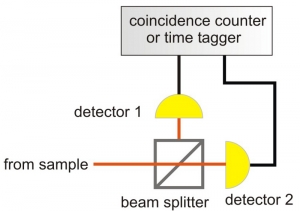
Descripción de la experiencia: sea un divisor de haz, BS, con igual probabilidad, 50%, de reflexión y transmisión, y sean un par de sendos detectores preparados para recoger los pulsos reflejado y transmitido, de modo que, bajo incidencia monofotónica, en pura teoría nunca deberían detectar señales en coincidencia.
El que así se observe experimentalmente, será una confirmación de que la luz incidente es verdaderamente monofotónica.

$\rightarrow$ Éste fue el procedimiento que utilizaron Grangier et al en su artículo de 1986, consiguiendo unos resultados imposibles de reproducir con una teoría semi-clásica, esto es, que no involucre cuantización de la radiación electromagnética en sí misma: se deriva, por tanto, la necesidad de introducción del concepto teórico de «fotón».

Nota: sin embargo, aunque son escasos, algunos investigadores siguen todavía intentando desarrollar vías teóricas semi-clásicas, en un esfuerzo por eludir la necesidad del fotón:

Trevor W. Marshall, Emilio Santos: The myth of the photon

Referencias

- [GAR-08] Garrison, J. C. and R. Y. Chiao, Quantum Optics, Oxford Univ. Press, Oxford, 2008. ISBN: 978-0-19-850886-1.

Curioso e interesante: Markiewicz, M., Kaszlikowski, D., Kurzyński, P. et al. From contextuality of a single photon to realism of an electromagnetic wave., Quantum Inf 5, 5 (2019); https://doi.org/10.1038/s41534-018-0117-8; https://www.nature.com/articles/s41534-018-0117-8.

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

El fotón y su necesidad

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta