Luz coherente y luz caótica

coherente-caotica-luz — imagen: https://departamentofisicaequimica.wordpress.com/category/2015-ano-internacional-da-luz/celda-12/

Fuentes: esta entrada se basa principalmente en:

Cap. 5, Introductory Quantum Optics, de Gerry y Knight ([GER-05]).
Cap. 5, Quantum Optics, de Garrison y Chiao ([GAR-08]).
Caps. 2, 5 y 6, Quantum Optics. An introduction, de M. Fox ([FOX-04]).

Coherencia clásica

Clásicamente, la coherencia de la luz describe su estabilidad, distinguiéndose las coherencias espacial y temporal. La primera de ellas interviene en los dispositivos de interferencia, como los interferómetros de Michelson, y viene determinada por la dispersión angular con que la radiación alcanza el dispositivo.

La coherencia de la luz describe su «estabilidad»:
-Sólo las ondas coherentes pueden mostrar un patrón estable de interferencia.
-Ondas coherentes, en teoría ondulatoria clásica, pueden definirse en general como aquéllas que tienen una diferencia finita y estable entre sus frecuencias y fases: Coherencia.

La coherencia temporal de un haz de luz se cuantifica por el tiempo de coherencia $\tau_c$ o, equivalentemente, por la longitud de coherencia $L_c=c\tau_c = c\frac{2\pi}{\Delta \omega}$ , donde $\Delta \omega$ es la anchura espectral de la fuente. El tiempo de coherencia proporciona el intervalo de tiempo durante el cual la fase de un tren de ondas se mantiene constante: dada la fase de la onda en $(\vec{r},t_1)$ , se mantiene estable para intervalos $\Delta t=|t_2-t_1| \ll \tau_c$ ; equivalentemente, conocida la fase de la onda en $(\vec{r}_1,t)$ , no cambiará apreciablemente siempre que $\Delta r =|\vec{r}_2-\vec{r}_1|\ll L_c$ . Es obvio que una fuente perfectamente monocromática, $\Delta \omega=0$ , poseerá un tiempo de coherencia $\tau_c$ infinito.

-Así, en un experimento de doble rendija (véase también la correspondiente entrada en estos apuntes), se observarán interferencias siempre que la diferencia de caminos ópticos entre sendos haces de luz procedentes de dos rendijas satisfaga $\Delta L \ll L_c=c/\Delta \omega$ .

Coherencia de primer orden

La función general de coherencia de primer orden se define como:

$g^{(1)}(\vec{r}_1,t_1;\vec{r}_2,t_2)=\frac{<E(\vec{r}_1,t_1)E(\vec{r}_2,t_2)>}{ [<|E(\vec{r}_1,t_1)|^2><|E(\vec{r}_2,t_2)|^2>]^{\frac{1}{2}}}$

donde $<>$ representa promedio estadístico sobre una colectividad (ensemble: para estados no estacionarios, como pulsos, un ensemble se compondría de muchos pulsos).

-Para estados estacionarios, en los que las propiedades estadísticas se mantienen constantes en el devenir temporal, el promedio sobre la colectividad se reemplaza por el promedio temporal.

-Para ondas planas paralelas, tomando $\vec{r}_i=z$ (detectores a la misma distancia), el resultado no depende de $t_1$ , sino del retardo o diferencia $\tau=t_1-t_2$ .

La coherencia temporal clásica de la luz se cuantifica mediante la función de coherencia temporal de primer orden, $g^{(1)}(\tau)$ , definida como:

$g^{(1)}(\tau)=\frac{<E(t)E(t+\tau)>}{<|E(t)|^2>}$

donde $<>$ indica promedio sobre un intervalo de tiempo $T$ suficientemente largo,

$<E(t)E(t+\tau )>=\frac{1}{T}\int_T \ E(t)E(t+\tau)dt$

Sea un campo cuasi-monocromático de frecuencia central $\omega_0$ :

$E(t)=E_0e^{-i\omega_0t}e^{i\phi t}$

$\Rightarrow g^{(1)}(\tau)=e^{-i\omega_0\tau}<|e^{i[\phi(t+\tau)-\phi(t)]}|>$

de forma que la parte real de $g^{(1)}(\tau)$ oscila con período $\frac{2\pi}{\omega_0}$ . Esta oscilación es la responsable de la aparición del patrón de franjas en las situaciones interferenciales.

Para coherencia temporal, es el módulo $|g^{(1)}(\tau)|$ el que contiene la información sobre la coherencia de la luz, teniéndose:

Si $|g^{(1)}(\tau)|=1\; \forall \tau$ : luz perfectamente coherente, anchura espectral nula, tiempo de coherencia $\tau_c=\infty$ . Idealmente, una luz perfectamente monocromática; por ejemplo, un modo longitudinal de láser es una buena aproximación al concepto.
$|g^{(1)}(\tau)| \approx 1 \; \mbox{si} \quad 0<\tau \ll \tau_c \; (\phi(t+\tau)\approx \phi(t))$
$|g^{(1)}(\tau)|$ decrece al aumentar $\tau$ .
Si $0<|g^{(1)}(\tau)|<1$ : luz parcialmente coherente o caótica, anchura espectral $\Delta \omega \ne 0$ , tiempo de coherencia $\tau_c \approx \frac{1}{\Delta \omega}$ .
Si $|g^{(1)}(\tau)|\approx 0\;,\; \forall \tau$ : luz totalmente incoherente (completamente caótica); anchura espectral efectivamente infinita; tiempo de coherencia $\tau_c=0$ .
Para $\tau \gg \tau_c$ , $\phi(t+\tau)$ no está correlacionado con $\phi(t)$ , de forma que $|g^{(1)}(\tau)|=0$ .
Por tanto, la función es decreciente entre y en términos de la variable ; la forma funcional específica cambia reflejando el grado de coherencia:
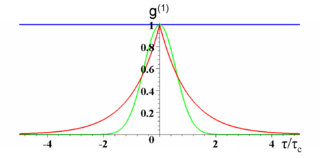
$Plot of $latex g^{(1)}$ as a function of the delay normalized to the coherence length $latex \tau/\tau_c$ . The blue curve is for a coherent state (an ideal laser or a single frequency). The red curve is for Lorentzian chaotic light (e.g. collision broadened). The green curve is for Gaussian chaotic light (e.g. Doppler broadened) (from Wikipedia)$
Representación de $g^{(1)}$ como función del retardo normalizado a la longitud de coherencia, $\tau/\tau_c$ . La curva azul corresponde a un estado coherente (un láser ideal o una frecuencia sola). La curva roja corresponde a luz caótica lorentziana (por ejemplo, ensanchada por colisiones). La curva verde corresponde a luz caótica gaussiana (ensanchamiento Doppler) (texto y figura de la Wikipedia).
1. A: curva roja: Para luz con anchura espectral $\Delta \omega$ respondiendo a una distribución de Lorentz,
  $g^{(1)}(\tau)=e^{-i\omega_0\tau}e^{-\frac{|\tau|}{\tau_c}}\;,\;\tau_c=\frac{1}{\Delta \omega}$
2. B: curva verde: Para luz con anchura espectral $\Delta \omega$ respondiendo a una distribución de Gauss,
  $g^{(1)}(\tau)=e^{-i\omega_0\tau}e^{-\frac{\pi}{2}(\frac{|\tau|}{\tau_c})^2}\;,\;\tau_c=\frac{\sqrt{8\pi\ ln2}}{\Delta \omega}$ .

Para la función general de coherencia de primer orden, es el módulo $|g^{(1)}(x_1,x_2)|$ ( $x_i \equiv (\vec{r}_i,t_i)$ ) el que contiene la información sobre la coherencia de la luz, cumpliendo:

Completa coherencia: $|g^{(1)}(x_1,x_2)|=1$

Coherencia parcial: $0< |g^{(1)}(x_1,x_2)|<1$

Completa incoherencia: $|g^{(1)}(x_1,x_2)|=0$

La visibilidad o contraste de las franjas de interferencia observadas se define por la fórmula de Rayleigh:

$Vis=\frac{I_{max}-I_{min}}{I_{max}+I_{min}}$

donde $I_{max}$ e $I_{min}$ representan, respectivamente las intensidades registradas en lo máximos y mínimos,

$I_{max(min)}=I_1+I_2 +(-)2\sqrt{I_1I_2}|g^{(1)}(x_1,x_2)|$ ,

de modo que:

$Vis=\frac{2\sqrt{I_1I_2}|g^{(1)}(x_1,x_2)|}{I_1+I_2}$

-Este parámetro viene pues determinado por la coherencia de la luz, de modo que, cuando la coherencia es completa,

$|g^{(1)}(\tau)|=1$ ,

se tiene que la visibilidad es máxima,

$Vis=\frac{2\sqrt{I_1I_2}}{I_1+I_2}$ ,

mientras que para incoherencia completa, la visibilidad es mínima, se anula.

-Nota: La condición de coherencia completa, $|g^{(1)}(x_1,x_2)|=1$ , es quivalente a la condición de factorización $<E^*(x_1)E(x_2)>=<E^*(x_1)><E(x_2)>$ .

-En la coherencia de primer orden, sólo la intensidad media se ve afectada por el número de fotones, de modo que los experimentos asociados no permitirán distinguir entre estados de luz que presenten idéntica distribución espectral pero diferente distribución en número de fotones. Cuando en los años 50 H. Brown y R. Twiss desarrollaron una nueva clase de experimentos, en la que se involucraban la correlación entre intensidades y no ya entre los campos, se requirió pasar al siguiente orden de coherencia para comprender los resultados.

Coherencia de segundo orden: óptica no lineal

La respuesta dieléctrica de un medio viene determinada por el vector polarización eléctrica o momento dipolar eléctrico por unidad de volumen $\vec{P}$ , satisfaciéndose

$\vec{D}=\epsilon_0\vec{E}+\vec{P}$

donde $\vec{D}$ es el vector desplazamiento eléctrico y $\vec{E}$ el vector campo eléctrico

-En un medio isótropo, los dipolos microscópicos se alinean según la dirección del campo eléctrico aplicado, y se aplica relación lineal aproximada

$\vec{D}=\epsilon_0\epsilon_r\vec{E}\;,\; \epsilon_r=1+\chi^{(1)}$

siendo $\chi=\chi^{(1)}$ la permitividad relativa del medio.

-Pero si la amplitud del campo es grande, la relación no puede suponerse lineal:

$P=\epsilon_0 \chi^{(1)}E+\epsilon_0 \chi^{(2)}E^2+\epsilon_0 \chi^{(3)}E^3+\cdots$

debiendo considerarse términos adicionales del desarrollo, proporcionales respectivamente a las potencias $n$ -ésimas de la intensidad $E$ del campo eléctrico, con constantes $\chi^{(n)}$ , las denominadas susceptibilidades no lineales de orden $n$ .

En segundo orden, si el medio se excita con dos ondas cosenoidales de frecuencias $\omega_i$ y amplitudes $E_i\;,\; i=1,2$ , la polarización no lineal viene dada por:

$P^{(2)}(t)=\epsilon_0\chi^{(2)}\times E_1\cos \omega_1 t \times E_2\cos \omega_2 t$

$=\epsilon_0\chi^{(2)}E_1E_2\frac{1}{2}[\cos(\omega_1 + \omega_2)t\cos(\omega_1 - \omega_2)t]$

-Así que la respuesta no lineal de segundo orden genera una polarización que oscila con frecuencias igual a la suma $\omega_+$ y a la diferencia $\omega_-$ de los campos aplicados, siendo éstas las frecuencias que radiará el medio, pudiendo diferenciándose las situaciones:

$\omega_1=\omega_2 \Rightarrow \omega_+=2\omega$ : duplicado de frecuencia
$\omega_1 \ne \omega_2 \Rightarrow \omega_+=|\omega_1 + \omega_2|$ : mezcla con suma de frecuencias
$\omega_1 \ne \omega_2 \Rightarrow \omega_-=|\omega_1 - \omega_2|$ : mezcla con resta de frecuencias

-Y también en procesos no lineales de segundo orden pueden aparecer fenómenos reversos, por ejemplo, casos en que luz incidente monocromática $\omega$ se desdobla en dos frecuencias $\omega_s$ y $\omega_i$ que suman a la inicial, $\omega=\omega_s +\omega_i$ (como en SPDHC: conversión paramétrica espontánea a la baja).

Función de coherencia de de segundo orden

La función de coherencia de de segundo orden, $g^{(2)}(\vec{r}_1,t_1;\vec{r}_2,t_2)$ , se define:

$g^{(2)}(\vec{r}_1,t_1;\vec{r}_2,t_2)=\frac{\left\langle E^*(\vec{r}_1,t_1)E^*(\vec{r}_2,t_2)E(\vec{r}_2,t_2)E(\vec{r}_1,t_1)\right\rangle}{[<|E(\vec{r}_1,t_1)|^2> <|E(\vec{r}_2,t_2)|^2>]}$

-Como para la función de primer orden, si los detectores están a la misma distancia, para ondas planas paralelas, tomando $\vec{r}=z$ , el resultado no depende de $t_1$ , sino del retardo $\tau=t_1-t_2$ .

La función de coherencia de segundo orden temporal, $g^{(2)}(\tau)$ , se define:

$g^{(2)}(\tau)=\frac{<E^*(t)E^*(t+\tau)E(t)E(t+\tau)>}{<|E(t)|^2><|E(t+\tau)|^2>}=\frac{<I(t)I(t+\tau)>}{<I(t)><I(t+\tau)>}$

donde $<>$ indica promedio sobre un intervalo de tiempo $T$ suficientemente largo; $E(t)$ y $I(t)$ representan, respectivamente, la intensidad del campo eléctrico y de la radiación en el instante $t$ ,

$<C(t,\tau)>=\frac{1}{T}\int_T \ C(t,\tau)dt$

$\rightarrow$ Mientras que $g^{(1)}(\tau)$ cuantifica las fluctuaciones temporales del campo eléctrico $E$ , la de segundo orden cuantifica las fluctuaciones temporales de la intensidad de la radiación $I$ .

El parámetro tiempo de coherencia $\tau_c$ de la fuente emisora determina las fluctuaciones en la intensidad:

Cuando $\tau \gg \tau_c$ , las fluctuaciones de intensidad en dos instantes $t$ y $t+\tau$ no presentarán correlación alguna, de forma que:
$I(t)=< I > + \Delta I(t) \quad \mbox{y} \quad <\Delta I(t)>=0$
$\Rightarrow <I(t)I(t+\tau)>_{\tau \gg \tau_c}=<I>^2$ $\Rightarrow g^{(2)}(\tau \gg \tau_c)=\frac{<I(t)I(t+\tau)>}{<I(t)>^2}=\frac{<I(t)>^2}{<I(t)>^2}=1$
Cuando $\tau \ll \tau_c$ , las fluctuaciones de intensidad en dos instantes $t$ y $t+\tau$ estarán correlacionadas, de forma que, en particular:
$g^{(2)}(\tau=0)=\frac{<I(t)>^2}{<I(t)>^2}\ge 1$
Para cualquier función $I(t)$ se satisface:
$g^{(2)}(0) \ge g^{(2)}(\tau)$
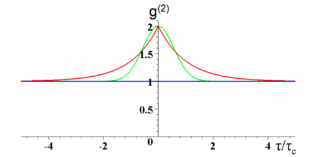
$Plot of $latex g^{(2)}$ as a function of the delay normalized to the coherence length $latex \tau/\tau_c$ . The blue curve is for a coherent state (an ideal laser or a single frequency). The red curve is for Lorentzian chaotic light (e.g. collision broadened). The green curve is for Gaussian chaotic light (e.g. Doppler broadened) (from Wikipedia).$
Representación de $g^{(2)}$ como función del retardo normalizado a la longitud de coherencia, $\tau/\tau_c$ . La curva azul corresponde a un estado coherente (un láser ideal o una frecuencia sola). La curva roja corresponde a luz caótica lorentziana (por ejemplo, ensanchada por colisiones). La curva verde corresponde a luz caótica gaussiana (ensanchamiento Doppler) (texto y figura de la Wikipedia).

En general, la radiación clásica ofrece el rango de valores para la función de coherencia de segundo orden:

Para toda radiación:
1. $1 \le g^{(2)}(0) < \infty$
2. Para intensidad constante: $g^{(2)}(0)=1$
3. $g^{(2)}(\tau)\le g^{(2)}(0)$
4. Luz incoherente o caótica:
  $g^{(2)}(\tau)=1+|g^{(1)}(\tau)|^2 \Rightarrow 1\le |g^{(2)}(\tau)| \le 2$ y $g^{(2)}(0)=2$
(desigualdades que violará la luz cuántica)
Para luz perfectamente coherente:
$g^{(2)}(\tau)=1$
Coherencia clásica de segundo orden:
$|g^{(1)}(x_1,x_2)|=1=g^{(2)}(x_1,x_2;x_2,x_1)$
Para luz parcialmente incoherente o caótica, distribución de Gauss:
$g^{(2)}(\tau)=1+e^{-\pi(\tau/\tau_c)^2}$
Para luz parcialmente incoherente o caótica, distribución de Lorentz:
$g^{(2)}(\tau)=1+e^{-2|\tau|/\tau_o}$
( $\tau_o$ es la vida media de la correspondiente transición espectral)
La luz termal presenta efecto HBT o agrupamiento (bunching) fotónico. Es coherente en primer orden pero no en segundo («coherencia despreciable»).

En general, la teoría de la coherencia clásica se ha centrado en el primer orden, estudiando las correlaciones entre los valores del campo en puntos separados tanto espacial como temporalmente, determinando las condiciones que permiten observar franjas de interferencia, como en un experimento de doble rendija de Young, donde lo que interviene son cantidades cuadráticas en la intensidad de campo E. Antes del desarrollo de la aplicación del formalismo cuántico a las funciones de correlación ópticas, tan sólo algunos pocos experimentos, como el de Hanbury Brown-Twiss de 1955, proporcionaron medidas de los promedios de las potencias cuartas de las intensidades del campo, cantidades pertenecientes ya a la óptica no lineal.

-Experimentos de este tipo en definitiva van a medir razones de coincidencia diferida: tras hacer incidir radiación sobre un divisor de haz, un detector registra contaje en un tiempo dado $t$ mientras que un segundo detector, a la misma distancia del divisor que el anterior, registra en $t + \tau$ . Si el tiempo de retardo $\tau$ es menor que el tiempo de coherencia de la radiación, se obtiene información sobre la distribución o estadística fotónica del haz de luz incidente sobre el divisor de haz. La función de correlación de segundo orden va a dar cuenta de la probabilidad de registrar una coincidencia para un tiempo de retardo $\tau$ .

-HBT, puesto que $g^{(2)}(\tau=0)=2$ para cualquier luz caótica, trabajando en la hipótesis de que las sendas radiaciones que llegaban a los dos detectores, compuestas de fotones que se suponía eran emitidos de forma independiente por la fuente primaria (coherencia en primer orden) y que, al incidir sobre el divisor de haz, meramente reflejaban o transmitían, siempre de forma íntegra, explicaron el porqué detectaban para tiempos de retardo nulos el doble de ratio de contaje que para retardos $\tau$ muy largos (esperaban una razón de coincidencias uniforme, independiente del tiempo) asumiendo que los fotones para retardo nulo llegaban agrupados en pares, «photon bunching effect«, o efecto HBT, justificándolo, de forma innecesaria, en el carácter bosónico del fotón: ha de ser incorporado a la descripción teórica con un tratamiento en segundo orden.

Funciones de correlación y coherencia cuánticas

Roy Glauber fue el autor que desarrolló principalmente, en los años 60, una teoría cuántica de la coherencia en paralelismo con la clásica, introduciendo los operadores mecano-cuánticos para definir las funciones de correlación cuánticas.

Roy J. Glauber, Quantum Theory of Optical Coherence: Selected Papers and Lectures, Wiley VCH, ISBN-13 ‏ 978-35274068.

Roy J. Glauber: The quantum Theory of Optical Coherence, Physical Review 130-6 (1963) 2529:
The present paper, which is the first of a series on fundamental problems of optics, is devoted largely to defining the concept of coherence. We do this by constructing a sequence of correlation functions for the field vectors, and by discussing the consequences of certain assumptions about their properties. The definition of coherence which we reach differs from earlier ones in several significant ways. The most important difference, perhaps, is that complete coherence, as we define it, requires that the field correlation functions satisfy an infinite succession of coherence conditions. We are led then to distinguish among various orders of incomplete coherence, according to the number of conditions satisfied. The fields traditionally described as coherent in optics are shown to have only first-order coherence. The fields generated by the optical maser, on the other hand, may have a considerably higher order of coherence. A further difference between our approach and previous ones is that it is constructed to apply to fields of arbitrary time dependence, rather than just to those which are, on the average, stationary in time. We have also attempted to develop the discussion in a fully quantum theoretical way.
It would hardly seem that any justification is necessary for discussing the theory of light quanta in quantum theoretical terms. Yet, as we all know, the successes of classical theory in dealing with optical experiments have been so great that we feel no hesitation in introducing optics as a sophomore course. The quantum theory, in other words, has had only a fraction of the infuence upon optics that optics has historically had upon quantum theory. The explanation, no doubt, lies in the fact that optical experiments to date have paid very little attention to individual photons. To the extent that observations in optics have been confined to the measurement of ordinary light intensities, it is not surprising that classical theory has offered simple and essentially correct insights.
Experiments such as those on quantum correlations suggest, on the other hand, the growing importance of studies of photon statistics. Such studies lie largely outside the grasp of classical theory. To observe that the quantum theory is fundamentally necessary to the treatment of these problems is not to say that the semiclassical approach always yields incorrect results. On the contrary, correct answers to certain classes of problems of photon statistics’ may be found through adaptations of classical methods. There are, however, distinct virtues to knowing where such methods succeed and where they do not.

J. O. Cortés-Tamayo: Estados coherentes del campo de radiación , Revista Mexicana de Física 38, No. 2 (1992) 309-331:
Por un lado, el concepto de coherencia usado convencionalmente en óptica clásica implica que dos valores del campo de un haz de luz en puntos espacio-tiempo muy separados se encuentran correlacionados y que cuando se usan medios ópticos para superponerlos resultan franjas de intensidad; el ejemplo típico es el experimento de interferencia de Young. No obstante, este concepto requiere de un solo detector, el cual mide la intensidad o en otras palabras el cuadrado de la amplitud del campo y está confinado a describir haces monocromáticos y estacionarios en el tiempo. Con esto es posible caracterizar todos los experimentos típicos de la óptica clásica, como son los experimentos de difracción e interferencia. Esta coherencia clásica se introduce a través de la función de visibilidad de las franjas de interferencia en el experimento de Young, y se formula mediante la teoría estadística de cuasiprobabilidad.
Como la coherencia de un haz de luz está relacionada con las correlaciones que éste experimenta en intervalos considerables de distancia y tiempo, la idea de R.J. Glauber en 1963 fue examinar un experimento más general en que se colocan $n$ detectores en diferentes puntos espacio-tiempo para registrar correlaciones de $n$ fotones.

Los detectores miden la intensidad de los haces de radiación vía la absorción de fotones, es decir, atenuándolos. Supuesto un detector ideal monoatómico, en el que la dimensión atómica característica es mucho menor que la longitud de onda de la radiación, la absorción de luz produce la ionización y subsiguiente emisión de un fotoelectrón: el contaje de estos electrones de ionización dará cuenta de las propiedades estadísticas de la radiación.

Sea un detector ideal para la componente en frecuencia positiva del campo, $\hat{\vec{E}}^{(+)}(\vec{r},t)$ , es decir, que trabaja vía la absorción de fotones que matemáticamente se representa por la aplicación del correspondiente operador destrucción.

-En la absorción de un fotón del campo, éste realiza una transición desde el estado $|i>$ hacia el $|f>$ , y la razón de transición para esa absorción viene dada por la regla de oro de Fermi, $W_{fi}=\frac{dP_{fi}}{dt}$ :

$W_{fi}=|<f|\hat{\vec{E}}^{(+)}(\vec{r},t)|i>|^2$

-Sumando sobre todos los estados $|f>$ , ya que se busca determinar la razón de contaje del detector, se obtiene la intensidad detectada $I(\vec{r},t)$ :

$I(\vec{r},t)=\sum_f |<f|\hat{\vec{E}}^{(+)}(\vec{r},t)|f>|^2$

$=<i|\hat{\vec{E}}^{(-)}(\vec{r},t)|f><f|\hat{\vec{E}}^{(+)}(\vec{r},t)|i>$

$=<i|\hat{\vec{E}}^{(-)}(\vec{r},t)\hat{\vec{E}}^{(+)}(\vec{r},t)|i>$

-En el caso de que el estado inicial del campo fuese una mezcla estadística de estados, descrita por el operador densidad $\hat{\rho}$ , el anterior resultado se expresaría:

$I(\vec{r},t)=Tr(\hat{\rho}\hat{\vec{E}}^{(-)}(\vec{r},t)\hat{\vec{E}}^{(+)}(\vec{r},t))$

Un ejemplo sencillo: Sea el estado inicial dado por un estado de Fock $|n_k>$ ; sea la componente del campo que describe la absorción es la componente de frecuencia positiva, que es la que contiene el operador aniquilación,

$\hat{\vec{E}}^{(+)}(\vec{r},t)=i\sum_{\vec{k},s}(\frac{\hbar\omega_k}{2\epsilon_0})^{\frac{1}{2}}\vec{u}_{\vec{k}s}(\vec{r})\hat{a}_{\vec{k}s} e^{i\omega_k t}$ ;

su adjunto, la componente en frecuencia negativa, tiene la expresión

$\hat{\vec{E}}^{(-)}(\vec{r},t)=(\hat{\vec{E}}^{(+)}(\vec{r},t))^{\dagger}$

donde $u_{\vec{k}s}(\vec{r})$ es la componente en el modo correspondiente $(\vec{k}s)$ del desarrollo en serie de Fourier para el campo eléctrico en un volumen finito; en el caso de un cubo de lado $L$ con condiciones de contorno periódicas se expresa como

$u_{\vec{k}s}(\vec{r})=\frac{1}{L^3}\vec{e}_{\vec{k}s}e^{i\vec{k}\cdot \vec{r}}$

-Se obtiene entonces para la intensidad:

$I(\vec{r},t)=<n_k|\hat{\vec{E}}^{(-)}(\vec{r},t)\hat{\vec{E}}^{(+)}(\vec{r},t)|n_k>=n_k\frac{\hbar\omega_k}{2\epsilon_0}|u_{\vec{k}s}(\vec{r})|^2$

Las funciones de correlación cuántica, de orden $n$ , se definen como:

(notación: $x_i \equiv (\vec{r}_i,t_i)$ )

$G^{(n)}(x_1,\ldots ,x_n;x_n,\ldots ,x_1)=Tr(\rho \hat{\vec{E}}^{(-)}(x_1)\ldots \hat{\vec{E}}^{(-)}(x_n)\hat{\vec{E}}^{(+)}(x_{n})\ldots \hat{\vec{E}}^{(+)}(x_{1}))$

cumpliéndose

$I(\vec{r},t)=G^{(1)}(x_i;x_i)$

-De estas funciones:

$G^{(1)}(x_i;x_i)$ es la intensidad de la luz que llega a un detector desde $x_i$

$G^{(1)}(x_i;x_j)$ es una medida de la correlación entre la luz que llega desde $x_i$ y $x_j$ , o sea, una medida de su interferencia.

$G^{(2)}(x_i,x_j;x_j,x_i)$ es el promedio sobre el ensemble del producto de intensidades $I(x_i)I(x_j)$ .

La función de coherencia cuántica de orden $n$ se define ( $x_i \equiv (\vec{r}_i,t_i)$ ):

$g^{(n)}_Q (x_1,\ldots ,x_n;x_n, \ldots ,x_1)=\frac{G^{(n)}(x_1,\ldots ,x_n;x_n,\ldots ,x_1)}{[G^{(1)}(x_1,x_1)\ldots G^{(1)}(x_n,x_n)]}$

de forma que las de órdenes primero y segundo son:

$g^{(1)}_Q(x_1,x_2)=\frac{G^{(1)}(x_1,x_2)}{[G^{(1)}(x_1,x_1)G^{(1)}(x_2,x_2)]^{\frac{1}{2}}}$

$g^{(2)}_Q (x_1,x_2;x_2,x_1)=\frac{G^{(2)}(x_1,x_2;x_2,x_1)}{[G^{(1)}(x_1,x_1)G^{(1)}(x_2,x_2)]}$

donde $g^{(2)}_Q (x_1,x_2;x_2,x_1)$ representa la probabilidad conjunta de detección de un fotón en $(\vec{r}_1,t_1)$ y otro en $(\vec{r}_2,t_2)$ .

Un campo se dice que es $m$ -coherente si cumple:

$|g^{(n)}_Q (x_1,\ldots ,x_n;x_n, \ldots ,x_1)|=1\;,\; \forall n\le m$

para lo que debe satisfacerse $\forall n\le m$ que

$G^{(m)}(x_1,\ldots ,x_m;x_m,\ldots ,x_1)=G^{(1)}(x_1,x_1)G^{(1)}(x_2,x_2)\ldots G^{(1)}(x_m,x_m)$ ,

condición que cumplen todos los estados coherentes.

-Y se dice que es totalmente coherente cuando lo es para todo $n$

(lo es en el límite $\lim_{n\rightarrow \infty}$ ).

En una posición fija, $g^{(2)}_Q$ depende sólo del retardo o diferencia $\tau=t_2-t_1$ , convirtiéndose en la función de coherencia temporal de segundo orden:

$g_Q^{(2)}(\tau)=\frac{\left\langle \hat{E}^-(t)E^-(t+\tau)\hat{E}^+(t+\tau)\hat{E}^+(t)\right\rangle}{<\hat{E}^-(t)\hat{E}^+(t)> <\hat{E}^-(t+\tau)\hat{E}^+(t+\tau)>}$ ,

Función de correlación de segundo orden (imagen de https://www.kth.se/social/files/5cb1833856be5bf03c8165fa/Lecture%203%20Second-order%20Intensity%20Correlation%20Function.pdf )

Véase http://qutip.org/docs/3.1.0/guide/guide-correlation.html .

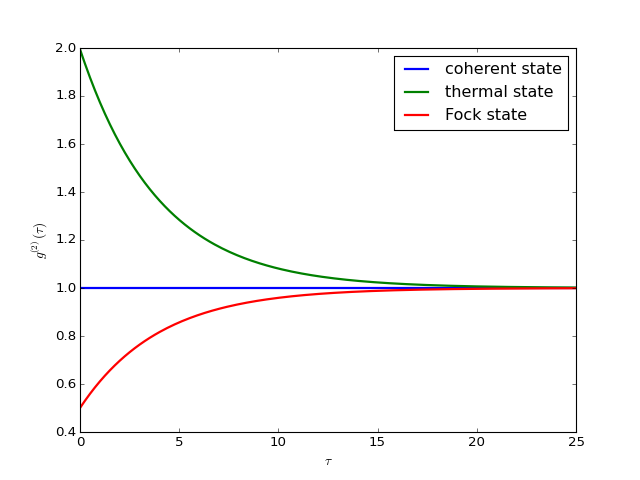
representando la probabilidad condicional de que se detecte, en una posición dada, un fotón en $t$ y también otro en $t+\tau$ , esto es, con un retardo $\tau$ .
–Si $g_Q^{(2)}(\tau)=1$ , entonces los fotones van llegando de forma independiente.

$\rightarrow$ Puede esperarse que $\lim_{\tau \rightarrow \infty} g_Q^{(2)}(\tau)\rightarrow 1$ para cualquier estado del campo, es decir, que, transcurrido un intervalo de tiempo suficientemente grande, la memoria del primer fotón detectado desaparezca.

Estas funciones cuánticas satisfacen:

Función de correlación de primer orden:
1. $G^{(1)}(x_1,x_2)=[G^{(1)}(x_2,x_1)]^*$
2. $G^{(1)}(x_i,x_i)\ge 0$
3. $G^{(1)}(x_1,x_1)G^{(1)}(x_2,x_2)\ge |G^{(1)}(x_1,x_2)|^2$
  (si se da la igualdad, $G^{(1)}(x_1,x_1)G^{(1)}(x_2,x_2)=|G^{(1)}(x_1,x_2)|^2$ , se implica máxima visibilidad de las franjas de interferencia).
Función de coherencia de primer orden:
1. $0 \le |g_Q^{(1)}(x_1,x_2)|\le 1$
2. Completa coherencia: $|g_Q^{(1)}(x_1,x_2)|=1$
3. Coherencia o caos parcial: $0< |g_Q^{(1)}(x_1,x_2)|<1$
4. Completa incoherencia o caos total: $|g_Q^{(1)}(x_1,x_2)|=0$
La caracterización de la coherencia en términos de la función de primer orden es por completo análoga a la clásica.
Función de coherencia de segundo orden:
1. Sobre un estado del campo correspondiente a un solo modo de excitación, propagándose con vector número de ondas $\vec{k}$ ( $\hat{E}^{(+)}=i(\frac{\hbar \omega}{2\epsilon_0 V})^{\frac{1}{2}}e^{i\vec{k}\cdot \vec{r} -\omega t}$ ) :
  $g_Q^{(2)}(\tau)=1+ \frac{<\hat{a}^{\dagger} \hat{a}^{\dagger} \hat{a} \hat{a} >}{< \hat{a}^{\dagger} \hat{a} > }=1+\frac{<(\Delta \hat{n})^2>-<\hat{n}>}{<\hat{n}>^2}=g_Q^{(2)}(0) \ne f(\tau)$
2. Sobre un estado de campo que es coherente o estado Glauber $|\alpha>$ :
  $g_Q^{(2)}(\tau)=g_Q^{(2)}(0)=1$ :
  
  $\rightarrow$ los fotones llegan distribuidos al azar.
  
  $\rightarrow$ este estado es coherente en segundo orden.
  
  $\rightarrow$ la probabilidad de una detección en coincidencia es independiente del tiempo.
  
  $\rightarrow$ luz cuasi-clásica.
3. Sobre un estado del campo en un solo modo térmico (modo de radiación en una cavidad en equilibrio térmico): $g_Q^{(2)}(\tau)=g_Q^{(2)}(0)=2$ $\rightarrow$ hay alta probabilidad de que se produzcan detecciones en coincidencia de fotones.
4. Sobre un estado del campo multimodal térmico (mezcla de modos de radiación en una cavidad en equilibrio térmico):
  $1 \le (g_Q^{(2)}(\tau)= 1 + |g_Q^{(1)}(\tau)|^2)\le 2$
  $\rightarrow$ el resultado coincide con el clásico.
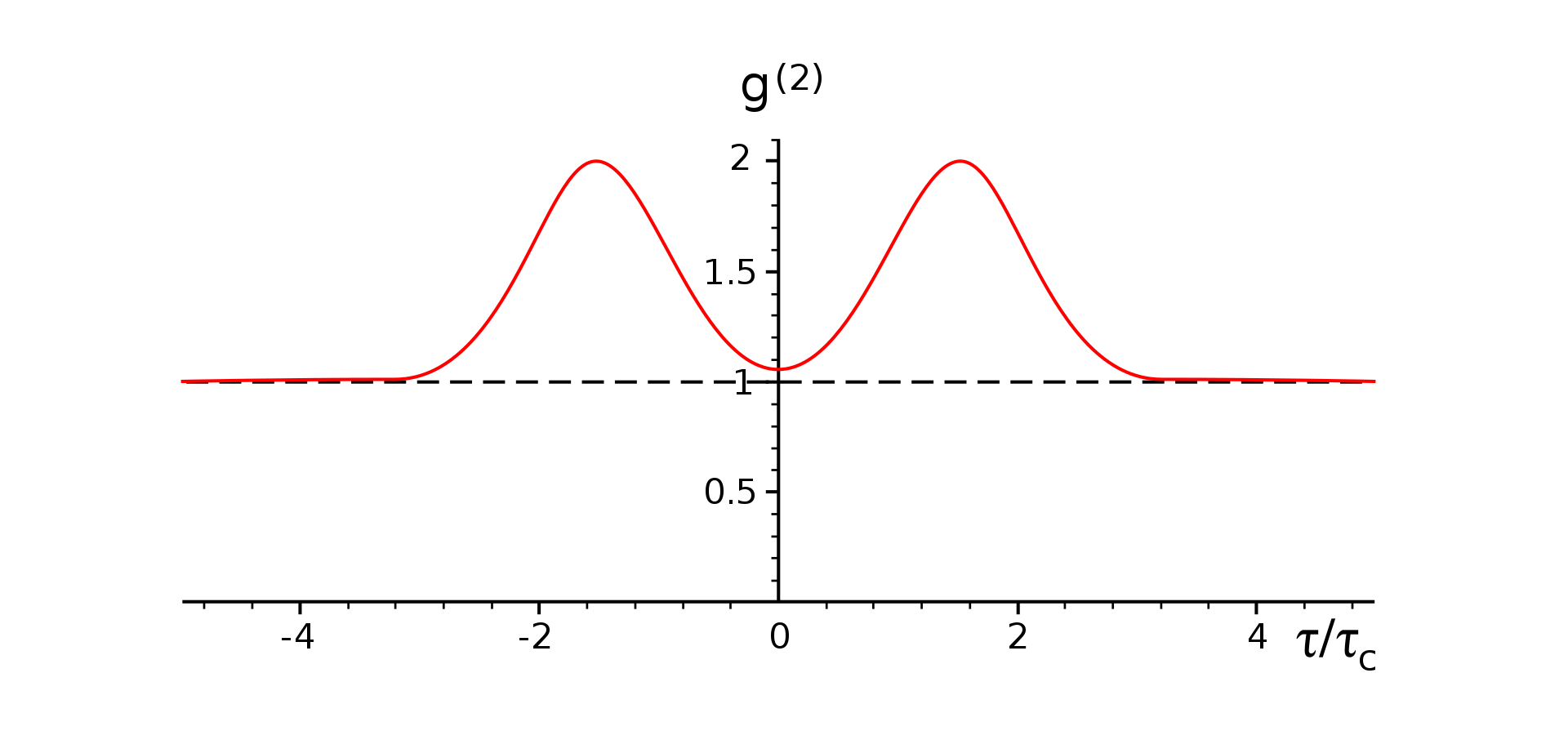
5. Puede tenerse $g_Q^{(2)}(\tau)<g_Q^{(2)}(0)$ ;
  
  $\rightarrow$ photon bunching: los fotones tienden a aparecer juntos.
  
  $\rightarrow$ la probabilidad de que se produzca la detección de un segundo fotón después de un retardo $\tau$ decrece con $\tau$ .
  
  $\rightarrow$ se trata de un efecto clásico.
  
  $Plot of $latex g^{(2)}$ as a function of the delay normalized to the coherence length $latex \tau/\tau_c$ . The blue curve is for a coherent state (an ideal laser or a single frequency). The red curve is for Lorentzian chaotic light (e.g. collision broadened). The green curve is for Gaussian chaotic light (e.g. Doppler broadened) (from Wikipedia).$
  Representación de $g^{(2)}$ como función del retardo normalizado a la longitud de coherencia, $\tau/\tau_c$ . La curva azul corresponde a un estado coherente (un láser ideal o una frecuencia sola). La curva roja corresponde a luz caótica lorentziana (por ejemplo, ensanchada por colisiones). La curva verde corresponde a luz caótica gaussiana (ensanchamiento Doppler). La luz caótica es super-Poissoniana y «buncheada» (texto y figura de la Wikipedia).
  
  -El efecto no es posible sobre un estado de un solo modo de campo.
  
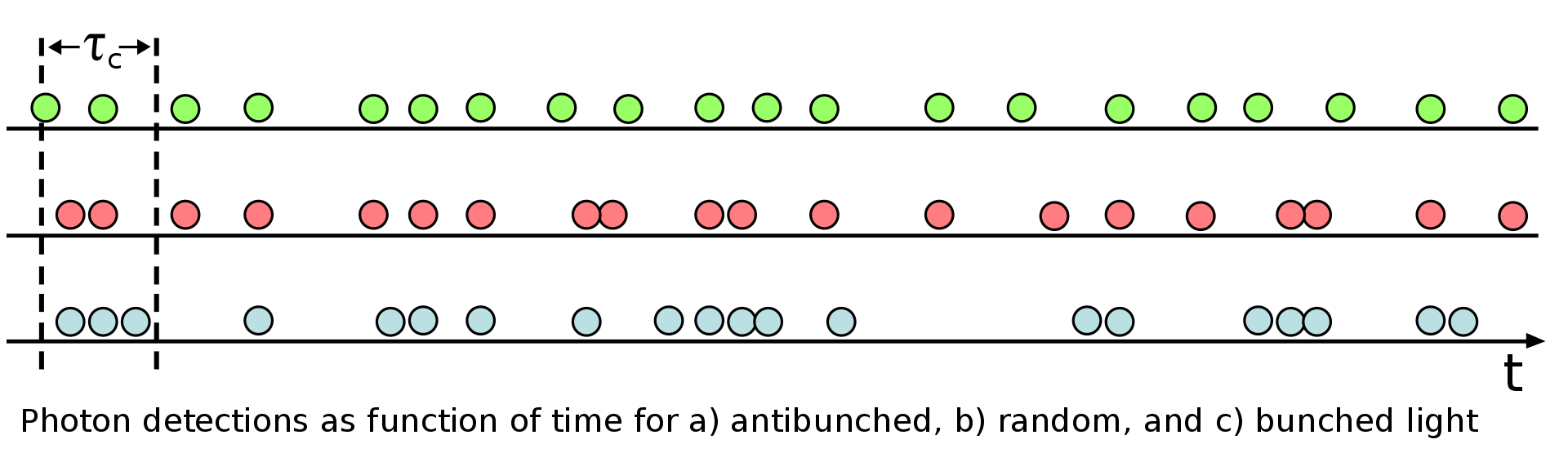
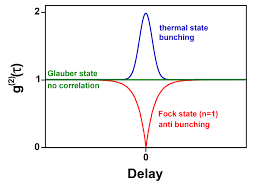
  Posibles tipos de agrupamientos fotónicos: detecciones de fotones como función del tiempo para un a) antibunching (p. ej. luz emitida por un solo átomo), b) luz random o aleatoria (p. ej. un estado coherente, haz de láser), y c) bunching (luz caótica); τc es el tiempo de coherencia (la escala de tiempo de las fluctuaciones del fotón o de la intensidad) (Wikipedia).
6. Puede tenerse $g_Q^{(2)}(\tau)>g_Q^{(2)}(0)$ :
  
  Luz antiagrupada (y, en particular, no subpoissoniana) (imagen de la Wikipedia).
  
  $\rightarrow$ photon antibunching: los fotones tienden a aparecer separados.
  $\rightarrow$ la probabilidad de que se produzca la detección de un segundo fotón después de un retardo $\tau$ crece con $\tau$ .
  
  $\rightarrow$ los fotones tienden a llegar con intervalo temporal fijo.
  
  $\rightarrow$ la probabilidad de que se produzcan detecciones en coincidencia de fotones en un intervalo $\tau$ es menor que en el caso de estado coherente.
  -El efecto no es posible sobre un estado de un solo modo de campo.
  
  $\rightarrow$ resultado incompatible con la teoría clásica.
7. Puede tenerse $g_Q^{(2)}(0)<1$ :
  
  $\rightarrow$ estados sub-poissonianos.
  $\rightarrow$ la condición puede ser simultánea con la de antibunching o no: son efectos diferentes.
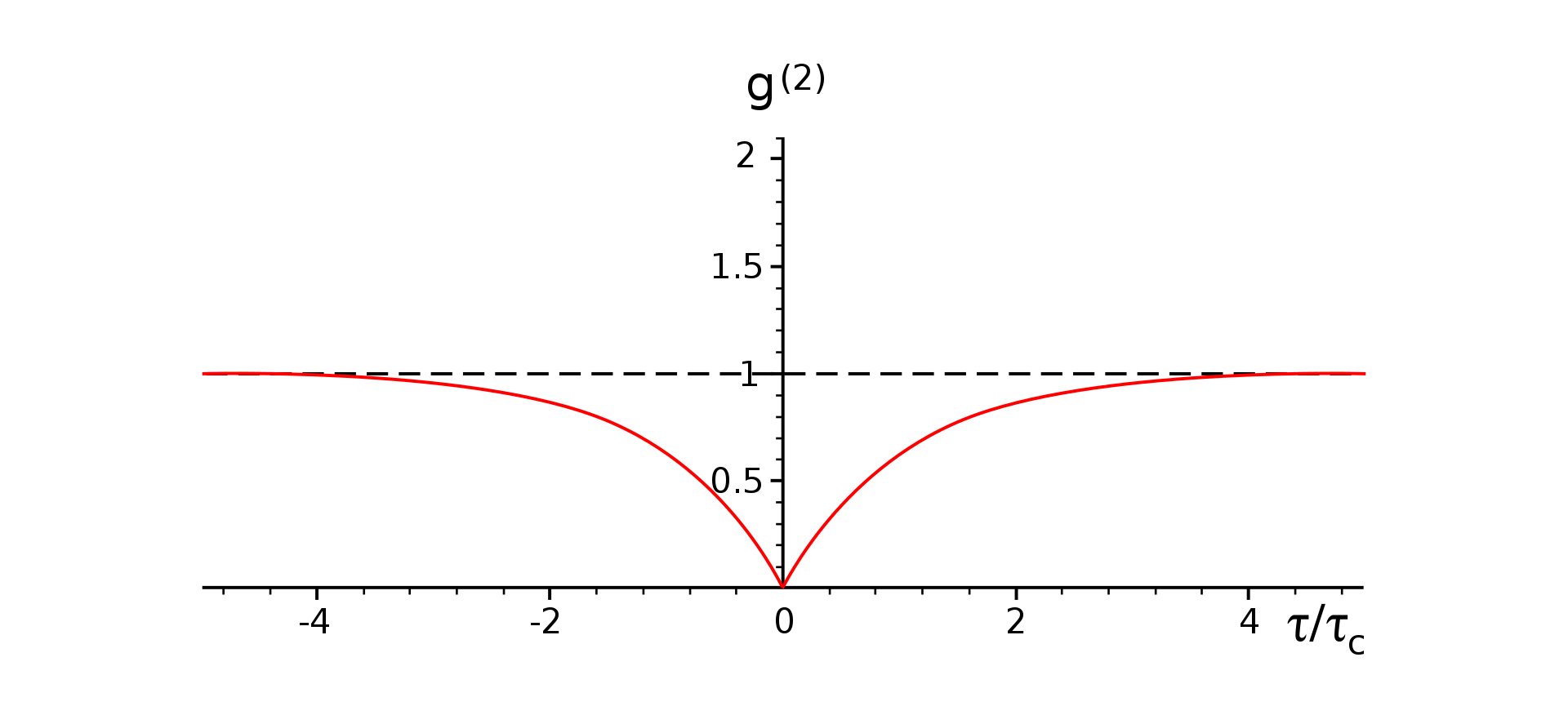
  $\rightarrow$ la condición indica también anti-bunching cuando, siempre que $g_Q^{(2)}(\tau)$ no sea constante, se tenga $\lim_{\tau \rightarrow \infty} g_Q^{(2)}(\tau)\rightarrow 1$
  
  Luz antiagrupada y subpoissoniana (imagen de la Wikipedia).
  
  -Por ejemplo, para el caso de un solo modo de excitación de campo, se tiene $g_Q^{(2)}(\tau)=g_Q^{(2)}(0)$ , constante, y no hay antibunching.
  
  $\rightarrow$ la probabilidad de que se produzcan detecciones en coincidencia de fotones en un intervalo $\tau$ es menor que en el caso de estado coherente.
  
  $\rightarrow$ resultado incompatible con la teoría clásica.
8. Sobre un estado de Fock $|n>$ , autoestado del operador número:
  $g_Q^{(2)}(0)=\frac{n(n-1)}{n^2}<1$
  
  $\rightarrow$ estado sub-poissoniano.
  
  -En particular, para un estado de Fock de un solo fotón, $\hat{n}|\Psi>=|\Psi>$ , se tiene $g_Q^{(2)}(0)=0<1$ .