El experimento de Franck-Hertz

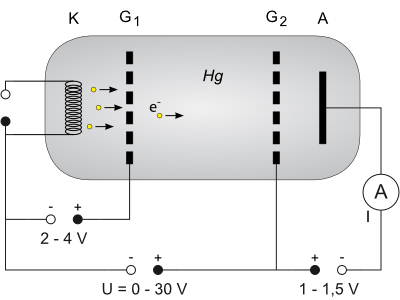
Experimento de Franck-Hertz

En 1914, apenas un año después de la publicación del modelo atómico de Bohr, J. Franck y G. Hertz realizaron un experimento que demostró la existencia de estados excitados discretos en los átomos de mercurio, lo que confirmó la predicción del modelo de Bohr de que los sistemas ligados atómicos ocupaban solamente determinados estados de energía, es decir, su energía estaba cuantizada. En otras palabras: el correspondiente espectro de energía no era continuo, sino discreto.
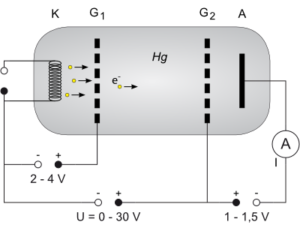
La figura siguiente muestra un esquema del dispositivo experimental usado:
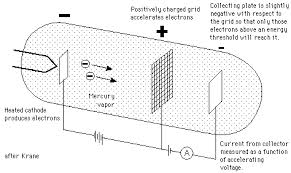
En el dispositivo, vapor rarificado (a baja presión) de un elemento dado ocupa el interior de un tubo de descarga , donde puede ser bombardeado con electrones de energía conocida, $K$ , emitidos por por un filamento calentado a temperatura $T$ , que actúa de cátodo. Los electrones son acelerados hacia una rejilla interpuesta, de forma que se emiten con energía cinética $K=\frac{1}{2}mv^2=|e|V$ . La rejilla interpuesta es mantenida a una diferencia de potencial $V_r$ respecto a la lámina colectora trasera, de signo opuesto respecto al del filamento, de manera que $V_r$ actúa como potencial retardador para los electrones.
Parte de los electrones atravesarán la rejilla-ánodo, con suficiente energía todavía para vencer la diferencia de potencial adicional $-V_r=|V_r| \ll V$ , o potencial de frenado, establecido entre la rejilla y una placa tras ésta, y cuyo orden es del voltio o voltio y medio, permitiendo que el amperímetro correspondiente mida una corriente de intensidad $I$ .
El primer gas que usaron fue vapor de mercurio, y los resultados medidos para la corriente $I$ se representan en la siguiente gráfica:
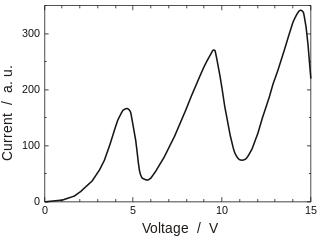
Dependence of the anode current upon the voltage in the 1914 Franck-Hertz experiment. The tube temperature was about 115 C (redrawing of a figure from the original 1914 paper of Franck and Hertz; image by Ahellwig).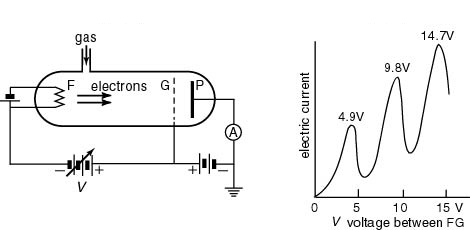
Análisis de los resultados:
1. Conforme $V$ aumenta, partiendo del origen, la intensidad $I$ también va aumentando, un resultado esperable, puesto que los electrones tendrán cada vez más energía cinética y, en consecuencia, un mayor número de ellos podrá superar el potencial retardador y contribuir a la corriente.
2. Si los electrones se involucraran tan sólo en colisiones elásticas con los átomos de $Hg$ en el tubo, de forma que sólo experimentasen desviaciones de su trayectoria, sin intercambiar energía, la corriente $I$ debería seguir creciendo de forma continua al hacerlo $V$ , lo que proporcionaría la gráfica de una función monótonamente creciente, similar para cualquier gas en el tubo.
3. Sin embargo, lo que se observa es una gráfica donde la intensidad $I$ experimenta bruscas caídas para algunos de los valores del potencial $V$ , valores que depende del gas específico presente en el tubo. En particular, para el $Hg$ la primera caída se produce para el valor $V=4,88 \,$ V; posteriores caídas se observan a otros valores de $V$ ; en particular, también para valores $V=9,76 \,$ V y múltiplos enteros del primer máximo.
La explicación del fenómeno es que se están produciendo colisiones inelásticas entre los electrones que se desplazan hacia el ánodo y los átomos del gas presente, de manera que el electrón pierde parte de su energía cinética, pasando ésta a tener un valor $K'=\frac{1}{2}mv'^2=(|e|V-E_{ced})$ , donde $E_{ced}$ representa la energía cedida en el choque y $v'$ la nueva velocidad. Si se tiene que $|e|V \gtrapprox E_{ced}$ , entonces la energía que le queda al electrón es insuficiente para que pueda superar el pequeño potencial de retardo $V_r$ aplicado, de forma que estos electrones son incapaces de alcanzar la placa colectora tras la rejilla.
Por su parte, el átomo de mercurio ha absorbido esa energía $E_{ced}$ , y el hecho de que el proceso no ocurra hasta que la energía de los electrones involucrados alcanza precisamente ese valor específico $E=|e|V_R$ , donde $V_R$ se denomina «potencial de resonancia», característico del gas empleado, es interpretado como debido a la existencia de una cuantización en los niveles de energía atómicos, teniendo en particular el $Hg$ un primer estado excitado con un valor de energía de excitación de $4,9\,eV$ , lo que le permite absorber precisamente esa cantidad de energía, pero no una menor.
Las caídas posteriores de energías, a múltiplos enteros del potencial de resonancia, se explican como relacionadas con electrones que, en su viaje hacia la rejilla, han sufridos dos, tres, etc., colisiones con átomos del gas en el tubo. Las caídas a otros valores de $V$ se corresponderán con otros estados excitados (en la gráfica adjunta no aparecen; una mejorada nos mostraría también un pico adicional para $V=6,7\,V$ ).
Si la anterior explicación es correcta, se infiere que, en el espectro de líneas correspondiente a cada átomo en fase de vapor empleado, podría encontrarse una línea con números de ondas $\tilde{\nu}=\frac{eV_R}{hc}$ ; Franck y Hertz, por ejemplo, verificaron en efecto la presencia en el espectro del mercurio de una línea espectral con número de ondas $\tilde{\nu}=\frac{4,88\, eV}{hc}=\frac{4,88 \, eV}{12398,51\,eV \cdot \AA}=39350\, cm^{-1}$ ( $\lambda \approx 2537\,\AA$ ). Por ello, dedujeron que el primer estado excitado del $Hg$ se encontraba a $4,88\,eV$ por encima del estado fundamental.
Nota 1: Para un experimento con mejor resolución, pueden usarse un cátodo indirectamente calentado y una segunda rejilla tras el cátodo, con el fin de lograr una zona libre de colisiones y así obtener una distribución en energía de los electrones más uniforme (consultar Haken-Wolf, p. 109). De esta forma, se obtienen gráficas como la siguiente, en que se amplía en detalle el pico primero (potencial de resonancia $V_R\approx 4,9\, V$ ):
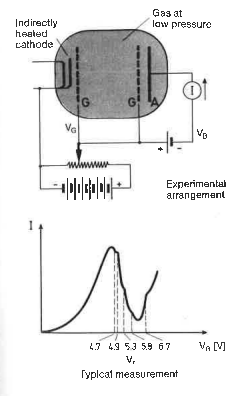
En la gráfica, el escalón a $6,73\,eV$ se corresponde con una intensa línea de $1850\,\AA$ en el espectro del $Hg$ .
Nota 2: No todas las caídas de potencial se pueden correlacionar con líneas en el correspondiente espectro: hay reglas de selección ópticas, que operan prohibiendo transiciones ópticas (con emisión/absorción de radiación) entre algunos estados, y hay también, por otra parte, reglas de selección para las excitaciones posibles para el átomo como resultado de colisiones, y los dos conjuntos de reglas son diferentes.
En definitiva: el experimento supuso la confirmación de la cuantización de los niveles de energía correspondientes a los estados ligados atómicos.

A los fenómenos comentados se superpondrá el Bremsstrahlung o radiación de frenado, que puede dificultar las observaciones.

Práctica en Laboratorio

http://fm127.ugr.es/lfc/Frank_Hertz_poster.html

https://laboratoriofisica.uc3m.es/guiones_ing/qp/Franck-Hertz_guide_english.pdf

https://myprojectideas.com/the-franck-hertz-experiment/

Bibliografía:

H. Haken y H. C. Wolf; Atomic and Quantum Physics. An Introduction to the Fundamentals of Experiment and Theory; Springer-Verlag; Berlin, 1987; pp. 107-110.

Páginas complementarias:

http://www.ptolomeo.unam.mx:8080/xmlui/bitstream/handle/132.248.52.100/627/A4.pdf?sequence=4

https://culturacientifica.com/2019/10/22/la-realidad-de-los-estados-estacionarios/

https://www.vaia.com/en-us/textbooks/chemistry/principles-of-modern-chemistry-8th-edition/introduction-to-qyantum-mechanics/q18p-in-a-franckhertz-experiment-on-hydrogen-atoms-the-first/#step-by-step-solution

APPS:

http://www.sc.ehu.es/sbweb/fisica/cuantica/frankHertz/frankHertz.htm
Franck-Hertz Experiment from the Wolfram Demonstrations Project by S. M. Blinder.
Universidad de Ceara, simulación del experimento de Frank-Hertz:
https://www.laboratoriovirtual.fisica.ufc.br/experimento-de-frank-hertz?lang=en

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

El experimento de Franck-Hertz

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta